引言

数值天气预报在气象领域得到了广泛应用，世界较为先进的国家着手发展了多种数值模式，并逐渐开始了业务运行。我国也自主开发了新一代数值模式GRAPES(Global and Regional Assimilation and Prediction Enhanced System)(陈德辉等，2006；张人禾等，2008)，包含全球和区域两个版本，其中区域版本GRAPES_Meso已业务运行(王雨等，2010)，为我国的天气预报，尤其是灾害性强天气预报提供了一个有效工具。然而由于初值误差、模式误差及大气的混沌特性，使得单一的数值预报存在不确定性，自Leith(1974)提出集合预报思想以来，集合预报已成为数值预报领域一个重要的发展方向，世界上较为先进的国家陆续基于各自的模式发展了集合预报系统(Ensemble Prediction System，EPS)(Buzzia et al，1995；Molteni et al，1996；Toth et al，1993; 1997；Bowler et al，2008)，且在各国的业务中占有越来越重要的地位。目前我国业务运行的全球集合预报系统是T213全球集合预报(任志杰等，2011)，基于GRAPES全球模式的集合预报也有所发展(刘永柱等，2013)；业务区域集合预报系统是基于WRF中尺度模式的WRF区域集合预报(邓国等，2010)。随着GRAPES模式的业务升级、计算资源的增加，基于GRAPES区域模式发展新一代的区域集合预报系统已经具备了较好的条件，并受到GRAPES发展团队的高度重视。

中小尺度强天气具有突发性和转折性，其预报不确定性因素难以把握。如何基于区域模式，通过合适的扰动方法来构建有效的区域集合预报，以描述中尺度灾害天气的不确定性，成为了目前的研究热点和难点，目前国际上一些天气预报中心也开始越来越关注区域集合预报系统的发展，如NCEP的短期集合预报计划(Short Range Ensemble Forecast，SREF)(Du et al，2003；Stensrud et al，2007)，采用了增长模繁殖法(Breeding Growing Mode, BGM)(Toth et al，1993)生成初值扰动，并结合了多模式组合方案进行模式扰动，结果表明SREF系统能够提高概率定量降水预报效果；Met Office的全球区域集合预报系统(MOGREPS)中，采用全球集合预报扰动降尺度的方法来驱动区域集合预报系统，结果表明区域集合预报系统能够捕捉小尺度不确定性信息(Bowler et al，2009a; 2009b)。国内学者对区域集合预报也进行了一系列的试验性探索，并取得了一定成果，陈静等(2005)提出了异物理模态初值扰动方法，并应用于区域集合预报，结果表明该方案产生的扰动具有显著的中尺度特征，集合预报效果明显优于控制预报；王太微(2008)基于GRAPES区域模式，采用集合变换卡尔曼滤波法(Ensemble Transform Kalman Filter，ETKF)和BGM两种初值扰动方法进行集合预报试验，结果表明两种方案均具有一定的概率预报技巧，基于BGM方法的集合预报离散度及降水预报效果略好于ETKF方法；龙柯吉等(2011)基于GRAPES_MesoV2.5模式，采用ETKF初值扰动方法建立了区域集合预报系统，并进行了一系列试验，结果表明ETKF方案优于随机扰动方案。傅娜等(2013)基于华东区域中尺度快速更新同化数值预报模式系统，应用时间滞后平均法进行集合预报试验，表明降水概率预报优于集合平均预报，具有较好的指示作用，但该集合预报的离散度不够理想。目前国内区域集合预报研究受限于计算资源较少无法开展大批量试验，模式版本陈旧以及模式分辨率较低等因素，使得试验结果不够理想，另外区域模式的误差会导致预报存在很大的模式不确定性(张涵斌等，2012)，使得仅采用初值扰动方法的区域集合预报系统存在离散度不足的问题。为了充分体现区域集合预报的不确定性，有学者尝试引入模式扰动方法(Houtekamer et al，1996；Buizza et al，1999)来提高区域集合预报技巧。陈静等(2003)研究了模式物理过程参数化方案对中尺度集合预报的影响，试验结果表明物理过程扰动可以有效应用于中国的暴雨集合预报；谭燕等(2007)基于GRAPES区域模式构建了模式物理过程扰动方案，结果表明该扰动方案可以有效捕捉中尺度过程信息，且物理过程扰动结合初值扰动能够获得更好的集合离散度和概率预报技巧。

在GRAPES模式性能的逐渐提高以及区域集合预报扰动方法逐渐完善的基础上，有必要开展大量试验，以研究GRAPES区域集合预报系统的应用效果。本文基于业务版本的GRAPES区域模式，采用ETKF初值扰动方法和多物理过程组合模式扰动方法建立了GRAPES区域集合预报系统(GRAPES-REPS)，通过40 d的批量试验，对GRAPES-REPS的扰动特征、集合预报检验效果以及降水预报性能进行了分析，本研究可以为系统的进一步业务化提供参考。

1 GRAPES-REPS扰动方法介绍 1.1 ETKF初值扰动

集合预报扰动方法是集合预报的关键。对于初值扰动，国外最初发展了Monte Carlo随机扰动法(Hollingsworth，1980；Mullen et al，1994)和滞后平均法(Hoffman et al，1983)，随后又发展了具有动力学扰动结构的增长模繁殖法和奇异向量法(Singular Vectors, SVs)(Buzzia et al，1995)，目前较新的初值扰动方法侧重于代表由资料同化产生的分析场的不确定性，如集合转置法(Ensemble Transform，ET)(Wei et al，2008)和ETKF方法(Wang et al，2003)。

GRAPES-REPS的初值扰动采用国际上较新的ETKF方法。ETKF方法基于卡尔曼滤波理论，最初应用于适应性观测(Bishop et al，2001)，Wang等(2003)将该方法应用于集合预报初值扰动的生成。其基本思路与BGM方法类似，通过繁殖循环来使产生的初值扰动具有随流型依赖的动力学结构，识别快速增长的误差方向，另外由于ETKF方法中吸收了观测信息，因此其生成的扰动场能对观测分布具有较好的响应，且不同成员的初值扰动是相互正交的，该方法还有一个优点是计算耗费较小。ETKF方法的基本计算思路是通过繁殖循环将上一时次预报到当前时刻的预报扰动更新为该时刻的初值扰动(称为分析扰动)。但与BGM方法中乘以一个固定的尺度化算子不同，ETKF方法通过一个变换矩阵T来对扰动进行更新，即

$ {X^a} = {X^f}\mathit{\boldsymbol{T}} $

(1)

式中，X^a为分析扰动，X^f为预报扰动，变换矩阵T的推导过程见Wang等(2003)。

由于模式预报相空间的自由度远大于集合成员数，有限数目的集合扰动的发展方向并不能充分代表误差可能的发展方向，式(1) 得到的分析扰动的方差小于实际的分析误差方差，此时需要在每一次循环引入一个放大因子Π_i来使分析扰动方差与实际的分析误差方差大体相当(Wang et al，2003)，即t_i时刻的分析扰动为：

$ X_i^a = X_i^f{\mathit{\boldsymbol{T}}_i}{\mathit{\Pi }_i} $

(2)

为了使集合扰动成员相对于集合平均中心化，引入球面单形中心化方案，在式(2) 的基础上乘以矩阵C^T，其中矩阵C的列向量为经过观测误差协方差标准化后的预报扰动协方差矩阵的特征向量，详见Wang等(2004)，C^T为C的转置矩阵。ETKF的最终表达式为：

$ X_i^a = X_i^f{{\bf{T}}_i} \cdot {{\bf{C}}^{\rm{T}}} \cdot {\mathit{\Pi} _i} $

(3)

1.2 多物理过程组合模式扰动

仅采用初值扰动方法并不能充分代表模式大气演变的不确定性(Harrison，1999)，区域模式本身具有模式误差，通过模式扰动可以描述模式的不确定性信息。目前的模式扰动方法多针对模式物理过程的不确定性，即通过物理过程扰动来表征物理过程参数化方案计算中的对流的潜热释放、云对辐射的影响、行星边界层热量和动量输送以及小尺度地形摩擦效应的方法、边界层强迫等不确定因素。物理过程扰动方法主要有多物理过程组合法(Houtekamer et al，1996)以及随机物理过程扰动法(Buizza et al，1999；谭宁等，2013)。本文对GRAPES-REPS引入了模式扰动，采用的方法是多物理过程组合。

由于各种物理过程参数化方案在设计原理、复杂程度和成熟程度等方面存在差异，会使各方案在不同的情况下具有不同的表现。GRAPES_Meso的物理过程中，微物理过程和积云对流参数化方案与降水密切相关，而边界层过程能显著影响行星边界层热量和动量输送，本文最初尝试对此三种物理过程进行多方案组合，通过试验发现微物理过程的某些选项存在积分不稳定的情况，因此本文最终仅对边界层过程及积云对流参数化方案进行组合。对于边界层过程，选取了Medium Range Forecast Model (MRF)方案和Yonsei University (YSU)方案参与组合；对于积云对流参数化方案，选取了Kain Fritsch(KF)，Simplified Arakawa Schubert(SAS)和Betts Miller Janjic(BMJ)三个方案参与组合，具体组合方式见表 1，这样即得到了不同成员的模式扰动。

2 集合预报试验方案设计

系统采用GRAPES_Meso V3.3.2.4版本业务模式，模式水平分辨率为0.15°×0.15°，垂直层次为地形追随坐标的33层模式面，以及26层等压面，模拟区域为15°~65°N、70°~145°E，覆盖了中国范围，控制预报背景场和边界条件采用GFS全球预报场，初值采用GRAPES-3dvar系统生成分析场。模式积分步长为300 s，预报时效为72 h。集合数目为一个控制预报加上14个扰动成员共15个集合成员，预报结果通过一系列后处理方法得到集合预报产品。本文试验时段为2013年6月5日至7月15日共40 d。

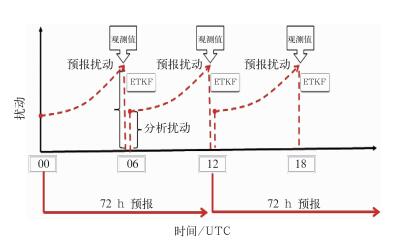
图 1是GRAPES-REPS的更新循环流程，该系统循环间隔为6 h，即每天的00：00，06：00，12：00和18：00 UTC起报，其中00：00与12：00 UTC两个起报时次积分72 h，06：00与18：00 UTC两个起报时次仅积分6 h。对于每个起报时刻，首先从上一循环的6 h预报结果中提取预报扰动(fcst per)，通过ETKF方法对扰动进行变换，得出该时刻的分析扰动(ana per)，随后将初值扰动叠加到分析场上得到各成员的扰动初值场，再进行积分。由于ETKF的集合扰动变换是在观测空间中进行的，且放大因子的计算需要观测资料来计算更新向量(innovation)(Wang et al，2003)，所以本文引入了模拟观测资料(obs)，目前的试验系统中，参照马旭林等(2008)的方法，每次循环采用GFS分析场插值到观测空间作为模拟观测资料。

3 集合预报扰动特征及演变分析

集合预报初值扰动的性能对集合预报效果至关重要，合理的初值扰动能够体现分析场的不确定性信息，捕捉快速增长的分析误差，而分析场的不确性一部分是由于背景场误差导致，另一部分是由于观测误差导致，初值扰动需要具有准确捕捉这些误差的能力。同时对于模式预报而言，集合成员间需要保持合理的发散，最大限度的确保预报集合能够包含真实大气状态的可能分布，这就需要集合扰动在预报过程中保持合理的增长，以体现出预报误差随预报时效的增长。

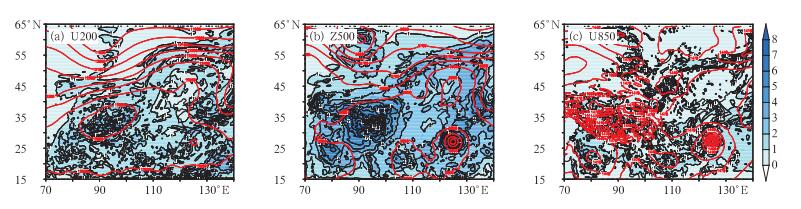
3.1 ETKF初值扰动结构分析

合理的集合预报初值扰动能够捕捉初始场中快速增长的“高能误差”，这些误差往往与动力不稳定区域相联系，因此集合扰动需要具有动力学特性，即“流依赖(flow dependent)”。图 2是2013年6月6日12：00 UTC的200 hPa U分量风(U200)，500 hPa位势高度(Z500) 以及850 hPa U分量风(U850) 的初值扰动绝对值的水平分布，同时给出分析场对应层次的位势高度场。可以看出，在等位势线较平缓的区域，扰动较小，而在槽脊区，扰动较大，说明ETKF方法可以识别初始场中不确定性较大区域，使该地区扰动较大。

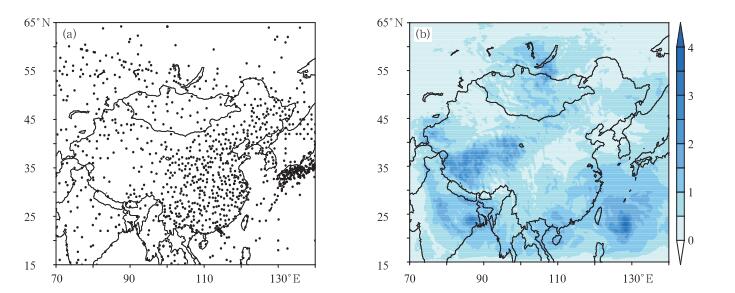
ETKF方法的一个重要特征是能够吸收观测信息，对扰动进行调整。图 3是观测空间水平分布以及连续40 d垂直平均的U分量风扰动绝对值的分布。可以看出图 3a中观测分布不均匀，在高原地区以及西太平洋海洋地区，观测较为稀疏，因此这些地区初始分析场的不确定性较大，与之相对应的是，图 3b在青藏高原地区以及西太平洋海洋地区扰动量级较大，如西太平洋地区扰动最大值可达4 m·s^-1，而在观测分布较密集的中国大陆东部地区，扰动量级较小，说明ETKF的调整使得分析扰动能够体现观测的不确定性。

3.2 集合扰动的方差分布

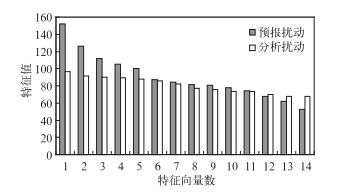
对于有限的集合成员数来说，ETKF方法通过集合变换，能够将集合方差平均分配到正交的特征方向，集合扰动中能够在14个正交、不相关的特征向量方向保持均衡的误差方差，而不是仅在少数方向保留较大的误差方差，这就是ETKF方法的滤波效应，这样带来的好处就是每个扰动成员都能参与贡献来描述误差方差，在今后随着集合成员数的增加，会给集合预报系统带来更明显的正效果。图 4是连续40 d平均的预报扰动协方差矩阵和分析扰动协方差矩阵特征值谱，可以看出，分析扰动协方差的特征值谱更加平缓，说明通过ETKF的滤波效应，系统在每个正交方向上均保持了相当大小的误差方差。

3.3 集合扰动变化分析

为了进一步看出扰动的总体演变特征，本文采用集合方差总能量来进行分析(Wang et al，2003；马旭林等，2008)，定义一个扰动的总能量为：

$ \frac{1}{2}\left[ {{{u'}^2}\left({i, j, k} \right) + {{v'}^2}\left({i, j, k} \right)} \right] + \frac{{{c_p}}}{{{T_r}}}{{T'}^2}\left({i, j, k} \right) $

(4)

式中u′，v′和T′分别为水平风场和温度的扰动，扰动值为集合成员预报和集合平均之差，c_p为干空气定压比热，T_r是参考温度，i，j，k分别是格点的水平与垂直维数。

首先对每个成员各个层次的总能量全场求平均，随后对各个成员求平均，这样便得到了不同预报时效集合扰动总能量离散度的垂直廓线图(图 5)。可以看出，随着预报时效的延长，总能量离散度是在不断增长的。各预报时效的总能量离散度在200~300 hPa均存在一个极大值区，该层的总能量离散度增长幅度也较大，6 h预报时效的总能量离散度极大值位于200 hPa附近，为5.5 J·kg^-1，30 h预报时效总能量离散度极大值位于250 hPa附近，达到了9.8 J·kg^-1；中低层总能量离散度涨幅较小，其中700 hPa的总能量离散度在6 h预报时效为3.3 J·kg^-1，30 h预报时效达到5.3 J·kg^-1。总体上集合扰动随预报时效的延长呈现出发展的状态，能在一定程度上代表模式预报误差的增长。

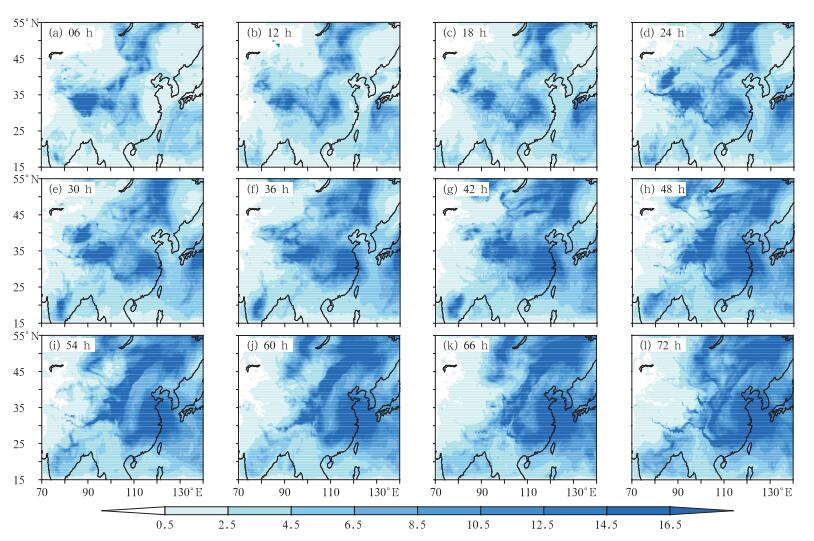
为了了解集合扰动的水平增长特征，图 6给出了各层垂直平均及不同成员平均的集合扰动总能量离散度在不同预报时效的水平分布图，时间间隔6 h。可以看出，总能量离散度有东移发展的趋势，这与流型的演变是相吻合的，说明集合扰动具有较好的随流型发展的能力。

4 集合预报批量试验的检验分析

评估一个集合预报系统的效果需要通过一系列概率预报检验方法来进行检验。本文采用了一系列典型的集合预报检验方法，如集合均方根误差和集合离散度，Talagrand分布以及CRPS评分来对GRAPES-REPS连续40 d批量试验效果进行检验，其中对于每个预报时效，用以检验的分析场采用的是对应时刻GRAPES_Meso模式自身的分析场。

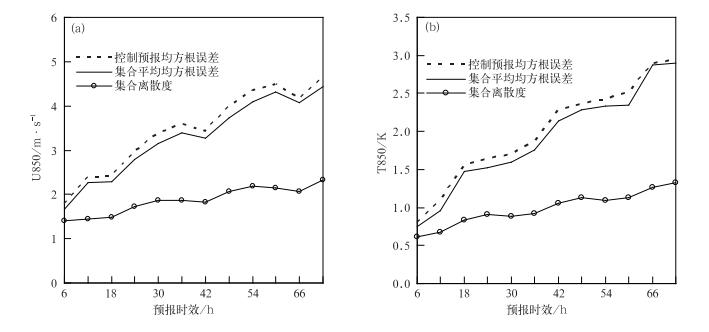
4.1 集合均方根误差和集合离散度

图 7是U850及T850两个等压面变量连续40 d统计平均的控制预报和集合平均均方根误差(root mean square error，rmse)，以及集合离散度(ensemble spread)随预报时效的演变。可以看出两个变量随着预报时效的延长，均方根误差是不断增长的，而集合离散度也随之增长，说明集合预报能在一定程度上代表预报不确定性；其次，集合平均的均方根误差小于控制预报，说明集合预报能够改善确定性预报的效果；但是集合离散度总体上低于均方根误差，如对于U850，72 h预报时效的集合均方根误差为4.4 m·s^-1, 而集合离散度为2.3 m·s^-1，对于T850, 72 h预报时效的集合均方根误差为2.9 K，而集合离散度为1.3 K，其他变量情况也类似(图略)，这种集合离散度小于均方根误差的情况也是国际上区域集合预报普遍存在的问题。

4.2 Talagrand分布

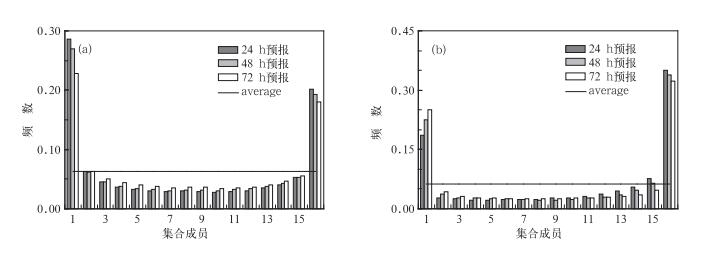
对于一个理想的集合预报系统，观测实况应该以近似相等的概率落在集合成员附近，Talagrand分布可以描述这种集合成员与观测真值的一致性，通过Talagrand分布可以了解集合预报系统的可靠性以及系统偏差特征。图 8是连续40 d统计平均的U850和Z500两个等压面变量24、36和48 h预报时效的Talagrand分布。可以看出两个变量预报均产生了一定的集合离散度，且随着预报时效的延长，Talagrand分布趋于平缓，表明集合成员间的发散度随预报时效延长不断增长。各变量的Talagrand分布距离理想的平均线还存在一定差距，图 8a显示U850的Talagrand呈一定的U型分布，集合离散度略有不足，图 8b显示Z500的Talagrand略呈J型分布，说明500 hPa高度场预报存在一定的系统性负偏差，这可能与模式本身的性能有关。

4.3 CRPS评分

连续分级概率评分(CRPS)是集合预报中常用的评分方法，其能够定量比较集合预报累计概率与真实观测累计分布概率的距离，CRPS值越小表示预报的概率密度和观测的差越小，预报系统预报能力越高。

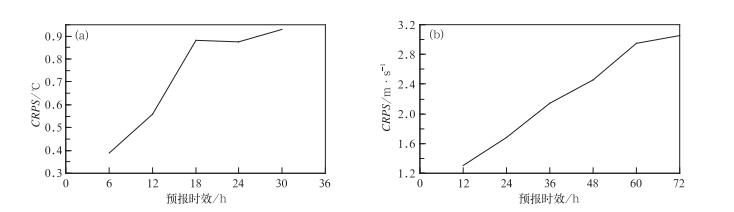
图 9是T850与U850连续40 d统计平均的CRPS随预报时效演变图。本文参照Met Office区域集合预报系统(MO-REPS)的CRPS评分(Bowler et al，2009a；2009b)(图略)进行对比。对于T850的6 h预报，GRAPES-REPS的CRPS值为0.38℃左右，小于MO-REPS的0.74℃，随着预报时效的延长，18 h预报时效的GRAPES-REPS的CRPS值为0.9℃，超过了MO-REPS的0.8℃；对于30 h预报时效，GRAPES-REPS的CRPS值为0.94℃而MO-REPS为0.9℃左右。对于U850预报，12 h预报时效GRAPES-REPS的CRPS值(1.3 m·s^-1)低于MO-REPS(1.67 m·s^-1)；而随着预报时效的延长，GRAPES-REPS的CRPS值逐渐增大，72 h预报时效的值为3 m·s^-1，略超过了MO-REPS的2.25 m·s^-1，总体上两个系统相差不大。

5 与业务WRF-REPS的降水评分对比

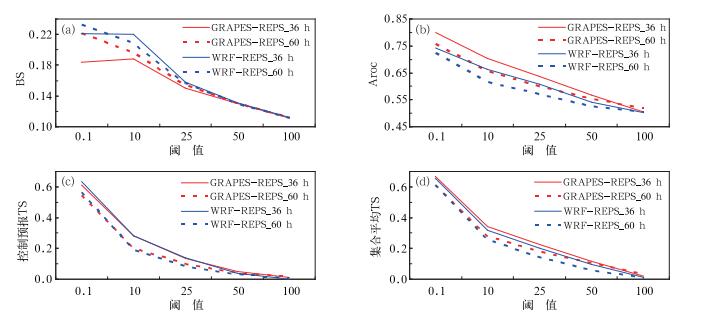
降水预报能力的好坏是衡量区域集合预报系统优劣的重要指标。肖玉华等(2013)指出GRAPES和WRF两种模式在我国西南地区的单模式降水预报性能相差不大，基于两种区域模式的集合预报系统表现如何值得研究。目前基于WRF的集合预报系统WRF-REPS已业务运行，该系统采用BGM初值扰动方法以及多物理过程组合模式扰动方法，能够提供较好的降水概率预报(邓国等，2010)。本节主要关注GRAPES-REPS降水预报能力如何，与WRF-REPS相比具有怎样的差异。采用一系列降水评分方法对GRAPES-REPS和WRF-REPS两套区域集合预报系统36和60 h预报时效的24 h累计降水预报进行检验，检验时段为2013年6月24日至7月13日，所采用的评分为BS评分、Aroc和TS评分(图 10)。由图 10a可以看出，对于小雨(阈值0.1 mm)和中雨(阈值10, 25 mm)量级，GRAPES-REPS的BS评分明显小于WRF-REPS，说明GRAPES-REPS预报误差更小，预报更准确，而随着降水量级的增加，两者的预报能力趋于接近；图 10b可以看出GRAPES-REPS的Aroc值要更大，且各量级降水预报表现均好于WRF-REPS，尤其是对于小雨和中雨，GRAPES-REPS优势相当明显；对于TS评分，GRAPES-REPS和WRF-REPS的控制预报(图 10c)水平很接近，但是集合平均(图 10d)，GRAPES-REPS要明显优于WRF-REPS，显示了GRAPES-REPS集合预报对控制预报较好的改进效果。

6 一次典型的强降水个例分析

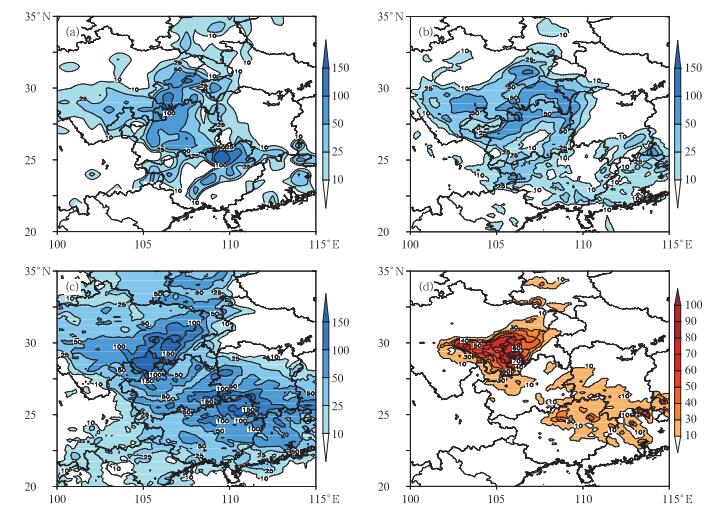
为了进一步检验GRAPES-REPS的降水预报能力，本文选取了2013年6月8—9日西南至华南强对流过程进行个例分析，集合预报从2013年6月8日12：00 UTC起报。图 11是6月8日12：00 UTC至9日12：00 UTC 24 h累计降水量的实况、控制预报、最大降水量预报以及大雨量级概率预报分布。从实况(图 11a)可以看出，该时段有两个强降水中心，一个位于四川—重庆—贵州交界地区，另一个位于广西东北部。控制预报(图 11b)对四川—重庆—贵州降水中心预报较好，但是对广西东北部的强降水中心漏报；图 11c为集合预报最大降水量，即各个预报成员的预报最大值，可以看出最大降水中心与实况对应较为准确，在四川—重庆—贵州与广西东北部存在两个明显的强降水中心；图 11d是大于50 mm降水概率分布，在实况降水中心附近，降水概率分布值均为最大，表明集合预报对该个例的概率预报是成功的。

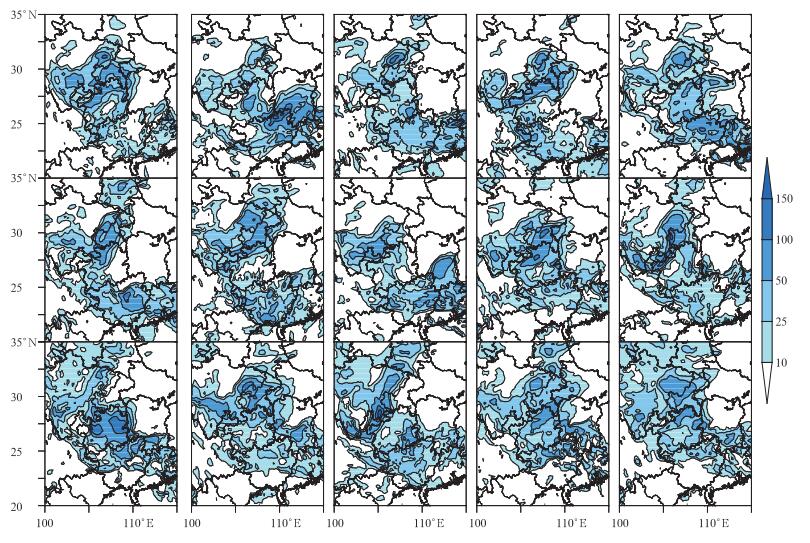
图 12是2013年6月8日12：00UTC至6月9日12：00 UTC的24 h累计降水量预报的邮票图，从左上至右下分别为控制预报和member1—member14共15个集合成员。可以看出，控制预报未报出广西东北部强降水中心，而若干集合成员对该降水中心的预报较好，如member1和member4均报出了广西东北部强降水中心，说明集合预报对确定性预报有很好的改进作用。

7 结论与讨论

本文基于GRAPES_Meso区域模式，采用ETKF初值扰动方法以及多物理过程组合模式扰动方法建立了GRAPES区域集合预报系统(GRAPES-REPS)，设计了具有业务运行潜力的试验流程，并针对2013年暖季开展了连续40 d的集合预报批量试验，通过集合预报检验以及降水检验等手段，综合对比分析了GRAPES区域集合预报系统的表现，得出如下结论：

(1) 采用ETKF初值扰动方法的GRAPES区域集合预报系统能够产生具有合理结构，随流型依赖的初值扰动，且扰动能够反映观测信息，扰动成员间是正交的。

(2) 随着预报时效的延长，各个层次的集合扰动均有所发展，且集合扰动具有随流型发展的能力。

(3) 集合预报检验表明该区域集合预报系统的集合预报平均优于控制预报，随着预报时效的延长系统能够保持合理的集合离散度，该系统的性能与国际上先进的区域集合预报系统相差不大。

(4) 降水检验表明，该区域集合预报系统的降水预报能力较好，优于业务的WRF区域集合预报系统。

虽然目前的GRAPES-REPS系统已具有较好的应用效果，但仍有一些方面有待完善。目前ETKF方法的计算中使用的是模拟观测资料，引入真实观测资料是今后的工作重点。另外，从目前的结果来看，仅采用初值扰动与物理过程扰动的GRAPES-REPS离散度略显不足，目前该系统并未采用侧边界条件扰动，今后将尝试与T639全球集合预报系统实现集成，用大尺度集合预报场为区域集合预报提供边界条件扰动，以进一步提高集合离散度。