2. 中国气象局气象探测中心,北京 100081;
3. 北京大学物理学院大气科学系,北京 100029
2. CMA Meteorological Observation Centre, Beijing 100081;
3. Department of Atmospheric Sciences, School of Physics, Peiking University, Beijing 100029
在前期联合估测区域降水量研究中,由于与雷达观测相匹配的地面雨量站数量不足,研究者(王叶红等,2001)基本上都是把参与联合校准的雨量站(校准站),也用于估测精度的评估,因此,雷达估测雨量站点的降水精度可以达到90%以上(李建通等,1997;2000)。事实上,在校准站点之外的区域,雷达估测精度远远低于该精度,限制了评估效益的发挥。显然,采用未参加校准的雨量站数据进行方法估测精度评估,其结果更为客观和合理。
许多研究用雷达资料估测降水,取得了一些进展(陈小华等,2013;李柏等,2013;东高红等,2012;庄薇等,2013)。2000—2004年,中国气象局和水利部联合开展“黄河淮河流域暴雨洪水预报系统”项目,利用两个部门的联合优势开展外场试验,采集了大量的雷达和地面站降水观测资料,为降水估测的研究提供了很好的基础。特别是2003年梅汛期间,淮河流域爆发了继1991年后的全流域持续性暴雨和大洪水,此次大洪水过程和亚欧中高纬地区高压活动密切相关。2003年6月20日至7月12日的降水过程是由于亚洲北部阻塞形势发展成熟,活动显著的原因造成的(李峰等,2008),该降水过程的类型为典型梅雨期降水。项目组成员全面收集该降水过程的雷达和地面雨量站网数据,为雷达估测降水区域降水量方法研究和精度评估提供大量的研究样本。在此降水过程期间,安徽省合肥市新一代天气雷达(CINRAD/SA)以降水观测模式(每隔6 min)对降水过程进行采样,降水区域主要维持雷达半径90~200 km的范围内。降水过程共获取雷达立体扫描(VOL)5520个基数据。同时,与雷达观测资料匹配的1 h雨量观测数据为河南、安徽省水文部门和气象部门的雨量站。
利用上述的资料,本文从雨量站观测值和雷达估测值之间的相关系数、平均相对误差、平均相对误差标准差等评估参数,对前期的Z-I关系法(ZI)、平均校准法(AVG) (Wilson et al,1979; 张亚萍等,2013)、变分校准法(VAR) (伍志方, 1989;1991; 张培昌等,1992;李建通等,1997)、自适应最优插值校准法(OPT)(李建通等,2000)、卡尔曼滤波校准法(KLM)(尹忠海等,2005)、自适应卡尔曼滤波校准法(SKM)(赵坤等,2005)、卡尔曼-变分校准法(KVR) (赵坤等,2001)、卡尔曼-最优插值法(KOP)(李建通等,2009)、临界概率集成法(EMS)、平均权重集成法(EAV)(李建通等,2014)等10种降水估测方法进行系统检验和评估,以期为进一步开展降水估测方法研究和降水估测产品应用提供有益参考。
1 资料质量控制与分析 1.1 质量控制由于雷达、雨量站自身问题,以及地形等原因,使得雷达和雨量站采集的数据存在一些不合理数据,它们的存在对降水估测校准和评估产生会不良影响,因此,在使用前必须进行质量控制,消除不合理的数据。质量控制剔除的雨量站数据主要为:
(1) 雨量站有降水量,但雷达降水估测结果为零的数据。这些数据通常是由于地形或其他原因造成的地面观测到降水而相应时间雷达上无回波的数据。
(2) 相对误差绝对值平均大于200%的数据。这些数据通常是混杂在降水中的地物回波造成,使得雷达估测的降水量远远大于地面的实际降水量。
(3) 地面雨量数据观测值大于实际雷达估测3倍以上的数据。这些数据通常是由于仪器或其他原因造成的。
1.2 雨量站分组为了充分利用雨量站数据进行检验、评估,同时也使检验评估更具客观性,将逐时雨量站网数据分为3组:R0、R1、R2。具体分组方法如下:
(1) 首先,将同一小时内所有观测到降水的雨量站按经纬度从上到下、从左到右顺序排列,然后,分别将序列号对3取余数,余数(0,1,2) 相同编为一组,即将同一小时的雨量站网数据在空间上基本均匀地分为3组(R0、R1、R2)。
(2) 将雨量站R0的数据用于雷达降水估测的校准,其余两组雨量站(R1、R2用于评估。然后,分别将R1和R2用于校准,相应的(R0、R2)和(R0、R1)作为评估雨量站。循环使用3组雨量站分别用于校准和评估。
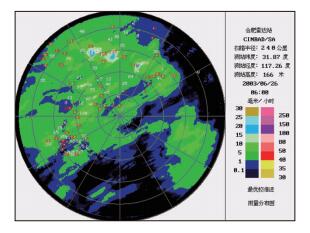
(3) 对过程所有的逐时雨量数据重复上述的工作。图 1是2002年6月26日06时校准站和评估站(非校准站)的空间分布图,其中红色为校准站,白色为评估站。
|
图 1 校准雨量站和评估雨量站分布示意图 (红色是校准站,白色是评估站) Fig. 1 Distribution diagram calibration rainfall stations (red color) and assessment rainfall stations (white color) |
(4) 把所有参加校准的雨量站数据和相应雷达估测的数据合并形成一个数据集,用于自评估,称为校准雨量站评估数据(简称校准组);把所有未参加校准的雨量站数据和相应雷达估测的数据合并形成一个数据集,用于非自评估,称为非校准雨量站评估数据(简称非校准组)。
1.3 数据分类汇总在统计学上,对数据进行分类汇总就是按照指定分类变量值的观测量进行分组,获得每组观测量和分类变量统计关系。在上述样本组,雨强、距离都与精度存在一多对应的关系。为了研究估测精度与雨强之间、以及其与测站距离之间的统计关系,将上述数据分别按雨强和雨量站进行汇总。通过汇总,可以分别建立雨强与精度,距离与精度的一对一的统计关系,并用于评估检验。
雨强汇总的过程是:以等雨强作为汇总变量,把雷达估测同一雨强在不同时间、雨量站点降水时的误差和误差标准差,按等权重方法进行平均,获取不同雨强等级所对应雷达估测的平均相对误差及其标准差。雨量站汇总的过程是:以雨量站点位置为汇总变量,把雷达估测同一个雨量站在不同雨强、时间点降水时的误差和误差标准差,按等权重方法进行平均,获取不同雨量站距离所对应雷达估测降水的平均相对误差及其标准差。
1.4 资料特征分析在此次降水过程中,按照1.1节中的方法进行质量控制后,气象和水利部门地面雨量站观测到逐时雨量站样本有35793站时,称为总样本组;雨量站观测到地面有降水的总时数为347 h,平均每小时有58个站同时观测到降水;出现同一个时次最多171雨量站同时测量到降水;50个以上雨量站在同一时次内都测量到降水的时次有177 h;雨量站测量的最大雨强为79.5 mm·h-1。
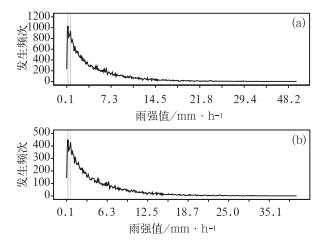
按照1.2节方法分组,非校准雨量站的数据共有16595站时,称为非校准组;校准雨量站的数据共有19198站时,称为校准组。表 1给出了两种样本组在不同累积率对应的雨强。图 2给出了两种样本组的雨强累积概率分布图,其中,图 2a为总样本组,图 2b为非校准组。
|
|
表 1 两种样本组中,不同累积率相对应的雨强情况 Table 1 Rainfall intensity corresponding to different cumulative rate in two sample groups |
|
图 2 不同雨强等级的频次分布图 (a)总样本组, (b)非校准组 Fig. 2 Frequency distribution of the different rainfall intensities (a) sample group, (b) non-calibration group |
从表 1中可知:对于总样本组,0.1~0.5 mm·h-1的降水事件占过程降水事件的10%,降水事件主要发生在0.5~11.1 mm·h-1,约占总降水事件的80%,高于11.1 mm·h-1的降水也仅占10%左右,高于14.9 mm·h-1的雨强仅占5%;对于非校准组,其累积概率分布特征基本一致,具体数据有小的差异,如降水事件在0.5~11.0 mm·h-1之间,约占总降水概率的80%。从表 1中也可以看出:80%以上的降水事件都在7.5 mm·h-1以下。
从图 2中可知:对于总样本组,有两个峰值,分别是0.7和0.3 mm·h-1,出现频次最多为0.3 mm·h-1,总共有1032次,占2.9%,其次,是0.7 mm·h-1的降水,总共有935次,占2.6%;对于非校准组,也具有总样本组的双峰值结构特征,具体数值也一样,出现频次最多的也是0.3 mm·h-1,共计450个,占2.7%,其次是0.7 mm·h-1,共计429个,占2.6%。综合来看,两个样本组的空间分布结构基本一致。
另外,从图 1中可以看出校准站和非校准站的空间分布也是基本均匀,上述的雨量站分组具有较好随机性和代表性。
综上所述,采用质量控制和雨量站分组方法后,非校准组的数据特征与总样本组基本一致;逐时的非校准和校准站站网空间分布合理,以此数据作为检验和评估是客观可行的。
2 单站评估前期研究表明,雷达估测降水的最佳估测范围为50~150 km距离段。为了检验各种方法在不同距离档时的估测精度情况,分别在最佳估测范围内和外,各选一个降水时次较多的站。
一个是河口集雨量站,该站和雷达的距离为112 km,位于雷达估测降水的最佳范围内。在此次降水过程中,该站地面测量的最大雨强为23.2 mm·h-1。
另一个是马汊河雨量站,该站和雷达的距离为201 km,位于雷达估测降水最佳范围之外。在整个降水过程中,该站地面测量的最大雨强为29.6 mm·h-1。
为了表述方便,简称评估的相关系数为α,偏差标准差为δ,平均相对误差为β,平均相对误差标准差为γ。
2.1 校准站评估在整个降水过程的样本中,马汊河站参与校准的时次共有79次,因此,可参加评估的样本79个,按雨强汇总后有58个样本(58个等级雨强);河口集站参与校准的时次共有113次,因此,可参加评估的样本113个,按雨强汇总后有68个样本(68个等级雨强)。
比较3个评估参数(表略),图 3a~3c分别是相关系数α、平均相对误差β和平均相对误差标准差γ的比较曲线。

|
图 3 校准站评估参数比较 (a)相关系数,(b)平均相对误差(单位:%),(c)平均相对误差标准差(单位:%) Fig. 3 Comparison of assessment parameters for calibration stations (a) correlation coefficient, (b) average relative error (unit: %), (c) standard deviation of average relative errors (unit: %) |
(1) 从相关系数变化(图 3a)看:① OPT、KOP和VAR 3种空间域上校准方法的相关系数都为1;② 除去上述3种方法外,EAV和EMS方法的相关系数都大于其他5种方法,EAV方法始终大于EMS方法;③ 河口集(雷达最佳估测范围内)处的相关系数均大于马汊河站(雷达最佳估测范围外)处。
(2) 从平均相对误差(图 3b)来看:① OPT、KOP和VAR 3种空间域上校准方法的平均相对误差明显小于其他7种方法,<6%;② 集成类的EAV和EMS方法略大于前面3种,但优于其他5种方法,EMS方法好于EAV方法;③ 余下的5种方法中,除了SKM和KVR方法,河口集站平均相对误差不大于马汊河站。
(3) 从平均相对误差标准差(图 3c)来看:① OPT、KOP、VAR方法的平均相对误差标准差最小;② 除去上述3种,EAV和EMS方法的都小于其他5种方法,EAV方法始终小于EMS方法;③ EAV、EMS、KVR、KLM、AVG方法,河口集(雷达最佳估测范围内)处优于马汊河站(最佳估测范围外)处。
2.2 非校准站评估在整个降水过程的样本中,河口集站未参与校准的时次共有96次,因此,可参加评估的样本为96个,按雨强汇总后有63个样本;马汊河站未参与校准的时次共有79次,因此,可参加评估的样本为79个,按雨强汇总后有57个样本。
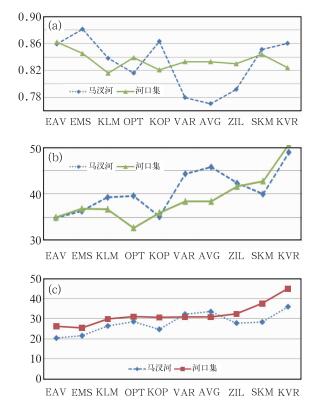
比较非校准站处3个评估参数(表略),图 4a~4c分别是相关系数α、平均相对误差β,平均相对误差标准差γ的比较曲线。
|
图 4 非校准站评估参数比较 (a)相关系数,(b)平均相对误差(单位:%),(c)平均相对误差标准差(单位:%) Fig. 4 Comparison of assessment parameters for non-calibration stations (a) correlation coefficient, (b) average relative error (unit: %), (c) standard deviation of average relative errors (unit: %) |
(1) 从相关系数(图 4a)来看:① EAV方法始终都小于EMS方法。对于河口集站处(最佳估测范围内),EAV或EMS两种方法的相关系数均大于其他8种方法, 且EAV方法大于EMS方法;对于马汊河站处(最佳估测范围外),EMS方法大于EAV方法,且大于其他8种方法, EAV方法略小于KVR和KOP方法,但大于其他6种方法;② 空间域上校准的方法如OPT、VAR、ZIL、AVG,河口集站处大于马汊河,时间域上校准的方法如KLM、SKM,以及空间和时间域上两次校准的方法如KOP、KVR,河口集相关系数小于马汊河。
(2) 从平均相对误差(图 4b)来看:① 对于马汊河站处,EAV方法的平均相对误差都是最小的;EMS方法除了在马汊集站处的KOP方法外,小于其他7种方法,且EAV方法小于EMS方法;对于河口集站,EMS方法除了在河口集站处的OPT方法外,EMS方法小于其他8种方法;② 采用OPT、KLM、VAR、AVG、ZIL方法时,河口集站处优于马汊河。
(3) 从平均相对误差标准差(图 4c)来看:① EAV和EMS方法的平均相对误差标准差都优于其他8种方法,对河口集站,EMS方法优于EAV方法,对于马汊河,EAV方法优于EMS方法;② 除了VAR、AVG方法外,马汊河站处都优于河口集站处。
(4) 河口集汇总前的相关系数大小的排序是:EAV、EMS、SKM、OPT、VAR、AVG、ZIL、KVR、KOP、KLM, 但相应的平均相对误差大小从小到大的排序是:EAV、OPT、EMS、VAR、AVG、KOP、KLM、ZIL、SKM、KVR。
2.3 综合评估综合上述的结果,可以得知:
(1) 各种方法估测结果与地面实际测量值之间的相关系数较大。除了KVR方法在马汊河站外,其余相关系数都大于0.7。因此,各种校准方法估测结果与地面观测值之间都存在显著相关。
(2) 相关系数大小与和估测平均相对误差不是一一对应的关系。相关系数主要反映的是两组数据变化的一致性,相关系数越大,说明两者的一致性好,也就是说平移时重合程度也越好,但其系统性的偏差可大可小。因此,不能仅凭相关系数就能确定估测结果的准确性,还需要平均相对误差等评估参数。
(3) EAV和EMS方法的平均相对误差及其标准差总体好于其他的8种方法,其估测的精度和稳定度优于其他8种方法。
(4) 从各种方法估测的精度和稳定度上来看,河口集站(最佳估测范围内)总体优于马汊河(最佳估测范围外)。
2.4 分雨强特征分析图 5是马汊河站和河口集站作为校准站时,各种方法估测值和雨量站测量值的比较;图 6是马汊河站和河口集站作为非校准站时,各种方法估测值和雨量站测量值的比较;图 7是马汊河站和河口集站作为非校准站时,EAV方法估测值和雨量站值的比较。
|
图 5 雷达估测值和雨量站值的比较(校准站) (a)河口集站,(b)马汊河站 Fig. 5 Comparison of radar estimation values and rainfall station observed values (calibration station) (a) Hekouji Station, (b) Macha River Station |
|
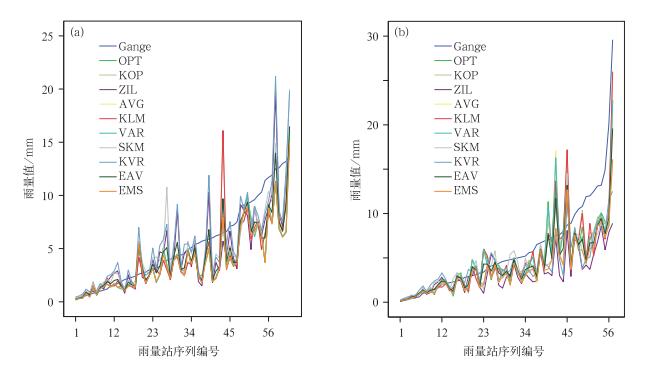
图 6 雷达估测值和雨量站值的比较(非校准站) (a)河口集站,(b)马汊河站 Fig. 6 Comparison of radar estimation values and rainfall station observed values (non-calibration station) (a) Hekouji Station, (b) Macha River Station |
|
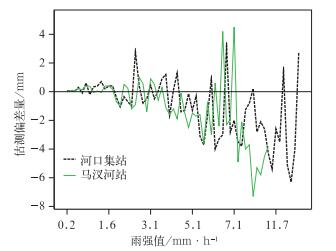
图 7 EAV方法估测偏差的比较 Fig. 7 Comparison of estimated deviations using EVA approach |
(1) 无论是校准站还是非校准站,对于雨强4.0 mm·h-1以下的降水,各种方法估测结果都呈高估的趋势;对于雨强4.0 mm·h-1以上的降水,各种方法都呈低估的趋势。
(2) 随着雨强的逐渐增强,雷达估测偏差量也随之增大。
(3) 从图 7可以知道:相比较于马汊河站(实线),河口集(虚线)估测偏差在大小和振幅上都比较小,即在最佳范围内的降水估测,雷达估测的偏差在大小和振幅上总体优于最佳范围外。
3 多站综合评估 3.1 逐时估测精度评估 3.1.1 分雨强评估为了考察估测区域内逐时降水估测的平均精度情况,把16595组成的非校准组称为样本组A。为了探讨雷达对不同雨强估测精度的情况,对上述样本组按照雨强进行汇总,汇总可以得到不同雨强时对应的评估参数的值。图 8给出了平均相对误差随雨强的变化曲线,图 9给出了雷达估测和地面雨量站观测雨强值的对比。为了清楚表现变化情况,图中仅给出了KOP和EAV方法的变化曲线,其余方法结果相似。
|
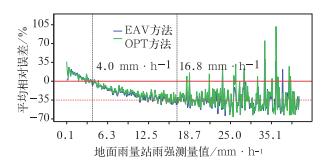
图 8 平均相对误差随雨强的变化曲线 Fig. 8 Curve of relative errors average changing with rainfall intensity |
|
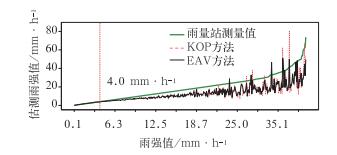
图 9 雷达估测雨强值和雨量站观测雨强值的比较 Fig. 9 Comparison of radar estimation values and rainfall station observed values |
(1) 当雨强在0.0~4.0 mm·h-1区间时。各种方法估测基本上高估;随着雨强增大,平均相对误差减小。也就是说,随着雨强增大,估测精度提高;当雨强为4.0 mm·h-1时,其平均相对误差最小,各种方法估测的精度最高。
(2) 当雨强在4.0~16.8 mm·h-1区间时,随着雨强增大,雷达估测的偏差和平均相对误差增大;当雨强不小于16.8 mm·h-1时,平均相对误差基本稳定,但振幅加大。
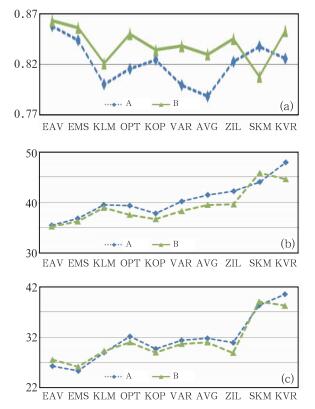
3.1.2 综合评估为了考察估测区域内逐时降水估测的平均精度情况。我们选取此次过程降水中范围较大、时间较长的一天(2003年6月26日)作为一个样本组,对日累积降水量估测精度进行评估。该日24 h内逐时雨量数据经质量控制后,共有1813个站时,把该日内逐时非校准数据组成的样本组B。图 10给出了样本组A和B中三个评估参数的比较。
|
图 10 两种样本组评估系数比较 (a)相关系数,(b)平均相对误差(单位:%),(c)平均相对误差标准差(单位:%) Fig. 10 Comparisons of assessment coefficients of two sample groups (a) correlation coefficient, (b) average relative error (unit: %), (c) standard deviation of average relative errors (unit: %) |
从图 10可知:
(1) 各种方法估测值与地面雨量测量值之间的相关系数都大于0.7;由此也反映各种方法估测的有效性。
(2) 除了SKM方法外,样本B组的相关系数同比都大于样本A,而样本B组的平均相对误差及其标准差都小于样本组A;由此可见,相关系数与平均相对误差不是一一对应关系。
(3) EAV和EMS方法的3个评估参数,都优于其他的8种方法,亦即集成方法估测降水的精度和稳定度优于其他8种方法。
(4) EAV方法的相关系数大于EMS,平均相对误差小于EMS,但平均相对误差标准差略大于EMS方法;EAV方法具有更强的适用性。
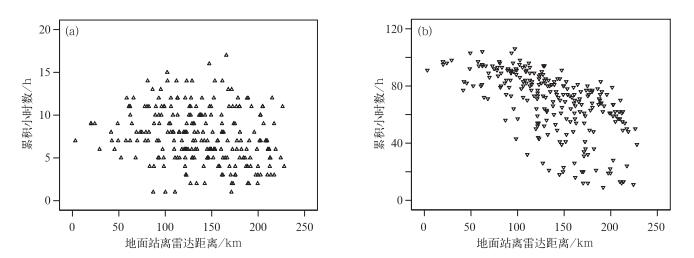
3.2 累积估测精度评估为了评估各种方法估测日降水量和过程降水量精度的情况,把样本组B按雨量站进行汇总(即累积各站日降水量)得到样本组C,共有239个站,平均时数7.59 h,方差3.23 h,平均站距为136.88 km,方差为47.65 km。对总样本组A按雨量站进行汇总(即累积各站过程的降水量)得到样本组D,共有243站。平均站距为137.22 km,方差为47.38 km。在该过程中总降水时间共有106 h,最少的是9 h,平均时数是68.29 h,方差为22 h。
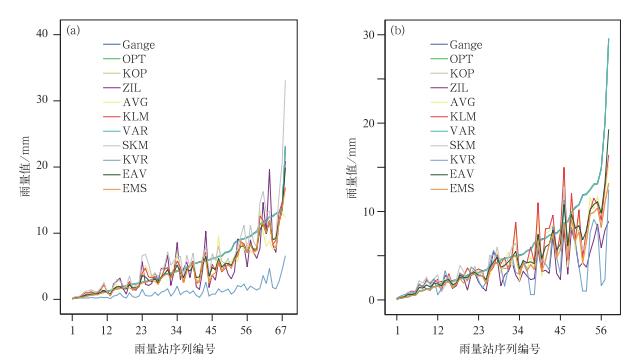
图 11是日和过程降水累积时数与距离的散点图,数据给出了4种样本组条件下,3种评估参数的比较表,图 12是各种评估参数的比较图(表略)。
|
图 11 累积时数与雨量站距离的散点图 (a)日累积,(b)过程累积 Fig. 11 Scatter diagram of accumulated hours and distance between rainfall stations (a) daily accumulation, (b) process accumulation |
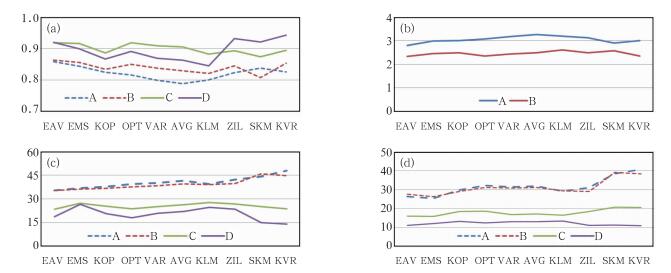
从数据(表略)和图 12可以知道:
|
图 12 各种方法4个评估参数的比较 (a)相关系数,(b)偏差标准差(单位:mm·h-1),(c)平均相对误差(单位:%),(d)平均相对误差标准差(单位:%) Fig. 12 Comparison of four estimation parameters using various approaches (a) correlation coefficient, (b) standard deviation (unit: mm·h-1), (c) average relative error (unit: %), (d) standard deviation of average relative errors (unit: %) |
(1) 相关系数(α)的比较(图 12a)。各种方法日累积和过程累积的相关系数都一致性大于相应逐时的相关系数。对于A、B、C 3种样本组,在相同样本组时,EAV方法的相关系数是最大的,但对于过程累积的样本D,EAV方法的相关系数小于ZIL、SKM和KVR。EMS方法相比较于EAV方法,其变化趋势和EAV方法一致,但同比小于EAV方法;ZIL、SKM和KVR方法过程累积后的相关系数大于24 h累积的相关系数,EAV方法不变,其余减小。
(2) 估测偏差标准差(δ)的比较(图 12b)。对于A、B两种样本组,在相同样本组时,EAV方法估测偏差标准差是最小的,EMS方法相比较于EAV方法,其变化趋势基本一致,但同比大于EAV方法,个别比单独的方法也还大。由于C、D样本组对应的是日累积和过程累积降水量,它们和逐时降水量不在同一数量级,在此不作比较。
(3) 平均相对误差(β)的比较(图 12c)。对于逐时降水量的估测,样本组A和B的平均相对误差量级相当,除了SKM方法外,样本组A略大于样本组B;随着时间累积的增加,各种方法的逐时、日累积和过程累积的平均相对误差基本呈减小的趋势,对于EAV方法分别是35.42%,35.19%,23.47%和18.78%,基本上是日累积比逐时10%~20%左右; 过程累积又比日累积降低5%~10%左右。对于SKM和KVR方法,过程累积比日累积减小约10%,明显高于EAV和EMS方法;在A、B、C三组样本中,EAV方法的平均相对都是最小的。
(4) 平均相对误差标准差(γ)的比较(图 12d)。对于逐时降水量的估测,样本组A和B的平均相对标准差误差量级相当;随着时间累积增加,各种方法的平均相对误差标准差基本呈减小的趋势,对于EAV方法分别是26.32%,16.08%和11.07%;基本上是日累积比逐时10%~20%左右,过程累积又比日累积降低5%~10%左右。对于SKM和KVR方法,过程累积比日累积减小约10%,明显高于EAV和EMS方法;在A、B、C 3组样本中,EAV方法的平均相对都是最小的。
综合来看:
(1) 在OPT、KLM和KOP方法中,KOP方法综合了OPT和KLM方法优点,估测的精度和稳定度优于二者(李建通等,2009)。
(2) 随着时间累积的增加,各种方法估测的平均相对误差及其标准差都减小;日累积和过程累积的相关系数都一致性大于逐时的相关系数,时间累积可以改善各种方法估测降水量的精度和稳定性。
(3) 在A、B、C样本组中,EAV方法无论从相关系数,估测偏差标准差还是从平均相对误差及其标准差来看,其估测结果基本都优于其他方法。EMS方法稍逊于EAV方法,但相对非集成的8种方法,总体还是有所改善。
值得注意的是:对于KVR方法,在过程累积降水估测中(样本组D),其相关系数最大,偏差标准差、平均相对误差及其标准差都是最小的,且小于EAV方法,KVR方法在长时间序列的降水量估测中有优势,其理论机制有待进一步研究。
4 评估参数距离分档的特征为了研究相关系数等评估参数与距离之间的关系,本文将总样本组数据50 km为一档,分为5档,分别是0~50 km(Ⅰ档)、50~100 km(Ⅱ档)、100~150 km(Ⅲ档)、150~200 km(Ⅳ档)和200~240 km(Ⅴ档)5档。对上述5档的数据分别计算各种方法的评估参数,具体结果如下:
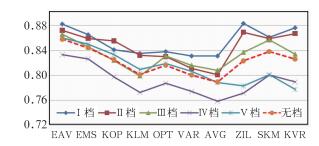
4.1 相关系数(α)结果(表略)和图 13是在不同距离档时,各种方法相关系数的比较。可看出:
|
图 13 不同分档时,各种方法相关系数的比较 Fig. 13 Comparison of correlation coefficients by different approaches in different grades |
(1) 除了Ⅰ档中ZIL方法外,EAV方法的相关系数都是大于其他方法,且EAV方法的相关系数同比都大于EMS方法。
(2) 除了OPT、VAR和AVG第Ⅲ档的相关系数大于第Ⅱ档,KOP第Ⅱ档的相关系数大于第Ⅰ档的4种特例外,在Ⅰ、Ⅱ、Ⅲ、Ⅳ的4个距离档中,各种方法的相关系数基本都随距离增加而减小。
(3) 除了KOP方法在最大相关系数出现在第Ⅱ档内(即50~100 km档)外,其余方法的最大相关系数都出现在第Ⅰ档内(即0~50 km档)。这主要由于雷达观测数据接近地面,雷达与雨量的二者观测时空一致性好,充塞系数大有关。
(4) 除了KVR方法最小的相关系数出现在第Ⅴ档外,其余方法最小相关系数都出现在第Ⅳ档(150~200 km)。导致150~200 km的雷达估测降水的相关系数最小的原因,主要是随着距离的增加,雷达充塞系数减小。理论上200~240 km的减小应多于150~200 km,但当地面有雨量站进行校准时,雷达和地面充塞的差异大,通过周边雨量站实现校准,得到了较好的订正,而对于150~200 km,这种差异相对也小,订正的效果也差。由此可见,对于远距离雷达估测系统性偏差的较大区域,地面雨量站对降水估测的意义是十分重大的,在实际应用中要加以考虑。
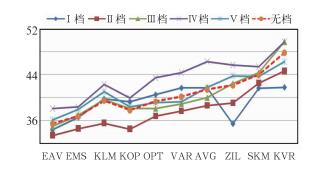
4.2 平均相对误差(β)分析数据(表略)和图 14是在不同距离分档条件下,各种方法平均相对误差的比较,可以看到:
|
图 14 在不同距离档时,平均相对误差(单位:%)的比较 Fig. 14 Comparison of average relative errors in different distance grades |
(1) 无论评估数据是分档,还是不分档,EAV、EMS方法的平均相对误差都是小于其他8种单独的方法,且EAV方法平均相对误差同比都小于EMS方法。
(2) 在0~150 km内,各种方法的平均相对误差基本小于不分档,也就是说,0~150 km是逐时降水的最佳估测范围;除了ZIL、SKM和KVR方法的最小平均相对误差出现在第Ⅰ档外,其余的最小平均相对误差都出现在Ⅱ档(50~100 km),第Ⅱ档(50~100 km)的平均相对误差总体最小。
(3) Ⅴ档(200~240 km)的平均相对误差小于Ⅳ档(150~200 km)。
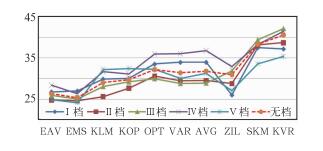
4.3 平均相对误差标准差(γ)分析数据(表略)和图 15是在不同距离档时,各种方法平均相对误差标准差的比较,可以得到:
|
图 15 在不同距离档时,平均相对误差标准差(单位:%)的比较 Fig. 15 Comparison of standard deviations of average relative errors in different distance grades |
(1) 无论评估数据是分档,还是不分档,EAV、EMS方法的平均相对误差标准差都是小于其他8种单独的方法。
(2) 第Ⅱ档(50~100 km)的平均相对误差标准差总体同比最好;第Ⅰ档(0~50 km)和第Ⅲ档(100~150 km)档次之;第Ⅳ档(150~200 km)最差。
5 结论和讨论 5.1 评估参数空间结构特征综合分析上述评估参数的空间和结构特点,可知:
(1) 在Ⅰ、Ⅱ、Ⅲ、Ⅳ的4个距离档中,相关系数基本都随距离增加而减小,第Ⅴ档的相关系数基本大于第四档,最小的相关系数出现在第Ⅳ档。
(2) 在0~150 km内,其平均相对误差都小于不分档,也就是说,0~150 km是逐时降水估测较为理想的范围, 且Ⅱ档平均相对误差最小,Ⅴ档的平均相对误差小于Ⅳ档(150~200 km), 第Ⅳ档的平均相对误差最大。也就是说50~100 km时雷达估测降水的最佳区间,0~50 km和100~150 km次之,150~200 km是估测误差最大的区间。
(3) 对于小于4.0 mm·h-1的降水,各种方法估测基本偏高,随着雨强增大,平均相对误差减小;在4.0 mm·h-1左右,估测降水偏差最小;对于4~16.8 mm·h-1降水,各种方法估测偏低随着雨强增大,平均相对误差增大;当大于16.8 mm·h-1的雨强时,平均相对误差基本稳定,但振幅加大。
(4) EAV方法的相关系数总体大于其他方法,且EAV方法的相关系数同比都大于EMS方法; EAV、EMS方法的平均相对误差都是小于其他8种单独的方法,且EAV方法的平均相对误差同比都小于EMS方法。
综上来看,对于逐时降水量的估测,模式集成法可以改善降水估测中的不确定性,提高雷达估测的精度和稳定度,是较好的降水估测新方法。
5.2 评估参数时间特征综合本文分析,可以有以下几个主要结论:
(1) 在雷达估测降水的范围内,无论雨量站距离雷达远近,KOP、OPT和KVR方法校准后,雨量站站点处雷达估测的平均相对误差小,不大于6%,相关系数为1。
(2) 随着时间的累积的增加,逐时、日降水量和过程降水量的平均相对误差呈减小的趋势。总的来看,时间累积可以提高降水估测的精度。
(3) 对于逐时、日降水的降水估测,EAV方法无论从相关系数,估测偏差标准差还是从平均相对误差及其标准差来看,它估测的结果基本都好于其他各种方法。EMS方法稍逊于EAV方法,但相对非集成的8种方法,总体还是有所改善。因此,EAV集成估测法可以改善逐时和日降水估测精度和稳定度。
(4) 对于过程累积降水的估测来说,KVR方法的估测效果总体好于包括EAV和EMS方法在内的其他9种方法,初步显现了体现了KVR方法在估测降水长时间累积过程中的订正效果,也体现了方法组合对降水估测的重要意义。KVR方法对长时间序列降水过程的降水量估测值得进一步研究。
5.3 讨论前期和本文研究的结果表明:对于非集成类的降水估测方法,KOP方法优于OPT和KLM方法(李建通等,2009);对于集成类估测方法,EAV方法具有更大的适用性;时间累积可以提高估测区域降水的精度;50~100 km区间是雷达降水估测的最佳区间;雷达估测降水精度与雨强之间存在非线性关系等。
上述研究成果,给雷达估测产品开发与应用提供了一些有益的启示:
(1) 对于相对稠密雨量站网数据,本文采用先空间排序,再用相同余数进行取样的分组方式,可以保持评估站和总样本站的空间和统计一致性,同时保持评估数据和校准数据的相对独立性,提高检验评估效果的客观性和可用性。
(2) 降水估测算法的改进。研究结果提供了降水估测在空间和时间的一些结构特征,可以作为下一步降水估测改进的客观依据,进一步优化各种算法,提高雷达估测区域降水量的精度。
(3) 降水估测算法的选择。
① 对于逐时和日降水量的估测,集成法估测降水量是目前较为理想的降水估测方法,但涉及的算法和代码实现较复杂,需要进一步结合各地实际情况进行完善;对于非集成的降水估测方法而言,KOP方法具有较好的适用性,估测结果较好,且容易实现。
② 对于过程降水量的估测,KVR方法的结果最好。
上述的结论也启示我们:由于降水过程自身的复杂性和各种校准方法的非完美性,在方法选用时要根据实际和应用的情况进行考虑。
(4) 估测产品应用的选择。对于精细化应用的需求,如高分辨数值预报模式雷达降水产品的同化需求、局地暴雨的预报决策等,最好选用优选方法在50~100 km范围估测结果;对于大范围降水量的分布需求,如水文洪水预报模式或中尺度以上雷达产品的同化、SWAN系统中雷达产品输入、水库蓄水和泄洪的决策等最好采用时间累积的产品;对于非最佳估测范围的估测产品,可以适当粗化降水估测产品,提高产品应用的有效性。
陈小华, 段旭, 2013. 基于卫星和雷达资料估测滇中地区降水量方法研究[J]. 气象, 39(2): 203-209. DOI:10.7519/j.issn.1000-0526.2013.02.009 |
东高红, 刘黎平, 2012. 雨量计密度对校准雷达估测降水的影响及单点对校准的贡献[J]. 气象, 38(9): 1042-1052. |
李柏, 古庆同, 李瑞义, 等, 2013. 新一代天气雷达灾害性天气监测能力分析及未来发展[J]. 气象, 39(3): 265-280. DOI:10.7519/j.issn.1000-0526.2013.03.001 |
李峰, 丁一汇, 鲍媛媛, 2008. 2003年淮河大水期间亚洲北部阻塞高压的形成特征[J]. 大气科学, 32(3): 469-480. |
李建通, 高守亭, 郭林, 等, 2009. 基于分步校准的区域降水量估测方法研究[J]. 大气科学, 33(3): 501-512. |
李建通, 杨维生, 郭林, 等, 2000. 提高最优插值法测量区域降水量精度的探讨[J]. 大气科学, 24(2): 263-270. |
李建通, 张培昌, 1997. 欧拉方程中三个参数选取与雷达测定区域降水量的精度[J]. 气象, 23(9): 1-7. DOI:10.7519/j.issn.1000-0526.1997.09.011 |
李建通, 李柏, 杨洪平, 等, 2014. 雷达-雨量计联合估测区域降水量方法研究(Ⅰ)——模式集成法的提出[J]. 气象科技, 42(4): 556-562. |
王叶红, 崔春光, 赵玉春, 等, 2001. 变分技术在校准数字化天气雷达定量估测降水中的应用[J]. 气象, 27(10): 3-7. DOI:10.3969/j.issn.1000-0526.2001.10.001 |
伍志方, 戴铁丕, 张培昌, 1991. 天气雷达定量测量区域降水量的校准技术及误差分析[J]. 气象, 17(10): 9-14. DOI:10.7519/j.issn.1000-0526.1991.10.002 |
伍志方, 戴铁丕, 张培昌, 等, 1989. 用变分法校准天气雷达测定区域降水量的数值计算和精度分析[J]. 气象科学, 9(3): 224-235. |
尹忠海, 张沛源, 2005. 利用卡尔曼滤波校准方法估算区域降水量[J]. 应用气象学报, 16(2): 213-219. DOI:10.11898/1001-7313.20050226 |
张培昌, 戴铁丕, 1992. 用变分方法校准数字化天气雷达测定区域降水量基本原理和精度[J]. 大气科学, 16(2): 248-256. |
张亚萍, 张勇, 廖峻, 等, 2013. 天气雷达定量降水估测不同校准方法的比较与应用[J]. 气象, 39(7): 923-929. DOI:10.7519/j.issn.1000-0526.2013.07.013 |
赵坤, 葛文忠, 刘国庆, 等, 2005. 在雷达测雨和洪水预报中自适应卡尔曼滤波法的应用[J]. 高原气象, 24(6): 956-965. |
赵坤, 刘国庆, 葛文忠, 2001. 用卡尔曼滤波确定变分方法中的权重系数进行雨量校正[J]. 气候与环境研究, 6(2): 180-185. |
庄薇, 刘黎平, 胡志群, 2013. 青藏高原零度层亮带的识别订正方法及在雷达估测降水中的应用[J]. 气象, 39(8): 1004-1013. DOI:10.7519/j.issn.1000-0526.2013.08.007 |
Wilson J W, Brandes E A, 1979. Radar measurement of rainfall-A summary[J]. Bull Meteor Soc, 60(9): 1048-1058. DOI:10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2 |
 2015, Vol. 41
2015, Vol. 41 