引言

在全球大气数值模拟中平流输送过程是一种重要的动力过程，平流传输过程不仅会影响物理量的分布，而且会产生平流传输量与波动的非线性相互作用。平流输送过程也和数值方法的计算稳定性、计算精度和计算效率密切相关(Ritchie，1987)。目前，全球大气数值模式许多是基于普通的球面经纬网格上开发的，其动力框架中通常是采用欧拉方法或谱转换的方法计算平流(Li et al，2006)。普通经纬网格由于存在极点奇异和经线辐合的数值计算问题，采用欧拉方法计算平流会受到严格的CFL条件的限制，使得计算时间步长受限，计算误差偏大且计算效率降低。而采用谱转换的方法计算平流会出现非物理数值解，如负地形、负水汽等。针对全球大气数值模式动力框架中平流计算存在的问题，从20世纪60年代开始众多科学家就开始探索解决的办法，大致可以分为两个方向：一是采用基于半拉格朗日平流的动力框架；二是构造准均匀的球面网格。

对于半拉格朗日平流动力框架，自从Fjφrtoft(1952；1955)尝试采用拉格朗日方法进行描述流体的运动规律之后，拉格朗日方法思想便逐步引起众多气象学家的关注。Wiin-Nielse(1959) 鉴于采用拉格朗日方法对固定粒子积分一段时间后出现变形的问题提出了半拉格朗日平流方法，和欧拉方法处理平流相比，该方法能够突破CFL条件的限制，允许大的积分时间步长和避免非线性计算不稳定，同时该方法和隐式处理快波问题方法相结合能够提高计算效率和计算稳定性(Robert，1982)。最近几十年，采用半拉格朗日方法处理平流问题的思想逐渐发展起来，也逐步应用到模式预报中。Bates等(1982) 在分裂显式多尺度原始方程模式中采用半拉格朗日平流方法得到了准确的预报结果，Staniforth等(1986) 将半拉格朗日方法和半隐式处理问题的方法相结合并将其应用到有限元浅水方程区域模式中，也获得了比较理想的结果。此外，Staniforth等(1991) 对半拉格朗日方法在一维、二维及三维上的应用做过详细论述，包括被动平流、强迫平流及浅水方程组的处理。我国气象学家廖洞贤等(1982)、曾庆存(1978)、王宗皓(1981) 对拉格朗日方法进行过相关研究，包括差分格式的设计及数值算法的设计等等。我国新一代自主研发大气数值模式GRAPES也是采用半拉格朗日方案处理平流过程(徐枝芳等，2013；朱振铎等，2007)。

关于构造准均匀球面网格方面，Kurihara(1965) 最早提出了“精简网格”，此后Sadourny等(1968)和Williamson(1968) 提出“正二十面体网格”，Sadourny(1972) 提出了“立方体球面网格”等。“精简网格”由于在每一纬度都减少一定的格点会产生波动的位相误差，同时也会引起波动的经向坡度加大；“立方体球面网格”由于其非正交性增加了模式的计算量；“正二十面体网格”由于网格长度和网格角度的变化不是非常规则，对其无法应用常规的有限差分方法，同时也存在弱的奇异点。但是球面准均匀网格是改进模式多尺度模拟能力和负载平衡能力很好的选择(Zerroukat et al，2012)，也是未来解决极点问题的重要途径(Washington et al，2009)。基于上述考虑，论文尝试采用一种“阴阳网格”来讨论球面平流传输问题。球面阴阳网格是Kageyama等(2004) 提出的一种准均匀无奇异重叠网格系统，它设计简单而且是正交的，同时也不存在坐标奇异、极区网格辐合物理问题。论文以球面阴阳网格为主线，在球面坐标下采用新型的LE水平跳点网格(刘宇迪，2004；刘宇迪等，2006)，设计一种两时间层半拉格朗日平流方案讨论球面平流传输问题，以期为开发全球高分辨球面阴阳网格数值模式的相关学者提供可行性参考。

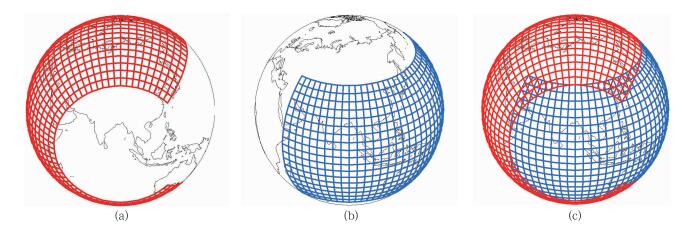
1 基本网格 1.1 阴阳网格

阴阳网格是一种球面上的重叠网格，它由两个相同的经纬网格扣合组成，如图 1c所示。以n表示阳网格，e表示阴网格，在笛卡尔坐标系中，阴阳网格之间的关系表达式为：

$ \left({{x}^{n}}, {{y}^{n}}, {{z}^{n}} \right)=\left(-{{x}^{e}}, {{z}^{e}}, {{y}^{e}} \right) $

(1)

阴阳网格是普通经纬网格的低纬部分，对于每一分量网格(图 1a或1b)，设λ、φ分别代表球坐标系下的经向及纬向坐标，则其经纬度的范围为：

$ {\pi }/{4}\;\le \lambda \le {7\pi }/{4}\; $

(2)

$ -\pi /4\ \le \varphi \le \pi /4\ $

(3)

在球坐标系下，按照式(1) 可得：

$ {{r}^{n}}={{r}^{e}} $

(4)

$ \cos {{\varphi }^{n}}\cos {{\lambda }^{n}}=-\cos {{\varphi }^{e}}\cos {{\lambda }^{e}} $

(5)

$ \cos {{\varphi }^{n}}\sin {{\lambda }^{n}}=\sin {{\varphi }^{e}} $

(6)

$ \sin {{\varphi }^{n}}=\cos {{\varphi }^{e}}\sin {{\lambda }^{e}} $

(7)

式(4)~(7) 是阴阳网格进行边界数据交换的基本关系式，其中为了方便对阴阳网格的边界进行数据交换，通常需要扩展各分量网格的边界。

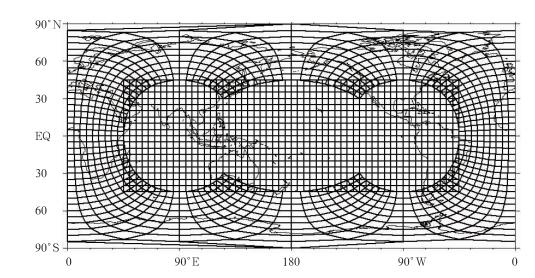
为了更清晰地看到阴阳网格的重叠属性，图 2绘制阴阳网格在圆柱等面积的投影示意图。由图可知，阴阳网格是重叠网格，阴网格和阳网格在边界处交错重叠。关于阴阳网格的优点，Kageyama等(2004)、Peng等(2006)、Baba等(2010)、Staniforth等(2012)和Zerroukat等(2012) 都进行过相关介绍，包括网格正交性、准均匀无奇异、易于区域分解和并行运算、易于编程及全球和局地数值模式的转换等。

1.2 LE网格

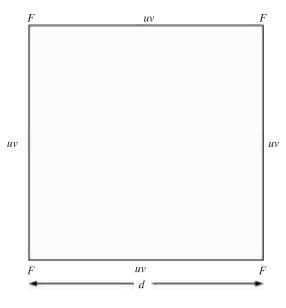
20世纪60年代Winninghoff(1968) 对水平网格变量配置的研究进行过论述，此后刘宇迪等(2001；2002)参照Winninghoff的思路对现今出现的所有水平网格从模拟大气波动的角度进行过较为深入的分析，发现尽管Arakawa C网格是现有的水平网格的最好网格，但在科氏项存在平均，数值计算也会出现误差。鉴于此，刘宇迪(2004) 提出的一种新的水平跳点LE网格，如图 3所示，它主要是将平流量F放在格点上，u，v风场同时放在x和y方向格点中间。刘宇迪采用一种推导波动频散关系的通用方法，在可分辨和不可分辨情形下，借助二阶中央差和四阶紧致差分格式将LE网格和Arakawa A、B、C、D及E网格在模拟Rossby波及惯性重力波的特性进行了对比分析，结果表明无论可分辨还是不可分辨, ，亦或是采用二阶中央差还是四阶紧致差分格式，在频率和群速两方面，LE网格描述惯性重力波产生的误差均较Arakawa A-E网格要小，同时也表明只有LE网格和Arakawa C网格采用差分精度较高的紧致差分格式时，模拟惯性重力波的精度才会提高。因此，本文在设计球面阴阳重叠网格平流方案过程中，尝试采用LE网格配置方案来离散变量，也为后续设计三维球面阴阳网格模式做好铺垫。

2 阴阳网格上半拉格朗日平流方案设计

关于半拉格朗日方法，本文研究的是基于全球的省时两时间层半拉格朗日格式，这种格式在不丧失数值精度的情况下时间步长能比三时间层半拉格朗日格式取得更长(Staniforth et al，1991)。如前所述，阴阳网格是普通经纬网格的低纬部分，平流方程在两网格中的表达形式类似，以阳网格为例，在极坐标系下二维平流方程可以表示为：

$ \;\;\;{l_3}\left( {{x_3}} \right)F_D^e\left( {{x_p},{y_3}} \right)\frac{{{\rm{d}}F\left( {{\lambda ^n},{\varphi ^n}} \right)}}{{{\rm{d}}t}} = \psi $

(8)

式中，标量F(λⁿ, φⁿ)代表阳网格中的平流量，ψ为物质源汇项，d/dt是物质导数，且满足，

$ \frac{\text{d}}{\text{d}t}\left({} \right)=\frac{\partial }{\partial t}\left({} \right)+\frac{u}{a\cos \theta }\ \frac{\partial }{\partial \lambda }+\frac{v}{a}\ \frac{\partial }{\partial \theta }\left({} \right)$

(9)

式中u、v分别为纬向和经向速度分量，a为地球半径。对式(8) 采用两时间层半拉格朗日方法思想，将平流量F(λⁿ, φⁿ)从t^m=mΔt到t^m+1=(m+1)Δt沿空气质点轨迹积分，有：

$\frac{F_{i, j}^{m+1}-F_{i-a, j-b}^{m}}{\Delta t}=\frac{1}{2}\left(\varphi _{i.j}^{m+1}+\varphi _{i-a.j-b}^{m} \right) $

(10)

式中，(i, j)代表流体质点在(m+1)时刻到达的格点位置，(i-a, j-b)代表流体质点在m时刻的出发点位置。若忽略源汇项ψ，方程(8) 变为：

$\frac{\text{d}F\left({{\lambda }^{n}}, {{\varphi }^{n}} \right)}{\text{d}t}=0 $

(11)

则由式(10) 可知

$ F_{i, j}^{m+1}=F_{i-a, j-b}^{m} $

(12)

由式(12) 可知，在不考虑源汇项的情况下，到达点未来时刻的数值来源于其上游点数值，这就是半拉格朗日平流。从中我们也可以知道为了求得到达点未来时刻的平流数值必须确定上一时刻出发点位置(i-a, j-b)，而(i-a, j-b)所处的位置不一定是格点，因而需要通过已知时刻的平流值插值获得上游点的值，因此球面阴阳网格半拉格朗日平流方案设计关键问题之一为半拉格朗日轨迹的计算。

本文所涉及的半拉格朗日平流方案是在球面阴阳网格上进行，因而着重考虑半拉格朗日方法在球面上的轨迹计算，而阴网格是阳网格经过旋转后得到的，阴阳网格的轨迹计算可以共用一套源程序，下面以阳网格为例来探讨半拉格朗日轨迹的计算。

在阳网格中流体质点运动轨迹的控制方程可以表示为：

$ \frac{\text{d}{{\lambda }^{n}}}{\text{d}t}=\frac{u}{a\cos {{\varphi }^{n}}}$

(13)

$ \frac{\text{d}{{\theta }^{n}}}{\text{d}t}=\frac{v}{a} $

(14)

在球面坐标上考虑上游点的位置B、到达点位置A及中间点C，(λ_d, φ_d)、(λ_a, φ_a)和(λ₀, φ₀)分别为其相应的经纬度坐标, 采用如下的两步格式确定出发点：

${{\lambda }_{0}}={{\lambda }_{a}}-u\left({{\lambda }_{a}}, {{\varphi }_{a}}, {{t}^{m}} \right)\ {\Delta t}/{2}\; $

(15)

${{\varphi }_{0}}={{\varphi }_{a}}-v\left({{\lambda }_{a}}, {{\varphi }_{a}}, {{t}^{m}} \right)\ {\Delta t}/{2}\; $

(16)

$ {{\lambda }_{d}}={{\lambda }_{a}}-u\left({{\lambda }_{0}}, {{\varphi }_{0}}, {{t}^{m+\frac{1}{2}}} \right)\ \Delta t$

(17)

$ {{\varphi }_{d}}={{\varphi }_{a}}-v\left({{\lambda }_{0}}, {{\varphi }_{0}}, {{t}^{m+\frac{1}{2}}} \right)\ \Delta t$

(18)

Ritchie等(1994) 在球面中低纬度对式(15)~(18) 给出一种很好的近似，其表达式为：

$ {{\lambda }_{0}}={{\lambda }_{a}}-\frac{{{u}_{0}}\ \Delta t}{a\cos {{\varphi }_{a}}}\left[ 1+\frac{\Delta {{t}^{2}}}{6{{a}^{2}}}\left( u_{0}^{2}{{\tan }^{2}}{{\varphi }_{a}}-v_{0}^{2} \right) \right]$

(19)

$ {{\varphi }_{0}}={{\varphi }_{a}}-\frac{{{v}_{0}}\ \Delta t}{a}+{{\left(\frac{{{u}_{0}}\ \Delta t}{a} \right)}^{2}}\ \frac{\tan {{\varphi }_{a}}}{2}$

(20)

$ {{\lambda }_{d}}={{\lambda }_{a}}-\frac{2{{u}_{0}}\ \Delta t}{a\cos {{\varphi }_{a}}}\left[ 1-\frac{{{u}_{0}}\ \Delta t}{a}\tan {{\varphi }_{a}} \right]$

(21)

$ {{\varphi }_{d}}={{\varphi }_{a}}-\frac{2{{v}_{0}}\ \Delta t}{a}+\left({{\sec }^{2}}{{\varphi }_{a}}-\frac{2}{3} \right){{\left(\frac{{{u}_{0}}\ \Delta t}{a} \right)}^{2}}\frac{{{v}_{0}}\ \Delta t}{a}$

(22)

式中(u₀, v₀)代表中间点C的风速，可以采用线性插值获得该风场。经过数值验证，通常迭代两次就可以求得球面上游点位置(λ_d, φ_d)。阴阳网格是球面经纬网格的低纬部分，因此本文主要借助Ritchie等(1994) 算法确定上游点的位置。

球面阴阳网格半拉格朗日平流方案设计关键问题之二为阴阳网格重叠区的平流数据交换。阴阳网格是重叠网格，而对重叠网格的数据交换一般采用的是插值的方法(McDonald，1989)。关于阴阳网格边界的数据插值交换问题，Quaddouri等(2008)、Li等(2008)、Baba等(2010) 均采用三次拉格朗日插值来完成阴阳网格的边界数据交换，Peng等(2006) 在阴阳网格上应用了双线性插值进行边界数据的过渡。为了比较插值方案对阴阳网格重叠区交换的影响，本文将分别采用三次拉格朗日插值及双线性插值进行比较分析。下面针对阴阳网格重叠区数据交换，详细讨论三次拉格朗日插值在阴阳网格上的应用，关于双线性插值Peng等(2006) 进行过详细的介绍。

由前所述，阴阳网格的边界插值通常是在分量网格的扩展区δ内进行。设在阳网格边界扩展区上某点的坐标为(λ_hⁿ, φ_hⁿ)，由式(5)和(6) 可知，该点可用阴网格点的坐标(λ_in^e, φ_in^e)表示为：

$\varphi _{h}^{n}={{\sin }^{-1}}\left(\cos \varphi _{in}^{e}\sin \lambda _{in}^{e} \right) $

(23)

$ \lambda _{h}^{n}={{\sin }^{-1}}\left( {\sin \varphi _{in}^{e}}/{\cos \varphi _{h}^{e}}\; \right)$

(24)

由式(23)和(24) 可以方便确定阳网格边界扩展区上的点在阴网格的位置，从而可以在阴网格中对其进行拉格朗日插值求解。拉格朗日插值处理过程如下：设在经向方向上分布着x₀, x₁, …, x_n的n+1个离散格点，则一维拉格朗日插值基函数l_i(x)为：

$ {{l}_{i}}\left(x \right)=\prod\limits_{j=0, j\ne i}^{n}{\frac{x-{{x}_{i}}}{{{x}_{i}}-{{x}_{j}}}\left(i=0, 1, \cdot \cdot \cdot n \right)}$

(25)

式(25) 的插值具有n阶精度，同理在纬向方向上对于分布着的y₀, y₁, …, y_n的n+1个离散格点, 可以得出其插值基函数l_j(y)。对于三次拉格朗日插值可知纬向一维基底函数为：

${{l}_{0}}\left({{x}_{0}} \right)=\frac{\left(x-{{x}_{1}} \right)\left(x-{{x}_{2}} \right)\left(x-{{x}_{3}} \right)}{\left({{x}_{0}}-{{x}_{1}} \right)\left({{x}_{0}}-{{x}_{2}} \right)\left({{x}_{0}}-{{x}_{3}} \right)} $

(26)

$ {{l}_{1}}\left({{x}_{1}} \right)=\frac{\left(x-{{x}_{0}} \right)\left(x-{{x}_{2}} \right)\left(x-{{x}_{3}} \right)}{\left({{x}_{1}}-{{x}_{0}} \right)\left({{x}_{1}}-{{x}_{2}} \right)\left({{x}_{1}}-{{x}_{3}} \right)}$

(27)

$ {{l}_{2}}\left({{x}_{2}} \right)=\frac{\left(x-{{x}_{0}} \right)\left(x-{{x}_{1}} \right)\left(x-{{x}_{3}} \right)}{\left({{x}_{2}}-{{x}_{0}} \right)\left({{x}_{2}}-{{x}_{1}} \right)\left({{x}_{2}}-{{x}_{3}} \right)}$

(28)

$ {{l}_{3}}\left({{x}_{3}} \right)=\frac{\left(x-{{x}_{0}} \right)\left(x-{{x}_{1}} \right)\left(x-{{x}_{2}} \right)}{\left({{x}_{3}}-{{x}_{0}} \right)\left({{x}_{3}}-{{x}_{1}} \right)\left({{x}_{3}}-{{x}_{2}} \right)}$

(29)

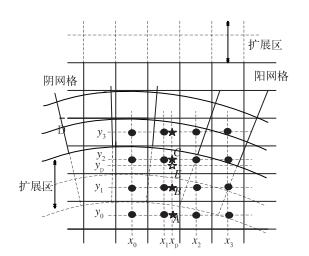
如图 4所示，设阳网格边界扩展区(虚线表示)E点为所要的插值点，其坐标为(x_p, y_p)，其在阴网格对应的物理量值设为F_E^e(x_p, y_p)。通过经向方向上三次拉格朗日插值求出F_A^e(x_p, y₀)，F_B^e(x_p, y₁)，F_C^e(x_p, y₂)，F_D^e(x_p, y₃)。对应的求解公式如下：

$ \begin{align} & F_{A}^{e}\left( {{x}_{p}},{{y}_{0}} \right)={{l}_{0}}\left( {{x}_{0}} \right){{F}^{e}}\left( {{x}_{0}},{{y}_{0}} \right)+{{l}_{1}}\left( {{x}_{1}} \right){{F}^{e}}\left( {{x}_{1}},{{y}_{0}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{2}}\left( {{x}_{2}} \right){{F}^{e}}\left( {{x}_{2}},{{y}_{0}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{3}}\left( {{x}_{3}} \right){{F}^{e}}\left( {{x}_{3}},{{y}_{0}} \right) \\ \end{align} $

(30)

$ \begin{align} & F_{B}^{e}\left( {{x}_{p}},{{y}_{1}} \right)={{l}_{0}}\left( {{x}_{0}} \right){{F}^{e}}\left( {{x}_{0}},{{y}_{1}} \right)+{{l}_{1}}\left( {{x}_{1}} \right){{F}^{e}}\left( {{x}_{1}},{{y}_{1}} \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{2}}\left( {{x}_{2}} \right){{F}^{e}}\left( {{x}_{2}},{{y}_{1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{3}}\left( {{x}_{3}} \right){{F}^{e}}\left( {{x}_{3}},{{y}_{1}} \right) \\ \end{align} $

(31)

$ \begin{align} & F_{C}^{e}\left( {{x}_{p}},{{y}_{2}} \right)={{l}_{0}}\left( {{x}_{0}} \right){{F}^{e}}\left( {{x}_{0}},{{y}_{2}} \right)+{{l}_{1}}\left( {{x}_{1}} \right){{F}^{e}}\left( {{x}_{1}},{{y}_{2}} \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{2}}\left( {{x}_{2}} \right){{F}^{e}}\left( {{x}_{2}},{{y}_{2}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{3}}\left( {{x}_{3}} \right){{F}^{e}}\left( {{x}_{3}},{{y}_{2}} \right) \\ \end{align} $

(32)

$ \begin{align} & F_{D}^{e}\left( {{x}_{p}},{{y}_{3}} \right)={{l}_{0}}\left( {{x}_{0}} \right){{F}^{e}}\left( {{x}_{0}},{{y}_{3}} \right)+{{l}_{1}}\left( {{x}_{1}} \right){{F}^{e}}\left( {{x}_{1}},{{y}_{3}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{2}}\left( {{x}_{2}} \right){{F}^{e}}\left( {{x}_{2}},{{y}_{3}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{3}}\left( {{x}_{3}} \right){{F}^{e}}\left( {{x}_{3}},{{y}_{3}} \right) \\ \end{align} $

(33)

根据式(30)~(33)，在纬向方向上进行插值可以得到F_E^e(x_p, y_p)，其表达式如下：

$ \begin{align} & F_{E}^{e}\left( {{x}_{p}},{{y}_{p}} \right)={{l}_{0}}\left( {{x}_{0}} \right)F_{A}^{e}\left( {{x}_{p}},{{y}_{1}} \right)+{{l}_{1}}\left( {{x}_{1}} \right)F_{A}^{e}\left( {{x}_{p}},{{y}_{1}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{2}}\left( {{x}_{2}} \right)F_{C}^{e}\left( {{x}_{p}},{{y}_{2}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ {{l}_{3}}\left( {{x}_{3}} \right)F_{D}^{e}\left( {{x}_{p}},{{y}_{3}} \right) \\ \end{align} $

(34)

式(34) 完成了阴阳网格边界处的数据交换，而对于阴阳网格中的矢量数据的交换其处理过程会有所不同，其具体参见Kageyama等(2004) 一文。通过上述的所有步骤，完成了阴阳网格边界数据交换，下面将进行相应的理想数值试验，以揭示半拉格平流方案在阴阳重叠网格中的设计效果。

3 理想数值试验

本文采用球面浅水方程最为广泛使用的刚体平流试验、变形流试验及正弦波试验，对半拉格日平流方案在球面阴阳重叠网格上的设计效果进行分析和评估。在进行数值试验前，先介绍在试验结果分析过程中用到的误差估计标准。根据Williamson等(1992) 的定义，同时兼顾阴阳网格的特殊性，定义全球积分为：

$ \begin{align} & {{I}_{yinyang}}\left( F \right)=\frac{1}{4\pi }\int\limits_{\frac{\pi }{4}}^{\frac{7\pi }{4}}{\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{4}}{{{F}^{n}}\left( \lambda ,\varphi \right)\cos {{\varphi }^{n}}\text{d}{{\varphi }^{n}}\text{d}{{\lambda }^{n}}}+} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{4\pi }\int\limits_{\frac{\pi }{4}}^{\frac{7\pi }{4}}{\int\limits_{-\frac{\pi }{4}}^{\frac{\pi }{4}}{{{F}^{e}}\left( \lambda ,\varphi \right)\cos {{\varphi }^{e}}\text{d}{{\varphi }^{e}}\text{d}{{\lambda }^{e}}}}\ \ \\ \end{align} $

(35)

全球归一化误差为：

$ {{l}_{1}}\left(F \right)=\frac{{{I}_{yinyang}}\left| F-{{F}_{T}} \right|}{{{I}_{yinyang}}\left| {{F}_{T}} \right|}$

(36)

${{l}_{2}}\left( F \right)=\frac{{{\left\{ {{I}_{yinyang}}\left[ {{\left( F-{{F}_{T}} \right)}^{2}} \right] \right\}}^{\frac{1}{2}}}}{{{\left\{ {{I}_{yinyang}}\left| F_{T}^{2} \right| \right\}}^{\frac{1}{2}}}} $

(37)

$ {{l}_{\inf }}\left(F \right)=\frac{\max \left[ \left| {{F}^{n}}\left(\lambda, \varphi \right)-F_{T}^{n}\left(\lambda, \varphi \right) \right|, \left| {{F}^{e}}\left(\lambda, \varphi \right)-F_{T}^{e}\left(\lambda, \varphi \right) \right| \right]}{\max \left[ \left| F_{T}^{n}\left(\lambda, \varphi \right) \right|, \left| F_{T}^{e}\left(\lambda, \varphi \right) \right| \right]}$

(38)

其中下标T的物理量代表平流量的解析值。根据Li等(2006) 的定义，收敛率ε的定义如下：

$ \varepsilon \left({\Delta {{x}_{2}}}/{\Delta {{x}_{1}}}\; \right)=\frac{{{\text{l}}_{\text{n}}}\left[ {E\left(\Delta {{x}_{2}} \right)}/{E\left(\Delta {{x}_{1}} \right)}\; \right]}{{{\text{l}}_{\text{n}}}\left({\Delta {{x}_{2}}}/{\Delta {{x}_{1}}}\; \right)}$

(39)

式中，Δx为网格单方向的分辨率，E为总误差，其衡量的表达式为，

$E=\frac{1}{N}\sum\limits_{N}{\left| F\left(\lambda, \varphi \right)-{{F}_{T}}\left(\lambda, \varphi \right) \right|} $

(40)

式中N为总格点数。

3.1 刚体平流试验

Williamson等(1992) 提出一个在二维无辐散风场中刚体平流试验，该试验被广泛应用于测试全球平流数值方案性能中(Hall et al，2013)。试验中由于采用无辐散风场，平流过程中“余弦钟”形状应保持不变。本文针对平流方程(11)，在定常无辐散风场下模拟平流传输问题。在经纬网格系统内，定常无辐散风场为：

$u={{u}_{0}}\left(\cos \varphi \cos\alpha +\sin\varphi \cos \lambda \sin\alpha \right)$

(41)

$v=-{{u}_{0}}\sin \lambda \sin \alpha $

(42)

式中，α为刚体旋转轴和极轴的夹角，u₀为旋转的线速度，其定义为u₀=2πa/(12×24×3600), 大概为40 m·s^-1。试验中平流量的初始分布为：

$ F\left(\lambda, \varphi \right)=\left\{ \begin{align} &0.5\left[ 1+\cos \left({\pi r}/{R}\; \right) \right], \\ &当\ r<R={a}/{3}\; \\ &0, \\ &当\ r\ge R={a}/{3}\; \\ \end{align} \right.$

(43)

式中r=acos^-1[sinφ₀sinφ+cosφ₀cosφcos(λ-λ₀)]表示(λ, φ)与“余弦钟”中心(λ₀, φ₀)的大圆距离，试验中余弦钟的中心定位在λ₀=3π/2，φ₀=0。

本次刚体平流试验，针对不同的分辨率，一共进行了三组试验，选取分辨率为0.3125°×0.3125°，0.625°×0.625°，1.25°×1.25°，相应的时间步长为1200 s、2400 s和4800 s，且所有测试均绕地球一圈。试验中的CFL条件保持不变，分别在旋转角α等于0°、45°和90°下进行，关于半拉格朗日处理的方法，比如球面上游点的确定采用的是前述的Ritchie和Beaudoin方法，阴阳网格边界数据插值交换采用的是三次拉格朗日插值方法，空间离散采用的是LE网格水平离散方式。

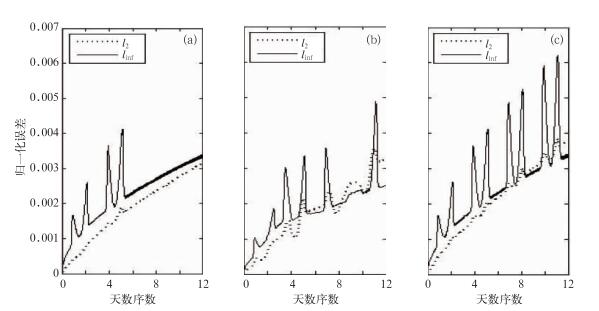
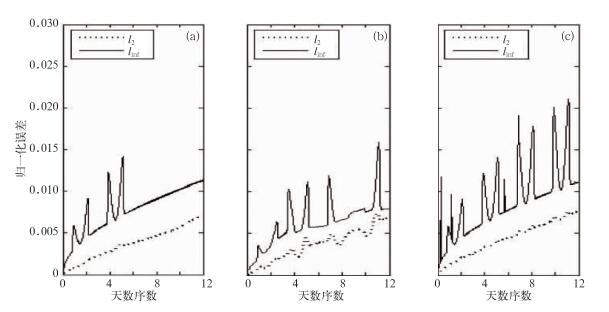
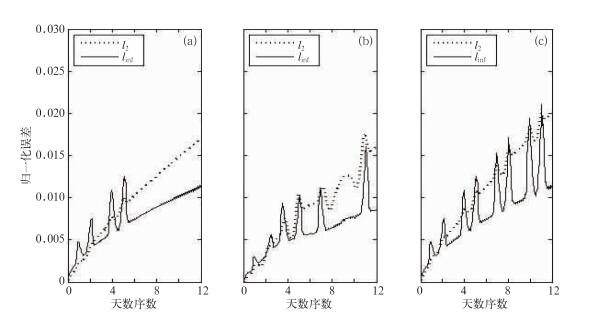
图 5给出了刚体平流试验在网格分辨率为1.25°×1.25°情形下，绕0°、45°、90°旋转下的l₂、l_inf随时间的演变图。从图可以看出，不管在何种旋转角下，l₂、l_inf的总体趋势是随着时间的积分在向上增长，且l₂、l_inf在时间演变过程中存在不同程度的脉冲状的跳跃，这主要是刚体平流在不同的旋转角度情况下通过阴阳网格的边界次数所致(这主要是因为参照式(35) 的全球积分的定义在球面阴阳网格重叠边界处积分计算了两次)。从图 5a、5b、5c通过分析不同旋转角度下l₂、l_inf的最大值，可以发现对于绕极平流其l₂、l_inf的最大值明显大于绕赤道和绕45°平流，l₂、l_inf的最大值都达到了0.0210，说明在阴阳网格平流数值模拟中，通过阴阳网格的边界次数越多，其计算的误差相应地会增大。图 6和图 7给出刚体平流试验在网格分辨率为0.625°×0.625°和0.3125°×0.3125°情形下，绕0°、45°、90°旋转下的l₂、l_inf、随时间的演变图。从图 6和图 7，可以看出随着模式分辨率的提高，l₂、l_inf随时间演变的趋势不变，都在向上增大，且针对不同的旋转角度也会出现相应程度的脉冲状跳跃。但是分析不同旋转角度下l₂、l_inf的最大值时，随着模式分辨率的提高虽然仍保持着绕极地平流大于绕赤道和绕45°平流的特点，其最大值明显小于在网格分辨率为1.25°×1.25°的情形下。对于网格分辨率为0.625°×0.625°，绕极地平流l₂、l_inf的最大值分别为0.0038和0.0062，而对于网格分辨率为0.3125°×0.3125°，绕极地平流l₂、l_inf的最大值则骤减为0.000767和0.0021。从中可以得知随着模式分辨率提高，虽然l₂、l_inf的总体变化趋势没有太大变化，但是其误差的极值随着分辨率的提高急剧下降，说明阴阳网格适合于高分辨率的数值模拟。

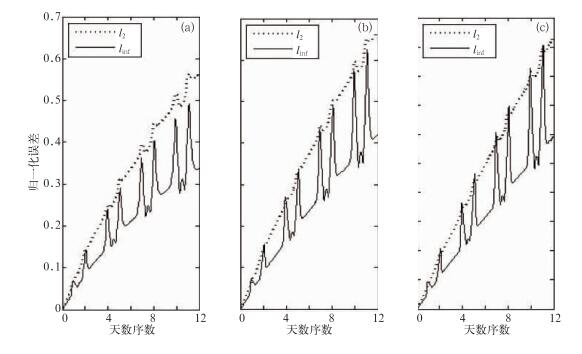
同时为了比较边界数据插值方案对数值解的敏感性，结合上述分析，仅考虑绕极地平流，图 8给出了在双线性边界数据插值方案下不同分辨率绕极地的l₂、l_inf的时间演变图，试验中其他条件和三次拉格朗日插值方案一样。从图中可知，对于绕极地平流，采用双线性插值方案l₂、l_inf的总体变化趋势和三次拉格朗日插值模拟效果一致，都在随时间演变而向上增长，且通过阴阳网格的边界时，也出现了不同程度的脉冲状跳跃。但是对双线性插值方案，其绕极地平流的l₂、l_inf的最大值明显大于采用三次拉格朗日插值。同样对于网格分辨率为1.25°×1.25°，采用三次拉格朗日插值方案，如前所述绕极地平流的l₂、l_inf的最大值都为0.0210，而采用双线性插值绕极地平流的l₂、l_inf的极值分别为0.5640和0.4910，是采用三次拉格朗日插值的26倍和23倍之多，虽然采用双线性插值方案随着模式分辨率的提高，l₂、l_inf的最大值减小，但是相对三次拉格朗日插值方案，其误差也明显偏大，说明对于半拉格朗日平流方案采用双线性插值处理阴阳网格的边界是不恰当的，边界的数据交换对插值方案非常敏感。

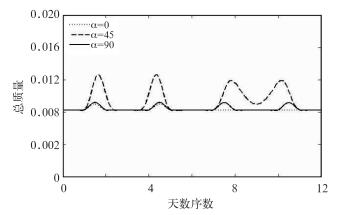
为了分析采用三次拉格朗日插值下，半拉格朗日平流方案的数值守恒性和稳定性。图 9给出网格分辨率为1.25°×1.25°下刚体平流试验中在不同旋转角度下全球总质量积分的时间系列。从图中可以可出，在不同的旋转角度下，全球总质量积分也出现了相应程度的脉冲状的跳跃，这和归一化误差的时间相似，说明对于全球总质量积分，当刚体通过阴阳网格边界时会出现质量不守恒，存在着数值突变，也进一步说明了阴阳网格的数值守恒是一个急需研究的问题。表 1给出了刚体平流试验在网格分辨率为1.25°×1.25°绕极地旋转一圈后不同CFL条件下的归一化误差，从表可知随着CFL的条件的增大，l₁、l₂、l_inf误差没有突变，误差仍保持在一定的范围之类，说明半拉格朗日平流计算方案比较稳定，有利于大时间步长的模拟。

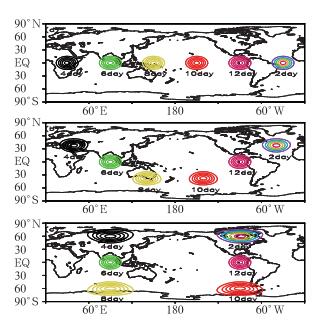
为了进一步揭示半拉格朗日平流方案模拟平流的性能及阴阳网格在数值模式的优越性，图 10描绘了刚体平流在不同分辨率、不同旋转角度情形下绕地球积分一圈后的平流量的分布情形。对于分辨率为1.25°×1.25°，刚体平流在旋转角为0°、45°和90°的情形下，绕地球积分一圈后能够准确回到出发时的位置，并保持着原来的形状，且在积分过程中当刚体平流经过阴阳网格边界的重叠区域时的形状保持不变，图中所显示的刚体平流的变形是由于采用圆柱投影造成的，相当于刚体在东西方向的拉伸，说明阴阳网格完全消除了常规经纬网格存在的坐标奇异和极区格点辐合问题，也进一步揭示了阴阳网格的重叠区处理方案是合理的。

3.2 变形流试验

变形流试验(Nair et al，2002) 是测试数值平流方案更为严格的试验，其考虑在一个平直的气流上加上变形的涡度流以测试其随时间演变情况，同时也叫球面锋生试验(Nair et al，1999)。变形流试验是Doswell(1984) 涡旋问题的一种演变，在旋转坐标系上两个对称的静止涡旋同时生成。为了方便讨论，本文考虑涡旋中心基于(π+0.025，π/2.2) 的涡度流。根据Nair等(2002) 的定义，稳定的涡度风场，切线方向速度为:

$ {{V}_{t}}=\cos {{\varphi }^{'}}\frac{\text{d}{{\lambda }^{'}}}{\text{d}t}=\frac{3\sqrt{3}}{2}\tanh \left( {{r}^{'}} \right)\sec {{h}^{2}}\left( {{r}^{'}} \right) $

(44)

式中，(λ',φ')是旋转坐标系的经纬度，r'=r₀cosφ'是距涡旋中心的距离，且r₀=3。角速度的定义为：

$ \overline{\omega }'\left( {{\varphi }^{'}} \right)=\left\{ \begin{align} & {{{V}_{l}}}/{{{r}^{'}}}\;,\ \ \ 当\ {{r}^{'}}\ne 0 \\ & 0\ \ \ \ \ \ \ \ \ \ {{r}^{'}}=0 \\ \end{align} \right. $

(45)

锋生的解析表达式为：

$ F\left( {{\lambda }^{'}},{{\varphi }^{'}},t \right)=1-\tanh \left\{ {{{r}^{'}}}/{d\times \sin \left( {{\lambda }^{'}}-{{\overline{\omega }}^{'}}t \right)}\; \right\} $

(46)

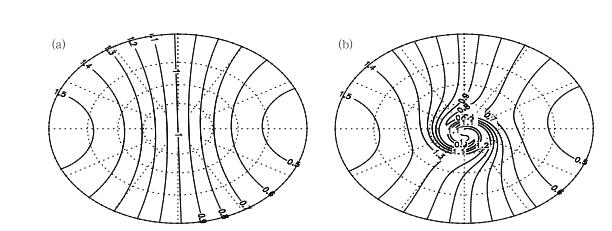
式中，d=5是平滑参数，初始值为F(λ', φ, 0)，对应图 11a。试验中条件和刚体平流试验一样，但是采用三次拉格朗日插值方案。试验中选取的分辨率为2.8125°×2.8125°，积分时间为3 s，该时刻的解析解对应图 11b。

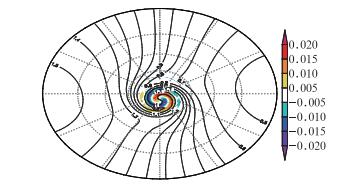
图 12描述试验积分32步后的数值结果及数值结果和解析解的差值(阴影区域表示)，从图中可以得知，在阴阳网格上采用半拉格朗日方法计算平流能较好地描述变形流的演变过程，且计算误差不大，最大最小误差分别为+0.02和-0.02，相对应Peng等(2006) 的数值误差明显偏小，也进一步说明本文采用的数值平流方案在阴阳网格上具有较好的模拟能力。

3.3 正弦波试验

正弦波试验是相对刚体平流更为平缓的试验，主要是考虑平流算法的收敛性，本文中主要为了分析采用三次拉格朗日插值方案下球面阴阳重叠网格半拉格朗日平流方案的设计的数值精度。试验中条件和刚体平流试验一样，试验中的初始场为，

$ F\left(\lambda, \varphi \right)={{F}_{\text{o}}}{{\cos }^{2}}\varphi \sin \left(k\lambda \right) $

(47)

式中，F₀为常数，k为波数。试验过程中考虑平流绕赤道和极地旋转的情况，表 2和表 3分别给出正弦波试验l₁、l₂、l_inf在不同分辨率下的大小及收敛阶数。对于绕赤道旋转，随着模式分辨率的提高，各归一化误差明显减小，通过分析各归一化的阶数，可知在阴阳网格上采用三次拉格朗日插值方案进行数据交换时，其精度能接近3阶。同时对于绕极地旋转，同样随着模式分辨率的提高，各归一化误差也明显减小，精度也能接近3阶。正弦波试验表明在阴阳网格上采用三次拉格朗日插值处理边界数据交换时具有较高的数值精度，这和Li等(2006) 基于Arakawa-C网格设计的阴阳网格的数值平流方案计算精度相当。

4 结论和讨论

为了模拟球面平流传输过程，本文基于球面阴阳重叠网格上设计了一种两时间层半拉格朗日平流方案。该方案在球面坐标下采用新型的LE水平跳点网格，同时针对阴阳网格重叠区，采用了不同插值方法进行比较分析，且进行了相关的理想数值试验对方案设计效果进行评估。

刚体平流试验表明：(1) 在球面阴阳网格上实施半拉格朗日积分方案处理平流时，当刚体平流通过阴阳网格边界时会出现脉冲状的跳跃，且绕极地平流的误差大于绕赤道和绕45°平流，随着模式分辨率的提高，数值误差明显减小，说明阴阳网格适合高分辨率的数值模拟；(2) 刚体平流数值解对于边界插值方案比较敏感，试验中当采用双线性边界插值时误差会成倍的增大；(3) 在球面阴阳网格上采用三次拉格朗日插值方案下对半拉格朗日平流方案的数值守恒性和稳定性分析得知，刚体平流通过阴阳网格边界时全球总质量积分会出现脉冲状跳跃，表明该方案不能有效的保证全球的质量守恒，但是对于CFL的条件数值模拟得知该方案具有较好的稳定性；(4) 对刚体平流绕地球积分一圈后平流量的分布情况分析得知，刚体平流能很好保持着初始时刻形状回到出发点，说明阴阳网格的重叠区处理方案是合理的。

变形流试验表明：在球面阴阳网格上采用半拉格朗日方案处理平流能较好地给出变形涡旋的结构、位置和演变过程，且数值误差相对较小。

正弦波试验表明：在球面阴阳网格上采用三次拉格朗日插值处理边界数据交换时具有较高的数值精度。

阴阳网格是重叠网格，网格重叠处的数据交换一直是比较棘手的问题，特别是对于矢量场。如果在阴阳网格边界重叠处没有很好地处理风场，气流通过边界时会造成紊乱，会影响风场的预报效果，因此阴阳网格重叠区守恒格式构造也是个值得关注的问题，特别是采用半拉格朗日平流方案后阴阳网格重叠区的守恒问题及上游点的精确确定问题，还有待于后续文章进一步阐明。