引言

数值天气预报(NWP)中心通常使用一种观测资料和短期预报结果统计结合的方法来产生初值，这就是我们所说的“资料同化”(卡莱尼，2005；邹晓蕾，2009；朱国富，2015)。观测资料的一个重要来源是极轨卫星大气探测资料(张兴海等，2014)，但是极轨卫星大气探测资料不是完美的，它们通常是有误差的。误差产生的原因非常多，比如：辐射传输模式本身的误差；辐射传输模式的基础光谱数据以及输入数据(温度廓线、湿度廓线、臭氧总量等)的误差。此外，仪器的灵敏度、定标、云污染等的影响，传感器的响应特性的改变，也将造成观测数据的系统偏差。这些偏差的存在限制了对卫星观测资料的利用，甚至有些资料根本没有办法被利用。除非误差可以控制和订正到一定范围内，否则如果将卫星观测资料应用于数值天气预报模式，那么这些系统观测偏差会破坏数据同化，并且最终影响预报的质量。因此，我们需要对偏差进行有效的订正。

目前为止，世界各国的数值预报中心应用的偏差订正方法主要经历了传统的静态偏差订正方法与比较先进的动态偏差订正方法，动态偏差订正方法又分为变分偏差订正与偏差订正的动态更新技术两种。

关于静态偏差订正方法，ECMWF最初采用了全球平均扫描订正和以微波探测通道2、3、4的观测辐射率为预报因子的线性气团订正(McMillin et al，1989); 而Eyre(1992)引用了云辐射对此方案进行了调整，但本质上没有改变。Harris等(2001)提出的方案，使得辐射偏差订正有了本质的突破性的进展。一方面，他们发现对于某些通道，特别是微波通道的辐射率数据，扫描偏差具有一定的纬度依赖性。于是，新方案在偏差订正中考虑了扫描偏差的纬度依赖性。另一方面，他们发现使用模式背景信息，而不是MSU微波通道信息，更能反映出气团和地表性质，所以应用来自背景场的“气团”预报因子进行气团订正更为合理。对于这种方法，国内也有许多学者进行了深入的研究和探索，其中突出的是刘志权等(2007)针对ATOVS(Advanced TIROS-N Operational Vertical Sounder)微波辐射率资料提出的偏差订正方案。该方案在ECMWF原全球TOVS辐射偏差订正方案基础上，结合ATOVS资料特征和中国的实际情况，建立了适用于区域NOAA-15/16/17极轨气象卫星ATOVS辐射资料的偏差订正方案。

目前GRAPES中采用的偏差订正方法还是传统的静态偏差订正方法，这种方法属于统计方法，其实质是一种数据分析方法, 在积累了大量数据的基础上, 总结出一定的统计规律, 运用这些统计规律来预报未来。这个方程是以历史资料为样本建立的, 它包含着探测仪器的特性及大气运动的历史演变联系或规律, 但并不一定包含最新的大气运动信息、仪器老化、观测定标等影响，而存在于历史资料中的这种联系或规律, 未来并不一定能保持, 所以统计方法常常为此所窘。为了能够解决上述问题，国外在NWP系统中对卫星数据提出了动态的偏差订正方法(Auligné et al, 2007; Dee et al, 1998; McNally et al, 2006)。动态方法减少了对手动调整程序的需要，并且在分析过程中不断加入新的观测资料。它对一些通道可能出现的漂移会做出补偿，同时也能处理未预期到的事件带来的突变。

变分偏差订正(Dee, 2004)与变分分析同步进行，即在极小化迭代过程中直接对模式状态变量和控制参数同时进行调整。但由于变分偏差订正需要其他观测资料和较为准确的预报模式的配合，而中国目前可用的观测资料有限，特别是在模式高层，其他观测资料很少，此外预报模式在高层偏差很大，所以相当长的一段时间内变分偏差订正技术在中国不适用。

偏差订正动态更新技术与Harris和Kelly方案采用相同的偏差模型。该方案不但可以在每次同化分析前不断地更新控制参数，而且可以自动地感应到给定传感器下特定通道的偏差的变化，并作出相应的订正。这样可以更好地解决上述问题，使分析更为准确，提高NWP的效果。

1 偏差订正方法

三维变分同化方法的基本思想是将资料同化归结为一个表征分析场与观测场、分析场与背景场偏差的二次泛函极小值问题。该泛函一般定义为：

$ \begin{align} & \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{x}})=\frac{1}{2}{{\left( \mathit{\boldsymbol{x}}-{{\mathit{\boldsymbol{x}}}_{b}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{B}}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}}-{{\mathit{\boldsymbol{x}}}_{\mathit{b}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}{{\left[ \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{x}} \right)-{{\mathit{\boldsymbol{y}}}_{\rm{0}}} \right]}^{\rm{T}}}{{\mathit{\boldsymbol{R}}}^{\rm{-1}}}\left[ \mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{x}} \right)-{{\mathit{\boldsymbol{y}}}_{\rm{0}}} \right] \\ \end{align} $

(1)

其增量形式为：

$ \begin{align} & \mathit{\boldsymbol{J}}(\delta \mathit{x})=\frac{1}{2}\delta {{\mathit{x}}^{\rm{T}}}{{\mathit{\boldsymbol{B}}}^{\rm{-1}}}\delta x+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}{{\left(\mathit{\boldsymbol{{H}'}}\delta x+\mathit{d} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{R}}}^{\rm{-1}}}\left(\mathit{{H}'}\delta x+d \right) \\ \end{align} $

(2)

式中，δx=x-x_b, d= H(x_b)-y₀，x_b是背景场向量(来自数值预报模式的短期预报，一般也作为迭代的初估场)；y是观测向量，包括常规和卫星等所有类型的观测资料；x是控制向量，即要求解的温度、湿度和风等模式参数向量；B是背景场误差协方差矩阵；R是观测和向前模式误差协方差矩阵；H是观测算子，它变换控制向量x到观测向量x, H′=$\triangledown $H为切线性观测算子。

变分同化理论基本假定是背景x_b，y及观测算子H的误差满足高斯分布并且是无偏的。一般而言，由于仪器定标、预处理，以及向前模式中的误差，这种无偏的假定并不成立，所以需要对系统偏差进行订正。

1.1 静态方法——Harris和Kelly的方法

偏差订正动态更新技术是在传统静态偏差订正技术(Harris et al，2001)的基础上展开的。订正方案分为两步。

1.1.1 扫描偏差订正

对于每个通道，利用扫描角信息计算每个扫描位置相对于中心位置的全球或区域平均差：

$ {{\mathit{d}}_{\mathit{j}}}\left(\theta \right)={{{\mathit{\bar{R}}}}_{\mathit{j}}}\left(\theta \right)-{{{\mathit{\bar{R}}}}_{\mathit{j}}}\left(\theta =0 \right) $

(3)

式中，R是平均观测辐射率，d是观测残差，θ是扫描角，j是扫描位置。同时，将偏差对于纬度的依赖性纳入考虑，将地球分成18个纬度带，每个纬度带10°，计算每个扫描位置和每个纬度带平均值，然后利用它们计算扫描订正系数：

$ {{d}_{j}}\left(\phi, \theta \right)={{{\bar{R}}}_{j}}\left(\phi, \theta \right)-{{{\bar{R}}}_{j}}\left(\phi, \theta =0 \right) $

(4)

式中ϕ是纬度带。为避免纬度带之间扫描偏差订正不连续，在跨纬度带地区采用平滑技术产生连续订正系数。平滑扫描订正系数计算方法：

$ \begin{align} & {{{{d}'}}_{j}}\left(\phi, \theta \right)=\frac{1}{4}{{d}_{j}}\left(\phi -1, \theta \right)+\frac{1}{2}{{d}_{j}}\left(\phi, \theta \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{4}{{d}_{j}}\left(\phi +1, \theta \right) \\ \end{align} $

(5)

这样，扫描偏差订正系数d′_j(ϕ, θ)就计算出来了。若单纯想消除因扫描位置的变化而引起的相对误差，则将其代入下式便得到经过扫描偏差订正的观测残差：

$ {{{{R}'}}_{j}}\left(\phi, \theta \right)={{R}_{j}}\left(\phi, \theta \right)-{{{{d}'}}_{j}}\left(\phi, \theta \right) $

(6)

1.1.2 气团偏差订正

气团偏差订正方案使用一组偏差预报因子X_i(i=1, 2, …, n)来与气团偏差相联系，利用下面的线性方程计算每个通道j的气团偏差：

$ {{B}_{j}}=\sum\limits_{i=1}^{n}{{{\mathit{A}}_{\mathit{ji}}}}{{\mathit{X}}_{\mathit{i}}}+{{\mathit{C}}_{\mathit{j}}} $

(7)

式中，系数A_ji和C_j是利用大样本(通常两周的数据)通过最小二乘法拟合计算的。系数可以由下式给出：

$ {{A}_{ji}}=\sum\limits_{k=1}^{n}{\left\langle \left. {{\mathit{D}}_{\mathit{j}}}, {{\mathit{X}}_{\mathit{k}}} \right\rangle \right.\cdot \left[ \left\langle \left. \mathit{\boldsymbol{X}}, \mathit{\boldsymbol{X}} \right\rangle \right. \right]_{ki}^{-1}} $

(8)

式中，$ \left\langle \left. \ldots, \ldots \right\rangle \right.$表示协方差，X是X_k的向量，D_j是通道j的偏差：

$ {{\mathit{D}}_{\mathit{j}}}={{\left[ y-\mathit{\boldsymbol{H}}\left(\mathit{x} \right) \right]}_{j}} $

(9)

1.1.3 预报因子的选择

气团偏差订正关键是预报因子的选择。对于不同的传感器和不同的通道，偏差是不同的。所以，根据仪器和通道的不同，预报因子的选择是有弹性的。GRAPES中用模式背景场作为预报因子，能够更好地消除辐射传输模式所带来的系统偏差，并且可以在同化方案中考虑偏差订正的梯度。本研究仍采用现GRAPES模式中使用的预报因子：模式初始场厚度(1000~300 hPa)，模式初始场厚度(200~50 hPa)。

1.2 偏差订正的动态更新技术

由于偏差不仅来自于观测，还来源于观测算子。所以在偏差订正动态更新技术中，定义了修改后的观测算子：

$ \mathit{\boldsymbol{\tilde{H}}}\left( \mathit{\boldsymbol{x}},\beta \right)=\mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{x}} \right)+\mathit{\boldsymbol{f}}\left( \beta \right) $

(10)

式中，$\mathit{\boldsymbol{f}}\left(\beta \right)=\sum\limits_{i=0}^{N}{{{\beta }_{i}}{{\mathit{p}}_{\mathit{i}}}\left(\mathit{\boldsymbol{x}} \right)} $。订正后的观测算子可以满足无偏的假定，模式偏差参数β是预报因子p的系数，x是模式状态向量，N是预报因子的个数。

目标函数定义为：参数背景误差协方差的逆矩阵所加权的参数β与参数初估值β_b的距离，加上被观测误差协方差的逆矩阵所加权的x与观测y_o的距离，所谓偏差订正的动态更新就是在每一次分析循环之前，调整β使得相应目标函数：

$ \begin{align} & \mathit{\boldsymbol{J}}(\beta )=\frac{1}{2}{{\left( \beta -{{\beta }_{\mathit{h}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}_{\beta }^{-1}\left( \beta -{{\beta }_{\mathit{b}}} \right)+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}{{\left[ \mathit{\boldsymbol{\tilde{H}}}\left( {{\mathit{x}}_{\mathit{b}}},\beta \right)-{{\mathit{y}}_{\mathit{o}}} \right]}^{\rm{T}}}{{\mathit{\boldsymbol{R}}}^{\rm{-1}}}\left[ \mathit{\boldsymbol{\tilde{H}}}\left( {{x}_{b}},\beta \right)-{{y}_{\mathit{o}}} \right] \\ \end{align} $

(11)

达到极小。其中R代表了观测误差协方差矩阵。B_β代表偏差参数背景误差协方差矩阵。在偏差订正动态更新中，β的更新需要使用前一次分析循环得到的偏差参数β_b作为初估值，然后把更新的β应用于订正数据。

1.3 增量分析

为了能够减少计算量，节省机时，我们采用增量分析的方法。

由泰勒公式可得：

$ \mathit{\boldsymbol{f}}(\beta)=\mathit{\boldsymbol{f}}\left({{\beta }_{b}}+\delta \beta \right)\approx \mathit{\boldsymbol{f}}\left({{\beta }_{\mathit{b}}} \right)+\mathit{\boldsymbol{F}}\delta \beta $

(12)

其中

$ \mathit{\boldsymbol{F=}}\frac{\partial \mathit{\boldsymbol{f}}}{\partial \beta }, \ \ \ \delta \beta =\beta -{{\beta }_{b}} $

(13)

则有，

$ \begin{align} & \mathit{\boldsymbol{\tilde{H}}}\left( x,\beta \right)-{{y}_{\mathit{o}}}=\mathit{\boldsymbol{H}}\left( {{x}_{b}} \right)+\mathit{\boldsymbol{f}}\left( \beta \right)-{{y}_{\mathit{o}}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\mathit{\boldsymbol{H}}\left( {{x}_{b}} \right)+\mathit{\boldsymbol{f}}\left( {{\beta }_{b}} \right)+\mathit{\boldsymbol{F}}\delta \beta -{{y}_{\mathit{o}}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =d+\mathit{\boldsymbol{f}}\left( {{\beta }_{b}} \right)+\mathit{\boldsymbol{F}}\delta \beta \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={d}'+\mathit{\boldsymbol{F}}\delta \beta \\ \end{align} $

(14)

式中，

$ d=\mathit{\boldsymbol{H}}\left( {{x}_{b}} \right)-{{y}_{\mathit{o}}},\ \ {d}'=d+\mathit{\boldsymbol{f}}\left( {{\beta }_{b}} \right) $

(15)

利用上述变换，对之前给出的目标函数进行变形可得：

$ \begin{align} & \mathit{\boldsymbol{J}}(\delta \beta)=\frac{1}{2}\delta {{\beta }^{\rm{T}}}\mathit{\boldsymbol{B}}_{\beta }^{-1}\delta \beta + \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}{{\left[ \mathit{{d}'}+\mathit{\boldsymbol{F}}\delta \beta \right]}^{\rm{T}}}{{\mathit{\boldsymbol{R}}}^{\rm{-1}}}\left[ \mathit{{d}'}+\mathit{\boldsymbol{F}}\delta \beta \right] \\ \end{align} $

(16)

可求得：

$ {{\triangledown }_{\delta \beta }}\mathit{\boldsymbol{J=B}}_{\beta }^{-1}\delta \beta +{{\mathit{\boldsymbol{F}}}^{\mathit{T}}}{{\mathit{\boldsymbol{R}}}^{\rm{-1}}}\left(\mathit{{d}'}+\mathit{\boldsymbol{F}}\delta \beta \right) $

(17)

其二阶导数(Hessian矩阵)为：

$ \triangledown _{\delta x}^{2}\mathit{\boldsymbol{J=B}}_{\beta }^{-1}+{{\mathit{\boldsymbol{F}}}^{\mathit{T}}}{{\mathit{\boldsymbol{R}}}^{\rm{-1}}}\mathit{\boldsymbol{F}} $

(18)

令B_β为对角矩阵：

$ \begin{align} & \ \ {{\mathit{\boldsymbol{B}}}_{\beta }}=diag\left( {{\sigma }_{\beta 1}}, \cdots , {{\sigma }_{\beta n}} \right), \\ & {{\sigma }_{\beta i}}=\sigma _{oj}^{2}/{{N}_{j}},j\rm{=1},\cdots ,\mathit{n} \\ \end{align} $

(19)

式中，β_j表示第j个偏差参数，N_j是给定通道的观测值数目，每一个通道对应的总方差为σ_oj²。当N_j充分大的时候(比如，N_j≫100)，忽略参数背景误差协方差矩阵非对角线元素的影响就可以忽略不计的。这是因为O(N_j)观测值只用来估计几个偏差参数，即使估计是次优的，估计的误差也很小。所以我们可以令B_β为对角矩阵。

在现有GRAPES偏差订正及质量控制的基础上，由极小化迭代求得δβ，由β=β_b+δβ可得β。

2 试验方案 2.1 数据选择

本文研究偏差订正的主要目的是消除卫星测量辐射值和根据NWP模式背景场和前向辐射传输模式计算的辐射值之间的相对系统偏差，改善数据漂移的问题，使其可以直接应用于NWP变分同化模式中。为此，模式背景场选择GRAPES模式的6 h预报场，前向辐射传输模式采用目前国际上应用最广的RTTOV-7。卫星辐射资料采用经过预处理的NOAA18-AMSUA微波温度计资料。

2.2 质量控制

为了保证历史样本资料的有效性，必须在利用数据计算系数之前，对它们进行如下质量控制：

(1) 极值检验:如果任何一个预报因子通道的亮温超出给定极限(150~350 K)或任何亮温偏差超出给定极限(-20~+20 K)，则所有通道数据被丢弃。

(2) 云检测:尽管AMSU有穿透云层探测大气温度和湿度的能力，但是在降水云中水滴和冰晶比辐射波长要大，就会减弱云层以下的信号。这就会影响探测的结果，所以必须要检测降水云的存在。

(3) 偏差检验:使用阈值检验，如果辐射亮温数据不能满足|y_bi-y_oi|≤kσ₀则被剔除。其中y_bi和y_oi分别是通道的背景场和观测的真实值。σ₀是辐射亮温的矩阵，k为参数。

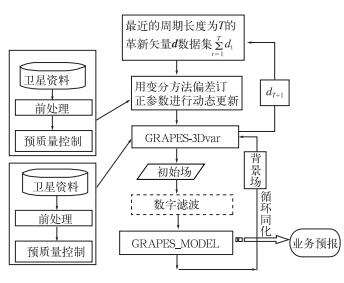
2.3 业务流程

图 1给出了偏差订正动态更新技术在GRAPES模式中的实现流程。首先要收集一定周期长度(本文为5月1—10日共10天的数据)的最近的革新矢量d进行偏差订正参数的动态更新，其中，质量控制是关键。然后，更新后的系数与背景场一起输入GRAPES三维变分系统，进行变分。同时，GRAPES三维变分系统会产生一个新的d_T+1, 与本次循环前的T-1个d组成新数据集，作为下一次偏差订正参数动态更新的样本资料。

2.4 影响试验

计划用NOAA18-AMSUA辐射率进行动态更新试验，试验周期为5月11日到6月30日，作者由于缺乏具有漂移特性的数据，为了检验偏差订正动态更新方案的有效性，就对原GRAPES偏差订正模式预报因子的系数进行扰动，使其订正效果变差从而构造一个退化的偏差订正方程，人为地构造观测数据漂移现象，即

$ {{\beta }_{i}}={{\beta }_{bi}}\left(1+{{\alpha }_{i}} \right) $

(20)

式中，β_i是预报因子p经过扰动后的系数，β_bi为预报因子p的原系数，α_i为(0，1) 范围内的随机扰动。

利用上述方案进行偏差订正的动态更新，进行逐步优化，看其能否恢复甚至超过原局部最优的方程。我们进行两个试验：

控制试验：偏差订正方程采用静态的、上述人为退化的偏差订正方程，观测资料包括常规观测及卫星NOAA18-AMSUA辐射率观测资料。

动态更新试验：观测资料与控制试验相同，偏差订正采用动态更新方案。

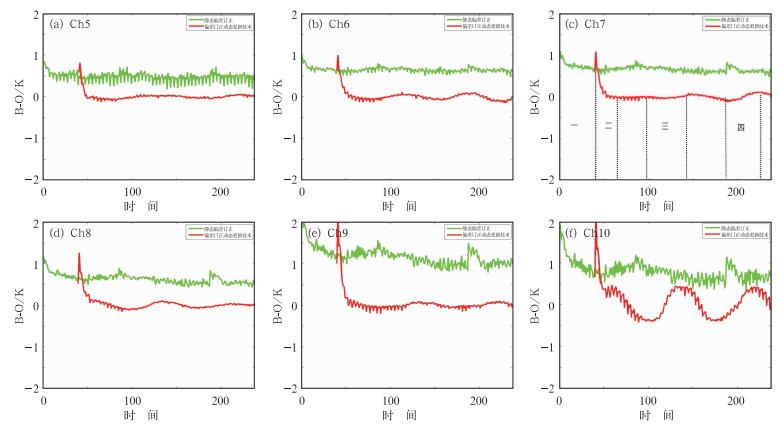
3 结果分析与评价 3.1 与静态偏差订正效果的比较 3.1.1 订正效果稳定性分析

图 2给出了采用静态偏差订正(5月1日至6月30日)与偏差订正动态更新技术(5月11日至6月30日)后偏差的时间序列图。每天要进行4次循环同化，分别为00、06、12和18时，每天的12时更新预报因子的系数。横坐标时间以每次的循环同化作为单位坐标。静态偏差订正前10天为偏差订正的动态更新技术提供了样本资料。从图中可以看出，静态偏差订正后平均观测残差还是很大，出现数据漂移现象，而采用偏差订正动态更新技术订正后，刚开始的平均观测残差会变大，但经过短暂的调整期(5月11—16日)后平均观测残差会稳定在0附近，并且随着时间演变表现比较稳定。虽然通道10的平均观测残差随时间的变化会有小幅度的波动，但总体来说平均观测残差变小。

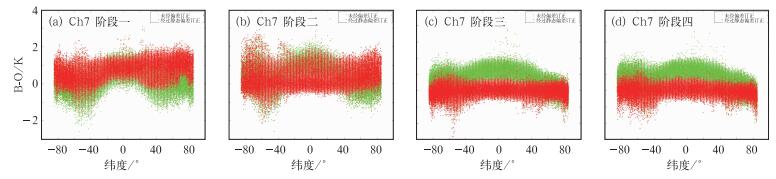
以通道7为例，图 3给出了阶段一(图 3a)(未更新期，5月1—10日)、阶段二(图 3b)(偏差订正动态更新技术调整期，5月11—16日)、阶段三(图 3c)(稳定期, 5月25日至6月5日)以及阶段四(图 3d)(稳定期，6月15—25日)四个阶段偏差随纬度变化的图。由图可以看出阶段一数据存在系统性误差，阶段二即偏差订正动态更新技术调整期比阶段一有所好转，系统性偏差减小，但仍然比较发散，而经过一段时间的动态更新之后，结果趋于稳定，发散性明显减小，并且偏差保持在0附近。左下与右下两幅图基本相似，所以我们无论选取哪一段时间的数据与静态偏差订正效果作对比，对结论都不会有很大影响。

3.1.2 全球偏差及订正效果

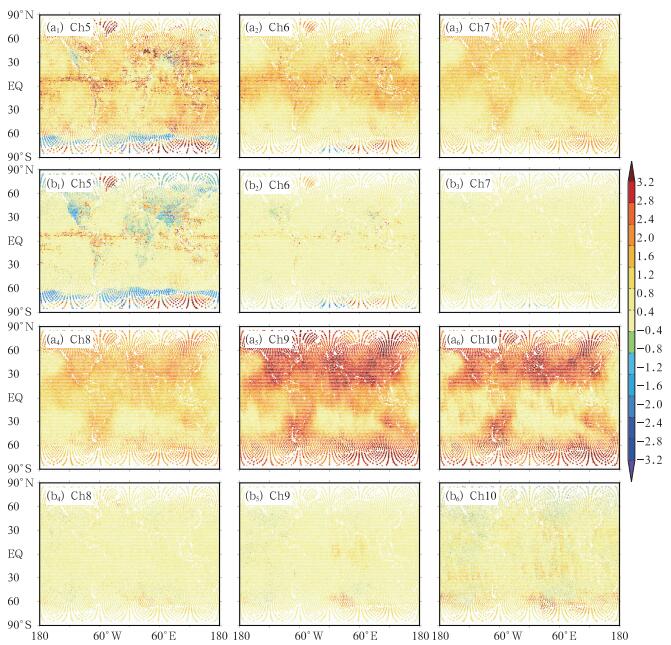
图 4给出了这16天分别采用静态偏差订正(图 4a)和偏差订正动态更新技术(图 4b)后通道偏差的比较。由图可知，采用静态偏差订正后，通道5、6的热带和高纬度地区偏差仍很大，通道7、8北半球偏差仍未被订正过来，而通道9、10效果最差，北半球与南半球高纬偏差都很大。而采用偏差订正动态更新技术订正后，系统性偏差显著减小。其中通道5除了在高纬和赤道附近仍有部分残余偏差外，总体上来看，即从全球分布来看，新方案是有效的。通道6热带地区偏差减小；通道7、8北半球偏差被订正过来了；通道9、10南半球高纬附近有极少数资料订正效果不好，但比起静态偏差订正效果仍改进明显。总体来说，采用偏差订正动态更新技术之后样本偏差明显变小，并且效果随高度增加越来越显著。

3.1.3 偏差概率密度函数

图 5给出了未经偏差订正的数据(蓝色)以及采用静态偏差订正(绿色)与偏差订正的动态更新技术(红色)订正后的概率密度函数图。峰值越接近零说明背景减去观测的残差越接近无偏。可以看到，采用静态偏差订正后的观测残差计数的峰值全都不在零附近，存在系统性偏差，而通道7、8、9、10，订正后的效果甚至还不如未订正的数据效果好。而经偏差订正动态更新技术订正后，不仅使得观测残差计数的峰值全都在零附近，而且相比于静态偏差订正，偏差的分布更集中，更接近高斯型，尤其是对于通道7、8、9、10，订正效果更为明显。

3.1.4 同化效果分析

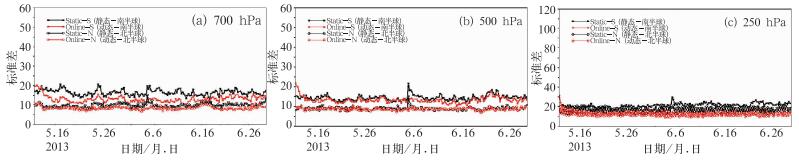
图 6为位势高度均方根误差分析图。同化结果的误差以NCEP分析作为标准来统计。我们选择了700、500与250 hPa三层来分析同化效果。由图可以看出，偏差订正的动态更新刚开始时有一个偏差下降的过程，也就是上文说的调整期。与静态偏差订正效果相比，偏差订正的动态更新技术不论在南半球还是北半球都有改进，不仅在低层的700 hPa有明显的改进，而且在500以及250 hPa的改进效果也是相当明显。所以偏差订正的动态更新技术的订正效果整体优于静态偏差订正的效果，并且南半球的整体改进效果要优于北半球。

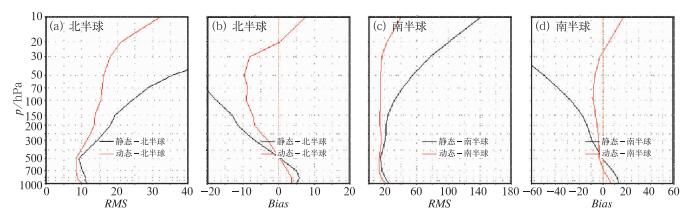
图 7为位势高度廓线的偏差与均方根误差分析图。通过比较廓线图我们可以知道，采用偏差订正动态更新技术后，虽然仍有一定的误差，但相比于静态偏差订正的廓线图分析结果改进明显，能够起到积极的作用。

3.2 与局部最优偏差订正效果的比较

原GRAPES模式偏差订正预报因子的系数是由5月上旬共10天资料获得的统计样本，采用最小二乘法计算出来的，所以在5—6月我们可以把原偏差订正模式看做是局部最优的。

将采用偏差订正动态更新技术后获得的数据与偏差系数扰动前的数据作比较，看看能否达到甚至超过原偏差订正模式即局部最优效果。

3.2.1 订正效果分析

使用经过调整期后5月16日到6月30日的数据，可以从时间序列图(图略)看出动态更新方案达到甚至超过原偏差订正模式，偏差订正的动态更新方案通道5至通道9订正结果比最优偏差订正更接近零，动态更新技术是比较稳定的；概率密度函数分析图(图略)表明，动态更新技术的订正效果与最优偏差订正的效果在通道5、6、7、8是差不多，而在通道9、10，动态更新技术订正效果比最优偏差订正的效果还要好一些。

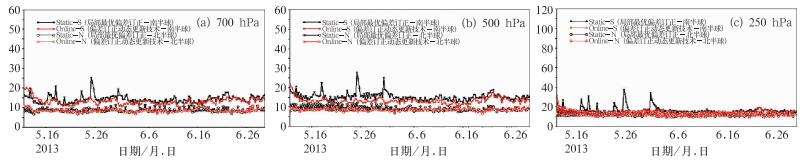
3.2.2 同化效果分析

图 8为采用偏差订正动态更新技术(红色)以及最优偏差订正(黑色)后，位势高度均方根误差分析图。由图我们可以看出，与局部最优偏差订正效果相比，新方案对位势高度场，在中低层，南半球偏差订正的动态更新效果要略好一些，在高层与北半球，两者相差不大。

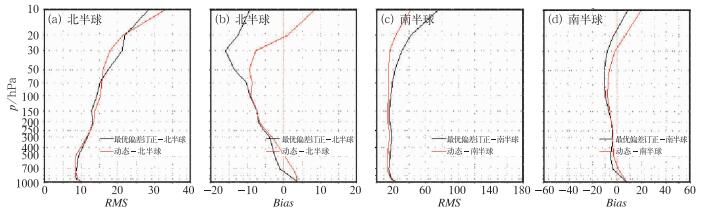
图 9为位势高度廓线的均方根误差与偏差分析图。通过比较廓线图可以知道，相比于最优偏差订正，除了高层外，南北半球都优于局部最优偏差订正的效果。综上所述，可以说偏差订正的动态更新技术达到甚至某些地区超过了最优偏差订正的效果。

4 结论和讨论

本文在Harris和Kelly的TOVS辐射偏差订正方案以及国外NWP系统中对卫星数据提出的偏差订正动态更新概念的基础上，结合GRAPES系统和国家卫星气象中心的卫星预处理系统的特点以及仪器特征，提出了GRAPES偏差订正动态更新方案，解决了数据的漂移问题。在确定准备使用的背景场和卫星辐射资料之后，偏差订正分三步进行：第一步，收集适当周期长度的卫星观测偏差数据；第二步，在同化分析之前，利用变分方法对偏差订正系数进行动态更新；第三步，对当前观测数据进行订正，实现同化分析。从试验结果来看，比起静态偏差订正，动态更新方案可以自动、迅速地优化已经退化的偏差订正方程，并且保持偏差订正的效果，运行稳定，达到了期待的效果。

需要说明的是，此方案只是初步的尝试，今后还有很多工作。第一，通道10的偏差有小幅度的波动，未来还可以考虑怎样进行改进；第二，本文只对预报因子的系数进行了动态更新，扫描偏差仍然是在分析之前完成，日后还可以考虑同时对扫描角系数进行动态更新；第三，本文的预报因子采用的是GRAPES模式原有的预报因子，下一步希望能够根据偏差订正动态更新技术的特点，重新选取预报因子，进行偏差订正。