2. 大连市气象服务中心,大连 116001;
3. 大连市气象台,大连 116001
2. Dalian Meteorological Service Centre of Liaoning, Dalian 116001;
3. Dalian Meteorological Observatory of Liaoning, Dalian 116001
冰雹是一种直径大于0.5 cm的冰相降水粒子,多数为椭圆形、球形和锥形,在强对流云体中上部的上升气流中反复增长形成冰雹,最后在降落过程中穿过0℃层高度后部分融化。盛夏高温时随着0℃层高度的增加,冰雹直径在下落过程中受热融化的影响增大,对于相同的雷达回波指标,在春秋季节可以出现冰雹,而在盛夏季节往往只有强降水。许焕斌等(2004)、段英(2009)、李大山(2002)的统计表明:我国降雹主要出现在西北、东北、华北、西南,尤其是山区,雹块直径一般在0.5~2 cm,也出现过直径大于15 cm的降雹,但这样大的雹块少见。当雹块直径较小时,依然可以对农作物产生较大损坏,如苹果被小雹击伤后无法长时间保存,烟叶受雹击后会造成经济很大损失等。
雷雨顺等(1978)对冰雹天气进行过系统深入的研究,国内外科学家在应用雷达识别冰雹云方面做了大量的工作,Mather等(1976)、樊鹏等(2005)、段鹤等(2014)和王秀玲等(2012)讨论了45 dBz高度、0℃层高度与地面降雹之间的关系。目前对于冰雹半径的预报方法较少,其中WSR-88D的增强HDA算法(Arthur et al, 1998)中开发了基于反射率因子的算法,是在垂直累积液态水(VIL)算法(Eric et al, 1998)成功的基础上设计的(俞小鼎等,2000)。该算法在预测强冰雹方面效果较好,但由于只考虑了冰雹在冻结层以上的形成过程,而没有很好考虑冰雹下降到冻结层之下的融化过程,邵玲玲等(2006)、朱君鉴等(2004)、王瑾等(2011)的研究表明增强HDA算法容易产生虚报或高估。一些地区根据当地历史资料统计,通过提高雷达回波强度参数的阈值等方法降低误差。
大连市气象局2002年安装了CINRAD/SA雷达,使用过程中发现也存在冰雹预警的虚警率偏高现象。在大连防雹作业指挥系统中尝试根据增强HDA算法和探空资料计算一项自动实时输出的冰雹尺寸估算的产品,为冰雹预警和防雹作业提供辅助参考和订正依据。为降低融化作用的影响,本文尝试分析0℃层高度与对冰雹尺寸变化的关系,尽管冰雹融化过程比较复杂,徐家骝(1979)、黄美元(1980)的研究表明冰雹融化能力与0℃层高度关联性较大,本文通过建立理想状态下0℃层高度、0℃层冰雹半径和地面冰雹半径之间的近似关系可以根据探空资料得到一种降低融化作用对增强HDA算法影响的简单方法。
1 计算方法和结果分析 1.1 计算方法徐家骝(1979)在《冰雹微物理与成雹机制》一文中对冰雹融化过程的微物理机制进行了详细的研究,本文尝试在此基础上通过简化计算,讨论0℃层高度、0℃层冰雹半径和地面冰雹半径之间的近似关系。
假设冰雹在理想热力环境和低速状态下从0℃层下落过程中融化所需的热量
若0℃层高度为h0、大气压
| $ c{\rm{d}}m = - [1.68k{\left({\frac{v}{\eta }} \right)^{0.5}}{D^{\frac{3}{2}}}({t_d} - {t_a}) + \frac{{{C_1}{D_w}}}{T}{\left({\frac{v}{\eta }} \right)^{0.5}}{D^{\frac{3}{2}}}({e_{sh}} - {e_{sv}})]\theta \frac{{{\rm{d}}h}}{v} $ | (1) |
| $ v = 204\sqrt r $ | (2) |
式中,
| $ \begin{array}{l} \int_{{r_g}}^{{r_0}} {{r^{3/4}}{\rm{d}}r} = \int_0^{{h_0}} {{K_{cc}}\frac{{k({h_0} - h)}}{{\sqrt \eta }}{\rm{d}}h} + \int_0^{{h_{\rm{0}}}} {{K_{es}}} \cdot \\ \;\;\;\frac{{k{p_g}({e_{sh}} - {e_{sv}})}}{{pT\sqrt \eta }}{(\frac{{273.15 + \gamma ({h_0} - h)}}{{273.15}})^{\frac{3}{2}}}{\rm{d}}h \end{array} $ | (3) |
或
| $ \begin{array}{*{35}{l}} \int_{{{r}_{g}}}^{{{r}_{0}}}{{{r}^{3/4}}\text{d}r}=\int_{0}^{{{h}_{0}}}{{{K}_{cc}}\frac{k({{h}_{0}}-h)}{\sqrt{\eta }}\text{d}h}+\int_{0}^{{{h}_{\text{0}}}}{{{K}_{es}}} \\ \ \ \ \frac{6.11k\left\{ \exp \left[ \frac{17.62\gamma ({{h}_{0}}-h)}{243.12+\gamma ({{h}_{0}}-h)} \right]-1 \right\}{{\left[ 273.15+\gamma ({{h}_{0}}-h) \right]}^{\frac{1}{2}}}}{{{273.15}^{\frac{3}{2}}}\sqrt{\eta }{{(\frac{273.15+\gamma ({{h}_{0}}-h)}{273.15+\gamma {{h}_{0}}})}^{\frac{g}{{{R}_{d}}\gamma }}}}\text{d}h \\ \end{array} $ |
式中,
| $ {r_0}^{\frac{7}{4}} - {r_g}^{\frac{7}{4}} = f({h_0}) = {C_{cc}} + {C_{es}} $ | (4) |
考虑到强对流天气的0℃层高度一般在2000~6000 m左右,本文重点讨论该范围内的热融化作用。通过式(4) 得到不同0℃层高度的计算结果可以比较热传导和水汽凝华作用对冰雹融化的贡献(表 1):在2000~6000 m高度范围内两项贡献为同一量级;当0℃层较低时两者数值接近,不过随着0℃层抬高,水汽凝华作用的贡献明显增大。
|
|
表 1 热传导和水汽凝华对冰雹融化的贡献 Table 1 Contribution of thermal conduction and vapor sublimation to hail melting |
式(3) 得到地面冰雹半径与0℃层冰雹半径的曲线关系(图 1)和典型数值表(表 2),设rg<0.2cm时认为冰雹可以忽略。以下讨论0℃层分别在2000、4000和6000 m高度的情况。

|
图 1 不同0℃层高度的冰雹半径与地面冰雹半径关系 Fig. 1 Relations of hail radius at different 0℃ layer heights |
|
|
表 2 地面冰雹半径(单位:cm)、0℃层高度与0℃层冰雹半径的关系 Table 2 Relation of ground hail radius (unit: cm), 0℃ layer height and 0℃ layer hail radius |
h0高度在2000 m左右的冰雹云回波一般出现在初春或深秋季节,表 1显示当r0达到0.35 cm以上时地面就出现降雹。由于临界冰雹半径小、雷达反射功率低,单依靠回波强度和顶高指标不易识别,不过雷达垂直剖面图上在最大半径冰雹位置可以看到强度中等的回波核。
h0高度在4000 m左右的冰雹云回波比较多见,r0要达到0.65 cm时地面出现降雹。由于临界冰雹半径较大、雷达反射功率较强,除了在雷达垂直剖面图上回波核的特征明显之外,较大冰雹所在位置的回波强度也比较强。
h0高度在6000 m左右的冰雹云回波一般出现在盛夏季节,图 1显示当r0>1.25 cm以上时地面才出现降雹,而且夏季上升气流旺盛、云体内0℃层高度往往比探空资料显示的环境高度更高,因此热融化效应对地面冰雹大小的影响很大。
在分析强对流回波与冰雹关系时地面冰雹半径随0℃层冰雹半径和0℃层高度变化,冰雹云的雷达回波高度和中心强度等指标也应当随之变化,因此设定冰雹云判别的雷达指标时应当综合考虑0℃层高度和强回波中心强度的关系。
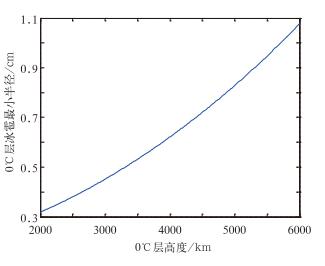
1.2.2 地面出现降雹时0℃层冰雹最小半径地面出现临界降雹时取rg=0.2 cm,根据式(4) 可以得到临界降雹时0℃层高度h0与0℃层冰雹最小半径rmin0之间的关系(图 2)。随着0℃层高度从2000 m抬高到6000 m,0℃层冰雹最小半径临界值在0.32~1.08 cm,变化范围较大,当0℃层高度较高时必须考虑热融化因素对冰雹尺寸预报的影响。
|
图 2 临界降雹时0℃层高度与0℃层冰雹最小半径关系 Fig. 2 Relation of 0℃ layer height and minimum 0℃ layer hail radius at critical the moment of hail falling |
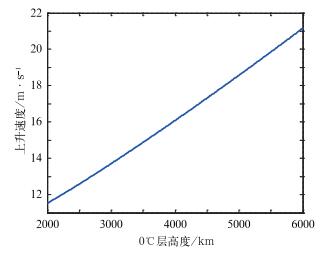
在许多冰雹云模型中上升气流的最大值一般出现在0℃层高度附近,分析在垂直温压场配置下0℃层高度的潜在上升气流速度能否达到产生冰雹条件对预报冰雹有指导意义。取rg=0.2 cm,可得到临界降雹时0℃层高度h0与0℃层最小上升气流vmin0之间的关系。结果显示随着0℃层高度从2000 m抬高到6000 m,临界降雹的最小上升气流在11.5~21.2 m·s-1(图 3)。
|
图 3 临界降雹时0℃层高度与最小上升速度关系 Fig. 3 Relation of 0℃ layer height and minimum updraft velocity at the moment of critical hail falling |
WSR-88D的增强HDA算法中开发了基于反射率因子的算法,是在垂直累积液态水(VIL)算法成功的基础上设计的。根据冰雹动能(E)的通量值E=5×10-6×100.0084zW(Z), 其中
| $ W(Z) = \left\{ \begin{array}{l} 0, z \le {z_L}\\ \frac{{z - {z_L}}}{{{z_u} - {z_L}}}, {z_L} \le z \le \\ 1, z \ge {z_u} \end{array} \right.{z_u} $ |
| $ {W_T}(H) = \left\{ \begin{array}{l} 0, H \le {H_0}\\ \frac{{H - {H_0}}}{{{H_{ - 20}} - {H_0}}}, {H_0} \le H \le \\ 1, H \ge {H_{ - 20}} \end{array} \right.{H_{ - 20}} $ |
得到强冰雹指数
以上算法中冰雹尺寸MEHS并未考虑冰雹热融化的影响。假定根据增强HDA算法预报结果为冰雹半径等于1 cm,如果考虑热融化的影响,那么当0℃层高度分别在2000、4000和6000 m时得到的地面冰雹半径(表 2)分别为0.96、0.76和0.0 cm,可见0℃层高度变化对于小尺寸冰雹的热融化影响比较明显。如果根据增强HDA算法原理把MEHS计算结果作为r0的函数,然后通过式(4) 得到地面冰雹实际尺寸rg似乎更加合理,可以降低由于0℃层以下的融化作用引起该算法结果偏高的问题。
因大连地区尚未开展冰雹尺寸的HDA算法与实况对比工作,以下引用的是2002—2005年济南13次冰雹过程的CINRAD/SA雷达计算、融化订正与实况(刁秀广等, 2007)进行比较(表 3),其中融化订正为将HDA算法作为0℃层冰雹半径代入式(4) 进行计算的结果。结果显示:直径的平均绝对误差从1.46 cm下降到1.19 cm,平均相对误差从44%下降到36%。
|
|
表 3 冰雹直径预测与实况对照表 Table 3 Forecast and observation of hail diameter |
(1) 本算法基于理想大气垂直分布状态,在发展非常强盛的对流云中首先云体内的0℃层高度可大大高于T-lnp资料反映的环境温度高度场配置,利用T-lnp资料计算时h0值会偏低;其次v-r关系未考虑环境垂直气流,当上升气流w>0时实际冰雹下落速度
(2) 实际冰雹不会是完全的圆形粒子,粗糙订正因子θ可大于1;实际降雹过程中环境水汽压为饱和状态的条件也不一定能够满足。
(3) 俞小鼎(2014)认为与干球温度0℃层高度相比,把湿球温度0℃层高度作为冰雹融化层高度更合理,因此对于冰雹融化的过程有待进一步研究。
4 结论(1) 地面冰雹半径与0℃层高度和0℃层冰雹半径相关,冰雹的热融化作用随着0℃层高度产生较大变化,因此设定冰雹云判别的雷达回波高度和中心强度等指标时应当综合考虑0℃层高度的影响。
(2) 当0℃层高度在2000~6000 m时,0℃层冰雹最小半径临界值在0.32~1.08 cm,临界降雹的最小上升气流在11.5~21.2 m·s-1。
(3) 将增强HDA算法的冰雹尺寸MEHS结果作为r0,通过计算得到地面冰雹实际尺寸rg更加合理,可以降低由于融化作用引起该算法结果偏高的问题。
总之,在理想大气垂直分布状态及低速下落状态下对于0.5 cm≤r≤3.5 cm范围内的冰雹,公式可建立地面冰雹半径与0℃层高度、0℃层冰雹半径之间的关系。计算结果分析可初步了解0℃层高度对冰雹融化的影响,为冰雹预报及人工防雹作业提供重要参考、应用于多普勒雷达冰雹尺寸预报可以降低WSR-88D增强HDA算法的虚警率。
刁秀广, 黄秀韶, 任钟冬, 等, 2007. CINRAD/SA雷达冰雹探测算法效果检验及参数本地化[J]. 气象科技, 35(5): 727-731. |
段鹤, 严华生, 马学文, 等, 2014. 滇南冰雹的预报预警方法研究[J]. 气象, 40(2): 174-185. DOI:10.7519/j.issn.1000-0526.2014.02.005 |
段英, 2009. 冰雹灾害[M]. 北京: 气象出版社.
|
樊鹏, 肖辉, 2005. 雷达识别渭北地区冰雹云技术研究[J]. 气象, 31(7): 16-19. DOI:10.7519/j.issn.1000-0526.2005.07.004 |
黄美元, 1980. 人工防雹导论[M]. 北京: 科学出版社.
|
卡尔L.约斯, 2003. Matheson气体数据手册[M]. 北京: 化学工业出版社.
|
雷雨顺, 吴宝俊, 吴正华, 1978. 冰雹概论[M]. 北京: 气象出版社, 56-110.
|
李大山, 2002. 人工影响天气现状与展望[M]. 北京: 气象出版社.
|
邵玲玲, 黄宁立, 王倩怡, 等, 2006. 冰雹指数产品剖析及在灾害性强降水预报中的应用[J]. 气象, 32(11): 48-54. DOI:10.3969/j.issn.1000-0526.2006.11.008 |
王瑾, 刘黎平, 2011. WSR-88D冰雹探测算法在贵州地区的评估检验[J]. 应用气象学报, 22(1): 96-106. DOI:10.11898/1001-7313.20110110 |
王秀玲, 郭丽霞, 高桂芹, 等, 2012. 唐山地区冰雹气候特征与雷达回波分析[J]. 气象, 38(3): 344-348. |
徐家骝, 1979. 冰雹微物理与成雹机制[M]. 北京: 农业出版社.
|
许焕斌, 段英, 刘海月, 等, 2004. 雹云物理与防雹的原理和设计[M]. 北京: 气象出版社.
|
俞小鼎, 2014. 关于冰雹的融化层高度[J]. 气象, 40(6): 649-654. DOI:10.7519/j.issn.1000-0526.2014.06.001 |
俞小鼎, 姚秀萍, 熊廷南, 等, 2000. 新一代天气雷达原理与应用[M]. 北京: 气象出版社.
|
朱君鉴, 刁秀广, 黄秀韶, 2004. 一次冰雹风暴的CINRAD/SA产品分析[J]. 应用气象学报, 15(5): 579-589. |
Arthur W, Michael D E, Gregory J S, 1998. An enhanced hail detection algorithm for the WSR-88D[J]. Wea Forecasting, 13(2): 286-303. DOI:10.1175/1520-0434(1998)013<0286:AEHDAF>2.0.CO;2 |
Eric L, Henry E F, 1998. An evaluation of WSR-88D severe hail algorithms along the Northeastern Gulf Coast[J]. Wea Forecasting, 13: 1029-1045. DOI:10.1175/1520-0434(1998)013<1029:AEOWSH>2.0.CO;2 |
Mather G K, Treddenick D, Parsons R, 1976. Observed relationships between the height of the 45dBZ contours in storm profiles and surface hail reports[J]. J Appl Meteor, 15(12): 1336-1340. DOI:10.1175/1520-0450(1976)015<1336:AORBTH>2.0.CO;2 |
 2015, Vol. 41
2015, Vol. 41 