引言

作为简化的描述，台风中的基本流场可看作是一级环流和次级环流的叠加(孙子平等，1990；Holton，2004；Fudeyasu et al，2011)，一级环流是一个轴对称的、满足梯度风平衡及静力平衡关系的暖心涡旋，次级环流是叠加于其上的、主要指径向及高度方向的环流。次级环流对台风的维持和增强(Fudeyasu et al，2011；Shapiro et al，1982；Möller et al，2002)乃至结构的改变如眼墙替换过程(Willoughby et al，1982；Sun et al，2013；Zhu et al，2014；Sawyer, 1956)都起着很大的作用。

台风中的次级环流可基于一级环流的基本场并配合热力及动力强迫场使用Sawyer-Eliassen (SE)方程进行诊断，该方程最早由Eliassen(1951)导出，而后Sawyer(1956)、Eliassen(1962)导出了适用于锋面的次级环流方程，这之后有许多相关的理论工作(Willoughby，1979；Shapiro et al，1982；Schubert et al，1983)，孙子平等(1987)对20世纪90年代前的工作做了相关的综述。这之后也有些理论工作，如Shapiro等(1993)得到了包含SE方程的非对称平衡方程，Bui等(2009)及Pendergrass等(2009)分别在高度坐标下推导了SE方程。

用于研究台风的各种不同形式的SE方程都使用了严格的梯度风平衡关系，台风中该平衡关系在边界层以上、对流层中低层能够较准确地成立(Willoughby，1990；Bell et al，2008)。然而，在边界层以及在紧邻边界层的对流区，梯度风平衡关系有很大的误差(Gray et al，1973；Bell et al，2008；Miyamoto et al，2014；Montgomery et al，2014)，例如Gray等(1973)用航测资料发现对流层低层台风最大切向风半径处的切向风比梯度风大25%，Miyamoto等(2014)用7 km分辨率的全球模式发现切向风局地最大可超过梯度风的40%，Montgomery等(2014)根据观测资料发现眼墙下方的平均最大切向风可以超过梯度风的20%~60%。

因为描述台风次级环流的SE方程本身基于梯度风平衡，梯度风平衡关系的较大误差也就可能导致SE方程在描述次级环流上有较大误差。关于SE方程的台风研究，早年的工作多是诊断理想场，或低分辨率合成场(刘月贞等，1988；孙子平等，1990)，这一定程度上回避了该问题。本世纪以来，随着数值模式的发展和计算条件的改善，越来越多的工作将SE方程应用于台风个例的研究中(Möller et al，2002；Hendricks et al，2004；Montgomery et al，2006；Bui et al，2009；Pendergrass et al，2009；Fudeyasu et al，2010；2011；Fang et al，2011；Sun et al，2013；Abarca et al，2014a；2014b；Ohno et al，2014；Zhu et al，2014)，如Hendricks等(2004)发现“黛安娜”(1984) 台风的生成过程的次级环流可用平衡方程来诊断，Fang等(2011)发现“多利”(2008) 台风的增强过程主要是由轴对称的非绝热加热场主导的，Ohno等(2014)用SE方程诊断理想台风的模拟结果显示台风眼区的位温倾向主要由非绝热加热及切向风的次网格摩擦强迫出的次级环流主导着，且两者呈负相关。那么，基于严格梯度风平衡的SE方程求解出的次级环流在结构上及强度上是否真实可信呢？

本文发现，在使用SE方程求解出的次级环流的结构上，存在明显的变形，在本文第三节会详细描述，而在强度上，从现有的实际个例的应用上看，存在着相互矛盾之处，许多结果显示SE方程得到的入流比模拟结果明显偏小(Bui et al，2009；Abarca et al，2014a)，另一些结果却显示SE方程得到的入流明显偏强(Montgomery et al，2006；Fudeyasu et al，2011)，而SE方程所能捕捉到的次级环流相对实际次级环流的大小在台风原理增强的分析中是个很关键的因素(Bui et al，2009；Fudeyasu et al，2011)。本文的个例研究显示，这种不一致可能与本文称之为正规化处理的过程有关：为了使SE方程稳定求解出次级环流，常需要人为对流场进行调整(Möller et al，2002；Bui et al，2009；Abarca et al，2014b)。Bui等(2009)和Abarca等(2014a)的工作中明确指出对边界层区域的流场进行调整后，他们得到的径向入流明显偏小。而Montgomery等(2006)和Fudeyasu等(2011)没有对边界层区域的流场进行调整，求解出的径向入流明显偏大。Bui等(2009)对此进行过一定的讨论。该调整具有很强的主观性，详见本文第二节。

基于现有的描述台风次级环流的SE方程存在的问题，是否能用更广泛的平衡关系来代替梯度风平衡？文中将基于完整的径向风方程来推导SE方程。并对其效果进行检验。

1 推导

这里从f平面、Boussinesq近似、水平面使用极坐标、垂直方向使用假相当高度坐标(Hoskins et al，1972)下的方程出发推导SE方程，选用该坐标是因为形式简单且使用广泛(Hendricks et al，2004；Montgomery et al，2006；Fudeyasu et al，2010；2011；Fang et al，2011；)，设物理场H可分解为H=H+H′，其中H为切向平均场，H′为切向扰动场，则切向平均的基本方程组可写为：

$ \mathit{\bar v}\left({{\mathit{f}_0} + \frac{{\mathit{\bar v}}}{\mathit{r}}} \right) = \frac{{\partial \bar \phi }}{{\partial \mathit{r}}} + \mathit{\bar S} $

(1)

$ \frac{{\partial \mathit{\bar v}}}{{\partial \mathit{t}}} + \mathit{\bar u\bar \eta } + \mathit{\bar w}\frac{{\partial \mathit{\bar v}}}{{\partial \mathit{\bar z}}} = \mathit{\bar F} $

(2)

$ \frac{1}{\mathit{r}}\frac{{\partial \mathit{r\bar u}}}{{\partial \mathit{r}}} + \frac{1}{\mathit{r}}\frac{{\partial \mathit{r\bar w}}}{{\partial \mathit{z}}} = 0 $

(3)

$ \frac{{{\partial ^{\rm{2}}}\bar \phi }}{{\partial \mathit{t}\partial \mathit{z}}} + \mathit{\bar u}\frac{{{\partial ^{\rm{2}}}\bar \phi }}{{\partial \mathit{r}\partial \mathit{z}}} + \mathit{\bar w}\frac{{{\partial ^{\rm{2}}}\bar \phi }}{{\partial {\mathit{z}^{\rm{2}}}}} = \frac{\mathit{g}}{{{\mathit{\theta }_0}}}\bar Q $

(4)

$ \frac{{\partial \bar \phi }}{{\partial \mathit{z}}} = g\frac{{\mathit{\bar \theta }}}{{{\mathit{\theta }_0}}} $

(5)

以上五个方程分别为径向动量方程、切向动量方程、连续方程、热力学方程、静力方程，其形式同Montgomery等(2006)，除了这里在切向方程中补充了超梯度力项S，其中$\bar S = - {{\bar F}_u} - \overline {v'v'} /r + \overline {\partial u/\partial t + u\partial u/\partial r + w\partial u/\partial z} ,$，$\bar F = {{\bar F}_v} - \overline {u'\eta '} - \overline {w'\partial v'/\partial z} $，F_u及F_v分别为数值模式中径向及切向的次网格过程，主要为边界层摩擦，$ \bar Q = {{\bar Q}_d} - \overline {u'\partial \theta '/\partial r} {\rm{ }} - \overline {w'\partial \theta '/\partial z} $，Q_d为非绝热加热率，$ \bar \eta = {f_0} + \left({1/r} \right){\rm{ }}(\partial r\bar v/\partial r)$为绝对涡度的垂直分量，ϕ=gh为重力位势，z=[1-(p/p₀)^κ](c_pθ₀/g)为假相当高度，z与实际高度h的转化关系为θdz=θ₀dh，κ=R_d/c_p，R_d是干空气比气体常数，c_p是定压比热容，p₀和θ₀为参考气压及参考位温，分别为1000 hPa及300 K。

式(1) 中若忽略S，就是经典的梯度风平衡关系：

$ {\mathit{f}_{\rm{o}}}\mathit{\bar v} + \frac{{{{\mathit{\bar v}}^{\rm{2}}}}}{\mathit{r}} = \frac{{\partial \bar \phi }}{{\partial \mathit{r}}} $

(6)

其反映的是科氏力、离心力、气压梯度力的平衡。引言已指出，该平衡关系在台风边界层以上的大部分区域都能较好地满足，但在台风边界层及紧邻边界层的对流区有很大误差。本文使用包含超梯度力的径向方程(1) 来推导次级环流方程。

式(1) 对z求偏导，式(5) 对r求偏导，代换掉$\frac{{{\partial ^2}\bar \phi }}{{\partial \mathit{r}\partial \mathit{z}}} $项，得

$ - \frac{{\partial \mathit{\bar S}}}{{\partial \mathit{z}}} + \mathit{\bar \xi }\frac{{\partial \mathit{\bar u}}}{{\partial \mathit{z}}} = \frac{\mathit{g}}{{{\mathit{\theta }_0}}}\frac{{\partial \mathit{\bar \theta }}}{{\partial \mathit{r}}} $

(7)

式中ξ=f₀+2v/r为涡旋惯性场。式(7) 若忽略第一项，就是轴对称涡旋的热成风平衡关系，反映径向的位温梯度与切向风速随高度变化之间的平衡。

式(7) 对时间t求偏导，得

$ - \frac{{{\partial ^{\rm{2}}}\mathit{\bar S}}}{{\partial \mathit{t}\partial \mathit{z}}} + \frac{\partial }{{\partial \mathit{z}}}\left({\mathit{\bar \xi }\frac{{\partial \mathit{\bar v}}}{{\partial \mathit{t}}}} \right) = \frac{\mathit{g}}{{{\mathit{\theta }_0}}}\frac{\partial }{{\partial \mathit{r}}}\frac{{\partial \mathit{\bar \theta }}}{{\partial \mathit{t}}} $

(8)

由式(2) 得$ \frac{{\partial \bar v}}{{\partial t}}$，由式(5) 代入式(4) 得$\frac{{\partial \bar \theta }}{{\partial t}} $，都代入式(8)，得

$ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial r}}\left( {\frac{g}{{{\theta _0}}}\frac{{\partial \bar \theta }}{{\partial r}}\bar u + {{\bar N}^{\rm{2}}}\bar w} \right) + \frac{\partial }{{\partial z}}\left( { - \bar \xi \bar \eta \bar u - \bar \xi \frac{{\partial \bar v}}{{\partial z}}\bar w} \right)}\\ {\;\;\;\;\;\;\;\;\; = \frac{g}{{{\theta _0}}}\frac{{\partial \bar Q}}{{\partial r}} - \frac{{\partial \left( {\bar \xi \bar F} \right)}}{{\partial z}} + \frac{{{\partial ^{\rm{2}}}\bar S}}{{\partial t\partial z}}} \end{array} $

(9)

由连续方程(3)，引入流函数ψ以减少变量：$\bar u = - \frac{1}{r}\frac{{\partial \psi }}{{\partial z}}, \mathit{\bar w = }\frac{1}{r}\frac{{\partial \psi }}{{\partial r}} $，式(9) 可化简为

$ \begin{array}{l} \frac{\partial }{{\partial \mathit{r}}}\left({\frac{{\mathit{\bar A}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{r}}}\mathit{ + }\frac{{{{\mathit{\bar B}}_1}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{z}}}} \right) + \frac{\partial }{{\partial \mathit{z}}}\left({\frac{{{{\mathit{\bar B}}_{\rm{2}}}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{r}}}\mathit{ - }\frac{{\mathit{\bar C}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{z}}}} \right)\\ \;\;\;\;\;\;\;\;\; = \frac{\mathit{g}}{{{\mathit{\theta }_0}}}\frac{{\partial \mathit{\bar Q}}}{{\partial \mathit{r}}} - \frac{{\partial \left({\mathit{\bar \xi \bar F}} \right)}}{{\partial \mathit{z}}} + \frac{{{\partial ^{\rm{2}}}\mathit{\bar S}}}{{\partial \mathit{t}\partial \mathit{z}}} \end{array} $

(10)

其中A=N²=g/θ₀∂θ/∂z为静力稳定度，B₁=-g/θ₀∂θ/∂r为以水平位温梯度表征的斜压性场，B₂=-ξ∂v/∂z=-(f₀+2v/r)∂v/∂z为以切向风垂直切变表征的斜压性场，C=ξη=(f₀+2v/r)[f₀+(1/r)(∂rv/∂r)]为惯性稳定度。

方程(10) 由于右侧含有时间的偏导项，通常还不能作为诊断方程使用，而下一节中通过对实际个例的诊断能够发现，方程右侧的∂²S/(∂t∂z)项很小，若略去这一项，就得到关于次级环流的诊断方程

$ \begin{array}{l} \frac{\partial }{{\partial \mathit{r}}}\left({\frac{{\mathit{\bar A}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{r}}}\mathit{ + }\frac{{{{\mathit{\bar B}}_1}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{z}}}} \right) + \frac{\partial }{{\partial \mathit{z}}}\left({\frac{{{{\mathit{\bar B}}_{\rm{2}}}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{r}}}\mathit{ - }\frac{{\mathit{\bar C}}}{\mathit{r}}\frac{{\partial \mathit{\psi }}}{{\partial \mathit{z}}}} \right)\\ \;\;\;\;\;\;\;\;\; = \frac{\mathit{g}}{{{\mathit{\theta }_0}}}\frac{{\partial \mathit{\bar Q}}}{{\partial \mathit{r}}} - \frac{{\partial \left({\mathit{\bar \xi \bar F}} \right)}}{{\partial \mathit{z}}} \end{array}\ $

(11)

当D=AC-(B₁+B₂)²/4 > 0时，方程(11) 为关于台风次级环流流函数ψ的椭圆型方程，可用数值方法如超松弛法求解出次级环流(Press et al, 1992)，方程右侧的两项分别为热力强迫相关的源项及动量强迫相关的源项。

方程(11) 中，B₁≠B₂，若将严格的热成风关系代入，得B₁=B₂，这就回到了经典的SE方程，各文献中出现的都是以B₂代替B₁的形式，其椭圆型方程的判别式为D=AC-B₂² > 0。B₁或B₂代表的是斜压作用，而超梯度力的存在导致这两项不一致，即超梯度力是通过调节次级环流方程中与斜压作用有关的系数来影响次级环流的。

边界条件可取为在内边界及上、下边界没有穿越边界的流动，即ψ|_{r=0, or z=0, Z}=0，而在外边界可认为对流已很弱，垂直速度为零，即(∂ψ/∂r)|_r=R=(rw)|_r=R=0，其中Z为涡旋顶的高度，R为涡旋外边界。

这样处理后，次级环流方程包含了超梯度力的作用，而求解中需要用到的仍然是切向平均位温及切向风场，超梯度力自然隐含于其中，无需显式计算。

2 试验设置

本文使用“森拉克”(2008) 台风的模拟个例来进行次级环流的诊断。使用WRF V3.1.1(Skamarock et al，2008)，外层区域分辨率为10.8 km格点数为174×210，内层区域分辨率为3.6 km，格点数为169×169，采用涡旋跟随的双向嵌套方案，垂直方向为σ坐标设置为40层，参数化方案边界层为YSU，微物理为WSM6，外层区域的积云对流方案为Kain-Fritsch。模拟开始时间为2008年9月9日0000 UTC，选用NCEP的FNL数据作为初始条件及边界条件，并且在初始时刻植入了bogus涡旋，积分96 h。在该设置下积分，模拟出了“森拉克”台风快速增强、第二眼墙生成以及眼墙替换的过程，详见Sun等(2013)。

跟随着模拟出的“森拉克”台风中心，可以建立一个柱坐标系，将各物理场插值到该柱坐标系，其径向分辨率为3.6 km，高度方向分辨率为0.5 km，使用The NCAR Command Language(2014)的wrf_user_intrp3d函数进行插值。该柱坐标系的顶高20 km，径向范围450 km，由于内层嵌套区域的半径不足450 km，超出该区域的格点值用粗网格线性插值到对应位置后的值代替。对各物理场再做切向平均，就得到切向平均场。从而可以作为SE方程的输入场来进行次级环流的诊断。

关于求解时的正规化处理，首先对绝对涡度做了径向18 km，垂直方向1 km的滑动平均，这可增强求解的稳定性而对结果的影响很小。不满足椭圆形方程的区域主要有两片，一是高层出流区，二是边界层内的对流区，对于高层出流区的不稳定，本文将即惯性稳定度的最小值设置为5×10^-9 s^-2，类似的处理可见于Möller等(2002)，Bui等(2009)及Fudeyasu等(2011)，这样能增强求解的稳定性，对求解结果尤其是中低层的流场没有明显影响。对于边界层入流区的不稳定，本文在求解时每个时次都做了3组实验：(1) 不做处理，求解改进后的SE方程；(2) 不做处理，求解原始的SE方程；(3) 在AC-B₂² < 0的区域，将B₂设置为其0.5倍，再求解原始的SE方程，与这一处理类似的如Bui等(2009)选用的系数是0.8，Abarca等(2014b)选用的系数是0.15。还有许多前人的工作中没有明确写出如何处理边界层区域的不稳定，可见这里有相当大的主观性，本文选用0.5是因为这样处理后得到的不稳定区域与不做处理的改进的SE方程相当，从而方便对比两者对次级环流的描述效果。且若以改进后的SE方程作为标准，可认为0.5是原始SE方程中B₂的最优修正系数。

3 结果与分析

这一节将对比改进后的SE方程与原始的SE方程在“森拉克”台风的模拟个例中对其次级环流的求解效果。首先，确认第一节方程推导中出现的源项∂²S/(∂t∂z)确实是可忽略的。图 1为SE方程中各源项的最大值的时间演变曲线。由图可见80 h之前最大的项是蓝线所示的切向摩擦作用相关项，该项最大值在眼墙替换之前逐渐增大，这与切向风速逐渐增大相一致，眼墙替换过程开始后，随着最大风速半径外扩，该项迅速减小。与加热作用相关的源项构成台风次级环流的另一个重要的源项，其最大值在图中多数时段不及切向摩擦相关的源项大，在80 h之后开始成为最大的项。图中黑色实线为与超梯度力对应的源项即∂²S/(∂t∂z)，可见该项在模拟过程的绝大部分时段都非常小，远小于前述两项，唯一的例外是在第72至75 h出现了峰值，其时从最大值看与前述两项作用相当，这段时间正好对应着内眼墙的入流被外眼墙切断，径向风的分布有较大变化，这导致该项在这段时间相对较大。经计算，即使在最大的这段时间，加入或不加入该项对求解出的次级环流影响很小。图 2给出了第73 h的求解对比，可见两者并没有明显差异。进一步地诊断表明这是由于该时次∂²S/(∂t∂z)的大值区域很小，故对次级环流的影响也很小。因此，包含超梯度力的SE方程中确实可以忽略该源项。此外，图 1黑色虚线为∂²F_u/(∂t∂z)项，从极值上看，与边界层径向的次网格动量强迫对应的源项多数时候可以代表与超梯度力对应的源项。

图 3为第18 h次级环流的模拟场及SE方程的求解场的对比图。此时“森拉克”台风处于初始的发展增强阶段，已形成稳定的主眼墙，但强度还远没有发展到最强(此时模拟的海平面最低气压是973 hPa)。由图可见，该时次总体而言三组求解试验都较好地再现了模拟场的次级环流，不同的是：(1) 原始SE方程求解结果在1 km以下的眼墙对流区靠近入流一侧，相对原始垂直速度场，有向地面延伸的较强的垂直速度(图 3c)，与之对应的眼墙外侧的径向入流也较强(图 3g)。从物理意义上讲，这是可能是由于原始的SE方程忽略了边界层内对入流起阻碍作用的径向摩擦，故入流增强，在连续方程的约束下垂直速度也相应增强。(2) 人为调整斜压系数B₂后，入流明显减弱(图 3h)。另外图中可见，改进后的SE方程在边界层区域的D明显增大(图 3i和3j)，即能更好地满足椭圆方程的条件，而人为调节B₂为0.5倍的效果从D上看与改进的SE方程相当(图 3i和3k)。

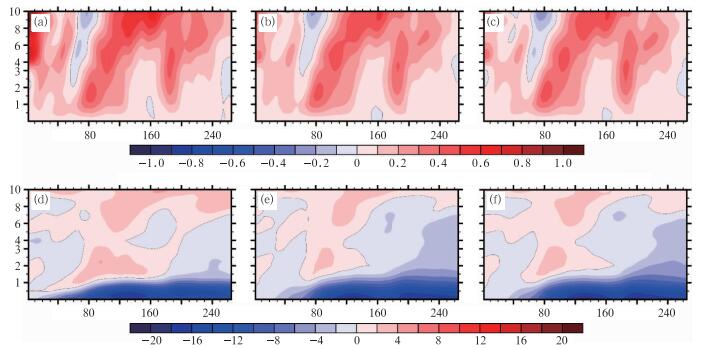
图 4为第65 h的各试验对比图，此时第二眼墙正在形成，在低层距台风中心120 km处已明晰可见对流极大值区域。各试验的求解结果在第一眼墙附近差异不大，而在形成中的第二眼墙附近能看出明显区别：具体的，原始SE方程得到的垂直速度(图 4c)可见两个虚假的大值区，一是主眼墙外侧，相对模拟结果略微偏大，二是第二眼墙外侧，明显可见向外向下延伸的垂直速度偏大的区域。人为系数修正后的原始SE方程的求解结果也仍然能看出这样的畸变(图 4d)；原始SE方程得到径向入流(图 4g)在外眼墙区域明显有虚假增大，且从形态上看，有向内向上虚假凸起的趋势，下面还将看到，该虚假形变在图 5中表现得尤为明显。这两类虚假畸变也常见于前人的研究，如Fudeyasu等(2011)的图 12，Abarca等(2014a)的图 3。

图 5为第80 h的各试验对比图，此时眼墙替换已完成，该时次外围眼墙的对流较强，其低层约2 km处有强对流，其外围边界层内有下沉气流，由图可见，该时次各试验有明显不同：改进后的SE方程能较好地还原次级环流，原始的SE方程求解出的次级环流存在前述的两种虚假形变，且对流场在200 km附近处边界层内出现虚假强下沉，径向风场在140~200 km的边界层内出现了虚假出流。人为调节系数后的原始SE方程求解出的次级环流相对未调节有明显改善，但仍然可见明显畸变。该个例表明包含超梯度力作用的SE方程有可能明显改进台风次级环流的求解效果。

4 结论与讨论

本文首先基于包含超梯度力的径向风方程，推导出了包含超梯度力作用的诊断台风次级环流的SE方程，从方程形式上看，超梯度力对次级环流的影响主要有两方面，一是调节方程中与斜压性相关的系数，二是增加了一个含有时间偏导的源项。而根据实际个例的诊断结果可知，后者即增加的源项的作用非常小，可以忽略，于是方程仍然可作为诊断方程使用。对于次级环流结构改变较快的情形，该结果的适用性尚需进一步验证。

使用改进后的SE方程对“森拉克”台风的模拟个例进行了次级环流的诊断，结果显示使用改进的SE方程能较好地还原次级环流场。而原始的SE方程求解出的次级环流，结构上看会有畸变，即在边界层附近，眼墙对流会有向外侧向下的虚假扩展，径向入流有向内侧向上的虚假扩展；从强度上看，若不经过人为的系数调节，边界层入流会明显偏大。

从文中的三个示例来看，当台风眼墙的半径较大时，改进的SE方程的优势更明显，这可能是因为较大半径处的惯性稳定度比较小半径处要小很多，从而受斜压性的影响更大。而第一节已指出，超梯度力是通过调节改进的SE方程中与斜压作用有关的系数来影响次级环流的，所以该改进在半径较大处对次级环流的影响就更大。而文中后两个时次的差别可能是由于眼墙强弱的差异造成的，即眼墙对流较强时，与之相伴随的边界层内入流区的超梯度力也较大，从而使用新的SE方程求解出的次级环流效果提升较明显。

针对前人用SE方程捕捉次级环流得到的相矛盾的结果，本文的数值试验揭示了这可能是前人为了尽量让SE方程满足椭圆方程的条件而人为调节SE方程中与斜压性相关的系数而造成的，即人为减小该系数后，椭圆型方程条件更易满足，但入流也会随之明显减小。而使用改进的SE方程，就可能避免这一因人为调节的程度不同而导致的问题。

使用原始的SE方程研究实际台风个例的困难可总结如下：若不进行正规化处理，次级环流会有畸变，且入流明显偏强；若进行正规化处理，边界层入流强度又很大程度上受人为调节的影响，且次级环流结构上仍然有畸变。本文改进的SE方程可广泛应用于模拟台风的诊断，如可应用于高拴柱等(2009)，杨文霞等(2011)，周冠博等(2012；2015)，杨文霞(2013)的工作中。前人的许多工作将SE方程求解出的次级环流尤其是边界层入流相对原始场偏小完全归因于平衡过程，本文的结果显示这方面尚有待进一步的研究。

致谢：感谢谭本馗教授和黄嘉佑教授的指导和鼓励，受益匪浅。