β中尺度天气系统是典型的中尺度系统,其水平分布位于20~200 km之间。人们利用天气雷达和加密观测网提供的产品和数据,围绕中尺度对流系统的结构(陈敏等,2005;赵宇等,2011;王啸华等,2012)、发生发展(孙建华等,2015;杨吉等,2015)、天气性质(鲁德金等,2015;井喜等,2014)、传播规律(苏君毅,2006)以及与大尺度系统的相互作用(辜旭赞等,2014)等问题展开了大量的研究和统计分析,推进了对这类系统可能引发的局地灾害天气的短临预报工作(郝莹等,2012;孙靖等,2010;袁美英等,2010;杜小玲,2013)。
强对流系统极可能引发短时强降水、冰雹、对流性大风等不同类型的灾害天气或几种类型的复合灾害天气。一个能够对它们进行客观分类识别的业务系统,需要首先抓住或提取出冰雹系统和暴雨系统间具有显著性差异的形态、结构以及强度分布等方面的特征,并在这些具有优良分类品质的特征向量的描述下训练出客观模型。
研究发现,β中尺度下水平范围达到50 km以上的较大型的冰雹系统与强降水系统在三维形态(例如是否出现窟窿)、垂直空间延伸高度以及系统核反射率均值等方面差异比较显著,王萍等(2013)据此设计并实现了“悬垂度”等多个特征提取算法,实验验证了各项指标的分类能力,选用支持向量机训练出强冰雹与强降水的分类识别模型,并取得很好的测试效果。但在50 km以内雷暴系统中,区别于强降水的窟窿形态特征并不强烈甚至并不出现;强度较弱、高度较低、面积较小的系统可能因其移动极其缓慢同样会诱发短时强降水。因此,适合于辨析出较大型系统引发天气类型的特征及分类模型(王萍等,2013)在用于50 km以内雷暴系统时往往表现不佳。本文的工作重点就是构建适用于50 km以内雷暴系统的新特征并进行客观建模,以实现对50 km以内雷暴系统引发的冰雹、短时强降水等进行分类识别。
1 50 km以内雷暴系统特征提取图 1是“悬垂度”特征(王萍等,2013)为0的50 km以内冰雹系统和强降水系统的反射率因子图像(0.5°仰角),虽然它们核区内部的反射率值均超过了55 dBz,但其分布特点是有差异的。首先,冰雹系统从核区过渡到边界(取35 dBz)的距离差异大,因此核区偏离单体几何中心较远。再看强降水系统,其核区相对较大,位置比较接近单体几何中心。

|
图 1 冰雹系统和强降水系统示例(a)冰雹系统,(b)强降水系统 Fig. 1 Examples of hail system (a) and severe precipitation system (b) |
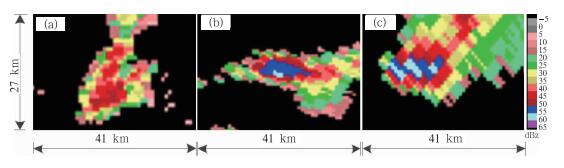
图 2是单时刻看上去较弱的强降水系统和单时刻看上去较强的强降水+冰雹系统和冰雹系统。第一种情况虽然强度偏低,但移速较慢;第二种情况也因移速缓慢会同时引发冰雹和暴雨天气;第三种情况则因移动快速而不伴有强降水。经统计分析,在大量50 km以内雷暴系统中,图 1和图 2展现出来的特点是具有共性的。
|
图 2 引发不同天气类型的系统示例 (a)强降水系统,(b)强降水+冰雹系统,(c)冰雹系统 Fig. 2 Examples of systems generating different weather systems (a) severe precipitation, (b) hail and severe precipitation, (c) hail |
采用16级量化方案的雷达反射率图是一张由16种颜色构成的伪彩图像,图中除表示背景的黑色以外的15种颜色分别代表≥65, 60, 55 dBz, …, 0和-5 dBz的量化反射率值。为刻画系统核区与系统几何中心的偏移度,设计算法如下:
(1) 将50 km以内雷暴系统的最高反射率和次高反射率所占区域称作系统核区,将系统中≥35 dBz区域称作系统区域。以图 1a所示系统为例,系统核区和系统区域如图 3a和3b所示。

|
图 3 系统内轮廓和外轮廓提取过程示意图 (a)系统核区,(b)系统区域,(c)闭运算前的两轮廓,(d)闭运算后的两轮廓 Fig. 3 Extracting process of inner and outer contours (a) inner area, (b) system area, (c) two contours before closing operation, (d) two contours after closing operation |
(2) 运用数学形态学闭运算(阮秋琦,2009)分别对两个区域进行操作以避免直接提取区域轮廓所存在的严重的突变现象(图 3c),然后提取区域轮廓(图 3d),且称系统核区轮廓为内轮廓,系统区域轮廓为外轮廓。考虑到待处理的系统尺度较小,闭运算时使用的结构元素选择简单的3×3方形。
(3) 求内外轮廓间距离均值
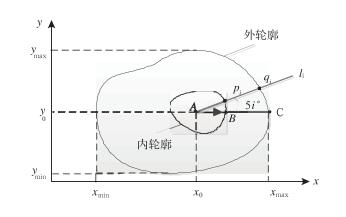
记P, Q为系统内外轮廓点集,设内轮廓外包矩形的中点A(x0, y0)为定位点(参见图 4)。
|
图 4 内外轮廓距离均值计算示意图 Fig. 4 Calculation of average distance of inner contour and outer contour |
1) 从A点出发以间隔5°做72根射线li
| $\begin{array}{*{20}{c}} {{l_i}:{y_i} = \left[ {\tan {{\left( {5i} \right)}^ \circ }} \right]\left( {x - {x_0}} \right) + {y_0},}&{i = 0, \cdots ,71} \end{array}$ | (1) |
式中,x∈{x0, xmax}或{x0, xmin},y∈{y0, ymax}或{y0, ymin};
2) 在外轮廓的外包矩形内,量化x或y, 经四舍五入得到该直线点集Ui;
3) 计算射线li与内轮廓的交点pi和与外轮廓的交点qi,方法如下:设fmx(P, Ui)为P中元素pm与Ui中元素uk间距离,fnk(Q, Ui)为Q中元素qn与Ui中元素uk间距离,则:
| ${p_i} = \min \left\{ {{f_{mk}}\left( {P,{U_i}} \right)|{p_m} \in P,{u_k} \in {U_i}} \right\}$ | (2) |
| ${q_i} = \min \left\{ {{f_{nk}}\left( {Q,{U_i}} \right)|{q_n} \in Q,{u_k} \in {U_i}} \right\}$ | (3) |
4) 计算(5i)°方向上内轮廓和外轮廓之间的距离
5) 依据下式计算轮廓间距离均值:
| $d = \frac{1}{{72}}\sum\limits_{i = 0}^{71} {\left\| {\overrightarrow {{p_i}{q_i}} } \right\|} $ | (4) |
根据对d的构建过程容易分析出,系统核紧凑时,则d值升高,系统核紧凑且偏向一侧时,则d值同样较高,而系统核松散时,则d值偏小。因此称d为50 km以内雷暴系统结构疏密性特征。
(4) 系统结构疏密性类间显著性分析
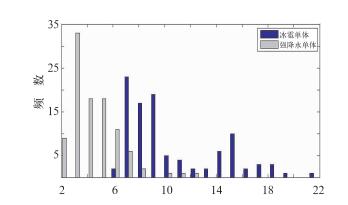
选择天津地区和山东地区共7个过程100个50 km以内冰雹系统以及天津地区10个过程共100个50 km以内强降水系统进行系统结构疏密性特征统计,结果如图 5所示。可以看出,冰雹系统结构疏密性特征普遍偏高,而短时强降水系统结构疏密性特征普遍偏低。
|
图 5 强冰雹/短时强降水系统的疏密性特征分布 Fig. 5 Distribution of density feature of hail systems and short-time severe precipitation systems |
设特征d所描述的冰雹和短时强降水系统样本分别来自两个服从正态分布的总体,且其方差相同,使用服从t分布的统计量[见式(5)],展开置信水平(1-α)的假设检验。
| $\begin{array}{l} t = \frac{{\left( {{m_1} - {m_2}} \right)}}{{\sqrt {\frac{{\left( {{n_1} - 1} \right)S_1^2 + \left( {{n_2} - 1} \right)S_2^2}}{{{n_1} + {n_2} - 2}} \cdot \left( {\frac{1}{{{n_1}}} + \frac{1}{{{n_2}}}} \right)} }}\\ \quad \quad \sim t\left( {{n_1} + {n_2} - 2} \right) \end{array}$ | (5) |
式中,m1、m2分别为冰雹和短时强降水系统的d特征均值,S12和S22分别为对应的方差,n1、n2分别为两类样本数。假设特征d对冰雹和短时强降水两类样本无显著性差异,根据式(5) 算得t=13.623,取α=0.01,则tα/2(n1+n2-2)=t0.005(198),查表得t0.005(198)<t0.005(180)=2.603,显然,t>t0.005,因此推翻原假设,认为系统结构疏密性特征在冰雹系统和短时强降水系统之间具有显著性差异。
1.2 50 km以内雷暴系统液态水含量受垂直累积液态水含量的启发(肖艳姣等,2009),通过下式计算50 km以内雷暴系统总体液态水含量:
| $\mathop {\smallint \smallint }\limits_{S{H_{\rm{L}}}}^{{H_{\rm{U}}}} k\left( h \right) \cdot M{\rm{d}}h{\rm{d}}s$ | (6) |
式中,M=3.44×10-3z4/7,s为系统组合反射率图中≥35 dBz的区域面积,k为与高度有关的系数,可以令
| $k\left( h \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{h \le {H_0}}\\ { < 1,}&{h > {H_0}} \end{array}} \right.$ |
式中,H0为0℃层高度。为简化系统液态水含量特征计算,本文采取了两条简约措施:
(1) 用z取代M;
(2) 将垂直积分上限限定在0℃层和-20℃层之间,同时令k=1。
于是得单时刻50 km以内雷暴系统液态水含量特征估算办法:
| $LE=\iint\limits_{S}{_{{{H}_{L}}}^{\frac{{{H}_{0}}+{{H}_{-20}}}{{{H}_{L}}}}}z\text{d}h\text{d}s$ | (7) |
算法实现时,首先用0.5°, 1.5°, …, 19.5°等9个仰角的系统雷达数据,通过双线性插值法生成其三维格点数据(李聪,2014),并认为低于30 dBz的反射率值对强降水贡献不大,置为0。按照纵向0.1 km、水平1 km的分辨率计算:
| $LE=\sum\limits_{i\in S}{\sum\limits_{j\in \left[ {{H}_{L}},\left( {{H}_{0}}+{{H}_{-20}} \right)/2 \right]}{0.1\times {{z}_{ij}}}}$ | (8) |
如果系统移动速度较慢甚至基本不动,即使系统反射率强度及延伸厚度有限,经时间累积也可能导致短时强降水的发生,反之,即使50 km以内雷暴系统单个体扫液态水含量较高,但若移动快速,达到短时强降水量级的可能性也会偏小,为此特构建系统移出率特征。
如图 6所示BRmin为某系统某时刻(后文称初始时刻)的正最小外包矩形,将其左下角点设为参照点,以后第i个体扫相对于前一体扫的位移为Si,那么,第n个体扫后,该系统相对于初始时刻的位移为S;求出初始时刻的系统在向量S的方向上的跨宽W,并定义第n个体扫后系统相对于初始时刻的移出率为:
| $\rho =\frac{\left\| \sum\limits_{i=1}^{n}{\mathit{\boldsymbol{S}}} \right\|}{W}$ | (9) |

|
图 6 移出率计算示意图 Fig. 6 Calculation of emigration rate |
移出率可以反映系统在一段时间内的位置重叠情况,因此也可以为计算系统累加液态水含量提供权重。
1.4 50 km以内雷暴系统累加液态水含量50 km以内雷暴系统在固定区域的降水效应与两方面因素有关,即液态水含量的多少和系统在该位置停留的时间。据此,预测一个系统是否引发强降水天气需要综合考虑多个体扫的情况。
(1) 定义从初始时刻历经至第n个体扫时,系统在相应位置的累加液态水含量:
| ${{E}_{a}}=\sum\limits_{i=1}^{n}{\left( 1-{{\rho }_{i}} \right)}L{{E}_{i}}$ | (10) |
式中,ρi为系统从初始时刻发展到第i个体扫时的移出率,LEi为系统在第i个体扫的液态水含量。按照相邻体扫时间间隔6 min考虑,本文取nmax=5。
(2) 50 km以内雷暴系统累加液态水含量特征的类间显著性分析
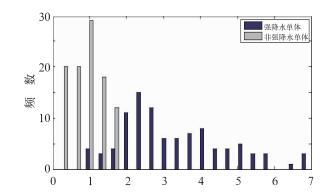
选择天津地区8个过程共100个50 km以内非强天气系统和10个过程共100个50 km以内强降水系统进行系统累加液态水含量统计,结果如图 7所示。可见看出,非强降水系统累加液态水含量相对偏低,而短时强降水系统累加液态水含量相对偏高。
|
图 7 非强天气/短时强降水系统的累加液态水含量特征分布 Fig. 7 Distribution of cumulative liquid water content of non-severe weather system and short-time severe precipitation system |
设特征Ea所描述的非强天气和短时强降水系统样本分别来自两个服从正态分布的总体,且其方差相同,使用服从t分布的统计量[见式(5)],展开置信水平(1-α)的假设检验。假设特征Ea对非强天气/短时强降水两类样本无显著性差异,取显著性水平α=0.01,则tα/2(n1+n2-2)=t0.005(198),查表得到t0.005(198)<t0.005(180)=2.603,根据式(5) 算得t=16.031,显然,t>t0.005,因此推翻原假设,认为系统累加液态水含量特征在非强天气系统和短时强降水系统之间具有显著性差异。
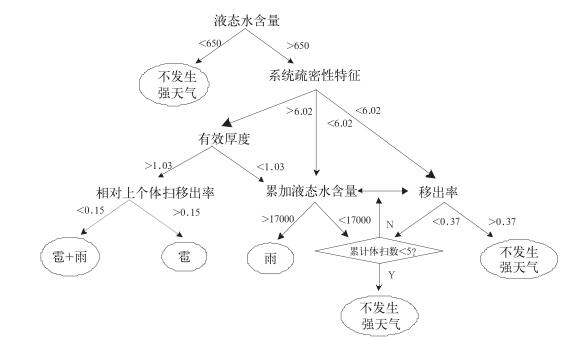
2 分类决策由单体结构的疏密性、有效厚度(王萍等,2013)、移出率、液态水含量及累加液态水含量形成对50 km以内雷暴系统的5维向量描述,选择2005—2007年间天津地区和2014年山东地区部分50 km以内雷暴系统样本共27个过程作为建模样本,根据各特征对强降水以及冰雹发生过程的分布情况,采取如下构建原则:优先选用误分率较小的特征,用该特征在一类建模样本中分布的边界值作为分类阈值,剩余不可分样本寻找新的分类特征和分类阈值,最终得到50 km以内雷暴系统分类识别决策树如图 8所示,其中分类阈值确定方法如下:
|
图 8 50 km以内雷暴系统分类识别决策模型 Fig. 8 Classification tree of thunderstorm system less than 50 km |
(1) 液态水含量的分类阈值选训练样本中强天气系统的最小值;
(2) 系统结构疏密性特征的分类阈值选训练样本中冰雹系统的最小值;
(3) 移出率的分类阈值选训练样本中强降水系统的最大值;
(4) 累加液态水含量的分类阈值选训练样本中不发生强天气的系统的最大值;
(5) 有效厚度的分类阈值选训练样本中冰雹系统的最小值;
(6) 相对上下体扫的移出率阈值选训练样本中冰雹系统的最小值。
3 测试及分析为验证本文算法及分类模型的有效性,选择未参加训练的2014年6月1日和2012年6月7日南昌地区10个50 km以内雷暴系统序列,2005—2015年天津地区12个50 km以内雷暴系统序列共229个体扫作为测试样本,各类样本数及测试结果如表 1所示。其中,对于同时发生强降水和冰雹的35个系统,既视为强降水样本也视为冰雹样本,对这35个系统的识别结果是23个完全正确、9个仅识别成强降水、3个无强天气识别结果,因此强降水样本数记为102+35,击中90+23+9;冰雹样本数记为49+35,击中44+23。可以看出,就测试样本而言本模型对50 km以内雷暴系统引发的强降水击中率达到89.1%,同时带来9.5%的误报;对50 km以内雷暴系统引发的冰雹的击中率为79.8%,同时带来3.5%的误报;会对27.9%的强天气系统误报成非强天气。平均临界成功指数达到80.0%。
|
|
表 1 测试结果 Table 1 Testing results |
下面给出几种具有代表性的示例分析。
(1) 反射率值较大的50 km以内冰雹系统和强降水系统
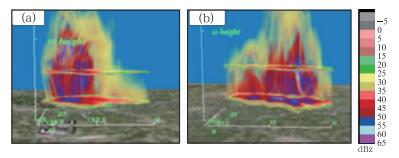
图 9a和9b分别是出现在天津地区的冰雹系统和强降水系统的三维图。两者的反射率值均较大,具有一定的延伸厚度,但前者移动较快(ρ=0.1755, 见表 2)故未产生强降水,后者因结构较松散(d=4.8307<6.02) 而不产生冰雹、又因移动较慢(ρ=0.0668) 而出现强降水。
|
图 9 反射率值较大的冰雹系统和强降水系统的三维显示图 (a)冰雹系统(200906361100,最大水平跨度25 km),(b)强降水系统(200808100142,最大水平跨度30 km) Fig. 9 Three-dimensional graphs of hail system and severe precipitation system with high reflectivity (a) hail system (200906361100, maximum horizontal width is 25 km), (b) severe precipitation system (200808100142, maximum horizontal width is 30 km) |
|
|
表 2 示例(1) 系统特征取值 Table 2 Feature values of systems in Example 1 |
(2) 冰雹单独出现和冰雹、强降水同时出现
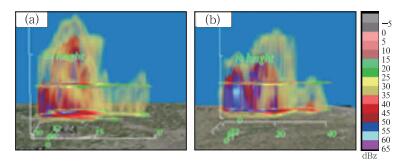
图 10a和10b分别是冰雹系统和冰雹+强降水系统的三维图,两者延伸厚度较深、结构均较紧密(d>6.02, 见表 3),均发生了冰雹,但因前者移动较快(ρ=0.2636) 而不伴有强降水,而后者移动较慢(ρ=0.0837) 则同时发生强降水。
|
图 10 冰雹系统和冰雹强降水系统三维图 (a)冰雹系统(天津201406261118,最大水平跨度30 km),(b)冰雹强降水系统(南昌201406010612,最大水平跨度40 km) Fig. 10 Three-dimensional graphs of hail system and severe precipitation system (a) hail system (Tianjin 201406261118, maximum horizontal width is 30 km), (b) hail and severe precipitation system (Nanchang 201406010612, maximum horizontal width is 40 km) |
|
|
表 3 示例(2) 系统特征取值 Table 3 Feature values of systems in Example 2 |
(3) 累加液态水含量在辨析强降水系统和非强水系统的作用
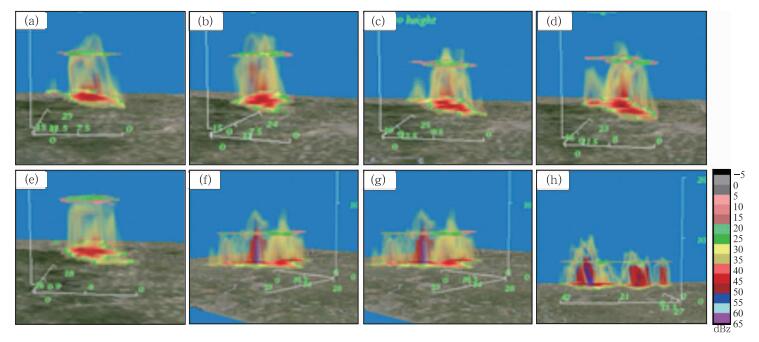
图 11a~11e是天津地区某50 km以内非强天气系统连续5个体扫的三维图,图 11f~11h是南昌地区某50 km以内强降水系统连续3个体扫的三维图,它们的特征取值如表 4所示。单看每一个体扫,它们的液态水含量均较低(LE≪17000 g·m-2),结构非常松散(d≪6.02 km),延伸厚度有限,但它们移动较慢,经3个体扫后,后者的累加液态水含量就超过了强降水阈值,而前者经5个体扫后累加液态水含量仍达不到强降水阈值,且移出率已变得较高,因此前者不会发生强天气。
|
图 11 (a)~(e)天津小型无实况系统,最大水平跨度30~50 km,(f)~(h)南昌小型强降水系统,最大水平跨度30~50 km (a)天津201507160754,(b) 201507160800,(c) 201507160806,(d) 201507160812,(e) 201507160818,(f)南昌201406100700,(g) 201406100706,(h) 201406100712 Fig. 11 (a)-(e) small systems without severe weather in Tianjin, maximum horizontal width is 30-50 km; (f)-(h) small precipitation systems in Nanchang, maximum horizontal width is 30-50 km (a) Tianjin 201507160754, (b) 201507160800, (c) 201507160806, (d) 201507160812, (e) 201507160818, (f) Nanchang 201406100700, (g) 201406100706, (h) 201406100712 |
|
|
表 4 示例(3) 系统特征取值 Table 4 Feature values of systems in Example 3 |
站在审视50 km以内雷暴系统所引发的不同天气类型之间差异性角度,在分析其三维结构、强度分布以及移动特点的基础上,提出了50 km以内雷暴系统结构疏密性、移出率、液态水含量及累加液态水含量4项特征的构建算法,通过对这些特征在一定数量的历史样本上的分布分析,构建了分类决策树。其间,将冰雹系统和短时强降水系统互视为反例形成训练样本集,同时,还特别准备了一组未发生强天气的样本,以使对50 km以内雷暴系统的冰雹/短时强降水的两分类识别问题扩展为冰雹/短时强降水/非强天气的三分类识别;另外,根据引发冰雹+强降水的复合天气的系统应具有双重特性的观点,选用了在特征使用上比较灵活的分类树模型。
测试结果表明,本文方法能够在一定程度上解决50 km以内雷暴系统冰雹和短时强降水之间的分类识别问题,能够将冰雹+短时强降水这种复合天气识别出来。总体来看,本文算法对短时强降水的击中率(89.1%)高于对冰雹的击中率(79.8%),所带来平均误报率为10.6%。
本文实现的50 km以内雷暴系统强天气分类识别模型是强天气分类识别系统的有效补充,将两者融合后,可整体上提升强天气分类识别的品质。
本文研究工作尚未涉及对雷雨大风这种强对流天气的识别,未使用温、压、湿、风等环境物理场数据,将基于雷达数据的强对流天气分类识别工作置于大的背景场之中是本文作者后续欲展开的工作。
致谢:本项研究所用数据由天津市气象台、山东气象台和江西气象台提供,在此表示真诚的感谢!
陈敏, 郑永光, 王洪庆, 等, 2005. 一次降水过程的中尺度对流系统模拟研究[J]. 气象学报, 63(3): 313-324. DOI:10.11676/qxxb2005.031 |
杜小玲, 2013. 2012年贵州暴雨的中尺度环境场分析及短期预报着眼点[J]. 气象, 39(7): 861-873. DOI:10.7519/j.issn.1000-0526.2013.07.007 |
辜旭赞, 于晓晶, 唐永兰, 等, 2014. 一次华南-江南持续暴雨的大尺度水汽场和中尺度特大暴雨模拟诊断分析[J]. 气象, 40(1): 18-27. DOI:10.7519/j.issn.1000-0526.2014.01.003 |
郝莹, 姚叶青, 郑媛媛, 等, 2012. 短时强降水的多尺度分析及临近预警[J]. 气象, 38(8): 903-912. DOI:10.7519/j.issn.1000-0526.2012.08.002 |
井喜, 井宇, 陈闯, 等, 2014. 黄土高原β中尺度致洪暴雨特征及成因[J]. 气象, 40(10): 1183-1193. DOI:10.7519/j.issn.1000-0526.2014.10.003 |
李聪. 2014. 强冰雹自动识别技术与防雹作业决策方法研究. 天津: 天津大学.
|
鲁德金, 陈钟荣, 袁野, 等, 2015. 安徽地区春夏季冰雹云雷达回波特征分析[J]. 气象, 41(9): 1104-1110. |
阮秋琦, 2009. 数字图像处理基础[M]. 北京: 清华大学出版社, 125.
|
苏君毅. 2006. 引起中尺度对流系统移动传播的环境场研究. 上海: 华东师范大学.
|
孙建华, 李娟, 沈新勇, 等, 2015. 2013年7月四川盆地一次特大暴雨的中尺度系统演变特征[J]. 气象, 41(5): 533-543. DOI:10.7519/j.issn.1000-0526.2015.05.002 |
孙靖, 王建捷, 2010. 北京地区一次引发强降水的中尺度对流系统的组织发展特征及成因探讨[J]. 气象, 36(12): 19-27. DOI:10.7519/j.issn.1000-0526.2010.12.003 |
王萍, 潘跃, 2013. 基于显著性特征的大冰雹识别模型[J]. 物理学报, 62(6). DOI:10.6038/cjg20130601 |
王啸华, 吴海英, 唐红昇, 等, 2012. 2009年7月7日南京短时暴雨的中尺度特征分析[J]. 气象, 39(9): 1060-1069. |
肖艳姣, 马中元, 李中华, 2009. 改进的雷达回波顶高、垂直积分液态水含量及其密度算法[J]. 暴雨灾害, 28(3): 210-214. |
杨吉, 郑媛媛, 夏文梅, 等, 2015. 雷达拼图资料上中尺度对流系统的跟踪与预报[J]. 气象, 41(6): 738-744. DOI:10.7519/j.issn.1000-0526.2015.06.008 |
袁美英, 李泽椿, 张小玲, 2010. 东北地区一次短时大暴雨β中尺度对流系统分析[J]. 气象学报, 68(1): 125-136. DOI:10.11676/qxxb2010.013 |
赵宇, 崔晓鹏, 高守亭, 2011. 引发华北特大暴雨过程的中尺度对流系统结构特征研究[J]. 大气科学, 35(5): 945-962. |
 2016, Vol. 42
2016, Vol. 42 