降水预报是天气预报业务体系的核心组成部分。由于降水本身物理过程的复杂性、模式次网格过程参数化的局限性等客观原因,模式输出的降水场相比其他物理量的预报准确性差。在降水预报业务中,天气型和物理量阈值判别相结合的分析方式得到普遍应用 (刘国忠等,2013),而确定适当的阈值在实际操作中并非易事,因为这些阈值往往随区域和季节而改变,这也是基于构成要素的预报方法的主要局限性之一 (俞小鼎,2011)。因此,对数值模式进行统计释用,建立降水预报客观模型,是提高模式降水预报准确率的一项有益尝试,所得结果也便于实现客观化、自动化业务运行。常用的模式输出统计 (MOS) 方法建立在多元线性回归技术基础之上,此技术对某些物理量的释用简单而行之有效,能提高模式预报结果的准确率,比如温度的预报 (刘还珠等,2004;陈豫英等,2005)。但对降水预报而言,该技术却有固有的局限性——多元线性回归最有效的预报是对正态分布的物理量所做的回归预报 (Goldberger,1962),但众多研究表明降水量多呈显著的非正态分布 (Ananthakrishnan et al,1989;Husak et al,2007)。因而从理论上讲,多元线性回归方法并不十分适合降水预报。
在降水预报中,最为关注的是强降水预报,其准确程度对于气象防灾减灾至关重要。强降水预报的第一步就是判别这种天气是否会出现,因而可转化为判别预报的问题。在判别预报领域已有较多的研究进展 (Sohn et al,2005;陈长胜等,2007;赵声蓉等,2009),其本质就是在所选众多影响因子的某一数值组合下,判断强降水发生的可能性有多大,即为条件概率的问题。而对于这种条件概率问题的处理,也有较多成熟方法,Logistic判别模型就是其中之一 (Hosmer et al,2004;徐晶等,2007;Prasad et al,2010;Imon et al,2012)。
Logistic判别模型有诸多优点,比如降水值会依据某一阈值转化成 (0,1) 的伯努利分布,其非正态分布的影响可得到一定程度消除、该模型能考虑条件概率的非线性变化、模型设计相对简单等。但它同样有一般多元线性回归的缺点,其一是当变量之间高度线性相关时,参数方程会出现类似“方程欠定”的情况,导致回归系数不稳定,进而影响到模型预报的稳定性 (许美玲等,2009);其二是可能存在模型拟合效果好而预报效果却不佳的问题。
本文将采用Logistic判别技术建立6 h间隔的强降水客观预报模型,并针对上述两个问题分别采用主成分分析技术和Bootstrap样本抽样技术 (Felsenstein,1985;Efron et al,1986) 设计3种不同模型技术方案,进行对比试验和评估。
1 资料和方法 1.1 资料本文使用的降水量资料为国家气象中心整编的666个国家站6 h间隔的降水观测资料。建模所用的物理因子取自美国大气海洋中心的FNL分析资料,该资料是经过同化的格点分析场资料,其准确性已在一些文章中讨论过 (Fu et al,2006);该资料集包含不同层次的风场、高度场、温度场、相对湿度场、垂直速度场等,共计96个变量,空间分辨率为1°×1°,时间分辨率为6 h。两种资料时间长度均为2002—2012年,其中前10年资料用于统计建模,2012年资料用于模型预报试验。
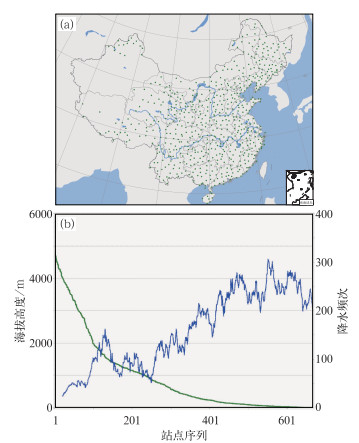
观测站点分布如图 1a所示,图 1b为各站点海拔高度与6 h降水量≥13 mm的强降水 (根据中央气象台现行业务规定,6 h降水量在13~25 mm为大雨,25~60 mm为暴雨,本文研究的是大雨及以上量级的强降水) 出现的频次。由图 1a可知,在我国中东部地区,降水观测站点分布密集并相对均匀,而西部高海拔地区的站点分布稀疏且不均匀。图 1b表明,强降水发生频次较高的站点海拔多在1000 m以下,部分等压面位于地表以下,因此对应的FNL物理量资料为根据大气垂直分布规律插值得到,但考虑到插值规律的确定性,以及这些物理量受其地表上层物理量的影响,其变化也可表征天气系统对相应站点的影响;且本工作针对每个站点选取因子建模,站点之间互不影响。
|
图 1 666个降水测站分布 (a)、站点海拔高度 (绿线) 与强降水频次 (蓝线)(b) Fig. 1 Disturbution of 666 observation stations (a), station altitude (green curve) and frequencies of heavy rainfalls (blue curve) (b) |
Logistic模型是一种常用的判别分析模型 (Hosmer et al,2004),其计算公式为
| $ P(\boldsymbol{X}) = \frac{1}{{[1 + \exp (- \boldsymbol{X\beta })]}} $ |
式中, X为影响因子矩阵,每个影响因子Xi以列向量的形式存储,每个行向量代表一次影响因子组合取样;β为参数列向量,采用最大似然原则估计;P (X) 代表在某次影响因子组合取样下强降水发生的概率值。如图 2所示,当影响因子组合Xβ逐渐增大时,表示强降水发生可能性的概率值P (X) 也在增大;反之亦然。另外,模型需要根据计算出来的概率值P (X) 判断是否发生强降水,因此存在一个判别阈值pc—若P (X) 计算结果≥pc则认为有强降水发生;反之亦然。基于现行预报业务中对强降水预报效果的检验方法,此处将使降水预报的TS评分最大作为pc取值的依据。

|
图 2 Logistic模型示意图 Fig. 2 Schematic diagram of the logistic discriminant model |
作为统计模型的第一步,便是计算各因子与强降水的相关性。根据降水量与物理量的统计相关关系和显著性检验结果,并结合业务预报实践经验,选取了14个物理量因子 (表 1) 为建模所用,并通过双线性插值方法插值到站点上,且以该降水时段内的物理量平均值作为该站的影响因子。表 2是物理量与降水量的相关系数。
|
|
表 1 影响因子选取表 Table 1 Impact factors used in the LDM |
|
|
表 2 影响因子与降水相关系数表 Table 2 Correlation coefficients between impact factors and precipitation |
由表 2可见,此相关关系与天气学基本原理是一致的:各层的相对湿度、比湿及露点温度等均和降水量呈正相关,各层的垂直速度和降水量呈负相关,表明丰沛的水汽和强烈的上升运动有利于强降水的发生。同时,各影响因子之间的相关性 (相关系数矩阵表略) 分析表明,部分因子之间存在着明显的相关性,即共线性特征比较显著。
2.2 3种方案的模型设计本文设计了3种使用Logistic模型的技术方案对比说明其预报效果,同时以北京站 (54511) 的7月降水模型为例,描述模型改进的具体过程和效果;对不同方案整体预报效果的检验评估则以666个站的统计结果加以讨论。
方案1:直接使用上述14个影响因子建立Logistic判别模型。
方案2:将上述14个影响因子进行主成分分析,并截取含有90%以上信息的主成分作为影响因子进行Logistic参数回算。
由于大气物理量内在的关联性,很多物理量之间存在着明显的共线性关系。为此提出参与回归计算的不是原始影响因子,而是经过主成分分析后的主成分。这样处理在理论上讲有两个优点:一是主成分分析可以根据需要截取一定数目的主成分,从而去除数据中的噪音部分以提高影响因子的信噪比,使计算出的参数是根据影响因子中有用的信号得到的;第二由于主成分之间是正交的,两两线性无关,因此避免了因子共线性问题对模型参数的影响。
方案3:使用Bootstrap有放回抽样技术来处理模型拟合效果好但预报效果较差的问题,同时在一定程度上解决强降水样本少造成的模型判别不稳定的问题。
很多预报模型的拟合结果较好,但是实际预报效果并不是很好。其中有两点重要的原因:第一是减小拟合的方差并不能代表模型对于真实物理过程的拟合更加准确——相反由于过分考虑数据中的细节特征,将很多噪音虚假信息也做了拟合考虑,反而增大了与真实物理过程的差异性,导致预报效果不佳,此即数据处理中所谓的“过拟合”现象;第二是大气波动的波谱很广,且为非平稳随机过程,利用某一时段内的数据做出的拟合计算,并不能对多种谱段都做出很好拟合。
为此提出使用Bootstrap有放回抽样技术来处理这一问题。Bootstrap技术的核心是通过对原有样本进行有放回重复抽样来构造新样本,每次抽样构造的新样本成员数与原样本相等,这样便得到更多的样本组合用于训练模型。在有放回抽样过程中,一个样本成员可能被抽到多次,也可能不会被抽到。本方案对该技术运用的思路如下:对原始样本按一定数量比例 (80%) 进行有放回抽样,利用每次抽样的子样本数据进行Logistic模型参数β的计算;进行1000次抽样,就可计算1000次模型参数,最终对这1000次参数计算平均值作为最终参数结果。从理论上讲,由于随机抽样的缘故,每次样本分别随机来自不同年份,原始大气的波动会被打乱,保留下来的就是平稳信息部分。
2.3 3种方案的模型结果对比分析如方案设计部分所述,为了便于对比不同方案产生的模型细节变化,将使用北京站 (54511)7月大雨判别模型为例加以说明,3套方案均通过χ2分布的显著性检验,但预报性能却各不相同。
首先利用方案1进行建模,得到Logistic模型的β参数如表 3。
|
|
表 3 方案1的Logistic模型β参数表 Table 3 The β parameter of the LDM in Scheme 1 |
由表 3可见,部分β参数出现了和相关分析 (表 2) 矛盾的结论,比如850 hPa比湿和降水量相关系数为0.174,为正相关,表明850 hPa比湿越大越有利于降水的发生。而在方案1的Logistic模型中其参数为-2.983,对概率值起到负作用,即850 hPa比湿越大越不利于降水的发生。这样建立的模型显然是违背天气学基本原理的。产生这一现象的主要原因就是影响因子之间存在显著的共线性,导致确定模型参数时出现类似“方程欠定”的现象。虽然此模型由于拟合自由度较大,拟合结果较好;但当在预报阶段使用时,只要存在微小的影响因子扰动,便会对方程的预报效果产生较大影响——而这些微小的扰动是不可避免的。因此使用方案1设计的模型做强降水判别预报是不稳定的,且有可能出现违背天气学基本原理的现象。
利用方案2进行建模,首先对影响因子进行主成分分析,得到如下累积方差表 (表 4)。
|
|
表 4 方案2主成分分析累积方差表 Table 4 Accumulated variances of principal component analysis in Scheme 2 |
由表 4可见,虽然有14个影响因子,但是影响因子所包含的信息却集中在少数几个主成分上。如第一个主成分就占51.9%的解释方差,包含了影响因子一半的信息量;前6个主成分共占93.6%的解释方差,包含绝大部分有用的信息。而后面8个主成分仅占6.4%的解释方差,所占比例已非常小,几乎可认为是噪音信号。因此通过主成分分析,既可以提取主要的影响因子信息用于建立模型,同时可以保证主成分之间的正交性,避免了参数受影响因子共线性的影响。
通过主成分分析,截取前6个主成分用于Logistic模型参数的计算,最后反算到14个影响因子上得到β参数。具体反算方法为
| $ {\boldsymbol{\beta} _{{\rm{fact}}}} = {\boldsymbol{V}_{\bmod {\rm{el}}}} \times {\boldsymbol{\beta }_{\bmod {\rm{el}}}} $ |
式中,β fact为影响因子系数,V model为主成分模态,β model为主成分序列的系数。由表 5可见,方案1中出现的参数β与相关系数的矛盾 (表 3) 被去除了,相对湿度、比湿、露点温度对应的参数都为正值,垂直速度的参数为负值,这和前面的相关分析以及天气学基本原理一致。同时,参数β的绝对值总和相比于方案1的绝对值总和要小很多,而在影响因子与预报因子量级一致的情形下,参数β的绝对值总和越小代表预报方程越稳定 (赵进文,1995)。因此方案2模型的稳定性优于方案1。此外,参数β有明显的相对大小。如在相对湿度因子中,700 hPa相对湿度的系数就显著高于850及925 hPa,也就是说对于北京地区7月的降水,700 hPa相对湿度的重要性高于850和925 hPa。其他影响因子也存在类似的相对重要性,可为预报员把握重要预报信息提供依据。
|
|
表 5 方案2的Logistic模型β参数表 Table 5 The β parameter of the LDM in Scheme 2 |
利用方案3进行建模,由Bootstrap抽样的特性,可定义一个表征参数优劣性的指标量
|
|
表 6 方案3的Logistic模型β参数及指标量G表 Table 6 The β parameter of the LDM and the G index in Scheme 3 |
由表 6可见,通过Bootstrap抽样建立的模型,不仅可以给出参数β的估计值,而且可以给出这个参数值的相对优劣性。比如850及925 hPa相对湿度就不如700 hPa相对湿度稳定且重要。同时,某些影响因子的参数相比于方案2(表 5) 的调整较大:如850 hPa相对湿度、700 hPa垂直速度等,说明这些影响因子受大气的周期性影响较大,在时间序列中不够平稳;有些则调整较小,如700 hPa比湿、500 hPa垂直速度,说明这些影响因子受周期性影响较小,在时间序列中相对平稳。因此这些调整本质与上述参数在强降水判别中的重要性及稳定性有关,而通过Bootstrap抽样可以在数据信息量一定的情况下做到最优化处理。
为展现3种方案统计意义上的效果,以2012年7月全国666个站大雨及以上量级强降水的6 h预报试验结果加以说明。
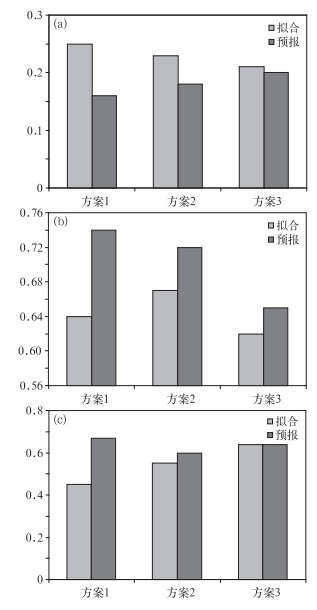
图 3a为3种方案模型的2012年7月全国大雨及以上量级降水的6 h预报TS评分对比,可见从第1到第3种方案的拟合TS评分逐渐降低,但是预报TS评分却逐渐升高。第1种方案拟合TS评分为0.25,但预报TS评分却只有0.16,相比拟合效果差了许多。原因正如上文所述:由于完全引入14个影响因子拟合自由度较大,拟合评分自然会高;但由于因子共线性作用以及噪音信号的影响,导致参数β不稳定,实际微小的因子变化都会使模型结果发生变化,因而预报效果是3种方案里最差的。方案2对影响因子做了主成分分析,只保留了前几个信号显著的主成分,虽然拟合自由度降低,导致拟合的评分不如方案1,但是预报的TS评分却高于方案1,主要原因就是消除影响因子的共线性作用并减少噪音信号的影响。而方案3,拟合的TS评分相比方案2要低,但是预报的TS评分却高于方案2,主要原因在于去除了大气波动的影响仅保留了平稳信息部分。图 3b为3种方案的空报率对比图,可见方案3拟合及预报的空报率均为最低,拟合和预报结果相差也最小,表明模型预报稳定性最高。图 3c为漏报率对比图,方案1的拟合漏报率虽然最低,但预报漏报率最高;方案3的拟合及预报漏报率虽然不是最低,但两者之间差异最小也说明模型稳定性在三者中为最高。
|
图 3 3种方案模型对2012年7月全国666个站6 h间隔6 h预报时效的大雨预报TS评分 (a),空报率 (b) 及漏报率 (c) Fig. 3 The TS scores (a), false alarm ratio (b) and false negative rate (c) of the three schemes in forecasting the 6 h heavy rainfall in July 2012 |
根据上述技术方案的对比分析,在中央气象台建立了基于Logistic回归模型的6 h间隔强降水客观预报系统并业务化运行。图 4为其技术路线和业务流程。该系统分为参数训练模块和业务计算模块,采用欧洲中心数值模式预报场计算物理因子,每日03和15时共运行2次,每次运行时间约15 min,输出产品有站点和格点两种格式,可以满足实时业务使用需求。由于该模型运用的是二分法判别思路,即“有或无”大雨,因此最终预报产品是6 h降水量≥13 mm的站点或格点,而非具体降水量。

|
图 4 基于Logistics回归模型的强降水客观预报系统技术路线和业务流程 Fig. 4 Technique route and operational flow of the LDM heavy rainfall forecasting system |
采用NCEP FNL逐6 h分析场资料建模,用NCEP、EC和T639等模式进行预报对比试验,发现基于EC预报场的模型预报性能最好 (图略)。同时,考虑到EC模式的中短期预报性能一般优于其他数值模式,因此,实时业务中采用EC模式预报场资料作为模型物理量的输入场。
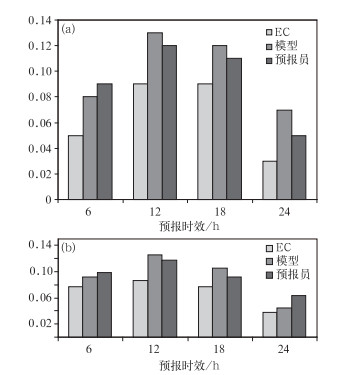
图 5分别是2013和2014年汛期本模型与EC数值模式、预报员的强降水预报TS评分对比。由图可知,模型对6 h间隔的强降水预报较数值模式本身有较明显而稳定的订正作用,部分时段TS评分高于预报员,具有一定的业务参考价值。进一步分析发现,模型较高的TS评分得益于其分别降低了数值模式的漏报率和主观预报的空报率 (图略)。
|
图 5 2013年 (a) 和2014年 (b)6—8月全国6 h间隔24 h预报时效强降水预报TS评分 Fig. 5 Comparison of the TS scores of LDM, EC model and forecasters in forecasting 6 h heavy rainfall from June to August in 2013 (a) and 2014 (b) |
强降水客观预报一直是统计释用领域的重点和难点。本文根据强降水与物理量场的相关关系,利用Logistic判别模型并对其进行一定的技术改进 (如对物理量进行主成分分析、采取有放回抽样技术等),建立强降水客观预报模型,得到如下结论:
(1) 影响因子不加处理而直接应用于Logistic模型,会导致部分模型参数与相关分析的结论及天气学基本原理相矛盾,同时模型参数受共线性和噪音影响表现得不甚稳定,拟合效果虽较好,但预报效果较差。
(2) 将影响因子通过主成分分析,提取前几个主成分应用于Logistic模型,可有效消除影响因子的共线性作用并去除噪音信号。虽然拟合自由度下降,拟合效果降低,但预报效果却明显改善。
(3) 由于大气非平稳随机过程,存在多时间尺度波动,因此使用Bootstrap抽样技术,去除受波动影响部分仅保留平稳过程信息,同时改善强降水样本数偏少造成的模型判别效果不佳的状况。这样改进后的Logistic模型,虽然拟合效果进一步下降,但预报效果却是3种方案里最好的;并且拟合与预报效果非常接近,说明模型的稳定性也是3种方案里最优的。
(4) 连续两年的业务化运行表明,经过技术改进的Logistic强降水预报模型较数值模式直接输出的降水预报性能有一定提高,且预报效果较为稳定,可为强降水预报业务提供参考依据。
3种方案虽逐步改进,但TS评分仍然不及0.2,预报和实际降水分布仍有较大差异,主要原因是强降水大多是由中尺度系统直接造成,而目前考虑的影响因子仅包含大尺度信息;同时,模型建立在数值模式输出场的基础上,不可避免地受到模式偏差的影响。因此,如何引入多尺度有效信息进入模型,并尝试订正模式系统性误差,是以后改进的重要方向。
陈长胜, 王慧敏, 慕秀香, 等, 2008. 吉林省旬降水量的客观分级方法探讨[J]. 气象, 33(11): 87-92. |
陈豫英, 陈晓光, 马金仁, 2005. 基于MM5模式的精细化MOS温度预报[J]. 干旱气象, 23(4): 52-56. |
刘国忠, 黄开刚, 罗建英, 等, 2013. 基于概念模型及配料法的持续性暴雨短期预报技术探究[J]. 气象, 39(1): 20-27. DOI:10.7519/j.issn.1000-0526.2013.01.003 |
刘还珠, 赵声蓉, 陆志善, 等, 2004. 国家气象中心气象要素的客观预报——MOS系统[J]. 应用气象学报, 15(2): 181-191. |
徐晶, 张国平, 张芳华, 等, 2007. 基于Logistic回归的区域地质灾害综合气象预警模型[J]. 气象, 33(12): 3-8. DOI:10.7519/j.issn.1000-0526.2007.12.001 |
许美玲, 段旭, 丁圣, 2009. 客观预报方程中因子的选取及应用效果分析[J]. 气象, 35(9): 112-118. DOI:10.7519/j.issn.1000-0526.2009.09.015 |
俞小鼎, 2011. 基于构成要素的预报方法——配料法[J]. 气象, 37(8): 913-918. DOI:10.7519/j.issn.1000-0526.2011.08.001 |
赵进文, 1995. 复共线影响点的主成分诊断[J]. 数理统计与应用概率, 10(2): 22-28. |
赵声蓉, 赵翠光, 邵明轩, 2009. 事件概率回归估计与降水等级预报[J]. 应用气象学报, 20(5): 521-529. DOI:10.11898/1001-7313.20090502 |
Ananthakrishnan R, Soman M K, 1989. Statistical distribution of daily rainfall and its association with the coefficient of variation of rainfall series[J]. Inter J Climat, 9(5): 485-500. DOI:10.1002/(ISSN)1097-0088 |
Efron B, Tibshirani R, 1986. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy[J]. Statis Sci, 1(1): 54-77. DOI:10.1214/ss/1177013815 |
Felsenstein J, 1985. Confidence limits on phylogenies: An approach using the bootstrap[J]. Evolution: 783-791. |
Fu G, Guo J, Xie S P, et al, 2006. Analysis and high-resolution modeling of a dense sea fog event over the Yellow Sea[J]. Atmos Res, 81(4): 293-303. DOI:10.1016/j.atmosres.2006.01.005 |
Goldberger A S, 1962. Best linear unbiased prediction in the generalized linear regression model[J]. J Amer Statis Assoc, 57(298): 369-375. DOI:10.1080/01621459.1962.10480665 |
Hosmer Jr D W, Lemeshow S. 2004. Applied logistic regression. New York: John Wiley & Sons.
|
Husak G J, Michaelsen J, Funk C, 2007. Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications[J]. Inter J Climat, 27(7): 935-944. DOI:10.1002/(ISSN)1097-0088 |
Imon A H M R, Roy M C, Bhattacharjee S K, 2012. Prediction of rainfall using logistic regression[J]. Pakistan J Statis Opera Res, 8(3): 655-667. DOI:10.18187/pjsor.v8i3.535 |
Prasad K, Dash S K, Mohanty U C, 2010. A logistic regression approach for monthly rainfall forecasts in meteorological subdivisions of India based on DEMETER retrospective forecasts[J]. Inter J Climat, 30(10): 1577-1588. |
Sohn K T, Lee J H, Lee S H, et al, 2005. Statistical prediction of heavy rain in South Korea[J]. Adv Atmos Sci, 22(5): 703-710. DOI:10.1007/BF02918713 |
 2016, Vol. 42
2016, Vol. 42 