2. 南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044;
3. 江苏省大数据分析技术重点实验室,南京 210044
2. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044;
3. Jiangsu Key Laboratory of Big Data Analysis Technology, Nanjing 210044
近年来,因人们对能源需求的不断增加,煤、石油和天然气等不可再生资源被大量开采,其储量不断减少,同时这些能源的广泛使用也带来全球气候变暖的加快和环境污染的加剧,寻求清洁可再生能源的课题日益受到人们的关注。风电作为环保清洁的可再生资源,正逐渐受到各个国家的重视。由于风速具有随机性和间歇性,必然增加风能并入电网的难度,因此准确的风功率预测日益成为人们研究的热门和重点(雷亚洲等,2002)。风速的预测是风电功率预测的基础,若能提前准确的对风电场中的风速进行预报和评估,就可以有效地解决大规模风力运行和并网的难题(张保会等,2012)。
风电场风速在时间尺度上分为超短期(未来15 min到4 h内)、短期(未来72 h内)、长期(数周或数月),短期风速预测的准确性有利于电力调度部门调整计划,减轻风能的并入对电网的不利影响。本文重点关注风电场短期风速的订正研究。目前,常采用MM5、WRF等中尺度数值模式来预报短期风速。WRF模式使用数值天气预报资料降尺度来预报风速,预报时间更长、准确率更高(孙川永等,2009)。但由于现阶段WRF模式受物理参数化方案不完善、分辨率较低、地形不够精确等因素的影响,导致WRF模式的预报结果误差较大、预报结果具有不确定性(常俊等,2015;张宇等,2013;王益柏等,2014)。由于风能与风速的三次方成正比,较小的风速误差就可能带来较大的风电功率误差,因而有必要对WRF模式预报风速进行订正,进一步提高短期风速预报的准确度(方艳莹等, 2012, 许杨等,2013)。李茜等(2014)利用相似Kalman滤波法对WRF模式预报风速进行订正研究,结果表明对预报风速进行订正后,模式预报误差减小,预报准确率提高了。徐晶晶等(2013)利用相似误差法对WRF模式预报风速进行订正,减小了系统误差和随机误差,提高了短期预报的准确率;祝赢等(2013)利用线性滚动极值处理方法对WRF模式预报风速进行订正,结果表明采用滚动极值处理方法订正后的WRF模式预报风速的误差得到有效的降低,预报精度有了较大提高。这些研究表明经过了订正后的WRF模式预报风速精度明显提高,但在这些研究中,风速订正方法需要进行大量的实验研究,预报误差的大小取决于各个模型建立的复杂与否。ELM算法比传统的学习算法速度更快,数学模型简单,具有良好的泛化性能,在短期风速订正的研究中具有突出的优势。
本文利用WRF模式预报70 m高度处风速,分析预报风速与风电场风机轮毂高度70 m处的实际风速的误差,再利用ELM算法订正WRF模式预报风速。结果表明,该方法能够有效地减小WRF模式预报的误差,提高了短期风速预报的精度。
1 资料与方法 1.1 WRF模式介绍WRF模式是由美国NCAR、NOAA联合一些大学和研究机构开发的区域中尺度数值预报模式(章国材,2004)。本文中WRF模式采用三重嵌套网格,网格数分别为79×77、91×91和112×112,网格间距分别为27、9和3 km。WRF模式边界资料采用美国国家环境预报中心(NCEP)的全球大气环流模式GFS初始场资料,每6 h一次、分辨率为1°×1°。模拟时段为2014年1—12月。模拟结果输出时间间隔为15 min。模式输出要素为70 m处的气象数据,包括风速、风向、气温、气压及空气湿度等。
1.2 风电场及资料选取本文以我国东部沿海某风电场为研究对象,所用资料为风电场风机轮毂高度70 m处的实测风速值,风速数据由SCADA系统采集,时间分辨率为15 min。
以2014年全年的WRF预报风速作为实验资料,采用ELM订正算法逐月对WRF模式预报风速进行订正:从每月中随机抽取1500组预报风速数据,以前1000组数据作为训练样本建立订正模型,后250组数据作为检验样本检验模型,最后利用训练好的模型订正最后250组数据。
1.3 极限学习机(ELM)算法极限学习机(ELM)是单隐藏层前馈神经网络(Single hidden Layer Feed forward Networks,SLFNs)中一种很有效的学习算法(Huang et al,2006)。设M个不同的样本{(xi, ti), i=1, …, N},其中x=(xi1, xi2, …, xin)T∈Rn,t=(ti1, ti2, …, tim)T∈Rm,含有N个隐层神经元及激活函数为g(x)的标准SLFNs数学建模可表示为:
| $ \begin{array}{*{20}{l}} {\sum\limits_{i = 1}^N {{\mathit{\boldsymbol{\beta }}_i}g({x_j})} = \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{\beta }}_i}g} ({\mathit{\boldsymbol{w}}_i} \cdot {x_j} + {b_i})}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1, \cdots ,M} \end{array} $ | (1) |
式中,wi=[wi1, wi2, …, win]T是连接第i层输入结点与隐层结点的权值向量;βi=[ βi1, βi2, …, βin]T是连接第i个隐层结点与输出结点的权值向量;bi是第i层隐层结点的阈值;(wi·xj)表示wi和xj的内积,输出结点为线性结点。若含有N个隐层神经元及激活函数为g(x)的标准SLFNs可以零误差的逼近这M个样本,即网络实际输出等于期望输出,则式(1) 可以表示为:
| $ \begin{array}{*{20}{l}} {\sum\limits_{i = 1}^N {{\mathit{\boldsymbol{\beta }}_i}g({x_j})} = \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{\beta }}_i}g} ({\mathit{\boldsymbol{w}}_i} \cdot {x_j} + {b_i}) = {t_j}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1, \ldots ,M} \end{array} $ | (2) |
以上N个等式可以写成:
| $ \boldsymbol{H}\boldsymbol{\beta} = \boldsymbol{T} $ | (3) |
式中,
| $ \begin{array}{l} \mathit{\boldsymbol{H}}({w_1}, \cdots {w_N}, {b_1}, \cdots, {b_N}, {x_1}, \cdots, {x_M}) = \\ {\left[ {\begin{array}{*{20}{c}} {g({w_1}, {x_1} + {b_1})}& \cdots &{g({w_N}{x_1} + {b_N})}\\ { \vdots \;\;\;\;\; \vdots \;\;\;\;\; \vdots }&{}&{}\\ {g({w_1}, {x_M} + {b_1})}& \cdots &{g({w_N}{x_M} + {b_N})} \end{array}} \right]_{M \times N}}\\ \mathit{\boldsymbol{\beta }} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\beta }}_1^T}\\ \vdots \\ {\mathit{\boldsymbol{\beta }}_N^T} \end{array}} \right]_{N \times m}}, \mathit{\boldsymbol{T}} = {\left[ {\begin{array}{*{20}{c}} {t_1^T}\\ \vdots \\ {t_N^T} \end{array}} \right]_{N \times m}} \end{array} $ |
H是隐层输出矩阵,H第i行代表第i个训练样本关于所有隐层结点的输出;H的第j列代表所有训练样本关于第j个隐层结点的输出。ELM学习算法过程如下:
(1) 首先确定隐含层神经元个数,输入层与隐含层间的连接权值w以及隐含层神经元的偏置b随机赋值。
(2) 选择隐含层神经元的激活函数,该函数必须无限可微,进而求出H。
(3) 计算输出层权值
本文采用了相对均方根误差(rRMSE)和相对平均绝对误差(rMAE)衡量模型的订正效果。均方根误差(RMSE)如式(4) 所示,rRMSE是在原来均方根误差(RMSE)的基础上除以观测的平均值,表示均方根误差占实际观测的百分率,这种衡量指标更加客观评价了一个序列变化产生误差的相对大小,如式(5) 所示。rMAE是平均绝对误差除以平均观测值,如式(6) 所示。
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{[{{\hat x}_k}(i) - {x_k}(i)]}^2}} } $ | (4) |
| $ \begin{array}{l} rRMSE = \\ \left\{ {\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{[{{\hat x}_k}(i) - {x_k}(i)]}^2}} } /\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{x_k}(i)} } \right]} \right\} \times 100\% \end{array} $ | (5) |
| $ \begin{array}{l} rMAE = \\ \left\{ {\frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\hat x}_k}(i) - {x_k}(i)} \right|/\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{x_k}(i)} } \right]} } \right\} \times 100\% \end{array} $ | (6) |
式中,N表示样本序列的长度,
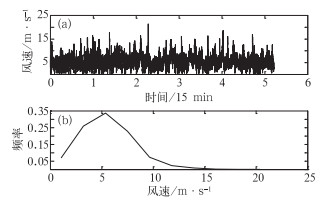
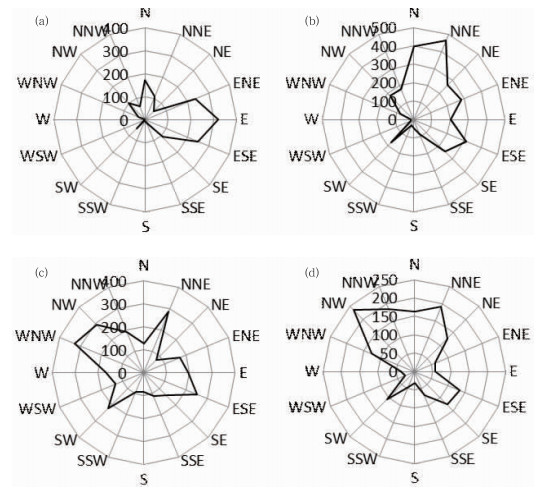
该风电场2014年全年测风塔70 m处风速数据和风速频率分布如图 1所示。从图 1可知,风速主要集中在3~10 m·s-1,风能分布较为集中。风电场四个季度的风向玫瑰图如图 2所示。图 2a表示春季的风向,主风向为E;图 2b表示夏季,主风向为NNE;图 2c代表秋季,方向多分布在WNW和ESE;图 2d代表冬季,主风向为NW。相比春、夏季,秋和冬季的风向变化幅度较大,各个方位的风向所占比例都较大,但总体上,四个季节的风向都相对较集中在主风向上。由图 1、图 2可知该风电场风向较为稳定,风能分布集中,适合风力发电。
|
图 1 全年风速数据(a)和风速频率(b)分布 Fig. 1 Annual wind speed data (a) and frequency distribution of wind speed (b) |
|
图 2 春(a)、夏(b)、秋(c)和冬(d)四个季度的风向分布 Fig. 2 Wind statistics of the four seasons of spring (a), summer (b), autumn (c), winter (d) |
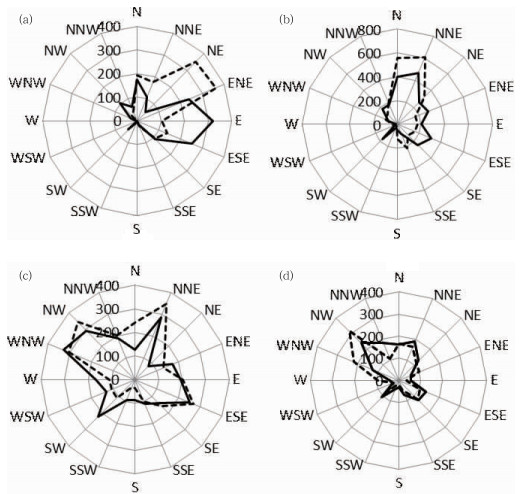
图 3为2014年测风塔与WRF模式预报风向玫瑰图的比较,图 3a~3d分别代表春、夏、秋、冬四个季节。从图 3中可知,除了春季WRF模式预报主风向略有偏差;夏、秋、冬三季的WRF模式预报风向与测风塔实测的风向有较好的一致性,风向概率分布相似,盛行风向一致,风频大小接近,说明WRF模式预报数据能较好地反映风速、风向等特征,利用WRF模式预报风电场短期风速是可行的。
|
图 3 春(a)、夏(b)、秋(c)和冬(d)四个季度的预测(虚线)与实测(实线)风向玫瑰图比较 Fig. 3 Comparison of wind rose diagram between prediction (dotted line) and observed (solid line) of the four seasons of spring (a), summer (b), autumn (c), winter (d) |
表 1为2014年12个月的WRF模式预报风速与测风塔风速(70 m处)的误差分析。从表 1中可以看出,WRF模式预报风速的rRMSE在30%~50%,误差最小的为7月,值为34.06%,误差最大的为9月,值为48.60%,各个月的相对均方根误差都较高。也导致了全年的平均RMSE为3.55 m·s-1,rRMSE为42.84%,rMAE为33.20%。由此可知,WRF模式预报风速相比测风塔实测风速的误差较大。因此,仅仅依靠WRF模式预报出的风速来预测风能是不够的,有必要采用一些智能算法对WRF模式预报风速订正,可以进一步提高WRF模式预报风速的准确率。
|
|
表 1 12个月风速的误差分析 Table 1 Wind speed error analysis of the twelve months |
为了解决WRF模式预报风速误差较大的问题,本文利用极限学习机(ELM)算法对WRF模式预报风速进行订正。表 2为经过ELM算法订正后各个月份WRF模式预报风速与测风塔实测风速的误差比较,RMSE在1.8 ~3.3 m·s-1,全年平均RMSE为2.42 m·s-1;rRMSE在14%~24%,全年平均rRMSE为18.74%;rMAE在10%~20%,全年平均rMAE为14.61%。与表 1相比,经过ELM算法订正后的12个月的rRMSE和rMAE均明显减小,均降低了20%~30%,全年平均RMSE减小了1.13 m·s-1。但各个月的订正结果也有着差异。春和秋季中,有两个月的rRMSE大于20%,其余月的rRMSE均小于20%。总体上来说,ELM算法对WRF模式预报风速进行订正提高了风速的预报能力,减小了模式的系统误差和随机误差,提高了预测风速的精度。
|
|
表 2 订正风速与实际风速的误差比较 Table 2 The error comparison of the revised wind speed and the observed wind speed |
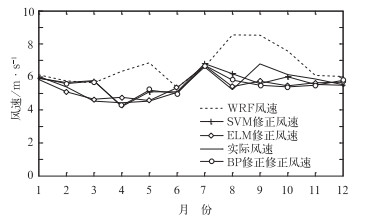
另外,本文也采用BP神经网络方法和SVM算法对WRF模式预报风速进行了订正,将ELM算法与SVM算法、BP神经网络算法的订正结果进行了比较,结果如图 4所示。从图 4中可以看出,通过SVM、BP、ELM算法对WRF模式预报风速订正,订正后的各月平均风速更接近于测风塔实测同期风速。因此,用WRF模式进行短期风速预测时,必须要进一步订正,才能得到更准确的风速,从而提高短期预测的精度。同时,与SVM、BP相比,ELM订正后的风速更接近实测风速。
|
图 4 不同模型的订正风速分布 Fig. 4 The distribution of revised wind speeds of different models |
表 3列出了不同订正算法对WRF模式预报风速订正结果的年均误差比较。从表 3中可以看出,ELM算法订正后的年均RMSE、rRMSE和rMAE相比BP神经网络、SVM订正结果小,ELM算法在短期风速订正中的精度比其他算法高,说明该算法的订正效果优于其他智能算法,同时在对全年WRF模式预报风速进行训练时,ELM算法较其他算法训练速度快,具有良好的泛化性能,从而验证了ELM算法的高效性。
|
|
表 3 三种订正算法的年均误差比较 Table 3 Comparison of the three revised algorithms annual error |
本文以我国东部沿海某风电场风机轮毂高度70 m处的2014年全年实测风速与同时刻WRF模式预报风速数据(70 m处)为实验资料,利用极限学习机(ELM)方法对WRF模式预报风速进行订正研究。主要结论如下:
(1) WRF模式对风速、风向等气象要素有着较好的预报效果,用于预报风电场短期风速是可行的。
(2) 用WRF模式进行短期风速预测时,必须要进一步订正,才能得到更准确的风速,从而提高短期风功率预测的精度。
(3) 使用ELM算法对WRF模式预报风速进行订正,订正后的WRF预报风速相对均方根误差和相对平均绝对误差降低了20%~30%,经过订正后的预报风速更趋近于实测风速,预报精度明显提高,说明利用ELM算法对预报风速进行订正可有效减小模式的系统误差和随机误差,能够提高风速预测的准确率。
(4) 相比其他的智能算法(BP神经网络、SVM算法),ELM算法在风速修正中的精度比其他的算法高,训练速度快,具有良好的泛化性能。ELM算法在风速订正研究中具有突出的优势。
常俊, 彭新东, 范广洲, 等, 2015. 结合历史资料的数值天气预报误差订正[J]. 气象学报, 73(2): 341-354. DOI:10.11676/qxxb2015.021 |
方艳莹, 徐海明, 朱蓉, 等, 2012. 基于WRF和CFD软件结合的风能资源数值模拟试验研究[J]. 气象, 38(11): 1378-1389. |
雷亚洲, 王伟胜, 戴慧珠, 2002. 风电对电力系统运行的价值分析[J]. 电网技术, 26(5): 10-14. |
李茜, 孙娴, 程路, 2014. 基于WRF模式与相似Kalman滤波法订正后的风速预报效果分析[J]. 水电能源科学, 32(6): 197-201. |
孙川永, 陶树旺, 罗勇, 等, 2009. 高分辨率中尺度数值模式在风电场风速预报中的应用[J]. 太阳能学报, 30(8): 1097-1099. |
王益柏, 梅娜, 范磊, 等, 2014. WRF模式对2013年1月华北一次大雾的数值对比试验[J]. 气象, 40(12): 1522-1529. DOI:10.7519/j.issn.1000-0526.2014.12.011 |
徐晶晶, 胡非, 肖子牛, 等, 2013. 风能模式预报的相似误差订正[J]. 应用气象学报, 24(6): 731-740. DOI:10.11898/1001-7313.20130610 |
许杨, 陈正洪, 杨宏青, 等, 2013. 风电场风电功率短期预报方法比较[J]. 应用气象学报, 24(5): 625-630. DOI:10.11898/1001-7313.20130512 |
张保会, 李光辉, 王进, 2012. 风电接入电力系统故障电流的影响因素分析及对继电保护的影响[J]. 电力自动化设备, 32(2): 1-8. |
章国材, 2004. 美国WRF模式的进展和应用前景[J]. 气象, 30(12): 27-31. DOI:10.3969/j.issn.1000-0526.2004.12.006 |
张宇, 郭振海, 林一骅, 等, 2013. 中尺度模式风电场风速短期预报能力研究[J]. 大气科学, 37(4): 955-962. DOI:10.3878/j.issn.1006-9895.2012.12092 |
祝赢, 柳艳香, 程兴宏, 等, 2013. 线性滚动极值处理方法对数值模拟风速的订正研究[J]. 热带气象学报, 29(4): 681-686. |
Huang G B, Zhu Q Y, Siew C K, 2006. Extreme learning machine: Theory and applications[J]. Neural Computation, 70: 489-501. |
 2016, Vol. 42
2016, Vol. 42 