2. 江苏省气象台,南京 210008;
3. 江苏省气象信息中心,南京 210008;
4. 江苏省气象服务中心,南京 210008
2. Jiangsu Meteorological Observatory, Nanjing 210008;
3. Jiangsu Meteorological Information Center, Nanjing 210008;
4. Jiangsu Meteorological Service Center, Nanjing 210008
短时强降水属于强对流天气的一种,是指对流系统在短时间内造成的较大雨量,降水强度超过20 mm·h-1,持续时间不超过6 h,降水集中时段一般在3 h以内。由于短时强降水历时短、降水强度大,其在短时间内形成的较大降水可形成城市暴洪,往往容易造成重大经济损失和人员伤亡(段鹤等,2014)。
江苏地处长江中下游地区,梅雨期间暴雨频发,特别是夏季短时强降水天气的发生频率更是呈显著上升趋势。由于短时强降水往往是中小尺度天气系统造成的,发生发展十分迅速,局地性较强,对短时强降水落区和时效的预报预警一直都是预报中的难点(郝莹等,2012;仇娟娟等,2013;牛金龙等,2015)。近年来,国内外关于强对流天气的预报方法已有很多研究成果,特别是利用对流参数进行潜势预报成为重要的方法之一(陈秋萍等,2010;冯民学等,2012;庞古乾等,2012; 樊李苗等,2013;李娜等,2015;郑栋等,2005; 李佰平等,2016;陈元昭等,2016)。同时,中尺度模式的发展也为基于对流参数的分类强对流天气预报提供了有效的途径(雷蕾等,2012;曾明剑等,2015a;2015b)。各种对流参数从不同侧面反映了环境特性,其在不同季节、不同种类的强对流天气下显示出的特性差异对判断对流发展与否以及预报对流天气类型都有一定的帮助(刘玉玲,2003;李耀东等,2004;孙继松等,2012)。郝莹等(2007)选取与雷暴相关性好的对流参数,在考虑了预报因子季节特征的基础上,对比使用判别分析法、指标叠加法对安徽地区的雷暴天气进行潜势预报研究。周后福等(2006)将稳定度指标和能量指标作为强对流天气的短时预报指标,结果表明:A指数和K指数具有一定的预报能力;位势不稳定指标在各地具有不同的临界值;当能量平衡高度较高时,强对流天气易于发生。
上述研究主要针对的是雷暴事件、闪电活动等强对流天气,而对短时强降水天气与各种物理量参数之间关系的研究较少,并且各地所研制的强对流天气物理量参数的阈值具有不同的侧重点。本文利用2004—2013年6—8月江苏省三个常规探空站(徐州、射阳、南京)的逐日高空探测资料,分析了物理量参数对上述三个地区短时强降水天气预报的指示作用,建立了江苏夏季短时强降水预报模型,以期为汛期短时强降水天气的预报提供参考依据。
1 数据和方法利用江苏省三个探空站(包括徐州、射阳以及南京)的逐日常规高空探测资料,借助MICAPS系统的物理量参数计算模块,计算了2004—2013年6—8月逐日08和20时的51个物理量参数。规定:若徐州市、盐城市以及南京市在当日08—14时或当日20时至次日02时内,出现任意1 h降水量在20 mm以上的降水过程,则将当日08或20时的相应探空站数据作为一个短时强降水样本,否则作为非短时强降水样本。剔除缺测资料后,共得到4905个样本,其中短时强降水的样本为223个,非短时强降水的样本为4682个。
其中,1 h降水量指的是整点小时值,来自于探空站所在行政区域的各国家基准气候站、基本气象站以及一般气象站的常规地面降水观测资料,包括徐州市的徐州站、丰县站、沛县站、邳州站、睢宁站和新沂站,盐城市的盐城站、射阳站、滨海站、大丰站、东台站、阜宁站、建湖站和响水站以及南京市的南京站、六合站、浦口站、溧水站和高淳站。
2 51个物理量参数的相关性分析为了选取与短时强降水有关的物理量参数,对51个物理量参数进行了计算,逐一进行挑选及分析,旨在找到对短时强降水预报有指示意义的判据。
假设短时强降水样本的Y=1,非短时强降水样本的Y=0,Xi为各物理量参数的值(i=1, 2, …, 51)。逐一分析Xi与Y之间的相关系数,并进行显著性检验,最后得到22个通过α < 0.01水平双侧检验、且相关系数 > 0.08的物理量参数,如表 1。其中剔除的参数包括:修正深对流指数MDCI、抬升指数LI、最大抬升指数LIMax、最优抬升指数BLI、斯拉维指数SLW、Faust指数、对流温度Tg、对流稳定度指数IC、条件对流稳定度指数ILC、最大对流稳定度指数BIC、Barber对流不稳定指数ICC、对流稳定度指数BI、杰弗逊指数JI、修正杰弗逊指数mJI、对流有效位能CAPE、抑制有效位能CIN、归一化有效位能GCAPE、能量螺旋度EHI、最大上升速度w_cape、大风指数VV、粗理查森数BRN、粗理查森数切变Shr、风暴强度指数SSI、Doswell云的厚度、地面温度、地面露点、850 hPa温度、700 hPa温度、500 hPa温度。
|
|
表 1 通过检验的物理量参数与短时强降水事件的相关系数 Table 1 The correlation coefficients of physical parameters having passed the significance test and the flash-heavy-rain events |
可以看到,整层比湿积分、A指数、干暖盖指数、强天气威胁指数、700 hPa比湿以及700 hPa相对湿度与短时强降水事件发生与否的相关系数达到0.18以上,对短时强降水有较好的指示意义,其中整层比湿积分的相关系数最高,达到0.22。
3 物理量参数的选定和分析理想情况下,如果物理量参数在有短时强降水的情况下和无短时强降水的情况下是完全不同的,即物理量参数在短时强降水样本与非短时强降水样本中的数值分布是没有任何交集的,则可以认为该物理量参数对短时强降水的发生有较好的指示意义(樊李苗等,2013)。实际上,出现这种理想情况的可能性是很小的,所以只有选择交集相对较小的物理量参数作为对短时强降水发生具有指示意义的参数。首先,统计出各物理量参数涵盖75%以上短时强降水样本的取值区间,如表 2。
|
|
表 2 各物理量参数涵盖75%以上短时强降水样本的取值区间 Table 2 The thresholds of physical parameters covering more than 75% of flash-heavy-rain samples |
对于非短时强降水样本,各物理量参数的取值落在上述涵盖75%以上短时强降水样本的取值区间的概率差异较大(图 1),热力稳定度参数和水汽参数平均分别仅为36.9%和36.5%,而动力及综合类参数则达到44.7%。其中,0~6 km垂直风矢量差ΔV0-6、风暴相对螺旋度SRH、通气管参数TQG以及Charba总指数ChTT对短时强降水事件指示性较差。
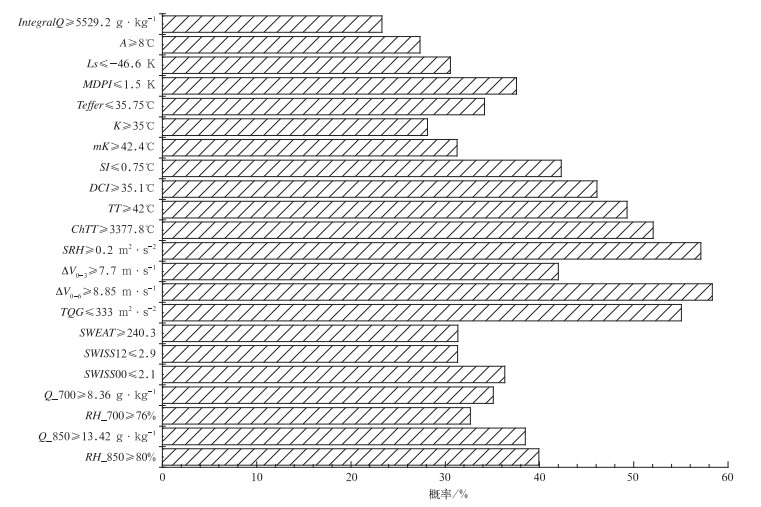
|
图 1 涵盖75%以上短时强降水样本的物理量参数取值区间在非短时强降水样本中的概率 Fig. 1 The probability of non flash-heavy-rain samples in the thresholds of physical parameters covering more than 75% of flash-heavy-rain samples |
从以上分析可以看出,仅仅反映了850 hPa一层的水汽情况以及中低层稳定度大小的总指数、Charba总指数、深对流指数以及沙氏指数对短时强降水的预报指示性均不是很强。然而,无论是考虑到700 hPa湿度的K指数和修正K指数,还是关注到500、700以及850 hPa温度露点差的A指数,甚至仅仅是代表整层比湿积分的IntegralQ参数,均对强降水的发生具有明显的指示意义。
中低层较厚的湿层有利于短时强降水天气的发生,反映中低层温湿差异的干暖盖指数和潜在下冲气流指数,与短时强降水呈反相关关系,也具有较好的指示意义。
3.2 动力及综合类参数强降水常发生于深层垂直风切变较弱的环境下(俞小鼎,2012),与雷雨大风或强冰雹等强对流天气的差异较大,但是却与普通雷暴单体产生的降水天气差异不大,从而也就使得风暴相对螺旋度参数以及0~6 km的垂直风矢量差失去了对短时强降水天气的指示作用。但是由于绝大多数的强降水都伴随低空急流(陶诗言,1980),结果显示0~3 km垂直风矢量差可以作为强降水发生的判据之一。
除此之外,由于短时强降水天气经常发生在高低空急流相互耦合造成的中小尺度对流系统中,所以描述低层850 hPa风矢与高层300 hPa风矢差异大小的通气管参数在短时强降水天气与无高低空急流发展的普通天气中的取值几乎没有差别,因此对是否发生短时强降水天气并不具有良好的指示意义。
表征850~500 hPa大气状态的热力学和动力学参数的组合物理量——瑞士雷暴指数和强天气威胁指数均可以较好地反映短时强降水天气发生的潜势大小。
3.3 水汽参数短时强降水虽然是属于强对流天气的一种,但其对水汽条件的要求比其他强对流天气要高得多。由前面的分析可知,水汽参数和热力稳定参数在短时强降水样本与非短时强降水样本中的数值分布的交集相较于动力参数及综合类参数要小得多,可以认为,水汽参数与热力稳定度参数对短时强降水事件的发生均较动力及综合类参数具有更显著的指示意义。
3.4 其他常用参数根据预报员的经验,我们还对850和500 hPa温差、850 hPa温度露点差、地面和925 hPa露点平均值以及925和850 hPa平均风速这四个常用的参数进行了计算和分析,结果显示:850和500 hPa温差与短时强降水事件的相关系数较小,只有-0.02,指示意义不强,不能选用。对850 hPa温度露点差、地面和925 hPa露点平均值以及925和850 hPa平均风速这三个参数来说,其在短时强降水样本与非短时强降水样本中数值分布的交集较大,对短时强降水事件的指示意义也略差些。
综上所述,选择取值区间涵盖75%以上短时强降水样本的、非短时强降水样本处于该取值区间的概率小于45%的、并且对短时强降水天气有一定指示意义的物理量参数进行重点分析。因此最终选取16个物理量参数(整层比湿积分、A指数、干暖盖指数、潜在下冲气流指数、Teffer指数、K指数、修正K指数、沙氏指数、0~3 km垂直风矢量差、强天气威胁指数、瑞士第二雷暴指数、瑞士第一雷暴指数、700 hPa比湿、850 hPa比湿、700 hPa相对湿度以及850 hPa相对湿度)用于建立短时强降水预报模型。
4 建立夏季短时强降水预报模型 4.1 物理量参数的月分布特征通过端须图可以得到发生短时强降水和未发生短时强降水时各月物理量参数的分布情况。假定各物理量参数的样本呈正态分布,则每个方框的上下底分别表示(准)正态分布两端占该物理量参数样本总数(包括短时强降水样本以及非短时强降水样本)25%个例的物理量参数值;方框中的黑线表示占样本总数50%个例的物理量参数值;从方框上下边延伸出的黑线的端点(*号)分别表示样本的最大和最小值(不包括异常值)(杨贵名等,2005)。
定义各月各物理量参数取值区间涵盖75%以上短时强降水样本为必要条件,得到:(1) 若非短时强降水样本处于该取值区间的概率小于25%,则将该物理量参数的取值区间作为该月判断短时强降水事件的指标;(2) 若非短时强降水样本处于该取值区间的概率在25%~50%,则将该物理量参数的取值区间作为该月短时强降水事件发生的有利条件;(3) 若非短时强降水样本处于该取值区间的概率大于50%,则认为该物理量参数对该月的短时强降水事件并无明显指示意义。
4.1.1 热力稳定度参数6月热力稳定度参数对短时强降水的发生具有较好的指示意义(图 2),非短时强降水样本落在涵盖75%短时强降水样本取值区间的概率仅为17.9%,其次是8月,为36.3%,而在7月,则达到43.3%,指示意义较差。其原因在于初夏时的6月,冬季风仍能够不时地渗透至江苏地区,使得中低层的热力稳定度参数呈现出过程性的变化,而随着夏季风的增强北抬,冬季风的减弱北缩,7月以后,江苏逐渐转为被副热带高压控制的盛夏天气,中低层的温度及湿度均明显增大,大气经常处于不稳定的状态下,热力不稳定参数的指示性也明显下降。
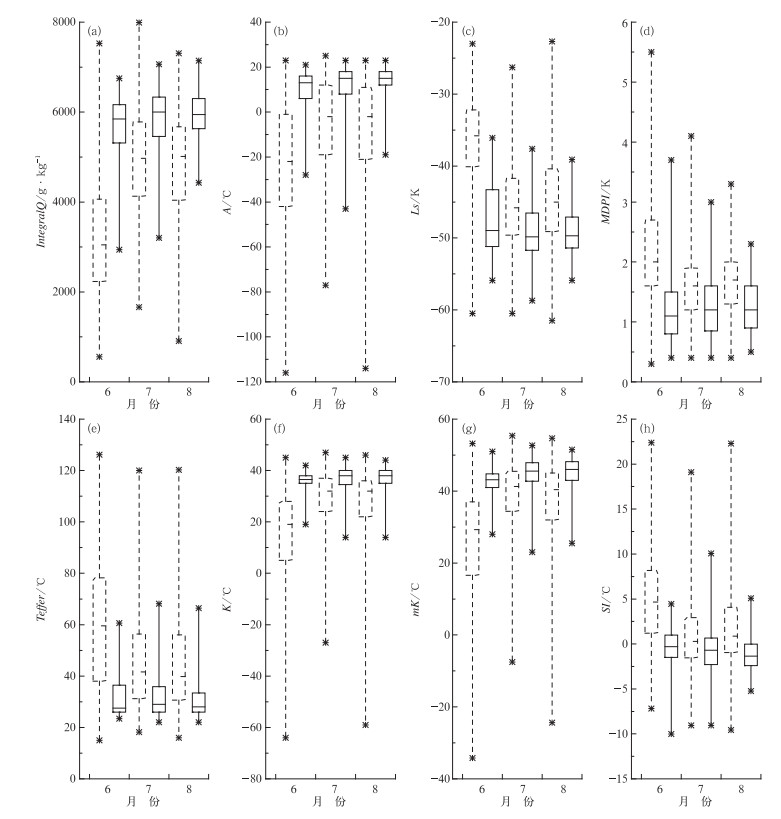
|
图 2 2004—2013年6—8月热力稳定度参数的端须图 (a)整层比湿积分, (b)A指数, (c)干暖盖指数, (d)潜在下冲气流指数, (e)Teffer指数, (f)K指数, (g)修正K指数, (h)沙氏指数(虚线框:非短时强降水样本;实线框:短时强降水样本) Fig. 2 Box-whisker plots of the thermal stability parameters from June to August 2004-2013 (a) IntegralQ, (b) A index, (c) dry and warm lid strength, (d) microburst-day potential index, (e) Teffer index, (f) K index, (g) modified K-index, (h) showalter index (dashed box: non flash-heavy-rain samples; solid box: flash-heavy-rain samples) |
因此,将IntegralQ≥5300 g·kg-1(图 2a)、A≥5℃(图 2b)、Ls≤-43 K(图 2c)、MDPI≤1.5 K(图 2d)、K≥34℃(图 2f)以及mK≥41℃(图 2g)作为判断6月短时强降水事件的指标,Teffer≤38℃(图 2e)以及SI≤1.2℃(图 2h)作为6月短时强降水事件发生的有利条件;将A≥9℃(图 2b)作为判断7月短时强降水事件的指标,IntegralQ≥5400 g·kg-1(图 2a)、Ls≤-47 K(图 2c)、Teffer≤36℃(图 2e)、K≥34℃(图 2f)以及mK≥43℃(图 2g)作为7月短时强降水事件发生的有利条件,而MDPI指数(图 2d)以及SI指数(图 2h)对7月短时强降水事件无明显指示意义;将IntegralQ≥5700 g·kg-1(图 2a)以及A≥11℃(图 2b)作为8月短时强降水事件的指标,Ls≤-47 K(图 2c)、Teffer≤34℃(图 2e)、K≥35℃(图 2f)、mK≥43℃(图 2g)以及SI≤0℃(图 2h)作为8月短时强降水事件发生的有利条件,而MDPI指数(图 2d)对8月短时强降水事件无明显指示意义。
4.1.2 动力及综合类参数与热力稳定度参数一样,6月动力及综合类参数同样对短时强降水的发生具有较好的指示意义(图 3),非短时强降水样本落在涵盖75%短时强降水样本取值区间的概率为20.3%,其次是8月,为42.1%,而在7月,则达到47.8%,指示意义较差。其原因在于动力参数或综合类参数中的动力因子均与中低层的垂直风切变相关,而6月中下旬至8月,随着夏季风的不断北推,江苏地区的中低层风速自南向北逐渐增大,导致垂直风切变的均值增大,进而使得动力及综合类参数的指示性变差。
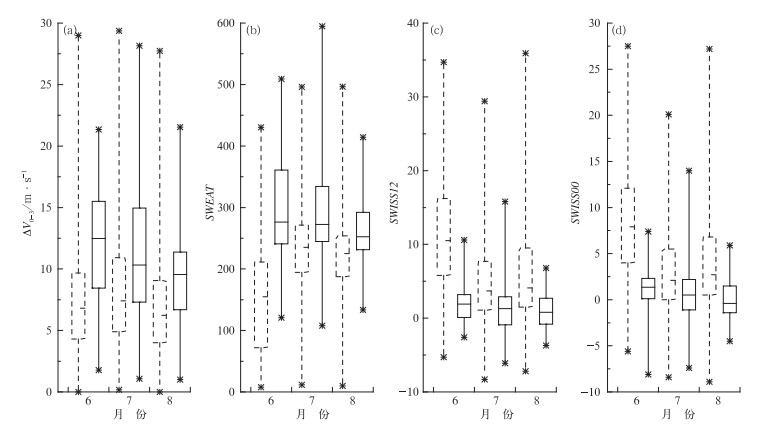
|
图 3 2004—2013年6—8月动力及综合类参数的端须图 (a)0~3 km垂直风矢量差, (b)强天气威胁指数, (c)瑞士第二雷暴指数, (d)瑞士第一雷暴指数(虚线框:非短时强降水样本;实线框:短时强降水样本) Fig. 3 Box-whisker plots of the dynamic and comprehensive parameters from June to August 2004-2013 (a) vertical wind vector difference of 0~3 km, (b) SWEAT, (c) SWISS00, (d) SWISS12 (dashed box: non flash-heavy-rain samples; solid box: flash-heavy-rain samples) |
因此,将SWEAT≥240(图 3b)、SWISS12≤3.3(图 3c)以及SWISS00≤2.5(图 3d)作为判断6月短时强降水事件的指标,ΔV0-3≥8.2 m·s-1(图 3a)作为6月短时强降水事件发生的有利条件;将SWEAT≥245(图 3b)以及SWISS12≤2.9(图 3c)作为7月短时强降水事件发生的有利条件,而ΔV0-3(图 3a)以及SWISS00(图 3d)对7月短时强降水事件均无明显指示意义;将ΔV0-3≥6.6 m·s-1(图 3a)、SWEAT≥230(图 3b)、SWISS12≤2.7(图 3c)以及SWISS00≤1.6(图 3d)作为8月短时强降水事件发生的有利条件。
4.1.3 水汽参数6月水汽参数对短时强降水事件的指示意义比动力及综合类参数显著,与热力稳定度参数相当(图 4),非短时强降水样本的取值落在涵盖75%短时强降水样本取值区间的概率为21.5%,其次是8月,为39.5%,而7月,则达到44.6%,指示意义较差。其原因与热力稳定度参数类似,也是由于春夏交替,夏季风携带大量水汽向北推进,使得水汽参数的均值增大而导致的。
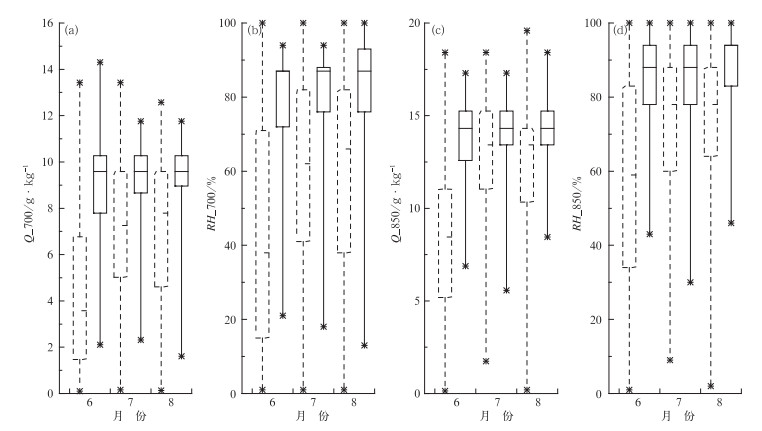
|
图 4 2004—2013年6—8月水汽参数的端须图 (a)700 hPa比湿, (b)700 hPa相对湿度, (c)850 hPa比湿, (d)850 hPa相对湿度(虚线框:非短时强降水样本;实线框:短时强降水样本) Fig. 4 Box-whisker plots of the moisture parameters from June to August 2004-2013 (a) 700 hPa specific humidity, (b) 700 hPa relative humidity, (c) 850 hPa specific humidity, (d) 850 hPa relative humidity (dashed box: non flash-heavy-rain samples, solid box: flash-heavy-rain samples) |
因此,将Q_700≥7.5 g·kg-1(图 4a)、RH_700≥72%(图 4b)、Q_850≥13.0 g·kg-1(图 4c)作为判断6月短时强降水事件的指标,将RH_850≥78%(图 4d)作为6月短时强降水事件发生的有利条件;将Q_700≥8.5 g·kg-1(图 4a)、RH_700≥76%(图 4b)作为7月短时强降水事件发生的有利条件,而850 hPa的比湿(图 4c)及相对湿度(图 4d)对7月短时强降水事件无明显指示意义;将Q_700≥9 g·kg-1(图 4a)、RH_700≥77%(图 4b)以及RH_850≥83%(图 4d)作为8月短时强降水事件发生的有利条件,而850 hPa的比湿(图 4c)对8月短时强降水事件亦无明显指示意义。
4.2 模型建立由上述分析可以看出,物理量参数的数值分布及其对短时强降水天气的指示性在不同月份存在较大差异,相较于7和8月,热力稳定度参数、动力及综合类参数以及水汽参数在6月对短时强降水天气的发生具有更好的指示意义。同时,不同类型的物理量对短时强降水天气的指示性也相差较大。一方面,由于短时强降水天气呈现出的是“湿”对流风暴的特征,其形成需要充沛的水汽,而热力不稳定又是对流风暴中上升气流发展的驱动力,这两类参数均是短时强降水发生的必要条件;另一方面,动力及综合类参数大多与垂直风切变相关,而强垂直风切变下强的高空风将冰晶粒子带到云砧处容易造成冰晶蒸发从而降低降水效率(俞小鼎,2012),弱垂直风切变又很难使得风暴有组织的增长。所以,水汽参数与热力稳定度参数对短时强降水事件的发生均较动力及综合类参数具有更显著的指示意义。因而,需要根据各月各类型物理量参数指示性的不同及其对短时强降水天气的不同判定指标分别建立预报模型。
选取4.1节分析的16个物理量参数,首先建立各参数的隶属函数。隶属函数值动态范围取-1~2,正值越大表示短时强降水天气发生的可能性越大,0表示短时强降水天气发生的可能性为零。因此,在各参数的隶属函数中,将上节分析得到的短时强降水事件指标区间的函数值取为2,有利条件区间的函数值取为1,不利条件区间的函数值取为-1,其他区间的函数值取为0。然后,通过隶属函数将对应的物理量转换到[-1, 2],得到单个参量对应的短时强降水事件的可能性大小。最后采用加权平均法,得到一个与短时强降水事件可能性大小相对应的组合量,作为预报短时强降水天气发生的指数S。
| $ S = \frac{{\sum {{w_i}{f_i}(x)} }}{{\sum {{w_i}} }} $ |
式中,fi(x)为物理量的隶属函数,wi为权重。本文根据6—8月各物理量参数对短时强降水天气指示性的强弱,分别赋予取值范围在1~10的权重。由此得到观测时刻(08时、20时,下同)之后0~1 h、2~3 h、4~6 h出现短时强降水天气以及观测时刻后0~6 h内未出现短时强降水天气的指数S。
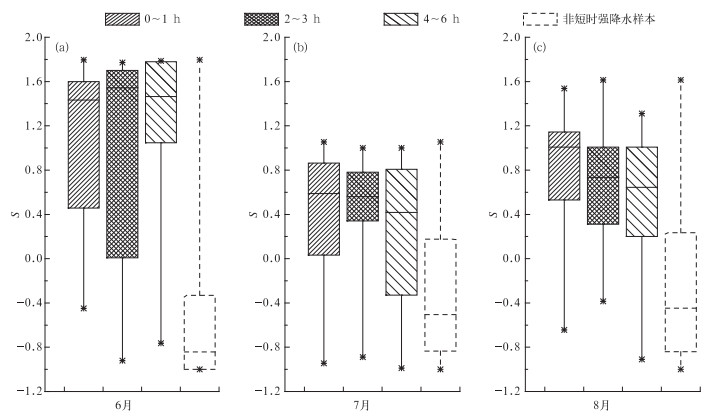
4.3 预报模型拟合率检验 4.3.1 2004—2013年样本拟合率分析结果显示(图 5),短时强降水样本S值的分布与非短时强降水样本的交集较小,区分度较好,可以认为该模型得到的指数S对短时强降水天气的发生具有一定的指示意义。
|
图 5 2004—2013年6—8月(a, b, c)观测时刻后0~1 h、2~3 h、4~6 h出现短时强降水天气以及观测时刻后0~6 h内未出现短时强降水天气的指数S的分布 Fig. 5 Box-whisker plots of the index S of flash heavy rain seen after 0-1 h, 2-3 h, 4-6 h of the observation time and no flash heavy rain after 0-6 h of the observation time from June to August 2004-2013 |
从观测时刻之后0~1 h、2~3 h以及4~6 h发生短时强降水天气的指数S的分布来看,其值阈区间几乎一致,并不是距离短时强降水发生时刻越近,S值就越大。所以,不能利用指数S做短时强降水天气发生时间的预报。
分析拟合结果(表 3):6月,有96.0%的样本拟合完全正确,对短时强降水样本拟合的准确率(TS评分)为25.0%,其中空报率为71.7%,漏报率为31.6%;7月,有80.9%的样本拟合完全正确,对短时强降水样本拟合的准确率(TS评分)为19.3%,其中空报率为79.1%,漏报率为29.5%;8月,有90.2%的样本拟合完全正确,对短时强降水样本拟合的准确率(TS评分)为19.6%,其中空报率为76.4%,漏报率为46.6%。拟合结果显示,由于短时强降水样本数明显偏少,导致模型对短时强降水样本的空报率偏高。
|
|
表 3 预报模型对2004—2013年6—8月短时强降水样本的拟合情况 Table 3 The fitting test of the flash heavy rain samples based on flash-heavy-rain forecast model from June to August in 2004-2013 |
使用该模型对2014年6—8月的短时强降水天气进行预报试验评估,共385个样本,其中短时强降水样本15个,非短时强降水样本370个。检验结果为:有94.3%的样本预报完全正确,对短时强降水样本预报的准确率(TS评分)为26.6%,具体各月情况见表 4。可以看到,各月的预报准确率均在25%以上,但由于样本较少,拟合结果并不具有普遍的代表性,模型优劣还需要更多的样本来验证。
|
|
表 4 预报模型对2014年6—8月短时强降水天气的预报情况 Table 4 The evaluation of forecasting test of flash heavy rain by flash-heavy-rain forecast model from June to August 2014 |
(1) 通过计算51个物理量参数与短时强降水事件的相关系数,并进行显著性检验,得到22个通过α < 0.01水平双侧检验、且相关系数 > 0.08的物理量参数:整层比湿积分、A指数、干暖盖指数、潜在下冲气流指数、Teffer指数、K指数、修正K指数、沙氏指数、深对流指数、总指数、Charba总指数、风暴相对螺旋度、0~3 km垂直风矢量差、0~6 km垂直风矢量差、通气管参数、强天气威胁指数、瑞士第二雷暴指数、瑞士第一雷暴指数、700 hPa比湿、850 hPa比湿、700 hPa相对湿度以及850 hPa相对湿度。
(2) 水汽参数与热力稳定度参数对短时强降水事件的发生均较动力及综合类参数具有更显著的指示意义。相较于7和8月,热力稳定度参数、动力及综合类参数以及水汽参数在6月对短时强降水天气的发生具有更好的指示意义。
(3) 通过分析22个物理量参数在短时强降水样本和非短时强降水样本中的值域分布特征,最终选取了16个物理量参数。利用端须图的方法,得到物理量参数在各月短时强降水事件中的阈值并将其作为判定指标,采用隶属函数转换法,建立了江苏夏季短时强降水预报模型。
(4) 按照灾害性天气评分标准,对2014年6—8月观测时刻后0~6 h内的短时强降水天气进行拟合率检验,以省辖市为区域,TS评分为25.0%~28.6%。
陈秋萍, 冯晋勤, 李白良, 等, 2010. 福建强天气短时潜势预报方法研究[J]. 气象, 36(2): 28-32. DOI:10.7519/j.issn.1000-0526.2010.02.004 |
陈元昭, 俞小鼎, 陈训来, 2016. 珠江三角洲地区重大短时强降水的基本流型与环境参量特征[J]. 气象, 42(2): 144-155. DOI:10.7519/j.issn.1000-0526.2016.02.002 |
段鹤, 夏文梅, 苏晓力, 等, 2014. 短时强降水特征统计及临近预警[J]. 气象, 40(10): 1194-1206. DOI:10.7519/j.issn.1000-0526.2014.10.004 |
樊李苗, 俞小鼎, 2013. 中国短时强对流天气的若干环境参数特征分析[J]. 高原气象, 32(1): 156-165. DOI:10.7522/j.issn.1000-0534.2012.00016 |
冯民学, 周俊驰, 曾明剑, 等, 2012. 基于对流参数的洋口港地区雷暴预报方法研究[J]. 气象, 38(12): 1515-1522. |
郝莹, 姚叶青, 陈焱, 等, 2007. 基于对流参数的雷暴潜势预报研究[J]. 气象, 33(1): 51-56. DOI:10.7519/j.issn.1000-0526.2007.01.008 |
郝莹, 姚叶青, 郑媛媛, 等, 2012. 短时强降水的多尺度分析及临近预警[J]. 气象, 38(8): 903-912. DOI:10.7519/j.issn.1000-0526.2012.08.002 |
雷蕾, 孙继松, 王国荣, 等, 2012. 基于中尺度数值模式快速循环系统的强对流天气分类概率预报试验[J]. 气象学报, 70(4): 752-765. DOI:10.11676/qxxb2012.061 |
李佰平, 戴建华, 张欣, 等, 2016. 三类强对流天气临近预报的模糊检验试验与对比[J]. 气象, 42(2): 129-143. DOI:10.11898/1001-7313.20160201 |
李娜, 冉令坤, 孙建华, 等, 2015. 基于NCEP/GFS资料的中国东部地区雷暴预报研究[J]. 气象学报, 73(3): 459-470. DOI:10.11676/qxxb2015.029 |
李耀东, 刘健文, 高守亭, 2004. 动力和能量参数在强对流天气预报中的应用研究[J]. 气象学报, 62(4): 401-409. DOI:10.11676/qxxb2004.041 |
刘玉玲, 2003. 对流参数在强对流天气潜势预测中的作用[J]. 气象科技, 31(3): 147-151. |
牛金龙, 黄楚惠, 李国平, 等, 2015. 基于高分辨率资料的湿螺旋度指标及其对成都强降水的预报应用[J]. 高原气象, 34(4): 942-949. DOI:10.7522/j.issn.1000-0534.2014.00053 |
庞古乾, 伍志方, 叶爱芬, 等, 2012. 珠三角地区前后汛期强对流过程物理量指数对比分析及阈值选取[J]. 热带气象学报, 28(6): 919-923. |
仇娟娟, 何立富, 2013. 苏沪浙地区短时强降水与冰雹天气分布及物理量特征对比分析[J]. 气象, 39(5): 577-584. DOI:10.3969/2012jms.0153 |
孙继松, 陶祖钰, 2012. 强对流天气分析与预报中的若干基本问题[J]. 气象, 38(2): 164-173. |
陶诗言, 1980. 中国之暴雨[M]. 北京: 科学出版社.
|
杨贵名, 宗志平, 马学款, 2005. "方框_端须图"及其应用示例[J]. 气象, 31(3): 53-55. DOI:10.7519/j.issn.1000-0526.2005.03.012 |
俞小鼎, 2012. 2012年7月21日北京特大暴雨成因分析[J]. 气象, 38(11): 1313-1329. |
曾明剑, 王桂臣, 吴海英, 等, 2015a. 基于中尺度数值模式的分类强对流天气预报方法研究[J]. 气象学报, 73(5): 868-882. |
曾明剑, 张备, 吴海英, 等, 2015b. 基于接近度概念的强对流天气预报方法研究[J]. 高原气象, 34(5): 1357-1368. |
郑栋, 张义军, 吕伟涛, 等, 2005. 大气不稳定度参数与闪电活动的预报[J]. 高原气象, 24(2): 196-203. |
周后福, 邱明燕, 张爱民, 等, 2006. 基于稳定度和能量指标作强对流天气的短时预报指标分析[J]. 高原气象, 25(4): 716-722. |
 2016, Vol. 42
2016, Vol. 42 