云是由悬浮在大气层中的水滴或冰粒子组成的可见集合体。云通过影响太阳的短波辐射和地球的长波辐射,对于地气系统的能量收支和水汽循环具有重要的调节作用,是影响气候变化的重要因子。同时,云对天气变化也有着显著的影响,任何一次降水的形成与发展都离不开云的参与。云顶高度(CTH)作为一个宏观参量,对于云微观参量的反演(Baum et al, 1994; Weisz et al, 2007; Garrett et al, 2009; 周非非等, 2010; 顾成明等, 2016)、云结构的分析(韩丁等, 2013; 严卫等, 2013; 孙晶等, 2015; 张晓等, 2015)、强对流天气的预警(Mack et al, 1983; Hasler et al, 1991; 郄秀书等, 2014; 张一平等, 2014)、卷云的时间演变研究(Mace et al, 2006; 寿亦萱等, 2014)等方面均具有非常重要的作用。
目前,通过卫星遥感手段反演云顶高度的方法主要分为几何关系法和通道辐射特性法。几何关系法直接测量距离,通常来说精度较高,但时间和空间覆盖范围小,探测效率低(Simpson et al, 2000; Weisz et al, 2007; 马烁等, 2014)。通道辐射特性法通过卫星接收到的辐亮度,间接反演云顶高度。通道辐射特性法精度通常低于几何关系法,但时间和空间覆盖范围大,利于连续性大范围探测。
最早的利用通道辐射特性的方法是亮温-廓线法(Fritz et al, 1962),该方法建立在对云的发射率已有先验知识的基础上。通常选用10~12 μm的红外波段,根据亮温计算实际温度,结合大气温度廓线插值得到云顶高度。该方法只适用于光学厚度较大的云。随后,Reynolds等(1977)加入了一个可见光通道,对亮温-廓线法进行了改进。通过使用一个多次散射模型,可见光通道辐亮度用来计算云的光学厚度,进而计算云的红外发射率,避免了使用先验发射率的主观性。之后,学者又提出了许多利用通道辐射特性反演云顶高度的算法,比较著名的有红外-水汽拟合法(Szejwach, 1982)、氧气A吸收带法(Fischer et al, 1991)、CO2薄片法(Menzel et al, 1992; Baum et al, 1994)等,目前都已在业务上得到应用,并取得了很好的效果。
以上提到的几种算法虽然大大促进了云顶高度反演的发展,但它们至少存在下面几种缺点之一:
(1) 算法过于简单,精度很低。
(2) 用到了可见光通道数据,无法计算夜间的云顶高度。
(3) 需要多个特定的光谱通道,目前许多卫星并不满足要求。
红外分裂窗法是一种快速有效的计算温度的方法,广泛应用于地表、海面和云顶温度的反演。该方法的优点是仅使用红外窗区通道1(~11 μm)的亮温T11和通道1与通道2(~12 μm)的亮温差BTD11-12,这两个通道是目前卫星传感器的常用通道,且不受白天和夜间的限制。Inoue (1985)利用NOAA-7上的AVHRR通道4(10.5~11.5 μm)和通道5(11.5~12.5 μm)的亮温,通过建立云顶温度和红外窗区的两个通道(11和12 μm)的亮温值的关系,反演出热带海洋上空半透明卷云的云顶温度和发射率。随后,Inoue (1987)提出了一种通过设定阈值判断云分类的方法,将云分成卷云、密卷云、积雨云和积云。在此基础上,Hamada等(2008;2010)提出云顶高度可以表述为(T11, BTD11-12)的函数,分别将静止卫星的(T11, BTD11-12)数据与船载(Hamada et al, 2008)和星载(Hamada et al, 2010)毫米波雷达云顶高度数据匹配,通过核回归法建立云顶高度查找表,取得了不错的效果。但是,由于计算时未对云进行分类,不同类型的云高度分布差异较大,导致核回归时高云和低云互相影响使误差增加,尤其是T11>270 K时反演效果较差。
本文首先提出一种云分类方法,基于支持向量机(SVM)原理,借助CloudSat光学厚度产品构建分类模型,将云分为透明云、半透明云和不透明云三类。然后依据红外分裂窗理论,用核回归法分别对三类云顶高度进行反演。最后将所得的结果与CloudSat的几何-激光雷达廓线产品进行对比,并选择个例进行分析,讨论反演方法的精度。
1 数据介绍本文主要用到同属A-Train卫星编队(Stephens et al, 2002)的Aqua、CloudSat和Calipso卫星数据产品。这三颗卫星在同一轨道上飞行,且彼此相差2 min以内,有效地解决了时空一致性问题,实现了多探测平台、多光谱频段及多传感器的协同观测。Aqua卫星上搭载的中分辨率成像光谱仪(MODIS)含有36个光谱通道,分布在0.4~14.4 μm的波长范围内,覆盖了可见光与部分红外波段。其中,通道31(中心波长11.03 μm)和通道32(中心波长12.02 μm)的辐亮度为本文所用到的红外分裂窗数据。CloudSat卫星上搭载的唯一有效载荷是94 GHz云廓线雷达(CPR)。CPR具有很强的穿透云层的能力,可以准确地描绘云内部的详细结构信息。CloudSat采取沿轨道垂直扫描的方式,可以提供星下点水平分辨率为1.7 km(沿轨)×1.3 km(跨轨),垂直分辨率为240 m的廓线。Calipso卫星上搭载了一部双波长激光雷达CALIOP,能提供气溶胶和云的垂直结构信息。CPR侧重于探测光学厚度较大的云层,而CALIOP则对纤细的薄卷云较为敏感。
当A-Train卫星编队穿过待探测的区域时,CloudSat的数据处理中心(DPC)将CPR的每条廓线都与其对应的A-Train卫星编队的其他传感器数据以及欧洲中期天气预报中心(ECMWF)提供的数值预报产品进行了汇编,并发布为10种标准数据产品和4种辅助数据产品。本文所采用的数据产品如表 1所示。数据产品的详细信息可参考http://cswww.cira.colostate.edu/。
|
|
表 1 本文所采用的数据产品描述 Table 1 Description of the data product used in this study |
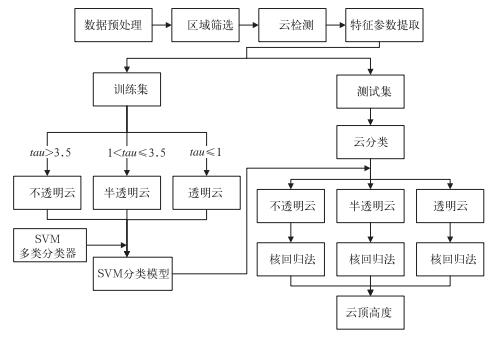
图 1为基于A-Train综合资料的云顶高度反演流程图,基本流程如下:
|
图 1 基于A-Train综合资料的云顶高度反演流程图 Fig. 1 Flowchart of CTH retrieval based on A-Train data |
(1) 数据预处理。剔除无效数据,将MODIS红外分裂窗通道的辐亮度转换为亮温。
(2) 进行区域筛选。选取纬度范围15°S~15°N的数据。
(3) 进行云检测。将云掩膜值大于30,T11范围200~285 K,云顶高度范围0~20 km的区域视为有云区域,并获取有云区域内各种物理参数。
(4) 提取特征参数。将MODIS通道31的亮温T11和通道31与通道32亮温差BTD11-12作为SVM分类的特征参数。
(5) 将样本集分为训练集和测试集,对于训练集,根据光学厚度tau的大小,分为透明云(tau≤1)、半透明云(1 < tau≤3.5) 和不透明云(tau>3.5)。
(6) 采用SVM多类分类器对训练集进行训练,得到SVM分类模型。
(7) 利用上一步得到的SVM分类模型对测试集进行分类,得到透明云、半透明云和不透明云。
(8) 对于三类不同类型的云,分别用核回归法反演云顶高度。
2.1 支持向量机简介支持向量机(Support Vector Machine, SVM)是在统计学习理论和结构风险最小化原理的基础上,一种解决分类问题的机器学习方法。SVM将分类问题转化为凸二次规划,进而求出全局最优解,克服了传统方法容易陷入局部极值的问题。SVM通过引入核函数,将线性不可分的样本向量映射到高维特征空间。SVM有效地解决了过学习和维数灾难等问题,具有较好的分类精度。目前SVM已在模式识别、基因分类、卫星遥感领域得到广泛的应用。
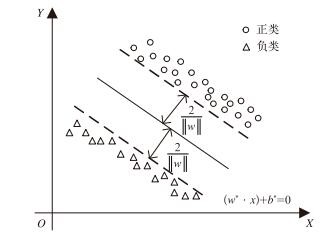
SVM的基本原理如图 2所示。对于两类分类问题,寻找最优超平面,该超平面能区分出两类样本点,并使两类样本集与该超平面的间距达到最大。对于多类分类问题,假设样本有M个类别(M>2),在处理时主要有两种方法:一类对余类分类(one versus the rest)和成对分类(one verse one)。本文中M=3,因此采用适合类数较少的成对分类方法:选取所有两类组合构造子分类器,共有M(M-1)/2个,在构造类别i和类别j的子分类器时(i < j, i, j=1, 2, …, M),将第i类样本看作正类,第j类样本看作负类,计算样本在每个类上的票数,票数最多的类别为最终结果。
|
图 2 SVM的基本原理示意图 Fig. 2 Schematic diagram of SVM |
核回归(kernel regression, KR)以核密度估计(kernel density estimation, KDE)理论为基础,是统计学中一种非参数随机变量条件期望的估计方法。KR具有学习能力强、健壮性高、计算复杂度低、容易实现等优点(Botev et al, 2010)。
对于二维概率密度,随机变量Z的变化与随机变量(X, Y)的分布有关,且X和Y相互独立。这里,X代表MODIS通道31亮温T11,Y代表通道31与通道32亮温差BTD11-12,Z代表云顶高度。
记Z对(X, Y)的联合概率密度的估计为
| $ \hat f\left({x, y} \right) = \frac{1}{{n{h_x}{h_y}}}\sum\limits_{i = 1}^n K \left({\frac{{x - {x_i}}}{{{h_x}}}} \right)K\left({\frac{{y - {y_i}}}{{{h_y}}}} \right) $ | (1) |
式中,K(·)是核函数,hx和hy分别是X和Y的窗口宽度。
常用的核函数有Boxcar核、Triangular核、Epanechnikov核、Quartic核、Tricube核、Gaussian核等。本文选用Gaussian核,具体表达式为:
| $ K\left(u \right) = \frac{1}{{\sqrt {2\pi } }}{{\rm{e}}^{ - \frac{{{u^2}}}{2}}} $ | (2) |
记:
| $ {K_h}\left(x \right) = \frac{1}{h}K\left({\frac{x}{h}} \right) $ | (3) |
则:
| $ \hat f\left({x, y} \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{K_{{h_x}}}} (x - {x_i}){K_{{h_y}}}(y - {y_i}) $ | (4) |
对于给定的数据集
| $ D = \{ ({x_i}, {y_i}, {z_i})|{x_i} \in \mathscr{R}, {y_i} \in \mathscr{R}, {z_i} \in \mathscr{R}, i = 1, 2, \cdots, n\} $ |
核回归方法试图通过构建如下的回归模型求解未知的回归函数m(x, y)去拟合数据集D并对新数据(x, y, z)作预测:
| $ \hat z = m\left({x, y} \right) + \varepsilon $ | (5) |
其中,
| $ m\left({x, y} \right) = E(Z|X = x, Y = y) $ | (6) |
误差项ε满足E(ε|X=x)=0。将式(6) 展开可得:
| $ \begin{array}{l} m\left({x, y} \right) = E\left({Z|X = x, Y = y} \right)\\ \;\;\;\;\;\;\; = \smallint _{_{ - \infty }}^{^{ + \infty }}zf\left({z|x, y} \right){\rm{d}}z\\ \;\;\;\;\;\;\; = \frac{{\smallint _{_{ - \infty }}^{^{ + \infty }}zf\left({x, y, z} \right){\rm{d}}z}}{{\smallint _{_{ - \infty }}^{^{ + \infty }}f\left({x, y, z} \right){\rm{d}}z}} \end{array} $ | (7) |
而f(x, y, z)用样本的估计
| $ \begin{array}{l} \hat f\left({x, y, z} \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{K_{{h_x}}}} (x - {x_i}) \times \\ \;\;\;\;\;\;\;{K_{{h_y}}}(y - {y_i}){K_{{h_z}}}(z - {z_i}) \end{array} $ | (8) |
展开并整理,得云顶高度反演公式:
| $ \hat z = \frac{{\sum\limits_{i = 1}^n {{K_{{h_x}}}} (x - {x_i}){K_{{h_y}}}(y - {y_i}){z_i}}}{{\sum\limits_{i = 1}^n {{K_{{h_x}}}} (x - {x_i}){K_{{h_y}}}(y - {y_i})}} $ | (9) |
本文选取2007年的CloudSat单层云数据,含有2B-GEOPROF、2B-GEOPROF-LIDAR、2B-TAU和MODIS-AUX产品的共1168轨。考虑到云的物理属性在不同地区存在差异性,将纬度范围设置为[15°S, 15°N]。T11的范围设置为[200 K,285 K],经筛选共得到48393个样本点。随机抽取其中80%作为训练集,剩余的20%作为测试集。样本点的分布情况如表 2所示,其中测试集的括号内表示用SVM分类模型预测的样本大小。
|
|
表 2 样本的分布情况 Table 2 Distribution of samples |
在红外波段,卫星接收到的辐射主要由两部分构成:一部分是云和云上大气的辐射,另一部分是地表和云下大气的辐射。无论水处于固、液、汽哪种相态,11 μm的透过率都大于12 μm。随着云光学厚度的减小,来自地表和云下大气的辐射将增加,同时BTD11-12将增大。因此,可以根据T11和BTD11-12的二维分布对云进行分类。图 3显示了样本特征参数的散点分布图,其中图 3a表示训练集,图 3b表示测试集。横轴表示通道31亮温T11,纵轴表示通道31与通道32亮温差BTD11-12,红、蓝、绿色点分别代表不透明云、半透明云和透明云。从图 3可以看出,三类云具有明显的分布特征。不透明云主要分布在T11 < 240 K或BTD11-12 < 2 K的区域,半透明云主要分布在T11>260 K且BTD11-12>2 K的区域,透明云主要分布在T11>275 K且BTD11-12>2 K的区域。当BTD11-12>2 K时,随着T11的增大,云逐渐变成半透明云和透明云。Inoue (1987)指出,通过给T11和BTD11-12划定简单的阈值,可以将云分为卷云、密卷云、积雨云和积云。从图 3可以看出当T11>260 K时,该结论成立,但当T11 < 260 K时,BTD11-12阈值随着T11的减小而增大,无法用简单的阈值来区分。

|
图 3 样本特征参数的散点分布图 Fig. 3 Scatter diagrams of sample characteristic parameters |
本文使用SVM多类分类器,核函数选用高斯径向基核函数,对多类问题采用成对分类方法。对训练集进行10折交叉验证,其正确率为90.3%。对于测试集,预测正确率为90.6%。
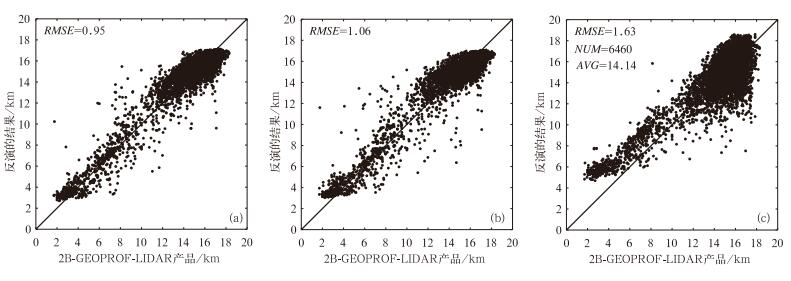
3.2 云顶高度反演结果 3.2.1 不透明云图 4所示的是不透明云反演结果,其中图 4a是进行云分类后的核回归法反演结果(下文简称L15法),图 4b是Hamada等(2010)所用的未将云分类的核回归法反演结果(下文简称H10法),图 4c是T11与ECMWF-AUX产品中的温度廓线对比所得的结果。RMSE、NUM和AVG分别代文献表均方根误差、样本大小和平均值。可以看出,L15法和H10法的反演效果均明显优于亮温-廓线法。当CTH>12 km时L15法和H10法反演误差较小,当CTH < 12 km时误差开始增大。H10法对于CTH < 8 km以下的云效果较差,个别样本点由于半透明云和不透明云样本的影响,出现偏高5~10 km的情况。而L15法预先对云进行了分类,避免了这一情况,使RMSE比H10法减小了10.4%。
|
图 4 不透明云反演的结果:(a)L15法,(b)H10法,(c)亮温-廓线法 Fig. 4 The results of opaque clouds: (a) L15 method, (b) H10 method, (c) method based on brightness temperatures and temperature profiles |
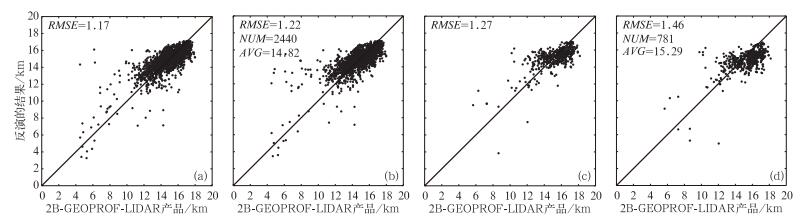
图 5所示的是半透明云和透明云的核回归法反演结果。从图中可以看出,L15法反演的半透明云和透明云的误差均比H10法要小。L15法对于高云效果较好,当CTH>13 km时L15法反演误差较小,对于低云的效果较差。L15法反演结果大多数比真实值偏大,RMSE分别达到1.17和1.27 km。主要原因是薄云更容易在高空出现,使高云在这两类云中占了绝大部分,反演时CTH值大的样本点所占权重较大,使结果偏高。薄云出现在低空时,下垫面更加复杂,对反演影响很大。H10法未将云分类,低云的比例增大,因此反演结果有的偏大,有的偏小。
|
图 5 半透明云和透明云反演的结果(a)L15法,半透明云;(b)H10法,半透明云;(c)L15法,透明云;(d)H10法,透明云 Fig. 5 The results of (a) L15 method, semi-transparent clouds; (b) H10 method, semi-transparent clouds; (c) L15 method, transparent clouds; (d) H10 method, transparent clouds |
个例1是一次典型的过冲云顶及其云砧,所用的数据轨道号为04293,时间为2007年2月17日04:16:06到04:17:10,经纬度范围是(141.98°E、0.11°N)到(141.19°E、3.83°N)。从图中可以看出,L15法和H10法的结果较为一致。在图 6a的A处有两层云叠加在一起,且高度差达到10 km。从图 6b和6c中看出A处的T11和BTD11-12均有突变,说明上层云较薄,卫星接收到了来自下层云的辐射,使反演结果偏小。对于B和C处的半透明云,L15法和H10法的反演效果依然较好,而亮温-廓线法的结果偏小,且误差随着云砧光学厚度的减小而急剧增加。对于其他地方的不透明云,L15法和H10法的反演效果都比较理想,而亮温-廓线法结果偏大。

|
图 6 个例1:过冲云顶及其云砧(a)CloudSat沿轨的雷达反射率因子垂直分布、2B-GEOPROF-LIDAR产品的云顶高度和三种方法反演的结果;(b)T11的分布;(c)BTD11-12的分布 Fig. 6 Case 1:an overshooting cloud and its anvil (a) vertical distribution of the radar reflectivity factor along track, the 2B-GEOPROF-LIDAR product, and the results of three methods; (b) distribution of T11; (c) distribution of BTD11-12 |
个例2所用的数据轨道号为05927,时间为2007年6月9日09:09:53到09:11:10,经纬度范围是(70.06°E、10.39°S)到(69.08°E、5.85°S)。卫星扫描带穿过一段高的半透明云,雷达反射率因子和反演结果如图 7所示。从图中可以看出,L15法和H10法对大部分样本点的反演效果都比较好,而亮温-廓线法的误差较大。对于A、B、C处的透明云,L15法和H10法的反演结果都偏高。而对于其他地方的半透明云,L15法和H10法都取得了不错的效果。
4.3 个例3低的不透明云个例3所用的数据轨道号为04290,时间为2007年2月16日23:16:15到23:16:39,经纬度范围是(141.36°W、11.49°S)到(141.68°W、10.04°S)。卫星扫描带穿过一段低的不透明云,雷达反射率因子和反演结果如图 8所示。从图中可以看出,亮温-廓线法对于低云效果明显较差。经过云分类的L15法排除了高的半透明云和透明云样本的干扰,因而效果优于未经分类的H10法。
5 结论利用MODIS红外分裂窗区两个通道的辐亮度实测数据和CloudSat光学厚度产品,基于SVM原理将云分为不透明云、半透明云和透明云3类,对这3类云分别用核回归法反演云顶高度,与CloudSat的几何-激光雷达产品进行对比,并分析了3个个例,得出如下结论:
(1) L15法对不透明云的RMSE达到0.95 km,比H10法误差减少了10.4%。对于高的半透明云的反演效果较好,但由于对少数低的不透明云误差较大,使RMSE达到1.17 km。对于透明云,L15法反演出的RMSE为1.27 km。与H10法相比,L15法对三种类型云的反演效果都有一定改善。
(2) 不透明云和透明云更容易出现在高空,高云在这两类云中占了绝大部分。L15法预先将云分类,反演半透明云和透明云时高云的样本点所占权重较大,使结果偏大。而H10法未分类,样本中含有大量不透明云中的低云样本,因此反演的半透明云和透明云结果有的偏高,有的偏低。
(3) L15法适用性较强,在仅有两个红外分裂窗通道的情况下就可以反演出云顶高度。大多数卫星传感器都具备这两个通道,而核回归所用的云顶高度数据源可以选用地基毫米波雷达、无线电掩星、探空资料、静止卫星云顶高度产品等。因此,可以将该方法推广,发挥更多卫星资源的效用。
顾成明, 王云峰, 张晓辉, 等, 2016. 云参数对微波亮温模拟计算的影响试验[J]. 应用气象学报, 27(3): 380-384. DOI:10.11898/1001-7313.20160313 |
韩丁, 严卫, 陆文, 等, 2013. 基于cosmic掩星资料的中国及周边地区云垂直结构特征研究[J]. 地球物理学进展, 28(1): 36-48. DOI:10.6038/pg20130105 |
马烁, 黄云仙, 严卫, 等, 2014. 三线阵云立体探测技术[J]. 红外与毫米波学报, 33(2): 164-171. |
郄秀书, 刘冬霞, 孙竹玲, 2014. 闪电气象学研究进展[J]. 气象学报, 72(5): 1054-1068. DOI:10.11676/qxxb2014.048 |
寿亦萱, 陆风, 王捷纯, 等, 2014. 华南冷季暴雨中热带卷云羽特征研究[J]. 气象, 40(6): 687-696. DOI:10.7519/j.issn.1000-0526.2014.06.005 |
孙晶, 史月琴, 蔡淼, 等, 2015. 南方三类云系云结构预报和增雨作业条件分析[J]. 气象, 41(11): 1356-1366. DOI:10.7519/j.issn.1000-0526.2015.11.005 |
严卫, 韩丁, 周小珂, 等, 2013. 利用CloudSat卫星资料分析热带气旋的结构特征[J]. 地球物理学报, 56(6): 1809-1824. DOI:10.6038/cjg20130603 |
张晓, 段克勤, 石培宏, 2015. 基于CloudSat卫星资料分析青藏高原东部夏季云的垂直结构[J]. 大气科学, 39(06): 1073-1080. |
张一平, 俞小鼎, 孙景兰, 等, 2014. 2012年早春河南一次高架雷暴天气成因分析[J]. 气象, 40(1): 48-58. DOI:10.7519/j.issn.1000-0526.2014.01.006 |
周非非, 周毓荃, 王俊, 等, 2010. Fy-2卫星反演的云顶高度与多普勒雷达回波顶高的关系初探[J]. 气象, 36(4): 43-50. DOI:10.7519/j.issn.1000-0526.2010.04.008 |
Baum B A, Wielicki B A, 1994. Cirrus cloud retrieval using infrared sounding data:Multilevel cloud errors[J]. J Appl Meteor Clim, 33(1): 107-117. DOI:10.1175/1520-0450(1994)033<0107:CCRUIS>2.0.CO;2 |
Botev Z, Grotowski J, Kroese D, 2010. Kernel density estimation via diffusion[J]. The Annals of Statistics, 38(5): 2916-2957. DOI:10.1214/10-AOS799 |
Fischer J, Grassl H, 1991. Detection of cloud-top height from backscattered radiances within the oxygen a band. Part 1:Theoretical study[J]. J Appl Meteor Clim, 30(9): 1245-1259. DOI:10.1175/1520-0450(1991)030<1245:DOCTHF>2.0.CO;2 |
Fritz S, Winston J S, 1962. Synoptic use of radiation measurements from satellite tiros Ⅱ1[J]. Mon Wea Rev, 90(1): 1-9. DOI:10.1175/1520-0493(1962)090<0001:SUORMF>2.0.CO;2 |
Garrett K J, Yang P, Nasiri S L, et al, 2009. Influence of cloud-top height and geometric thickness on a MODIS infrared-based ice cloud retrieval[J]. J Appl Meteor Clim, 48(4): 818-832. DOI:10.1175/2008JAMC1915.1 |
Hamada A, Nishi N, 2010. Development of a cloud-top height estimation method by geostationary satellite split-window measurements trained with cloudSat data[J]. J Appl Meteor Clim, 49(9): 2035-2049. DOI:10.1175/2010JAMC2287.1 |
Hamada A, Nishi N, Iwasaki S, et al, 2008. Cloud type and top height estimation for tropical upper-tropospheric clouds using GMS-5 split-window measurements combined with cloud radar measurements[J]. SOLA, 4: 47-60. |
Hasler A F, Strong J, Woodward R H, et al, 1991. Automatic analysis of stereoscopic satellite image pairs for determination of cloud-top height and structure[J]. J Appl Meteor Clim, 30(3): 257-281. DOI:10.1175/1520-0450(1991)030<0257:AAOSSI>2.0.CO;2 |
Inoue T, 1985. On the temperature and effective emissivity determination of semi-transparent cirrus clouds by bi-spectral measurements in the 10μm window region[J]. J Meteor Soc Jap, 63(1): 88-99. DOI:10.2151/jmsj1965.63.1_88 |
Inoue T, 1987. A cloud type classification with NOAA 7 split-window measurements[J]. J Geophys Res, 92(D4): 3991-4000. DOI:10.1029/JD092iD04p03991 |
Mace G G, Deng M, Soden B, et al, 2006. Association of tropical cirrus in the 10-15-km Layer with deep convective sources:An observational study combining millimeter radar data and satellite-derived trajectories[J]. J Atmos Sci, 63(2): 480-503. DOI:10.1175/JAS3627.1 |
Mack R A, Hasler A F, Adler R F, 1983. Thunderstorm cloud top observations using satellite stereoscopy[J]. Mon Wea Rev, 111(10): 1949-1964. DOI:10.1175/1520-0493(1983)111<1949:TCTOUS>2.0.CO;2 |
Menzel W P, Wylie D P, Strabala K I, 1992. Seasonal and diurnal changes in cirrus clouds as seen in four years of observations with the VAS[J]. J Appl Meteor Clim, 31(4): 370-385. DOI:10.1175/1520-0450(1992)031<0370:SADCIC>2.0.CO;2 |
Reynolds D W, Vonder Haar T H, 1977. A bispectral method for cloud parameter determination[J]. Mon Wea Rev, 105(4): 446-457. DOI:10.1175/1520-0493(1977)105<0446:ABMFCP>2.0.CO;2 |
Simpson J J, McIntire T, Jin Z, et al, 2000. Improved cloud top height retrieval under arbitrary viewing and illumination conditions using AVHRR data[J]. Remote Sens Environ, 72(1): 95-110. DOI:10.1016/S0034-4257(99)00095-4 |
Stephens G L, Vane D G, Boain R J, et al, 2002. The cloudsat mission and the a-train[J]. B Ame Meteor Soc, 83(12): 1771-1790. DOI:10.1175/BAMS-83-12-1771 |
Szejwach G, 1982. Determination of semi-transparent cirrus cloud temperature from infrared radiances:Application to Meteosat[J]. J Appl Meteor Clim, 21(3): 384-393. DOI:10.1175/1520-0450(1982)021<0384:DOSTCC>2.0.CO;2 |
Weisz E, Li J, Menzel W P, et al, 2007. Comparison of AIRS, MODIS, cloudSat and CALIPSO cloud top height retrievals[J]. Geophys Res Lett, 34(17): L17811. DOI:10.1029/2007GL030676 |
 2016, Vol. 42
2016, Vol. 42 

