引言

目前，多普勒天气雷达已被普遍用来测量各种大气现象内部的流场。由于多普勒天气雷达只能测量三维大气运动沿雷达波束的一维分量，多普勒速度不能直观地解释大气流场结构。为此，人们常采用多普勒速度模式来解释测量的多普勒速度。Wood等(1986)使用随高度变化的水平均匀风场模拟了晴空和大范围降水情况下的观测径向速度。Brown等(1991)使用几种简单的解析流场模式(例如均匀流场、轴对称旋转流场和轴对称辐散流场)的叠加产生模拟多普勒速度模式，用作识别强雷暴内准水平流场特征的标志。夏文梅等(2003)从大量观测实践中总结出“大面积降水的产生、维持和消散往往与中低层的大尺度辐合辐散和冷暖平流有关，大尺度风场往往是冷暖平流和大尺度辐合辐散相结合的结果”，并在前人研究基础上，模拟了大尺度辐合辐散与冷暖平流运动叠加的多普勒速度场。虽然所有这些多普勒速度模式的模拟都有助于预报员分析和判断多普勒速度观测场中隐含的实际风场和冷暖平流信息(郑媛媛等，2004；张腾飞等，2006；王丽荣等，2006；张家国等，2010；刁秀广等，2011；金巍等，2013；王福侠等，2014；傅朝等，2015；孔凡超等，2016)，但是，对于从多普勒速度观测场中客观提取各种尺度的流场信息和冷暖平流信息也是迫切需要的。对于风暴内的小尺度辐合辐散和涡旋流场特征，人们已能根据其模式特征使用计算机自动识别(Smith et al，2004；Robert et al，2004；王彦等，2008；冯晋勤等，2010)。对于雷达上空大尺度平均流场和散度信息的反演最常用的是VAD(Velocity Azimuth Display)(Lhermitte et al，1961；Browning et al，1968；周小刚等，2015)和EVAD(extended-VAD)(Srivastava et al，1986；Matejka et al，1991；Matejka，1993)技术。Waldteufel等(1979)提出从多普勒雷达观测资料中反演三维风场信息的VVP技术。该技术把雷达体扫资料分割成多个小的扇形分析体积，在假设各个分析体积内风场线性的条件下，通过多元回归分析来估计各个分析体积的平均三维风、散度和形变等风参量。Holleman(2005)把VVP技术的扇形分析体积改为以高度分层的圆锥环分析体积，反演出雷达上空一定区域内的分层平均水平风、散度和形变等风参量，并使用探空测风作为参考比较了VAD和分层VVP技术反演的垂直风廓线VWP(Vertical Wind Profile)的差异，得出分层VVP方法要优于VAD方法的结论。肖艳姣等(2015)利用2010年阳江高精度探空仪国际比对试验中观测的探空测风资料、CINRAD-SA型多普勒天气雷达体扫资料及其基于PUP-VAD方法反演的垂直风廓线产品资料，基于分层VVP方法反演了雷达站上空的VWP，以探空测风为参考，以平均风向、风速均方差和相关系数作为评估因子，分雷达站周围降水回波分布较均匀和不均匀两种情况，对比分析了基于分层VVP方法和PUP-VAD方法反演的垂直风廓线。结果表明，在这两种情况下，相比PUP-VAD方法，分层VVP方法都能提供更实用、质量更好的垂直风廓线。在雷达周围降水分布均匀的情况下，基于分层VVP方法得到的垂直风廓线的平均风向、风速的均方差和相关系数分别为10.17°、1.98 m·s^-1、0.90和0.72，而基于PUP-VAD方法得到的这4个量分别为15.46°、2.98 m·s^-1、0.73和0.51。Cifelli等(1996)比较了EVAD和分层VVP方法得到的散度和垂直速度，认为两者的效果很接近，但是使用分层VVP方法得到的风场信息能伸展到更高高度。对于如何从径向速度资料中客观定量地提取冷暖平流信息还很少有人涉及，预报员常常根据径向速度PPI(Plane Position Indicator)图上零速度线呈S型还是反S型弯曲或是根据VWP产品中风向随高度是顺转还是逆转来判断冷暖平流(支树林等，2015)。

本文目的就是基于多普勒雷达径向速度资料，使用分层VVP方法反演雷达上空一定区域内的平均垂直散度廓线，基于分层VVP方法反演的垂直风廓线反演垂直温度平流廓线，以期为预报员提供关于大尺度辐合辐散和冷暖平流的定量分析产品。

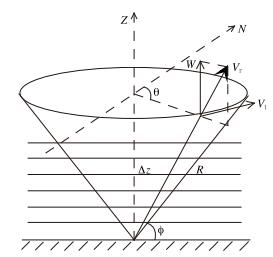
1 基于分层VVP方法反演垂直风廓线和垂直散度廓线

多普勒天气雷达进行三维扫描，可提供作为斜距、方位和仰角函数的平均径向速度。为了从径向速度中提取局地风场信息，我们必须假设观测的风矢量等于局地风矢量。图 1给出了典型的多普勒天气雷达扫描几何原理和相关的局地风场示意图。对于单多普勒雷达风场反演来说，常采用一个线性风场模式来近似雷达附近的风场。这个线性风场模式以雷达所在地上空的某高度z₀点为中心，局地风场在X、Y、Z向上的分量分别为U(r)、V(r)、W(r)，如果忽略垂直速度的水平偏导和所有速度分量的垂直偏导项，它们可以近似为：

$ U\left(\mathit{\boldsymbol{r}} \right) = {u_0} + x\frac{{\partial u}}{{\partial x}} + y\frac{{\partial u}}{{\partial y}} $

(1)

$ V\left(\mathit{\boldsymbol{r}} \right) = {v_0} + x\frac{{\partial v}}{{\partial x}} + y\frac{{\partial v}}{{\partial y}} $

(2)

$ W\left(\mathit{\boldsymbol{r}} \right) = {w_0} $

(3)

式中, u₀、v₀和w₀是局地风场位于中心点的分量，∂u/∂x、∂u/∂y、∂v/∂x和∂v/∂y是风场在中心点的偏导。

降水粒子除了因局地风场而运动外，它们本身还有一个末端下落速度W_f。由于Z轴指向天顶，所以W_f是负的，它一般大于局地风场的垂直分量(Holleman，2005)。

某点(x，y，z)的模式径向速度F(局地风沿雷达波束的分量)可以用线性风场模式U(r)、V(r)、W(r)和粒子末端下落速度W_f来表示：

$ \begin{array}{l} F = \frac{x}{{\left| \mathit{\boldsymbol{r}} \right|}}U\left(\mathit{\boldsymbol{r}} \right) + \frac{y}{{\left| \mathit{\boldsymbol{r}} \right|}}V\left(\mathit{\boldsymbol{r}} \right) + \frac{z}{{\left| \mathit{\boldsymbol{r}} \right|}}[W\left(\mathit{\boldsymbol{r}} \right) + {W_f}]\\ = {\rm{sin}}\theta {\rm{cos}}\phi U\left(\mathit{\boldsymbol{r}} \right) + {\rm{cos}}\theta {\rm{cos}}\phi V\left(\mathit{\boldsymbol{r}} \right) + \\ ({\rm{sin}}\phi + \left| \mathit{\boldsymbol{r}} \right|co{s^2}\phi /17000)[W\left(\mathit{\boldsymbol{r}} \right) + {W_f}]\\ = {u_0}{\rm{sin}}\theta {\rm{cos}}\phi + {v_0}{\rm{cos}}\theta {\rm{cos}}\phi + \\ ({w_0} + {W_f})({\rm{sin}}\phi + \left| \mathit{\boldsymbol{r}} \right|{\rm{co}}{{\rm{s}}^2}\phi /2{R_m}) + \\ \frac{{\partial u}}{{\partial x}}\left| \mathit{\boldsymbol{r}} \right|{\rm{si}}{{\rm{n}}^2}\theta {\rm{co}}{{\rm{s}}^2}\phi + \frac{{\partial v}}{{\partial y}}\left| \mathit{\boldsymbol{r}} \right|{\rm{co}}{{\rm{s}}^2}\theta {\rm{co}}{{\rm{s}}^2}\phi + \\ \left({\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)\left| \mathit{\boldsymbol{r}} \right|{\rm{sin}}\theta {\rm{cos}}\phi {\rm{co}}{{\rm{s}}^2}\phi \end{array} $

(4)

式中，|r|是斜距，θ和ϕ分别为方位角和仰角，R_m为等效地球半径，在标准大气情况下，R_m=8500 km，当不考虑地球曲率影响的情况下，可略去|r|cos²ϕ/2R_m项。式(4) 又可简写为：

$ F = \sum\limits_{j = 1}^K {\frac{{\partial F}}{{\partial {u_j}}}} {u_j} $

(5)

式中，u_j为风场变量，∂F/∂u_j为极坐标中各系数，K为风场变量个数。

分层VVP方法是把雷达体扫分割成以高度分层的多个圆锥环分析体积(图 1)，在假设各个圆锥环分析体积内风场线性的条件下，使用模式径向速度方程对分析体积内的观测径向速度资料进行多元回归分析来估计分析体积内的平均三维风分量、散度和形变等参量。在分析体积内，使观测得到的径向风场V_r与由线性假设得到的模式径向风场F之间的差值平方和$ H = \sum\limits_{i = 1}^N {{{\left({{V_n} - {F_i}} \right)}^2}} $达到最小，即：

$ \frac{{\partial H}}{{\partial {u_k}}} = - 2\sum\limits_{i = 1}^N {({V_{ri}} - \sum\limits_{j = 1}^K {\frac{{\partial {F_i}}}{{\partial {u_j}}}} {u_j})} \frac{{\partial {F_i}}}{{\partial {u_k}}} = 0 $

(6)

式中，i是分析体积内的资料点，N是分析体积内的有效资料个数，u_k是风场的变量。展开式(6) 有：

$ \sum\limits_{j = 1}^K {(\sum\limits_{i = 1}^N {\frac{{\partial {F_i}}}{{\partial {u_j}}}\frac{{\partial {F_i}}}{{\partial {u_k}}}})} {u_j} = \sum\limits_{i = 1}^N {\frac{{\partial {F_i}}}{{\partial {u_k}}}} {V_{ri}} $

(7)

式(7) 可写成：

$ \mathit{\boldsymbol{AX = B}} $

(8)

其中矩阵A、X、B分别为：

$ \begin{array}{l} \mathit{\boldsymbol{A}} = \sum\limits_i {\left\{ {\begin{array}{*{20}{c}} {{d_1} \times {d_1}} & {{d_1} \times {d_2}} & \cdots & {{d_1} \times {d_6}}\\ {{d_2} \times {d_1}} & {{d_2} \times {d_2}} & \cdots & {{d_2} \times {d_6}}\\ \cdots & \cdots & \cdots & \cdots \\ {{d_6} \times {d_1}} & {{d_6} \times {d_2}} & \cdots & {{d_6} \times {d_6}} \end{array}} \right\}}, \\ \mathit{\boldsymbol{X = }}\left({\begin{array}{*{20}{c}} {{u_0}}\\ {{v_0}}\\ {{w_0} + {W_f}}\\ {\partial u/\partial x}\\ {\partial v/\partial y}\\ {\partial u/\partial y + \partial v/\partial x} \end{array}} \right), \mathit{\boldsymbol{B = }}\sum\limits_i {\left({\begin{array}{*{20}{c}} {{d_1} \times {V_{r, i}}}\\ {{d_2} \times {V_{r, i}}}\\ {{d_3} \times {V_{r, i}}}\\ {{d_4} \times {V_{r, i}}}\\ {{d_5} \times {V_{r, i}}}\\ {{d_6} \times {V_{r, i}}} \end{array}} \right)} \end{array} $

式中，d₁=sinθcosϕ，d₂=cosθcosϕ，d₃=sinϕ+|r|cos²ϕ/2R_m，d₄=|r|sin²θcos²ϕ，d₅=|r|cos²θcos²ϕ，d₆=|r|sinθcosθcos²ϕ。使用简单共轭函数方法(邱崇践等，1996；石燕等，2009)求解式(8) 就可以得到各高度层的平均水平风u₀、v₀和散度∂u/∂x+∂v/∂y等风参量。简单共轭函数方法能克服因系数矩阵中各元素在量级上存在显著差异而导致的系数矩阵严重病态造成的解的严重误差。在使用分层VVP方法反演风参量之前对径向速度数据进行了退模糊处理(肖艳姣等，2012)。

2 基于垂直风廓线反演垂直温度平流廓线

在热成风的假定下，根据标准大气特性，温度平流的计算公式(章国材等，2007)为：

$ {\rm{ - }}\mathit{\boldsymbol{V}}\cdot\nabla T = \frac{{ - Pf}}{{{R_d}}}\mathit{\boldsymbol{V}}\cdot\left({\mathit{\boldsymbol{k}} \times \frac{{\partial v}}{{\partial p}}} \right) $

(9)

式中，f为科氏参数，R_d为空气气体常数。在等压面p₁和p₂上(p₁≥p₂)，风速风向分别为(V₁, θ₁)和(V₂, θ₂), 则式(9) 可以写成：

$ \begin{array}{l} {\rm{ - }}\mathit{\boldsymbol{V}}\cdot\nabla T \approx - \frac{{\bar pf}}{{{R_d}}}\left({\frac{{{V_1} + {V_2}}}{2}} \right)\cdot\left({\mathit{\boldsymbol{k}} \times \frac{{{V_1} - {V_2}}}{{\Delta p}}} \right)\\ \;\;\;\;\;\;\;\;\;\; = \frac{{\bar pf}}{{{R_d}\Delta p}}{V_1}{V_2}{\rm{sin}}({\theta _1} - {\theta _2}) \end{array} $

(10)

式中，Δp=p₁-p₂，=(p₁+p₂)/2。

在标准大气条件下，位势高度Z与气压之间的关系(章国材等，2007)为：

$ Z = 44331\left[ {1 - {{\left({\frac{p}{{1013.255}}} \right)}^{0.1903}}} \right] $

(11)

而高度h与位势高度之间的关系(章国材等，2007)为：

$ Z = \frac{{9.80616[1 - 0.00259{\rm{cos}}\left({2\phi } \right)]{{\left({1 + \frac{h}{{{R_0}}}} \right)}^2}}}{{9.80665}}\frac{{{R_0}}}{{{R_0} + h}} $

(12)

式中，R₀为地球半径，ϕ为雷达站纬度。

由于该方法计算温度平流是在假设地转平衡条件下进行的，所以只适用基本满足地转平衡条件的较大尺度天气系统，对于剧烈的中小尺度天气系统，因不满足地转平衡条件，该方法是不适用的。此外，对于1 km以下的低层大气因摩擦力的影响也难以满足地转平衡条件，用该方法计算的1 km以下的温度平流也不一定可靠。

在雷达周围有大范围降水回波的情况下，使用分层VVP方法可从雷达体扫资料中反演出较完整的垂直风廓线，得到的u₀、v₀代表线性风场条件下雷达有效探测范围内的平均水平风，可近似满足地转平衡条件。在这种情况下，可从垂直风廓线中反演出较为合理的垂直温度平流廓线。对于局地强对流天气来说，上述温度平流反演方法是不适用的，因为在这种天气情况下基于雷达观测不能得到比较完整的垂直风廓线，而且不满足地转平衡条件。

3 个例分析 3.1 2007年7月18日济南大暴雨分析

2007年7月18日山东省发生了一次大范围强降水过程，全省大部分地区降大到暴雨，强降水集中在18日14时(北京时，下同)至夜间。产生强降水的环境背景为：18日08时，850~500 hPa高空西太平洋副热带高压在华南沿海加强西伸，低层850~700 hPa从华南沿海到山东形成一股强盛的西南风急流；500 hPa中高纬度在贝加尔湖地区有低涡东移，低涡后部的冷空气在槽后西北气流的引导下东移南下，在地面上表现为冷锋。低层850 hPa冷空气从东北回流南下到达40°N附近，东北气流与西南暖湿气流之间形成明显的切变线，位于河北和山西上空。18日20时，西风槽和低层切变线到达山东上空，切变线西部的偏北气流与强盛的西南风急流在山东上空汇合，产生较强的辐合上升运动，触发不稳定能量释放，产生中尺度对流系统，造成山东大范围暴雨(杨晓霞等，2008)。

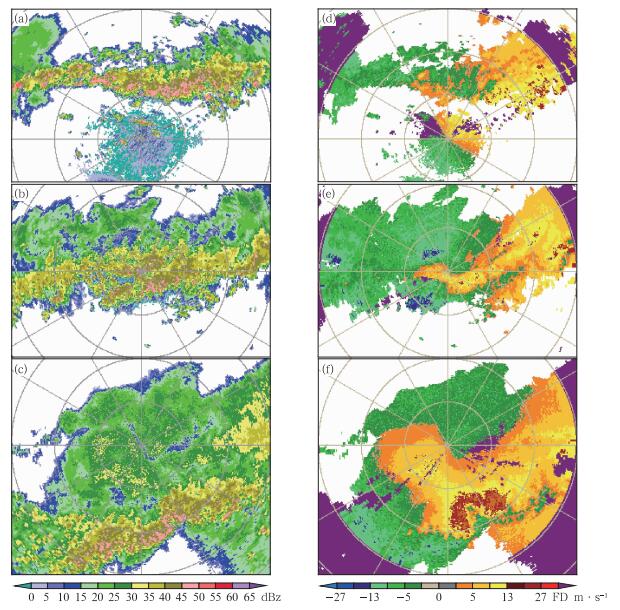
降水带影响济南的时间主要在17—19时，图 2给出了15:32、18:36和20:32济南雷达观测的1.5°仰角的反射率因子和径向速度图，其中每个距离圈代表50 km(下同)。从图 2a可看出降水回波呈近乎东西向的带状分布，其西侧南移速度大于东侧，致使降水回波带逐渐转为东北—西南向(图 2c)。从图 2d可看出雷达站上空低层为西南风，在雷达北侧50多千米处有一条东西向分布的切变线。从图 2e可看出，在40 km以内，同一距离圈上正速度区面积大于负速度区面积，说明低层有辐散存在；在40 km以外，负速度区面积远大于正速度区面积，说明中高层有明显的风向性辐合存在，此时地面冷锋刚过了雷达站。比较图 2e和2f，发现图 2f中同一距离圈上正速度面积大于负速度面积的范围扩大了，说明辐散的厚度随时间推移逐渐加大。从图 2e和2f可看出经过雷达的零速度线随离开雷达的距离(离开地面的高度)增加呈反S形弯曲，说明有冷平流存在。虽然从径向速度图上可以定性分析出一些辐合辐散和冷暖平流信息，但是难以细致分析其垂直分布情况。

图 3给出了基于济南雷达资料反演的15:32—22:23每间隔约半小时的垂直风廓线(时间轴从右至左，下同)。从图中可看出，在17:04—19:06，3.0~4.0 km高度的风向变化为西南风—西风—西北风；在18:05—20:04，4.6~5.8 km高度的风向变化为西南偏西风—西风—西北风，这反映了700和500 hPa高空槽经过雷达站的过程，槽前为西南气流，槽后为西北气流。济南强降水时段对应700 hPa高空槽过境时段。在17:04之前，8 km以下都为偏西南风，且风向随高度顺时针旋转，风速随高度增大, 有暖平流存在。到17:04，底层(0.9 km以下)开始出现偏西北风，说明地面冷锋到达雷达站，这与济南强降水开始时间对应。在这之后，底层的风随时间推移逐渐转为北—东北风，风向随高度逆时针旋转并且逆转厚度逐渐增大，这反映了冷锋锋面经过雷达站的过程，槽后的垂直风切变逐渐加深，冷平流厚度逐渐增大。

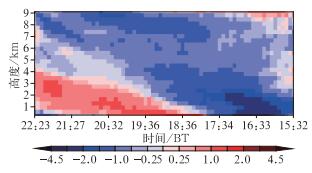
图 4给出了基于济南雷达资料反演的15:32—22:23的垂直散度廓线分布图。从图中可看出，在16:00之前，在3 km之上有弱辐散，之下为较强辐合；在16:00—17:20，9 km以下均为辐合，但是低层辐合强于高层辐合。高层辐合是由于雷达同时观测到高空槽后西北气流及槽前西南气流，因此在径向速度场中表现为辐合特征。低层辐合主要是由于偏北冷空气南下与西南气流交汇形成的强风向、风速辐合。槽前低层辐合、高层辐散或者低层强辐合、高层弱辐合有利于上升运动的发展。到17时左右，地面冷锋到达济南，济南较强降水开始，随着地面降水的加强(18时左右)，近地层因降水拖曳和冷空气共同作用开始转为辐散场。随着冷锋锋面逐渐经过雷达站，冷空气厚度不断增加，近地层辐散场逐渐向中层扩散，济南雷达站附近的上升运动减弱，对应强降水逐渐减弱。反演的垂直散度廓线随时间的演变与从径向速度图中分析同距离圈上的正负速度面积比来判断辐合、辐散的情况是一致的。

图 5给出了基于济南雷达资料反演的15:32—22:23的垂直温度平流廓线分布，从图中可看出，在约17时之前，5 km高度以下为较深厚的暖平流，表明槽前西南气流向强降水区域输送充足的不稳定能量和水汽，有利于不稳定层结的建立和维持。之后，随着高空槽和冷空气东移南下，底层暖平流转为冷平流。济南强降水出现在17—19时，表明冷空气对对流的触发作用。随着冷锋锋面逐渐经过雷达站，冷平流逐渐向中层扩展，不利于不稳定层结的建立，这对应济南强降水减弱。对比图 3和图 5可知，温度平流特征与垂直风廓线所反映出的冷暖平流是基本一致的，主要由于前者遵循了热成风平衡原理，对环境场的分析具有较好参考意义。

3.2 2013年7月6—7日梅雨期武汉大暴雨分析

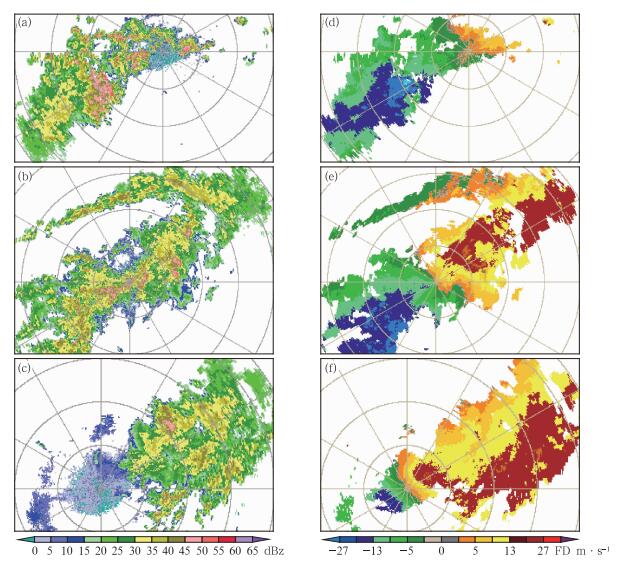
2013年7月6—7日，受高空槽东移和西南急流共同影响，湖北省出现了入梅以来最强降水过程，其中鄂东北、江汉平原中南部和鄂东南北部出现了暴雨或大暴雨。分析6日20时和7日08时850、700和500 hPa的高空天气图，发现6日20时武汉上空这3个高度都是暖平流，7日08时武汉上空500 hPa为冷平流，其他2个高度为暖平流。图 6给出了6日21:52、7日04:31和10:57武汉雷达观测的1.5°仰角的反射率因子和径向速度图。由反射率因子图可知，降水回波自湖南北部进入江汉平原，发展成东北—西南向的带状回波，向东北方向移动产生强降水。由径向速度图可知，在强降水移出武汉之前，一直有深厚的西南气流存在，在强降水移出武汉之后，低层依然维持很强的西南气流，而在中高层，大的正速度区明显南压，说明风随高度向偏西、偏北方向转向。

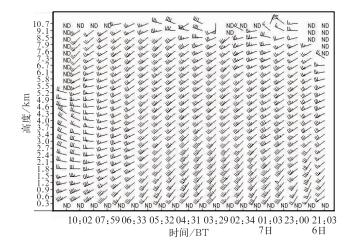
图 7给出了武汉雷达资料反演的6日21:03至7日10:57的垂直风廓线分布。由于武汉雷达资料最低仰角的杂波比较多，在反演过程中没有使用该仰角资料，故反演高度从0.6 km开始，图中没有资料的地方标记为ND。从图中可看出，强降水形成前期武汉受较深厚西南气流控制，且强度发展，形成急流，低空西南急流一直维持至强降水回波移出武汉。7日07:59—10:02，在2~5 km高度，风向由西南风逐渐转为西北风，反映了高空槽的过境过程。由此可见，反演的垂直风廓线反映的高空风随时间和高度的变化与实际情况基本一致，西南急流向武汉地区输送了充足的水汽和不稳定能量，有利于强降水回波的发展和维持，而随着高空槽东移，降水回波逐渐移出武汉。

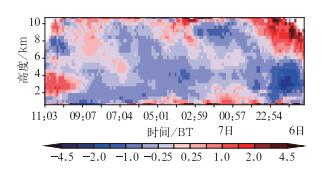
图 8给出了基于武汉雷达资料反演的6日21:03至7日11:03的垂直散度廓线分布, 由图可知，21:03之后，5 km以下高度辐合明显增强，此后在该高度以下维持辐合流场，这主要因西南急流自西南方向发展造成，对应武汉强降水发展。22:54之后，2 km以下出现辐散，到7日01时达到最强，高度扩展至3 km，对应强降水有所间歇。此后辐散高度下降，中低层辐合再度加强，对应强降水回波再次自西南方向发展影响武汉。降水减弱阶段，2~4 km高度转为辐散风场，径向速度图中表现为偏西气流加速远离雷达站。可见中低层散度变化与降水演变过程比较一致。

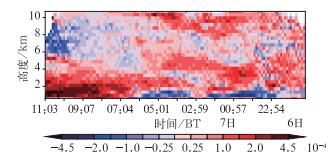
图 9给出了基于武汉雷达资料反演的6日21:03至7日11:03的垂直温度平流廓线分布。由图可知，在降水期间，武汉上空以暖平流为主，但在反演的垂直风廓线图中，风向随高度顺转不明显，且径向速度图中零速度线未呈明显的S形弯曲，因此暖平流强度主要取决于较大的西南风速。6日22时至7日06时，1 km以下高度为冷平流，这与图 8中的辐散场对应，可能是由降水下沉气流导致的浅薄冷空气层引起。在降水后期，随着高空槽过境，高空转为冷平流，中低层的暖平流加强，这与图 7中的风向先随高度顺转再逆转对应，也与使用高空天气图分析的冷暖平流基本一致。

4 结论

(1) 在雷达周围有大范围降水回波的情况下，使用分层VVP方法能合理地反演出雷达站上空的垂直风廓线和垂直散度廓线。

(2) 在雷达周围有大范围降水回波的情况下，反演的垂直风廓线代表各个高度雷达有效探测范围内的平均水平风，可近似满足地转平衡条件，在这种情况下，可从垂直风廓线中反演出较为合理的垂直温度平流廓线。

(3) 对于文中个例，可用天气学理论和天气实况来解释3个反演产品的合理性，其有助于预报员推断本站降水演变趋势。