2. 宁波市气象局,宁波 315012
2. Ningbo Meteorological Bureau of Zhejiang Province, Ningbo 315012
台风暴雨是影响我国东部沿海地区(地形复杂,多丘陵、山地)的灾害性天气之一。台风造成的特大暴雨,易引发山洪和泥石流等次生灾害(樊建勇等,2012;张亚萍等,2013;陆桂荣等,2015),对人民生命财产造成巨大的损害。雷达是目前监测台风最有效的手段,如何利用雷达资料提高台风降水估测的精度,对减少台风造成的灾害具有重要意义。
研究表明(Marshall et al, 1947),雷达反射率因子(Z)和降雨效率(R)之间存在有效性关系:Z=ARb。降水估计精度主要取决于两方面因素:近地面反射率和最优估计参数A和b。前者实际应用时一般采用最低仰角反射率,但当低层反射率廓线存在随高度递增或递减时,如在台风等降水过程中,反射率随高度增大递减,则容易造成降水低估,因而相关研究通过反演低层垂直反射率因子廓线(vertical profiles of reflectivity, VPR)来获取近地面最优反射率(胡胜等,2014;Qi et al, 2014; Wen et al, 2011;2013; Wang et al, 2014)。后者主要通过降水类型分类,如分为暖云、对流、层云等,然后获取每一类的最优Z-R关系(Xu et al, 2008)。虽然台风降水更接近暖云降水,但实际过程尤为复杂,尤其在复杂地形区域,单一的Z-R关系来进行降雨估测容易导致极值的偏差。
雷达具有较高的时空分辨率、覆盖范围大,而自动雨量计具有单点观测雨量较精准的特点,因此针对上述单一的Z-R关系降雨估测的缺陷问题,研究在Z-R关系提升降雨估测的基础上,采用雷达-雨量计的融合方法来进一步提升定量降雨估测精度。该类方法主要有两类:卡尔曼滤波方法和变分方法(Ninomiya and Akiyama, 1978)。赵坤等(2001)对卡尔曼滤波方法客观进行了应用评估,结果显示该方法具有较高估测精度。变分方法也取得了较好的估测效果(东高红和刘黎平,2012),而改进的变分理论,则进一步提升了降雨估测精度(马慧等,2008)。除了上述两类方法,克里金法和最优插值法也被一些研究工作者应用于雷达估测降水(黄小玉等,2009;李建通等,2015;勾亚彬等, 2014)。
上述雷达-雨量计的融合方法主要是数学算法优化更新过程,但对降雨的微物理结构特性(如不同的降雨类型和地区的Z-R关系差异,强风环境下雷达和雨量计时空匹配等)以及雷达探测相关的问题(如低层垂直反射率结构观测不完整,反射率强度的距离衰减等)并没有特殊处理,而复杂地形下此类问题尤为突出(杨杰等,2014;温龙等,2015)。复杂地形下,台风的暖湿气流环境下更易形成地形增雨进而导致低层的VPR递增特征更为显著(Smith et al, 2010; Zhang et al, 2014)。
针对复杂地形下的VPR结构观测不完整问题,最近十几年,许多研究使用反演VPR来修正计算近地面反射率,而后再通过Z-R关系估算降水进而提高降水估测精度。Bellon et al(2005)、Germann and Joss(2002)提出整场平均VPR法,改善了高大山脉(例如阿尔卑斯山脉)迎风坡的降雨估测低估问题,但平均的VPR并不能反映复杂地形下不同雷达单点的VPR的差异。针对此,Vignal et al(2000)和Vignal and Krajewski(2001)提出了局地的VPR法,降雨评估结果要相对优于之前整场平均的VPR方法,但实际应用中,由于计算量较大,并没有推广。近些年,随着综合观测系统的不断完善,许多研究则考虑联合其他观测资料来修正VPR廓线,进而修正用于估测的反射率。例如,针对地形增雨造成雷达降水估测低估问题,Zhang et al(2014)建立了联合雷达、自动站和复杂地形降水月气候统计信息的混合法,在一定程度上提高了复杂地形下稳定性层云降雨的降水估测精度。又如,针对复杂地形下地物和地形遮挡造成的降雨低估问题,Chang et al(2009)利用雷达反射率和地面观测分析的统计参数修正获得近地面反射率,一定程度上改善台湾地区的台风降雨低估问题。
尽管上述研究不同程度上改进了降水估测精度,但因为台风降雨在复杂地形下的降雨分布复杂性,尤其是强降水估测,仍旧存在较大的误差,部分原因是以往的研究只考虑其中的某一方面。本文将在上述研究的基础上,有机结合上述联合自动站、全局与区域VPR廓线算法以及动态的Z-R关系三种算法来提高复杂地形下台风降雨估测精度。
1 资料和方法 1.1 资料及质量控制本文选取浙江东部地区为研究区域(图 1a),该区域是受台风灾害影响较为严重的区域之一。区域内地形复杂,平地、丘陵、山地混合存在,其中靠海岸线多平地,而内陆则丘陵和山地更多。本研究所用的资料包括区域内多普勒天气雷达的基数据(Level-Ⅱ)资料、加密自动站10和1 min雨量资料,以及为了获取高精度反射率廓线而使用的高精度地形数据。

|
图 1 研究区域内的自动站分布(a)以及台风海葵(b)、凤凰(c)和菲特(d)的路径 (红色三角形位置为宁波雷达位置,紫色圈为宁波雷达150 km半径圈;图 1a中蓝色圆点为自动站位置;图 1b, 1c, 1d中红色曲线为台风路径,图中的雷达回波为台风靠近登陆时间点附近的雷达回波图) Fig. 1 Locations of of automatic weather stations (a) and paths of the three typhoons, (b) Typhoon Haikui; (c) Typhoon Fungwong; (d) Typhoon Fitow (Red triangle indicates the position of Ningbo Radar, purple circle indicates the 150 km radius of radar; Blue dots indicate the positions of automatic weather stations in Fig. 1a; Red curves indicate the paths of typhoons, the radar echoes of the typhoon near the leading time are showed in Figs. 1b-1d) |
研究区域内使用多普勒天气雷达为宁波S波段雷达。该雷达位于慈溪达蓬山,站点海拔485 m。为保证雷达观测精度,这里选取了雷达监测的150 km半径区域(图 1a)。采用南京大学单雷达批处理软件Single Radar Batch Processing System(SRPRO)对雷达资料进行预处理。采用参考切面质量控制算法对雷达反射率资料进行质量控制。水平方向上使用双线性样条方法将极坐标等仰角面数据插值到1 km×1 km等间距网格,垂直方向上使用Zhang et al(2005)提出的三维格点线性插值方法将多仰角层数据处理成垂直0.5 km间隔等高面反射率数据。为获取高精度VPR廓线,试验使用SRTM3高精度地形数据,分辨率为90 m。对地形进行了简单划分:海拔高度低于100 m、且10 km半径的水平尺度对应的坡度低于1°,划分为平原地区(如果下垫面为海洋,则定义为洋面),其余划分为复杂地形区域,包括海拔低于500 m的丘陵和高于500 m的山地。
宁波地区自动站布网平均间隔距离6~7 km,图 1a是雷达扫描半径内自动站分布图。对自动站雨量观测数据进行了质量控制,包括去除重复站点、时间与空间的一致连续性检验,以及联合雷达估测降水去除奇异点等。
表 1列出了本文研究所用的三个台风(台风海葵、凤凰和菲特)历史个例。图 1b~1d分别为选取台风对应某一时刻的反射率以及移动路径。台风海葵(图 1b)于2012年8月7日19:20(世界时,下同)在浙江省宁波市象山县鹤浦镇登陆,登陆时强台风级别。浙江省大部分地区普降中到大雨,局部暴雨,东部沿海部分出现暴雨到大暴雨,局部特大暴雨,最大过程累积雨量达到540 mm。台风菲特(图 1c)2013年10月6日17:15在浙闽交界处(福鼎沙埕镇)登陆,登陆时强度为强台风级别。该台风是2014年之前10月登陆我国大陆最强台风,其强降水范围广,总量大,破多项历史极值纪录。浙江省内普遍出现300 mm以上过程累积雨量,部分400 mm以上,局部地区500 mm以上,最大雨量达到695 mm。台风凤凰(图 1d)2014年9月22日11:35在宁波市象山鹤浦镇登陆,登陆时强热带风暴级别,最大过程累积雨量达到331 mm。
|
|
表 1 台风定量降雨估测方法研究中用到的3个台风个例 Table 1 Summary of the three typhoon cases in the study |
台风强的水平风影响以及地形抬升造成的强扰动对雷达和自动站雨量观测的时空匹配偏差影响是降水估测误差的其中一个原因之一。复杂地形下对于雷达和自动站的数据的时空匹配影响主要体现在:(1)雷达的最底层监测到雨滴降落到不同高度的自动站的时间存在一定差异。(2)抬升气流的速度大小对于在山区降雨的频率以及激烈程度都有着最大的影响,而风向决定了降雨的分布以及激烈程度。
在雷达和雨量站的配对分析,采用Xu et al(2008)所使用的热带暖云Z-R关系(A=230,B=1.25)生成每个时次的雷达瞬时雨强(换算成逐分钟雨量),最后按照每个雷达体扫所覆盖的时间,生成分析时间段内的逐分钟雨量。这里第i个体扫所覆盖的逐分钟时段开始时间为从当前体扫时间ti和上一个体扫时间ti-1的平均时间;结束时间为当前体扫时间ti和下一个体扫时间ti-1的平均时间。将换算为逐分钟的雷达降雨估测时序数据和自动站分钟观测雨量时序数据进行时空偏移的皮尔逊相关系数计算,最后获得两者的时空匹配关系分布统计图。台风海葵的雷达和自动站的数据的时空匹配关系统计(图 2a)表明,自动站相对于雷达资料的滞后5~6 min存在最佳的匹配关系,1 h时间尺度的是最佳选择。两者空间匹配关系(图略)表明,在不考虑时间滞后性问题的情况下,时间累积尺度越大,其空间匹配相关性特征越显著。对台风海葵过程而言,雷达反射率数据需要x方向平移0 km,y方向需要向上平移1 km,可以获得和自动站相关系数最好的空间匹配(图 2b),即相关性最大的偏移位置。

|
图 2 台风海葵2012年8月7日03时至8日15时UTC的自动站雨量和雷达反射率时空匹配关系 (a)自动站雨量和雷达反射率时间匹配关系, (b)60 min时间尺度的自动站雨量和雷达反射率空间偏移相关性匹配图 Fig. 2 The relation of temporal and spatial matching of Typhoon Haikui rainfall in automatic weather station and radar reflectivity from 03:00 UTC 7 to 15:00 UTC 8 August 2012 (a) the relation of temporal matching, (b) the relation of spatial matching |
目前,由于国内缺乏根据地面风场观测资料或模式风场观测资料,校正地面雨量计观测资料的研究,现有的QPE方法基本都没有考虑自动站和雷达资料的时空偏移问题,所以在台风过程中,直接依据雷达-雨量计观测资料拟合得到的Z-R关系存在着和潜在Z-R关系“真值”之间的偏离问题(勾亚彬等,2014)。本文的算法因为联合自动站获取1 h时间尺度上的全局和区域最优的VPR廓线,因此可有效地避免此类问题。
1.3 区域垂直反射率因子廓线修正降雨估测方法本文提出了一种基于区域垂直反射率因子廓线修正的雷达定量估测方法(Region VPR QPE,RVQ)。针对传统降水估测方法在复杂地形下的缺陷,RVQ采用目标函数迭代获取站点全局和区域最优的VPR以及最优Z-R关系,最后插值获取对应格点的VPR,并反演获得格点降雨。RVQ的具体计算按照如下步骤(图 3)。

|
图 3 RVQ流程 Fig. 3 The flowchart of RVQ |
构建目标函数J为雷达降雨估测与自动站雨量计标准偏差:
| $ J = {\left[ {\frac{1}{N}\sum\limits_{j = 1}^N {\left({{P_j} - {O_j}} \right)^2} } \right]^{1/2}} $ | (1) |
式中,P为利用Z-R关系(A, B)计算的雷达估测小时雨量(单位:mm·h-1),并通过雷达体扫所覆盖的时间权重加权计算取得小时估测雨量(单个时次体扫所覆盖时间权重系数即其覆盖时段长度:时段开始时间为从该体扫时间和上一个体扫时间的平均时间,结束时间为该体扫时间和下一个体扫时间的平均时间);O为对应自动站的小时观测雨量,其中Z-R关系如下:
| $ R = {10^{\left({0.1Z - \lg A} \right)/B}} $ | (2) |
通过最小二乘迭代求解目标函数J极小值,步骤如下:
(a) 假设初始的近地面反射率Z0等于雷达最低仰角面反射率E,利用最小二乘法计算获得初始(A0, B0)。定义近地面反射率增量为ΔZ=Z-E,则初始值为0。
(b) 在每一步迭代(第k次迭代)计算中,选取每个自动站(第j个自动站)附近相邻站点构建德洛内(Delaunay)三角网格区域作为该自动站的分析区域(图 4和图 5),在该分析区域内利用区域内平均面雨量以及雷达估测降水量,通过最小二乘求解区域的第k次迭代近地面估测反射率Gj, k,区域与全场增量加权平均求得最优近地面反射率Zj, k。

|
图 4 自动站三角网格示意图 (图中黑线为自动构建的Delaunay三角网格,背景为地形图) Fig. 4 Triangular mesh diagram of automatic weather station (Black lines indicate triangular Delaunay network, the background is topographic map) |

|
图 5 区域VPR示意图 (a)垂直剖面示意图, (b)图 5a VPR阴影区域对应的近地面三角网格示意图 (图中黑色区域表示地形;阴影区域表示以黑边白色圆代表的自动站区域,实心圆代表其相邻三角网格连接的周边自动站;图 5a中上下垂直方向箭头线段表示该区域空间的VPR) Fig. 5 The diagram of VPR (a) the diagram of vertical section, (b) the diagram of triangular mesh (Black area indicates terrain; shaded area indicates the analysis area of automatic weather station, the solid circles indicate the neighboring automatic weather stations connected by the adjacent triangular mesh; the vertical arrow line indicates the VPR of the area in Fig. 5a) |
| $ {Z_{j, k}} = {E_j} + 0.5({G_{j, k}} - {E_j}) + 0.5\Delta {Z_{j, k - 1}} $ | (3) |
联合自动站降水以及估测的近地面反射率,再次利用最小二乘计算得到拟合获得Z-R关系(Ak+1, Bk+1)。
(c) 当|Jk-Jk-1| < 0.01,则迭代收敛;另外为了保证计算的稳定性,需同时满足|Ak-Ak-1| < 0.01和|Bk-Bk-1| < 0.001。
1.3.2 计算格点的区域VPR利用观测反射率和计算的近地面反射率构建自动站区域VPR(图 5),采用三角权重线性矢量插值方法插值获取到等间距网格的区域VPR;这里VPR顶高设为4 km,主要是便于线性矢量插值。
1.3.3 估测格点降水联合反演的格点VPR和最低仰角反射率计算格点反射率,利用步骤1.3.1获得最优Z-R关系估算格点降水。
加密自动站的相关性研究(刘雨佳等, 2014)表明,站点之间距离越近,观测资料之间的相关性越大,因此,RVQ算法采用相邻站点构建Delaunay三角网格区域作为分析区域来拟合区域VPR,理论上是可以更合理地描述复杂地形下的非均一VPR问题。此外,该算法因为是基于时间、空间尺度统计意义上进行最优Z-R关系以及近地面反射率的求解,因此其可以有效避免自动站和雷达数据资料配对的时间、空间偏移问题。通过计算近地面反射率以及获取最优的Z-R关系,可以有效解决地形等因素造成台风降水低估问题。下文将通过对比试验来检验算法的准确性。
2 台风个例应用本节将对RVQ降水估测精度进行评估,并将其与最优Z-R关系法(OZR)、热带暖云(WARM:A=230,B=1.25)、对流云(CON:A=300,B=1.4,其为敏视达雷达业务算法)、层云Z-R关系(STR:A=200,B=1.6),以及美国业务常用的算法(Xu et al,2008)提出降水估测方法,简称Z08,下同)等传统估测方法比较,分析RVQ方法在不同地形条件下改进台风降雨估测精度的效果。这里Z08法采用Xu et al(2008)默认方案和阈值,在判断出该雷达区域的整体VPR结构具有热带暖云结构特征之后,对分析范围内各个格点分不同降雨类型进行降雨估测(小于30 dBz的格点采用层云Z-R关系;大于30 dBz且小于42 dBz格点采用热带暖云关系;大于42 dBz格点采用对流云Z-R关系)。评估方法则参考Xu et al(2008)方法,采用RMSE、CC以及Bias来进行评估,计算公式如下:
| $ RMSE = {\left\{ {\sum\limits_{i = 1}^N {{{\left[ {{B_{\rm{R}}}\left(i \right) - {B_{\rm{G}}}\left(i \right)} \right]}^2}/N} } \right\}^{0.5}} $ | (4) |
| $ CC = \frac{{\sum\limits_{i = 1}^N {{B_{\rm{R}}}\left(i \right){B_{\rm{G}}}\left(i \right)} - \frac{1}{N}\sum\limits_{i = 1}^N {{B_{\rm{R}}}\left(i \right)} \sum\limits_{k = 1}^N {{B_{\rm{G}}}\left(i \right)} }}{{{{\left\{ {\left[ {\sum\limits_{i = 1}^N {B_{\rm{R}}^2\left(i \right)} - N{{\bar B}_{\rm{R}}}^2} \right]\left[ {\sum\limits_{k = 1}^N {B_{\rm{G}}^2\left(i \right) - N{{\bar B}_{\rm{G}}}^2} } \right]} \right\}}^{1/2}}}} $ | (5) |
| $ Bias = \sum\limits_{i = 0}^N {{B_{\rm{R}}}\left(i \right)} /\sum\limits_{i = 0}^N {{B_{\rm{G}}}\left(i \right)} $ | (6) |
式中,RMSE、CC和Bias分别为降水估测与观测的雨量误差(小时雨量估测误差单位为mm·h-1;平均过程累积降水估测误差单位为mm)、相关系数以及偏差。这里BR和BG分别代表了1 h段内的雷达降水估测和自动站观测配对的雨量(平均过程累积降水估测评估则采用整个过程时段累积估测雨量和自动站观测累积雨量比较)的样本数组,样本数为N。这里BR代表对数组BR的平均数值, BG代表对数组BG的平均数值。
2.1 不同地形的反射率因子垂直廓线分析依据地形高度分为洋面、平原、山丘和山地四类。图 6分析了不同地形条件下反演的反射率廓线特征差异。不同地形条件下的VPR比较(图 6)表明,近海海面和沿海陆地的下界面区域对应VPR结构是存在显著差异的:沿海海面的VPR呈现出3~4 km随高度降低基本维持不变,而在3 km向近地面随高度降低呈现微弱线性递减的特征,陆地则随高度降低线性递增的特征;沿海海面的回波强度要整体弱于陆地,表明海面的雨滴大小要小于陆地上的雨滴。这主要是因为海上通常对流比较浅,水汽比陆地更充足,粒子下落过程中碰并增长时间短,导致粒子浓度偏大而粒径偏小;而在4 km高度,由于该高度靠近0℃层底部高度,在其附近冰相粒子的存在导致了回波变强,在雨滴的下落过程中不断融化和蒸发等,因而使得到达地面时雨滴相对偏小(Nesbitt et al, 2000; Cecil and Zipser, 2002; Chen et al, 2012)。而在陆地区域,由于所产生的抬升气流要明显强于海面,因此抬升气流能使得雨滴在空中停留维持更长时间,进而通过碰并等作用产生相对更大的雨滴,因而导致近地面反射率强度相对更强。

|
图 6 不同地形条件下的VPR比较 (a)海葵,(b)凤凰,(c)菲特(近地面反射率>30 dBz以上的统计结果) Fig. 6 Comparison of VPRs in different terrain conditions (a) Typhoon Haikui, (b) Typhoon Fungwong, (c) Typhoon Fitow (the statistical results of near surface refectivity that greater than 30 dBz) |
山地和丘陵地区的VPR的随高度降低递增比平原地区更显著(尤其在近地面倾斜递增程度较大),8月台风海葵和9月台风凤凰尤其显著(图 6a和6b)。这主要是由于台风深厚的暖湿气流在爬升过程中,大量的水汽迅速转变为云中的雨滴;而在强风速环境的地形的强迫抬升作用使得雨滴在空中停留更长时间,通过碰并增长成更大雨滴,最后在山区形成强降雨(对应近地面回波更强)。地形强迫有利于生成低层辐合和高层辐散的环境,进而加剧降水的非均一的分布(钮学新等,2005;柴东红等,2010)。此外,在台风影响下,播撒机制在复杂地形下地形增雨过程非常迅速, 进一步促进了地形增雨,而台风的充足的水汽对于地形增雨机制的维持起到了重要作用(Smith et al, 2009;2010; 程婧和倪允琪, 2009)。
综合来看,RVQ较好地反映了台风在不同地形条件下的VPR结构特征差异,相比传统只利用Z-R关系的算法并不考虑此类特征的算法,或只是获取整场的平均获取单一的VPR结构的算法,RVQ法反演的VPR修正反射率可以获得更接近于地面实际情况的反射率分布,从而提高降水估测精度。
2.2 登陆后1 h降雨精度评估这里选取美国业务算法Z08与RVQ法做比较。图 7~图 9分别为三个台风小时雨量估测误差分布图。台风海葵登陆后,从图 7b散点图可以看到,Z08算法对小于20 mm·h-1的降水存在高估,而对大于20 mm·h-1的降水则存在低估。从分布上看,高估区域主要集中在平原以及丘陵和平原的衔接地带的站点,而在山区和丘陵则明显低估了降雨估测。RVQ法较好地修正降水估测精度,从图 7d散点分布看,低值高估问题得到明显的改善;虽然高值还存在一定程度的低估,但相比Z08法,已明显改进,从空间分布图上看,山区和丘陵误差明显减少;RVQ与观测的相关系数为0.77,明显优于Z08的0.46。同时RVQ的估测误差为3.6 mm·h-1,明显低于Z08的6.7 mm·h-1。
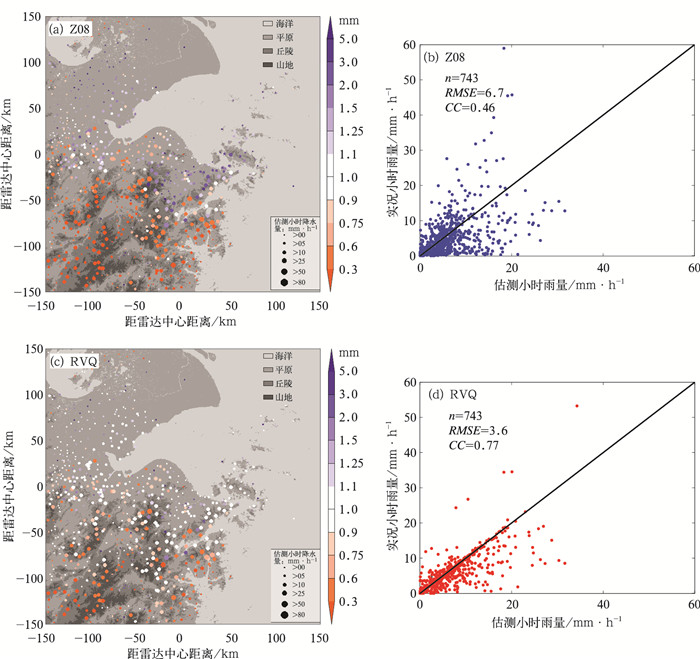
|
图 7 2012年8月7日20:20 UTC Z08方法(a, b)和RVQ方法(c, d)小时雨量误差分布比较图 (a, c)1 h降雨估测误差空间分布,(b, d)1 h降雨估测和实况观测比较散点图(时间为台风海葵登陆后1 h) Fig. 7 Comparison of 1 h QPE of Typhoon Haikui obtained by Z08 (a, b) and RVQ (c, d) methods at 20:20 UTC 7 August 2012 (a, c) the distribution of QPE errors, (b, d) the scatterplot of radar 1 h QPE |

|
图 8 同图 7,但为2014年9月22日12:36 UTC台风凤凰登陆后1 h的比较结果 Fig. 8 Same as Fig. 7, but for 1 h QPE of Typhoon Fungwong at 12:36 UTC 22 September 2014 |

|
图 9 同图 7,但为2013年10月6日18:16 UTC台风菲特登陆后1 h的比较结果 Fig. 9 Same as Fig. 7, but for 1 h QPE of Typhoon Fitow at 18:16 UTC 6 October 2013 |
台风凤凰登陆后,大部分实况小时雨量集中在10 mm·h-1以下,强度没有台风海葵强,Z08估测算法明显低估了强降水(图 8a和8b),对于此个例,RVQ法较成功地修正了降水估测误差,RVQ法估测降水散点分布基本集中在对角线,相关系数从0.8升至0.92左右;误差从4.5 mm·h-1降低至2.3 mm·h-1。
台风菲特的降水强度是三个台风中最强的,同之前的台风相比,Z08明显低估了强降水(图 9c)。从空间分布图看(图 9a),即使在平原地区,降水也明显低估,RVQ则比较成功地修正了降水估测低估的问题,相关系数从0.73升至0.92;误差从11.6 mm·h-1降至4.6 mm·h-1(图 9d)。空间分布上看(图 9d),RVQ法成功减少了不同地形区域降水估测误差,可以看到误差分布接近于零。
总的来说,传统Z08法存在低值高估,高值低估的问题,RVQ法明显减少了不同地形区域的降水估测误差,与观测降水的相关性也明显提高,要明显优于传统的Z08降水估计业务方法。
2.3 过程累积降雨精度评估本节对三个台风过程累计降水量估测进行比较。表 2是采用Xu et al(2008)的降雨估计评估方法对RVQ法估算与美国(Z08)业务方法估算的降水误差进行比较分析。相比较Z08方法,RVQ方法在定量降雨估测精度上有较显著提升。相关系数从0.61~0.79提升到0.85~0.94;累积估测误差明显减少(减少50%以上),其中台风菲特,从109.4 mm (Z08)降低到38.8 mm(RVQ);偏差系数也明显改善,如台风凤凰采用Z08方法偏差系数仅为0.3,台风降水估测强度明显低估,采用RVQ后,虽然仍旧存在一定程度的低估(强度较弱的台风在复杂地形区域的地形增雨所形成的对流性发生较浅,因而对应雷达最底层仰角面探测到反射率偏弱;而RVQ法为了迭代收敛性,对反射率修正范围进行阈值约束,因此,这就导致修正后的近地面反射率仍存在一定低估问题),但偏差系数已提升至0.67,降雨强度估算有明显改进;台风菲特RVQ算法改进更明显,改进后的偏差系数为0.93,接近无偏。
|
|
表 2 三个台风的整体定量降雨估测误差(Z08和RVQ比较) Table 2 QPE estimated errors of three typhoon cases (Z08 vs RVQ) |
图 10将降水估测误差进一步分为不同地形区域,这里简单将其划分为复杂地形(山地、丘陵)和平原地区。对于上述两种算法,三个台风在复杂地形区域降水估测误差远大于平原地区,其原因主要是降水估测强度在复杂地形区域存在明显低估。相比Z08,RVQ方法明显减少了复杂地形区域的降水估测误差;与观测降水的相关性明显提升,复杂地形区域在0.8以上,平原地区相关系数则接近于1;与观测降水的偏差也明显减少,更接近无偏估计。总的来说,不同的台风个例结果表明,RVQ方法减少了降水估测误差,与观测降水的相关性明显提高,偏差也明显减少。

|
图 10 Z08和RVQ方法在不同地形下的定量降雨估测误差比较 (a)平均过程累积雨量误差,(b)相关系数,(c)偏差 (Z08和RVQ在复杂地形下的估测结果采用Z08-T和RVQ-T表示,在平原下的估测结果采用Z08-P和RVQ-P表示) Fig. 10 Comparison of quantitative rainfall estimation errors in different terrains by Z08 and RVQ (a) cumulative process rainfall, (b) coefficient, (c) error (Z08-T and RVQ-T indicate the result of Z08 and RVQ in complex terrain, Z08-P and RVQ-P indicate the result of Z08 and RVQ in plain) |
RVQ法和不同降雨估测方法比较(图 11,图中的垂直虚线代表台风中心登陆时间)表明,在平原、山地、丘陵三种不同地形下,登陆前不同方法差异不大,主要差异集中在台风登陆以后。在不同地形下,RVQ法的累积降雨估测最接近于自动站实况观测(OBS)。RVQ法和最优Z-R关系(OZR)法的比较(图 11)表明,RVQ法全面优于OZR法,尤其在丘陵以及山地的复杂地形区域,RVQ法要显著优于OZR法。这说明RVQ法通过区域垂直反射率廓线修正可以获得更接近实况的近地面反射率,进而拟合出更稳定、准确的Z-R关系并提升了估测精度。RVQ和Z08等其他几种业务上常用的雷达降水估测结果表明,Z08法估测降水总量要明显低于RVQ,但由于进行了降雨分类,比其他依据某一类型的统计的Z-R关系接近实况;暖云的算法比对流和层云的算法要好,说明台风降水更接近暖云降水机制;依据对流云和层云统计的Z-R关系,估测强度类似,表现最差。

|
图 11 不同地形条件(a, d, g)平原,(b, e, h)丘陵,(c, f, i)山地的累积降雨估测和实况观测的时序比较图 (a, b, c)台风海葵,(d, e, f)台风凤凰,(g, h, i)台风菲特 (图中垂直虚线对应时间为台风登陆时间) Fig. 11 The time sequence comparison chart of cumulative rainfall estimation and observation in (a, d, g) plain, (b, c, h) hill, (c, f, i) mountain (a, b, c) Typhoon Haikui, (d, e, f) Typhoon Fungwong, (g, h, i) Typhoon Fitow (Vertical dotted lines indicate the time of typhoon landing) |
在台风海葵的平原地区的降雨估测(图 11a、11b、11c)中,除RVQ法外,OZR法、Z08法和热带暖云方法也较接近于实况,这主要是由于动态计算的最优Z-R关系以及固定Z-R关系(Z08法、热带暖云方法所用暖云Z-R关系在平原为主地形下的观测数据拟合取得)和夏季台风海葵的实际Z-R关系较为接近。而在山地和丘陵区域,RVQ法则通过区域VPR补充了近地面的地形增雨特征(图 6a),进而修正了近地面反射率;虽然还存在一定程度的低估,但RVQ法的估测雨量要明显优于其他算法,估测的降水总量更接近实况雨量。
台风凤凰的比较表明(图 11d、11e、11f),无论是平原,还是复杂地形下,所有的方法的估测精度都明显落后于RVQ法。这主要是以下两点原因造成的:(1)秋季台风降雨效率高,固定Z-R关系并没有考虑季节性差异对统计结果的影响,因而估测误差较大;因此,采用动态的Z-R关系拟合策略(RVQ,OZR)可以更好地适应不同季节的台风降雨估测;(2)台风凤凰的VPR统计(图 6b)表明,暖云以及地形增雨的特征十分显著, RVQ法考虑了全局与区域的最优,较好地拟合了低层VPR结构,修正了近地面反射率,从而提高了降水估测精度。
台风菲特(图 11g、11h、11i)也属于高效降水的秋季台风,其在登陆前5 h,无论是平原,还是复杂地形区域的实况观测雨量曲线都呈现出迅速递增特征,平均过程累积观测雨量整体都在200~250 mm,相比凤凰,其强降水分布面积较广,VPR统计(图 6c)表明,10月秋季台风的暖云结构特征要弱于其他两个台风,可以看到廓线结构近乎垂直。Z08法缺乏对秋季台风高效率降雨的统计,因而无论是平原还是复杂地形区域估测误差都较大,而RVQ法主要优势是通过动态Z-R关系的调整来改善不同地形条件下的降雨估测精度,其中RVQ法估测精度最高。
图 12降雨估测误差空间分布图。对于台风海葵,相比Z08,RVQ法改善了其在平原区域的降雨估测高估问题;降低了杭州湾以西的内陆平原地区的降雨估测误差,提升了估测精度;改善了大部分丘陵、山地等复杂地形区域的定量降雨估测低估问题(图 12a和12b)。对于台风凤凰,Z08在舟山海岛、宁波平原、丘陵和山地区域都存在显著低估问题(图 12c),同样,RVQ方法能自适应改善这些区域的降雨估测低估问题(图 12d)。对于台风菲特,Z08降雨估测低估问题更严重(图 12e),而RVQ法则显著改善了该过程的大面积降雨估测低估问题。

|
图 12 Z08(a, c, e)和RVQ法(b, d, f)的过程累积降雨估测误差空间分布比较图 (a, b)台风海葵,(c, d)台风凤凰,(e, f)台风菲特 Fig. 12 Comparison of spatial distribution of rainfall estimation errorsin process of Z08 (a, c, e) and RVQ (b, d, f) (a, b) Typhoon Haikui, (c, d) Typhoon Fungwong, (e, f) Typhoon Fitow |
总的来说,RVQ法可以较好地适应不同地形条件下的台风降雨估测。不同的降雨估测算法在台风登陆前差异较小,主要差异在台风登陆以后。台风登陆后,降水增强,尤其在遇到复杂地形时,低层反射率结构变化大,地形增雨明显。山地区域的平均累计降水量要明显高于平原地区。传统的估测算法因为没有考虑不同地形特征差异,估测降水递增相对缓慢,且平原与山地之间差异小,明显低估了降水强度。而RVQ法的估测的降水,无论是空间分布还是过程累计都最接近于实际观测;尤其在台风登陆后的复杂地形区域,RVQ法很好地体现了台风降水增强的特性,显著减少了降水低估问题。
3 结论针对传统降水估测方法在复杂地形下的缺陷,本文提出了一种基于区域垂直反射率因子廓线修正的定量降雨估测方法(RVQ)用于改善复杂地形下的台风降雨估测精度。该方法在通过全局与区域最优拟合的VPR廓线获取近地面的最优反射率,并在此基础上,进一步获取最优的动态Z-R关系。利用三个台风对RVQ法的精度进行检验,并将其与传统的降水估测算法比较,得到的结论如下:
(1) RVQ法考虑了区域以及全场最优拟合,使其估测的近地面反射率能够体现不同地形条件的差异,试验结果表明,RVQ法反演的VPR能够比较好地反映海洋、平原地区与复杂地形低层反射率结构的差异之间的存在差异,更符合实际。
(2) 相比传统的其他Z-R关系,RVQ自适应动态的Z-R关系估测的降水最接近实际观测,尤其在台风登陆后的复杂地形区域,RVQ法很好地体现了台风降水增强的特性,明显减少了降水低估问题。
(3) 与美国业务中Z08降水估测方法的比较分析表明,RVQ法显著地改进了复杂地形区域的定量降雨估测精度。相关系数看,RVQ法与观测相关性达到0.85~0.94,而美国业务算法(Z08)应用到本文的研究,相关性只有0.61~0.79;RVQ的累积估测误差也较Z08方法减少50%以上,尤其对造成强降水的台风,RVQ法优势更加明显。
尽管RVQ法较大幅度地改善了复杂地形下的降雨估测低估问题,但该方法对于局部的复杂地形区域(山地、复杂地形特征的丘陵区域)还存在些问题(图 12)。这一方面是由于RVQ法考虑了迭代收敛性,对近地面反射率修正范围进行了阈值约束,即上述ΔZk介于[-8 dB,8 dB],因此在一定程度上限制了修正范围(该参数依据气候统计,同时考虑到在台风的强风环境下的降水系统空间分布的不均匀性以及自动站观测资料空间采样的不确定性问题(张宁等,2010)。另一方面,在台风强度相对较弱(比如台风凤凰)的情况下,在丘陵和山地区域的地形增雨所形成的对流性发生较浅,而雷达最底层仰角面探测到反射率偏弱时候,也会导致修正后的近地面反射率偏低,进而造成降雨仍在一定程度上存在低估问题。因此,未来的一个工作重点是可以联合雨滴谱、其他空间要素观测仪器资料对其反演的VPR的空间精度进行进一步修正,来改进复杂地形下的短临降雨预报的精度。
柴东红, 景华, 孟凯, 等, 2010. 地形暴雨的多普勒天气雷达观测分析[J]. 气象科学, 30(3): 366-372. |
程婧, 倪允琪, 2009. 台湾地形对海棠台风影响的数值模拟研究[J]. 气象科学, 29(05): 575-583. DOI:10.3969/j.issn.1009-0827.2009.05.002 |
东高红, 刘黎平, 2012. 雷达与雨量计联合估测降水的相关性分析[J]. 应用气象学报, 23(1): 30-39. |
樊建勇, 单九生, 管珉, 等, 2012. 江西省小流域山洪灾害临界雨量计算分析[J]. 气象, 38(9): 1110-1114. |
勾亚彬, 刘黎平, 杨杰, 等, 2014. 基于雷达组网拼图的定量降水估测算法业务应用及效果评估[J]. 气象学报, 72(4): 731-748. DOI:10.11676/qxxb2014.050 |
胡胜, 张羽, 邓文剑, 等, 2014. 深圳新一代天气雷达山体阻挡的订正方案及效果检验[J]. 热带气象学报, 30(1): 1-10. |
黄小玉, 陈媛, 熊毅, 等, 2009. 漂移克里金方法在雷达和雨量计联合估测降水中的应用[J]. 气象学报, 67(2): 288-297. DOI:10.11676/qxxb2009.029 |
李建通, 李柏, 杨洪平, 等, 2015. 雷达-雨量计联合估测区域降水量方法检验与评估[J]. 气象, 41(2): 200-211. DOI:10.7519/j.issn.1000-0526.2015.02.008 |
刘雨佳, 陈洪滨, 金德镇, 等, 2014. 加密自动气象站雨量计资料的质量控制及其相关关系的研究[J]. 大气科学, 38(1): 159-170. DOI:10.3878/j.issn.1006-9895.2013.13116 |
陆桂荣, 王文, 郑美琴, 等, 2015. 海南台风暴雨的时空分布特征[J]. 大气科学学报, 38(5): 710-715. |
马慧, 万齐林, 陈子通, 等, 2008. 基于Z-I关系和变分校正法改进雷达估测降水[J]. 热带气象学报, 24(5): 546-549. |
钮学新, 董加斌, 杜惠良, 2005. 华东地区台风降水及影响降水因素的气候分析[J]. 应用气象学报, 16(3): 402-407. DOI:10.11898/1001-7313.20050315 |
温龙, 刘溯, 赵坤, 等, 2015. 两次降水过程的微降雨雷达探测精度分析[J]. 气象, 41(5): 577-587. DOI:10.7519/j.issn.1000-0526.2015.05.006 |
杨杰, 刘黎平, 勾亚彬, 2014. 影响浙江地区降水估测几个因素的分析[J]. 气象, 40(5): 589-597. DOI:10.7519/j.issn.1000-0526.2014.05.009 |
张宁, 江志红, 吴立广, 2010. 江苏省自动站与基础站降水观测资料质量分析[J]. 大气科学学报, 33(5): 606-614. |
张亚萍, 张勇, 廖峻, 等, 2013. 天气雷达定量降水估测不同校准方法的比较与应用[J]. 气象, 39(7): 923-929. DOI:10.7519/j.issn.1000-0526.2013.07.013 |
赵坤, 刘国庆, 葛文忠, 2001. 用卡尔曼滤波确定变分方法中的权重系数进行雨量校正[J]. 气候与环境研究, 6(2): 180-185. |
Bellon A, Lee G W, Zawadzki I, 2005. Error statistics of VPR corrections in stratiform precipitation[J]. J Appl Meteor, 44(7): 998-1015. DOI:10.1175/JAM2253.1 |
Cecil D J, Zipser E J, 2002. Reflectivity, ice scattering, and lightning characteristics of hurricane eyewalls and rainbands.Part Ⅱ: intercomparison of observations[J]. Mon Wea Rev, 130(4): 785-801. DOI:10.1175/1520-0493(2002)130<0785:RISALC>2.0.CO;2 |
Chang Paoliang, Lin Pinfang, Jou B J D, et al, 2009. An application of reflectivity climatology in constructing radar hybrid scans over complex terrain[J]. J Atmos Oceanic Technol, 26(7): 1315-1327. DOI:10.1175/2009JTECHA1162.1 |
Chen Baojun, Wang Yuan, Ming Jie, 2012. Microphysical characteristics of the raindrop size distribution in typhoon morakot (2009)[J]. J Trop Meteor, 18(2): 162-171. |
Germann U, Joss J, 2002. Mesobeta profiles to extrapolate radar precipitation measurements above the alps to the ground level[J]. J Appl Meteor, 41(5): 542-557. DOI:10.1175/1520-0450(2002)041<0542:MPTERP>2.0.CO;2 |
Marshall J M, Langille R C, Palmer W M K, 1947. Measurement of rainfall by radar[J]. J Meteor, 4(6): 186-192. DOI:10.1175/1520-0469(1947)004<0186:MORBR>2.0.CO;2 |
Nesbitt S W, Zipser E J, Cecil D J, 2000. A census of precipitation features in the tropics using TRMM: radar, ice scattering, and lightning observations[J]. J Climate, 13(23): 4087-4106. DOI:10.1175/1520-0442(2000)013<4087:ACOPFI>2.0.CO;2 |
Ninomiya K, Akiyama T, 1978. Objective analysis of heavy rainfalls based on radar and gauge measurement[J]. J Meteor Soc Japan, 56(3): 206-210. DOI:10.2151/jmsj1965.56.3_206 |
Qi Youcun, Zhang Jian, Kaney B, et al, 2014. Improving WSR-88D radar QPE for orographic precipitation using profiler observations[J]. J Hydrometeor, 15(3): 1135-1151. DOI:10.1175/JHM-D-13-0131.1 |
Smith B L, Yuter S E, Neiman P J, et al, 2010. Water vapor fluxes and orographic precipitation over northern California associated with a landfalling atmospheric river[J]. Mon Wea Rev, 138(1): 74-100. DOI:10.1175/2009MWR2939.1 |
Smith R B, Schafer P, Kirshbaum D J, et al, 2009. Orographic precipitation in the tropics: experiments in Dominica[J]. J Atmos Sci, 66(6): 1698-1716. DOI:10.1175/2008JAS2920.1 |
Xu Xiaoyong, Howard K, Zhang Jian, 2008. An automated radar technique for the identification of tropical precipitation[J]. J Hydrometeor, 9(5): 885-902. DOI:10.1175/2007JHM954.1 |
Vignal B, Galli G, Joss J, et al, 2000. Three methods to determine profiles of reflectivity from volumetric radar data to correct precipitation estimates[J]. J Appl Meteor, 39(10): 1715-1726. DOI:10.1175/1520-0450-39.10.1715 |
Vignal B, Krajewski W F, 2001. Large-sample evaluation of two methods to correct range-dependent error for WSR-88D rainfall estimates[J]. J Hydrometeor, 2(5): 490-504. DOI:10.1175/1525-7541(2001)002<0490:LSEOTM>2.0.CO;2 |
Wang Yadong, Zhang Pengfei, Ryzhkov A V, et al, 2014. Utilization of specific attenuation for tropical rainfall estimation in complex terrain[J]. J Hydrometeor, 15(6): 2250-2266. DOI:10.1175/JHM-D-14-0003.1 |
Wen Yixin, Cao Qing, Kirstetter P E, et al, 2013. Incorporating NASA spaceborne radar data into NOAA national mosaic QPE system for improved precipitation measurement: a physically based VPR identification and enhancement method[J]. J Hydrometeor, 14(4): 1293-1307. DOI:10.1175/JHM-D-12-0106.1 |
Wen Yixin, Hong Yang, Zhang Guifu, et al, 2011. Cross validation of spaceborne radar and ground polarimetric radar aided by polarimetric echo classification of hydrometeor types[J]. J Appl Meteor Climatol, 50(7): 1389-1402. DOI:10.1175/2011JAMC2622.1 |
Zhang Jian, Howard K, Gourley J J, 2005. Constructing three-dimensional multiple-radar reflectivity mosaics: examples of convective storms and stratiform rain echoes[J]. J Atmos Oceanic Technol, 22(1): 30-42. DOI:10.1175/JTECH-1689.1 |
Zhang Jian, Qi Youcun, Langston C, et al, 2014. A real-time algorithm for merging radar QPEs with rain gauge observations and orographic precipitation climatology[J]. J Hydrometeor, 15(5): 1794-1809. DOI:10.1175/JHM-D-13-0163.1 |
 2017, Vol. 43
2017, Vol. 43 
