2. 中国气象局国家气候中心气候研究开放实验室 & CMA-NJU气候预测研究联合实验室,北京 100081
2. Laboratory for Climate Studies, CMA and CMA-NJU Joint Laboratory for Climate Prediction Studies, Beijing 100081
厄尔尼诺和南方涛动(ENSO)现象是热带太平洋海气相互作用的重要系统,是全球气候系统所能观测到的最强年际变化信号,它以2~7年的周期循环往复,不仅造成热带太平洋地区的天气气候出现异常,还会以遥相关的方式间接地影响热带太平洋以外地区乃至全球的天气气候,造成世界许多地区严重的洪涝、干旱及其他灾害(Rasmusson and Carprnter, 1982; Rasmusson and Wallace, 1984; Zhang et al, 1996; 2012;臧恒范和王绍武,1984;伍红雨等,2014;王朋岭等,2015;陈丽娟等,2016;顾薇,2016;司东等,2016)。正是由于ENSO的显著影响,自从Zebiak and Cane(1987)首次使用简化海气耦合模式(ZCM)成功预测了1986/1987年的El Niño事件后,各国科学家对ENSO预测展开了广泛的研究。目前,ENSO预测主要依靠动力和统计两种方法,其中动力模式在短期气候预测业务中愈发重要,相关研究也取得了显著进展(Chen et al, 1995; 2004;Luo et al, 2005; 2008;Zheng et al, 2006; 2009;Cheng et al, 2010; Izumo et al, 2010)。然而,纯动力预测模式的预报能力仍然表现出不稳定性(Jin et al, 2008; Wang et al, 2008),例如,模式在物理过程参数化过程等方面不可避免地存在误差。
大量研究显示,在动力模式预测的基础上,采用统计方法对模式预测结果进行经验性订正,可以在一定程度上减小模式误差对预报的影响(任宏利和丑纪范,2007a;朱玉祥等,2016)。Zeng et al(1994)给出了平均误差订正、最大相似度、最小偏差和基于经验正交函数分解(EOF)4种订正模式误差的方法并用于气候预报误差订正。任宏利等(2006),任宏利和丑纪范(2005;2007b)提出了利用历史相似信息对模式预报误差进行预报的思路。在此基础上,Ren et al(2014)发展了一个相似-动力ENSO预报系统,通过运用相似状态提供的模式历史回报的误差分布信息对模式ENSO预报进行事后订正。Kang and Shukla(2006)和Kug et al(2007)依据耦合模态技术(Graham, 1994)的思想发展了一种模态投影方法并分别应用到降水与海温的预报订正中,得到了良好的效果。该方法首先对模式预报因子进行筛选,再利用投影和回归的方式将其有效信息反演出来,以达到提高预报技巧的效果。Kug et al(2008a;2008b)对最优因子集的选取方式进行改进并发展了逐步模态投影方法(SPPM),将其应用到多模式订正可使预报水平得到显著提高,其效果优于简单平均多模式集合以及奇异值分解集合方法。
国家气候中心近年来发展起来的气候系统模式(BCC_CSM1.1m)已经应用于业务预测,其对热带地区气候预测能力得到显著改善,但对ENSO的预报效果仍不令人满意,与国际水平仍存在一定差距(高峰等,2012;任宏利等,2015;2016)。本文拟采用SPPM对BCC_CSM1.1m模式的ENSO预报进行统计订正研究,将系统地从不同季节和不同提前预报月的角度多方面地分析该方法对BCC_CSM1.1m模式的订正技巧,同时还讨论该方法对El Niño中心纬向位置预报的订正效果。
1 数据与方法 1.1 数据本文选取的观测数据是美国国家海洋气象局(NOAA)1991—2015年的海表温度延长重构数据(Extended Reconstructed Sea Surface Temperature version 3b, ERSSTv3b),其数据空间分辨率为2°×2°,该数据将用来进行统计模型的构建和预测技巧的检验。
本文所选用的模式数据是国家气候中心开发的第二代气候系统模式BCC-CSM1.1m的海表温度(sea surface temperature,SST)。BCC_CSM1.1m是由国家气候中心在NCAR-CCSM框架基础上研发的全球海洋-陆地-海冰-大气多圈层耦合的全球气候-碳循环耦合模式,它是在BCC_CSM1.1基础上发展的一个较新版本,并已经参与了第五次耦合模式比较计划(Coupled Model Intercomparison Project Phase5,CMIP5),后文用BCC代替BCC_CSM1.1m。该模式可提供季节至年际尺度的全球气候预测产品,其水平分辨率为110 km,其大气分量模式为BCC_AGCM2.2,水平分辨率T106,垂直方向26层;海洋分量模式为MOM_L40,水平分辨率在热带为0.333°,热带外为1°。基于BCC_CSM1.1m的集合预报在每个月上中旬(使用月初初始场)生成未来13个月的预测产品,每次预测共有24个集合成员。关于该模式的更多具体细节描述可以参考文献Wu et al(2010;2014)。为了使模式数据与观测数据保持一致,研究中将模式数据插值成2°×2°。观测气候态选取为国际通用的1981—2010年30年平均,模式的气候态选取为1991—2014年平均(由于仅有1991年以后模式回报数据)。
1.2 统计订正方法本研究采用了Kug et al(2008a)提出的SPPM。该方法基于这样的假设:局地预报变量与预报因子场有很好的统计关系,局地预报变量可以通过一个适当的转换函数将预报因子场信息反演出来。本文中预报变量是局地观测的SST,用Y表示;预报因子场是模式预报的SST,用Ψ表示,x, y, t分别代表格点的纬度、经度和时间。该方法分为两步:第一步是选取最优预报因子集D;第二步是进行回归计算。现用前T年模式预报和观测的SST来预报第tf年SST,则首先利用回报数据得到局地预报变量与预报因子场的协方差矩阵,其表达式为:
| $\mathit{\boldsymbol{Cov}}\left( {x,{\rm{ }}y} \right) = \frac{1}{T}\sum\limits_{t = 1}^T {Y\left( t \right)} \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {x,{\rm{ }}y,{\rm{ }}t} \right)$ | (1) |
将预报因子场投影到该协方差矩阵上可以得到一个时间序列P即:
| $\mathit{\boldsymbol{P}}\left( {x,{\rm{ }}y} \right) = \sum\limits_{x,{\rm{ }}y}^D {\mathit{\boldsymbol{Cov}}} \left( {x,{\rm{ }}y} \right)\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {x,{\rm{ }}y,{\rm{ }}t} \right)$ | (2) |
建立预报变量与该时间序列之间的线性回归预报模型,如下:
| $Y\left( t \right) = \alpha P\left( t \right)$ | (3) |
利用最小二乘法求得时间序列的回归系数:
| $\alpha = \frac{{\frac{1}{T}\sum\limits_{t = 1}^T {Y\left( t \right)} P\left( t \right)}}{{\frac{1}{T}\sum\limits_{t = 1}^T {{P^2}} \left( t \right)}}$ | (4) |
将所求回归系数带入式(3),则第tf年的预测结果可表示为:
| $Y({t_f}) = \alpha P({t_f})$ | (5) |
在这一统计订正过程中,最优预报因子集D的选取尤为重要。以往的订正方法是选取一个固定的优化窗口,一旦确定了优化窗口后,在整个预报期内该优化窗口的大小以及位置都不再改变,该窗口外的有效信息也便不再能应用,这种方法只适用于区域预报变量,当预报变量范围较大时,主观地选定一个区域作为优化窗口可能使得该窗口包含的信息只对部分预报变量有意义。然而,SPPM是为每一观测预报变量选取出与其高相关的模式预报变量并排列重组成为最优预报因子集D,通过这种方式选取的预报因子集可以在避免优化窗口对预报变量不适用情况的同时充分提取预报变量中的有效信息。理论上预报因子量越多所得到结果越稳定可靠,但是随着预报因子量的增加计算成本也会显著增高,当预报因子量大于200时对预报技巧的提高不再显著,本文综合考虑计算成本和订正效果后,选定最优预报因子量为200。
本文选取出最优预报因子集的方法如下:首先计算出局地观测SST与同年所有模式预报SST之间的相关系数;然后将模式预报变量按相关系数从大到小的排列进行分组。当局地观测SST与模式预报SST之间相关系数≤0.3时,其相关性已经非常微弱了,因此本文中只将与局地观测SST之间相关系数>0.3的预报因子进行了分组,以0.05为步长,将数据分为了14组(即n取值为14),从第一组开始筛选,当第一组所选预报因子数不足200时,再将第二组选入最优预报因子集,依次向下进行,直到最优预报因子的数量达到200时停止筛选,这一过程可以将所有与预报变量相关性高的点都选入最优预报因子集中;最后将选定的最优预报因子集带入上述式(1)~式(5) 进行回归计算。
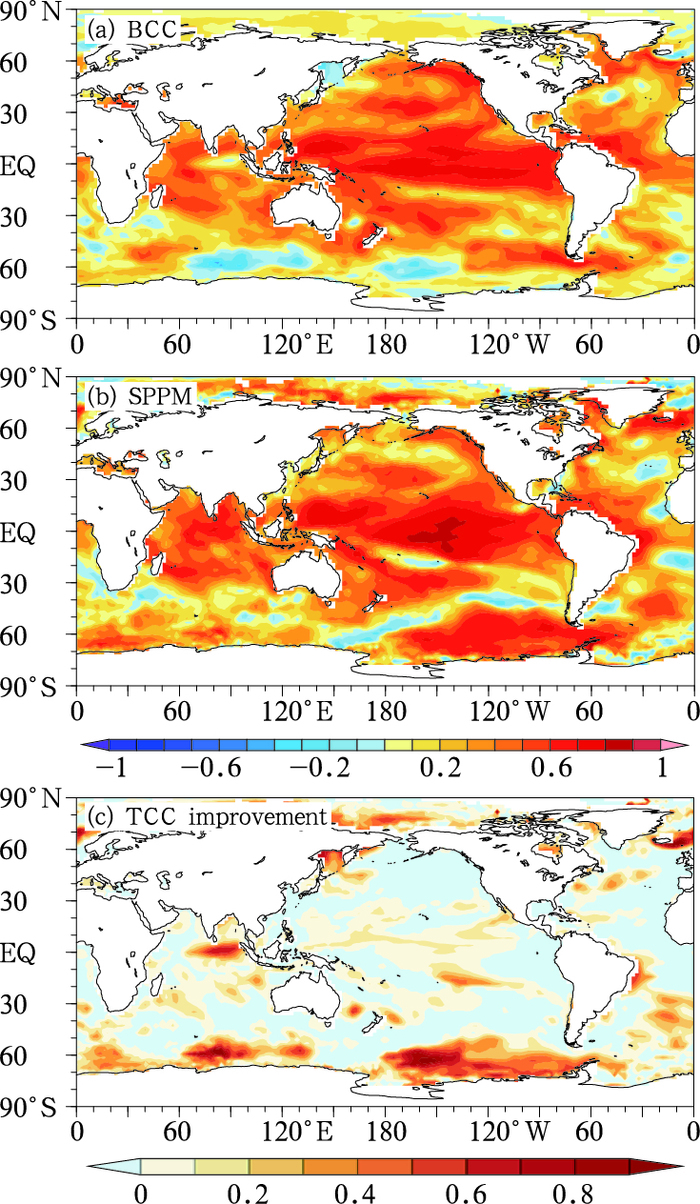
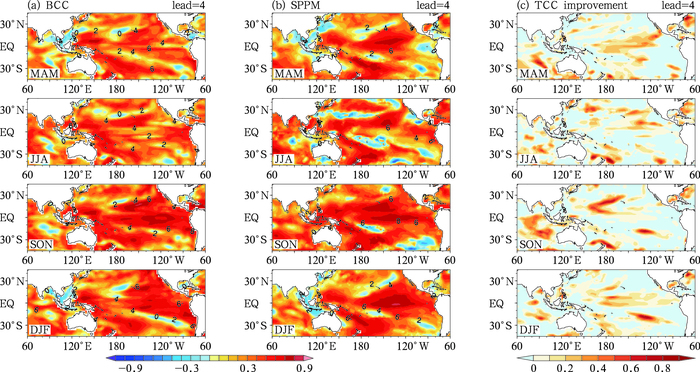
2 交叉检验 2.1 时间相关系数(TCC)检验本文首先对BCC模式预报以及SPPM订正预报进行了交叉检验分析,检验时段为1991—2014年。以提前4个月的预报为例,图 1分别给出了回报年期间观测SST与提前4个月BCC模式预报以及经SPPM订正后的SST时间相关系数(TCC)的空间分布。图 1a中全球范围内BCC模式与观测间普遍为正相关,最高TCC值出现在赤道太平洋附近,高值中心在0.7~0.8。从图 1中可以发现,在BCC模式的基础上,SPPM提高了全球范围内多个地区的预报技巧。并且与BCC高值中心相比,SPPM高于0.7的高值中心范围明显扩大且更为集中,尤其是在赤道太平洋以及印度洋海区,订正后最大TCC值超过了0.8。进一步分析了SPPM对各季节SST预报的技巧,图 2给出了提前4个月所预报的各季节订正前后TCC以及SPPM相对于BCC技巧提升的空间分布。对比图 2a和2b可看出,各季节订正后的预测效果与原模式结果相比都有了明显的改进,高技巧仍集中分布在赤道中太平洋地区,从图 2c中可以清晰看出,经SPPM订正后的预报技巧普遍在赤道区域有0.1~0.4的提高。对比各季节订正效果发现,在ENSO区域SPPM对秋季的预报结果相对较好,其TCC值超过0.8的范围最大,而夏季预报结果相对不够理想,这也在某种程度上体现了ENSO春季预报障碍问题在订正方法中仍存在(Webster and Yang 1992; Latif et al, 1994; McPhaden, 2003; Yu and Kao, 2007; Duan and Hu, 2016;张雅乐等,2013)。
|
图 1 交叉检验中(a)BCC和(b)SPPM提前4个月预报的SST与观测SST的时间相关系数分布以及(c)订正前后时间相关系数提升(SPPM-BCC)分布 Fig. 1 Spatial distribution of temporal correlation coefficients of (a) BCC predictions, (b) SPPM predictions and (c) improvement of temporal correlation coefficients (SPPM-BCC) at 4-month lead for the cross-validation, respectively |
|
图 2 交叉检验中各季节(a)BCC和(b)SPPM提前4个月预报结果与观测结果时间相关系数分布以及(c)订正前后时间相关系数提升(SPPM-BCC)分布 Fig. 2 Spatial distribution of temporal correlation coefficients of (a) BCC, (b) SPPM and (c) improvement of temporal correlation coefficients (SPPM-BCC) at 4-month lead in each season for the cross-validation, respectively |
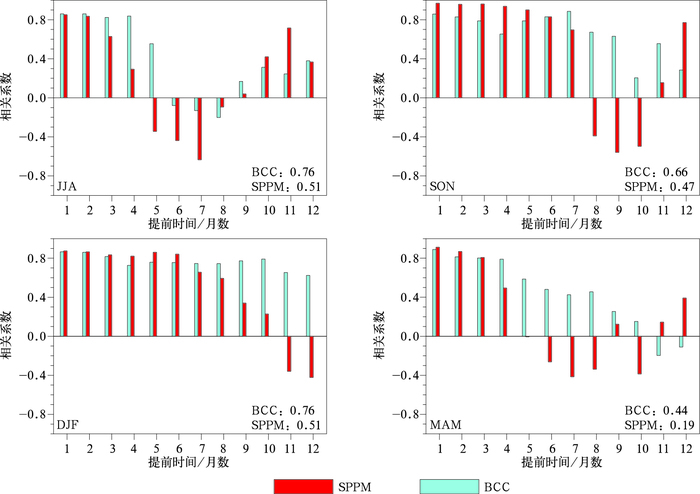
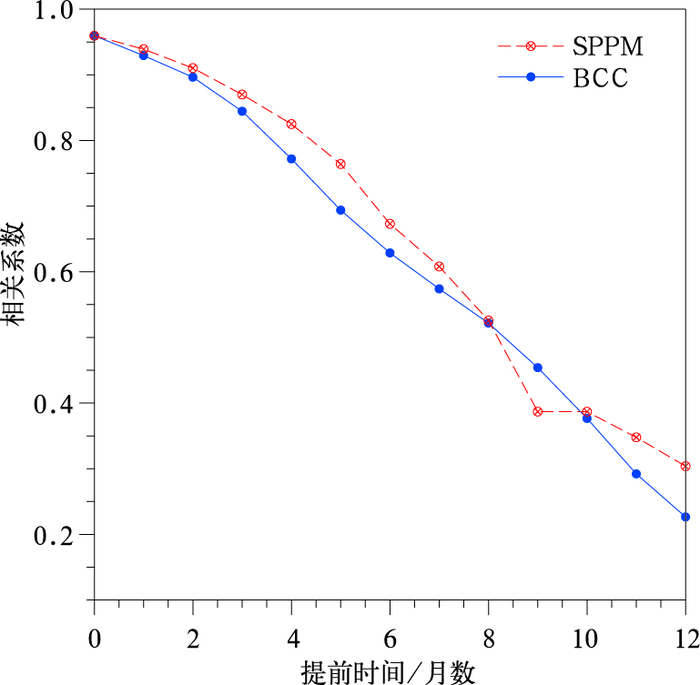
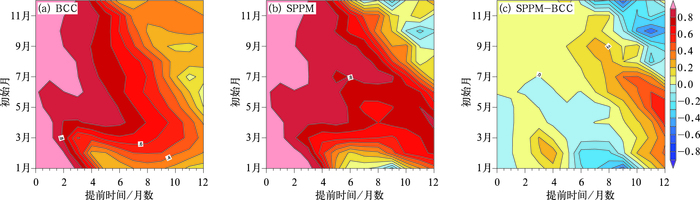
为了更整体性地看出SPPM对原模式预报技巧的提高效果,图 3给出了订正前后模式历史回报技巧检验。从Niño3.4区海表温度异常指数的时间距平相关系数上来看,相比于BCC模式预报,SPPM订正后的Niño3.4指数技巧总体上是提高的,除了极个别情况,SPPM的时间距平相关系数都高于BCC。订正前提前6个月对Niño3.4指数的预报技巧约为0.62,而订正后的提前6个月的预报技巧达到了0.67,提高了8%。其中SPPM相对于BCC模式Niño3.4指数的预报技巧在提前5个月时的改善效果最好,提高了10%。对于提前5个月以内的预报,随提前预报月份的增加,提高效果越明显。从图 4中各月起报的技巧分布来看,ENSO春季预报障碍问题在订正前后的预报中都存在,即模式在预报ENSO事件时,模式及持续性预报技巧在春季起报的月份快速下降且技巧最低(Webster and Yang, 1992)。值得注意的是,SPPM的技巧相比于BCC模式预报有大幅度提升,对春季预报障碍期间的预报效果有一定程度改善,但在某些较长超前时间的预报可能会有所变差。
|
图 3 1991—2014年交叉检验中BCC(蓝线)和SPPM(红线)的Niño3.4指数时间距平相关系数 Fig. 3 Skill score of temporal anomaly correlation coefficients of Niño3.4 index prediction by BCC (blue) and SPPM (red) during 1991-2014 for the cross-validation |
|
图 4 (a) BCC、(b) SPPM以及(c)订正前后时间相关系数差值(SPPM-BCC)分布 Fig. 4 Temporal anomaly correlation coefficients of Niño3.4 index prediction for (a) BCC, (b) SPPM and (c) their differences (SPPM-BCC)(x-axis is forecast month and y-axis is initial calendar month) |
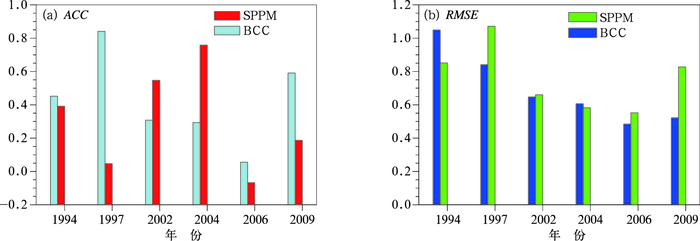
根据中国气象局业务监测规范,以Niño3.4区SSTA的3个月滑动平均值连续5个月≥0.5℃(≤-0.5℃)定义为一次El Niño(La Niña)事件,针对1991—2014年Niño3.4区SST异常值进行分析,一共可以确定出5次El Niño事件,分别是1994/1995年、1997/1998年、2002/2003年、2006/2007年以及2009/2010年事件。图 5分别给出了回报年期间5次El Niño事件Niño3.4区提前1~12个月预报的平均空间相关系数(ACC)和均方根误差(RMSE)。从12个提前预报月的平均空间相关系数上可以看出,BCC模式对1997/1998年个例的预报技巧最高,空间相关系数达到了0.85,对于2009/2010年个例的空间相关系数也较高达到了0.5,相反订正后的预报对于这两次事件技巧却偏低。图 5b中这两次事件BCC的RMSE也比SPPM低,表明BCC模式对于这两次事件的预报结果更加接近观测结果。如我们所知,1997/1998年事件是一次超强El Niño事件,2009/2010年事件也是一次中等强度的事件,而BCC模式已对这两次事件都表现出非常高的技巧。因此,可以看出BCC模式更擅长预报强事件,而SPPM订正方法对BCC模式强El Niño事件的预报订正改进能力相对较弱。
|
图 5 交叉检验中订正前后El Niño年赤道太平洋(5°S~5°N、120°E~90°W)区域提前1~12个月预报平均的(a)空间相关系数和(b)均方根误差 Fig. 5 Mean spatial anomaly correlation coefficients (a) and root-mean-square error (b) of BCC predictions and SPPM predictions for El Niño episodes from 1 to 12 months lead predictions at equatorial Pacific (5°S-5°N, 120°E-90°W) for the cross-validation |
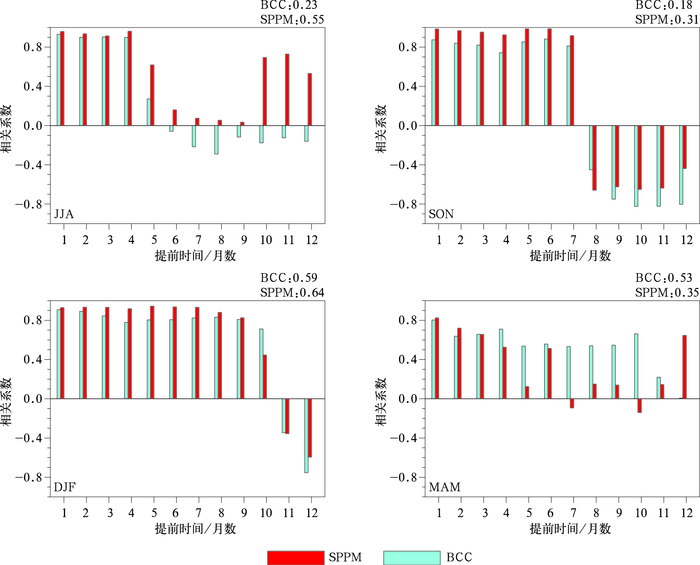
从上面的分析我们知道SPPM可以提高BCC模式的预报技巧,并且对El Niño事件预报技巧的提高主要表现在中等强度以及弱强度El Niño事件上。为了进一步分析各个季节SPPM对El Niño事件的订正效果,我们将回报年期间除1997/1998年和2009/2010年以外的El Niño事件做了合成并分析了订正前后模式对各季节的预报技巧。图 6给出了合成后各季节赤道太平洋(5°S~5°N、120°E~90°W)区域的空间相关系数,图中右上角分别为订正前后空间相关系数的平均值,从图中可以看出订正后的预报结果与原始结果相比有了一定改进。其中夏季、秋季、冬季订正后的平均空间相关系数分别提高了0.22、0.13、0.05。SPPM对夏季预报的提高最为明显,提前1~12个月预报的空间相关系数全部都高于BCC模式直接预报,并且对于提前6个月以上的预报,BCC模式的ACC几乎都<0而SPPM都提供了正技巧。然而,SPPM对春季订正的效果不理想,只对提前0~2个月和提前12个月的模式预报有提高。但总体来看,SPPM订正后的SST与观测SST的空间相关系数总体优于BCC预报的结果,除春季外,SPPM对提前7个月以内的模式预报都有改进。
|
图 6 交叉检验中订正前后合成El Niño事件各季节赤道太平洋区域(5°N~5°S、120°E~90°W)的空间相关系数 Fig. 6 Spatial anomaly correlation coefficients of the BCC predictions and SPPM predictions for SST at equatorial Pacific (5°S-5°N, 120°E-90°W) in each season for composited El Niño episodes for the cross-validation, respectively |
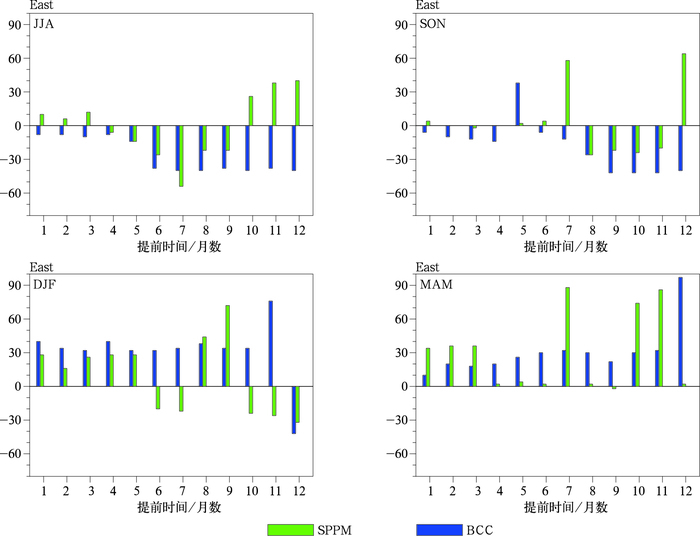
我们还发现BCC模式对El Niño事件中心纬向位置的预报普遍存在误差,对夏季和秋季中心位置的预报会较观测中心偏西而冬季和次年春季偏东,SPPM是否对中心位置的预报有改进呢?对此图 7分别给出了订正前后El Niño事件各季节平均中心位置与观测中心的距离。从图中可以看出SPPM对El Niño事件中心位置的订正也显示出一定的订正技巧。其中夏季和秋季SPPM对El Niño事件中心位置的订正效果最明显,对于绝大多数的提前预报月,SPPM预报的中心都比BCC模式更接近观测中心,并且提前6个月以内对秋季的预报中,订正后的中心位置与观测中心距离小于5个经度。对冬季El Niño中心位置的预报,SPPM提前8个月以内的预报都比BCC模式效果好。与空间相关技巧相似,SPPM对春季的预报结果相比于其他季节较差,在提前1~12个月的预报中,只有一半的预报效果较好,但预报的中心位置与观测中心的距离都小于5个经度。总体上看,该订正方法对El Niño事件中心纬向位置的订正具有一定的技巧。
|
图 7 交叉检验中订正前后El Niño事件各季节平均中心位置与观测中心的距离偏差 Fig. 7 Spatial distance deviation between the observed center and BCC predicted center and SPPM predicted center in each season for the cross-validation |
为了进一步检验该方法实际的应用效果,我们利用1991—2014年的回报数据对ENSO预报进行了滚动独立样本检验。在用SPPM方法订正过程中,首先选取前10年数据作为历史回报资料进行建模得到第11年的预报,此后预报每前进1年,用于建模的数据资料同时增加1年,然后以此类推,预报是滚动进行的,这样可以确保对于靠后的目标年有更多的回报数据可供使用。
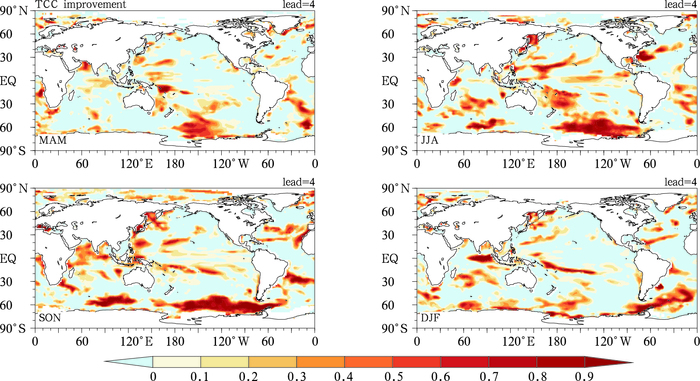
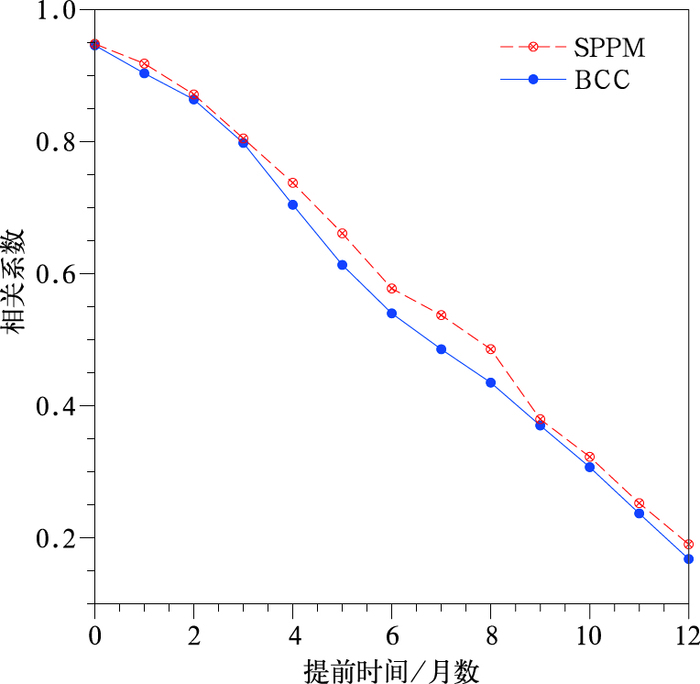
3.1 时间相关检验将独立样本检验得到的SPPM预报与BCC模式预报相比较,图 8给出了提前4个月各季节SPPM预报相对于BCC模式技巧提升的空间分布。从图中可以看出,独立样本检验结果中SPPM仍可以有效改善许多地区的预报技巧,并且对夏季和秋季的预报技巧提高效果最明显,这与交叉检验结果相似。然而对于冬季和次年春季的预报,SPPM订正技巧更集中出现在赤道外地区。图 9给出了订正前后模式独立样本检验的技巧,从Niño3.4区海表温度异常指数的时间距平相关系数上来看,订正后的模式预报技巧仍比原模式有提高。与图 3对比,独立样本检验的订正结果与交叉检验结果相比提高幅度较小,但在提前1~2个月以及提前9个月的预报结果,独立样本检验订正效果要略好于交叉检验,整体上看,独立样本检验中SPPM订正后的预报技巧与BCC模式相比仍然是提高的。
|
图 8 滚动独立样本检验中各季节订正前后提前4个月的预报时间相关系数提升(SPPM-BCC)的分布 Fig. 8 Spatial distribution of temporal correlation coefficients improvement between SPPM predictions and BCC predictions (SPPM-BCC) at 4-month lead in each season for the independent validation, respectively |
|
图 9 同图 3,但为2000—2014独立样本检验结果 Fig. 9 Same as in Fig. 3, but for the independent validation during 2000-2014 |
将独立样本检验结果的2002/2003年、2004/2005年以及2006/2007年El Niño事件做合成,分析独立样本检验中的SPPM对El Niño事件的订正技巧。图 10分别给出了合成后订正前后模式所预报的各季节赤道太平洋区域的空间相关系数。从图中可以看出独立样本检验结果的SPPM对秋季和冬季预报与观测的空间相关性较好,在提前6个月以内的ACC都高于BCC模式。而对夏季和次年春季的预报效果不理想,夏季SPPM与观测的空间相关性只有提前10~12个月的预报中可以高于原模式预报而春季在提前3个月以内的预报技巧可以与原模式技巧相当或略高于原模式。总体看来,独立样本检验不如交叉检验的效果好,独立样本检验效果较差的原因也与预报训练期长度有关,在Kug et al (2008a)的研究中表明SPPM订正方法对30年以上的数据效果稳定,少于30年的回报数据还不足以建立稳定的统计关系,并且随着数据量减少该方法的技巧显著下降。而本研究中独立样本训练期只有10~23年,因此对结果还是有较大的影响。
4 结论为了改进国家气候中心气候系统模式BCC_CSM1.1m对ENSO的预报,本文采用SPPM对该模式历史回算的SST输出结果进行了统计订正研究。该方法首先在所有模式预报变量中挑选出与局地观测变量相关性高的数据作为最优因子集,再将所挑选出的最优因子集投影到其与局地观测变量所建立的协方差矩阵上来提取最优预报因子集信息,以达到提高预报技巧的效果。交叉检验和滚动独立样本检验结果显示,SPPM可以有效提高BCC模式的预报技巧。
经过SPPM统计订正后,交叉检验结果的Niño3.4指数提前6个月的预报的相关系数技巧提高了8%~10%,预报误差得到显著降低,对春季预报障碍期间的预报效果也有一定程度改善。原模式预报技巧在很多地区都得到了明显提高,尤其是在热带太平洋地区以及印度洋海区,SPPM预报的SST与观测SST之间最高的TCC值超过了0.8。将回报年期间El Niño事件做合成分析发现,SPPM对不同季节的订正效果略有差异,其中对秋季的预报技巧提高最为显著。该统计订正方法对El Niño事件的订正效果主要表现在中等强度及弱强度事件上,并且对秋季和冬季的订正效果更佳,除春季外,提前7个月以内的空间相关技巧都高于BCC模式直接预报。交叉检验结果同时还显示SPPM针对模式预报的中心位置也有一定的预报技巧,其预报的中心位置与订正前相比要更接近于观测中心位置。以往的研究发现,最近20年一种与传统El Niño明显不同的El Niño事件发生的频率显著增加,这类El Niño事件特征是其暖中心不在赤道东太平洋,而出现在赤道中太平洋(Yeh et al, 2009;李智玉等,2015),有关这类ENSO现象预测的研究正面临着很大困难和挑战,而SPPM在对暖中心位置的预报中表现出的订正技巧可能对两类ENSO的预报提供借鉴,这些问题将在下一步工作中加以研究。
分析独立样本检验结果,经过SPPM订正的ENSO预报技巧同样得到了提高,但对个例分析的结果并没有交叉检验效果显著。这也体现了SPPM还存在一些局限性,Kug et al(2008a)指出SPPM对训练期较敏感,少于30年的回报数据还不足以建立稳定的统计关系,并且随着数据量减少该方法的技巧显著下降。本研究中样本训练期只有10~23年,所以当数据量增多时,该方法的预报技巧也将得到更显著的提高。
陈丽娟, 顾薇, 丁婷, 等, 2016. 2015年汛期气候预测先兆信号的综合分析[J]. 气象, 42(4): 496-506. DOI:10.7519/j.issn.1000-0526.2016.04.014 |
高峰, 辛晓歌, 吴统文, 2012. BCC_CSM1.1对10年尺度全球及区域温度的预测研究[J]. 大气科学, 36(6): 1165-1179. DOI:10.3878/j.issn.1006-9895.2012.11243 |
顾薇, 2016. 夏季热带西太平洋海温对厄尔尼诺发展阶段我国东部汛期降水的影响分析[J]. 气象, 42(5): 548-556. DOI:10.7519/j.issn.1000-0526.2016.05.004 |
李智玉, 张文君, 徐海明, 2015. 两类ENSO事件非对称性特征分析[J]. 气象学报, 73(6): 1019-1038. |
任宏利, 丑纪范, 2005. 统计-动力相结合的相似误差订正法[J]. 气象学报, 63(6): 988-993. DOI:10.11676/qxxb2005.094 |
任宏利, 丑纪范, 2007a. 数值模式的预报策略和方法研究进展[J]. 地球科学进展, 22(4): 376-385. |
任宏利, 丑纪范, 2007b. 动力相似预报的策略和方法研究[J]. 中国科学, 37(8): 1101-1109. |
任宏利, 刘颖, 左金清, 等, 2016. 国家气候中心新一代ENSO预测系统及其对2014/2016年超强厄尔尼诺事件的预测[J]. 气象, 42(5): 521-531. |
任宏利, 吴捷, 赵崇博, 等, 2015. MJO预报研究进展[J]. 应用气象学报, 26(6): 658-668. DOI:10.11898/1001-7313.20150602 |
任宏利, 张培群, 李维京, 等, 2006. 基于多个参考态更新的动力相似预报方法及应用[J]. 物理学报, 55(8): 4388-4396. |
司东, 柳艳菊, 邵勰, 等, 2016. 2015年海洋和大气环流异常及对中国气候的影响[J]. 气象, 42(4): 481-488. |
王朋岭, 周兵, 柳艳菊, 等, 2015. 2014年海洋和大气环流异常及对中国气候的影响[J]. 气象, 41(4): 489-496. |
伍红雨, 潘蔚娟, 王婷, 2014. 华南冬季气温异常与ENSO的关系[J]. 气象, 40(10): 1230-1239. DOI:10.7519/j.issn.1000-0526.2014.10.007 |
臧恒范, 王绍武, 1984. 赤道东太平洋水温对低纬大气环流的影响[J]. 海洋学报, 6(1): 16-24. |
张雅乐, 俞永强, 段晚锁, 2012. 四个耦合模式ENSO后报试验的"春季预报障碍"[J]. 气象学报, 70(3): 506-519. DOI:10.11676/qxxb2012.042 |
朱玉祥, 黄嘉佑, 丁一汇, 2016. 统计方法在数值模式中应用的若干新进展[J]. 气象, 42(4): 456-465. DOI:10.7519/j.issn.1000-0526.2016.04.009 |
Chen D, Cane M A, Kaplan A, et al, 2004. Predictability of El Niño over the past 148 years[J]. Nature, 428(6984): 733-736. DOI:10.1038/nature02439 |
Chen D, Zebiak S E, Busalacchi A J, et al, 1995. An improved procedure for El Niño forecasting:implications for predictability[J]. Science, 269(5231): 1699-1702. DOI:10.1126/science.269.5231.1699 |
Cheng Y, Tang Y, Zhou X, et al, 2010. Further analysis of singular vector and ENSO predictability in the Lamont model-part Ⅰ:singular vector and the control factors[J]. Clim Dyn, 35(5): 807-826. DOI:10.1007/s00382-009-0595-7 |
Duan W S, Hu J Y, 2016. The initial errors that induce a significant "spring predictability barrier" for El Niño events and their implications for target observation:results from an earth system model[J]. Clim Dyn, 46(11): 3599-3615. |
Graham N E, 1994. On the roles of tropical and midlatitude SSTs in forcing interannual to interdecadal variability in the winter Northern Hemisphere circulation[J]. J Climate, 7: 1416-1441. DOI:10.1175/1520-0442(1994)007<1416:OTROTA>2.0.CO;2 |
Izumo T, Vialard J, Lengaigne M, et al, 2010. Influence of the state of the Indian Ocean Dipole on the following year's El Niño[J]. Nat Geosci, 3(3): 168-172. DOI:10.1038/ngeo760 |
Jin E K, Iii J L K, Wang B, et al, 2008. Current status of ENSO prediction skill in coupled ocean-atmosphere models[J]. Clim Dyn, 31(6): 647-664. DOI:10.1007/s00382-008-0397-3 |
Kang I S, Shukla J, 2006. Dynamical seasonal prediction and predictability of the monsoon//Bin Wang (ed), The Asian Monsoon[M]chichester:Springer:585-612.
|
Kug J S, Lee J Y, Kang I S, 2007. Global sea surface temperature prediction using a multi-model ensemble[J]. Mon Wea Rev, 135(9): 3239-3247. DOI:10.1175/MWR3458.1 |
Kug J S, Lee J Y, Kang I S, 2008a. Systematic error correction of dynamical seasonal prediction of sea surface temperature using a stepwise pattern project method[J]. Mon Wea Rev, 136(9): 3501-3512. DOI:10.1175/2008MWR2272.1 |
Kug J S, Lee J Y, Kang I S, et al, 2008b. Optimal multi-model ensemble method in seasonal climate prediction[J]. Asia-Pacific J Atmos Sci, 44(3): 259-267. |
Latif M, Barnett T P, Cane M A, et al, 1994. A review of ENSO prediction studies[J]. Clim Dyn, 9(4): 167-179. |
Luo J J, Masson S, Behera S K, et al, 2005. Seasonal climate predictability in a coupled OAGCM using a different approach for ensemble forecasts[J]. J Climate, 18(18): 4474-4497. |
Luo J J, Masson S, Behera S K, et al, 2008. Extended ENSO predictions using a fully coupled ocean-atmosphere model[J]. J Climate, 21(1): 84-93. DOI:10.1175/2007JCLI1412.1 |
McPhaden M J, 2003. Tropical Pacific Ocean heat content variations and ENSO persistence barriers[J]. Geophys Res Lett, 30(9): 319-338. |
Rasmusson E M, Carpenter T H, 1982. Variations in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Niño[J]. Mon Wea Rev, 110(5): 354. DOI:10.1175/1520-0493(1982)110<0354:VITSST>2.0.CO;2 |
Rasmusson E M, Wallace J M, 1984. Meteorological aspects of the El Niño-Southern Oscillation[J]. Science, 222(4629): 1195-1202. |
Ren H L, Liu Y, Jin F F, et al, 2014. Application of the analogue-based correction of errors method in ENSO prediction[J]. Atmos Ocea Sci Lett, 7(2): 157-161. DOI:10.1080/16742834.2014.11447152 |
Wang B, Lee J Y, Kang I S, et al, 2008. How accurately do coupled climate models predict the Asian-Australian monsoon interannual variability[J]. Clim Dyn, 30(6): 605-619. DOI:10.1007/s00382-007-0310-5 |
Webster P J, Yang S, 1992. Monsoon and ENSO:selectively interactive systems[J]. Quart J Roy Meteorol Soc, 118(507): 877-926. DOI:10.1002/(ISSN)1477-870X |
Wu T, Song L, Li W, et al, 2014. An overview of progress in climate system model development at the Beijing Climate Center applications for climate change studies[J]. J Meteor Res, 28(1): 34-56. |
Wu T, Yu R, Zhang F, et al, 2010. The Beijing climate center atmospheric general circulation model:description and its performance for the present-day climate[J]. Clim Dyn, 34(1): 123-147. DOI:10.1007/s00382-008-0487-2 |
Yeh S W, Kug J S, Dewitte B, et al, 2009. El Niño in a changing climate[J]. Nature, 461: 511-514. DOI:10.1038/nature08316 |
Yu J Y, Kao H Y, 2007. Decadal changes of ENSO persistence barrier in SST and ocean heat content indices:1958-2001[J]. J Geophys Res-Atmos, 112(D13): 125-138. |
Zebiak S E, Cane M A, 1987. A Model El Niño-Southern Oscillation[J]. Mon Wea Rev, 115(10): 2262-2278. DOI:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2 |
Zeng Q C, Zhang B L, Yuan C G, et al, 1994. A note on some methods suitable for verifying and correcting the prediction of climate anomaly[J]. Adv Atmos Sci, 11(2): 121-127. DOI:10.1007/BF02666540 |
Zhang R, Sumi A, Kimoto M, 1996. Impact of El Niño on the East Asian monsoon:a diagnostic study of the 86/87 and 91/92 events[J]. J Meteor Soc Japan, 74(1): 49-62. DOI:10.2151/jmsj1965.74.1_49 |
Zhang W, Jin F F, Ren H L, et al, 2012. Differences in teleconnection over the north pacific and rainfall shift over the USA associated with two types of El Niño during boreal autumn[J]. J Meteor Soc Japan, 90(4): 535-552. DOI:10.2151/jmsj.2012-407 |
Zheng F, Wang H, Zhu J, 2009. ENSO ensemble prediction:initial error perturbations vs. model error perturbations[J]. Chinese Sci Bull, 54(14): 2516-2523. DOI:10.1007/s11434-009-0179-2 |
Zheng F, Zhu J, Zhang R H, et al, 2006. Ensemble hindcasts of SST anomalies in the tropical Pacific using an intermediate coupled model[J]. Geophys Res Lett, 331(19): 318-372. |
 2017, Vol. 43
2017, Vol. 43