2. 中国科学院深圳先进技术研究院,深圳 518055;
3. 深圳市国家气候观象台,深圳 518040;
4. 深圳南方强天气研究重点实验室,深圳 518040
2. Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055;
3. The National Climate Observatory in Shenzhen City, Shenzhen 518040;
4. Shenzhen Key Laboratory of Severe Weather in South China, Shenzhen 518040
短时临近强降雨是指在局部范围内较短时间里降水强度比较大,其降雨量达到或超过某一标准的常见天气现象(段鹤等,2014;何斌等,2015;张小玲等,2014;张庆云和郭恒,2014;宇如聪等,2014)。针对城市小尺度短时临近降雨(田付友等,2015;孙继松等,2015;闵晶晶,2014;刘娜和李双林,2015;洪伟等,2015),广东省在国内第一个建立了较为完善的精细化数字网格天气预报业务(陈元昭等,2016),提供精细化数字网格预报产品,满足公众对气象预报服务的定时、定点、定量的需求。珠三角地处亚热带且靠近太平洋,在全球气候异常增多的背景下,加上珠三角城市化进程加速的共同作用(陈子燊等,2015),珠三角城市群地区短时对流天气突发呈现出了局部差异与变化的特点,短时临近降雨事件发生的频率和强度不断增大,且预报难度比较大,导致城市内涝问题越来越严重(陈子燊等,2015)。
短时临近降雨比较常规的模式预报方法(王改利等,2007)主要是基于卫星云图(林奕桐等,2015;李冠林等,2016;汪亚萍等,2015)和雷达回波进行外推(韩雷等,2007),在数值模式临近预报技术还不成熟的情况下(陈明轩等,2010),专家系统基本代表了当今国际上临近预报业务的主流发展(段鹤等,2014;勾亚彬等,2014;高郁东等,2015;曾明剑等,2015)。深圳市精细化网格预报系统以数值预报为基础,采用最优集成预报技术进行客观化模式的解释应用,预报员对数值预报进行主观订正,生成文字、图形、表格和语音等预报产品,而主观订正因人而异,存在不确定性,对预报员的专家经验存在依赖,预测准确率较低且不稳定。深圳市气象台从2012年起逐时动态更新发布各分区天气预报,根据张蕾等(2015)的研究,在深圳市平均200 km2的预报范围内,定时、定点、定量预报短时强降水等小概率事件的预报能力较为有限,如果严格按TS标准评分,第一小时的准确率在10%以下,往后第二小时、第三小时的准确率下降很明显,使用价值有待提高。
近年来支持向量机(support vector machine, SVM)在气象领域得到了广泛应用,陈永义等(2004)分析了SVM在气象研究业务中的应用前景,冯汉中和陈永义(2004)将SVM应用于气象预报试验显示出该方法具有一定的预报能力,张乐坚等(2010)则比较了人工神经网络(artificial neural network, ANN)与SVM的1和3 h降雨预报效果,汪春秀(2011)利用SVM研究了灾害天气小概率事件的分类预测,王在文等(2012)利用SVM和MOS方法分析北京奥运气象要素后得出了整体预报效果SVM略优于MOS的推断。但对于SVM算法在气象预报中的应用,单一建模是目前普遍存在的一种思路,单一建模方法寻找的是大而泛的预测模型,预测的目标以面降雨为主,而本研究针对每个站点单独动态建模,充分考虑了不同站点、不同时刻的气象要素差异,可以解决单一建模过于注重整体规律、建立固定的整体预测函数模型而忽略不同站点、不同时刻局部气象变化的不足。同样是SVM建模,本文提出一种新的建模方法,该方法基于“受制于城市的局部环境因素,不同站点、不同时刻的气象变化不一样,对于每一时刻的降雨预测,其与临近的前一时间段的气象条件相关性更大”这一科学认识,这也正是本文思路的出发点。
本文立足于深圳市对于更高精度降水短时预报的实际需求,利用SVM在模式识别、分类和预测中解决非线性问题的能力和深圳市近两年多(2013年1月至2015年9月)的气象要素数据,建模方法为多时间尺度SVM,探索建立一种动态SVM短时临近降水预测模型,充分考虑不同站点、不同时刻的气象要素变化差异,并尝试提高短时临近降水预报的准确率。本方法属于探索性的研究,相比现有的数值预报方法(沈澄等,2016),本方法从纯数据的角度以一种简化的思路进行预测,比复杂的数值预报方法更具有计算成本上的优势。
1 资料和方法 1.1 研究区资料概况深圳地处华南沿海,暴雨、台风等灾害性天气频发,容易出现局地性的洪涝灾害和短时雷雨大风天气,在深圳经常可以看到全市范围多地局部出现不同的天气,天气突变的时间尺度和空间尺度都很小,而传统的基于雷达(龙清怡等,2014)和卫星云图的临近预报方法主要解决大尺度降雨预测问题。
深圳市全市范围内有大约100个自动气象站并且积累了5年以上的高密度气象数据(含雨量数据)(李磊等,2015)。深圳市气象自动站网平均探测密度为3.8 km×3.8 km(1988.2 km2),深圳市区(福田、罗湖、南山、盐田、前海)平均探测密度2.8 km×2.8 km(411.1 km2),市区外平均探测密度4.2 km×4.2 km(1577 km2)。本研究所采用2013年1月至2015年9月时间段内的自动站数据的时间分辨率为1 h,主要特征要素包括:风向、风速、温度、湿度、气压和降雨,在实际处理数据时发现,部分站点存在一定的数据缺失,缺失的数据主要是气压数据和湿度数据,在剔除掉部分数据缺失的站点后,选取数据质量比较好的站点(共44个)形成短时临近降雨样本集。
1.2 SVM原理和方法SVM是一种有效的小样本机器学习方法(丁世飞等,2011),1995年Vapnik(1995)在统计学习理论的基础上提出SVM(Vapnik et al,1995)作为模式识别的新方法之后,SVM一直倍受关注。1996年,Vapnik等(1996)又提出支持向量回归(support vector regression,SVR)的方法用于解决拟合问题。
支持向量机的基本思想为:在线性可分情况下,在特征空间寻找两类样本的最优分类超平面,使得该超平面在保证分类精度的同时,能够使分类间隔最大化。理论上,支持向量机能够实现对线性可分数据的最优分类,所谓最优分类面要求分类面不但能将两类正确分开,而且使分类间隔最大。因此,支持向量机被认为是目前针对小样本的分类、回归等问题的最佳理论。
设线性可分样本集为:(xi, yi),i=1, …, n, x∈Rd, y∈{±1},y是类别符号,d为样本空间维数。支持向量机分类的目标函数为:
| ${{\min }_{\omega ,b,\zeta }}\frac{1}{2}{{\omega }^{\text{T}}}\omega +C\sum\limits_{i=1}^{n}{{{\zeta }_{i}}}$ | (1) |
| ${y_i}[{\omega ^{\rm{T}}}\phi ({x_i}) + b] \ge 1 - {\zeta _i},{\zeta _i} \ge 0,i = 1,2, \cdots ,n$ | (2) |
式(1) 为目标函数,式(2) 为约束条件,式(1) 和式(2) 可以等价转化为式(3)、式(4)、式(5) 和式(6),αi为Lagrange乘数,其中式(6) 为将训练样本映射到高维空间的核函数,如下:
| ${{\min }_{\alpha }}\frac{1}{2}{{\alpha }^{\text{T}}}Q\alpha -{{\text{e}}^{\text{T}}}\alpha $ | (3) |
| ${y^{\rm{T}}}\alpha = 0,0 \le {\alpha _i} \le C,i = 1,2, \cdots ,n$ | (4) |
| ${Q_{i,j}} = {y_i}{y_j}K({x_i},{x_j})$ | (5) |
| $K({x_i},{x_y}) = \phi {({x_i})^{\rm{T}}}\phi ({x_j}) = \exp ( - \gamma {\left\| {{x_i} - {x_j}} \right\|^2}),\gamma > 0$ | (6) |
式(7) 为最终的分类决策函数,如下:
| $f(x) = {\mathop{\rm sgn}} \{ ({\omega ^*} \cdot x) + {b^*}\} = {\mathop{\rm sgn}} \{ \sum\limits_{i = 1}^n {\alpha _i^* \cdot {y_i}} \cdot K(x,{x_i}) + {b^*}\} $ | (7) |
样本数据训练建立的SVM模型的最终回归函数形式为:
| $R(x) = \sum\limits_{i = 1}^n {({\alpha _i} - \alpha _i^*)} K(x,{x_i}) + {b^*}$ | (8) |
对于非线性问题,SVM可以通过非线性变换(核函数)转化为某个高维空间中的线性问题,在变换空间求最优分类超平面。SVM核函数有线性核函数、多项式核函数、径向基核函数,考虑到本研究样本集中各数据之间并不是完全线性独立,样本变量中存在多重共线性问题,因此选择径向基核函数(冯汉中和陈永义,2004)(高斯核函数),见式(6)。
SVC在建模过程中有两个主要参数,分别是核函数中的Gamma和目标函数中的惩罚系数C,参数Gamma(默认1/d,d为样本空间维数)表示单个训练样本的影响距离,惩罚系数C的引入主要是为了平滑分类界面,使得结构风险最小化,增强模型的泛化能力。
1.3 短时临近降雨的评价本研究主要基于自动站的空间分布实现精细化的临近降雨预报,根据广东省精细化网格天气预报质量检验方法中关于短时临近预报检验的要求,地面气象要素降水检验标准采用所有观测站(国家站和选定的区域自动站)收录的降水实况资料,对于单站统计检验参数,检验统计量有:TS评分、命中率、空报率、预报偏差和预报效率。在本研究中采用的检验统计量主要为TS评分和预报效率,因为TS评分指标的好坏也同时反映了漏报率和空报率的高低,而预报效率则反映了预报的整体准确率(包括不降雨)情况。本研究的目的在于检验本方法的预测准确率,因此重点分析TS评分、命中率、空报率和预报效率(EH),降水预报检验分类见表 1。TS评分的计算公式如下:
|
|
表 1 降水预报检验分类表 Table 1 Classification of rainfall forecast test |
| $TS = \frac{{NA}}{{NA + NB + NC}} \times 100\% $ | (9) |
命中率的计算公式如下:
| $POD = \frac{{NA}}{{NA + NC}} \times 100\% $ | (10) |
空报率的计算公式如下:
| $FAR= \frac{{NB}}{{NA + NB}} \times 100\% $ | (11) |
预报效率的计算公式如下:
| $EH = \frac{{NA + ND}}{{NA + NB + NC + ND}} \times 100\% $ | (12) |
式中,NA为预报正确站(次)数, NB为空报站(次)数, NC为漏报站(次)数,见表 1;TS为降水预报的TS评分,EH为预报效率,整体准确率(包括不降雨)等于EH。
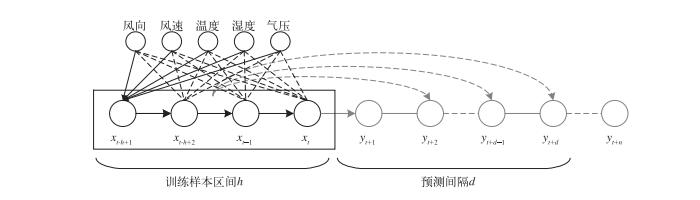
2 本文建模方法针对SVM处理小样本的特点和优势,建立多时间尺度SVM模型处理44个自动站数据,模型的输入为每个自动站的风向、风速、温度、气压和湿度。对于每一时刻的降雨概率预测和雨量峰值时间点预测,考虑到降雨预测模型在时间序列上与临近的前一时间段的气象条件相关性更大,虽然离预测时间点更远的历史数据中也包含了一定的未来降雨信息,但是我们认为该信息也体现了在离预测时间点比较近的气象数据中,因此使用较小间隔的多时间尺度SVM处理临近气象数据也能在一定程度上反映降雨时间序列的变化,降雨预测处理方法见图 1。
|
图 1 时间尺度为h小时SVM未来d小时降雨预测处理方法示意图 Fig. 1 Methods of h hours time scale SVM for future d hours rainfall prediction |
本研究方法基于简单气象条件进行降雨预测,其特点在于将当前时刻的气象条件与未来时刻的气象条件错位建模训练,建立当前气象条件与未来降雨的关系,解决了常规模型预测方法需要对训练样本中其他特征也同时进行预测的二次预测问题。多时间尺度SVM降雨预测的建模如下:
| ${Y_{t - 1}} = R_{t - 1}^*({X_{t - 1}})$ | (13) |
| ${X_{t - 1}} = {\left[ {{x_{t - h - d}},{x_{t - h - d + 1}}, \cdots ,{x_{t - d - 1}}} \right]^{\rm{T}}},d \in \left[ {0,5} \right],h = 3,6,8,12,24,48,72$ | (14) |
| ${Y_{t - 1}} = {\left[ {{y_{t - h}},{y_{t - h + 1}}, \cdots ,{y_{t - 1}}} \right]^{\rm{T}}},d \in \left[ {0,5} \right],h = 3,6,8,12,24,48,72$ | (15) |
| $y_t^* = R_{t - 1}^*({x_{t - d}})$ | (16) |
式中,Xt-1,Yt-1为训练样本;Rt-1*为根据训练样本所建立的模型;t为待预测时刻;h为训练样本的容量(时间尺度);d为预测时间间隔;yt*,xt-d分别为降雨预测值、待预测降雨的输入。
此处设置输入变量的时间尺度,时间尺度分别设置为:3,6,8,12,24,48,72 h,表示用3,6,8,12,24,48,72 h内的站点气象条件预测后续降雨。同时也设置预测时间间隔分别为:0,1,2,3,4,5 h,表示预测未来0,1,2,3,4,5 h的降雨,在建模、预测的检验过程中,对各特征变量进行标准化处理,消除量纲的影响。
以时间尺度6 h西丽自动站2014年4月6日11时的预测为例,此处d=1,h=6。
第一步,预处理并准备训练数据:
| ${X^{(11)}} = {\left[ {{x^{(8)}},{x^{(9)}},{x^{(10)}},{x^{(11)}},{x^{(12)}},{x^{(13)}}} \right]^{\rm{T}}}$ |
式中,x(8), x(9), x(10), x(11), x(12), x(13)分别为08、09、10、11、12和13时的气象条件。
| ${Y^{(11)}} = {\left[ {{y^{(9)}},{y^{(10)}},{y^{(11)}},{y^{(12)}},{y^{(13)}},{y^{(14)}}} \right]^{\rm{T}}}$ |
式中,y(9), y(10), y(11), y(12), y(13), y(14)分别为09、10、11、12、13和14时的降雨特征,X(11)与Y(11)错位匹配形成训练样本。
第二步,设置参数并训练模型:
利用SVM训练Y(11)=R11*X(11)得到模型R11*。
第三步,模型预测:
利用得到模型R11*,则12时(在11时预测未来1 h,即12时)的降雨预测结果为:y*(12)=R11*(x(11)),其中x(11)为11时的气象条件,y*(12)为预测得到的12时的降雨情况。
第四步,检验评价:
根据实际降雨情况,计算TS评分指标和预报效率EH。
在本研究中对有无降水两类天气进行了定性预报和分析,而在实际的天气预报中公众更关心未来可能出现多大强度的降水,因此对于降水量的预报采取如下方法,在预报出有降水的基础上,针对每个站点、每个季度的历史降雨类样本,单独建立各特征要素与降雨之间的多元回归关系,利用该多元回归模型进行降雨预测,该多元回归模型充分考虑到了不同站点、不同季节的特征差异,同时也避免了大而泛模型的局限。但是针对降雨量的分级预报将会是我们下一阶段的研究内容。
3 结果与分析 3.1 降水概率准确率比较表 2和表 3进一步说明本研究方法的预测效果。从各自动站2013年1月至2015年9月的降雨时间序列来看,降雨主要集中每年的春、夏季,在这个时间段内,降雨的密度和强度都比较大,对于是否降雨和降雨时间点的预测,时间尺度为3 h SVM模型都给出了较好的预测结果。特别是该预测结果基于自动站的气象数据,而自动站的地理分布位置不一样,由于深圳的气候特征,每个自动站所处位置的气象条件和降雨情况都存在明显的差异,而常规的气象预报往往针对的是深圳全市范围内的天气变化(如降雨),难以做到小尺度、精细化的降雨预报,因此该预测结果能够较好地反映更精细化的未来降雨趋势,为自动站周边范围内的社会经济生活提供气象保障,具备一定的实用价值。而且从表 2和表 3可以看出,不论是预测未来1 h,还是未来2 h的降雨预测,模型在降雨时间点上表现出了较好的准确率和吻合度。从表 2和表 3可以看出,随着时间尺度增大,命中率POD和空报率FAR增大,当时间尺度较大时,表面上命中率POD很高,其实预报效果比较差,从表 5的TS评分可以看出,主要因为时间尺度较大时,多了很多空报,也就是模型盲目的预报会产生降雨从而导致命中率POD较高,同时我们可以看到空报率FAR也很高,这与时间尺度较大时TS评分较低相符。
|
|
表 2 不同时间尺度SVM短时临近降雨预测的命中率POD均值(单位:%) Table 2 The POD average in different time-scale SVM for nowcasting rainfall prediction (unit: %) |
|
|
表 4 时间尺度为3 h的SVM短时临近降雨概率预测TS评分值(单位:%) Table 4 TS scores of 3 h time-scale SVM for future nowcasting prediction (unit:%) |
|
|
表 5 不同时间尺度SVM短时临近降雨预测的TS评分均值(单位:%) Table 5 The average of TS in different time-scale SVM for nowcasting rainfall prediction (unit:%) |
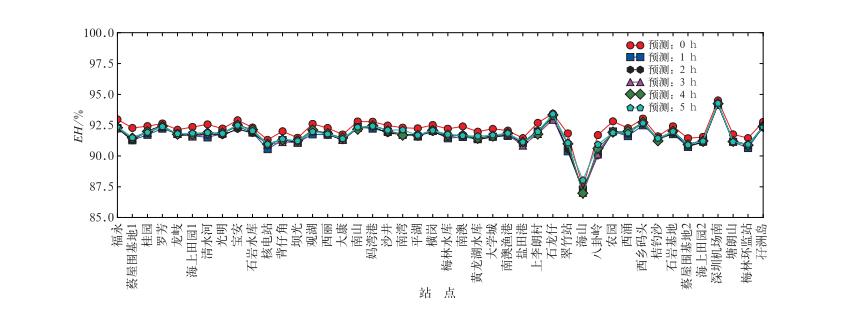
图 2所示的时间尺度3 h SVM未来1 h降雨预测的预报效率,其计算基于整个样本空间,表示各站点预测准确的降雨和无降雨时刻总数与样本容量的比值,可以明显看出各站点的整体预测准确率都比较好,除海山站点外,不论是当前时刻的预测,还是未来1~5 h的降雨预测,大多数站点的整体预测准确率都在90%以上,且不同预测时刻的准确率相差不大,石龙仔站点的整体预测率在94%以上。其中海山站点的整体预测效果比较差,根据分析,部分站点的数据质量不够好,数据连续性较差,这影响到了模型的预测结果。因此,好的数据质量是提高模型预测准确率的良好保证。
|
图 2 时间尺度3 h SVM未来1~5 h降雨预测预报效率(整体准确率) Fig. 2 The overall accuracy of 3 h time-scale SVM for future 1-5 h rainfall prediction |
在实验中发现,本文方法对于预测降雨开始与结束的时刻存在一定的误差,原因在于气象数据存在非平衡分布的特点,即训练集中两类样本(降雨类和非降雨类)的数量差别较大,降雨类样本与非降雨类样本的数量比值往往小于1:10,也就是说样本集中降雨时刻数远远小于非降雨时刻数,如果训练样本比较大,容易导致模型训练过程中的过拟合,使得分类超平面向降雨类倾斜,将真正的降雨样本点错误划分为非降雨类,同时模型的预测也会受到更长历史时间段内与当前预测相关性更低的样本的影响,导致预测效果较差;而如果训练样本比较小,容易导致训练集缺少正例(降雨)较难有效预测降雨突变和训练中缺少负例(晴天)较难有效预测降雨结束。但是这些时刻的误差对预测效率的影响不大,该不足的问题可以通过过采样降雨类和欠采样非降雨类得到平衡样本集来解决,这也是下一步的研究重点。
3.2 降水预测结果TS检验表 4给出了本研究所采用的时间尺度为3 h的预测结果的TS评分值,针对不同的预报时刻要求(1,2,3,4,5 h),计算预测结果的TS评分值。
总体来说,各站点的TS评分相对比较高,预测效果良好,不同站点的预测结果也不一样,可能特定位置站点的降雨受其他因素的影响也不一样,且不难看出,当预测时间后延时,TS评分有所降低,所有站点的各预测时段的TS评分值如表 5所示。
在表 5中,我们可以看到不同时间尺度短时临近降雨预测的TS评分均值结果,明显各站点的TS评分中,根据前3 h的气象数据对当前时刻降雨预测的TS评分最高,也就是降雨准确率最高。这也说明了与前3 h的气象数据越近的时间点,其降雨与前3 h的气象条件相关性越大。在本研究的分析中,在44个气象自动站中,部分自动站的TS评分较高,当前时刻的降雨预测TS评分接近50%,也有部分自动站的TS评分较低,当前时刻的降雨预测也有40%以上。随着预测时间点的后延,TS评分不断降低,也就是短时临近降雨预测的准确率有所下降。由表可知,在时间尺度为3 h SVM降雨预测中,即使预测时间点为后延5 h,TS评分也可以达到35%以上,模型并没有出现TS评分(预测准确率)迅速降低的情况,即模型对于后延5 h以内的降雨也具有一定的预测价值。同时,在表 5中可以看到除了当前时刻的降雨预测外,其他时刻的降雨预测TS评分非常接近,差异并不大,因此模型也具有一定的稳定性。
表 5中还可以看出时间尺度为6 h SVM降雨预测TS评分结果相比3 h的模型预测有所下降,且其他预测时刻的TS评分随着时间的后延逐渐降低,未来5 h的降雨预测TS评分最低,大多数站点未来5 h降雨预测的TS评分都只能达到30%左右。
表 5中所示时间尺度为12 h SVM降雨预测TS评分相比3,6,8 h时间尺度出现了较大幅度的下降,TS评分下降幅度约为8%。而对未来其他时刻的降雨预测则表现出了更低的TS评分,预测准确率下降明显。同样,我们分析时间尺度为24、48和72 h的SVM降雨预测TS评分结果,发现随着时间尺度的增大,降雨预测TS评分不断降低,预测的准确率也逐步降低,当时间尺度为72 h时,未来1 h的降雨预测TS评分不到20%。已经远远低于时间尺度为3 h SVM降雨预测的TS评分结果,且其他时刻的降雨预测TS评分也只有15%左右,该TS评分水平的降雨预测准确率已经比较低,在短时临近降雨预报中已经不具备实际应用价值。
根据表 5的TS评分结果可以看出,针对SVM小样本处理的特点,时间尺度越大,也就是训练样本的容量越大,模型预测的TS评分越低,反过来,时间尺度越小,即训练样本的容量越小,模型预测的TS评分越高。另外,也说明某一时刻的降雨与其临近的历史气象条件相关性更大,当历史时刻的气象条件与降雨发生的时间点相距较远时(如72 h),该气象条件所包含的未来较远时刻的降雨信息比较有限,难以有效地对未来较远时刻的降雨预测提供出有价值的参考,也可以说未来时刻的临近历史数据中已经包含了气象条件发生变化的信息,该信息对未来降雨的预测更有价值。因此,由表可知,时间尺度为3 h时,训练后的SVM模型降雨预测的TS评分最高,不管是预测未来1、2 h还是5 h,TS评分均接近或超过30%,具有一定的参考价值。
3.3 模型的稳定性模型的稳定性决定了模型能否持续有效地进行预测。本文计算多个时间尺度多个站点的TS平均值和标准差,用于描述模型的稳定性,多个站点的均值越接近,标准差越小,表明模型给出的预测结果越稳定。
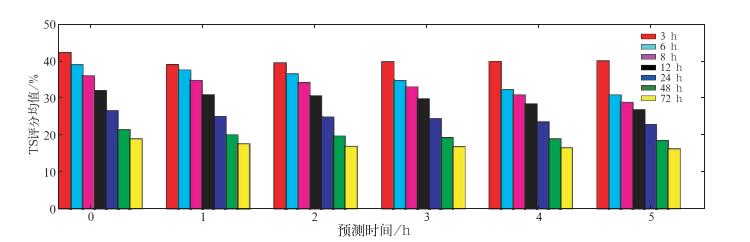
图 3描述了本研究所采用的全部44个气象自动站点的不同时间尺度SVM降雨预测TS评分均值,从图中的统计可以看出,时间尺度为3 h的降雨预测TS评分均值最高,其当前时刻的降雨预测TS评分均值超过40%,未来1 h的降雨预测TS评分均值接近40%,未来2~5 h的TS评分均值也都接近40%,这反映了各个站点的降雨预测TS评分的总体集中趋势。由图还可以看出,时间尺度为6 h时的降雨预测TS评分均值有所降低,且随着预测时间间隔的增大,下降幅度也在增大,当预测时间间隔为0 h(即当前时刻)时,所有站点TS评分均值下降到38%,而当预测时间间隔为5 h时,所有站点TS评分均值下降到30%左右。其次,时间尺度为8,12,24,48,72 h的降雨预测TS评分均值都呈现出了随着时间尺度和预测时间间隔的增大而逐步降低的趋势,这表明随着降雨预测模型的训练样本增大,模型中引入了较多的与未来降雨无关的气象因素,增加了模型的复杂度和不确定性。
|
图 3 不同时间尺度SVM降雨预测TS评分均值 Fig. 3 The mean of TS scores different time-scale SVM for rainfall prediction |
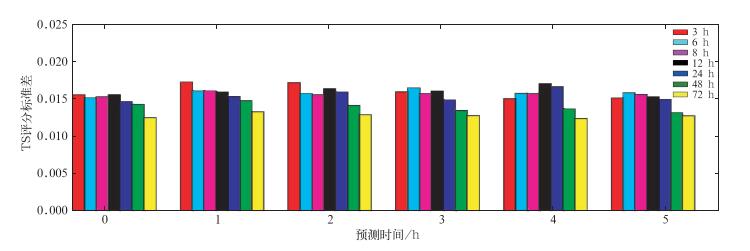
图 4所示为不同时间尺度SVM降雨预测TS评分标准差,TS评分标准差表达了所有站点降雨预测TS评分偏离均值的程度,时间尺度为3,6,8,12,24,48,72 h时不同预测时间间隔的TS评分标准差均比较小,只有0.015左右。通过该图的统计分析可以进一步看出,TS评分标准差反映了所有站点TS评分结果的离散程度,是该TS评分结果相对于TS评分均值的不确定性的一种测量,较小的标准差,代表大多数站点降雨预测的TS评分结果都比较接近整体平均值,而由图 3可知,整体TS评分平均值最好可达40%以上,而TS评分结果标准差较小为好,这样代表比较稳定,也表示不同站点的TS评分结果的数值波动比较小,反之,则波动较大。
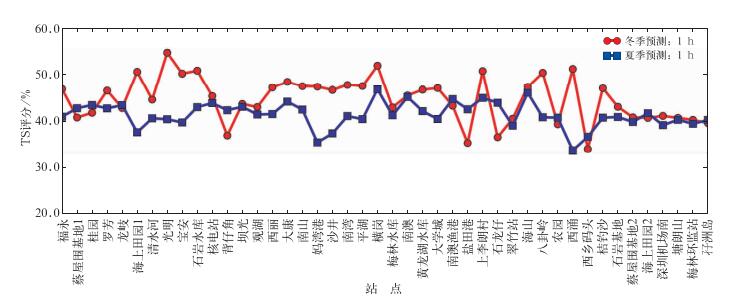
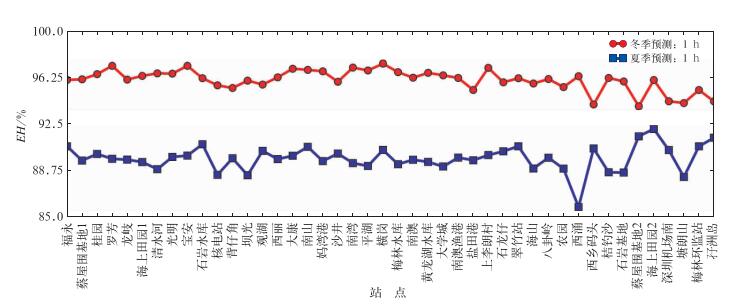
考虑到深圳的天气特点,在本节的稳定性讨论中,我们还将冬、夏两个半年的降雨预测结果进行了对比分析,以此验证本研究提出的方法在不同的季节均具有一定的适用性。夏半年是4—9月,而冬半年是10月到次年3月,预测效率(整体准确率)、3 h尺度预测未来1 h降雨的TS评分、TS评分均值和方差分别为图 5、图 6、图 7所示。
|
图 5 时间尺度3 h SVM未来1 h冬、夏半年降雨预测效率(整体准确率) Fig. 5 The overall accuracy of 3 hours time-scale SVM for future 1 h rainfall prediction in winter and summer |
|
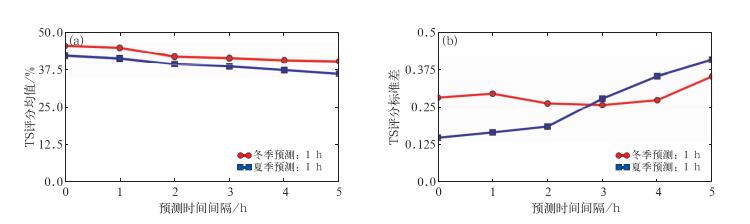
图 7 冬、夏季节时间尺度3 h SVM降雨预测TS评分均值(a)和标准差(b) Fig. 7 The mean (a) and standard deviation (b) of TS scores about 3 h time-scale SVM for rainfall prediction in winter and summer |
从图 5和图 6可以看出,冬、夏半年的降雨预测效率(整体准确率)和TS评分都存在一些差异,冬半年的降雨预测效率(整体准确率)和TS评分较高,分别为96%和45%左右,夏半年的预测效率(整体准确率)略低,分别为90%和41%左右,出现这种差异的主要原因在于:深圳地处华南沿海,夏半年的强对流天气比较多,天气突变的频率更大,小范围阵雨特别多,降雨预测的难度很大;而冬半年这类天气突变比较少,天气相对稳定,且降雨明显减少,降雨预测的难度较小。同时从图 7可以看出,冬、夏半年的TS评分均值也呈现出了夏低冬高的特点,但差别不大,而TS评分标准差都很小,说明冬、夏半年该模型方法对于不同站点的预测准确率很接近。虽然在冬、夏半年的预测结果会有一定的差异,但总体而言,考虑到深圳市的气候特点,这些差异是可以接受的。因此,可以认为本文提出的方法对季节不太敏感,能够较好地适用于深圳的各季节的气候环境。
综上所述,该方法建立的模型稳定性较好,不受站点位置和环境的影响,对于不同地理位置、地理社会环境的自动站点的降雨均具有一定的预测参考价值,同时对于站点的未来不同预测时间间隔的降雨也具有一定的效果。
4 结 论本研究使用深圳市气象自动站(共44个自动站)2013年1月至2015年9月时间段内的每小时气象观测资料作为样本数据,针对SVM处理小样本的特点和优势,结合降雨数据进行多时间尺度SVM建模,并进行验证、优化和完善,得到了以下结论:
(1) 本文利用站点的空间分布,初步研究了地理空间上更高密度、更精细化的降雨预测,降雨预测的时间分辨率为1 h,作为城市临近降雨精细预测的一种方法探索,对于深圳市频发性的小区域降雨异常和短时临近降雨的局部差异有一定的参考价值。
(2) 常规的气象预报主要借助数值预报系统和气象雷达来估计形势场,再结合专家经验进行降雨预报,也就是说在预报过程中要首先对与降雨相关的形势场进行预测,再利用预测的形势场预报降雨,实际上有两次预测过程,一次为预测形势场,一次为预测降雨。本文尝试建立上一时刻气象形势场(输入特征)与当前时刻降雨(预测输出)的非线性关系,并建立动态模型,无需预测当前时刻气象形势场的情况下,考虑到当前时刻降雨在时间序列上与上一时刻的气象条件更相关这一科学认识,可以避免二次预测过程中的随机误差及误差放大。
(3) 本研究提出的动态方法同时考虑了华南地区全年气候变化呈现冬夏两季的特点,分开建模与检验,针对目前SVM在气象预报中单一建模的普遍思路,本文认为,即使输入特征与降雨存在非线性关系,该非线性关系也不是固定的,而是随时间和地点动态变化,即在不同位置、不同时间段呈现出不同的非线性关系,基于这一点,本模型避免了单一建模方法寻找大而泛的预测模型的不足。
(4) 本研究针对每个站点建模的输入与输出特点,以及单一建模过于注重整体规律而忽略不同站点、不同时刻数据差异的现状,本方法从纯数据的角度以一种简化的思路进行预测,虽然使用的字段信息比较少,但是本方法的预测结果也有一定的参考价值。在多时间尺度SVM模型中,时间尺度越大,也就是训练样本的容量越大,模型预测的TS评分越低,反之模型预测的TS评分越高。发现随着时间尺度的增大,降雨预测TS评分不断降低,预测的准确率也逐步降低,说明某一时刻的降雨与其临近的历史气象条件相关性更大,临近历史数据中包含了气象条件发生变化的可能信息,因此选择时间尺度为3 h SVM降雨预测,1 h预测的TS评分可以达到40%以上,部分站点TS评分可以达到50%。且时间尺度越小,训练样本容量越小,模型计算的时间消耗更低。
下一步的研究计划包括继续改进本文的预测方法,进一步优化训练样本结构,引入云顶高度、云顶温度、云光学厚度、云粒子有效半径、辐射亮温、、辐射亮温梯度、亮温差异、总云量、云类型、对流层中上层水汽含量、云液水含量的垂直廓线及整层液水路径等气象参数及风云卫星等遥感数据,结合气象数据非平衡性的特点,改进现有模型,解决训练中缺少正例(降雨)无法预测降雨突变和训练中缺少负例(晴天)无法预测降雨结束的问题,解决气象突变预测问题,对降雨进行分级预测和降雨量的预测。这也是我们下一步的研究重点,期望进一步提高降水预测的准确度。
陈明轩, 高峰, 孔荣, 等, 2010. 自动临近预报系统及其在北京奥运期间的应用[J]. 应用气象学报, 21(4): 395-404. DOI:10.11898/1001-7313.20100402 |
陈永义, 俞小鼎, 高学浩, 等, 2004. 处理非线性分类和回归问题的一种新方法(Ⅰ)——支持向量机方法简介[J]. 应用气象学报, 15(3): 345-354. |
陈元昭, 俞小鼎, 陈训来, 2016. 珠江三角洲地区重大短时强降水的基本流型与环境参量特征[J]. 气象, 42(2): 144-155. |
陈子燊, 黄强, 李鸿皓, 等, 2015. 珠江三角洲城市短时强降水概率分布模型的对比分析[J]. 中山大学学报:自然科学版, 8(2): 127-132. |
丁世飞, 齐丙娟, 谭红艳, 2011. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 38(1): 2-10. |
段鹤, 夏文梅, 苏晓力, 等, 2014. 短时强降水特征统计及临近预警[J]. 气象, 40(10): 1194-1206. |
冯汉中, 陈永义, 2004. 处理非线性分类和回归问题的一种新方法(Ⅱ)——支持向量机方法在天气预报中的应用[J]. 应用气象学报, 15(3): 355-365. |
高郁东, 万齐林, 薛纪善, 等, 2015. 同化雷达估算降水率对暴雨预报的影响[J]. 应用气象学报, 26(1): 45-56. |
勾亚彬, 刘黎平, 杨杰, 等, 2014. 基于雷达组网拼图的定量降水估测算法业务应用及效果评估[J]. 气象学报, 72(4): 731-748. DOI:10.11676/qxxb2014.050 |
韩雷, 王洪庆, 谭晓光, 等, 2007. 基于雷达数据的风暴体识别、追踪及预警的研究进展[J]. 气象, 33(1): 3-10. |
何斌, 范晓红, 盛文斌, 等, 2015. "2013·7·21"杭州湾北岸短时大暴雨的中尺度分析[J]. 气象, 41(7): 842-851. |
洪伟, 任雪娟, 杨修群, 2015. 华南持续性强降水期间低频非绝热加热对低频环流的影响[J]. 气象学报, 73(2): 276-290. DOI:10.11676/qxxb2015.018 |
李冠林, 严卫, 王蕊, 等, 2016. 基于A-Train综合资料的云顶高度反演研究[J]. 气象, 42(8): 971-979. |
李磊, 张立杰, 力梅, 2015. 深圳降水资料信息挖掘及在气候服务中的应用[J]. 广东气象, 37(2): 48-51. |
林奕桐, 叶骏菲, 汪嘉杨, 等, 2015. 基于亮温和SVM模型的干球温度推算方法[J]. 遥感学报, 19(1): 172-178. DOI:10.11834/jrs.20153061 |
刘娜, 李双林, 2015. 基于时间尺度分离的中国东部夏季降水预测[J]. 应用气象学报, 26(3): 328-337. DOI:10.11898/1001-7313.20150308 |
龙清怡, 刘海文, 顾建峰, 等, 2014. 雷达资料与中尺度数值预报的融合方法研究及其在临近预报中的应用[J]. 气象, 40(10): 1248-1258. |
闵晶晶, 2014. BJ-RUC系统模式地面气象要素预报效果评估[J]. 应用气象学报, 25(3): 265-273. DOI:10.11898/1001-7313.20140302 |
沈澄, 孙燕, 魏晓奕, 等, 2016. 基于物理量参数的江苏短时强降水预报模型的研究[J]. 气象, 42(5): 557-566. DOI:10.7519/j.issn.1000-0526.2016.05.005 |
孙继松, 雷蕾, 于波, 等, 2015. 近10年北京地区极端暴雨事件的基本特征[J]. 气象学报, 73(4): 609-623. DOI:10.11676/qxxb2015.044 |
田付友, 郑永光, 张涛, 等, 2015. 短时强降水诊断物理量敏感性的点对面检验[J]. 应用气象学报, 26(4): 385-396. DOI:10.11898/1001-7313.20150401 |
汪春秀, 2011. 基于支持向量机的气象预报方法研究[D]. 南京: 南京信息工程大学.
|
汪亚萍, 崔晓鹏, 任晨平, 等, 2015. "碧利斯"(0604) 暴雨过程不同类型降水云微物理特征分析[J]. 大气科学, 39(3): 548-558. DOI:10.3878/j.issn.1006-9895.1408.14135 |
王改利, 刘黎平, 阮征, 2007. 多普勒雷达资料在暴雨临近预报中的应用[J]. 应用气象学报, 18(3): 388-395. |
王在文, 郑祚芳, 陈敏, 等, 2012. 支持向量机非线性回归方法的气象要素预报[J]. 应用气象学报, 23(5): 562-570. DOI:10.11898/1001-7313.20120506 |
宇如聪, 李建, 陈昊明, 等, 2014. 中国大陆降水日变化研究进展[J]. 气象学报, 72(5): 948-968. DOI:10.11676/qxxb2014.047 |
曾明剑, 王桂臣, 吴海英, 等, 2015. 基于中尺度数值模式的分类强对流天气预报方法研究[J]. 气象学报, 73(5): 868-882. |
张乐坚, 程明虎, 田付友, 2010. 人工神经网络及支持向量机在降雨量预报中的应用[J]. 高原气象, 29(4): 982-991. |
张蕾, 王明洁, 李辉, 2015. 短时强降水临近预报相对准确率的探讨[J]. 广东气象, 37(2): 1-6. |
张庆云, 郭恒, 2014. 夏季长江淮河流域异常降水事件环流差异及机理研究[J]. 大气科学, 38(4): 656-669. |
张小玲, 余蓉, 杜牧云, 2014. 梅雨锋上短时强降水系统的发展模态[J]. 大气科学, 38(4): 770-781. DOI:10.3878/j.issn.1006-9895.1401.13249 |
Vapnik V, 1995. The Nature of Statistical Learning Theory[M].
New York: Springer..
|
Vapnik V, Golowich S E, Smola A, 1996. Support vector method for function approximation, regression estimation, and signal processing[G]. Advances in neural information processing systems 9.
|
Vapnik V, Guyon I, Hastie T, 1995. Support Vector Machines[M].
New York: Springer.
|
 2017, Vol. 43
2017, Vol. 43