大气边界层是地球大气的最底层,在自由大气和地球表面之间的动量、热量以及水汽交换之间起着重要的作用。它主要受地表摩擦、蒸发、热量传输、污染物排放以及地形扰动等因素影响,其特征不仅对大气湍流和水汽垂直分布等存在重要意义,而且与大气污染物垂直扩散能力紧密相关。近年来,城市化进程的加快带动能源、工业和交通等需求的不断增加,由此产生的空气质量问题受到广泛关注。有研究表明,从污染源直接排放到大气中的污染物除受水平扩散条件影响之外,边界层的垂直扩散能力也是重要影响因素之一,对近地面污染物浓度分布有重要作用(廖晓农等,2016;徐敬等,2015;尤焕苓等,2010;马敏劲,2011)。
目前,边界层高度的计算方法主要分为两类,即基于廓线测量及基于参数化和简单模型计算。其中,基于廓线测量的常用方法有干绝热法、位温梯度法和总理查森数法等,基于参数化计算的最常用方法为罗氏法。如徐桂荣等(2014)采用气块法和总理查森数法估算青藏高原及下游地区的对流边界层和稳定边界层的高度特征;韩美等(2013)采用位温梯度法对青岛和台州两地稳定边界层、中性边界层以及对流边界层的特征进行分析;Ye et al(2013)首先对2004—2014年秋冬季节影响华北地区的天气型进行分类,结合总理查森数方法对边界层高度进行计算;程水源等(1997)利用首都机场多年探空资料和地面常规资料,采用干绝热法和罗氏法对边界层高度进行计算和比较。L波段探空雷达秒数据具有较高的垂直分辨率,可详细描述大气层结特征,因此被广泛应用于基于廓线测量的边界层研究(花丛等,2015)。在本地排放源近似不变以及没有上游天气系统影响的情况下,大气污染物在边界层内不断堆积,会导致近地面污染物浓度不断增加。低层大气污染物的扩散和输送能力在一定程度上依赖于边界层的高低,边界层高度越低,越有利于污染物的积累。因此,在雾-霾等污染天气的预报中,边界层高度成为重要的指标量。本文利用L波段探空雷达秒数据,采用多种方法计算北京地区2014年11—12月边界层高度,并通过与罗氏法的对比,探讨各种方法的异同点,以期加深对雾-霾多发季节边界层特征的了解。
1 资料本文选取北京市南郊观象台(站号54511) 的L波段探空雷达秒数据,观测时间为2014年11—12月,每日08和20时两个时次,数据包括每秒一组的温度、相对湿度、气压、风速和风向等气象要素。地面常规观测资料为每日8次(3 h每次)的MICAPS数据,包括温度、露点、风速、风向、气压、能见度以及天气现象等要素。PM2.5监测数据来源于全国城市空气质量实时发布平台(http://113.108.142.147:20035/emcpublish/),为方便与南郊观象台进行对比,选取北京城区8个国控站(万柳、奥体中心、古城、官园、东四、农展馆、万寿西宫、天坛)数据取平均值。
2 边界层高度计算方法概述 2.1 总理查森数法本文总理查森数(Ri)方法参照Sicard et al(2006)提出的方法,计算公式如下:
| $ Ri\left(z \right) = \frac{{g\left({z - {z_0}} \right)}}{{\theta \left(z \right)}}\frac{{\left[ {\theta \left(z \right) - \theta \left({{z_0}} \right)} \right]}}{{\left[ {u{{\left(z \right)}^2} + v{{\left(z \right)}^2}} \right]}} $ | (1) |
式中,g是重力加速度,z0是地面海拔高度,θ是位温,u和v分别代表纬向和经向风分量。理论和实验证明,当Ri>Rc(临界理查森数)时,湍流运动转变成层流运动,因此该方法主要依赖于临界理查森数Rc的选取。Joffre et al(2001)认为稳定状态的边界层高度常出现于风速风向、相对湿度以及总理查森数垂直廓线出现明显跃变时的高度,该高度所对应的Ri>1。因此本文将首次Ri/Rc>1的高度作为边界层高度。
2.2 逆温法Heffter(1980)提出可以利用位温垂直廓线确定边界层高度,因为在边界层顶部往往存在一个明显的顶盖逆位温。逆温法的主要依据基于两个条件,具体公式如下:
| $ \frac{{∂ \theta }}{{∂ z}} \ge 5\;{\rm{K}} \cdot {\rm{k}}{{\rm{m}}^{ - 1}} $ | (2) |
| $ {T_{{\rm{top}}}} - {T_{{\rm{base}}}} \ge 2\;{\rm{K}} $ | (3) |
因此,本文利用位温垂直廓线进行判断,满足上述两个条件的第一个高度作为边界层高度。
2.3 位温法由于混合层内温度、水汽分布相对均匀,位温变化较小,而在混合层高度以上位温梯度迅速变大。因此,本研究定义位温梯度最大处的高度作为边界层高度。位温梯度的计算常采用中央差分法
罗氏法是由Nozaki(1973)于1973年提出的一种基于常规地面气象资料估算混合层高度的方法,该方法认为大气混合层是热力湍流和机械湍流共同作用的结果,且大气边界层上部大气运动状况与地面气象参数存在反馈机制,可以用地面观测资料估算大气混合层高度。具体计算公式如下:
| $ H = \frac{{121}}{6}\left({6 - P} \right)\left({T - {T_{\rm{d}}}} \right) + \frac{{0.169P\left({{U_z} + 0.257} \right)}}{{12f\ln \left({Z/{Z_0}} \right)}} $ | (4) |
式中,T为地面温度,Td为露点温度,Uz为Z高度处的平均风速,Z0为地面粗糙度,f为科氏参数,P为帕斯奎尔稳定度级别。
由于此方法最大的优点在于不需要高空观测资料,对于在没有高空气象观测的地区有着重要应用价值,因而被广泛应用于国内大气边界层高度的研究中(饶晓琴等,2008;余剑蔚等,2009)。本文选取该方法与利用探空雷达秒数据进行计算的3种方法对2014年11—12月北京地区边界层高度计算结果进行对比,从而分析不同边界层高度计算方法的异同点。
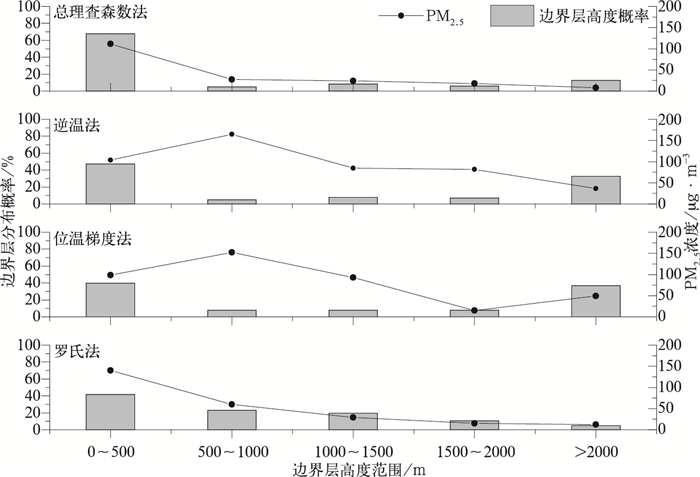
3 结果与讨论 3.1 颗粒物浓度与边界层高度利用第二节4种方法对2014年11—12月北京地区边界层高度进行计算分析。由表 1可知,总理查森数法和罗氏法计算得到的边界层平均高度相近,分别为653和763 m,而逆温法和位温梯度法得到的边界层平均高度较高,分别为1152和1296 m。4种方法计算得到的边界层高度与PM2.5浓度呈现出不同程度的负相关,均通过显著性为0.01的F检验,说明均能正确反映边界层高度的变化趋势。其中罗氏法和总理查森数法与PM2.5浓度相关性更好,分别为-0.60和-0.53,该结果较杜川利等(2014)对边界层高度与颗粒物浓度的统计结果略高(R=-0.32)。另外,由不同方法计算得到的边界层高度概率分布可知(图 1),4种方法均在0~500 m的概率分布最高,该研究结果与李梦等(2015)对2014年2月京津冀冬季大气混合层高度的计算结果相符。当边界层高度低于500 m时,4种方法计算得出的PM2.5平均浓度均超过75 μg·m-3,根据《环境空气质量指数(AQI)技术规定(试行)》(中华人民共和国环境保护部,2012),达到轻度污染以上标准。在其他高度区间上4种方法却存在差异,罗氏法和总理查森数法的边界层高度概率分布区间相似,对应的PM2.5平均浓度随边界层高度增加而降低。当边界层高度超过500 m时,PM2.5平均浓度低于75 μg·m-3,达到优或良的标准。逆温法和位温梯度法计算得出的边界层高度概率分布在2000 m以上明显增加,且PM2.5平均浓度的最大值出现在500~1000 m高度范围内,均与前期研究成果有所矛盾,说明这两种计算方法对部分时刻边界层高度的判断有偏差。
|
|
表 1 4种方法计算的北京地区2014年11—12月边界层高度 Table 1 Boundary layer height calculated by four methods in Beijing in November and December 2014 |
|
图 1 4种方法计算边界层高度统计分布结果 Fig. 1 Statistical probability distribution of boundary layer heights calculated by four methods |
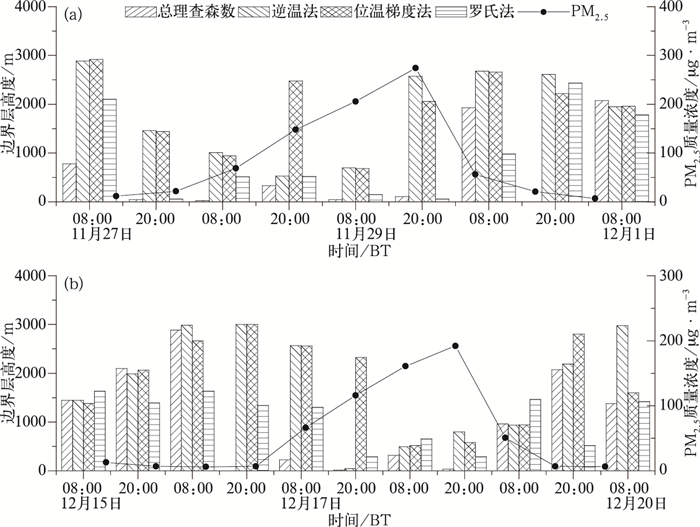
为深入了解污染天气在不同方法边界层高度计算结果的异同点,选取2014年11月27日至12月1日(过程1)、12月15—20日(过程2) 两次天气过程进行具体分析。在这两次过程中北京均受到静稳天气影响,出现了持续2 d以上的雾-霾天气,城区PM2.5浓度最高值分别达到274和192 μg·m-3,出现严重和重度污染。由图 2可知,两次过程中边界层高度和PM2.5浓度的整体趋势变化均表现出较为明显的负相关。过程前期,随静稳天气的建立,边界层高度逐渐降低,PM2.5浓度不断积累增加并达到峰值。后期受冷空气影响,静稳天气被破坏,边界层高度明显增加,PM2.5浓度迅速降低,污染天气结束。
|
图 2 2014年过程1(a)和过程2(b)4种方法计算边界层高度与PM2.5浓度变化关系 Fig. 2 The correlation between PM2.5 and boundary layer heights calculated by four methods (a) 27 November to 1 December 2014, (b) 15-20 December 2014 |
尽管整体变化趋势一致,但各种方法计算得出的边界层高度在部分时段仍体现出一定的差异性。过程1中,在静稳天气建立阶段(27日),总理查森数法的结果较逆温法和位温梯度法明显偏低;污染发展最强阶段(29日20时),总理查森数法和罗氏法得出的边界层高度均低于100 m,逆温法和位温梯度法得出的边界层高度却较前一时次明显增大,超过2000 m,与另两种方法有明显差别。过程2中,12月15—16日4种方法计算的边界层高度均在1000 m以上,对应的PM2.5浓度均低于35 μg·m-3,表现为典型的清洁时段边界层特征。18日,PM2.5浓度达到峰值时,4种方法边界层高度计算结果均低于800 m,表现出较好的一致性。
为深入了解污染天气不同发展阶段边界层高度计算结果的异同,选取11月27日20时、29日20时、12月16日08时和18日08时作为典型时次,利用L波段探空雷达秒数据对大气层结特征进行分析。
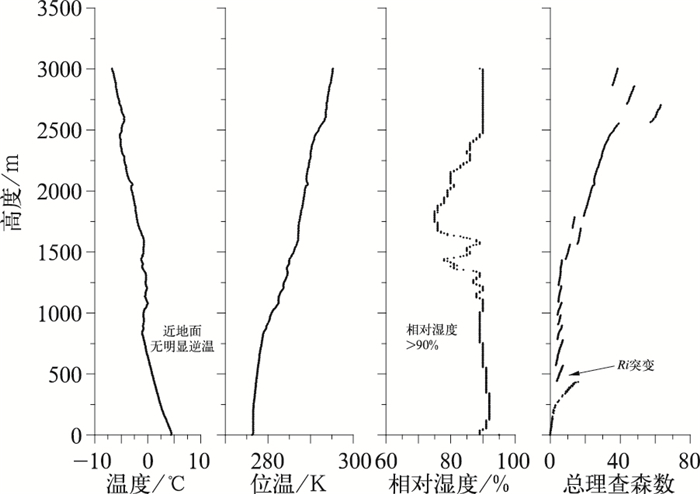
11月27日20时,北京位于地面均压场中,500 hPa西风带气流较为平直,静稳天气开始建立(图略)。从垂直廓线上看(图 3),气温随高度增加逐渐递减,1500 m附近出现浅薄逆温层。1450 m以下,位温随高度增加缓慢,呈现出等位温趋势,说明中低层为中性层结;1500 m附近位温出现跃变。相同高度上,相对湿度由40%突增到95%左右,达到近饱和状态。结合地面观测资料可知,该时刻总云量为8成,低云高2000 m,从而推测相对湿度的突增是受低云影响。由上述大气层结特征可主观判断该时刻边界层高度为1500 m左右。逆温法、位温梯度法的计算结果分别为1461和1442 m,与主观判断一致;总理查森数法计算结果为45 m,与实际相比出现明显偏差。通过Ri垂直廓线发现,Ri在45 m高度处第一次超过临界值,根据算法判断该高度为边界层顶。该高度向上,Ri在临界值附近摆动,未发生突变,直到1437 m处明显增加,而该高度正是符合客观实际的边界层高度,可见总理查森数法将首次超过临界值的高度作为边界层高度,忽略其垂直变化和突变等情况会导致判断出现偏差。该时刻,罗氏法计算得到的边界层高度为59 m,也与实际有明显差别,可能原因在于该方法利用地面要素计算高空边界层高度往往出现时间上的滞后性。
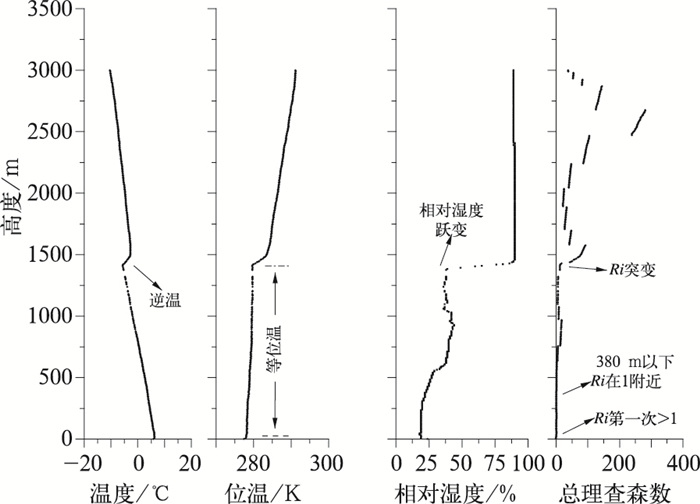
|
图 3 2014年11月27日20时各类要素垂直廓线 Fig. 3 Vertical profiles of meteorological elements at 20:00 BT 27 November 2014 |
11月29日20时,静稳天气形势维持,地面观测天气现象为间歇性小雨,降水量为微量。此时PM2.5质量浓度高达274 μg·m-3,达到严重污染级别。垂直廓线显示(图 4),1000 m以下未出现明显逆温,位温分布近于中性的等温层结。受降水影响,中低层相对湿度较高,基本在90%左右。可见,仅依据观测要素垂直廓线难以主观判断边界层高度。王耀庭等(2012)曾利用激光雷达和微波辐射计对夏季阴雨天气下的边界层高度进行研究,结果表明,北京地区在静稳天气条件下,阴雨天的大气边界层高度在200~300 m。这次过程发生在冬季,降水量小,近地面稳定的大气层结难以被突破,且降水造成的增湿对于细颗粒物的吸湿增长有促进作用,使得污染程度不断加剧。Ri在106 m处第一次超过临界值,400 m以下呈现出迅速增长的趋势,说明该高度层的大气层结动力特性发生了较明显变化,边界层被破坏。罗氏法计算结果(图 2)为60 m,与总理查森数法接近,均表明稳定层结的弱降水天气下,边界层集中在近地层。逆温法和位温梯度法计算结果均在2000 m高度以上,无法正确反映出边界层变化情况。因此,在对复杂天气下的边界层高度进行分析时,结合当前天气现象(有无降水)以及地面污染物浓度等情况,可有助于更好地确定边界层高度范围。
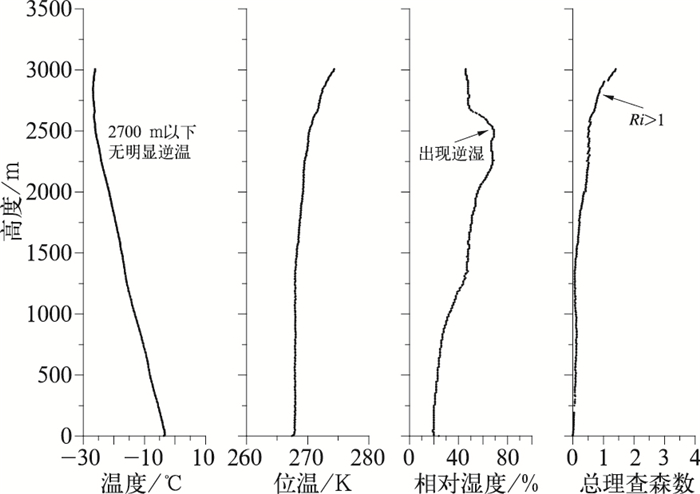
12月16日08时,由于华北平原受高空槽东移影响,中低空以西北气流为主,地面气压梯度较大,风速较大,有利于污染物的扩散,此时PM2.5浓度仅为6 μg·m-3。总理查森数法、逆温法和位温梯度法计算边界层高度分别为2886、2987和2664 m。该时刻的垂直廓线特征(图 5)与污染天气下有明显不同,中低层无明显逆温层,2500 m以下位温变化较小,接近常量。2500 m以上,相对湿度明显减小,而Ri第一次大于临界值,表明该高度以上气层性质发生变化。由上述大气层结特征,主观判断该时刻边界层高度为2500~3000 m。因此,该时刻总理查森数法、逆温法和位温梯度法计算结果与实际基本相符。罗氏法计算得到的边界层高度为1633 m(图 2),较实际情况明显偏低。
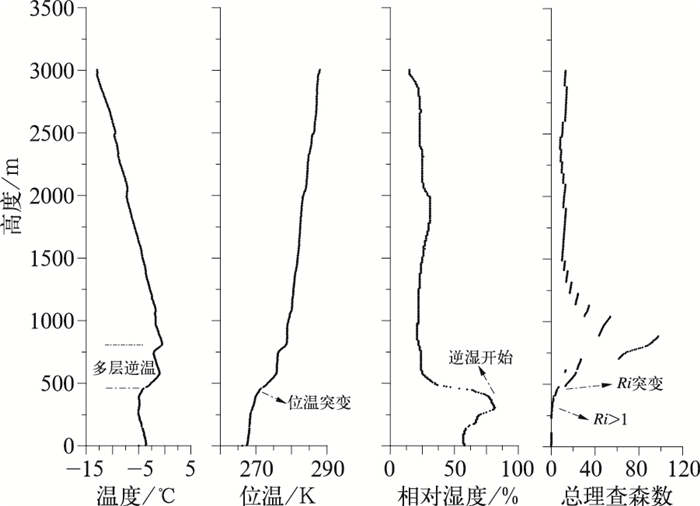
12月18日08时,地面观测显示该时刻天气现象为霾,能见度为3.3 km,PM2.5浓度为160.8 μg·m-3。总理查森数法、逆温法、位温梯度法以及罗氏法计算边界层高度分别为319、493、520和653 m,符合重污染天气条件下边界层高度较低的结论。垂直廓线显示(图 6),500~780 m高度内出现多层逆温,有利于低层稳定层结的维持。从逆温层底开始,对应高度上位温梯度显著增加,故位温梯度法判断该高度为边界层顶。通过湿度廓线发现,343 m以上相对湿度随高度迅速下降,出现梯度极大值,说明该高度以上,稳定层结被破坏,上、下气层交换作用加强。与之对应,Ri在319 m首次超过临界值,且在485 m处明显增大,表明大气运动由湍流向层流的转变。结合各要素垂直廓线分布等情况,可初步判断此时大气边界层高度在300~500 m。因此,该时刻4种方法计算结果与实际基本相符。
由以上分析可以看出,在不同的大气层结条件下,不同方法的计算结果有所不同。其中,在典型的晴空或云量较少的静稳天气中,各方法计算结果相近,且部分时段基于廓线的方法较罗氏法更符合客观实际;当云量较多或有弱降水时,由于计算方法中的局限性,不同算法结果相差较大,需根据廓线特征进行主观判断,或结合其他边界层观测资料加以判定。
4 结论和讨论(1) 利用L波段探空秒数据对2014年11—12月北京地区边界层高度进行分析,总理查森数法、逆温法和位温梯度法计算得到的边界层平均高度分别为653、1152和1296 m,均与PM2.5浓度呈现出较明显的负相关关系,且在0~500 m的概率分布最高,符合冬季边界层高度较低,且与大气污染垂直扩散能力密切相关的结论,证实了几种计算方法的合理性。
(2) 结合冬季两次典型污染过程,研究发现4种方法存在一定适用性和局限性。在典型的晴空或云量较少的静稳天气中,各方法计算结果相近;当出现弱降水和大气污染混合等复杂天气时,不同算法结果相差较大。
(3) 与罗氏法相比,利用廓线的计算方法在部分时段更能真实反映边界层高度情况。然而由于边界层特征的复杂性和算法本身的局限性,单一方法很难完全描述边界层高度状况。引入主观分析方法,并适当结合其他边界层观测资料有助于理解边界层内各种反馈机制和演变规律,能够更好地确定不同天气情况下边界层高度。
程水源, 席德立, 张宝宁, 等, 1997. 大气混合层高度的确定与计算方法研究[J]. 中国环境科学, 17(6): 512-516. |
杜川利, 唐晓, 李星敏, 等, 2014. 城市边界层高度变化特征与颗粒物浓度影响分析[J]. 高原气象, 33(5): 1383-1392. DOI:10.7522/j.issn.1000-0534.2013.00077 |
韩美, 张苏平, 尹跃进, 等, 2013. 基于L波段雷达探空数据的青岛与台州大气边界层特征分析[J]. 海洋湖沼通报, (3): 19-28. |
花丛, 张碧辉, 张恒德, 2015. 2013年1—2月华北雾、霾天气边界层特征对比分析[J]. 气象, 41(9): 1144-1151. |
李梦, 唐贵谦, 黄俊, 等, 2015. 京津冀冬季混合层高度与大气污染的关系[J]. 环境科学, 36(6): 1935-1943. |
廖晓农, 孙兆彬, 何娜, 等, 2016. 边界层低空急流导致北京PM2.5迅速下降及其形成机制的个例分析[J]. 环境科学, 37(1): 51-59. |
马敏劲, 2011. 中国西北地区极端天气大气边界层高度及其对化学追踪物质传输影响的数值模拟研究[D]. 兰州: 兰州大学: 17-18.
|
饶晓琴, 李峰, 周宁芳, 等, 2008. 我国中东部一次大范围霾天气分析[J]. 气象, 34(6): 89-96. DOI:10.7519/j.issn.1000-0526.2008.06.013 |
涂静, 张苏平, 程相坤, 等, 2012. 黄东海大气边界层高度时空变化特征[J]. 中国海洋大学学报, 42(4): 7-18. |
王耀庭, 李威, 张小玲, 等, 2012. 北京城区夏季静稳天气下大气边界层与大气污染的关系[J]. 环境科学研究, 25(10): 1092-1098. |
徐桂荣, 崔春光, 周志敏, 等, 2014. 利用探空资料估算青藏高原及下游地区大气边界层高度[J]. 暴雨灾害, 33(3): 217-227. |
徐敬, 马志强, 赵秀娟, 等, 2015. 边界层方案对华北低层O3垂直分布模拟的影响[J]. 应用气象学报, 26(5): 567-577. DOI:10.11898/1001-7313.20150506 |
尤焕苓, 刘伟东, 谭江瑞, 2010. 北京地区平均最大混合层厚度的时间变化特征[J]. 气象, 36(5): 51-55. DOI:10.7519/j.issn.1000-0526.2010.05.007 |
余剑蔚, 孙燕, 张备, 等, 2009. 江苏沿江一次重霾天气成因分析[J]. 气象科学, 29(5): 664-669. |
中华人民共和国环境保护部, 2012. 环境空气质量指数(AQI)技术规定(试行): HJ633-2012[S]. 北京: 中国环境科学出版社.
|
Heffter J L, 1980. Transport layer depth calculations[C]//Proceedings of the 2nd Joint Conference on Applications of Air Pollution Modeling.Amer Meteor Soc:787-791.
|
Joffre S M, Kangas M, Heikinheimo M, et al, 2001. Variability of the stable and unstable atmospheric boundary-layer height and its scales over a boreal forest[J]. Bound-Lay Meteorol, 99(3): 429-450. DOI:10.1023/A:1018956525605 |
Nozaki K Y, 1973. Mixing Depth Model Using Hourly Surface Observation[R].Report 7053, USAF Environment Technical Application Center.
|
Sicard M, Perez C, Rocadenbosch F, et al, 2006. Mixed-layer depth determination in the Barcelona coastal area from regular lidar measurements: methods, results and limitations[J]. Bound-Lay Meteorol, 119(1): 135-157. DOI:10.1007/s10546-005-9005-9 |
Ye Xinxin, Song Yu, Cai Xuhui, et al, 2013. Study on the synoptic flow patterns and boundary layer process of the severe haze events over the North China in January 2013[J]. Atmos Environ, 124(B): 129-145. |
 2017, Vol. 43
2017, Vol. 43