2. 中国科学院深圳先进技术研究院,深圳 518040;
3. 深圳南方强天气研究重点实验室,深圳 518040
2. Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518040;
3. Shenzhen Key Laboratory of Severe Weather in South China, Shenzhen 518040
近年来全国各地强降水导致地区局部积涝成灾的情况屡见报导(陈元昭等,2016),极端降雨事件频发,雨强纪录被不断刷新。目前应用较多的降雨预报方法主要是基于卫星云图和雷达回波进行外推(韩雷等,2007),这也是当前气象预报中天气雷达系统和强天气预警业务的基本组成部分(邹德龙等,2014)。新一代天气雷达(胡淳焓等,2015;陈明轩等,2016)的降雨预测数据可以为省域范围内的中小尺度降雨过程提供高时空分辨率的预报参考(尹忠海等,2014),而气象自动站的雨量计观测数据精度都可以达到0.1 mm,基于雷达的降雨预测产品和自动站雨量数据,可以有效建立省域范围内的QPE (定量降水估测)数据集(张强等,2007),这一方向的研究和应用目前普遍存在难度(孔荣等,2010),也是气象业务精细化发展的重点(王雨,2006)。为了进一步提高突发强降水等灾害天气的预报准确率,除了改进现有雷达预测技术(梁建茵和胡胜,2011;高郁东等,2015;曾明剑等,2015;胡胜等,2012)、发展新的预报技术外(陈明轩等,2004),找到更好的方法来利用实测数据对雷达产品进行有效的验证也很值得研究(潘旸等,2015;李佰平等,2016;田付友等,2015)。
国内外都进行了大量雷达降水估测再组网拼图的研究(王捷纯等,2007),并积极地推动了雷达降水估测的业务化(东高红和吕江津,2012),但是由于雷达本身的原理和技术特点在一定程度上限制了雷达降水估测算法的精度(高晓荣等,2012)。国内的很多省市气象部门都在使用中国气象科学研究院灾害天气国家重点实验室研发的雷达组网拼图(刘黎平等,2014)和显示系统及其构建的基于雷达三维组网拼图数据(王改利等,2010)的定量降水估测算法。目前针对不同级别降水过程的雷达定量降水评估(李建通等,2015;杨杰等,2014)及误差分析的研究比较少,特别是气象自动站的实测数据对雷达降雨数据的验证(包括形状验证和定量验证),其中对于定量验证的评价,已经有详细规范的评价标准且在气象预报中得到了广泛应用,而对于形状检验则缺少相应的评价标准。实际上在气象预报中,降雨往往是区域性的,呈面状分布,基于降雨区域的形状验证更为重要也更有检验价值。例如,Brown et al (2004), Ebert and Mcbride (2000)提出了面向对象的QPF (定量降水预报)降雨检验方法,该方法针对常规降雨检验的不足,利用模糊逻辑和图像统计分析从多个视角对降雨预报效果进行了验证。
本论文的研究在于提出一种雷达降雨预报的综合检验思路和具体的形状验证指标,包括预报区域重叠比例Ratiop、实况区域重叠比例Ratiot、计算雷达降雨预报区域形状与实况降雨区域形状相似度的杰卡德系数(Jaccard)和针对区域面积检验的指标FARshape、PODshape、TSshape,并利用该指标对降雨区域形状进行量化衡量,研究表明该形状验证方法和指标对雷达降雨预报的区域形状检验具有较好的指示作用和一定的验证价值。
1 资料和方法 1.1 资料概况本研究利用广东省1480个气象自动站点的实况降水数据,在研究过程中,通过动态的数据质量检查与筛选会删除部分存在严重数据缺失的站点,因此每次检验中实际使用的站点数少于1480个,时间分辨率为5 min,通过线性平均或插值与累加的结合,可以获得该站点与6 min分辨率的雷达数据时间点匹配的0.5、1、2、3 h累计实况降水。
本研究所使用的雷达数据的时间范围为2016年4月22日08:30—11:24,本次降水性质为对流、混合降水。雷达拼图范围为:19.0419°~26.0419°N、108.505°~117.505°E,空间分辨率为0.01°×0.01°,时间分辨率为6 min,本文中使用的QPF雷达降水数据根据动态Z-R关系和线性外推预报方法得到。为便于数值计算与可视化表达,同时将雷达数据网格化为700×900的矩形网格。
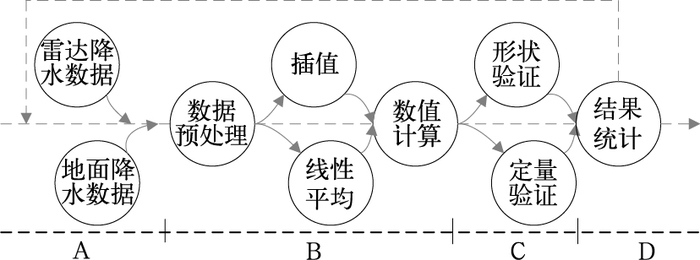
1.2 检验方法流程本论文0~3 h QPF雷达降雨检验方法研究的流程如图 1。本研究方法涉及的流程包含A、B、C、D四个部分,其中:A部分主要进行数据读取加载,包括雷达降雨估测数据的格点化、坐标转换、格式化和表格化;B部分主要进行雷达数据0.5、1、2、3 h的降雨计算和对应实况站点的数据提取,同时进行实况降水数据的质量控制、残缺站点动态过滤、时间序列数据缺失的插值补齐、线性平均再求和的匹配计算;C部分主要进行定量验证的评价指标计算,形状验证的空间区域插值运算、区域范围的Buffer控制、图像格式化输出、评价指标计算;D部分主要进行各评价指标的统计及分析。流程中各部分执行的先后顺序和串并行方式已经在图 1中完全体现。
|
图 1 雷达0~3 h QPF降雨检验方法流程 Fig. 1 Flow chart of radar forecast test method |
对于定量检验,根据气象预报中短期天气预报质量检验办法,有两种降水检验方法,有无降水的晴雨检验和针对某量级降水的分级检验,在本研究中同时采用了晴雨检验和分级检验办法,降水分级和降水预报检验指标分别见表 1和表 2。对于雷达估测降雨的准确率,常用TS评分方法。在本论文中同时使用了RMSE (均方根误差)、FAR (空报率)、POD (命中率)、TS评分四个指标来检验雷达降雨估测的准确率。以上四个指标采用的样本只是自动站上空的对比,并不包括插值区域的对比,计算公式如下:
|
|
表 1 降水预报分级表 Table 1 Classification of precipitation forecast |
|
|
表 2 降水预报检验分类表 Table 2 Classification of rainfall forecast test |
| $RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {} {{({R_{{\rm{QPF}}}} - {R_{{\rm{True}}}})}^2}} $ | (1) |
| $FA{R_k} = \frac{{N{B_k}}}{{N{A_k} + N{B_k}}} \times 100\% $ | (2) |
| $PO{D_k} = \frac{{N{A_k}}}{{N{A_k} + N{C_k}}} \times 100\% $ | (3) |
| $T{S_k} = \frac{{N{A_k}}}{{N{A_k} + N{B_k} + N{C_k}}} \times 100\% $ | (4) |
式中, NAk为预报正确站(次)数、NBk为空报站(次)数、NCk为漏报站(次)数(见表 2),TSk为预报准确率的TS评分,POD为命中率,FAR为空报率。其中k表示降雨的分级情况,当k=0时,表示不分级,不同的k值所代表的具体意义如表 1。
对于雷达降雨预报的形状检验,在图像结果中加入分级的等高线图形描述,引入了预报区域重叠比例(Brown et al,2004; Ebert and Mcbride, 2000)、实况区域重叠比例和杰卡德相似系数(Levandowsky and Winter, 1971)等指标进行检验,计算公式如下:
| $Rati{o_p} = \frac{{(Are{a_r} \cap Are{a_t}){\rm{ }}}}{{Are{a_r}}} \times 100\% $ | (5) |
| $Rati{o_t} = \frac{{(Are{a_r} \cap Are{a_t})}}{{Are{a_t}}}{\rm{ }} \times 100\% $ | (6) |
| $Jaccard = \frac{{(Are{a_r} \cap Are{a_t})}}{{Are{a_r} \cup Are{a_t}}}{\rm{ }} \times 100\% $ | (7) |
式中,Ratiop为预报区域重叠比例,Ratiot为实况区域重叠比例,Arear表示雷达估测降水区域面积,Areat为实况降水区域面积,Jaccard为计算不同样本间相似度的杰卡德系数(Levandowsky and Winter, 1971)。同时,参考站点的天气预报质量检验办法,也设置针对降雨覆盖区域检验的指标FARshape、PODshape、TSshape,各指标的定义见表 3。
|
|
表 3 降水覆盖区域检验分类表 Table 3 Classification of rainfall area test |
| $FA{R_{{\rm{shape}}}} = \frac{{N{B_{{\rm{shape}}}}}}{{N{A_{{\rm{shape}}}} + N{B_{{\rm{shape}}}}}} \times 100\% $ | (8) |
| $PO{D_{{\rm{shape}}}} = \frac{{N{A_{{\rm{shape}}}}}}{{N{A_{{\rm{shape}}}} + N{C_{{\rm{shape}}}}}} \times 100\% $ | (9) |
| $T{S_{{\rm{shape}}}} = \frac{{N{A_{{\rm{shape}}}}}}{{N{A_{{\rm{shape}}}} + N{B_{{\rm{shape}}}} + N{C_{{\rm{shape}}}}}} \times 100\% $ | (10) |
式中, NAshape为雷达降雨预报覆盖区域与实况降雨覆盖区域的交集、NBshape为实况降雨覆盖区域与雷达降雨预报覆盖区域的差集、NCshape为雷达降雨预报覆盖区域与实况降雨覆盖区域的差集(见表 3),TSshape为降雨区域的覆盖准确率,PODshape为降雨区域的覆盖命中率,FARshape为降雨区域的覆盖空报率,其中TSshape等于杰卡德系数。
2 数据质量控制 2.1 降雨时间序列数据的缺失插值本研究中对数据进行初步质量检查时,发现数据的质量参差不齐(赵瑞金等,2015),主要是数据缺失比较严重,存在多种形式的缺失情况(Yi et al,2016)。
在本研究中缺失的时间序列数据的插补思路为局部动态插补,而不是将各站点的记录进行一次性插补,一次性插补的插值算法拟合容易带来较大的数据波动和误差,不利于数据质量控制,同时设置局部插补的区间间隔为interval+5,interval为待检验的雷达降雨估测时间段(0.5、1、2、3 h)所包含的5 min间隔数(6、12、12、12)。
本研究使用的插值算法为三次样条插值(McKinley and Levine, 1998; Cubic Spline Interpolation),因为在局部小区间间隔内的插值计算中,三次样条插值即可以保证较好的拟合度,也具有一定的平滑性。对于待插值记录点[xi, yi](i=0, 1, 2, …, n),y=S (x),三次样条插值的计算公式(McKinley and Levine, 1998)如下:
| $\begin{array}{l} {S_i}\left( x \right) = {a_i}{(x - {x_i})^3} + {b_i}{(x - {x_i})^2} + {c_i}(x - {x_i}) + \\ \quad \quad \quad {d_i},x \in [{x_i},{x_{i + 1}}] \end{array}$ | (11) |
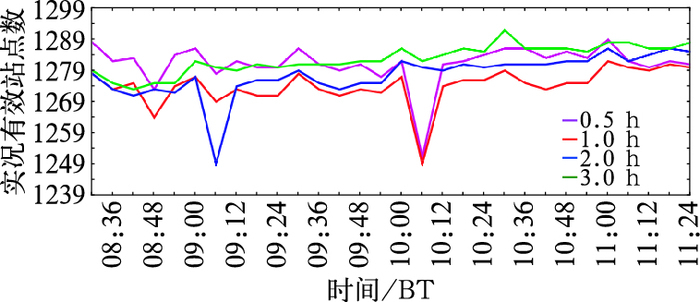
图 2给出了2016年4月22日08:30—11:24持续降雨过程检验中实况有效站点数的变化。
|
图 2 2016年4月22日08:30—11:24雷达降雨检验的实况有效站点数 Fig. 2 Effective stations with observations for radar rainfall test in 08:30-11:24 BT 22 April 2016 |
目前覆盖广东省的雷达数据时间分辨率为6 min,而全省范围内的气象自动站雨量数据时间分辨率为5 min,这两种数据只会在半点或整点时刻相遇,而雷达降雨检验不仅仅只是对半点或整点时刻进行,在实际应用中需要对雷达降雨估测进行6 min分辨率的检验,因此需要将自动站雨量数据与雷达估测数据进行匹配对齐。本研究在每一次的动态检验中,完成2.1节所述的数据质量检查与插补后,采用线性平均方法(勾亚彬等,2014)计算雨量计每隔6 min的0.5、1、2、3 h累计雨量。其中雨量计0.5 h累计雨量线性平均计算方法如下:
| ${G_{{\rm{hour}}}} = {g_{前}} + \sum\limits_{i = 1}^5 {} {g_i} + {g_{后}}$ | (12) |
| ${T_{前}} = \left( {{{\left\| {\frac{{{t_{前}}}}{5}} \right\|}_{取整}} + 1} \right) \times 5 - {t_{前}}$ | (13) |
| ${T_{后}} = {t_{后}} - \left( {{{\left\| {\frac{{{t_{后}}}}{5}} \right\|}_{取整}}} \right) \times 5$ | (14) |
| ${i_{前}} = \left( {{{\left\| {\frac{{{t_{前}}}}{5}} \right\|}_{取整}} + 1} \right) \times 5$ | (15) |
| ${i_{后}} = \left( {{{\left\| {\frac{{{t_{前}}}}{5}} \right\|}_{取整}} + 1} \right) \times 5$ | (16) |
| ${g_{前}} = \frac{{{t_{前}}}}{5} \times {g_i}_{前}$ | (17) |
| ${g_{后}} = \frac{{{T_{后}}}}{5} \times {g_i}_{后}$ | (18) |
式中, Ghour表示待计算的累计雨量,gi表示当前时刻之后的每个完整5 min累计雨量,g前表示当前时刻所在5 min间隔的部分累计雨量,g后表示最后时刻所在5 min间隔的部分累计雨量,T前表示当前时刻所在5 min间隔的累计时间,T后表示最后时刻所在5 min间隔的累计时间,t前表示当前时刻,t后表示最后时刻,i前表示g前所在5 min间隔的序号,i后表示g后所在5 min间隔的序号,gi前表示当前时刻所在5 min间隔的5 min累计雨量,gi后表示最后时刻所在5 min间隔的5 min累计雨量。因此,通过上述方法可实现每6 min计算自动站雨量计的0.5、1、2、3 h累计雨量,使得雷达估测降水与雨量计数据的匹配对齐。
2.3 空间区域一致性控制在雷达降雨估测的检验中,考虑到局部区域范围内的气象自动站比较少,单个站点的实况降雨数据不足以全面反映周边范围内降雨情况,因此需要完成单站点降雨数据到区域面状降雨数据的映射。在本论文研究中分别使用了多种网格插值算法将单点数据平滑插值为面状数据,所使用的插值算法包括IDW (反距离加权;Lu and Wang, 2008)、Nearest Neighbor (最近邻;Shepard,1968)、Bilinear (双线性;Gribbon and Bailey, 2004)和Bicubic (双三次;Keys,1981)。Bicubic (双三次)插值(Keys,1981)算法中,设单位矩形的四个角点坐标为(0, 0),(1, 0),(0, 1),(1, 1),同时这四个点的函数值和偏导数fx,fy,fxy均已知,则插值后的平面格点计算式如式(19),系数αij由偏导数所决定。
| $p{\rm{ }}\left( {x,y} \right) = \sum\limits_{i = 0}^3 {} \sum\limits_{j = 0}^3 {} {\alpha _{ij}}{x^i}{y^j}$ | (19) |
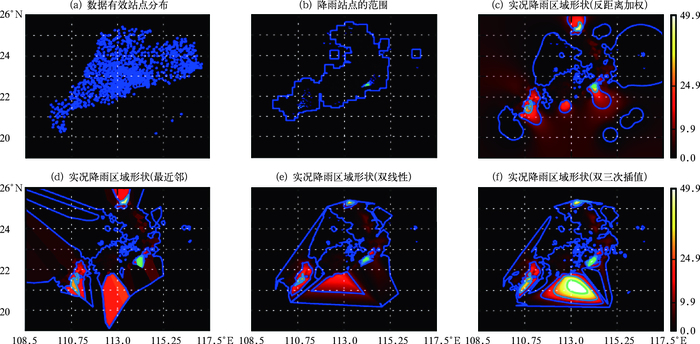
以时刻2016年4月22日08:30的1 h累计降雨为例,应用上述四种插值算法对站点实况降雨的网格数据进行计算,四种不同插值算法的插值效果如图 3。从图 3中可以看出Bicubic (双三次)插值算法得到网格最平滑,且插值区域形状存在有效边界,降雨量的梯度区分清晰。因此在后续的检验中采用该插值算法。由于插值算法针对的整个区域的降雨量,插值完成后,插值结果并不能完全代表研究区域的实况降雨。在本文中我们设置气象自动站的区域影响范围为20 km,也就是说只取以站点为中心的20 km范围内的网格插值结果,过滤掉20 km范围外的插值结果。从而实现由单站点实况降雨向区域范围的实况降雨映射。其中,图 3中数据有效站点是指当前时刻缺失比较少、数据质量有保证的站点,而降水站点是指在数据有效站点中存在降雨的站点,即没有包括不降雨的站点。
|
图 3 2016年4月22日08:30的1 h累计降雨区域插值比较(单位:mm) (a)数据有效站点分布,(b)降雨站点的范围,(c)反距离加权,(d)最近邻,(e)双线性,(f)双三次插值 Fig. 3 Comparision of accumulated rainfall areas between different interpolation methods (unit: mm) (a) effective stations of data, (b) range of rainfall station, (c) inverse distance weighting (ZDW), (d) nearest neighbour, (e) bilinear, (f) bicubic interpolation |
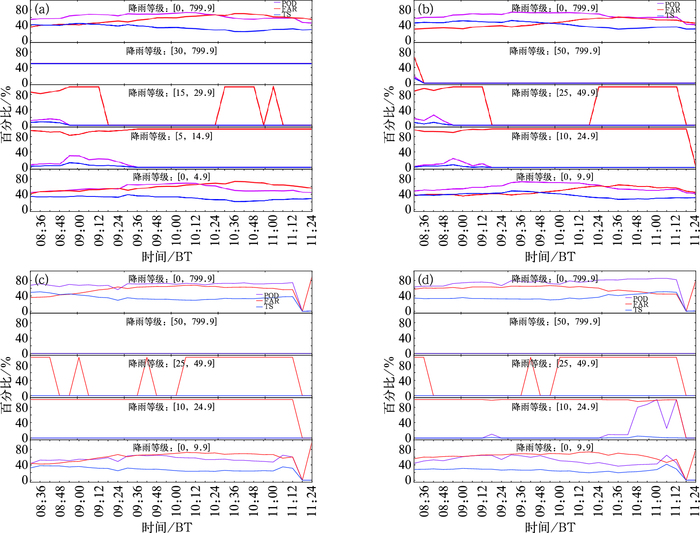
为了对雷达降雨预报进行更详细的定量评估,在本文中雷达预报降水量与自动站实况降水量分为五个降水等级,分别为0.5 h累计降雨分级([0, 4.9]、[5, 14.9]、[15, 29.9]、[30, 799.9]、[0, 799.9])和1 h累计降雨分级([0, 9.9]、[10, 24.9]、[25, 49.9]、[50, 799.9]、[0, 799.9]),其中降雨级别[0, 799.9]表示不分级,对预测间隔0.5、1、2、3 h雷达降雨预报的POD (命中率)、FAR (空报率)、CSI (TS)进行对比分析,随着雷达预报时长的延长,预报准确率不断下降,POD (命中率)、FAR (空报率)、CSI (TS)评分均出现了不同程度的下降。定量检验的结果也佐证了形状检验的指标,即随着预报时间间隔变大,雷达预报效果不断降低,0.5和1 h的雷达预报效果相对比较好。
图 4给出了2016年4月22日08:30—11:24持续降雨过程雷达预报定量检验的指标变化,图 4a~4d分别为0.5、1、2和3 h降雨预报分级定量检验,从图中可以看出该降雨过程中雷达0.5和1 h降雨预报的效果较好,分级检验中指标存在较大波动,因为雷达的分级预报效果有待改进,且分级检验中,发生大雨和暴雨的频次和区域相对较少,容易在指标的计算中产生波动。总的来说,分级检验中,空报率都比较高,说明降雨分级预报仍然是当前气象预报的难点与重点。
|
图 4 2016年4月22日08:30—11:24雷达降雨不同时间间隔预报定量检验 (a)0.5 h, (b)1 h, (c)2 h, (d)3 h Fig. 4 Quantitative analysis of radar forecast during 08:30-11:24 BT 22 April 2016 (a) 0.5 h, (b) 1 h, (c) 2 h, (d) 3 h |
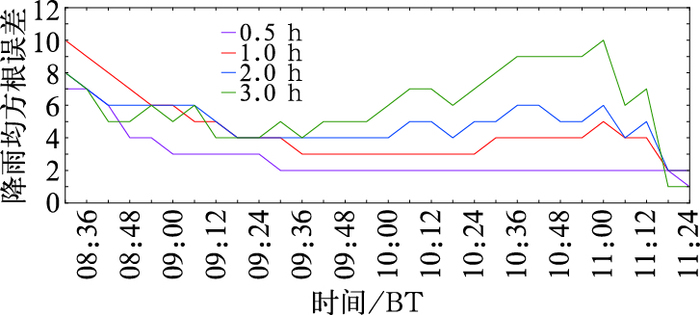
图 5给出了2016年4月22日08:30—11:24持续降雨过程中雷达降雨预报定量检验指标RMSE,从图中明显看到随着雷达降雨预报的时间间隔增大,RMSE不断增加,雷达0.5 h降雨预报的RMSE最小,且总体变化波动也很小,而2和3 h雷达降雨预报的RMSE及其变化波动都比较大。
|
图 5 2016年4月22日08:30—11:24雷达降雨预报定量检验RMSE Fig. 5 RMSE analysis of radar forecast during 08:30-11:24 BT 22 April 2016 |
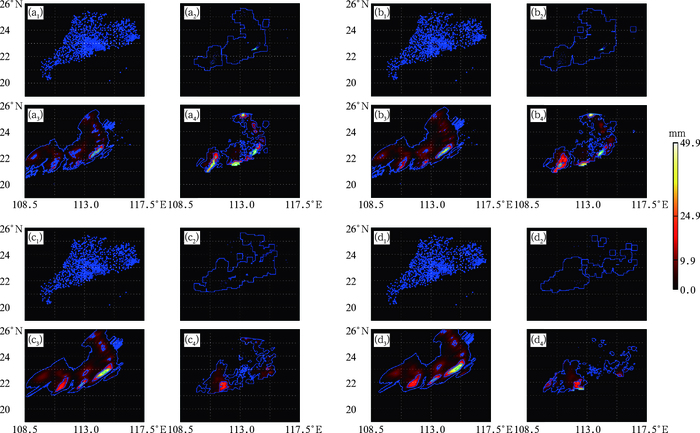
图 6a~6d分别为2016年4月22日08:36雷达预报0.5、1、2、3 h降雨区域形状与自动观测站测得的实况累积降水区域形状的对比图,其中0.5 h降雨检验使用单独的分级标准(见表 1)。由图 6可以看出,雷达0.5和1 h降雨预报的区域及形状与实况降雨的区域范围和形状比较接近,有较好的对应关系,而雷达2和3 h降雨预报的区域及形状与实况则有较大的差别。即随着时间的推移,累积降水量逐渐增加,雷达预报降雨的落区面积逐渐增大,形状也出现了较大变化。而在雷达0.5和1 h降雨预报中,较大降雨出现的落点区域与实况也大致相同,但是也存在漏报的情况,如在各时间间隔的实况降雨图中,20.0°N和113.0°E附近的高值降雨则没有在雷达预报中体现出来,特别是20.0°N以北范围内的降雨,雷达预报的降雨量存在明显低估。从形状检验上可以看出,相比2和3 h的预报,0.5和1 h的雷达预报效果更好。
|
图 6 2016年4月22日08:36雷达估测的(a)0.5 h, (b)1 h, (c)2 h, (d)3 h降雨形状与实况对比 (a1, b1, c1, d1)数据有效站点分布,(a2, b2, c2, d2)降雨站点的范围,(a3, b3, c3, d3)雷达预测降雨区域,(a4, b4, c4, d4)实况降雨区域形状(双三次插值) Fig. 6 Comparision of (a)0.5 h, (b)1 h, (c)2 h, (d)3 h rainfall areas between radar estimation and ground observation at 08:36 BT 22 April 2016 (a1, b1, c1, d1) effective stations of data, (a2, b2, c2, d2) ranges of rainfall stations, (a3, b3, c3, d3) radar-estimated rainfall areas, (a4, b4, c4, d4) observed rainfall areas (bicubic interpolation) |
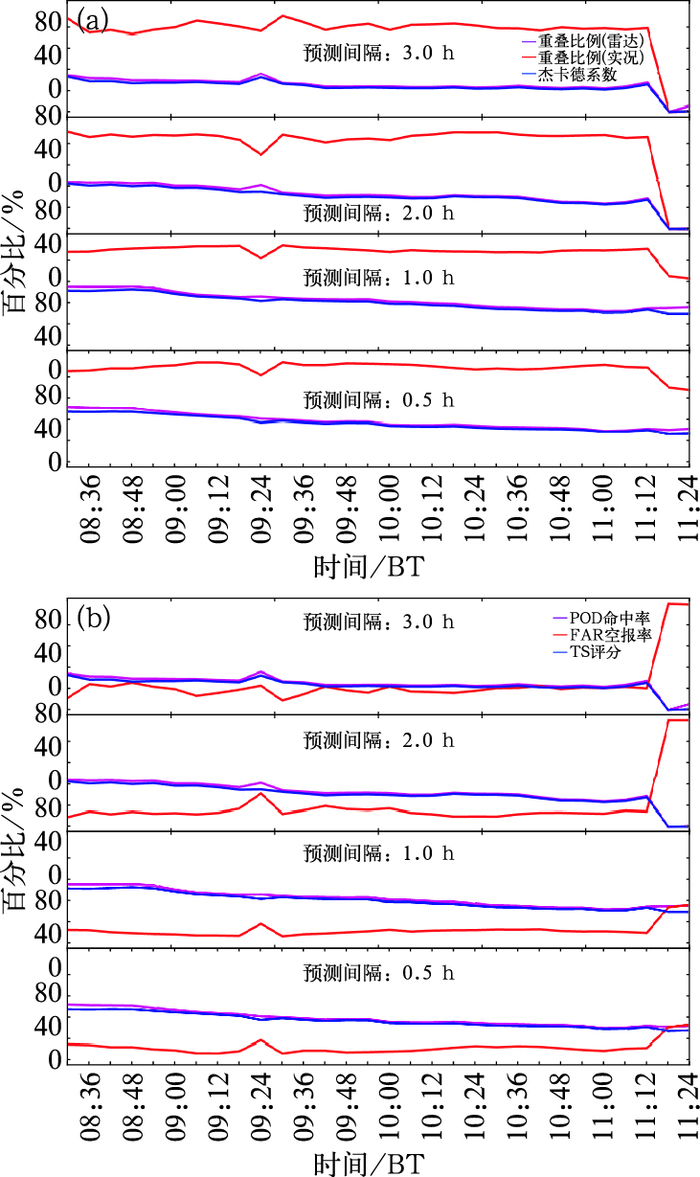
根据本文中提出的雷达降雨预报形状检验的指标(重叠比例和杰卡德系数),图 7给出了2016年4月22日08:30—11:24持续降雨过程检验的指标变化,从图 7a可以看出,雷达0.5和1 h降雨预报的预报区域重叠比例、实况区域重叠比例和杰卡德系数较高,分别为40%以上、80%以上、40%以上,与图 6形状检验的情形相符,随着雷达预报时间的后移,指标重叠比例(雷达)、重叠比例(实况)和杰卡德系数均出现了下降,同时,在本次持续降雨过程的检验中,各指标随时间的变化相对平稳,波动较小。从图 7b可以看出,根据本文中提出的针对雷达降雨预报形状面积检验的TS面积、POD面积、FAR面积指标,雷达0.5和1 h降雨预报的效果较好,TS面积、POD面积、FAR面积指标分别为40%以上、40%以上、30%以下,时间往后2和3 h的雷达降雨预报的效果较差。
|
图 7 2016年4月22日08:30—11:24雷达降雨形状检验的指标分析 (a)形状检验重叠比例和杰卡德系数, (b)形状检验的空报率、命中率和TS评分 Fig. 7 Index analysis of rainfall areas test during 08:30-11:24 BT 22 April 2016 (a) overlap ratio and Jaccard similarity coefficient of rainfall area test, (b) FAR, POD and TS of rainfall area test |
根据发生在2016年4月22日08:30—11:24的持续降雨过程,对本文中提出的雷达降雨预报综合检验方法中涉及的各项指标进行总体检验评价,分别对雷达降雨预报的区域形状检验指标和定量检验指标从均值和方差两个角度进行评价。
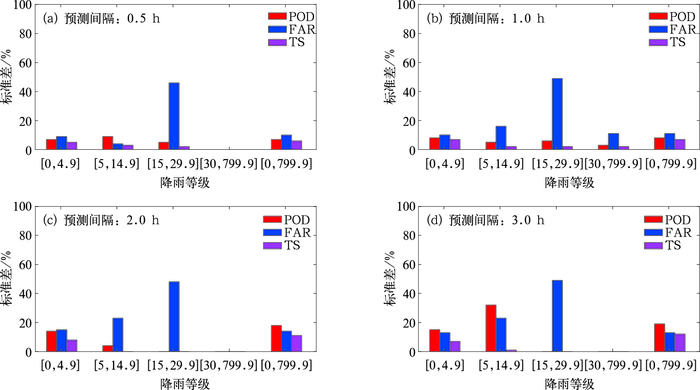
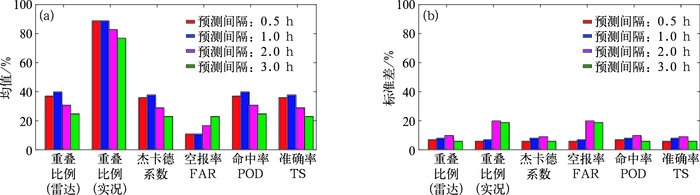
图 8给出了该持续降雨过程中不同预测间隔下雷达降雨预报的形状检验指标重叠比例、杰卡德系数、空报率、命中率以及准确率TS的均值和方差。从均值的角度来看,0.5和1 h雷达降雨预报的效果较好,重叠比例、杰卡德系数、命中率以及准确率TS的均值比较高,空报率的均值比较低,2和3 h雷达降雨预报的效果则较差。从标准差的角度来看,0.5和1 h雷达降雨预报的各项指标标准差都比较小,即数据波动性小,相对比较稳定,2和3 h雷达降雨预报的各项指标标准差都比较大,这也反映了0.5和1 h雷达降雨预报的效果更好。
|
图 8 2016年4月22日08:30—11:24雷达降雨形状检验指标均值(a)和标准差(b)的总体评价 Fig. 8 Overall evaluations of rainfall area index means (a) and standard difference (b) for radar forecast during 08:30-11:24 BT 22 April 2016 |
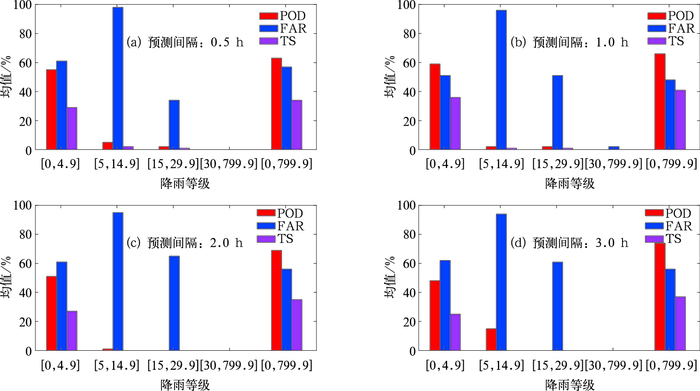
图 9和图 10则给出了该持续降雨过程中不同预测间隔下雷达降雨预报的分级定量检验指标命中率POD、空报率FAR和准确率TS的均值和方差。可能与本次降雨过程的降雨量特征有关,雷达分级降雨预报中,不分级的预报和小雨([0, 4.9])的预报效果比较好,大雨的预报效果比较差,空报率比较高。其中1 h雷达降雨预报的效果最好。而从图 10各指标的标准差特征中可以看出,0.5和1 h的预报准确率稳定性较好,同时不分级预报和小雨([0, 4.9])预报的准确率稳定性也较好,2和3 h的预报准确率稳定性较差、波动较大,大雨的预报准确率稳定性也较差。这也从一定程度上反映了雷达降雨预报效果的特点。
|
图 9 2016年4月22日08:30—11:24不同预测间隔下雷达降雨定量检验指标均值评价 Fig. 9 Means evaluation of quantitative test index for radar forecast in different forecast interval during 08:30-11:24 BT 22 April 2016 |
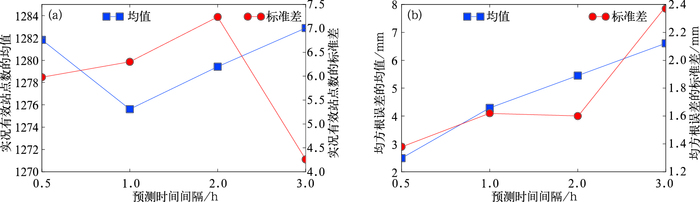
图 11给出了该持续降雨过程中不同预测间隔下雷达降雨定量检验的有效站点数和RMSE的均值和方差。RMSE的均值和方差都随着预测时间间隔的延长而增大,说明0.5和1 h的雷达降雨预报准确率更好,预报的稳定性也较好。由于实况有效站点数与实际的站点设备工作状态和维护保养有关,从图 11中并不能够分析出不同预测时间间隔下站点数的明显变化特征。
|
图 11 2016年4月22日08:30—11:24雷达降雨定量检验有效站点数(a)和RMSE (b)的评价 Fig. 11 Overall evaluations about number of effective stations (a) and RMSE (b) during 08:30-11:24 BT 22 April 2016 |
本文针对不同级别降水过程的雷达降雨预报提出了一种0~3 h QPF雷达降雨预报综合检验方法,包括形状验证和定量验证指标,并利用该综合检验方法对广东省2016年4月22日08:30—11:24的一次典型持续降雨过程进行了检验评价与分析,得到如下结论:
(1) 本文所述的方法流程充分考虑了实况降水数据的质量控制,并提出了数据质量控制的流程和方法,包括严重缺失站点动态过滤、时间序列数据常规缺失动态插补、不同时间分辨率一致性的数据匹配计算和空间区域一致性控制,一定程度上解决了数据质量参差不齐和精度控制的问题。
(2) 进行了更详细的雷达降雨预报分级检验评价,分别为针对半小时的分级([0, 4.9]、[5, 14.9]、[15, 29.9]、[30, 799.9]、[0, 799.9])检验和针对1、2、3 h的分级([0, 9.9]、[10, 24.9]、[25, 49.9]、[50, 799.9]、[0, 799.9])检验,检验结果表明小雨和不分级的雷达预报效果比较好,同时0.5和1 h的降雨预报效果整体好于2和3 h的预报效果。
(3) 对于雷达降雨预报的区域形状提出了一种结合空间插值与空间缓冲的形状验证方法,并进行了检验分析,其分析结果与雷达降雨预报的常规定量检验结果基本相符,即0.5和1 h的雷达降雨预报效果比较好。0.5和1 h雷达降雨预报的区域形状与实况较为一致。
(4) 在实际气象预报中,降雨往往是区域性的,呈面状分布,基于降雨区域的形状验证更为重要也更有检验价值,针对形状检验的难点和特点,提出了雷达降雨预报形状检验的量化指标,包括预报区域重叠比例Ratiop,实况区域重叠比例Ratiot,计算雷达降雨预报区域形状与实况降雨区域形状相似度的杰卡德系数和针对区域面积检验的指标FAR面积、POD面积、TS面积,并利用上述指标对持续降雨过程进行了检验分析与评价,研究表明该形状验证方法和指标对雷达降雨预报的区域形状检验具有较好的指示作用,对于雷达降雨预报具有一定的验证价值,该类指标能够较好地反映雷达降雨预报的效果。
后续的研究计划包括继续改进本文的综合检验方法,使其能够更好地反映雷达降雨预测与实况降雨之间的误差关系,为进一步提高雷达降雨预报的准确度提供更好的参考。
陈明轩, 肖现, 高峰, 等, 2016. 基于雷达四维变分分析系统的强对流高分辨率模拟个例分析和批量检验[J]. 气象学报, 74(3): 421-441. DOI:10.11676/qxxb2016.031 |
陈明轩, 俞小鼎, 谭晓光, 等, 2004. 对流天气临近预报技术的发展与研究进展[J]. 应用气象学报, 15(6): 754-766. |
陈元昭, 俞小鼎, 陈训来, 2016. 珠江三角洲地区重大短时强降水的基本流型与环境参量特征[J]. 气象, 42(2): 144-155. DOI:10.7519/j.issn.1000-0526.2016.02.002 |
东高红, 吕江津, 2012. 不同校准方法检验雷达定量估测降水的效果对比[J]. 气象与环境学报, 28(04): 38-42. DOI:10.3969/j.issn.1673-503X.2012.04.007 |
高晓荣, 梁建茵, 李春晖, 2012. 雷达定量降水估计技术及效果评估[J]. 热带气象学报, 28(01): 77-88. DOI:10.3969/j.issn.1004-4965.2012.01.009 |
高郁东, 万齐林, 薛纪善, 等, 2015. 同化雷达估算降水率对暴雨预报的影响[J]. 应用气象学报, 26(1): 45-56. |
勾亚彬, 刘黎平, 杨杰, 等, 2014. 基于雷达组网拼图的定量降水估测算法业务应用及效果评估[J]. 气象学报, 72(04): 731-748. |
韩雷, 王洪庆, 谭晓光, 等, 2007. 基于雷达数据的风暴体识别、追踪及预警的研究进展[J]. 气象, 33(01): 3-10. DOI:10.3969/j.issn.1002-252X.2007.01.002 |
胡淳焓, 黄娟, 王益琴, 等, 2015. 基于强度尺度法的雷达和数值模式定量降水预报检验对比[J]. 热带气象学报, 31(02): 273-279. |
胡胜, 罗聪, 黄晓梅, 等, 2012. 基于雷达外推和中尺度数值模式的定量降水预报的对比分析[J]. 气象, 38(3): 274-280. |
孔荣, 王建捷, 梁丰, 等, 2010. 尺度分解技术在定量降水临近预报检验中的应用[J]. 应用气象学报, 21(5): 535-544. DOI:10.11898/1001-7313.20100503 |
李佰平, 戴建华, 张欣, 等, 2016. 三类强对流天气临近预报的模糊检验试验与对比[J]. 气象, 42(2): 129-143. DOI:10.7519/j.issn.1000-0526.2016.02.001 |
李建通, 李柏, 杨洪平, 等, 2015. 雷达-雨量计联合估测区域降水量方法检验与评估[J]. 气象, 41(02): 200-211. |
梁建茵, 胡胜, 2011. 雷达回波强度拼图的定量估测降水及其效果检验[J]. 热带气象学报, 27(1): 1-10. |
刘黎平, 吴林林, 吴翀, 等, 2014. X波段相控阵天气雷达对流过程观测外场试验及初步结果分析[J]. 大气科学, 38(6): 1079-1094. |
潘旸, 沈艳, 宇婧婧, 等, 2015. 基于贝叶斯融合方法的高分辨率地面-卫星-雷达三源降水融合试验[J]. 气象学报, 73(1): 177-186. DOI:10.11676/qxxb2015.010 |
田付友, 郑永光, 张涛, 等, 2015. 短时强降水诊断物理量敏感性的点对面检验[J]. 应用气象学报, 26(4): 385-396. DOI:10.11898/1001-7313.20150401 |
王改利, 刘黎平, 阮征, 等, 2010. 基于雷达回波拼图资料的风暴识别、跟踪及临近预报技术[J]. 高原气象, 29(6): 1546-1555. |
王捷纯, 江吉喜, 冯建碧, 等, 2007. 广西热带气旋6h降水天气概略模型及其应用[J]. 应用气象学报, 18(6): 840-848. DOI:10.11898/1001-7313.200706126 |
王雨, 2006. 2004年主汛期各数值预报模式定量降水预报评估[J]. 应用气象学报, 17(3): 316-324. |
杨杰, 刘黎平, 勾亚彬, 2014. 影响浙江地区降水估测几个因素的分析[J]. 气象, 40(5): 589-597. DOI:10.7519/j.issn.1000-0526.2014.05.009 |
尹忠海, 张沛源, 程明虎, 2014. 雷达定量测量降水的检验"真值"求取方法研究[J]. 物理学报, 63(23): 456-466. |
张强, 涂满红, 马舒庆, 等, 2007. 自动雨量站降雨资料质量评估方法研究[J]. 应用气象学报, 18(3): 365-372. |
赵瑞金, 刘黎平, 张进, 2015. 硬件故障导致雷达回波错误数据质量控制方法[J]. 应用气象学报, 26(5): 578-589. DOI:10.11898/1001-7313.20150507 |
邹德龙, 冯业荣, 梁巧倩, 等, 2014. 0~3小时短时定量降水预报算法研究[J]. 热带气象学报, 30(02): 249-260. DOI:10.3969/j.issn.1004-4965.2014.02.006 |
曾明剑, 王桂臣, 吴海英, 等, 2015. 基于中尺度数值模式的分类强对流天气预报方法研究[J]. 气象学报, 73(5): 868-882. |
Brown B G, Bullock R R, Davis C A, et al, 2004.New verification approaches for convective weather forecasts[C].Conference on Preprints.
|
Ebert E E, Mcbride J L, 2000. Verification of precipitation in weather systems:determination of systematic errors[J]. J Hydrol, 239(1-4): 179-202. DOI:10.1016/S0022-1694(00)00343-7 |
Gribbon K T, Bailey D G, 2004.A novel approach to real-time bilinear interpolation[C].Second IEEE International Workshop on Electronic Design, Test and Applicadions.p.126-131.
|
Keys R, 1981.Cubic convolution interpolation for digital image processing[C].IEEE Transactions on Acoustics, Speech, and Signal Processing.p.1153-1160.
|
Levandowsky M, Winter D, 1971. Distance between sets[J]. Nature, 234(5323): 34-35. DOI:10.1038/234034a0 |
Lu G Y, Wong D W, 2008. An adaptive inverse-distance weighting spatial interpolation technique[J]. Computers & Geosciences, 34(9): 1044-1055. |
McKinley S, Levine M, 1998. Cubic spline interpolation[J]. College of the Redwoods, 45(1): 1049-1060. |
Shepard D, 1968.A two-dimensional interpolation function for irregularly-spaced data[C].Proceedings of the 1968 23rd ACM National Conference.ACM.p.517-524.
|
Yi Xiuwen, Zhang Junbo, Li Tianrui, 2016.ST-MVL:Filling Missing Values in Geo-sensory Time Series Data[C]. Proceedings of IJCAI 2016.
|
 2017, Vol. 43
2017, Vol. 43