2. 中国气象科学研究院, 北京 10008
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
降水过程与人民的生活和工业生产息息相关,因此对降水进行定量评估有着非常重要的意义。天气雷达作为我国定量估测地区降水量的主要工具之一,如何不断提高天气雷达的定量降水估测(Quantitative Precipitation Estimation,QPE)精度,一直是研究人员需要不断突破的重要课题。与传统多普勒雷达Z-R关系方法(简称PPS)相比,双线偏振雷达定量降水估测(简称DP-QPE)有着明显的优势(Bringi and Chandrasekar, 2001;Ryzhkov et al,2003)。双线偏振雷达不仅可以使用基本反射率因子ZH来计算降水强度,还增加了差分反射率因子ZDR、比差分传播相移KDP等偏振参量,能获得比常规天气雷达更多有关降水粒子形状和相态等微观物理信息,对进一步提高灾害性天气的监测和预报能力具有显著意义。过去30年,利用ZH、ZDR、KDP不同组合的降水估测公式被相继提出,如R(ZH, ZDR)、R(KDP)、R(KDP, ZDR)等。20世纪80、90年代国外做了很多关于偏振雷达定量降水估测方法的研究。在我国,对比常规雷达R(ZH)方法,人们对单个双极化雷达测雨公式R(ZH, ZDR)、R(KDP)、R(KDP, ZDR)的优势做了大量的比较研究。刘黎平等(1996)分析发现R(ZH, ZDR)的估测效果要优于R(ZH)。王建林等(2005)指出,在小雨阶段KDP存在比较大的系统误差,当反射率因子小于20 dBz时可采用R(ZH)进行估测降水。但都没有考虑雨滴谱的变化对降水估测的影响。殷秀良和张培昌(2002)研究发现,雷达反射率因子ZH对降雨谱各谱参量的变化也非常敏感,而差分传播相位变化率KDP对雨滴谱变化不敏感,R(KDP, ZDR)的测雨效果最佳。赵果等(2011)利用黑河流域观测雨滴谱数据得到的本地雷达测雨公式以及三参数方法R(KDP, ZDR, ZH)改进了双极化雷达测量降水精度。以上研究对我国双线偏振雷达降水估测的业务发展有着重要的指导意义,但都是基于科研用途的双极化雷达以及单个的测雨关系式。国外的双线极化雷达降水估计算法已经比较成熟和系统化,在国外,Chandrasekar et al(1993)探讨了把几种单个的降水估测公式联合起来进行降水估测,即对每一组测定值的偏振参量ZH、ZDR、KDP,选择一个最优的方法,这里我们称之为最优化算法(Optimization Algorithm,OA)。Cifelli et al(2003)研究提出了CSU-ICE最优化算法,通过设置冰晶系数和偏振参量ZH、ZDR、KDP阈值来建立降水强度估测公式选择机制。Ryzhkov et al(2005)在美国联合偏振试验(JPOLE)的基础上提出了JOPLE最优化算法,对于不同类型的降水强度使用不同降水估测公式。Giangrande and Ryzhkov(2008)将相态识别算法加入到降水估测中。相较而言,国内虽然也进行了双线偏振雷达相态识别方法的研究(曹俊武等,2005;刘亚男等,2012),但是并没有将其运用到定量降水估测方法中来。
双线偏振雷达是下一代天气雷达发展趋势。我国双线偏振雷达经过近30年的探索研究也逐步从科研外场试验发展为业务应用(刘黎平等,2016)。2013年底广东珠海和澳门市象局合作共建的S波段双偏振多普勒天气雷达进入了业务试运行阶段。2014年上海市气象局完成了对引进WSR-88D雷达的双偏振升级改造步骤和程序。2015年一部X波段双线偏振多普勒天气雷达在广东佛山市南海国家气象观测基地正式试用。在双偏振雷达的全国业务推广和偏振技术改造的过程中,也提出了更多亟待开展的研究课题。比如,双线偏振雷达业务资料的质量控制、其相态识别效果的评估、其业务探测降水能力的评估等。针对我国业务使用的双线偏振雷达降水估测能力的研究,本文利用华南地区雨滴谱数据计算得到的降水估测公式R(ZH)、R(ZH, ZDR)、R(KDP),参考CUS-ICE的液态降水类估测模型,建立了一种基于相态识别的S波段双线偏振最优化定量降水估测算法(简称HCA-LIQ)。该方法主要有两个特点,一是基于业务使用的双线偏振雷达,二是将相态识别方法运用到降水估测中。为了评估该最优化算法的估测效果,本文选取广东珠海业务使用的S波段双线偏振雷达和华南地面密集的自动站网络雨量资料,对该最优化算法的估测效果进行了统计分析,并且进一步与CUS-ICE算法、传统的R(ZH)方法进行了比较研究。
1 数据来源本文选取2014年5月9日以及11日珠海地区的两次降雨观测数据。据当地气象报道,从8—11日,珠海出现持续强降雨天气,历史上首次连续3天(9—11日)发布暴雨红色预警信号。11日是一次强对流降水过程,9日是一次大范围的混合云降水过程。该数据包括两部分:一部分是珠海S波段双线偏振雷达的观测数据,另一部分是华南自动雨量站网分钟级和小时级实测降雨量数据。降水过程信息统计如表 1所示。
|
|
表 1 降水过程的信息统计 Table 1 Information of precipitation processes |
珠海雷达资料共38个时段411个体扫数据样本。雷达的主要性能指标如下:偏振类型为双发双收,扫描方式为PPI体积扫描,雷达波长10.3 cm,雷达工作频率2.901 GHz,发射脉冲宽度1.57 μs,峰值功率650 kW,天线增益≥45 dB,天线海拔高度为257 m,波束宽度≤0.99°,其波束库长为250 m, 方位角分辨率为1°,探测半径为230 km。雷达的中心坐标位于22.026°N、113.370°E,雷达体扫数据为6 min·次-1,雷达基数据除了包含水平反射率因子、多普勒速度、谱宽,还包括差分反射率因子ZDR、差分传播相移率KDP等偏振参量。所取资料仰角皆为0.5°,查阅探空数据发现零度层高度为4.7 km左右,考虑到仰角较低和雷达探测半径,所以不考虑零度层亮带的影响(庄薇等,2013)。
1.2 自动站雨量资料自动站雨量资料来自于我国华南密集的地面雨量计网络,其降雨量分辨率为0.1 mm。其中能够提供与雷达形成对应的降水数据的雨量站数目为739个,这里我们选取逐小时雨量资料。其中雷达和雨量计的分布情况如图 1所示。

|
图 1 珠海偏振雷达位置与地面自动站分布 (★表示雷达,黑色的点表示雨量计) Fig. 1 Geographical distribution of radar stations (star) and gauges (black dots) in Zhuhai |
雷达的数据质量是使用雷达数据之前必须考虑的问题,它与雷达是否准确定标有关。通过中国气象局大气探测中心的硬件测试和日常观测数据的分析,认为珠海雷达在2014年得到了较为准确的标定,数据可靠。对于10℃层以下回波强度15~20 dBz的小雨回波和0℃层以上15~25 dBz的干雪回波,其ZDR在0 dB左右、ρhv接近1,均在合理的范围内。根据Liu et al(2010)对双偏振雷达资料质量的分析发现,信噪比偏低时噪声对差分反射率因子ZDR有着明显影响。因此,为了进一步提高可靠性,本文只选用信噪比大于20 dB时的雷达参数进行降水估测。
2.2 数据预处理在使用雷达资料之前,首先对数据进行质量控制。本文使用中值滤波方法(魏庆等,2016)对数据进行平滑预处理,中值滤波是一种非线性数据滤波技术,能够有效地处理脉冲噪声。取中值滤波窗口M=13,即采用13点滑动平均的方法对偏振雷达径向数据进行平滑处理。然后反演出逐6 min雷达降水强度估计,再经过时间累积,将每小时内的10次连续的逐6 min雷达降水强度估计累加为雷达小时雨量估计,当小时雨量小于0.1 mm时用0.1代替。接着将1 h雷达降水强度估计值与单点雨量站逐小时雨量测量值进行配对,雷达估计值与地面实际测量的空间不一致性是影响雷达定量降水估测精度的重要因素之一。高晓荣等(2012)指出,对于任一部单个雷达,雨量计降水强度与其上空9点平均的雷达回波强度的关系最为密切。因此这里我们选取雨量计站点正上方及周围共9个雷达观测数据进行算术平均,将平均值作为该点的雷达估测值与地面雨量计测量值对应进行匹配。
按以上准则对雷达与雨量计的小时雨量数据匹配完成以后, 5月9日和11日两次过程分别获取了15651组和11063组雷达-雨量计配对样本资料。然后按雷达与雨量计小时雨量的不同将配对样本分成四类,分别为雷达有值、雨量计空值,雷达空值、雨量计空值,雷达空值、雨量计有值和雷达有值、雨量计有值。结果如表 2所示,可以看到匹配样本中主要为雷达有值、雨量计有值和雷达空值、雨量计空值的情况,因此在对数据资料进行筛选时,只保留雷达有值、雨量计有值和雷达空值、雨量计空值的数据进行降水估测误差统计。
|
|
表 2 两次过程的雷达-雨量计小时雨量匹配样本统计 Table 2 Sample statistics of radar-gauge hourly accumulation in two rainfall events |
为了对降水估测的效果进行定量分析,本文选取了均方根误差(RMSE)、归一化偏差(NB)、皮尔逊相关系数(CORR)作为误差评估指标。其中均方根误差(RMSE)反映了雷达估测值和雨量计实测值之间的离散程度,其值越小离散程度也就越低,误差越小,单位为mm。归一化偏差(NB)的绝对值越低表示误差越小, 单位为%。皮尔逊相关系数(CORR)表示了估测值和实测值之间相关关系密切程度,其值越接近于1表示相关程度越高,无量纲。三个指标的具体定义如下:
均方根误差:
| $ RMSE={{\left[ \frac{1}{N}\sum\limits_{i=1}^{N}{\left( RA_{i}^{R}-R{{A}^{G}} \right)} \right]}^{1/2}} $ |
| $ 归一化偏差:NB=\left( \frac{\overline{R{{A}^{\rm{R}}}}-\overline{R{{A}^{\rm{G}}}}}{R{{A}^{\rm{G}}}} \right)\times 100 $ |
| $ 相关系数:CORR=\frac{Covar(R{{A}^{\rm{R}}},R{{A}^{\rm{G}}})}{{{\sigma }^{\rm{G}}},\sigma^ \rm{R}} $ |
式中,RAR、RAG分别表示雷达估测小时雨量和对应的雨量计实测小时雨量,i表示第i组雷达-雨量小时雨量匹配样本,上划线表示平均值。Covar()表示协方差,σ为标准差。
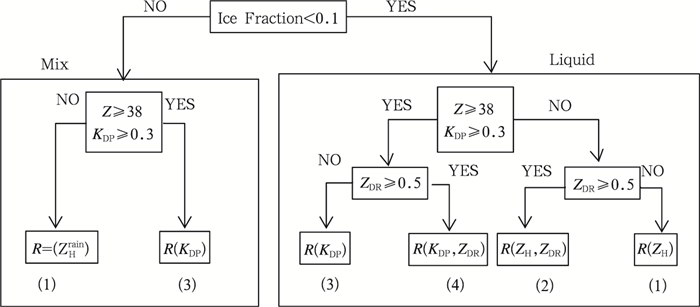
3 最优化定量降水估测方法 3.1 Colorado State University (CSU)-ICE最优化算法由于高原地区特殊的地理和气候条件,夏季的降水过程常伴有霰或者冰雹的出现。如果不能准确地分辨出非液态降水类,会使降水估测造成比较大的偏差。于是对高原地区的定量降水估测提出了更高的要求。美国科罗拉多州立大学利用世界先进的偏振雷达系统S波段CSU-CHILL雷达研究提出了Colorado State University (CSU)-ICE最优化算法,算法的流程图如图 2所示。根据差分反射率定义了一个冰晶因子(Ice Fraction,Golestani et al,1989),利用冰晶因子来区分出雷达扫描体积中的液态降水和冰雹混合区降水。然后基于ZH、ZDR、KDP阈值,分别对液态降水和冰雹混合区降水选择最优的降水估测公式,公式如下:
| $ R({{Z}_{\rm{H}}})=0.0170{{({{Z}_{\rm{H}}})}^{0.143}} $ | (1) |
| $ R({{Z}_{\rm{H}}},{{Z}_{\rm{DR}}})=0.0067{{({{Z}_{\rm{H}}})}^{0.927}}\times {{(10)}^{-0.343{{Z}_{\rm{DR}}}}} $ | (2) |
| $ R({{K}_{\rm{DP}}})=40.5\times {{\left( {{K}_{\rm{DP}}} \right)}^{0.85}} $ | (3) |
| $ R({{K}_{\rm{DP}}},{{Z}_{\rm{DR}}})=90.8\times {{K}_{\rm{DP}}}^{0.93}{{(10)}^{\left( -0.169{{Z}_{\rm{DR}}} \right)}} $ | (4) |
|
图 2 CSU-ICE最优化算法流程图 Fig. 2 Flow chart describing the CSU-ICE optimization algorithm logic |
水凝物分类算法(HCA),又称相态识别算法,是通过偏振雷达回波信息对雷达扫描体积中的水凝物进行分类识别的方法。目前最常用的是基于模糊逻辑的相态识别算法。模糊逻辑识别粒子相态的原理主要是,由于不同降水粒子时各偏振参量存在差异性,利用ZH、ZDR、KDP、ρhv等双偏振产品,根据不同相态降水粒子的散射和空间取向等特征建立模糊逻辑识别的隶属函数,可以判断目标粒子的形状、尺寸大小和相态等气象信息,从而得到降水粒子类型。这里的相态识别方法参考Park et al(2009)。将主要的降水粒子相态分为:地物回波(包括异常传播)(GC)、生物回波(BI)、干雪(DS)、湿雪(WS)、各相冰晶(IC)、霰(GR)、大雨滴(BD)、小到中雨(RA)、大雨(HR)、冰雹(HA)。作为本文方法的需要,在降水估测时我们将大雨滴(BD)、小到中雨(RA)、大雨(HR)归液态降水类。
本文的HCA-LIQ最优化方法选用基本估测公式R(ZH)、R(ZH, ZDR)、R(KDP)来定量评估地面降水,并且用相态识别来指导降水估测公式的选择,而不是使用冰晶因子。双线偏振雷达定量降水估测中一个最主要的问题就是,对雷达基数据中每一组测定的偏振参量ZH、ZDR、KDP,如何选择合适的降水强度估测公式。本文通过两个部分实现,(1) 对任一组雷达测定的ZH、ZDR、KDP、ρhv等参量,首先用相态识别的结果来区分液态降水类和其他相态。(2) 当相态识别的结果为液态降水类(雨、大雨、大滴)时,根据设置的ZH、ZDR、KDP阈值作为判别条件,来选择对应的最优降水强度估测公式(图 3)。其中ZH、ZDR、KDP阈值参考Cifelli et al(2003)里的设定。

|
图 3 最优化定量降水估测算法流程图 Fig. 3 Flow chart describing part of the HCA-LIQ optimization algorithm logic |
当相态识别的结果为其他冷冻水凝(如雪、雹、霰等)时,则直接选用相应的降水强度估测公式,如表 3所示。
|
|
表 3 不同的相态识别结果使用不同的降水估测方法 Table 3 Rainfall estimation method for each echo classification |
由于不同地区降水类型、粒子相态、雨滴谱参数存在差异,导致雷达参量与地面降水之间的统计关系也存在地区特性。因此,本文利用广东阳江的雨滴谱数据,观测起止时间为2014年4月27日至6月11日,在考虑不同降水强度采用不同偏振参量进行降水估测的情况下,采用非线性回归拟合和分段式拟合方法拟合出广东地区S波段双线偏振雷达降水估测公式,拟合结果如下:
| $ R({{Z}_{\rm{H}}})=0.0362{{({{Z}_{\rm{H}}})}^{0.687}} $ | (5) |
| $ R({{Z}_{\rm{H}}},{{Z}_{\rm{DR}}})=0.00786{{({{Z}_{\rm{H}}})}^{0.967}}\times {{({{Z}_{\rm{DR}}})}^{-4.98}} $ | (6) |
| $ R({{K}_{\rm{DP}}})=65.3{{\left| {{K}_{\rm{DP}}} \right|}^{0.806}}\times sign({{K}_{\rm{DP}}}) $ | (7) |
| $ \begin{align} &R({{K}_{\rm{DP}}},{{Z}_{\rm{DR}}})=136\times {{\left| {{K}_{\rm{DP}}} \right|}^{0.968}}\times \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{({{Z}_{\rm{DR}}})}^{-2.86}}\times sign({{K}_{\rm{DP}}}) \\ \end{align} $ | (8) |
R()表示降雨强度,单位为mm·h-1。ZH表示水平反射率因子,单位为dBz。ZDR为差分反射率。KDP为差分传播相移率,单位为°·km-1。
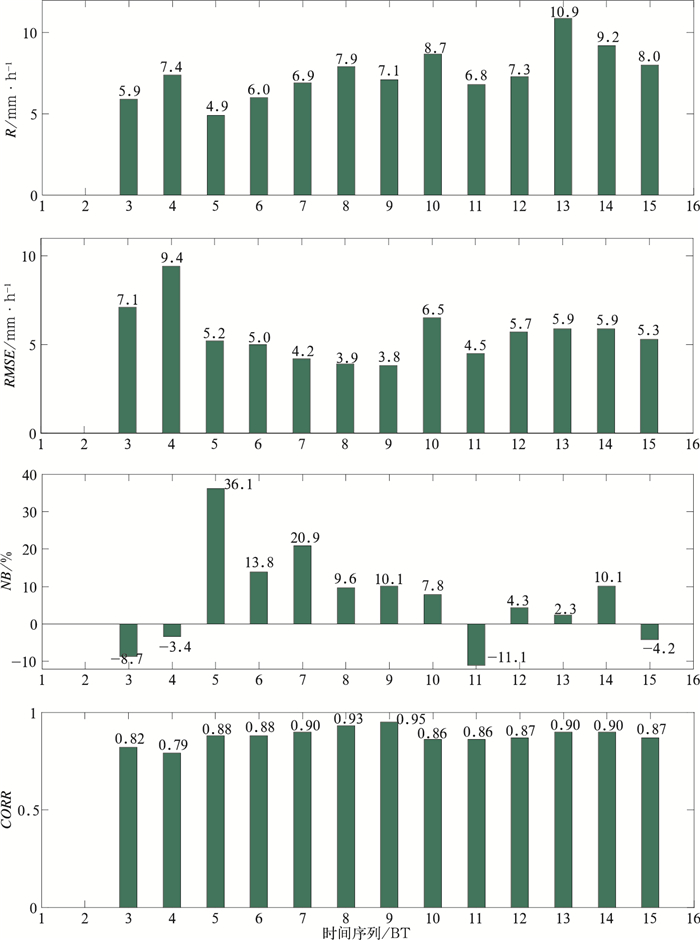
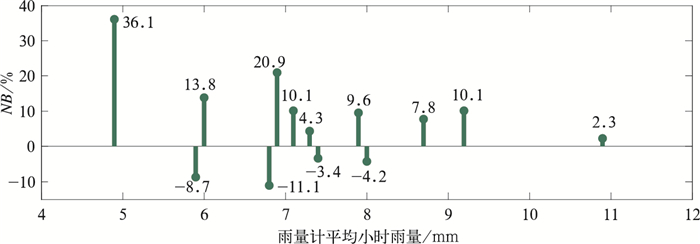
4 HCA-LIQ最优化算法测雨效果评估和时空变化分析由表 1可知,5月11日降水过程的平均雨量计小时雨量为7.8 mm,其中最大小时雨量达到了96.1 mm。这里以地面雨量计为标准,得到了该过程各时段的雨量计平均小时雨量,同时给出了雷达相对地面雨量计小时雨量估测的均方根误差(RMSE)、归一化偏差(NB)和相关系数(CORR)的误差评估结果,如图 4所示。由于01、02时有效匹配样本数据较少,故将其剔除。图 5给出了05、08、13时的雷达以及对应地面雨量计小时雨量估测的等直线图。由图 4得,03—15时,其均方根误差均小于9.4 mm,最小值达到了3.8 mm。相关系数在0.79~0.95,说明HCA-LIQ最优化算法估测结果与地面自动雨量站有着较好的相关性。并且,在图 5中,雷达估测结果相对于雨量计在雨量较多的区域以及雨量较少的区域都能较好的对应,进一步说明HCA-LIQ最优化算法的估测结果和地面雨量计具有较好的一致性。从归一化偏差来看,05时的归一化偏差最大为36.1%,此时雨量计平均小时雨量最小为4.9 mm。此外其他时段均小于20.9%,且当雨量计平均小时雨量≥7.1 mm(09时),其归一化偏差均小于10.1%,估测效果较为稳定。在13时其归一化偏差达到最小值只有2.3%,而此时对应的雨量计平均小时雨量达到最大为10.9 mm。为了初步分析偏差与雨强的关系,于是,给出了03—15时归一化偏差随雨量计平均小时雨量的变化,结果如图 6所示。随着雨量计平均小时雨量的增大,归一化偏差总体有变小的趋势。综上可知,整体上,HCA-LIQ最优化算法表现出与地面雨量计较强的相关性且有着较好的稳定性,随着雨量计平均小时雨量的增大,归一化偏差总体有变小的趋势。
|
图 4 2014年5月11日降水过程从03—15时各时段雷达-雨量计小时雨量估测的误差统计 (a)雨量计平均小时雨量(R), (b)均方根误差(RMSE), (c)归一化偏差(NB), (d)相关系数(CORR) Fig. 4 Error statistics of hourly radar-gauge rainfall accumulation from 03:00 BT to 15:00 BT 11 May 2014 (a) average hourly gauge accumulation, (b) RMSE, (c) NB, (d) CORR |
|
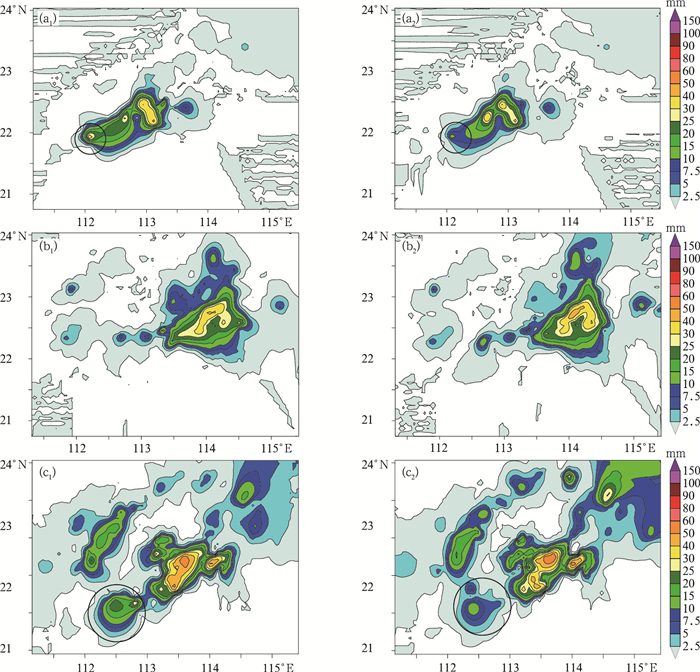
图 5 2014年5月11日降水过程小时雨量雷达估测结果(a1, b1, c1)和对应的雨量计实测结果(a2, b2, c2) (a1, a2)05时, (b1, b2)08时, (c1, c2)13时 Fig. 5 Contour line graph of the hourly radar (a1, b1, c1) and gauge (a2, b2, c2) accumulation for the 11 May 2014 (a1, a2) 05:00 BT, (b1, b2) 08:00 BT, (c1, c2) 13:00 BT |
|
图 6 归一化偏差随雨量计平均小时雨量的变化 Fig. 6 Variation of NB with the average gauge hourly rainfall |
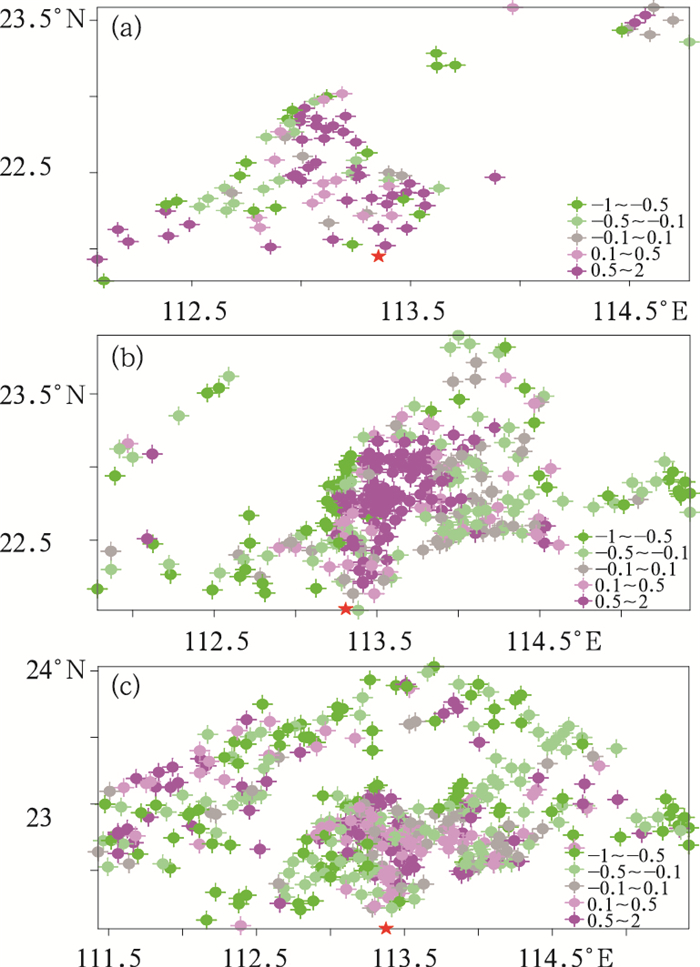
如图 5a、5c中的黑圈显示,与雨量计相比雷达更能观测到该区域强降水中心的极值降水,这可能和该区域雨量计分布较为稀疏有关。在图 5c1中,雷达的估测效果明显较弱,可能是雷达观测的边缘回波较弱造成的。图 7显示了雷达-雨量计小时雨量估测的偏差分布情况(杨杰等, 2014; 陈静等, 2015)。从图 7偏差的空间分布来看,偏差与离雷达的距离没有明显的分布关系,但是在雷达探测距离的边缘地带往往会出现负的偏差。图 5b2、5c2也可以明显地看到这种情况,其原因可能是远距离回波的衰减造成的。
|
图 7 2014年5月11日(a)05时, (b)08时, (c)13时雷达-雨量计小时雨量估测的偏差分布
( 表示雷达位置)
Fig. 7 NB distribution of hourly radar-gauge rainfall accumulation at (a) 05:00 BT, (b) 08:00 BT, (c) 13:00 BT 11 May 2014
( 表示雷达位置)
Fig. 7 NB distribution of hourly radar-gauge rainfall accumulation at (a) 05:00 BT, (b) 08:00 BT, (c) 13:00 BT 11 May 2014
( represents radar position) represents radar position)
|
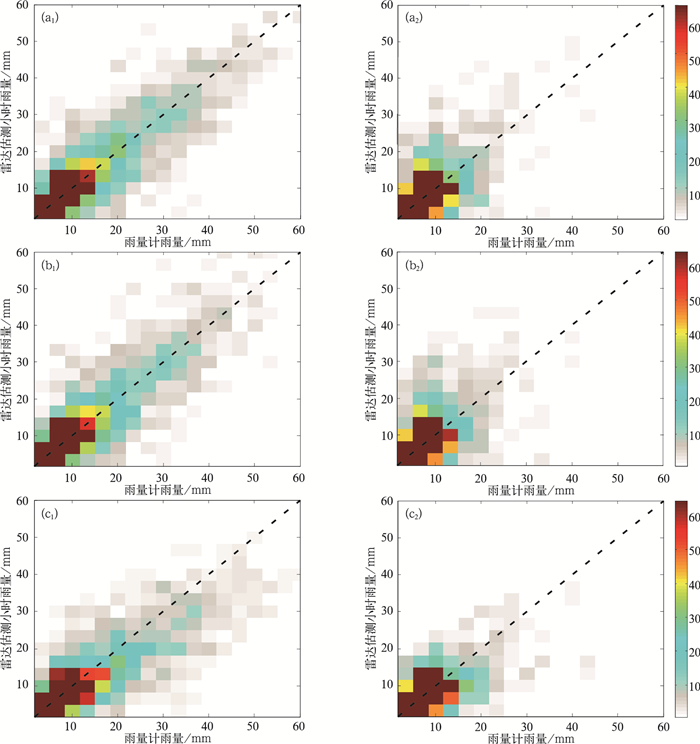
对两个降水过程分别使用两种最优化算法、传统R(ZH)方法(简称PPS)进行定量降水估测,并对三种方法的误差评估结果进行了统计,如表 4所示。图 8给出了对应的雷达-雨量计小时雨量的概率密度分布。表 4表明,对05月11日过程,与传统的R(ZH)方法相比两种最优化方法的估测效果明显更佳。尤其是HCA-LIQ方法,其均方根误差降低了11%,归一化偏差降低了67%,相关系数提高了4%。对比图 8也可以发现,两种最优化算法的概率密度图更集中于目标直线,而传统的R(ZH)方法则更多的偏向目标直线的下方。在对5月9日的过程进行估测时,三种方法的估测效果差别不大,R(ZH)方法要略好于最优化方法,图 8也可以看出这种情况。就两种最优化算法而言,HCA-LIQ方法在两个过程中RMSE、NB、CORR的统计表现均要优于CSU-ICE方法。综合以上分析可得,对强对流云降水,两种最优化算法要明显优于传统的R(ZH)方法;对混合云降水,最优化算法的效果则不如R(ZH)方法;HCA-LIQ最优化算法比CSU-ICE算法效果更佳。
|
|
表 4 两次降雨过程分别使用三种降水估测方法的误差统计结果 Table 4 Error statistic results of three rainfall estimation methods used for the two events |
|
图 8 2014年5月11日(a1, b1, c1)和5月9日(a2, b2, c2)雷达-雨量计小时雨量估测的概率密度图 (a1, a2)HCA-LIQ方法,(b1, b2)CSU-ICE方法,(c1, c2)传统R(ZH)方法 Fig. 8 Probability density plots of hourly radar-gauge rainfall accumulation for the 11 May event (a1, b1, c1) and the 9 May event (a2, b2, c2) (a1, a2) HCA-LIQ, (b1, b2) CSU-ICE, (c1, c2) R(ZH) |
根据气象标准规范:定义1 h内雨量≤2.5 mm的降水为小雨;1 h内雨量为2.6~8.0 mm的降水为中雨;1 h内雨量为8~16 mm的降水为大雨;1 h内雨量>16 mm的降水为暴雨(表 5)。为了更详细地分析在不同降雨强度情况下不同方法的估测精度。我们以雨量计小时雨量为标准,综合两个过程的数据,按降水强度大小进行分类统计(表 5)。
|
|
表 5 不同方法按雨强分类统计的结果 Table 5 Error statistic results according to the classification of rainfall intensity by different methods |
由归一化偏差可以看出,在小到中雨时,三种估测方法均高估了降水强度,在大到暴雨时均出现了低估。与传统的R(ZH)方法相比,两种最优化算法对大到暴雨的估测偏差显著降低。特别是大雨时,HCA-LIQ最优化方法的归一化偏差达到最小值。对小雨和暴雨的估测结果显示,CSU-ICE方法的效果最佳。统计分析来看,与传统的R(ZH)方法相比,HCA-LIQ最优化算法对小雨的估测偏差降低了23%,中雨时的估测偏差相当,对大雨、暴雨的估测偏差分别降低了71%、68%。
6 结论本文利用广东珠海业务应用的S波段双线偏振雷达资料,以及华南自动站网络雨量资料,结合双线偏振雷达在相态识别和降水估测中的优势,建立了一种基于相态识别的S波段双线偏振雷达最优化定量降水估测算法,为我国双偏振雷达估测降水业务提供了有价值的参考,所得结论如下:
(1) 以地面雨量计实测雨量为标准,对HCA-LIQ最优化算法的效果和估测结果的时空变化进行了评估、分析。整体上,HCA-LIQ最优化算法表现出与地面雨量计较强的相关性且有着较好的稳定性;随着雨量计平均小时雨量的增大,归一化偏差总体有变小的趋势;偏振雷达估测降水的偏差与离雷达的距离没有明显的分布关系。
(2) 对过程的估测结果显示,强对流云降水时,两种最优化算法要明显优于传统的R(ZH)方法;混合云降水时,最优化算法的效果则不如R(ZH)方法;HCA-LIQ最优化算法比CSU-ICE算法效果更佳。
(3) 按雨强进行分类统计的结果表明,在小到中雨时,两种最优化算法和传统R(ZH)方法均高估了降水强度,在大到暴雨时均出现了低估。与传统的R(ZH)方法相比,两种最优化算对大到暴雨的估测偏差显著降低,同时提高了对小雨的估测精度。与传统的R(ZH)方法相比,HCA-LIQ最优化算法对小雨的估测偏差降低了23%,中雨时的估测偏差相当,对大雨、暴雨的估测偏差分别降低了71%、68%。
曹俊武, 刘黎平, 葛润生, 2005. 模糊逻辑法在双线偏振雷达识别降水粒子相态中的研究[J]. 大气科学, 29(5): 827-836. |
陈静, 钤伟妙, 韩军彩, 等, 2015. 基于动态Z-I关系雷达回波定量估测降水方法研究[J]. 气象, 41(3): 296-303. DOI:10.7519/j.issn.1000-0526.2015.03.004 |
高晓荣, 梁建茵, 李春晖, 2012. 雷达定量降水估计技术及效果评估[J]. 热带气象学报, 28(1): 77-88. |
刘黎平, 胡志群, 吴翀, 2016. 双线偏振雷达和相控阵天气雷达技术的发展和应用[J]. 气象科技进展, 6(3): 28-33. |
刘黎平, 钱永甫, 王致君, 等, 1996. 双线偏振雷达测雨效果的对比分析[J]. 大气科学, 20(5): 615-619. |
刘亚男, 肖辉, 姚振东, 等, 2012. X波段双极化雷达对云中水凝物粒子的相态识别[J]. 气候与环境研究, 17(6): 925-936. DOI:10.3878/j.issn.1006-9585.2012.06.30 |
王建林, 刘黎平, 曹俊武, 2005. 双线偏振多普勒雷达估算降水方法的比较研究[J]. 气象, 31(8): 25-30, 41. DOI:10.7519/j.issn.1000-0526.2005.08.006 |
魏庆, 胡志群, 刘黎平, 等, 2016. C波段偏振雷达数据预处理及在降水估计中的应用[J]. 高原气象, 35(1): 231-243. |
杨杰, 刘黎平, 勾亚彬, 2014. 影响浙江地区降水估测几个因素的分析[J]. 气象, 40(5): 589-597. DOI:10.7519/j.issn.1000-0526.2014.05.009 |
殷秀良, 张培昌, 2000. 双线偏振雷达测雨公式的对比分析[J]. 南京气象学院学报, 23(3): 428-434. |
赵果, 楚荣忠, 张彤, 等, 2011. 偏振多普勒雷达定量测量降雨精度的改进[J]. 高原气象, 30(2): 498-507. |
庄薇, 刘黎平, 胡志群, 2013. 青藏高原零度层亮带的识别订正方法及在雷达估测降水中的应用[J]. 气象, 39(8): 1004-1013. DOI:10.7519/j.issn.1000-0526.2013.08.007 |
Bringi V N, Chandrasekar V, 2001. Polarimetric Doppler Weather Radar: Principles and Applications[M].
Cambridge: Cambridge University Press, 635.
|
Chandrasekar V, Gorgucci E, Scarchilli G, 1993. Optimization of multiparameter radar estimates of rainfall[J]. J Appl Meteor, 32(7): 1288-1293. DOI:10.1175/1520-0450(1993)032<1288:OOMREO>2.0.CO;2 |
Cifelli R, Barjenbruch D, Brunkow D, et al. 2003. Evaluation of an operational polarimetric rainfall algorithm[C]//32nd Conference on Broadcast Meteorology/31st Conference on Radar Meteorology/Fifth Conference on Coastal Atmospheric and Oceanic Prediction and Processes. Seattle, WA: American Meteorological Society.
|
Giangrande S E, Ryzhkov A V, 2008. Estimation of rainfall based on the results of polarimetric echo classification[J]. J Appl Meteor Climatol, 47(9): 2445-2462. DOI:10.1175/2008JAMC1753.1 |
Golestani Y, Chandrasekar V, Bringi V N. 1989. Intercomparison of multi-parameter radar measurements[C]//Proceedings of the 24th Conference on Radar Meteorology. Boston, MA: American Meteorological Society:309-314.
|
Liu Liping, Hu Zhiqun, Fang Wengui, et al, 2010. Calibration and data quality analysis with mobile C-band polarimetric radar[J]. Acta Meteor Sin, 24(4): 501-509. |
Park H S, Ryzhkov A V, Zrnic' D S, et al, 2009. The hydrometeor classification algorithm for the polarimetric WSR-88D: description and application to an MCS[J]. Wea Forecasting, 24(3): 730-748. DOI:10.1175/2008WAF2222205.1 |
Ryzhkov A, Giangrande S, Schuur T J. 2003. Rainfall measurements with the polarimetric WSR-88D radar[R].Norman, OK: National Severe Storms Laboratory:98.
|
Ryzhkov A V, Giangrande S E, Schuur T J, 2005. Rainfall estimation with a polarimetric prototype of WSR-88D[J]. J Appl Meteor, 44(4): 502-515. DOI:10.1175/JAM2213.1 |
 2017, Vol. 43
2017, Vol. 43 