引言

淮河流域地处中国东亚季风区，是我国气候的南北分界线。历史上淮河流域洪涝、干旱灾害频繁，具有典型的气象水文灾害代表性(Chen et al, 2007)。洪涝、干旱灾害主周期从19世纪的5年缩短为20年来的2~3年，洪旱灾害事件呈增加趋势(张崇旺，2012; 杨传国等，2014)。20世纪90年代以来，几乎每两年就发生1次洪涝，1996、1998、2000、2003、2005、2007、2008年发生了流域性或区域性大洪水，1992、1994、1997、2001、2016年发生了严重干旱灾害，1991年则为洪水和干旱共存的一年。另外，流域人均水资源量仅为世界人均水资源量的1/20、不足我国人均水资源量的1/4，属于严重缺水地区(沈宏，2013; 刘尚等，2013; 刘倩倩和陈岩，2016)。这些问题严重威胁着流域水资源安全和社会经济发展。短期气候预测对防御和减轻自然灾害，促进国民经济和社会发展具有重要意义。如果能提前预测出流域的降水信息，并进一步驱动水文模型给出流域径流预测信息，则能够为流域水库调度、防洪抗旱等水资源规划提供科学参考。WMO执行理事会第54次届会上关于天气和气候预报的科学基础和局限性的声明指出：温度和降水异常在某些较长的超前期甚至几个季节尺度上具有一定可预报性。

目前，短期气候预测方法可分为两类：基于资料统计分析的统计方法和基于气候系统变化规律的动力方法，后一种方法即动力气候模式预测方法是目前国际上开展气候预测的主要工具(张培群等，2004)。我国第一代季节气候模式预测业务系统于2001年10月在国家气候中心开始准业务运行(李维京等，2005)，第二代季节气候预测模式于2016年投入业务运行，每月预测未来13个月的气候趋势。两代模式在国家气候中心短期气候业务预测中发挥了重要作用。考虑到当前多数耦合模式都存在系统偏差问题，不可避免地降低了预报技巧，因此需要研究如何从模式集合预测中获取更详细准确的概率气候信息。本文基于国家气候中心第二代季节气候预测模式的集合回报数据集，应用时空统计降尺度结合的两步法预测淮河流域汛期分月降水概率，探讨评估其预测能力。考虑到现有业务中国家气候中心每年3月召开全国气候预测会商会预测当年全国及各大流域汛期气候趋势，之后每月滚动更新，本文重点关注3、4、5月起报的夏季降水预测。

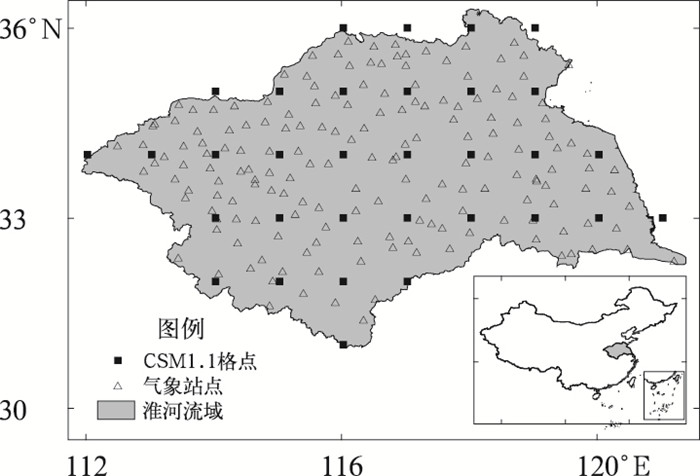
1 研究区与数据介绍 1.1 研究区介绍

淮河流域位于30°55′~36°36′N、111°55′~121°25′E (图 1)，面积270 000 km²，介于长江和黄河之间，地跨河南、安徽、江苏、山东及湖北5省。流域西部、西南部及东北部为山区、丘陵区，其余为广阔的平原。山丘区约占总面积的1/3，平原约占2/3。

流域地处我国南北气候的过渡带，北部为暖温带半湿润季风气候区，南部为亚热带湿润季风气候区，季节上表现为春、冬干旱少雨，夏、秋闷热多雨，冷暖和旱涝转变急剧(刘丽红等，2016)。1961—2016年流域年平均气温在13.46~15.58℃，最高月平均气温27.16℃，出现在7月，最低月平均气温在0.55℃，出现在1月。年降水量533.01~1265.37 mm，暴雨洪水集中在汛期6—9月，期间降水量约占全年降水量的64%。气温由北向南、由沿海向内陆递增。降水也表现为由北向南递增，北部极端降水较少且更为集中，易发生干旱，南部极端降水较多且强降水持续时间长，易发生洪涝灾害(叶金印等，2016; 郑泳杰等，2016)。洪涝的主要水汽来源为东南季风及南海季风(平凡等，2014)，夏季风异常是流域洪涝的主要原因(王东勇等，2008)。

1.2 使用数据 1.2.1 观测和再分析数据

本研究使用国家气象信息中心提供的1961—2015年淮河流域的171个站点(图 1)逐日和逐月降水观测资料，分别用于时间降尺度模型和空间降尺度模型的建立及检验。

海温场资料为NOAA最优插值海表面温度第二版本的逐月平均资料，网格距为1°×1°(Reynolds et al，2002)。海平面气压场资料为NCAR/NCEP再分析资料，网格距为2.5°×2.5°(Kalnay et al, 1996)，起始时间为1981年1月至2015年5月。用于空间统计降尺度模型建立，预测月降水异常。

1.2.2 气候模式数据

国家气候中心第二代季节气候预测模式(CSM1.1m)于2016年投入业务运行，大气分量模式采用BCC_AGCM2.2 T106L26;陆面分量模式采用BCC_AVIM1.0 T106;海洋分量模式采用MOM_L40，水平分辨率为1/3°~1°; 海冰分量模式采用GFDL的SIS; 各分量模式通过CPL5.1直接耦合在一起。基于模式系统开展实时预测时，首先应用多种观测资料生成大气、海洋、海冰模式中部分控制变量的初始驱动场，进而基于滞后平均和奇异向量扰动完成24个样本的集合预报作业。模式输出数据统一处理成1°×1°水平分辨率(图 1)。本研究采用1991—2017年每年3月1日、4月1日和5月1日起报的6、7、8月降水量集合回报预测数据集，用于统计模型建模及检验。

2 方法介绍 2.1 时空统计降尺度模型

应用月降水量异常确定性预测和随机天气发生器(WG)结合的两步法开展淮河流域汛期分月降水量集合概率预测，相似的方法已成功应用于中国地区延伸期月降水量与强降水日数(刘绿柳等，2011)、高温日数的预测(刘绿柳等，2008)。第一步基于国家气候中心的多模式解释应用集成预测系统(MODES)(刘长征等，2013)，利用CSM1.1m模式回报和观测资料，应用区域因子提取回归统计模型(杜良敏等，2016)、两个典型相关分析(Empirical Ortho- gonal Function-Canonical Correlation Analysis，EOF-CCA)统计模型(刘长征等，2013; 贾小龙等，2010)回报的1991—2015年各站汛期降水量异常。然后利用基于多元线性回归的经典超级集合方法(Krishnamurti et al，1999)对3种统计降尺度模型预测结果进行集合平均。两个EOF-CCA统计模型的预报量均为月降水量异常，其中一个统计模型以东亚H500为预报因子，另一个以东亚SLP为预报因子。

第二步利用逐日降水量观测序列计算国家气候中心研发的天气发生器(BCCWG-V2.1)(廖要明等，2004)的降水转移概率矩阵、降水量分布参数，然后应用Monte-Carlo方法生成10000个逐日降水随机序列，从中挑选出月降水量距平与超级集合预测距平最为相似的N个序列作为预测集合成员，集合样本数分别取12、14、16、18、20、22、24、26、28、30、32、34、36、38和40，共15个取样预测方案。考虑到随机过程的不确定性，每个方案运行100次。具体技术流程见图 2。

2.2 检验方法

采用交叉检验和独立样本检验方法检验评估时空统计降尺度模型对淮河流域夏季降水的模拟预测能力，并与CSM1.1m气候模式进行比较。

利用1991—2014年回报数据进行统计降尺度模型的交叉建模检验，采用世界气象组织(WMO)推荐的相对操作特征(Relative Operating Characteristic，ROC)的ROC面积(Area Under Curve，AUC)评估模型性能。AUC作为代表预报技巧的统计指数，其值介于0~1，越接近1，预测技巧越高，小于0.5代表无预测技巧。本研究针对3分位预测的正异常(Above Normal，AN)、负异常(Below Normal，BN)和接近正常(Near Normal，NN)3种事件的概率预报技巧进行评估。由于每个取样方案都随机运行100次，因此用公式(1)计算100次随机模拟的AUC平均值，用于评估每个概率预测项的预测技巧。为便于综合评估比较，用式(2)和式(3)进一步计算各起报月AUC平均值、3个起报月所有预测项AUC之和。如果统计模型有技巧预测频次高于模式，或者频次与模式相同但AUC之和高于模式，说明相应的方法能够提高降水概率预测技巧，反之预测技巧没有提高。

$ \overline {AU{C_{I, J, K}}} = \mathop \sum \limits_{l = 1}^{100} AU{C_{I, J, K, l}}(AU{C_{I, J, K, l}} > 0.5)/100 $

(1)

$ \overline {AU{C_I}} = \mathop \sum \limits_{J = 6}^8 \mathop \sum \limits_{K = 1}^3 \overline {AU{C_{I, J, K}}} (\overline {AU{C_{I, J, K}}} > 0.5) $

(2)

$ {T_I} = \mathop \sum \limits_{J = 6}^8 \mathop \sum \limits_{K = 1}^3 {\rm{count}}(\overline {AU{C_{I, J, K}}} > 0.5) $

(3)

式中：I=3，4，5，代表起报月; J=6，7，8，代表预测月; K=1，2，3，依次代表AN、NN和BN; l=1，2，3，…，100，表示随机模拟。$\overline {AU{C_{I, J, K}}} $：100次随机模拟AUC平均值; $ \overline {AU{C_{I}}} $、T_I：起报月为I时的有技巧的AUC值之和、有预测技巧总频次。

对于独立样本检验，首先基于第二代季节预测模式3、4、5月起报的2015—2017年汛期大尺度环流信息，利用所建的淮河流域时空降尺度模型逐站回报最近3年汛期各月降水。然后分析比较统计降尺度模型、CSM1.1m气候预测模式及观测的流域平均降水距平百分率。

3 结果分析 3.1 CSM1.1m预测技巧

从表 1可以看出，CSM1.1m模式4月起报的夏季3个月降水概率预测技巧之和最高，AUC值之和为3.28，对负异常预测均有预测技巧。其次是3月起报预测技巧，AUC值之和为3.08。5月起报的最差，AUC值之和仅为1.12，只对6月正异常降水、8月负异常降水具有预测技巧。对于夏季各月降水预测，对超前时间最短的6月预测技巧最高，超前时间最长的8月预测技巧次之。对于分级预测，异常级降水预测技巧略高于正常级降水预测技巧。

3.2 统计降尺度模型评估 3.2.1 交叉检验

表 2给出了时空统计降尺度模型对3个起报时次预测的6、7、8月三级降水的预测技巧与季节气候预测模式CSM1.1m的比较。对于各月分级降水预测，深灰表示统计模型AUC>0.5，且预测技巧高于模式。浅灰表示统计模型AUC值>0.5，但预测技巧低于模式或与模式相当。空白表示统计模型没有预测技巧。对于AUC总值和频次，深灰表示统计模型预测技巧优于模式，空白表示预测技巧低于模式或与模式相当。

分析表明，对于3月起报的夏季各月分级降水预测，17个取样预测方案中有8个方案(样本数分别为18、20、22、26、28、32、34、36)的预测技巧高于模式，有预测技巧的AUC之和由模式的3.08最大值提高到4.16，有预测技巧频次由6次增加为7~8次。大部分方案对于6月正常级降水、7月负异常降水、8月正常级降水，AUC最大值由模式低于0.50分别提高到0.56、0.57、0.56。对于4月起报的夏季各月分级降水预测，17个取样预测方案中也有8个方案(样本数分别为12、14、16、18、20、22、28、30)的预测技巧高于模式，有预测技巧的AUC之和由模式的3.28最大值提高到4.29，有预测技巧频次由6次增加为7~8次。大部分方案对于7月正异常和8月负异常降水预测，AUC最大值由模式低于0.50分别提高到0.54、0.56。所有方案对7月和8月三级降水有技巧预测的AUC值之和均高于模式。对于5月起报的夏季各月分级降水，全部17个取样预测方案均优于模式，有预测技巧的AUC之和从1.12最大值提高到4.79，有预测技巧频率从4次增加到5~9次。主要表现为CSM1.1m对6月正常级降水、负异常降水，7月各级降水、8月正异常和正常级降水没有预测技巧，而这些集合取样方案具有一定预测技巧，AUC最大值达到0.58。对于CSM1.1m有预测技巧的6月正异常降水和8月负异常降水，统计降尺度大多数方案也有一定预测技巧。

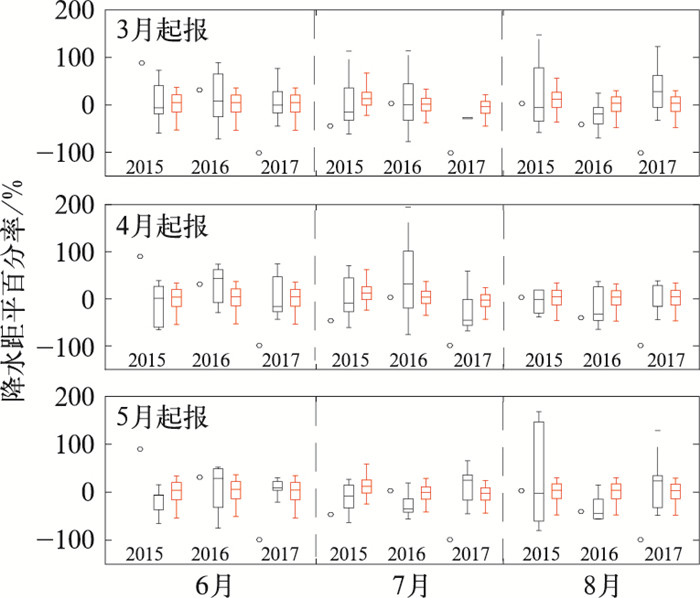
3.2.2 独立样本检验

2015—2017年夏季各月CSM1.1m气候预测模型、统计降尺度模型回报的淮河流域降水距平百分率与观测对比(图 3)分析表明，与CSM1.1m气候模式相比，统计降尺度模型3、4、5月起报的2015年和2017年6月、8月降水及2016年7月降水距平百分率与观测值更为接近。进一步对各起报月预测的近3年夏季3个月降水回报统计，与CSM1.1气候模式相比，统计降尺度3月起报的9次回报中有7次，5月起报的有6次，4月起报的有4次更接近观测值。可以认为通过统计降尺度能够在一定程度上提高预测可信度。

4 结论与讨论

(1) 对于夏季各月降水概率预测，CSM1.1m模式4月起报预测技巧最高，5月起报最低，对超前时间最短的6月降水分级预测技巧最高，对异常级降水预测优于对正常级降水预测。

(2) 交叉检验表明：有预测技巧AUC总和及总频次表明，时空统计降尺度结合的两步法的18、20、22、28个样本的取样方案对3个起报时次预测的夏季各月降水技巧预测均高于模式预测技巧，可选用这些方案用于淮河流域夏季分月降水分级预测。另外，3月起报时26、32、34、36个样本预测方案，4月起报时12、14、16、30个样本预测方案，及5月起报时所有其他预测方案均高于模式预测技巧，可用于相应起报时次的降水预测。

(3) 独立样本检验表明：统计降尺度方法可以降低3、4、5月起报的淮河流域夏季降水预测偏差，特别是3月、5月起报的6月和8月两个月的降水预测。

本文基于2016年最新投入业务应用的国家气候中心第二代季节气候预测模式，探讨了时空统计降尺度结合的两步法对淮河流域夏季分月降水概率预测的性能，研究结果还需在淮河流域降水预测及后续的水文集合预测中进一步应用验证。以往理论研究和实际预测试验都表明模式超级集合优于单模式结果和简单的集合平均结果(刘莹等，2013)，利用多模式超级集合预报可以减弱模式系统误差对预测结果的影响(张培群等，2004)。今后可以尝试基于多个气候模式的集合概率预报，进一步探讨这两种方法对降水概率预测技巧改善的可能性及改善空间。