2. 中国气象局气象探测中心,北京 100081
2. CMA Meteorological Observation Centre, Beijing 100081
全球卫星导航系统(GNSS)泛指所有的卫星导航系统,包括全球的、区域的和增强的,如美国的GPS、俄罗斯的GLONASS、欧洲的GALILEO和中国的北斗卫星导航系统(BSNS)(Guerova et al,2016)。GNSS气象学(GNSS/MET)中讨论了许多利用全球卫星导航系统遥感地球大气参数的方法,通过地面卫星导航信号接收设备测量穿过大气层的GNSS信号的时间延迟来获得大气折射率,进而获得大气的温、压、湿等信息(黄振等,2013),使用美国全球导航系统信号遥感被称为GPS/MET。水汽是大气时空变化中最活跃的成分之一,变化极其复杂,获取高精度的水汽就显得尤为困难(万蓉等,2015),目前我国GNSS/MET业务主要依托美国GPS星座信号和辅助信息探测对流层天顶总延迟(ZTD)和大气可降水量(PWV)。中国在2003年6月正式开通第一代北斗导航卫星试验系统,由于一代导航系统只有三颗卫星,只能覆盖我国本土的区域,2006年开始建设北斗二代卫星导航系统,主要由空间卫星系统、地面运控系统和用户应用系统三大部分组成,是继GPS、GLONASS之后第三个成熟的卫星导航系统,空间段是由5颗静止轨道卫星(GEO)、3颗倾斜同步轨道卫星(IGSO)和27颗中圆地球轨道卫星(MEO)组成(杨鑫春等,2013),目前,中国已经成功发射了16颗北斗导航卫星,在2012年就已经具备了覆盖亚太地区的定位、导航和授时以及短报文通信服务能力,计划在2020年完成覆盖全球的北斗卫星导航系统(杨元喜,2010)。
北斗卫星导航不仅在铁路交通、海运水运和航空运输方面得到了广泛的应用,在气象应用方面也是得到了极大的发展,如成方林等(2004)介绍了北斗系统在海洋水文和气象监测平台的应用,指出只要不断完善北斗系统就可以完全代替我们所使用的国外卫星系统。赵世军等(2012年)验证了北斗一号卫星导航系统在高空风探测的可行性,提出在未来十年内,北斗二号将成为我国高空气象探测的主要形式。周若和蔡宏(2014)介绍了湖北省水汽电离层监测系统,指出该系统对气象部门北斗基准站的建设具有一定的借鉴意义。郭巍等(2015)对上海北斗站反演的大气水汽总量的精度进行检验,并与GPS和探空对比,表明北斗与GPS的均方根误差小于3.5 mm,与探空的均方根误差为3.6 mm,能很好地反映出大气中水汽的变化特征。施闯等(2016)通过对北斗探测水汽的性能分析发现,北斗与探空相比,北斗的系统误差和标准偏差较大,需要进一步提高其稳定性。涂满红等(2016)研究了北斗卫星的反射信号在探测海风海浪中的实用性。刘持菊等(2017)详细地介绍了北斗气象预警信息发布系统的结构和应用。
本文利用北斗地基增强系统提供的数据资料,将目前北斗探测水汽精度的初步分析结果与成熟的GPS和探空系统进行对比,分析存在的误差因素,从而提高北斗卫星导航系统在天气分析和预报中的应用能力。
1 北斗地基增强系统北斗地基增强系统是我国北斗卫星导航系统(BDS)重要的地面基础设施,旨在通过地面基准站网的辅助,通过GNSS差分技术,充分利用地面移动通信、数字广播以及卫星转发等各种通信手段,实现对北斗卫星导航系统空间信号精度和完好性的性能增强。北斗地基增强系统是提升我国北斗卫星导航系统的服务质量和竞争优势,解决北斗规模应用推广与产业化中行业与大众对高精度导航定位服务需求的战略措施。
北斗地基增强网国家数据综合处理中心现有175个北斗站和GPS原始观测数据,以及24 h连续采集基准站的温度、气压和相对湿度等气象数据。气象行业数据处理系统将接受处理从北斗地基增强网国家数据综合处理中心发来的GNSS和气象观测数据,实现对全国175个北斗地基增强站的数据处理,获取高精度、高时空分辨率的水汽和电离层监测数据产品,满足数值预报、空间天气监测和预警业务的需求,推动北斗技术的发展,提高气象预报水平,在防灾减灾、气候变化应对中发挥重大作用。中国气象局将利用北斗地基增强网全国分布的175个框架站观测数据,经过数据中心处理,获取北斗大气对流层水汽含量和电离层产品,服务于天气、气候的研究。北斗地基增强网将加密我国地基GNSS对大气的水汽观测,提升现有探测能力,降低现有GNSS/MET观测网络对美国GPS系统的依赖,提高北斗卫星导航系统在气象行业的应用能力。
2 大气可降水量反演原理北斗和GPS的卫星信号在穿过大气层到达地面接收机时会受到电离层和对流层等大气折射的影响,造成信号的延迟。电离层折射引起的延迟可以根据它与信号频率的相关性得以消除,而剩下的对流层总延迟(ZTD)分为由干空气造成的干延迟,或静力延迟(ZHD)和水汽造成的湿延迟(ZWD)(何平等,2002),即ZTD=ZHD+ZWD。Elgered et al(1991)在假设流体力学平衡、理想气体的条件下,得到ZHD表达式:
| $ ZHD = \left[ {\left({0.002279 \pm 0.0000024} \right)} \right]\frac{{{p_0}}}{{f\left({\varphi, H} \right)}} $ | (1) |
| $ f\left({\varphi, H} \right) = 1 - 0.00266\cos 2\varphi - 0.00028H $ | (2) |
式中,p0为GPS接收机高度处的气压(单位:hPa),φ为测站纬度,H为观测站点的海拔高度(单位:km),上式对ZHD的估算精度可达1 mm。从GAMIT软件解算得到的ZTD中减去ZHD,就可以得到天顶湿延迟(ZWD),其数值大约为0~500 mm。运用以下关系式计算出地基GPS遥感水汽的大气可降水量(PWV),即:
| $ PWV = \mathit{\Pi } \cdot ZWD $ | (3) |
其中转换因子
| $ \mathit{\Pi } = \frac{{{{10}^6}}}{{\left[ {{R_v}\left({\frac{{{k_3}}}{{{T_m}}} + {{k'}_2}} \right)} \right]}} $ | (4) |
Tm为加权平均温度(单位:K),可以用地面温度来计算:Tm=a+b·TS,式中,TS为地面温度。Bevis et al(1994)给出经验系数a=70.2,b=0.72;李建国等(1999)利用中国的探空资料,给出了北京地区的回归系数:a=44.05,b=0.81。
水汽的比气体常数:
| $ {R_v} = 461.495{\rm{J}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}} $ | (5) |
式(4)中的k3, k′2为折射系数,一般都采用Thayer(Bevis et al, 1994)提供的值:
| $ {k_3} = \left({3.776 \pm 0.014} \right) \times {10^5}{{\rm{K}}^2} \cdot {\rm{hP}}{{\rm{a}}^{ - 1}} $ | (6) |
| $ {{k'}_2} = {k_2} - {k_1}\left({{R_d}/{R_w}} \right) = 16.48{\rm{K}} \cdot {\rm{hP}}{{\rm{a}}^{ - 1}} $ | (7) |
本文试验利用北斗地基增强系统和中国大陆构造环境监测网络(以下简称陆态网)中福建省霞浦、河南省济源、四川省天全六个同址的北斗与GPS观测站,将北斗地基增强系统生成的三种水汽模式,即北斗单模、GPS单模、GPS+BD双模,分别与陆态网中同址的GPS系统进行比较分析。同时,利用北斗地基增强系统中宁夏银川、福建省厦门两个测站的三种水汽模式与GNSS基准站同址的探空数据资料进行比较,探空数据来自俄怀明大学(http://weather.uwyo.edu/upperair/sounding.html)。本文处理分析了2017年3月12日至5月17日的北斗气象站、GPS气象站和探空站的数据,剔除由于数据传输或仪器故障产生的不合格的时次和产生的异常值,然后进行时间上的匹配,综合比较分析北斗卫星导航系统与GPS和探空系统探测水汽的精度。
3.2 北斗和GPS数据解算为了确定不同软件对PWV解算结果的影响,本文对于GPS数据采用两种解算方法:(1)对于陆态网GPS站点的数据采用美国麻省理工学院(MIT)和斯克里普斯海洋研究所(SIO)联合开发的GAMIT软件利用双差技术进行解算,将解算结果记为PGPS-G,GPS气象站使用的接收机类型为TRIMBLE NETR8,天线类型为TRM59800.00;(2)对于北斗地基增强网中北斗单模、GPS单模、GPS+BD双模采用PANDA软件进行单点定位技术解算,将解算结果分别记为PBD,PGPS-P,PGPS+BD,北斗气象站采用的接收机类型为司南PDB38,天线类型为HXCGX601A。其中PANDA软件是由武汉大学自主研发的一款高精度导航定位数据处理分析软件,具有支持GPS、GLONASS、北斗三种卫星定位系统数据的联合处理能力,该软件依照惯性系选用非差处理模式,为了尽可能地探测与修正周跳并剔除异常值,在数据预处理方面采用与Blewitt(1990)一致的单站数据预处理方法。对于未修正的周跳可以引入新的模糊度参数加以修正,在估计模块的质量控制中处理未探测的周跳与粗差观测值(陈克杰等,2011)。
卫星轨道主要是通过其初始时刻的参考状态和力学模型这两个参数值进行描述。轨道积分器采用Runge-Kutta起步,预报校正采用Adams-Moulton多步法。固体潮汐力、海洋潮汐力、太阳、月亮等第三体行星引力以及相对论效应引起的轨道摄动力模型参照IERS规范。重力场模型使用EGM96和EIGEN等模型。而GPS卫星采用ROCK,JPL,BERN等太阳光压模型。
PANDA软件采用的观测模型与IERS 2003标准一致,考虑了包括所有被各IGS数据分析中心运行软件所采用的改正模型。对于不能精确模型化的误差因素,通过参数估计吸收。软件采用逐个历元地建立观测方程的方法,这样有利于灵活应用于实时和动态定位。同时,为了节省计算时间和基于观测值残差数据的再编辑,在参数估计模块采用最小二乘估计器(刘光明等,2013)。
北斗数据在处理过程中是把残余的天顶延迟模型误差作为未知参数参与平差,引入大气的水平梯度参数,通过平差计算获取参数估计值,然后将待定参数采取分段线性的方式处理,每2 h估算一个参数,湿延迟参数可以采用一阶高斯-马尔科夫随机过程模拟,最终解算出每个测站上空的天顶总延迟(施闯等,2016)。
3.3 探空数据处理目前,探空站每天只进行两次观测,分别是在UTC时间00、12时。从探空资料计算大气可降水量需要先利用温度(t)、气压(p)、相对湿度(U)以及饱和水汽压(E)计算出水汽压(e)得到水汽混合比湿(q)(Bolton,1980;Wang and Zhang, 2008):
| $ E = 6.112\exp \left({\frac{{at}}{{b + t}}} \right) $ | (8) |
当t>0℃时,a=17.27,b=237.3;当t < 0℃时,a=21.87,b=265.5。
| $ e = \frac{{UE}}{{100}} $ | (9) |
| $ q = \frac{{\varepsilon e}}{{p - (1 - \varepsilon)e}} $ | (10) |
再通过积分计算PWV:
| $ PWV = \frac{1}{g}\int_0^{{p_0}} {q{\rm{d}}p} $ | (11) |
其中ε=0.622,表示经验常数;p0为测站地面气压;g为地球重力加速度。
4 PWV精度检验方法一般采用以下4种方法,从不同角度检验PWV的精度:
平均偏差
| $ bias = \sum\limits_{i = 1}^n {\frac{{({Y_i} - {{Y'}_i})}}{n}} $ | (12) |
均方差
| $ rms = {\left[ {\sum\limits_{i = 1}^n {{{({Y_i} - {{Y'}_i})}^2}/n} } \right]^{\frac{1}{2}}} $ | (13) |
相对方差
| $ ecpc = 100\% \times {\left[ {\sum\limits_{i = 1}^n {{{({Y_i} - {{Y'}_i})}^2}/\sum\limits_{i = 1}^n {Y_i^2} } } \right]^{\frac{1}{2}}} $ | (14) |
相关系数
| $ \begin{array}{l} r = \sum\limits_{i = 1}^n {\left[ {\left({{Y_i} - {{\bar Y}_i}} \right) \times \left({{Y_i} - {{\bar Y'}_i}} \right)} \right]} /\\ \;\;\;\;\;{\left\{ {\sum\limits_{i = 1}^n {\left[ {{{\left({{Y_i} - {{\bar Y}_i}} \right)}^2}\sum\limits_{i = 1}^n {} {{\left({{Y_i} - {{\bar Y'}_i}} \right)}^2}} \right]} } \right\}^{\frac{1}{2}}} \end{array} $ | (15) |
式中,Yi Yi分别表示GPS/PWV的值和其平均值,Y′i,Y′i分别表示北斗/PWV的值和其平均值,n为两者的样本总数。
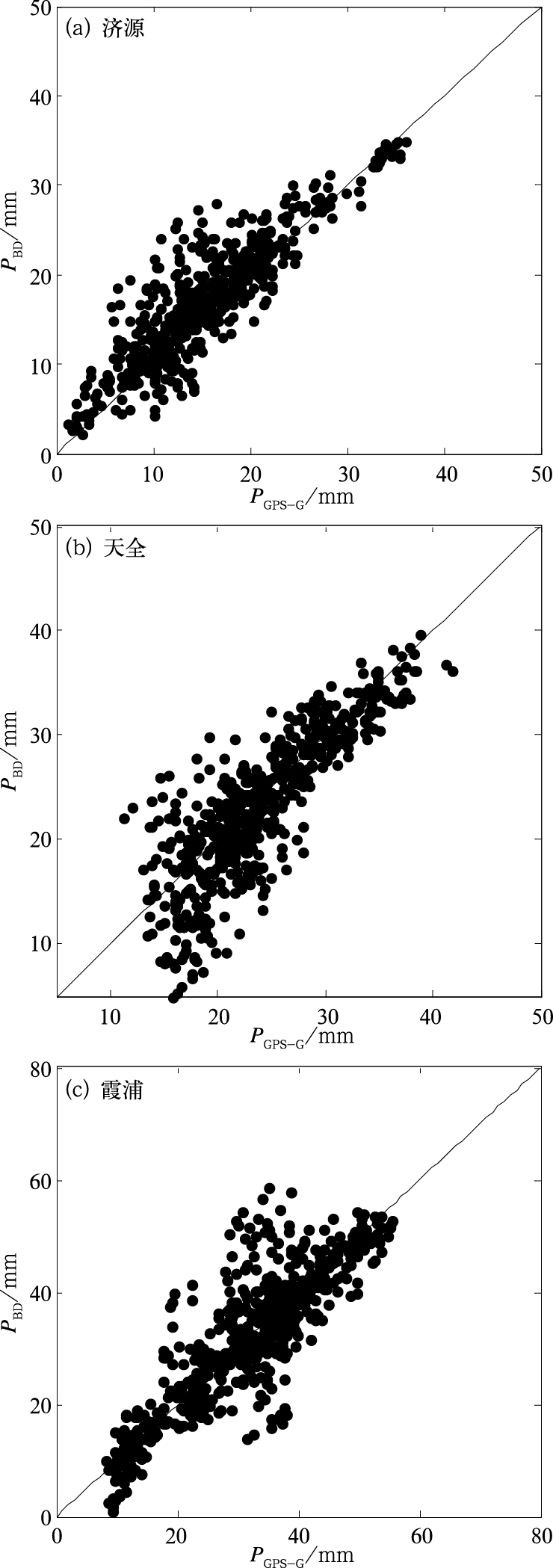
5 PWV精度检验结果分析 5.1 北斗和GPS的精度对比 5.1.1 PBD和PGPS-G的精度对比图 1显示了天全站、济源站和霞浦站PBD与PGPS-G的散点图,表 1为各站点对比分析结果。由图可知,PBD与PGPS-G的散点分布在y=x线的两侧,但并不是很集中,一部分点偏离较大,尤其是在水汽的低值和高值部分一致性较差。从平均偏差来看,除天全站为负的外,其余都为正值,表明北斗站反演的PWV略高于GPS站观测资料计算的PWV,与PGPS-G相比,济源、天全和霞浦北斗站的均方差分别偏高3.73、3.93和6.33 mm,相对方差分别偏高22.22%、15.83%和18.33%,在相关性方面,北斗/PWV与GPS/PWV的相关系数都不足0.90,这不仅与各地区GPS气象站与北斗气象站使用不同接收机和天线类型有关,而且北斗数据在解算过程中采用单点定位非差模式,不考虑测站之间的相关性,需要精确的卫星轨道和卫星钟差,而北斗卫星在定位方面与GPS卫星相比,北斗广播星历的卫星轨道精度整体偏低,GEO卫星精密定轨中切向分量存在1~4 m级的误差(耿涛等,2015),IGSO卫星的空间信号的稳定性较差(刘万科等,2015),所以北斗卫星获取的精密星历文件不完善对北斗反演PWV的精度影响较大,这也是造成北斗/PWV的相对偏差产生较大的主要原因之一。因此,与PGPS-G相比,北斗单模在处理水汽精度方面还有一些差距,尤其是在水汽的高值和低值区域,两者的一致性较差。
|
图 1 各站PBD与PGPS-G的散点图 Fig. 1 Scatter plot of PBD and PGPS-G for each station |
|
|
表 1 三种水汽模式与GPS系统反演PWV的结果比较 Table 1 Comparison of results between three water vapor models and GPS system inversion PWV |
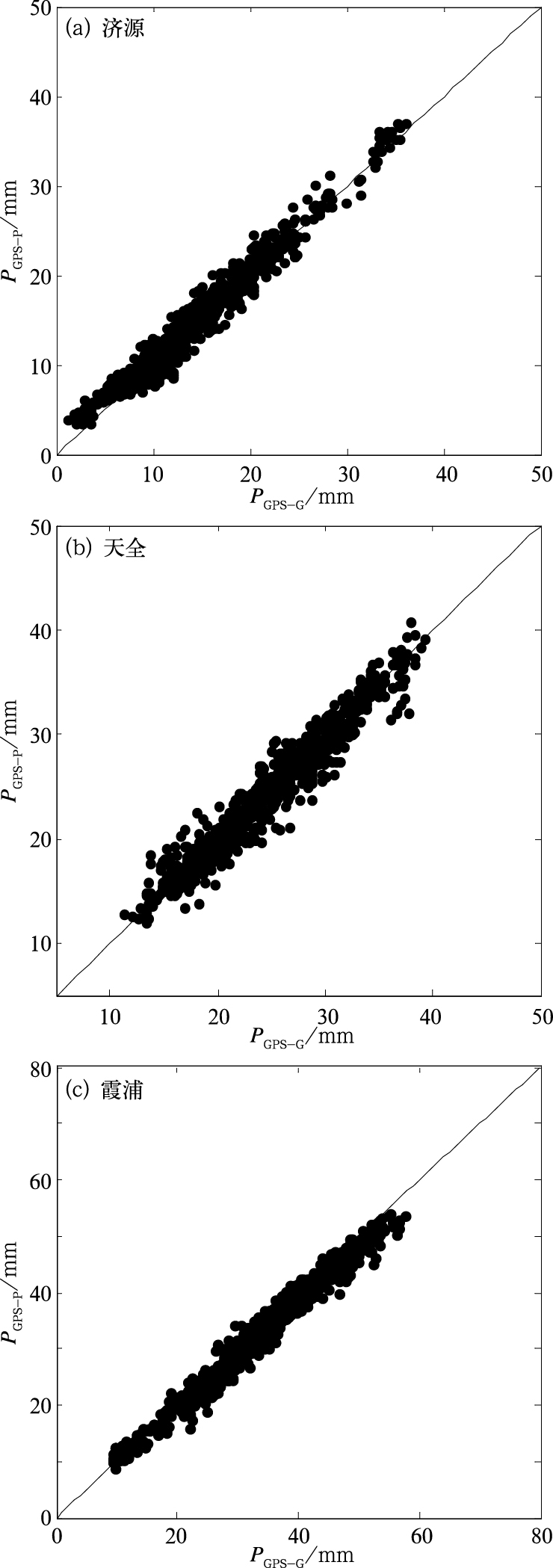
图 2显示了天全、济源和霞浦站PGPS-P与PGPS-G的散点图。由图可见,各站点的散点都均匀分布在y=x线的两侧,存在非常显著的相关性,由于PGPS-P和PGPS-G是分别使用PANDA和GAMIT软件进行解算,平均偏差都小于1 mm,相关系数都超过了0.97以上,两者在反演PWV的变化上基本趋于一致,均方差在2 mm之内,相对方差为5%~9%,表明不同解算方法对于GPS观测资料反演水汽的影响较小,两者精度结果相当,与GAMIT软件相比,我国自主研发的PANDA软件在技术功能上已经达到了一定的水平。
|
图 2 PGPS-P与PGPS-G的散点图 Fig. 2 Scatter plot of PGPS-P and PGPS-G for each station |
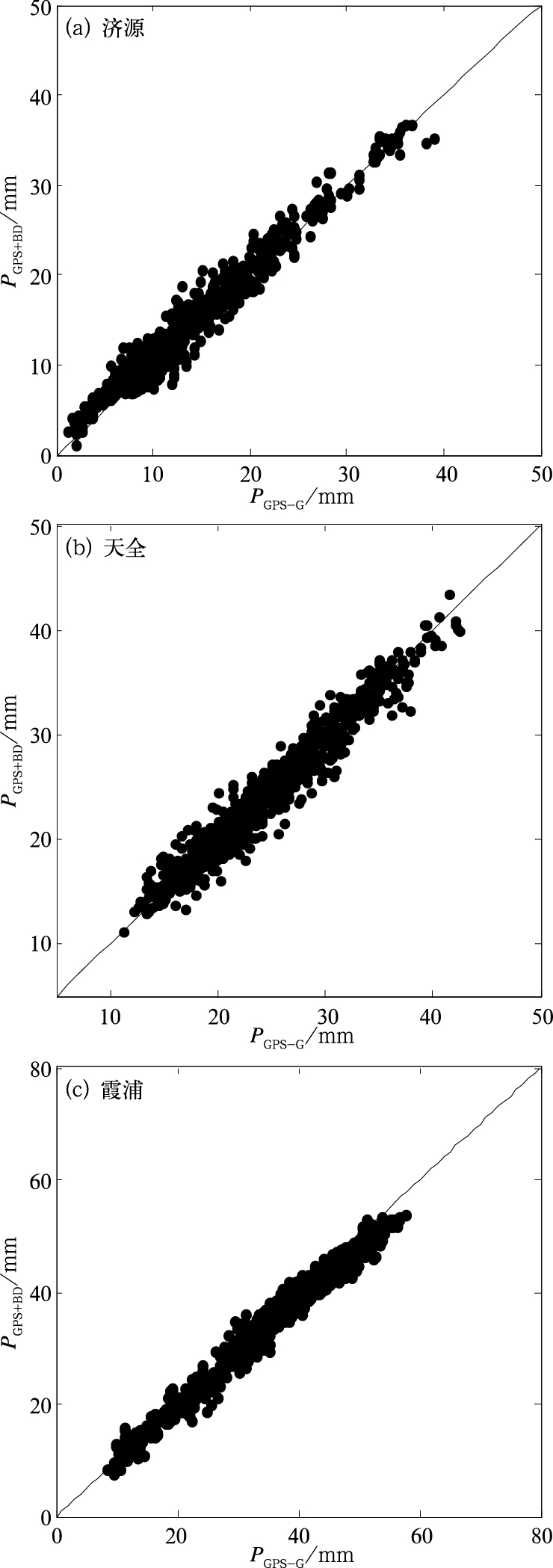
图 3显示了天全、济源和霞浦站PGPS+BD与PGPS-G的散点图,通过对比可见,GPS+BD双模与GPS系统反演的水汽值符合较好,两者之间存在非常显著的相关性,天全、济源、霞浦站的相关系数分别达到了0.9715、0.9788和0.9898,表明PGPS+BD与PGPS-G反演的PWV在变化上具有很好的一致性,均方差分别为1.5、1.65和1.87 mm,相对方差分别达到了5.86%、10.44%和5.24%,表示利用GPS+BD双模观测资料反演PWV具有一定的精度,可能是GPS观测资料起到了主要作用的结果,能满足气象应用的需要,对气象预报有一定的指示作用,并通过建立回归模型可以进行精度上的订正(郭巍等,2015),且与GPS系统反演PWV的精度相当,相比北斗单模要更加稳定。
|
图 3 各站PGPS+BD与PGPS-G的散点图 Fig. 3 Scatter plot of PGPS+BD and PGPS-G for each station |
探空系统是目前探测大气水汽含量最常规、最直接的手段,所获取的数据被认为是最准确的,常常作为其他气象探测系统的校准系统。本文将北斗地基增强系统中银川和厦门站点的北斗单模、GPS单模和GPS+BD双模数据的计算结果分别与GNSS基准站同址的探空数据进行对比分析。由于探空系统一天只观测两次,所以匹配的样本量较少(42)。
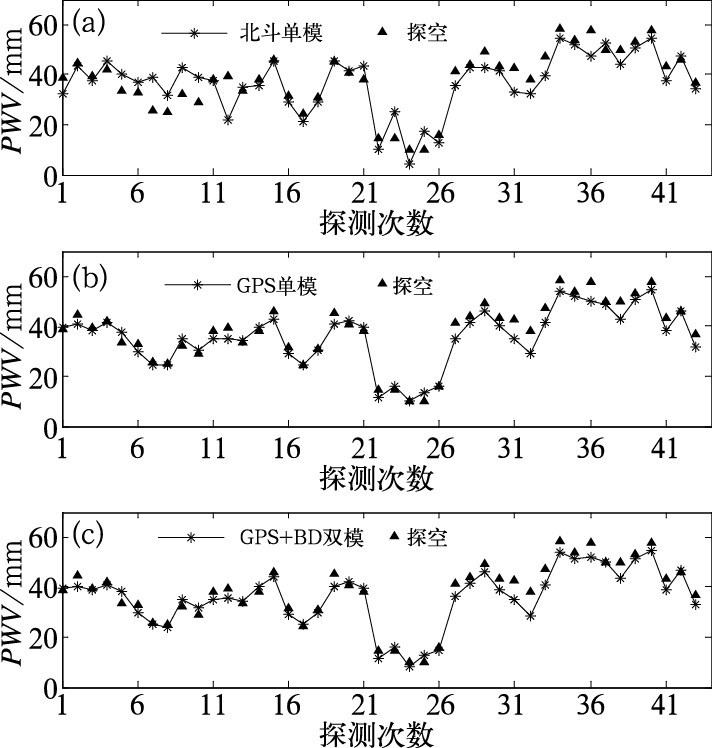
由图 4、图 5可知,三种水汽模式与探空系统在反演PWV变化上基本一致,能很好地反映出大气中水汽含量的变化情况,但是北斗单模的部分点与探空系统存在一定的偏差。根据表 2的统计结果,与探空对比,在平均偏差方面北斗单模、GPS单模和GPS+BD双模都小于1 mm,在水汽低值和高值区域GPS单模和GPS+BD双模都与探空测量的水汽值符合较好,相关系数都达到了0.96以上,均方差在3 mm左右,属于合理区间,这也说明了GPS单模和GPS+BD双模的观测资料在反演大气可降水量的变化方面有很高的精度,这也是GPS的高精度定位起到了主要作用的结果。而对于北斗单模,水汽值较低时均方差为2.14 mm,相对方差为20.84%。水汽值偏高时均方差达到了6.12 mm,相对方差为15.32%,是其他两种模式的两倍左右,且与探空的相关系数分别为0.9166和0.8734,相比于GPS+BD双模,北斗单模在反演水汽的精度上还有一定的差距,对比结果与施闯(2016)得出的结论相当。而引起偏差较大的主要原因可能与北斗系统对卫星轨道的定位精度不高有关,此外,地面接收机类型、台站位置以及数据处理方法也会对水汽的结果有一定的影响(郭巍等,2015)。

|
图 4 银川北斗(a)、GPS(b)、GPS+BD双模(c)和探空探测的PWV Fig. 4 Comparison between PWV detected by Beidou (a), GPS (b), GPS+BD (c) and radiosonde in Yinchuan |
|
|
表 2 北斗、GPS和探空反演PWV对比结果 Table 2 Comparison of results between Beidou, GPS and radiosonde inversion of PWV |
本文利用2017年北斗地基增强系统中北斗单模、GPS单模和GPS+BD双模的数据资料,对同址的北斗和GPS气象站反演大气可降水量进行分析,同时利用GNSS基准站同址的探空数据资料进行对比,经过分析发现:
(1) 经过数据研究表明,现行北斗地基增强系统所提供的数据,可以有效地用来反演大气柱总水汽含量,所得结果合理,能很好地反映大气中水汽含量的变化情况,可用于提高模式初始湿度场的精确性,从而有效地提高数值预报模式的水平。
(2) 以陆态网中GAMIT软件解算的GPS数据资料为参考,GPS单模和GPS+BD双模的解算结果要优于北斗单模的解算结果,三种模式的平均偏差都小于1 mm,北斗单模在水汽的低值和高值时段符合性较差,其均方差为3~6 mm,相对方差达到了15%~20%。对于GPS数据,使用不同解算方法对水汽结果产生的影响较小,表明与GAMIT软件相比,我国自主研发的PANDA软件在技术功能上已经达到了一定的水平。
(3) 由于探空采用直接测量方式,测得的水汽数据更为可靠(王继竹等,2014),与探空数据对比,三种模式在变化上与探空有很好的一致性,其中北斗单模与探空在个别时次变化趋势上存在不一致的情况,其均方差为2.14~6.12 mm,相对方差为15.32%~20.84%,同样证明目前北斗单模反演水汽的效果距离GPS系统和探空在精度上还有一些差距,可能是由于探测系统误差等因素造成的,而GPS+BD双模和GPS单模会更加稳定。
造成北斗系统探测水汽偏差大的原因主要与卫星的精密星历有关,同时地面接收机类型、天线类型以及数据解算方法也都会对其结果产生影响,但是随着北斗卫星导航系统的逐步发展,相信这些问题会逐步解决,并逐渐代替GPS系统应用于气象观测业务中。
致谢:对中国地震局和中国气象局气象探测中心提供的气象资料表示衷心的感谢。
陈克杰, 方荣新, 李敏, 等, 2011. PANDA软件在高频数据PPP动态定位中的应用研究[J]. 大地测量与地球动力学, 31(4): 132-134, 143. |
成方林, 冯林强, 张翼飞, 2004. "北斗"导航系统在海洋水文、气象监测系统中的应用[J]. 海洋技术, 23(3): 70-73. DOI:10.3969/j.issn.1003-2029.2004.03.017 |
耿涛, 苏醒, 许小龙, 等, 2015. 北斗卫星导航系统精密定轨和广播星历轨道精度分析[J]. 中国科技论文, 10(9): 1023-1026, 1032. DOI:10.3969/j.issn.2095-2783.2015.09.007 |
郭巍, 尹球, 杜明斌, 等, 2015. 利用地基北斗站反演大气水汽总量的精度检验[J]. 应用气象学报, 26(3): 346-353. |
何平, 徐宝祥, 周秀骥, 等, 2002. 地基GPS反演大气水汽总量的初步试验[J]. 应用气象学报, 13(2): 179-183. DOI:10.3969/j.issn.1001-7313.2002.02.006 |
黄振, 李万彪, 梁军, 2013. GPS遥感大气可降水量在降水天气过程分析中的应用[J]. 气象与环境学报, 29(4): 31-36. DOI:10.3969/j.issn.1673-503X.2013.04.005 |
李建国, 毛节泰, 李成才, 等, 1999. 使用全球定位系统遥感水汽分布原理和中国东部地区加权"平均温度"的回归分析[J]. 气象学报, 57(3): 283-292. DOI:10.3969/j.issn.1001-7313.1999.03.004 |
刘持菊, 李小汝, 王春芳, 等, 2017. 北斗气象预警信息发布系统及其在秭归的应用[J]. 气象科技, 45(4): 629-636. |
刘光明, 唐颖哲, 秦显平, 等, 2013. 陆态网GPS精密定轨方法与精度分析[J]. 测绘工程, 22(4): 38-41. DOI:10.3969/j.issn.1006-7949.2013.04.010 |
刘万科, 任杰, 曾琪, 等, 2015. 2013-2015年BDS空间信号测距误差的精度评估[J]. 国防科技大学学报, 38(3): 1-6. |
施闯, 王海深, 曹云昌, 等, 2016. 基于北斗卫星的水汽探测性能分析[J]. 武汉大学学报·信息科学版, 41(3): 285-289. |
涂满红, 曹云昌, 周丹, 2016. 基于北斗导航卫星反射信号探测海浪的实现与分析[J]. 安徽农业科学, 44(35): 188-190. DOI:10.3969/j.issn.0517-6611.2016.35.065 |
万蓉, 付志康, 李武阶, 等, 2015. 地基GPS斜路径水汽反演技术及资料应用初探[J]. 气象, 41(4): 448-455. |
王继竹, 郭英莲, 徐桂荣, 等, 2014. 湖北省不同资料反演大气可降水量的误差分析[J]. 气象, 40(11): 1308-1315. DOI:10.7519/j.issn.1000-0526.2014.11.003 |
杨鑫春, 徐必礼, 胡杨, 2013. 北斗卫星导航系统的星座性能分析[J]. 测绘科学, 38(2): 8-11, 31. |
杨元喜, 2010. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 39(1): 1-6. |
赵世军, 高太长, 刘涛, 等, 2012. 基于北斗一号的高空风探测方法研究[J]. 气象科技, 40(2): 170-174. DOI:10.3969/j.issn.1671-6345.2012.02.005 |
周若, 蔡宏, 2014. 湖北省北斗水汽电离层监测系统基准站设计与实施[J]. 气象科技, 42(4): 601-604. DOI:10.3969/j.issn.1671-6345.2014.04.013 |
Bevis M, Businger S, Chiswell S R, et al, 1994. GPS meteorology:mapping zenith wet delays onto precipitable water[J]. J Appl Meteor, 33(3): 379-386. DOI:10.1175/1520-0450(1994)033<0379:GMMZWD>2.0.CO;2 |
Blewitt G., 1990. An automatic editing algorithm for GPS data[J]. Geophys Res Lett, 17(3): 199-202. DOI:10.1029/GL017i003p00199 |
Bolton D, 1980. The computation of equivalent potential temperature[J]. Mon Wea Rev, 108(7): 1046-1053. DOI:10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.CO;2 |
Elgered G, Davis J L, Herring T A, et al, 1991. Geodesy by radio interferometry:water vapor radiometry for estimation of the wet delay[J]. J Geophys Res, 96(B4): 6541-6555. DOI:10.1029/90JB00834 |
Guerova G, Jones J, Dousa J, et al, 2016. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe[J]. Atmos Meas Tech, 9(11): 5385-5406. DOI:10.5194/amt-2016-125 |
Wang Junhong, Zhang Liangying, 2008. Systematic errors in global radiosonde precipitable water data from comparisons with ground-based GPS measurements[J]. J Climate, 21(10): 2218-2238. DOI:10.1175/2007JCLI1944.1 |
 2018, Vol. 44
2018, Vol. 44