2. 国家气象中心,北京 100081;
3. 香港理工大学,香港 999077
2. National Meteorological Centre, Beijing 100081;
3. The Hong Kong Polytechnic University, Hongkong 999077
众所周知,气象灾害是主要的自然灾害,约占我国自然灾害损失的70%左右(章国材,2006),而台风灾害又是气象灾害中的重中之重。随着社会经济的高速发展,政府等相关部门在防灾减灾方针、政策方法研究方面一直做着巨大的努力。为寻求和制定合理的、恰如其分的防灾减灾措施,一方面需要及时掌握较为准确的天气或其灾害的预报、预估产品信息;另一方面也需借鉴和考证历史中相关气象灾害发生规律及特征,对其进行定量评价后将之作为政府等部门的防灾减灾决策依据。
为研究台风灾害特征,国外部分学者早在20世纪70年代(Saffir,1972;Simpson,1974)就开展了台风灾害风险评估工作。中国相对起步较晚,但近些年来,台风灾害及其影响评估工作受到越来越多的重视(叶雯,2002;孙峥等,2007;马清云等,2008;石蓉蓉等,2008;刘少军等,2010;于小龙等,2011;石先武等,2017);运用GIS技术或模糊数学等方法针对台风引发的风雨潮灾害预估或风险划分等方面进行了大量研究,对台风致灾因子风、雨、潮与灾害之间的关系等进行了大量研判,得出一些有益的结论,但大部分研究多集中于东南沿海地区,没有对中国整个区域的台风灾害特征进行分析研判,且多没有涉及到对已经发生的灾情强度大小的评判;部分学者(梁必骐等,1999;钱燕珍等,2001;姚棣荣和刘孝麟,2001)运用台风造成的人员伤亡、农田受淹面积、房屋倒损数目三个指标通过规范化无量纲处理建立了灾情指数大小评判模型,大致反映了台风灾害的综合强度大小,但其没有考虑台风中引发的直接经济损失这一重要灾害指标;王秀荣等(2010)运用台风灾害中死亡人数、直接经济损失、倒损房屋数、农作物受淹面积共4个指标,通过函数转换及关联度分析法建立了台风灾害综合等级评判模型。该模型初步解决了台风灾害综合等级评判问题,当台风灾情统计上报后,可以很快捷地给出历史台风灾害的综合等级和排序,但在随后的研究和应用分析过程中发现,一是原来模型中倒损房屋(倒塌和损坏)数据中的损坏房屋精确数据经常难以获取,二是原模型中对直接经济损失的比较没有考虑通货膨胀的因素,导致在纵向比较失真,三是原模型中的各个指标等值权重取法有所欠缺。
基于以上,2016年以来,在原模型建模基础上,对其进一步的修订与完善,并对改进后的模型输出结果等进行检验与分析。
1 原模型简介 1.1 单项指标选取及分级标准首先参照2006年中国气象局预测减灾司在《气象灾情收集上报调查和评估试行规定》中对灾情的等级划分做的规定草案标准,选取台风灾害中死亡人数、房屋倒损数(倒塌房屋+损坏房屋)、农作物受灾面积数以及直接经济损失数4个指标;结合台风灾害历史数据中农作物受灾面积和倒损房屋数目的分布规律以及社会经济发展状况,给出全国范围内台风灾情单项指标灾害等级标准(王秀荣等,2010)。
1.2 建立单项指标转换函数首先对各个单项灾害指标进行函数转换。将各单项灾害指标进行归一化处理;且引入转换函数后,单项指标灾害等级与单项转换函数值的对应关系为:特大灾(0.8, 1)、大灾(0.6, 0.8)、中灾(0.4, 0.6)、小灾(0.2, 0.4)、微灾(0, 0.2)。按照以上思路,设计如下4个转换函数U(式中lg表示对数函数):
1.2.1 对于死亡人数(X1, i, 单位:人)的转换函数:| $ U\left(1, i \right)=\left\{ \begin{align} &1\ \ \ \ \ \ \ \ \ \ 1000<{{X}_{1, i}} \\ &0.8+\frac{1}{10}\text{lg}\frac{{{X}_{1, i}}}{10} \\ &\ \ \ \ \ \ \ \ \ \ \ 100<{{X}_{1, i}}\le 1000 \\ &0.6+\frac{1}{350}({{X}_{1, i}}-30) \\ &\ \ \ \ \ \ \ \ \ \ \ 30<{{X}_{1, i}}\le 100 \\ &0.4+\frac{1}{100}({{X}_{1, i}}-10) \\ &\ \ \ \ \ \ \ \ \ \ 10<{{X}_{1, i}}\le 30 \\ &0.2+\frac{1}{35}({{X}_{1, i}}-3) \\ &\ \ \ \ \ \ \ \ \ 3<{{X}_{1, i}}\le 10 \\ &0.1({{X}_{1, i}}-1) \\ &\ \ \ \ \ \ \ \ \ 1<{{X}_{1, i}}\le 3 \\ &0\ \ \ \ \ \ \ {{X}_{1, i}}\le 1 \\ \end{align} \right. $ | (1) |
| $ U\left(2, i \right)=\left\{ \begin{align} &1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 1000000<{{X}_{2, i}} \\ &0.2\text{lg}\frac{{{X}_{2, i}}}{10}\ \ \ \ \ 10<{{X}_{2, i}}\le 1000000 \\ &0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{X}_{2, i}}\le 10 \\ \end{align} \right. $ | (2) |
| $ U\left(3, i \right)=\left\{ \begin{align} &1\ \ \ \ \ \ \ \ \ \ \ \ 10000<{{X}_{3, i}} \\ &0.2\times \text{lg}(10{{X}_{3, i}}) \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ 0.1<{{X}_{3, i}}\le 10000 \\ &0\ \ \ \ \ \ \ \ \ \ \ \ {{X}_{3, i}}\le 0.1 \\ \end{align} \right. $ | (3) |
| $ U\left( 4,i \right)=\left\{ \begin{align} & 1\ \ \ \ \ \ \ \ \ \ \ 1000000<{{X}_{4,i}} \\ & 0.8+\text{ }\frac{1}{40000000}({{X}_{4,i}}-200000) \\ & \ \ \ \ \ \ \ \ \ \ 200000<{{X}_{4,i}}\le 1000000 \\ & 0.6+\frac{1}{500000}\text{ }({{X}_{4,i}}-10000) \\ & \ \ \ \ \ \ \ \ \ \ 100000<{{X}_{4,i}}\le 200000 \\ & 0.4+\frac{1}{350000}\text{ }({{X}_{4,i}}-30000) \\ & \ \ \ \ \ \ \ \ \ \ 30000<{{X}_{4,i}}\le 100000 \\ & 0.2+0.2\text{lg}\frac{{{X}_{4,i}}}{3000} \\ & \ \ \ \ \ \ \ \ \ \ 3000<{{X}_{4,i}}\le 30000 \\ & 0.2\text{lg}\frac{{{X}_{4,i}}}{300} \\ & \ \ \ \ \ \ \ \ \ \ \ 1<{{X}_{4,i}}\le 3000 \\ & 0\ \ \ \ \ \ \ \ \ {{X}_{4,i}}\le 1 \\ \end{align} \right. $ | (4) |
为将上述指标进行无量纲化处理,选取假定可能发生的最大台风灾情指标为参考序列U0, 该序列灾害的各单项指标的转换函数值皆为1,即假设其属于标准的巨灾。计算各灾害指标的转换函数值序列U(Xm, i)与参考序列U0的关联度(接近)系数,运用等权重法计算出综合关联度,据此划分灾害综合等级。
参照杨仕生(1997)提出的灰色关联系数的定义方法,引入比较序列与参考序列各项指标间的关联系数为:
| $ {{\lambda }_{0i}}\left(i \right)=\frac{1}{1+{{\Delta }_{0i}}\left(i \right)} $ | (5) |
式中,Δ0i(i)=|U0(x0i)-U(xmi)|,m=1,2,…, M; i= 1,2,…,I。Δ0i(i)表示参考序列U0与比较序列U的第m项灾情指标的第i个绝对差值,绝对差值越大,说明该单项指标与参考序列中的同项指标的距离就大,则关联系数就小;反之,关联系数就越大。关联系数的取值区间为[0.5, 1]。
在参照以上灰色关联分析方法对台风灾害的各单项指标与单项巨灾指标的关联系数量化和排序的分析基础上,为将每一比较序列各项指标的关联系数集中在一个值上, 采用等权处理的平均值法计算综合关联度:
| $ {{a}_{0i}}=\frac{1}{M}\sum\limits_{m=1}^{M}{{{\lambda }_{0i}}\left(i \right)} $ | (6) |
故此,用综合关联度的取值来划分灾害等级(表 1)。将综合关联度从大到小进行排序, 即可以得到各次灾情轻或重的比较关系。
|
|
表 1 关联度与灾害等级的对应关系 Table 1 Relationship between association degree and disaster grade |
2012年,在运用上述模型对后续台风灾害进行综合等级评估工作中发现,房屋损坏数目在很多台风灾害案例中不再统计,而仅统计倒塌房屋数目,使得灾情数据获得出现短缺。因此,在原来该项指标转换函数基础上,根据相关专家建议,将原来模型中的倒损(倒塌+损坏)房屋指标改为纯粹的倒塌房屋数,并根据统计分析得出历史台风灾害中房屋倒塌数量约为损坏房屋数量四分之一的平均关系特征,重新界定了房屋倒塌指标的分级标准(表 2),并重新设计了房屋倒塌指标的转换函数[式(7)],其他灾情指标转换函数仍沿用原来设定方法计算。
|
|
表 2 台风灾害中倒塌房屋数目分级标准 Table 2 Grade standard of number of houses collapsed by typhoon in China |
根据表 2给出的分级标准,为将房屋倒塌灾害指标进行归一化处理,将式(4)进行改进如下(X4, i为倒塌房屋数,单位:间):
| $ U\left(4, i \right)=\left\{ \begin{align} &1\ \ \ \ \ \ \ \ \ \ \ \ \ 250000<{{X}_{4, i}} \\ &0.8+\frac{1}{4750000}\text{ }({{X}_{4, i}}-50000) \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ 50000<{{X}_{4, i}}\le 250000\text{ } \\ &0.6+\frac{1}{150000}({{X}_{4, i}}-20000)\text{ } \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ 20000<{{X}_{4, i}}\le 50000\text{ } \\ &0.4+\text{ }\frac{1}{75000}({{X}_{4, i}}-5000)\text{ } \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 5000<{{X}_{4, i}}\le 20000\text{ } \\ &0.2+\frac{1}{22500}\text{ }({{X}_{4, i}}-500)\text{ } \\ &\ \ \ \ \ \ \ \ \ 500<{{X}_{4, i}}\le 5000\text{ } \\ &\frac{{{X}_{4, i}}}{2500}\ \ \ \ \ \ \ \ \ 1<{{X}_{4, i}}\le 500\text{ } \\ &0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{X}_{4, i}}\le 1 \\ \end{align} \right. $ | (7) |
由于通货膨胀、物价上涨的原因,同等强度的台风损坏相同生产资料、产品、资产所造成的经济损失会有较大的差异。而这种差异,并不是由于台风自身的强度大小为主要影响因素造成的。因此,为削弱通货膨胀、物价上涨的影响,对直接经济损失进行去通货膨胀化处理。
居民消费价格指数(consumer price index,CPI)是反映与居民生活有关的产品及劳务价格统计出来的物价变动指标,通常作为观察通货膨胀水平的重要指标。全国CPI涵盖全国城乡居民生活消费的食品、烟酒及用品、衣着、家庭设备用品及维修服务、医疗保健和个人用品、交通和通信、娱乐教育文化用品及服务、居住等八大类,包括262个基本分类的商品与服务价格。
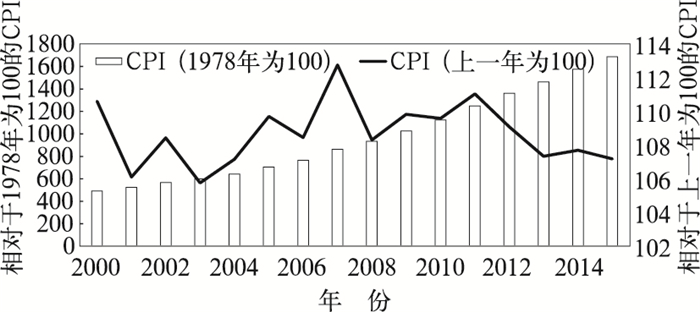
图 1即为反映我国2000—2015年CPI变化水平的图(图中所示以1978年为定基的CPI与以上一年为100的CPI数据均摘录自中国统计局官网“2016年中国统计年鉴”)。
|
图 1 2000—2015年中国CPI变化趋势 Fig. 1 Variation trend of CPI in China from 2000 to 2015 |
由图 1可以看出,自2000年始,我国的物价水平在以不低于6%的比率上升。2015年的物价水平近似于2000年的4倍。其背后隐含的是人民的消费水平、收入水平均大幅上升,对灾害造成的经济损失的承受水平也水涨船高。可见,在通过经济损失来衡量台风灾害水平的时候,去除通货膨胀是十分必要的。此方法与雷小途等(2009)划分灾情等级时的研究思想一致。
本研究选取2000年为基准年,以2000年为基准的当年CPI=以1978年为基准的当年CPI/以1978年为基准的2000年CPI。
那么,本研究中的去通货膨胀的可比较的台风直接经济损失数据计算公式为:X2, i=直接经济损失/以2000年为基准的当年CPI指数。
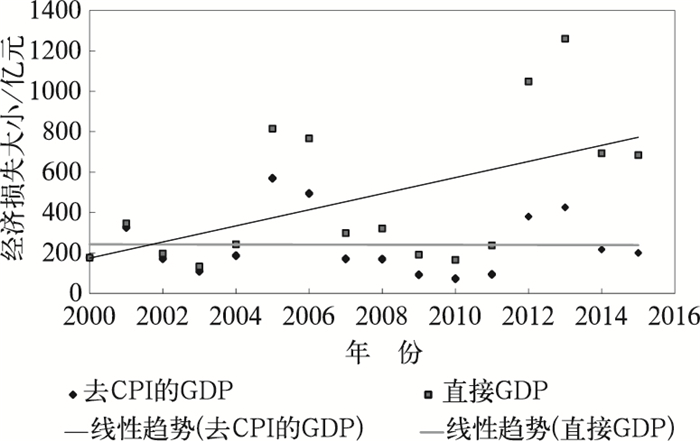
将2000—2015年登陆我国的台风逐年造成的累计直接经济损失和逐年的去CPI的累计直接经济损失绘制成图 2,通过图 2的对比,可以明显发现去CPI的逐年经济损失趋势近似于一条水平线,而逐年直接经济损失的趋势线是一条向上的斜线,且离散度更高。因为目前没有研究表明台风强度有逐年加强的趋势,明显去CPI的经济损失数值更贴合实际,能更好地揭示经济损失与台风灾害级别间的关系。
|
图 2 2000—2015年逐年因台风造成的直接经济损失与去CPI的经济损失逐年比较 Fig. 2 Comparison between direct economic loss per year and economic loss without CPI per year from 2000 to 2015 |
考虑到死亡人数指标为灾害损失评价中的最重要指标, 直接经济损失指标次之,而倒塌房屋指标以及农作物受灾面积指标与直接经济损失指标有交叉反应。因此,运用经验法以及专家咨询的方式,并经过多次计算调试,确定了综合关联度计算中死亡人数、直接经济损失、倒塌房屋、农作物受灾面积各项指标权重Km(m=1~4)分别为0.4、0.3、0.15、0.15。
根据以上分析,将式(6)中的综合关联度指数a0i计算方法改进为:
| $ {{a}_{0i}}=\frac{1}{4}\times \sum\limits_{m=1}^{4}{{{K}_{m}}{{\lambda }_{0i}}} $ | (8) |
用改进后的灾害综合等级评判模型对2000—2015年登陆我国的128个台风灾情[灾情数据来自中国气象灾害年鉴及全国气候影响评价(中国气象局,2000—2004;2005—2016)]进行分析。首先将登陆台风造成的死亡人数、去CPI的直接经济损失、农作物受淹面积、房屋倒塌数目4个灾害指标序列分别代入式(1)、式(2)、式(3)、式(7)进行函数转化,得到转换后的比较序列矩阵U(Xm, i);然后再运用式(5)计算其与参考序列的关联系数λ0, i;后将其代入式(8),最后得到每一次台风的综合关联度指数,也即是台风灾害综合等级评判指数, 然后依据表 3评判出每个台风的灾害综合等级。
|
|
表 3 改进模型与原模型对2000—2015年登陆我国台风等级划分结果对比 Table 3 Comparison of the results about different typhoon disaster classification from 2000 to 2015 analyzed by improved model and original model |
表 3给出了分别运用改进模型和原模型对2000—2015年登陆我国的台风灾害等级评判结果。改进模型评判结果可见,2000—2015年这16年间,共有4个特大灾、20个大灾、29个中灾、45个小灾、30个微灾,其中特大灾分别为0604号台风碧利斯、0608号台风桑美、0513号台风泰利、0414号台风云娜;原模型评判得出的特大灾1个(0604号台风碧利斯),大灾23个、中灾59个、小灾37个、微灾8个。
3.2 评判结果检验分析通过表 3的评判结果综合分析可见,模型改进后明显消弱了经济通货膨胀的影响,并在灾害评估过程中突出了以人为本的防灾减灾理念。
选取4个特大台风灾害以及2个比较典型的灾情较轻的台风案例来进行分析。从表 4可见,之所以改进后的模型将0604号台风碧利斯、0608号台风桑美、0513号台风泰利以及0414号台风云娜均被评判为特大灾,是因为此4个台风除了造成较为严重的直接经济损失和其他灾害以外,均造成了严重的人员死亡,分别为843、583、148、186人;而在原模型评判结果中,将“泰利”、“桑美”、“云娜”均化成大灾,且原模型中将“泰利”综合灾情等级排序为第二,而将“桑美”排序为第三(改进后“桑美”综合灾情等级排序第二,“泰利”为第三),显然也没有突出人员伤亡在灾情评判中的权重。再分析1321号台风蝴蝶和1521号台风杜鹃的各项灾情指标可见,“蝴蝶”虽然在原模型和改进模型输出结果中灾害等级均为小灾,但在原模型中历史排序为第108位,改进模型后历史排序上升为第78位,这是由于台风蝴蝶造成了62人死亡;对于1521号台风杜鹃,其造成了7.8万间房屋倒塌,但没有其他灾害损失,因此原模型评定为中灾,排序第78位,改进后模型评定为小灾,排序下降为第86位。
|
|
表 4 台风灾害典型案例及等级评判比对 Table 4 Comparison of typical typhoon disasters and their classification |
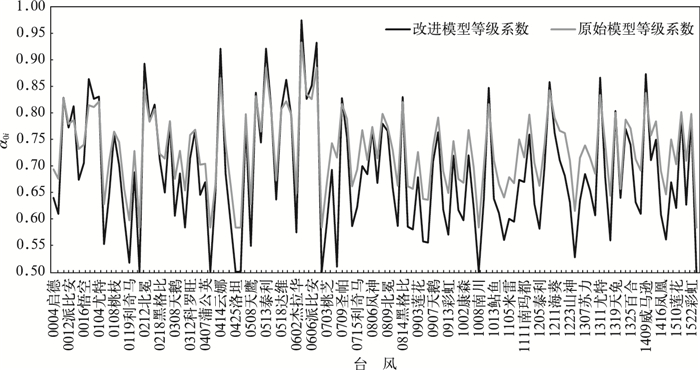
为进一步分析改进模型的优越性以及与原模型所得等级系数间的异、同,将两种模型输出的综合关联度指数(即等级指数)进行趋势比对(图 3)。
|
图 3 改进模型关联度指数与原模型关联度指数比较 (横坐标中由于空间限制,没有列出全部台风名称) Fig. 3 Comparison of correlation indices of improved model and original model (Since the space on abscissa is limited, the typhoon names are not shown completely) |
从图 3可明显看出,改进后模型和原模型两者之间具有非常相似的走势和分布状态。因此,改进模型可以有效地沿用原模型的“关联度与灾害等级对应关系”;同时,从图中观察可以发现改进模型结果具有更高的离散度。通过对原始模型得出的关联度序列与改进模型得出的关联度序列进一步数据分析得出,原始模型128个关联度数据方差为0.0054,改进模型128个关联度数据方差为0.0119,验证了观察结果。这表明,在同样能满足不同台风强弱程度的对比需要下,改进模型具有更好的分辨度,有益于台风灾害影响的分级划分。
另外,从前面表 3可见,改进后的模型较原模型输出结果增加了3个特大灾害、8个小灾和22个微灾,减少了3个大灾和30个中灾,既在灾害等级强度大、小两头增加了,而位于中间的灾害等级减少,也从另一角度验证了以上所说的改进后模型较原模型具有更好的灾害等级分辨度这一结论。
4 结论本研究中对原模型进行了如下改进,一是将倒损房屋指标替换为倒塌房屋指标,重新设计该项指标归一化处理的转化函数;二是在直接经济损失灾害指标中去除了通货膨胀因素,三是重新设计四个灾情指标在台风灾害综合等级计算时的权重系数。
利用改进的台风灾害综合等级评定模型,对2000—2015年登陆我国的历史台风灾害进行综合等级评定及历史排序,并结合原模型输出结果及实际台风灾情信息等对改进模型进行了检验分析。
通过检验证明,改善后的模型较原模型具备以下优点:一是改进模型明显消弱了经济通货膨胀,从而降低了原模型中直接经济损失比重过高对灾情综合等级评判的影响;二是改进后模型在灾害评估过程中通过调节各个灾情指标的权重系数更突出了以人为本的防灾减灾理念;三是改进后模型较原模型对灾害大小具备了更高的分辨度。
从上述分析可以看出,改进后模型较原模型能对历史台风灾害综合等级做出更客观、合理的评判;利用该模型,根据统计得到的各单项台风灾情指标,可快速分析输出某次台风灾害的综合等级划分结果,并能和历史上不同台风灾害个例进行排序比较(包括同一等级内的比较和不同等级内的比较)。
基于目前的业务需求,该模型可以用于历史台风灾害案例分析入库存档;模型输出结果可以试用于国家级台风气象服务业务中制作台风灾害综合等级的定量评价产品。另外,参照该模型的灾害综合评估的思路, 也可以建立其他不同气象灾种、不同地区范围的灾害综合等级评估模型。
雷小途, 陈佩燕, 杨玉华, 等, 2009. 中国台风灾情特征及其灾害客观评估方法[J]. 气象学报, 67(5): 875-883. DOI:10.11676/qxxb2009.085 |
梁必骐, 樊琦, 杨洁, 等, 1999. 热带气旋灾害的模糊数学评价[J]. 热带气象学报, 15(4): 305-311. |
刘少军, 张京红, 何政伟, 等, 2010. 基于GIS的台风灾害损失评估模型研究[J]. 灾害学, 25(2): 64-67. |
马清云, 李佳英, 王秀荣, 等, 2008. 基于模糊综合评价法的登陆台风灾害影响评估模型[J]. 气象, 34(5): 20-25. DOI:10.7519/j.issn.1000-0526.2008.05.004 |
钱燕珍, 何彩芬, 杨元琴, 等, 2001. 热带气旋灾害指数的估算与应用方法[J]. 气象, 27(1): 14-18, 24. DOI:10.7519/j.issn.1000-0526.2001.01.003 |
石蓉蓉, 雷媛, 王东法, 等, 2008. 1949—2007年影响浙江热带气旋灾情分析及评估研究[J]. 科技通报, 24(5): 612-616. |
石先武, 国志兴, 林国斌, 等, 2017. 河北省风暴潮灾害风险评估研究[J]. 灾害学, 32(2): 85-89. |
孙峥, 庄丽, 冯启民, 2007. 风暴潮灾情等级识别的模糊聚类分析方法研究[J]. 自然灾害学报, 16(4): 49-54. |
王秀荣, 王维国, 马清云, 2010. 台风灾害综合等级评估模型及应用[J]. 气象, 36(1): 66-71. DOI:10.7519/j.issn.1000-0526.2010.01.010 |
杨仕升, 1997. 自然灾害等级划分及灾情比较模型探讨[J]. 自然灾害学报, 6(1): 8-13. |
姚棣荣, 刘孝麟, 2001. 浙江省热带气旋灾情的评估[J]. 浙江大学学报(理学版), 28(3): 344-348. |
叶雯, 2002. 广东省台风灾害特点及减灾对策[J]. 灾害学, 17(3): 54-59. |
于小龙, 潘伟然, 张国荣, 等, 2011. 福建省台风灾害直接经济损失预评估模型[J]. 厦门大学学报(自然科学版), 50(6): 1047-1052. |
章国材, 2006. 防御和减轻气象灾害——2006年世界气象日主题[J]. 气象, 32(3): 3-5. DOI:10.7519/j.issn.1000-0526.2006.03.001 |
中国气象局, 2000. 2000—2004.全国气候影响评价[M]. 北京: 气象出版社.
|
中国气象局, 2005. 2005—2016.中国气象灾害年鉴[M]. 北京: 气象出版社.
|
Saffir H S, 1972. The Nature and Extent of Structural Damage Caused by Hurricane Camille[M]. Washington, D C: National Oceanic and Atmospheric Administration. http://www.researchgate.net/publication/291321798_THE_NATURE_AND_EXTENT_OF_STRUCTURAL_DAMAGE_CAUSED_BY_HURRICANE_CAMILLE
|
Simpson R H, 1974. The hurricane disaster-potential scale[J]. Weatherwise, 27(4): 169-186. DOI:10.1080/00431672.1974.9931702 |
 2018, Vol. 44
2018, Vol. 44 