2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081;
3. 南京大学,南京 210023;
4. 山西省朔州市气象局,朔州 036000
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Nanjing University, Nanjing 210023;
4. Shuozhou Meteorological Office of Shanxi Province, Shuozhou 036000
20世纪60—70年代,科学家们提出许多利用地基多普勒雷达径向速度资料反演雷达站上空平均风场信息的方法。Lhermitte and Atlas(1961)在水平风场均匀的假设下首次提出了速度方位显示技术(简称VAD技术),利用正余弦函数拟合等距离圈径向速度,计算雷达站上空平均水平风垂直廓线;Caton(1963)、Browning and Wexler(1968)在Lhermitte等人的基础上,在水平风场线性假设下得到雷达站上空各高度层平均水平风、平均散度以及平均变形。Srivastava et al(1985)与Matejka and Srivastava(1991),Matejka(1993)改进了VAD技术在高仰角计算平均散度误差较大的缺点。
传统VAD技术获得的雷达站上空平均水平风垂直廓线(即VWP)在降水系统发生发展实时监测、模式资料同化中得到广泛应用, 但径向速度模糊是影响其应用质量的一个因素(Collins, 2001;Germann, 1999;Yamada and Chong, 1999)。Tabary et al (2001)针对传统VAD技术受速度模糊影响较大的现象,提出利用径向速度方位梯度而不是径向速度反演雷达站上空平均风垂直廓线,该技术又称梯度VAD技术。Gao and Droegemeier(2004)进一步改进了GVAD技术,排除了计算中的人为阈值设置因素。本文首先理论描述了GVAD技术,进而研究了其在新一代天气雷达中的应用。
1 GVAD技术天气雷达径向速度资料Vr为空气速度(u, v, w)、粒子下落速度wt在径向上分量合成。
| $ \begin{array}{l} {V_r} = u\cos \theta \sin \phi + \upsilon \cos \theta \cos \phi + \\ \;\;\;\;\;\;\;\;\left({w - {w_t}} \right)\sin \theta \end{array} $ | (1) |
式中,θ为仰角,ϕ为方位角。
在水平风场线性假设下,传统VAD技术傅里叶级数拟合等距离圈上径向速度Vr,一阶系数a1=u0cosθ,b1=v0cosθ,式中u0, v0即为欲求雷达站上空平均速度分量(Doviak and Zrnic, 1984;Fabry, 1993)。
GVAD技术为等距离圈径向速度方位梯度拟合,因此其傅里叶展开式为
| $ \begin{array}{l} \frac{{\partial {V_r}}}{{\partial \phi }} = - {a_1}^\prime \sin \phi + {b_1}^\prime \cos \phi - 2{a_2}^\prime \sin 2\phi + \\ \;\;\;\;\;\;\;\;\;2{b_2}^\prime \cos 2\phi \end{array} $ | (2) |
式中,a1′=u0cosθ,b1′=-v0cosθ。
Gao et al(2004)利用低通滤波方法减弱噪声对径向速度方位梯度影响,如下式
| $ \left({\frac{{\partial {V_r}}}{{\partial \phi }}} \right)_{ob}^j = \sum\limits_{j = k - N/2}^{k + N/2} {{W_j}} \left({\frac{{\partial {V_r}}}{{\partial \phi }}} \right)_{ob}^j/\sum\limits_{j = k - N/2}^{k + N/2} {{W_j}} $ | (3) |
式中,N为滤波中径向速度方位梯度个数,Wj权重函数表达式为式(4):
| $ {W_j} = 1 - \frac{{ABS\left({j - k} \right)}}{N} $ | (4) |
式中,ABS代表求绝对值。
模拟理想均匀风场,理论分析GVAD技术在速度模糊中的应用。假设均匀风场风速20 m·s-1,最大不模糊速度为12 m·s-1,方位间隔1°,并加入随机噪声。
图 1为GVAD与传统VAD方法拟合模拟速度模糊径向速度方位资料。其中黑色线为径向速度Vr,方位大约0°~60°、130°~230°、300°~360°径向速度大于12 m·s-1时,出现速度模糊,若无速度模糊,均匀风场径向速度方位显示应为余弦曲线,锯齿状小波动为加入的随机噪声;红色线为传统VAD方法拟合,可见由于速度模糊,传统VAD方法并不能拟合出模拟均匀风场无速度模糊径向速度方位资料;而绿色GVAD方法拟合线可以在不退速度模糊的情况下,很好拟合出模拟均匀风场无速度模糊径向速度方位资料。
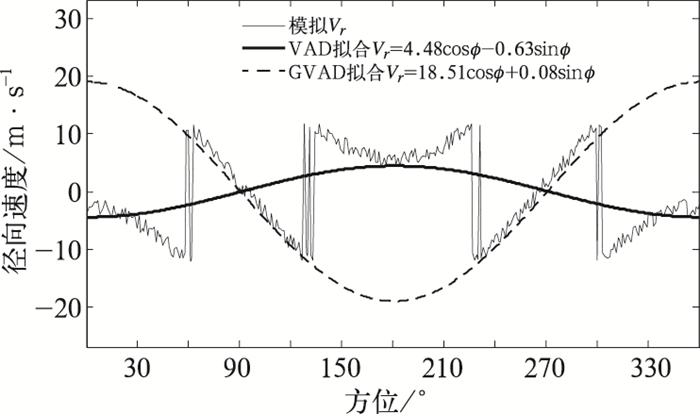
|
图 1 GVAD与传统VAD方法拟合模拟速度模糊径向速度方位资料 Fig. 1 The fitting of simulation of radial velocity aliasing by GVAD and VAD |
图 2为GVAD中径向速度梯度拟合。小圆圈代表径向速度梯度,可见随机噪声的添加使径向速度梯度值跳变明显,但低通滤波后(红色线表示),梯度值跳变减弱,梯度拟合可以拟合出理想的正余弦曲线,可见在此模拟个例中,随机噪声对GVAD技术计算影响不大。
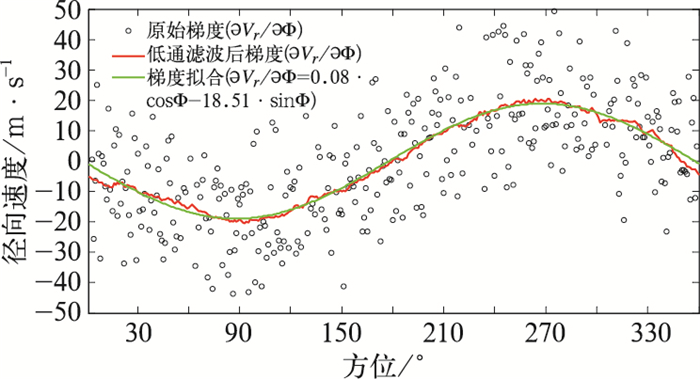
|
图 2 径向速度的原始梯度低通滤波和梯度拟合 Fig. 2 Original gradient low-pass filter and gradient fitting for radial velocity |
在模拟速度模糊均匀风场中,GVAD技术可有效反演出雷达站上空平均水平风,而传统VAD技术受速度模糊影响大。以下分析GVAD技术在新一代天气雷达速度模糊资料中的应用。
2 GVAD技术在新一代天气雷达中的应用 2.1 台风尤特实例应用2013年8月14日15:50台风尤特在广东省阳西附近沿海登陆,登陆时中心附近最大风力42 m·s-1。图 3为阳江SA波段雷达于14日01时对台风监测的2.4°仰角径向速度图,此时台风眼距离雷达站约100 km左右,基本满足VAD反演雷达站上空风场线性假设。阳江雷达最大不模糊速度为±27 m·s-1(俞小鼎等,2006),在图 3中黑色箭头所指为径向速度模糊区域(张培昌等,2001;王彦等,2008)。
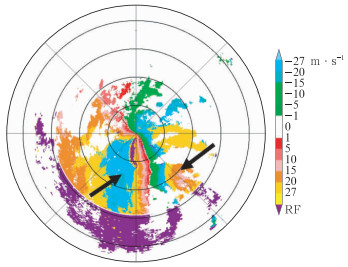
|
图 3 2013年8月14日01时阳江雷达监测台风尤特2.4°仰角径向速度 (黑色箭头所指为径向速度模糊区域) Fig. 3 Radial velocity of Typhoon Utor monitoring by 2.4° elevation of Yangjiang Weather Radar at 01:00 BT 14 August 2013 (Black arrow indicates the area of radial velocity aliasing) |
图 4为GVAD技术与传统VAD技术反演图 3对应时间阳江雷达站上空各高度层风速、风向。传统VAD技术就速度模糊与退速度模糊后资料分别进行了计算(实例中,GVAD技术在选择每个高度层距离圈时,与VAD技术一致,选择与等高面相交的斜距最接近30 km的仰角,如0.6 km等高面,选择0.5°仰角,该仰角到0.6 km等高面的斜距与其他仰角相比更接近30 km)(俞小鼎等,2006;朱丽娟等,2012)。

|
图 4 2013年8月14日01时阳江雷达监测尤特台风GVAD方法(红色)与VAD方法(黑色)反演风速(a, c)、风向(b, d)垂直廓线对比 (a)未退速度模糊反演风速,(b)未退速度模糊反演风向,(c)退速度模糊反演风速,(d)退速度模糊反演风向 Fig. 4 The contrast between GVAD fitting (red) and VAD fitting (black) for Typhoon Utor monitoring by Yangjiang Weather Radar at 01:00 BT 14 August 2013 (a) inversion speed without velocity aliasing, (b) inversion direction without velocity aliasing, (c) inversion speed with velocity dealiasing, (d) inversion direction with velocity dealiasing |
图 4a、4b中,传统VAD技术速度模糊资料反演风速、风向(黑色线),可见在4 km高度以下,由于速度模糊无法反演出平均水平风;而GVAD技术则可以得到各高度平均水平风(红色线)。图 4c、4d,传统VAD技术利用退速度模糊后资料反演风速、风向(黑色线),在各高度层都可以计算出平均水平风(除6 km高度外),比较两种VAD技术反演风速风向值,风向值相差不大,但GVAD技术反演风速值较传统VAD技术风速值相对小, 平均偏弱2~3 m·s-1。
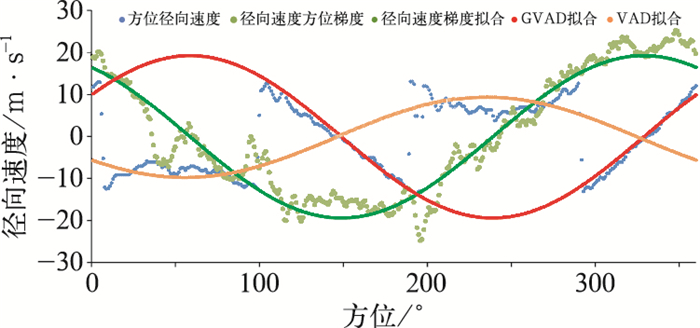
详细分析两种VAD技术在拟合2.9 km高度速度模糊径向速度方位资料情况(图 5)。在2.9 km高度,径向速度在方位约50°~100°速度模糊,传统VAD技术不能很好拟合各方位径向速度,拟合均方根误差太大,因此在图 4中VAD拟合对应2.9 km高度为无效值。径向速度的方位梯度,其在速度模糊方位跳变不明显,GVAD技术拟合径向速度方位梯度,可以较好拟合出各方位径向速度,可见GVAD技术在速度模糊资料中的优势。红色划线为绿色划线平移后GVAD技术最终拟合径向速度曲线。但也注意到,径向速度方位梯度在零径向速度附近(方位约160°、340°)波动较大,这也导致GVAD技术拟合谷峰值较原始径向速度略小。
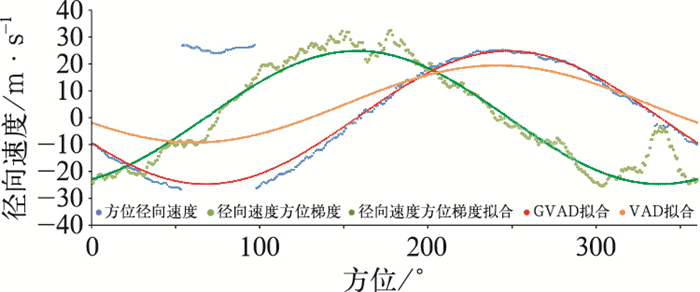
|
图 5 2013年8月14日01时阳江雷达监测台风尤特2.9 km高度径向速度方位资料拟合 (蓝色点线为2.9 km等距离圈方位径向速度,绿色点线为径向速度方位梯度,绿色划线为径向速度梯度拟合,红色划线为GVAD技术拟合,橙色划线为传统VAD技术拟合线) Fig. 5 Azimuth fitting of radial velocity at 2.9 km height for Typhoon Utor monitoring by Yangjiang Weather Radar at 01:00 BT 14 August 2013 (Blue dotted line is radial velocity of equidistance circle, green dotted line is azimuth gradients of radial velocity, green lineation is fitting of radial velocity gradients, red lineation is GVAD fitting result, orange lineation is VAD fitting result) |
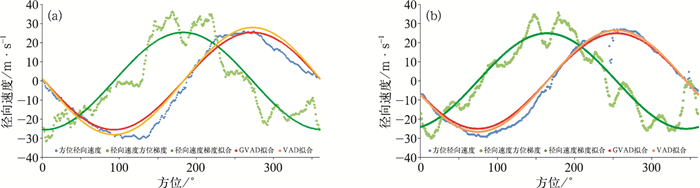
再分析4.3与7.1 km高度GVAD技术拟合(图 6)。由图可见,在4.3与7.1 km高度,没有出现速度模糊现象,径向速度方位梯度较方位径向速度波动大,方位径向速度中的小波动或者噪声会在径向速度方位梯度中放大,进而影响GVAD拟合的准确性。由图 6a与6b可见,GVAD拟合谷峰值较原始径向速度都略小,这也是造成本例中GVAD技术计算风速值较VAD技术风速值略小的原因。
|
图 6 同图 5,但为台风尤特4.3 km高度(a)与7.1 km高度(b)径向速度方位资料拟合 Fig. 6 Same as Fig. 5, but for azimuth fitting of radial velocity at 4.3 km (a) and 7.1 km (b) heights |
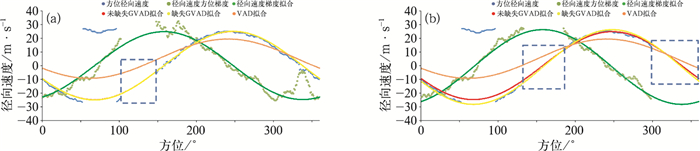
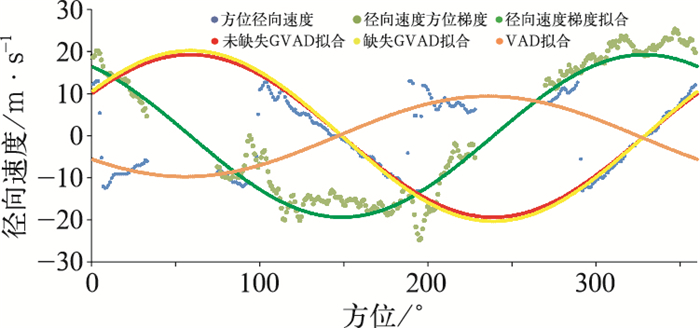
个例中雷达站附近回波面积较大,因此0°~360°方位径向速度较完整。为分析部分径向速度缺失对GVAD技术反演的影响,人为对图 5中2.9 km高度径向速度进行删减,进而进行判断分析(图 7)。
|
图 7 2013年8月14日01时阳江雷达监测台风尤特2.9 km高度模拟分析部分方位缺失对GVAD反演结果的影响 (a)约105°~145°方位缺失, (b)约135°~185°和约300°~360°方位缺失(缺失方位用蓝色方框标出) (蓝色点线为等距离圈方位径向速度,绿色点线为径向速度方位梯度,绿色划线为径向速度梯度拟合,红色划线为未缺失GVAD技术拟合,黄色划线为缺失GVAD技术拟合,橙色划线为VAD技术拟合) Fig. 7 Influence analysis of the lacking of azimuth for GVAD fitting at 2.9 km height for Typhoon Utor monitoring by Yangjiang Weather Radar at 01:00 BT 14 August 2013 (a) lacking azimuth between 105°-145°, (b) lacking azimuth between 135°-185° and between 300°-360° (blue square for lacking direction) (Blue dotted line is radial velocity of equidistance circle, green dotted line is azimuth gradients of radial velocity, green lineation is fitting of radial velocity gradients, red lineation is GVAD fitting result for original azimuth, yellow lineation is GVAD fitting result for lacking azimuth, orange lineation is VAD fitting result) |
图 7a为约105°~145°方位缺失情况,人为删减造成总缺失方位约40°,图中缺失GVAD拟合与未缺失GVAD拟合基本重合,可见方位的缺失并没有影响GVAD技术在速度模糊情况下的反演;图 7b为约135°~185°和约300°~360°方位缺失,人为删减造成总缺失方位约110°,这两个方位为径向速度零速度附近区域,也是造成径向速度梯度波动较大的区域,图中缺失GVAD拟合较未缺失GVAD拟合振幅略大,也就是反演的速度值略大,更贴近退速度模糊后VAD的反演速度值,可见如果部分径向速度方位的缺失使梯度波动减小,反而会提高GVAD反演的精度。
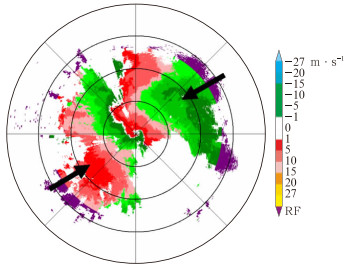
2.2 承德大范围强降水实例应用2013年6月16日承德发生大范围强降水过程,图 8为承德CB雷达于03时监测强降水2.4°仰角径向速度PPI图,承德雷达最大不模糊速度为±13 m·s-1(俞小鼎等,2006),黑色箭头所指为速度模糊区域,可见存在大范围速度模糊区域(张培昌等,2001;周小刚等,2015)。
|
图 8 同图 3,但为2013年6月16日03时承德雷达监测强降水 Fig. 8 Same as Fig. 3, but for heavy precipitation monitoring by of Chengde Weather Radar at 03:00 BT 16 June 2013 |
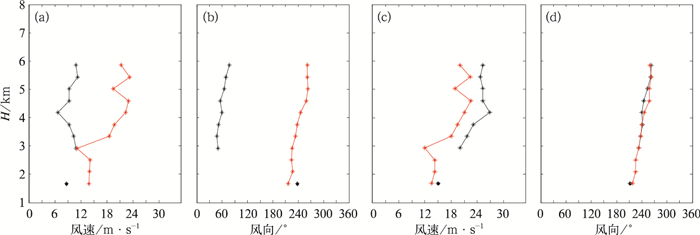
图 9为GVAD技术与传统VAD技术反演图 8对应时间承德雷达站上空各高度层风速、风向。同样,传统VAD技术就速度模糊与退速度模糊后资料分别进行了计算。
|
图 9 同图 4,但为2013年6月16日03时承德雷达监测强降水 Fig. 9 Same as Fig. 4, but for heavy precipitation monitoring by Chengde Weather Radar at 03:00 BT 16 June 2013 |
在台风尤特个例中,传统VAD技术在速度模糊情况下无法反演出低层平均风,而退速度模糊后能正确计算平均风。在本个例中,由图 9分析,传统VAD技术在低层大部分高度速度模糊与退速度模糊后都无法计算出平均风,原因是不满足传统VAD技术计算条件中拟合均方根误差不超过5 m·s-1的条件(俞小鼎等,2006)。而在中层,传统VAD技术在速度模糊情况下计算的风速、风向(图 9a、9b黑色)与退速度模糊后计算的风速、风向(图 9c、9d黑色)相差较大,速度模糊情况下计算的风速值较小,风向与退速度模糊后计算的风向相反,具体原因在下文中分析。GVAD技术计算的风速与台风尤特个例相似,较退速度模糊后传统VAD技术的风速偏小,平均偏弱2~3 m·s-1,风向较一致。
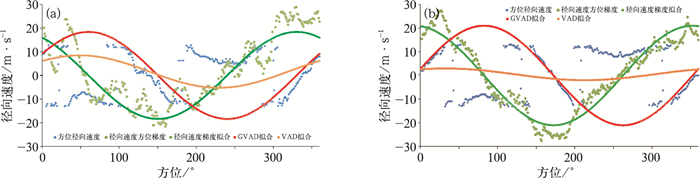
进一步分析两种VAD技术拟合3.3 km高度速度模糊径向速度方位资料(图 10)。在图 10中,径向速度方位约10°~100°与方位约185°~285°速度模糊,由于速度模糊方位太大,传统VAD技术以拟合速度模糊径向速度部分为主,因此反演得到的风向相反,风速值小。径向速度方位梯度受速度模糊影响不大,GVAD技术拟合径向速度方位梯度,可以较好拟合出各方位径向速度,同样可见GVAD技术在速度模糊资料中的优势。但也注意到径向速度方位梯度的波动对GVAD技术的影响。
|
图 10 同图 5,但为2013年6月16日03时承德雷达监测强降水3.3 km高度径向速度方位资料拟合 Fig. 10 Same as Fig. 5, but for azimuth fitting of radial velocity at 3.3 km height for heavy precipitation monitoring by Chengde Weather Radar at 03:00 BT 16 June 2013 |
分析3.7与5.3 km高度GVAD技术拟合,如图 11。在3.7 km(图 11a)与5.3 km(图 11b)高度,方位径向速度中的小波动或噪声同样会在径向速度方位梯度中放大,使径向速度方位梯度产生较大波动,也是造成本例中GVAD技术计算风速值较VAD技术风速值略小的原因。
|
图 11 同图 5,但为2013年6月16日03时承德雷达监测强降水3.7 km高度(a)与5.3 km高度(b)径向速度方位资料拟合 Fig. 11 Same as Fig. 5, but for azimuth fitting of radial velocity at 3.7 km height (a) and 5.3 km height (b) for heavy precipitation monitoring by Chengde Weather Radar at 03:00 BT 16 June 2013 |
同样为分析部分径向速度缺失对GVAD技术反演的影响,人为对图 10中3.3 km高度径向速度进行删减(图 12)。
|
图 12 2013年6月16日03时承德雷达监测强降水3.3 km高度模拟分析部分方位缺失对GVAD反演结果的影响 (缺失方位约35°~75°和约230°~275°,蓝色点线为3.3 km等距离圈径向速度,绿色点线为径向速度方位梯度,绿色划线为径向速度梯度拟合,红色划线为未缺失GVAD技术拟合,黄色划线为缺失GVAD技术拟合,橙色划线为传统VAD技术拟合线) Fig. 12 Influence analysis of the lacking of azimuth for GVAD fitting at 3.3 km height for heavy precipitation monitoring by Chengde Weather Radar at 03:00 BT 16 June 2013 (Lacking azimuth is between 105°-145° and between 300°-360°, blue dotted line is radial velocity of equidistance circle, green dotted line is azimuth gradients of radial velocity, green lineation is fitting of radial velocity gradients, red lineation is GVAD fitting result for original azimuth, yellow lineation is GVAD fitting result for lacking azimuth, orange lineation is VAD fitting result) |
这次人为删减,选择的方位为速度模糊方位,删减约35°~75°和约230°~275°,总删减约85°方位,但仍有速度模糊方位存在。由未缺失GVAD拟合与缺失GVAD拟合对比,拟合线基本重合,可见部分方位的缺失并不影响GVAD技术的反演精度。
3 结论本文就GVAD技术以及其在新一代天气雷达中的应用进行研究分析,从理论上对GVAD技术进行了讨论,再将其应用于一次台风个例与一次大范围强降水个例,初步得到如下结论。
(1) 在模拟个例与两次实际个例中,GVAD技术径向速度梯度拟合较传统VAD技术受速度模糊影响小,可较好反演出水平平均风。
(2) 在两次实际个例中,方位径向速度中的小波动或者噪声会在径向速度方位梯度中放大,尽管利用低通滤波进行了平滑,但其对GVAD技术反演精度影响仍然较大,尤其影响水平风速反演精度,在个例中GVAD技术反演风速较传统VAD技术平均偏弱2~3 m·s-1。同时,个例中模拟部分方位缺失并不影响GVAD技术的反演精度。
方位径向速度中的小波动或者噪声与天气个例以及雷达探测精度有关,需进一步分析大量个例来评估GVAD技术在新一代天气雷达中的应用,研究减少新一代天气雷达径向速度资料中小波动或者噪声对GVAD技术应用影响的方法。
王彦, 吕江津, 周海光, 等, 2008. 暴雨的多普勒天气雷达速度辐合风场特征[J]. 气象, 34(3): 63-68. DOI:10.7519/j.issn.1000-0526.2008.03.010 |
俞小鼎, 姚秀萍, 熊廷南, 等, 2006. 多普勒天气雷达原理与业务应用[M]. 北京: 气象出版社.
|
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学[M]. 北京: 气象出版社.
|
周小刚, 费海燕, 王秀明, 2015. 基于多普勒雷达VAD算法的业务应用讨论[J]. 气象, 41(1): 113-120. |
朱丽娟, 龚建东, 李泽椿, 等, 2012. 利用地面观测资料参考标定雷达VAD资料气压高度方法研究[J]. 气象, 38(2): 250-256. |
Browning K A, Wexler R, 1968. The determination of kinematic properties of a wind field using Doppler radar[J]. J Appl Meteor, 7(1): 105-113. DOI:10.1175/1520-0450(1968)007<0105:TDOKPO>2.0.CO;2 |
Caton P G F, 1963. Wind measurement by Doppler radar[J]. Meteor Mag, 92: 213-222. |
Collins W G, 2001. The quality control of velocity azimuth display (VAD) winds at the national centers for environmental prediction[C]//Proceedings of the 11th Symposium On Meteorological Observations and Instrumentation. Albuquerque, NM: American Meteor Society: 317-320.
|
Doviak R J, Zrnic D S, 1984. Doppler Radar and Weather Observations[M].
Orlando: Academic Press, 458.
|
Fabry F, 1993. Wind-profile estimation by conventional radar[J]. J Appl Meteor, 32(1): 40-49. DOI:10.1175/1520-0450(1993)032<0040:WPEBCR>2.0.CO;2 |
Gao J D, Droegemeier K K, 2004. A variational technique for dealiasing Doppler radial velocity data[J]. J Appl Meteor, 43(6): 934-940. DOI:10.1175/1520-0450(2004)043<0934:AVTFDD>2.0.CO;2 |
Gao J D, Droegemeier K K, Gong J D, et al, 2004. A method for retrieving mean horizontal wind profiles from single-Doppler radar observations contaminated by aliasing[J]. Mon Wea Rev, 132(6): 1399-1409. DOI:10.1175/1520-0493-132.1.1399 |
Germann U, 1999. Vertical wind profile by Doppler radars[C]//MAP Newsletter. Zurich, Switzerland: Swiss Meteorological Institute: 11.
|
Lhermitte R M, Atlas D, 1961. Precipitation motion by pulse Doppler radar[C]//Proceedings of the 9th Weather Radar Conference. Boston: American Meteor Society: 218-223.
|
Matejka T J, 1993. Concurrent extended vertical velocity azimuth display(CEVAD)[C]//Proceedings of the 26th Int. Conf. on Radar Meteorology. Norman, OK: American Meteor Society: 463-465.
|
Matejka T J, Srivastava R C, 1991. An improved version of the extended velocity-azimuth display analysis of single-Doppler radar data[J]. J Atmos Oceanic Technol, 8: 453-466. DOI:10.1175/1520-0426(1991)008<0453:AIVOTE>2.0.CO;2 |
Srivastava R C, Matejka T J, Lorello T J, 1985. Doppler radar study of the trailing anvil region associated with a squall line[J]. J Atmos Sci, 43(4): 356-377. |
Tabary P, Scialom G, Germann U, 2001. Real-time retrieval of the wind from aliased velocities measured by Doppler radars[J]. J Atmos Oceanic Technol, 18(6): 875-882. DOI:10.1175/1520-0426(2001)018<0875:RTROTW>2.0.CO;2 |
Yamada Y, Chong M, 1999. VAD-based determination of the Nyquist internal number of Doppler velocity aliasing without wind information[J]. J Meteor Soc Jpn, 77(2): 447-457. DOI:10.2151/jmsj1965.77.2_447 |
 2018, Vol. 44
2018, Vol. 44 
