引言

随着经济的发展，大气污染物的排放逐渐增多，空气污染问题日益突出，其中细颗粒物(PM_2.5)是影响空气质量的主要大气污染物，对能见度和人类健康有很大的影响(谢元博等，2014)。上海作为中国超大城市之一，市民对空气质量的关注度越来越高。

气象条件是影响PM_2.5浓度的最主要原因之一(张人禾等，2014；Flocas et al，2009；于庚康等，2015；郭蕊等，2016)，研究表明大气污染过程主要由上游污染物的输送和本地扩散条件较差引起的污染物累积两方面因素造成(王跃思等，2014；李零军等，2012；赵敬国等，2015)。国内外很多学者提出了一些空气污染气象指数，用来反映大气扩散条件对空气质量的影响。Allwine and Whiteman(1994)提出了滞留指数的概念，主要利用局地风场的时间变化来反映大气的水平扩散条件，计算表明滞留指数在一定程度上可以反映大气的静稳和通风状况。杨勇杰等(2006)通过对上海地区近15年的大气稳定度和混合层高度分析后发现，大气稳定度有明显的日变化和季节变化，夏季和白天不稳定性相对较大，大气的垂直扩散能力较强。Pasch et al(2011)研究发现，混合层高度越高、边界层内风速越大，大气通风效果越好，PM_2.5浓度则相对较低。有关学者(Wu et al，2013；吴蒙等，2015；王淑云等，2006)通过重污染天气过程的气象条件研究后同样发现，不利的天气形势会导致大范围持续的重污染过程，较小的通风系数不利于污染物的扩散，同时低层逆温引起的垂直扩散能力减小是导致重污染天气的重要原因。针对上游污染输送过程，需要确定输送源区和路径(王茜，2013；陈朝晖等，2008), 张磊等(2013)和王爱平等(2014)通过后向轨迹的滞留时间和污染物排放强度场，设计了可以评估污染物平流传输的输送强度参数。花丛等(2016)在此基础上通过对2013—2015年冬半年北京重污染天气气象传输条件分析后构建了传输气象指数，并发现与PM_2.5浓度的生消变化有较好的一致性。这些研究均能在一定程度上表征污染物的输送强度，但未能表现上游实时污染浓度对下游的影响。

上海地处华东中部，东部沿海，西部与江苏和浙江两省相邻，位于长三角核心地区，人口密集，工业生产等人类活动会产生大量的污染物。现有研究大都利用典型个例分析重污染天气过程的污染气象条件，而对空气污染气象指数的研发及在本地的适用性研究则相对较少，本研究主要利用常规气象资料研发了一些适合长三角地区的能够反映大气扩散条件的空气污染气象指数，并进一步探讨了这些空气污染气象指数在上海地区的适用性，并优化了空气污染气象指数，对空气污染预报方面起到技术支撑作用。

1 资料与方法

本文所采用的PM_2.5浓度资料来源于“全国城市空气质量实时发布平台”发布的逐小时数据(http://113.108.142.147:20035/emcpublish/)。气象数据来源于上海地区11个国家级地面观测站的常规观测数据。

滞留指数(RF)最初由Allwine and Whiteman(1994)提出，通过风场的变化特征，反映风场的通风和滞留程度，从而可以间接反映大气的水平扩散条件。当RF值(数值范围为0~1)趋于0时，表示一段时间内风向趋于一致，水平扩散条件较好，不利于本地污染物的堆积；当RF值趋于1时，表示一段时间内风向变化较大，风力较小，水平扩散条件较差，污染物容易滞留，其计算公式如下：

$ RF = 1 - \frac{{\sqrt {{{(\Delta T\sum\limits_{{i_{\rm{s}}}}^{{i_{\rm{e}}}} {{u_i}})}^2} + {{(\Delta T\sum\limits_{{i_{\rm{s}}}}^{{i_{\rm{e}}}} {{v_i}})}^2}} }}{{\Delta T\sum\limits_{{i_{\rm{s}}}}^{{i_{\rm{e}}}} {\sqrt {u_i^2 + v_i^2} } }} $

(1)

式中，u和v为速度分量，单位：m·s^-1；i_s为起始时间，单位：h；i_e为终止时间，单位：h；ΔT为时间间隔(本文所选时间间隔为1 h)。

混合层高度可以反映污染物在垂直方向上的扩散水平(李梦等，2015)，混合层高度越高，越有利于污染在垂直方向的扩散。混合层高度的计算方法较多(程水源等，1997)，其中罗氏法综合了热力和动力因素对混合层高度的影响，且在计算过程中考虑了地面粗糙度，对于局地混合层高度的计算效果较好，因此本文在计算混合层高度主要采取罗氏法。

$ H = \frac{{121}}{6}\left({6 - P} \right)(T - {T_{\rm{d}}}) + \frac{{0.169P({U_Z} + 0.257)}}{{12f{\rm{ln}}(Z/{Z_0})}} $

(2)

式中，H为混合层高度，单位：m；P为帕斯奎尔稳定度级别的取值(程水源等，1997)；(T-T_d)为温度露点差，单位：℃；U_Z为Z高度处所观测的平均风速(本文选取地面10 m风速)，单位：m·s^-1；Z₀为地面粗糙度；f为地转参数。

国内外一些学者构建了一些适用于本地的输送指数，主要思想是根据后向轨迹经过区域的污染在一定的时间衰减和距离衰减后到达终点的输送强度的累加，主要公式如下：

$ \begin{array}{l} {T_l}\left( {i,j} \right) = {R_l}\left( {i,j} \right){E_l}\left( {i,j} \right){W_d}\left( {i,j} \right) \times \\ {W_{{\rm{t}}l}}\left( {i,j} \right)PSCF \end{array} $

(3)

$ {W_d}\left({i, j} \right) = 1/[\frac{{d\left({i, j} \right)}}{5} + 1] $

(4)

$ {W_{{\rm{t}}l}}\left({i, j} \right) = 1/[\frac{{{t_l}\left({i, j} \right)}}{{18}} + 1] $

(5)

式中，T_l为输送强度; R_l为输送概率[轨迹l在网格(i, j)内的停留时间占总时间的比例]；E_l为PM_2.5排放强度；W_d为距离权重函数(权重随着输送距离的增加而减小)，式(4)中d代表网格(i, j)与观测点的距离；W_tl为时间权重函数(权重随着输送时间的增加而减小)，式(5)中t_l为网格(i, j)移动到观测点所需要的时间；PSCF为潜在源贡献因子；下标l和(i, j)为轨迹和网格(花丛等，2016)。

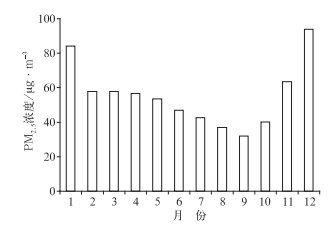
2 上海市空气质量概述

表 1给出了2013—2015年共1095 d上海PM_2.5污染等级分布情况，其中优和良日数共862 d，占总数的78.72%，污染日数共233 d，占总数的21.28%。图 1给出了2013—2015年上海PM_2.5浓度的逐月平均，冬季上海地区PM_2.5浓度较高，污染相对严重；夏季PM_2.5浓度较低，空气相对清洁。通过分析发现上海的重污染主要为静稳累积型和冷空气输送型。静稳累积型污染持续时间较长，时间变化表现为PM_2.5浓度缓慢上升，空间上常出现大范围污染区。冷空气输送型污染持续时间相对较短，时间变化表现为PM_2.5浓度迅速上升，峰值浓度较高。下面本文将根据不同类型对研发的空气污染气象指数在上海地区的适用性进行检验。

3 静稳条件下空气污染扩散指数

对2013—2015年上海地区PM_2.5浓度统计后发现，有、无降水时PM_2.5平均浓度分别为35.35和63.85 μg·m^-3，可见降水对PM_2.5的冲刷作用明显，因此本研究排除了降水日。

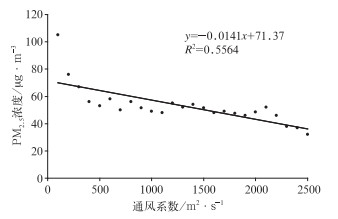
通过计算发现上海地区白天和夜间的混合层高度差别较大，白天的混合层平均高度为940 m，夜间的混合层平均高度为527 m，白天的混合层高度明显较高。因此分白天和夜间分别计算2013—2015年的上海地区通风系数，对比PM_2.5浓度后发现，当PM_2.5浓度达到轻度及以上污染时，白天的通风系数为1624 m²·s^-1，夜间为566 m²·s^-1；当PM_2.5为优和良时，白天的通风系数为2197 m²·s^-1，夜间为980 m²·s^-1。可见，污染越重，通风系数越低。上海地区通风系数和PM_2.5浓度呈显著负相关(图 2)，通风系数越低，垂直扩散条件越差，不利于污染物在垂直方向的扩散，污染程度越重。

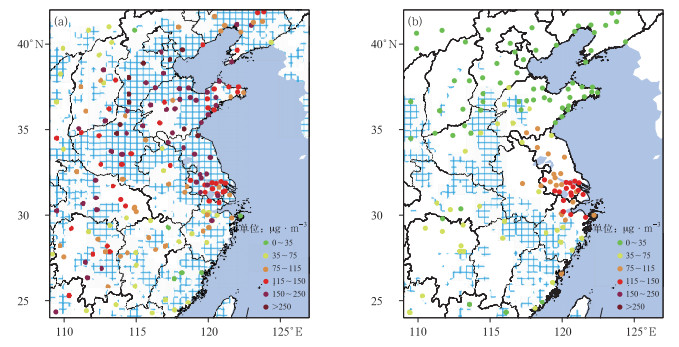
通风系数反映了大气垂直扩散能力，滞留指数则可以反映大气的水平扩散条件。图 3a为2015年1月4日的污染过程，华东中北部和京津冀等地出现了大范围的重污染天气，同期对气象场的分析后发现此次污染过程主要由静稳天气造成。由图 3a可见，滞留指数大于0.3的覆盖区和重污染区重合度较好，尤其在京津冀、河南、山东中东部和江苏地区，说明该地区的污染主要是由于水平扩散条件差导致。但山东西部和华东南部重合度较差，这主要由地形原因造成，因为滞留指数的计算主要由风场得出，而地形对地面风有很大影响。此外，通过分析滞留指数的公式后可以发现滞留指数在适用上有一定的局限性。在上海东部沿海，当主导风向为持续偏东风时，海上清洁空气对污染物有一定的稀释作用，因此滞留指数在使用过程中要考虑偏东风的作用；当主导风向为持续西北风时，滞留指数较小，但上游城市群污染物对上海产生输送，PM_2.5浓度相对较高，因此滞留指数在使用过程中要考虑风向的作用；此外，滞留指数无法表现输送的作用(图 3b)。

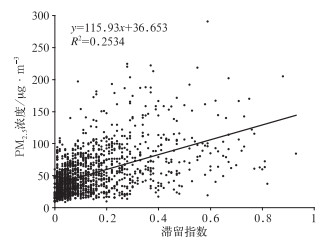
进一步对比分析滞留指数和PM_2.5浓度的关系后发现，对上海而言，在污染情况下，滞留指数平均值为0.34；在PM_2.5浓度未达到污染程度时，滞留指数平均值为0.14。可见，滞留指数越高，水平扩散条件越差，越容易导致污染的发生。同样对滞留指数和PM_2.5浓度进行回归分析后发现，PM_2.5浓度和滞留指数正相关(样本数n=1468，相关系数r=0.503，通过0.01的显著性水平检验)，见图 4。

通过前面的分析可以发现，通风系数和滞留指数作为反映大气垂直及水平扩散能力均与PM_2.5浓度相关性较好，本文综合考虑大气水平扩散条件和垂直扩散条件构建了扩散指数。

$ DI = x \times V{I_{{\rm{norm}}}} + \left({1 - x} \right) \times RF $

(6)

式中，DI代表扩散指数，VI为通风系数，RF为滞留指数，x为通风系数的权重，1-x则为滞留指数的权重。因通风系数的数值较大，而滞留指数为0~1的实数，因此在构建扩散指数之前先对通风系数作了归一化处理：

$ V{I_{{\rm{norm}}}} = 1 - \frac{{{\rm{arctan}}\left({VI/Mid} \right)}}{{({\rm{ \mathit{ π} }}/2)}} $

(7)

式中Mid为所有样本的中位数，主要是优化归一化效果。

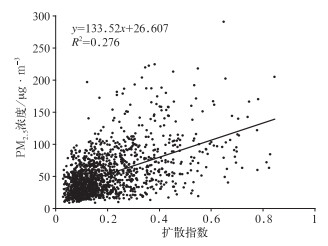
对于权重x的选择，我们做了敏感性试验，表 2为不同权重下扩散指数与PM_2.5浓度的相关系数，当通风系数的权重为0.15时，扩散指数与PM_2.5浓度的相关系数最大，因此，我们将x选取为0.15作为权重因子。图 5为扩散指数和PM_2.5浓度的相关关系，相关系数为0.525，对比图 4和图 5可见，综合考虑了大气水平扩散条件和垂直扩散条件创建的扩散指数与PM_2.5浓度的相关关系要优于单一的滞留指数，而且用一个指数可以同时表征大气的水平和垂直扩散能力，在实际业务中更加实用。

4 空气污染输送指数 4.1 颗粒物输送特征

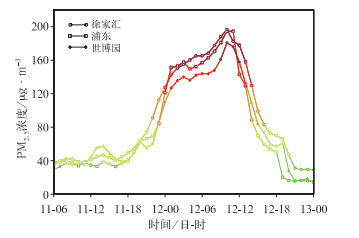
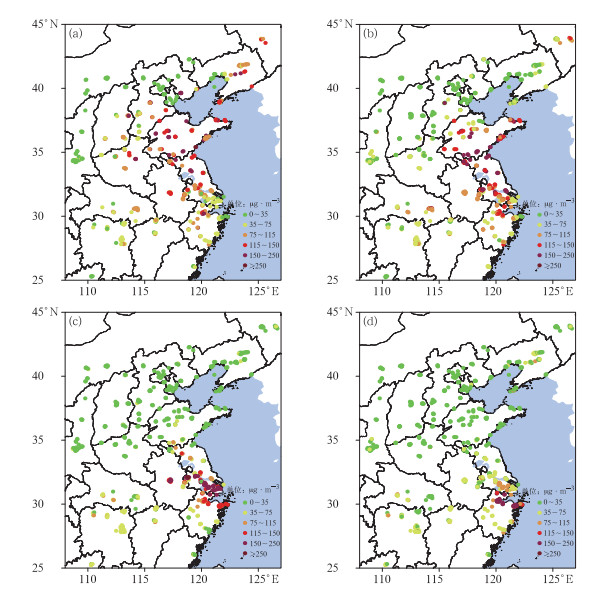
颗粒物的输送主要特征为空间上高污染带受风场等气象要素影响逐渐向下游推移的过程。在具体地区的反映则是颗粒物浓度梯度明显增加，随着高污染带的移出，颗粒物浓度又有一个明显的下降过程(曹钰等，2016；王艳等，2008；陈镭等，2016)。图 6给出了2014年11月11—12日上海地区三个环境监测站的典型颗粒物输送过程PM_2.5浓度的时间变化序列，11日20时之前三个测站的PM_2.5浓度都维持在较低值，20时以后快速上升，12日10时前后达到了峰值，之后便快速下降。结合图 7可以更清晰地看出这次污染物输送过程，11日12时高污染区主要分布在华东北部地区(图 7a)，受北方冷空气扩散南下影响，我国东部地区盛行西北风，20时高污染区有所南移(图 7b)，12日12时高污染区主要分布在上海及周边一带(图 7c)，随着污染带的进一步南压，上海的污染过程结束。

4.2 输送潜在源区分析

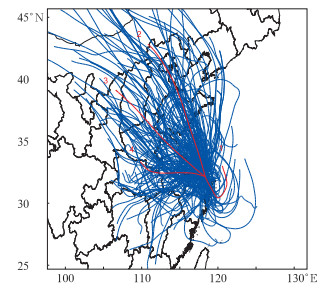
图 8给出了上海市PM_2.5逐6 h浓度均值(02、08、14和20时)达到中度污染过程的后向轨迹的分布，轨迹时长为48 h，通过聚类分析后发现，上海污染物的输送来源有4类主要路径：第一类路径为东路冷空气引导山东半岛的污染物对本市的输送；第二类主要为中路冷空引导的京津冀地区和山东中西部污染物对本市的输送；第三类和第四类路径则为西路冷空气引导陕西南部，河南和安徽的污染物对本市的输送。由于第一类路径经过我国东海地区，而海上清洁空气对污染物有一定的稀释作用，输送引起污染程度存在一定的不确定性，因此本文重点研究第二、第三和第四类路径。

为了进一步确定污染物输送的潜在源区，本文以上述路径的所有个例为样本，利用PSCF分析法绘制图 9，从图中可以看出PSCF的大值中心主要分布在京津冀中南部地区和山东西北部地区。

4.3 输送强度指数

根据上文所选的输送路径，筛选2013—2015年的输送个例，利用式(3)计算了这些污染个例的输送强度，并对输送强度做归一化处理。图 10给出了输送强度指数和PM_2.5浓度的关系，根据图中的结果发现输送强度指数和PM_2.5浓度的对应关系一般，并不能很好地体现输送强度指数和PM_2.5浓度的线性相关关系。

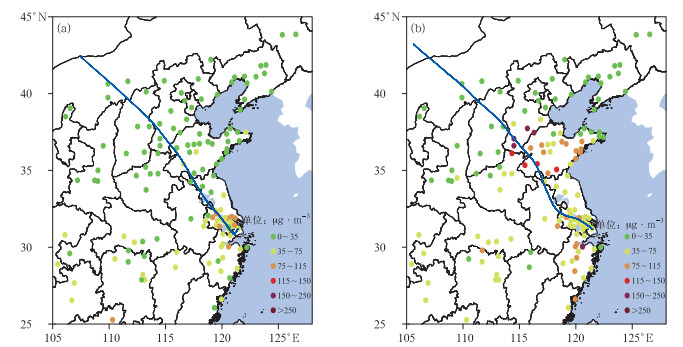
式(3)中E为排放源强度，排放源清单数据只有逐月数据，若同一月内有两条近似轨迹，根据式(3)的计算结果，输送强度值会相近。但结合个例分析后发现，如若两个个例轨迹近似，上游污染程度不同，输送强度会有很大差异。如图 11所示的两个冷空气输送个例，前者上游浓度较低(图 11a)，经过24~48 h的传输后，上海2014年12月2日夜间的空气质量(图略)为优到良；后者(图 11b)在轨迹上的京津冀南部和山东西部的浓度较高，同样经过24~48 h的传输后，上海的12月4日的空气质量(图略)达到了轻度污染，并出现了短时的中度污染。

4.4 改进的空气污染输送指数

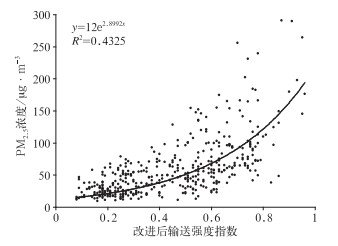
本文对式(3)做了改进，将式(3)中的E改为上游PM_2.5浓度实况ES[见式(8)]。进一步计算改进后的输送强度之后发现，输送强度指数和PM_2.5浓度有很好地对应关系，随着输送强度指数的增加，PM_2.5浓度呈指数增长(图 12)。两者相关关系达到0.658。在实际业务中，改进后的空气污染输送指数对上海地区典型的污染物输送过程有很好地指示意义，给预报员提供了很好的技术支持。

$ \begin{array}{l} {T_l}\left( {i,j} \right) = {R_l}\left( {i,j} \right)E{S_l}\left( {i,j} \right){W_{\rm{d}}}\left( {i,j} \right) \times \\ {W_{{\rm{t}}l}}\left( {i,j} \right)PSCF \end{array} $

(8)

5 结论和讨论

本文结合影响空气质量的天气条件，提出了静稳天气条件的空气污染扩散指数和输送条件下的空气污染输送指数，并对两个指数在上海的适用性进行验证，表明两个指数均能对上海的空气污染起到较好地提示作用，在空气污染预报业务及空气污染防治方面具有现实支撑意义。主要的结论有以下几点：

(1) 上海近三年平均每年有75次PM_2.5日平均浓度达到轻度及以上污染(>75 μg·m^-3)，统计结果显示上海的重污染主要为静稳累积型和冷空气输送型。冷空气输送型污染持续时间相对较短，时间变化表现为PM_2.5浓度迅速上升，峰值浓度较高。静稳累积型污染持续时间较长，时间变化表现为PM_2.5浓度缓慢上升，空间上常出现大范围污染区。

(2) 通风系数反映了大气垂直扩散条件，滞留指数则可以反映大气的水平扩散条件，两者和PM_2.5浓度线性相关。本文为研究大气扩散条件和PM_2.5浓度的关系，综合考虑大气水平扩散条件和垂直扩散条件创建了扩散指数，结果表明扩散指数和PM_2.5浓度的相关系数为0.525，扩散指数与PM_2.5浓度的相关关系要优于单一的通风系数和滞留指数。

(3) 输送强度指数在上海地区的适用效果一般，本文结合历史个例分析在输送强度指数公式的基础上做了一些改进，将公式中的排放源强度E改为上游PM_2.5浓度实况ES，计算结果表明改进后的输送强度指数和PM_2.5浓度呈指数正相关，相关系数达0.658，改进后的输送强度指数效果更佳。

上海地区污染程度有很明显的季节特征，夏季颗粒物污染浓度较低，污染日数较少；冬季则相反。扩散指数和输送指数对季节变化考虑不够全面，还需进一步深入研究。另外，上述指数在长三角其他地区的适用性还需进一步验证。