引言

土壤湿度和土壤温度的误差直接或间接影响着感热通量和潜热通量的模拟，进而反馈到气象模式中，影响2 m气温(T_{2 m})和2 m相对湿度(RH_{2 m})的模拟精度，对降水的模拟也有一定的影响。许多研究表明了土壤湿度和土壤温度在数值模式中的重要性(林朝晖等，2001；张生雷等，2006；黄春林和李新, 2006；Tian and Xie, 2008；Wang et al，2017)。土壤湿度的初始化数据对中尺度模式尤为重要，不合适的初始值可能会导致输出结果的失真。Giard and Bazile(2010)通过对模式进行72 h的敏感性试验，发现初始土壤湿度对模式2 m气温和湿度模拟的结果影响很大，误差分别能够达到4 K和0.50 kg·kg^-1。Miyakoda et al(1979)通过试验证明利用真实的初始土壤含水量数据，能够在夏季改进降水和蒸发的预报，而且对土壤湿度空间分布和时间变化的准确模拟，有助于了解能量和水分交换过程，提高降水预报准确率。Mahfouf(1991)通过对ISBA的两层陆面模式试验结果分析发现，下层土壤湿度对T_{2 m}和RH_{2 m}的模拟结果影响更大，这是由于表层土壤的“无记忆性”，因为ISBA模式的表层土壤深度只有1 cm，在模拟过程中很容易丢失土壤湿度和土壤温度的信息，所以他认为在进行土壤同化分析时，针对ISBA陆面模式，更应该注重对下层土壤的分析结果。王莉莉和陈德辉(2013)通过对比分析在中国中东部的降水试验结果发现，对于久旱过后的第一场雨，由于土壤水有一个从缺水到饱和或是接近饱和的过程，土壤含水量的变化对模式降水空间分布有一定的影响。

如何能利用观测及其与模式变量之间的关系，给数值模式提供一个最佳的初始场，就转化为如何推导出一个通用关系的问题。早在1986年，Lorenc(1986)就已经证明了数值模式中的同化方法(卡尔曼滤波、最优插值等方法)都和理想的分析方程有关，这种方式可利用地表参数对土壤水分含量进行估算。变分方法无疑是最有效的技术，因为它能够包含一段时间的观测，而且大气参数和土壤湿度都和地表方案中的非线性预报方程有关。但是，变分方法的计算量太大。另外一种广泛应用的分析技术是最优插值法。利用多元线性回归，假定大气参数的预报误差与土壤湿度修正有关，但需要一些与观测和预报误差统计有关的数据，而且这种方法自身就已经包含了土壤含水量静态修正的预报量。Mahfouf(1991)在假设短期预报误差是源于土壤湿度的前提下，扰动初始土壤含水量得到一组试验数据，利用Optimal Interpolation(OI)方法估算权重系数，得到ISBA-2L陆面模式表层和下层的土壤湿度，提出了原始的OI方案。其原则是考虑观测和预报误差的客观统计方法，利用两种信息来源，即观测2 m气温和湿度，而不仅仅是湿度，因为只有当两条信息相互支持时才会发生显著的增量。但是由于2 m气温和相对湿度的预报误差并不是总能够包含土壤湿度的信息，例如，在降水期间、夜晚以及太阳辐射较弱的时候，由于在这些情况下预报误差和土壤湿度误差关联性很弱，或没有关联，所以在这些情况下利用其分析土壤湿度增量是不合理的。这些结论在Bouttier et al(1993)发表的文章中已经被试验证明了。Douville et al(2000)以此为基础，在OI分析方法中加入了植被覆盖率、土壤类型和辐射的影响，也就是OI_EC(Optimal Interpolation European Centre for Medium-Range Weather Forecasts)陆面同化方法，通过试验结果对比，证明OI_EC方法更为可靠，能改善蒸发和土壤湿度，并能弥补陆面方案和降水强迫的偏差。OI_EC方法已经在欧洲中心进行了业务应用。Bouttier et al(1993)以Mahfouf(1991)提出的原始OI方法为基础，初步建立OI_MF(Optimal Interpolation Météo-France)陆面同化方法，认为模式对T_{2 m}和RH_{2 m}的预报误差不仅来源于土壤湿度，特别在大风或是辐射较弱的情况下，模式的预报误差受到其他因素的影响更大，同时这种大风或是辐射较弱的情况出现的频率较高，所以应该在方法中考虑此类因素的影响。又因为OI系数中包含了绝大多数信息(如观测误差等)，所以他们尝试利用分析方程对OI系数进行敏感性试验，对原始的OI方法(Mahfouf，1991)进行了改进，并在中尺度模式中得到较好的模拟结果。Giard and Bazile(1996)在此基础上，对OI_MF陆面同化方法进行了改进，解决了之前方法遇到的一些问题(如云量、季节性等)。1998年，OI_MF陆面同化分析方法在法国气象局ARPEGE全球模式中得到业务应用。2009年2月，OI_MF陆面同化分析方法应用到了ALADIN有限区域模式。

国内研究中，张生雷等(2006)等利用EKF(extended Kalman filter)方法结合VIC(variable infiltration capacity)模型进行试验，结果证明同化后的土壤湿度分布与站点观测资料基本一致。贾炳浩等(2010)基于微波亮温及集合Kalman滤波的土壤湿度同化方案，通过理想试验表明该同化方案可以明显改善表层土壤湿度的模拟精度，对深层土壤的模拟也有改善。田向军和谢正辉(2008)将双集合卡尔曼滤波应用于土壤湿度同化方法，并考虑次网格变异性和土壤冻融过程，提高了土壤湿度的模拟精度。杨晓春(2010)利用我国FY-2静止卫星降水和辐射资料，制作一套高分辨率、较真实的大气强迫数据用于陆面模式的土壤湿度模拟，经过试验结果表明可以有效提高模拟精度。杨袁慧等(2013)在WRFV模式中，采用同化后的土壤湿度，针对一次强降水进行模拟，证明土壤湿度能够有效提高模式的模拟能力。朱智和师春香(2014)利用中国区域土壤湿度站点观测数据，对中国气象局陆面同化系统和全球陆面同化系统进行评估，结果证明中国气象局陆面同化系统在中国区域的土壤湿度模拟效果较好。现在的GRAPES_Meso模式中，土壤湿度、温度初始场采用的是NCEP或T639的土壤数据，还未引入陆面土壤湿度、温度同化方法。而无论是NCEP或T639的土壤温度、湿度数据，与观测值还有一定的差距。又因为土壤观测站点的分布密度还不够高，不能达到模式对初始场时间和空间的需求。所以，本文选用两种OI陆面同化方法对土壤变量进行同化分析，这两种方法已经在欧洲中心和法国气象局等业务化。

1 Noah陆面模式介绍

GRAPES_Meso采用的是Noah陆面模式(Chen and Dudhia, 2001)，土壤分为四层，各层厚度从表层到底层分别为0.1、0.3、0.6和1.0 m。陆面热通量采用土壤温度热扩散公式，如下：

$ C\left( \mathit{\Theta } \right)\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial z}}\left[ {{K_t}\left( \mathit{\Theta } \right)\frac{{\partial T}}{{\partial z}}} \right] $

(1)

式中，K_t是导热率，Θ是土壤容积水含量，C是容积热容量，T是土壤温度，t是时间，z是土壤深度。

Noah对土壤容积水含量计算，采用以下公式：

$ \frac{{\partial \mathit{\Theta }}}{{\partial t}} = \frac{\partial }{{\partial z}}\left( {D\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right) + \frac{{\partial K}}{{\partial z}} + {F_\mathit{\Theta }} $

(2)

式中，D是土壤水扩散率，K是导水率，F_Θ代表了土壤水的源汇项(降水、蒸发等)。

通过公式(2)可以得到每层土壤含水量的公式如下：

$ {d_1}\frac{{\partial {\mathit{\Theta }_1}}}{{\partial t}} = - D{\left( {\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right)_1} - {K_1} + {P_d} - R - {E_{dir}} - {E_1} $

(3)

$ {d_2}\frac{{\partial {\mathit{\Theta }_2}}}{{\partial t}} = D{\left( {\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right)_1} - D{\left( {\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right)_2} + {K_1} - {K_2} - {E_2} $

(4)

$ {d_3}\frac{{\partial {\mathit{\Theta }_3}}}{{\partial t}} = D{\left( {\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right)_2} - D{\left( {\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right)_3} + {K_2} - {K_3} - {E_3} $

(5)

$ {d_4}\frac{{\partial {\mathit{\Theta }_4}}}{{\partial t}} = D{\left( {\frac{{\partial \mathit{\Theta }}}{{\partial z}}} \right)_3} + {K_3} - {K_4} $

(6)

式中，d_i是第i层土壤的土壤厚度，P_d是降水，R是地表出流，E_dir是植物的截留，E_i是土壤第i层的蒸发。

2 OI_EC方法介绍 2.1 OI_EC土壤湿度同化方法

在OI_EC方法中，2 m气温和2 m相对湿度的分析增量用于分析根系层的土壤含水量的变化。在Noah陆面模式中，上面的三层是根系层，所以在本次试验中，OI_EC和OI_MF方法只用于Noah陆面模式的上面三层土壤的同化分析。陆面土壤同化方法对每一层土壤含水量的分析都是独立的，每一层的土壤含水量增量是按照下面公式得到的，具体如下：

$ \Delta {w_i} = {\alpha _i}\Delta {T_{2m}} + {\beta _i}\Delta R{H_{2m}} $

(7)

$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {1 + {{\left( {\sigma _{{T_{2m}}}^O/\sigma _{{T_{2m}}}^f} \right)}^2}}&{{\rho _{R{H_{2{\rm{m}}}},{T_{2{\rm{m}}}}}}}\\ {{\rho _{R{H_{2{\rm{m}}}},{T_{2{\rm{m}}}}}}}&{1 + {{\left( {\sigma _{R{H_{2m}}}^O/\sigma _{R{H_{2m}}}^f} \right)}^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\frac{{{\sigma _{{T_{{\rm{2m}}}}}}}}{{{\sigma _{{w_i}}}}}{\alpha _i}}\\ {\frac{{{\sigma _{R{H_{{\rm{2m}}}}}}}}{{{\sigma _{{w_i}}}}}{\beta _i}} \end{array}} \right]}\\ { = \left( {\begin{array}{*{20}{l}} {{\rho _{{w_i},{T_{{\rm{2m}}}}}}}\\ {{\rho _{{w_i},R{H_{{\rm{2m}}}}}}} \end{array}} \right)} \end{array} $

(8)

式中，Δ是每个格点上的分析增量，w_i是第i层土壤的含水量，α_i和β_i是第i层土壤的分析系数，分别反映了T_{2 m}和RH_{2 m}的分析增量对每一层土壤含水量增量的贡献。利用下面公式计算：

$ \begin{array}{l} {\alpha _i} = \frac{{\sigma _{{w_i}}^f}}{{\mathit{\Phi }\sigma _{{T_{2{\rm{m}}}}}^f}}\left\{ {\left[ {1 + {{\left( {\frac{{\sigma _{R{H_{2m}}}^a}}{{\sigma _{R{H_{2m}}}^f}}} \right)}^2}} \right]{\rho _{{T_{{\rm{2m}}}},{w_i}}} - } \right.\\ \;\;\;\;\;\;\left. {{\rho _{{T_{{\rm{2m}}}},R{H_{2{\rm{m}}}}}} \cdot {\rho _{R{H_{{\rm{2m}}}},{w_i}}}} \right\}{F_1}{F_2} \end{array} $

(9)

$ \begin{array}{l} {\beta _i} = \frac{{\sigma _{{w_i}}^f}}{{\mathit{\Phi }\sigma _{R{H_{2{\rm{m}}}}}^f}}\left\{ {\left[ {1 + {{\left( {\frac{{\sigma _{{T_{2m}}}^a}}{{\sigma _{{T_{2m}}}^f}}} \right)}^2}} \right]{\rho _{R{H_{{\rm{2m}}}},{w_i}}} - } \right.\\ \;\;\;\;\;\;\left. {{\rho _{{T_{{\rm{2m}}}},R{H_{2{\rm{m}}}}}} \cdot {\rho _{{T_{{\rm{2m}}}},{w_i}}}} \right\}{F_1}{F_2} \end{array} $

(10)

$ \mathit{\Phi } = \left[ {1 + {{\left( {\frac{{\sigma _{{T_{2m}}}^a}}{{\sigma _{{T_{2m}}}^f}}} \right)}^2}} \right]\left[ {1 + {{\left( {\frac{{\sigma _{R{H_{2m}}}^a}}{{\sigma _{R{H_{2m}}}^f}}} \right)}^2}} \right] - {\rho _{{T_{{\rm{2m}}}},R{H_{2{\rm{m}}}}^2}} $

(11)

式中，ρ_{x, y}代表x与y之间预报误差的相关性，σ^f和σ^a分别是预报和分析误差的标准偏差，F₁和F₂是经验系数，用于在大气的误差不是由土壤误差引起的情况下，减小分析系数。Douville et al(2000)加入了经验系数F₁，用于在夜间和冬季的情况下，模拟土壤含水量的变化和大气之间的弱相关性，由下面公式：

$ {F_1} = \frac{1}{2}\left\{ {1 + \tanh \left[ {\lambda \left( {{\mu _M} - 0.5} \right)} \right]} \right\} $

(12)

式中，μ_M是分析前6 h的平均太阳天顶角，λ是常数。同时，在多云辐射弱的情况下，OI的系数也会减少，所以，Douville et al(2000)利用大气透射率T_r和分析前6 h的平均地表向下短波辐射$\overline {{R_g}} $，在OI系数中加入F₂经验系数，利用下面公式计算：

$ {T_r} = {\left( {\frac{{\overline {{R_g}} }}{{{S_0}{\mu _M}}}} \right)^{{\mu _M}}} $

(13)

$ {F_2} = \left( {\frac{{{T_r} - {T_{r\min }}}}{{{T_{r\max }} - {T_{r\min }}}}} \right) $

(14)

式中，S₀是太阳常数，T_rmin和T_rmax都是常数，分别是0.2和0.9。

Mahfouf(1991)通过48 h试验结果发现，土壤湿度增量的分析方程[式(7)]，不适用于土壤和大气之间联系较弱的情况，当符合以下任何一种情况时，土壤含水量分析增量为零：

(1) 在分析前6 h内，降水量>0.6 mm；

(2) 风速>10 m·s^-1；

(3) 气温 < 0℃(273.15 K)；

(4) 地面有雪。

2.2 OI_EC土壤温度同化方法

在OI_EC方法中，对表层土壤和下层土壤温度分析只与2 m气温相关，利用式(12)中的经验系数F₁进行计算，如下面公式：

$ \Delta {T_i} = {\gamma _i}\Delta {T_{{\rm{2m}}}} $

(15)

$ {\gamma _1} = 1 - {F_1},\;\;\;\;\;{\gamma _{2,3}} = \frac{{\left( {1 - {F_1}} \right)}}{{10}} $

(16)

式中，γ_i是土壤温度同化系数，T_i是第i层土壤温度，T_{2 m}是2 m气温。

3 OI_MF方法介绍 3.1 OI_MF土壤湿度同化方法

OI_MF对土壤湿度的分析方法是基于Mahfouf(1991)提出的原始OI方法，利用观测的2 m温度T_{2 m}和相对湿度RH_{2 m}误差的统计方法。在本次试验中，第一层土壤含水量增量采用式(17)计算，第二和第三层土壤含水量增量均是采用式(18)计算，公式如下：

$ \Delta {w_s} = {\alpha _1}\Delta {T_{{\rm{2m}}}} + {\beta _1}\Delta R{H_{{\rm{2m}}}} $

(17)

$ \Delta {w_p} = {\alpha _2}\Delta {T_{{\rm{2m}}}} + {\beta _2}\Delta R{H_{{\rm{2m}}}} $

(18)

式中，w_s是表层的土壤湿度，w_p是下层土壤湿度，系数α_i和β_i(Giard and Bazile, 1996)是与土壤类型、云量(CI)、辐射时间(t^*)和植被类型有关，其中α_i对应的是系数a_i^{T_{2 m}}，b_i^{T_{2 m}}和c_i^{T_{2 m}}，β_i对应的是系数a_i^{RH_{2 m}}，b_i^{RH_{2 m}}和c_i^{RH_{2 m}}，如下分析方程：

$ \begin{array}{*{20}{c}} {{\alpha _1}\left( {{\beta _1}} \right) = \frac{{\delta w}}{{\delta {w_r}}}B\left( {CI} \right)\left( {1 - veg} \right) \times \left[ {a_0^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right) + } \right.}\\ {\left. {a_1^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right)veg + \alpha _2^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right)ve{g^2}} \right]} \end{array} $

(19)

$ \begin{array}{*{20}{c}} {{\alpha _2}\left( {{\beta _2}} \right) = \frac{{\delta w}}{{\delta {w_r}}}B\left( {CI} \right)\left( {1 - veg} \right) \times \left\{ {\left( {1 - veg} \right) \times } \right.}\\ {\left[ {b_0^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right) + b_1^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right)veg + } \right.}\\ {\left. {b_2^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right)ve{g^2}} \right] + veg\frac{{LAI}}{{{R_{sm}}}}\left[ {c_0^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right) + } \right.}\\ {\left. {\left. {c_1^{{T_{{\rm{2m}}}}/R{H_{{\rm{2m}}}}}\left( {{t^ * }} \right)veg} \right]} \right\}} \end{array} $

(20)

式中，veg是植被覆盖率，LAI是叶面指数，R_sm是植被最小抗阻，δw_r由下面公式得到：

$ \delta {w_r} = {w_{fc}} - {w_{wilt}} $

(21)

式中，w_fc是田间持水量，w_wilt是凋萎含水量，δw_r是土壤类型为壤土的值。

式(19)和式(20)中B是前6 h平均云量的简单权重数：

$ B\left( {CI} \right) = 1 - {B_1}C{I^{{B_2}}} $

(22)

式中，B₁和B₂是参数。

公式(19)和(20)中，a_n^{T_{2 m}/RH_{2 m}}(t^*)，b_n^{T_{2 m}/RH_{2 m}}(t^*)，c_n^{T_{2 m}/RH_{2 m}}(t^*)，(n=0，1，2)，是通过在壤土中进行OI系数的敏感性试验，对所得到的试验结果进行最小二乘拟合得到的。其中，a_n^{T_{2 m}/RH_{2 m}}(t^*)，b_n^{T_{2 m}/RH_{2 m}}(t^*)，c_n^{T_{2 m}/RH_{2 m}}(t^*)反映了不同的辐射时长(t^*)对应的系数。由于试验是针对壤土进行的，所以要通过对比格点所对应的土壤的含水量和壤土含水量的关系，对系数做进一步的修正(Mahfouf，1991；Bouttier er al，1993；Giard and Bazile, 1996)。

3.2 OI_MF土壤温度同化方法

土壤温度的同化方法采用的是Coiffier et al(2015)提出的方法，表层土壤和下层土壤温度分析方法，如下面公式：

$ \Delta {T_s} = \Delta {T_{{\rm{2m}}}},\;\;\;\Delta {T_p} = \frac{{\Delta {T_{{\rm{2m}}}}}}{{2{\rm{ \mathsf{ π} }}}} $

(23)

式中，T_s是表层土壤温度，T_{2 m}是2 m气温，T_p是平均土壤温度。在本次试验中，对第二三层土壤温度分析增量的求解方法都是采用式(23)中ΔT_p的分析增量。

4 数据及试验设计

本次研究试验时间选取2013年夏季和冬季，两个植被状况差异较大的季节进行试验结果对比分析，夏季时间为6月21日00 UTC至28日00 UTC，冬季时间为12月1日00 UTC至10日00 UTC。其中，夏季时间内，全国大部分地区均有降水，过程性降水主要有三次：第一次为6月21—26日，华北至黄淮区域；第二次为6月22—26日，陕西南部、湖北中北部至黄淮、长江中下游；第三次为6月27—28日，西南地区东部至江南、华南北部。而冬季时间内，全国大部分地区降水较弱。其中，12月8日，吉林中部局地、长江干流中下游沿江局地有0.1～9.0 mm降水，福建沿海局地有0.1 ～12.0 mm降水，其余大部地区1—10日无降水，局部地区有弱降水，极少数自动站有小雨量级降水。模式的预报时长为24 h，以每日00 UTC进行滚动预报，试验覆盖区域为15°～64.5°N、70°～145.3°E，以分辨率为1°×1°的美国NCEP全球预报场作为初始场和侧边界条件，驱动模式。采用美国马里兰大学提供的全球30″×30″分辨率的植被覆盖数据，联合国粮农组织提供的全球5′×5′分辨率的土壤类型分布数据。T_{2 m}和RH_{2 m}的观测数据，选取全国2513个自动观测站的数据，采用Mahfouf et al(2009)所使用的OI方法，只选取格点附近的10个观测站点数据，插值成为T_{2 m}和RH_{2 m}的格点数据，本文中使用的方法中没有考虑到地形的影响。

为了对比OI_EC和OI_MF方法的同化分析效果，本次研究将试验分为以下三种：

OI_EC——控制试验，利用OI_EC方法同化土壤湿度和土壤温度；

OI_MF——控制试验，利用OI_MF方法同化土壤湿度和土壤温度；

OL——开放试验，土壤湿度和土壤温度自由更新。

其中，OI_EC和OI_MF试验的设计如图 1所示，本次试验是将陆面同化方法与GRAPES_Meso模式耦合起来，每6 h启动一次陆面同化，计算陆面模式中的土壤温度和土壤含水量的分析增量，返回陆面模式同化分析后的土壤温度和土壤含水量。

5 应用结果分析 5.1 陆面同化方法的系数

本次试验采用的两种陆面同化技术，都是基于统计的方法，其关键是对系数α和β的推求。这两个系数包含了很多日变化的信息，如模式误差、观测误差等，所以本节主要是对两种陆面同化方法所得到的系数，在24 h内的模拟分布进行对比。选取起始模拟时间为2013年6月21日00 UTC的24 h模式结果，由于是每6 h进行一次陆面同化分析，所以结果展示了第6、12、18和24 h的系数分布(图 2～图 6)，对比两种同化方法的结果，每个系数的分布都是有昼夜变化的。从α和β的分布图可以看到有些区域的系数为0(图 2a, 2b, 图 3a, 3b, 图 5a, 5b, 图 6a, 6b)，这是由于在这些区域土壤和大气之间的联系很微弱，即认为土壤误差对T_{2 m}和RH_{2 m}误差贡献非常小，例如气温 < 273.15 K，或是过去6 h累计降水量>0.6 mm，或是风速>10 m·s^-1(图 7a，7b，7c)。

从图 2和图 3的对比可以看出α和β的分布正好相反的。α是2 m气温的同化系数，白天时刻系数要小于夜晚时刻(图 2a，2c)，这是由于在白天，引起2 m气温误差的原因很多，土壤含水量的变化只是其中一项。β是2 m相对湿度的同化系数，白天时刻的系数要大于夜晚时刻(图 3a, 3c)，这是由于白天太阳辐射强。β系数为正值，说明第一层土壤含水量的增量与2 m相对湿度增量呈正相关，即2 m相对湿度增大，第一层土壤含水量增大；α系数为负值，说明第一层土壤含水量的增量与2 m气温的增量呈负相关的，即2 m气温升高，第一层土壤含水量减小。第一层土壤的湿度和温度变化和分布与深层土壤相同，只是第一层土壤对大气的变化更加敏感，而底层土壤需要通过第一层土壤和植物根系才能将能量和水量传递到大气中，影响T_{2 m}和RH_{2 m}的变化，所以下层土壤不如第一层土壤的变化大。由试验结果可以看到(图略)，第一层α的分布及昼夜变化与第二层的结果相近，只是第二层α的数值比第一层略小一些。

从式(19)和式(20)可以看出，在OI_MF方法中，辐射对其系数的推求影响很大(如向下短波辐射、太阳天顶角、辐射时长等)。从α系数的分布可以看到(图 5a)，有很明显的带状分布(每15°)，这是由于α系数与当地辐射时间相关。同样，α系数有正值出现，即第一层土壤含水量增量与2 m气温的增量呈现正相关，也是因为公式中由纬度计算当地辐射时间的原因，所以图 5a中，50°N以北都是正值，图 5b全部都是正值。50°N以南也有部分正值出现，这是因为在这些区域的植被类型的抗阻值，推求出的α系数为正值。对比图 2c, 2d, 图 3c, 3d, 图 5c, 5d, 图 6c, 6d，OI_MF方法在夜晚时刻系数分布与OI_EC方法的系数分布图相近。在植被覆盖率低于10%的区域中(图 7d)，OI_MF对第二层土壤第6 h模拟的β系数分布图(图略)，β系数出现了负值，在冬季的试验结果中(图略)更为明显，即第二层土壤含水量增量与2 m相对湿度的增量呈负相关。原因是OI_MF方法在试验设计上更多地考虑到辐射等因素对系数的影响。同时，又因为OI_MF方法的试验只考虑了几种植被类型在不同植被覆盖率下的模拟情况，所以对于某些植被抗阻较大的植被类型，以及植被覆盖率较低的区域，会出现系数为负数的情况。

从OI_EC土壤温度系数γ₁分布图可以看到(图 4)，系数的推求与过去6 h平均太阳天顶角的余弦值相关，且分布也是一致，如式(12)和式(15)所示。对于第一层土壤，温度的同化系数要远远大于第二、三层土壤，这说明了第一层土壤温度更加敏感，昼夜变化大，这和实际情况也是一致的：越深层的土壤温度日变化越小。OI_MF方法中，土壤温度同化系数是个定值，即第一层土壤系数是1，第二层土壤系数约为0.159，如式(22)所示。

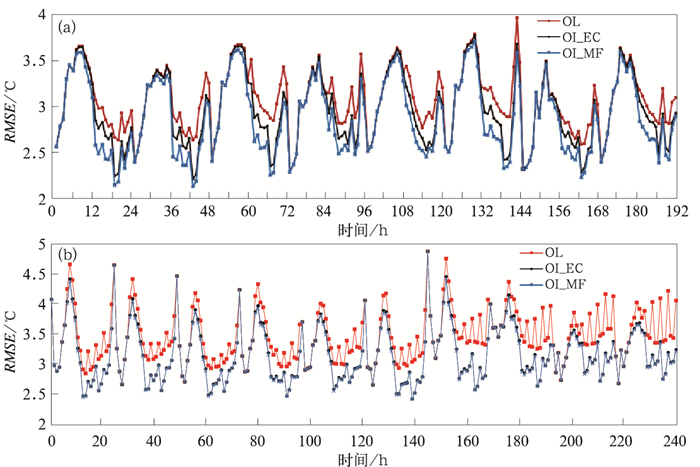
5.2 模拟结果对比分析

从连续试验的每小时均方根误差(root mean square error, RMSE)统计可以看出(图 8)，每种试验结果的均方根误差都有日变化，白天误差比夜晚大，而且陆面同化分析后的均方根误差要低于开放试验结果。从图 8、表 1和表 2的统计结果可以发现，对每24 h模拟时间中第一个6 h之前的结果，由于没有进行陆面同化分析，所以三个试验对T_{2 m}的RMSE结果都是一样的；从第二次陆面同化分析(即第12 h)开始，三个试验的结果有了比较明显的差别。从表 1的统计结果可看到，未加入陆面同化的试验(OL)，模拟结果从6～24 h误差逐渐减小，这是由于模式自身的调节作用；利用了OI_EC方法的试验，在12 h的模拟结果与6 h相同，这是由于OL试验中在第12 h的模拟误差增大了，所以OI_EC方法相对还是减小了模拟的误差；OI_MF方法的试验，对T_{2 m}的均方根误差一直有比较好的模拟效果，而且在第24 h的OI_EC与OI_MF两个模拟结果基本相同。从冬季试验结果可以看出(图 8b)，加入陆面同化后的误差明显小于无陆面同化的结果。这是由于在试验期间，全国绝大部分区域是弱降水，T_{2 m}和RH_{2 m}的误差与土壤温度、湿度误差之间的关联性比较强。从表 2统计结果可以看出，OI_EC的结果从第12 h开始，略好于OI_MF结果，这是由于冬季我国的植被覆盖率相对较低，OI_MF方法模拟的系数值不如OI_EC方法模拟的系数值合理。

从降水ETS评分和降水预报偏差对比可以看到(图略)，三个试验结果基本相同。本次试验是利用土壤含水量和温度的误差与2 m气温和相对湿度误差之间的关系，对土壤含水量和温度进行修正的，而在数值模式中，从土壤含水量到降水是一个复杂的过程，本次在夏季时间内的试验中，全国大部分地区有三次降水过程，而冬季试验时间降水较弱，所以只是从当前试验结果中很难判断其对降水的影响，需要更多的试验结果对比分析。

6 结论

陆面同化方法可以有效地改进模式对2 m气温的预报效果，这已经被很多科学家验证了(Mahfouf，1991；2005；Mahfouf and Bli žňák, 2011；Mahfouf and Bilodeau, 2007；Mahfouf et al，1995；Draper et al，2011；Reichle et al，2002；师春香等，2011)。在Mahfouf(1991)提出的最优插值陆面同化方法基础上，Douville et al(2000)提出的OI_EC和Giard and Bazile(2010)提出的OI_MF陆面同化方法，本文初步将这两种方法应用到GRAPES_Meso模式中。这两种方法都是通过统计方法，建立土壤湿度和温度与观测2 m气温和相对湿度之间的关系。最优插值系数(α和β)包含了很多土壤-大气日变化的信息，系数的变化与大气温度、表层含水量、深层土壤含水量的变化有关，通过感热通量、裸土蒸发、植被蒸腾等实现。为了更好地对比陆面同化方法结果，作者进行了夏、冬两个季节的试验，将两种同化方法的试验结果与未使用陆面同化的结果进行对比。通过分析试验结果发现，两种陆面同化方法得到系数均有日变化，而且系数在晚上的分布较为一致，白天时刻系数分布的差别是由于两种方法的不同试验设计所造成的。对比未使用陆面同化方法的试验结果，OI_EC和OI_MF两种方法对T_{2 m}模拟精度均有一定程度的提高，证明陆面同化方法可以有效地改善模式T_{2 m}的模拟效果，对降水模拟的影响不大。分析OI_MF方法模拟系数的分布和日变化结果，在推求系数时，有系数值不合理的现象出现，其原因：一是由于OI_MF方法在自身的试验设计上更多地考虑了辐射等因素的影响，所以受到数值模式的辐射模拟结果(如短波辐射等)的影响较大，反映在数值模式中，各个物理过程之间的耦合和配合；二是由于OI_MF方法的敏感性试验都是针对壤土进行的，对于其他的土壤类型，只利用土壤含水量对系数进行换算；三是由于只在几种植被类型上进行系数敏感性试验，所以在植被覆盖率低的区域，对下层土壤RH_{2 m}同化系数模拟值不合理。综合试验结果，证明OI_MF方法不适用于我国植被覆盖率低的地区，OI_EC方法更适用于GRAPES_Meso模式。本次试验只选取了夏、冬两个季节试验个例进行对比，还需要更多的试验以验证OI_EC和OI_MF两种陆面同化方法的分析效果。

本文中采用的两种OI陆面同化方法，都是利用2 m气温和相对湿度的短期预报误差来校正土壤温度和含水量，这种统计方法与地面观测网的密度相关，即站网密度大的区域效果好。对于下一步的研究计划，首先是如何能够得到质量更高的格点观测数据，本文中采用的OI方法没有考虑到地形的影响。另外，本文中采用的陆面同化OI_EC和OI_MF方法都是统计方法，不能利用除T_{2 m}和RH_{2 m}以外更多的观测资料，已经有很多国内外专家都证明了(Zhang et al, 2005；兰鑫宇等, 2015；Drusch，2007；Mahfouf et al，2009；Draper et al，2011；师春香等，2011；Xie et al，2011)，利用更多的观测资料(如亮温数据)能够有效地提高陆面同化的效果，所以EKF或是EnKF都是很好的选择，如法国气象局现在正是利用了EnKF方法进行陆面同化，本文作者也正在尝试利用EKF和EnKF方法进行陆面同化试验，希望能够利用更多的观测数据，进一步改进模式模拟结果。

致谢：特别感谢法国气象局的陆面同化专家Mahfouf Jean-Francois教授，在工作百忙之中指导我的工作，给予我有益的建议。