2. 中国科学院研究生院,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049
降水作为陆表系统中物质交换和能量平衡的重要元素,在水文模拟、气象灾害预报和生态模拟的研究中都扮演着重要角色(Xu et al, 2015)。因此,准确、高时空分辨率的降水数据对工农业生产及灾害预测都有重要意义(Ceccherini et al, 2015)。然而,在气象站点分布稀少的山区,降水信息的获取面临着巨大的挑战(Huang et al, 2014)。卫星遥感能提供全球范围内实时的降水信息,常用的卫星产品主要有:美国气象预测中心校正后的降水产品(climate prediction center morphing technique, CMORPH)(成璐等, 2014; Joyce et al, 2004)、全球卫星定位计划降水产品(Global Satellite Mapping of Precipitation Project,GSMaP)(Jia et al, 2011)、热带降水观测卫星(Tropical Rainfall Measurement Mission,TRMM)(周胜男等, 2015; Mantas et al, 2015;骆三等,2011)等。这些卫星降水产品在全球范围内已得到广泛应用,但仍存在很大的不确定性(Fang et al, 2013)。Cheema and Bastiaanssen (2012)将TRMM降水数据的误差分为时间误差(±8%~±10%)和空间采样误差(≈30%),如果不对这些误差进行校正,在应用时可能会导致更大偏差;另外,由于卫星降水产品的空间分辨率(0.25°~5°)较低,其难以满足中小尺度降水空间变异的研究,从而限制了其在流域内驱动水文、气象模型的应用(Duan and Bastiaanssen, 2013)。因此,对卫星降水产品进行误差校正及降尺度方法的研究很重要。
国内外许多学者对卫星降水产品的误差校正及降尺度工作做了大量研究,Condom et al (2011)等比较了加法修正模型(Additive Model)和乘法修正模型(Multiplicative Model)对秘鲁山区TRMM 3B43降水产品的校正,结果表明经过加法修正模型校正后的降水产品能更准确地反映秘鲁山区的降水变化。Cheema and Bastiaanssen (2012)运用回归分析(regression analysis,RA)和地理差异分析(geographical different analysis,GDA)对TRMM 3B43降水数据进行局部校正,通过验证发现GDA校正方法在山区表现最佳。宇婧婧等(2013)基于站点降水资料,通过PDF匹配的方法对CMORPH卫星降水资料进行误差订正,订正后系统误差明显减小。Jia et al(2011)将TRMM 3B43降水作为因变量,利用归一化植被指数(normalized difference vegetation index,NDVI)和数字高程模型(digital elevation model,DEM),建立TRMM年降水量与NDVI和DEM的多元回归模型,从而实现对TRMM的降尺度校正。Xu et al(2015)通过引入地理加权回归(Geographically Weighted Regression,GWR)模型进一步改善降尺度算法,将TRMM 3B43降尺度到1 km,并验证该方法在青藏高原及天山山区的适用性。Wanders et al(2015)基于粒子滤波的数据同化方法,利用水文模型(variable infiltration capacity, VIC)模拟土壤湿度(soil moisture,SM)和陆表温度(land surface temperature,LST)的变化,从而对TMPA-RT降水产品进行降尺度校正。以上结果均表明,经过误差校正及降尺度后的卫星降水产品精度更高,且能更详细地刻画降水的空间分布。
基于站点的误差校正算法虽然能有效改善卫星降水产品的精度,但是,在一些高海拔山区或冬季气象站网相对稀疏的情况下,该方法的适用性较差;而基于陆表环境变量的降尺度校正方法不仅能提高卫星降水产品的空间分辨率,还能改善卫星降水产品的精度。然而,降水与环境变量的关系受土壤类型、水文条件及人类活动的影响较大,导致回归模型难以准确预测降水的时空变化(Duan and Bastiaanssen, 2013),尤其是在沙漠和高寒草甸区,降水与NDVI的变化几乎没有线性关系。由于山区地形复杂,降水受到下垫面和小地形气象因子的影响,常表现出较大的空间差异(Krajewski et al, 2003)。Harmsen et al(2008)认为降水量在相邻两个GOES-12卫星像元(4 km×4 km)中可能会有显著差异,对山区生长季节内TRMM降水格点的内部降水格局进行均值比较,发现81%的TRMM格点内部降水存在显著性差异。
考虑到以上问题及研究区,本文基于新一代卫星降水产品——全球降水观测(Global Precipitation Measurement, GPM)及天山山区1998—2015年40个气象站点,提出了一种新的校正TRMM 3B42_V6 (TRMM)降水数据的方法,并通过气象站点交叉验证对比该方法与GDA方法的有效性。本文旨在结合GPM数据的高时空分辨率及站点数据的实时性,通过对TRMM降尺度及校正方法的研究,生成一套高精度、长时间序列(1998—2015年)山区降水产品, 从而为山区的水文及气候变化研究提供数据支持,以填补山区降水数据的空白。
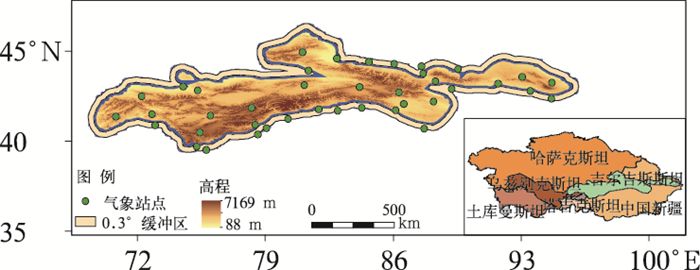
1 资料与分析方法 1.1 研究区概况天山位于欧亚大陆腹地(图 1),东西横跨中国、哈萨克斯坦、吉尔吉斯斯坦和乌兹别克斯坦四国,全长约2500 km(69°~97°E),宽约250~350 km(39°~47°N),平均海拔约5000 m。作为世界七大山系之一,天山是世界上最大的独立纬向山系,也是世界上距离海洋最远的山系和全球干旱地区最大的山系(李瑞雪,2010;张正勇等,2015;范彬彬等,2013)。山区的土地覆被表现出很大空间差异,东部和南部被沙漠(23.9%)所包围,而山区的中部和西北部主要以草地(62.3%)和森林(2.3%)为主(Ji and Chen, 2012)。受盛行西风的影响,大量水汽被迎风的北坡和西北坡拦截,形成丰沛的山区降水, 年平均降水量约为200 mm,且集中分布在夏秋两季(Ning et al, 2015)。同时,天山是众多河流的发源地,山区降水对于调节水量平衡及工农业发展都有重要意义。
|
图 1 天山位置示意图及40个气象站点分布 Fig. 1 Locations of Tianshan Mountains and 40 meteorological stations |
本文所使用的气象观测数据来源于中国气象科学数据共享网(http://cdc.cma.gov.cn/home.do)和吉尔吉斯斯坦国家气象局所提供的逐日气象数据,对于数据缺测大于20%的站点,均不予考虑,最终选取天山山区40个气象站点1998—2015年的降水数据,其空间分布如图 1所示。对山区40个气象站点的分析表明,1998—2015年的平均年降水量为165 mm,2008年降水量最少(120 mm),2010年降水最多(200 mm),而2011年降水最接近平均值(160 mm)。本文选取这3个典型年份来评价校正方法在不同气候条件下的表现能力。
1.2.2 卫星降水资料TRMM降水观测卫星于1997年11月成功发射,搭载了微波成像仪(TMI)、降水雷达(PR),可见/红外辐射仪(VIRS)、地球辐射能量探测器(CERES)等传感器,是第一颗专门用于观测热带、亚热带降水的气象卫星(唐国强等,2015)。本文使用的数据为1998—2015年TRMM卫星3级产品(3B42_V6)的日降水数据(http://pmm.nasa.gov/data-access/downloads/trmm),该产品融合了多源卫星传感器的降水数据与站点观测数据,提供精确的全球降水数据(张涛等,2015)。GPM作为新一代的降水观测卫星,其核心卫星于2014年2月27日发射,能够提供全球0.5 h以内的雨雪产品数据。GPM首次采用包含了Ka波段和Ku波段的双频雷达观测系统(DPR),从不同的角度提供云层降水粒子的物理信息(雨滴的形状、强度和对流过程),能更精确地刻画降水粒子的时空分布;相对于TRMM的传感载荷,GPM搭载的微波成像仪(GMI)增加了4个高频波段,提高了对微量降水及降雪的捕捉能力,而这两种降水类型是中高纬地区降水的重要组成部分。另外GPM数据除了使用站点数据进行统计校正外,还使用了基于地基观测试验的降水反演机理验证和以水文气象应用为导向的融合验证(Huffman et al, 2015)。本文使用的是GPM的3级融合产品(GPM_IMERG),时间为2014年3月至2016年3月(http://pmm.nasa.gov/data-access/downloads/gpm)。TRMM与GPM时空分辨率及主要参数对比如表 1所示。
|
|
表 1 TRMM与GPM卫星产品主要参数 Table 1 Main parameters of TRMM and GPM |
本文基于天山山区的40个气象站点,首先采用GDA方法对TRMM数据进行校正,该方法是由Cheema and Bastiaanssen(2012)首次提出,并与回归分析校正方法进行对比,结果表明经GDA校正后的降水数据表现最佳。因此,本文采用GDA校正方法与下文提出的MERGE方法作对比。GDA校正TRMM降水数据的具体步骤如下:
(1) 计算气象站点降水数据与其空间对应的TRMM数据的差值Pe。
(2) 使用反距离加权(IDW)插值方法将Pe插值到0.25°格网,得到误差的空间分布图Re。
(3) 将上述误差Re加到原始TRMM数据上,得到校正后的结果Pcal-GDA。
1.3.2 基于MERGE方法的校正相对于前人所做的卫星降水数据的校正工作,本文提出的降水校正方法基于两个假设:(1)GPM能提供准确实时的高时空分辨率降水数据,且能较好地刻画降水的空间分布特征。(2)TRMM降水的偏差并非是随机的,且能通过气象站点进行局部校正。详细校正算法步骤如下:
(1) 由于GPM(PGPM-0.1)与TRMM(PTRMM-0.25)的空间分辨率不同,为了建立两者在空间上的联系且得到更高精度的降水数据,首先将GPM的日降水数据重采样到0.05°空间分辨率PGPM-0.05,计算5×5块状范围内栅格的均值PGPM-0.25;然后计算PGPM-0.05每个栅格像元对其所在的PGPM-0.25下栅格像元的比例Pratio,这样,对于PGPM-0.25每一个栅格像元,都有一个Pratio与之对应。最后,利用两年的GPM的日降水数据,以月份为时间分段,即每个PTRMM-0.25栅格像元都对应60个PGPM-0.25栅格(两年的该月日降水),找出该月内日降水量与其最接近的PGPM-0.25像元,将对应的Pratio与PTRMM-0.25相乘,得到0.05°分辨率下的TRMM降水数据PTRMM-0.05。
(2) 基于山区气象站点降水数据,根据Vila et al (2009)提出的加法修正模型,由式(1)计算1998—2015年原始TRMM数据(PTRMM-0.25)与站点数据的平均误差,得到一个包含12个月平均误差的向量F1i,然后将F1i应用到式(2)得到校正后的TRMM月降水数据Pij。
| $ \frac{{\sum\limits_{t = 1}^j {\lg \left({TRM{M_{ij + 1}}} \right) - \lg \left({OB{S_{ij}} + 1} \right)} }}{j} = {F_{1i}} $ | (1) |
| $ {P_{ij}} = \left({TRM{M_{ij + 1}}} \right)\left({1 + {F_{1i}}} \right) - 1 $ | (2) |
式中,i表示月份(1, …, 12),j表示年份(1998, …, 2015),TRMMij,OBSij分别表示TRMM和站点第j年i月降水数据,F1i表示加法修正模型的修正系数,Pij是校正后的第j年i月降水数据。
(3) 经GPM校正后的PTRMM-0.05具有较高的空间分辨率且能准确刻画降水的空间分布,而通过加法模型校正后的Pij由于融合了站点降水信息更能反映降水的实时变化。基于隋玉正等(2016)提出的多元数据的融合方法,根据相关系数计算加权融合的权重组,从而构建联合融合函数:
| $ {V_j} = \sum\limits_{i = 1}^k {{w_{ij}}{v_{ij}}} $ | (3) |
| $ {w_{ij}}{\rm{ = }}\frac{{r_{ij}^2}}{{\sum\limits_{i = 1}^k {r_{ij}^2} }}\;\;\;\;\;{\rm{且}}1 = \sum\limits_{i = 1}^k {{w_{ij}}} $ | (4) |
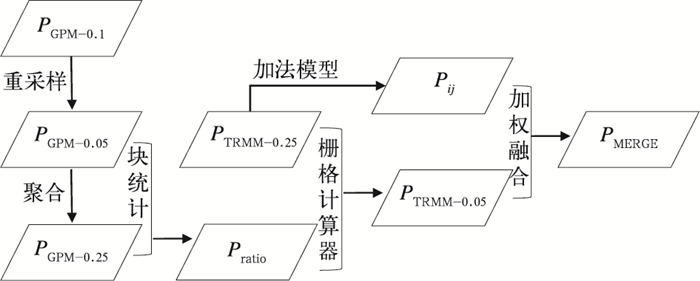
式中,Vj是融合后第j点的值,wij是第i种数据第j点的权重,vij是第i种数据第j点的值,rij是第i种数据第j点的相关系数,k是数据类型的总数。将第(1)步与第(2)步得到的PTRMM-0.05和Pij按上述融合函数,计算得到融合后的降水PMERGE即为最终结果。具体流程如图 2所示。
|
图 2 本文提出的校正TRMM降水数据的流程 Fig. 2 Flowchart of the TRMM precipitation datasets correction proposed in this study |
本文使用交叉验证的方法来检验两种校正方法的有效性。首先,随机选取80%的气象站点参与误差校正,然后利用余下20%站点对校正结果进行验证,将此过程重复5次,每次选取不重复的验证站点,以保证每个站点都参与到校正结果的验证中。另外,本文采用决定系数R2、均方根误差RMSE、相对误差Bias及平均绝对误差MAE 4个统计指标来评价校正后卫星产品的精度。R2反映了TRMM降水与实测站点的线性相关程度,Bias则描述了TRMM数据的系统误差,其正、负值表明TRMM数据对站点数据的高估或低估现象,而RMSE和MAE常被用来描述模拟值(TRMM)与观测值之间的差异,量测平均误差大小。当校正后TRMM数据具有较低的RMSE、MAE、Bias和较高的R2值时,表明其校正效果较好。各统计指标的计算公式如下所示。
| $ {R^2} = {\left({\frac{{\sum\limits_{i = 1}^n {\left({{M_i} - \overline M } \right)\left({{P_i} - \overline P } \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left({{M_i} - \overline M } \right)}^2}\left({{P_i} - \overline P } \right)} ^2} }}} \right)^2} $ | (5) |
| $ RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^n {({P_i} - } {M_i}{)^2}}}{n}} $ | (6) |
| $ Bias = \frac{{\sum\limits_{i = 1}^n {{P_i}} }}{{\sum\limits_{i = 1}^n {{M_i}} }} - 1 $ | (7) |
| $ MAE = \frac{{\sum\limits_{i = 1}^n {\left| {{P_i} - {M_i}} \right|} }}{n} $ | (8) |
式中,P和M分别表示校正后TRMM的降水值和站点观测值,P和M代表校正后TRMM与站点观测的平均降水量,n是研究区域内的站点数目。
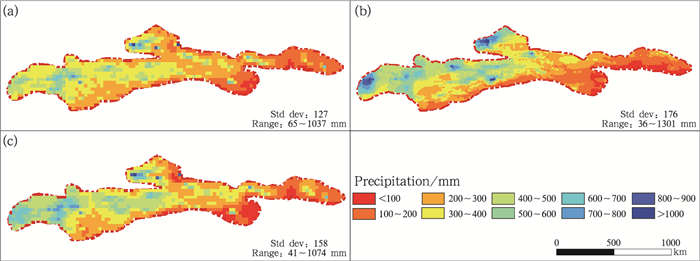
2 TRMM误差校正结果 2.1 对年降水的校正结果图 3分别表示原始TRMM_V6(V6)、经MERGE方法校正后的降水产品TRMM_MERGE (MERGE)和经GDA方法校正后的降水产品TRMM_GDA(GDA)在2011年的降水分布图。由图可见,三套产品均表现出相同的降水格局,位于吉尔吉斯斯坦境内的天山西部及伊犁河谷地区,降水量在600 mm以上;天山中部的主峰区降水量为300~500 mm;而东部吐哈盆地及南部部分山脉的降水最少,在200 mm以下,即山区的降水从西北向东南递减。相对于原始V6(Range:65~1037 mm,Std dev=127),MERGE (Range:36~1301 mm,Std dev=176)和GDA(Range:42~1074 mm,Std dev=158)的降水范围、标准差均明显增大,表明校正后的TRMM产品能捕捉到更大范围的降水变化,在量级上改变降水的分布;且MERGE方法提高了原始V6的分辨率(0.05°),能更精确地反映因局部地形变化所造成的降水差异。进一步分析可得,经GDA校正后的降水数据与原始V6数据降水空间分布基本一致,表明GDA方法对原始数据的依赖性较大,而经GPM校正和加法模型校正融合后的降水产品在局部地区起到平滑的作用,尤其在天山东部,V6和GDA存在少量异常点,而MERGE能够消除部分异常点,更准确地反映降水的空间分布。
|
图 3 2011年天山年降水量分布图
(a)原始TRMM_V6,(b)经过MERGE方法校正后降水TRMM_MERGE,(c)经过GDA校正后的降水TRMM_GDA (图 3a, 3c的分辨率为0.25°,图 3b的分辨率是0.05°) Fig. 3 Annual precipitation in Tianshan Mountains in 2011 (a) original TRMM_V6, (b) corrected precipitation with MERGE, TRMM_MERGE, (c) corrected precipitation with GDA, TRMM_GDA (Figs. 3a and 3c are at 0.25° resolution, Fig. 3b is at 0.05° resolution) |
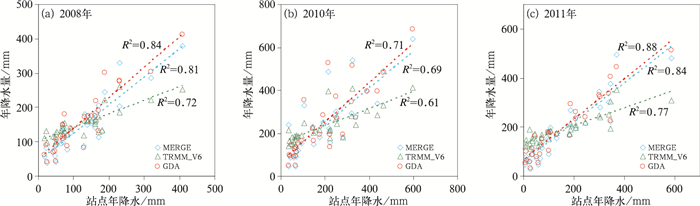
图 4是V6、GDA、MERGE与气象站点在三个特殊年份的年降水量散点图。图 4a~4c均表明V6同站点的相关性最差,即高估年降水量较少的站点,低估年降水量较大的站点。经过校正后的降水产品GDA与MERGE,明显改善了降水的误差情况,与站点的关系更接近1:1线;三套产品中,GDA与站点的相关性最好(例如,2011年GDA:R2=0.88,MERGE:R2=0.84,V6:R2=0.77),表明GDA方法对校正TRMM降水的稳健性。三个典型年份中,与站点降水产品拟合度最高的是2011年(平均降水年GDA:R2=0.88,MERGE:R2=0.84),2010年(降水最少年份)的拟合效果最差(GDA:R2=0.71,MERGE:R2=0.69),说明在降水较少的年份,GDA与MERGE的校正效果一般。原因可能是,基于TRMM的降水雷达很难观测到0.7 mm·h-1以下的降水,致使V6与站点拟合效果差,而GDA与MERGE都是基于V6产品进行校正的,会不可避免地引入原始降水产品的误差;所以,在降水较少的年份,GDA与MERGE的校正效果一般。同时,TRMM_V6也需要改进其数据生成算法以融合卫星、雷达、站点等多元观测数据。
|
图 4 天山三套卫星降水产品与气象站点年降水量散点图 Fig. 4 Scatterplot of the three sets of satellite products versus the measured annual precipitation in Tianshan Mountains |
表 2列出了对三个特殊年份进行交叉验证各统计量值。由表 2,GDA与MERGE都明显改善了V6产品的精度;相对于V6,GDA与MERGE的R2值增加,RMSE、MAE、Bias值均降低,说明两种方法均能有效降低V6产品的误差。然而,不同的统计指标可能会产生不同的评价结果。例如,在3个特殊年份,MERGE的RMSE、MAE、Bias值和R2均比GDA低(如2011年,GDA:RMSE=61.73 mm,MAE=51.29 mm,Bias=0.24,R2=0.88;MERGE:RMSE=60.81 mm,MAE=49.42 mm,Bias=0.17,R2=0.84),这可能是由于MERGE方法改善站点降水的非均匀性造成的。Willmott et al (2015)认为,尽管R2常被用来比较原始变量与模拟变量的相关程度,但它往往是一种误导性的精度评价指标(Xu et al, 2015)。另外,虽然GDA在3年中R2值最高,RMSE和MAE的值相对于V6也有所下降,但是Bias指数却比V6高,可能是在站点误差插值过程中,由于山区气象站点分布极不均匀,个别误差较大的站点插值后导致局部地区的降水量增大,从而使Bias值偏大。综合分析各项统计指标,MERGE表现最佳,能以较大R2值,和最小的误差(RMSE,MAE,Bias)校正V6年降水数据。
|
|
表 2 天山3个特殊年份内气象站点对三套产品年降水量验证的统计变量值 Table 2 Statistics of validation results of 40 meteorological stations on annual precipitation in three typical years in Tianshan Mountains |
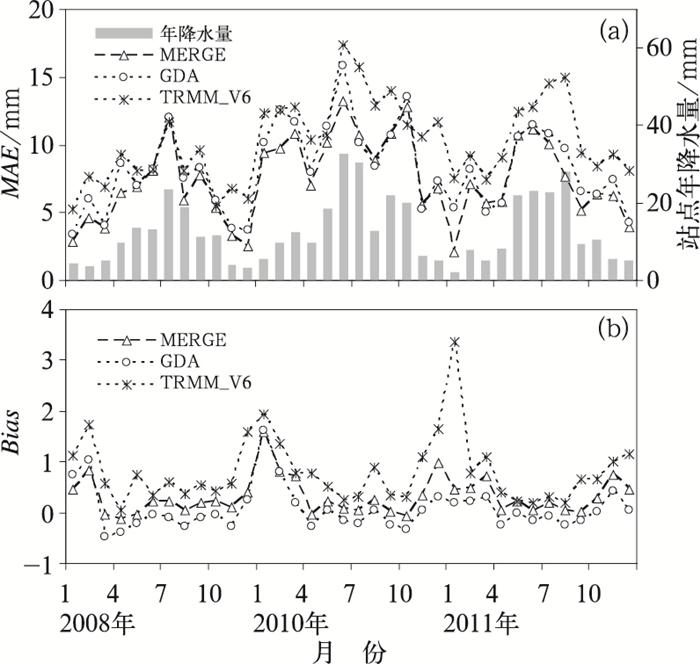
由于RMSE总是表现出与MAE相同的变化趋势,只是在数值上比MAE值大,且上文所述的R2往往带有误导性的精度评价结果,所以,仅采用MAE和Bias指数来评价V6月降水数据的校正结果。图 5是V6、GDA、MERGE在三个特殊年份的月降水与站点实测月降水MAE,Bias时间变化序列图,图 5a表明,在降水较多的雨季(4—10月)MAE>3 mm,在降水较少的干季(11月至次年3月)MAE < 3 mm,可能由于TRMM对山区夏季持续时间较短的对流雨误差较大,虽然进行了基于站点的误差校正,但这些误差不可避免地传递给GDA与MERGE,致使在雨季的平均误差较大。然而,图 5b中Bias则表现出同MAE相反的趋势,即在降水较多的雨季(4—10月)Bias值在0附近,在降水较少的干季(11月至次年3月)Bias值较大,说明经过校正后的GDA、MERGE依然高估干季的降水,而在雨季的偏差更接近0(可能是正负偏差平均的结果)。总体而言,GDA、MERGE均能有效降低V6产品的误差,MERGE产品融合了高时空分辨率的GPM与实测站点信息,表现最佳。考虑到GDA与MERGE在干湿季表现能力,有必要对干湿季节的V6产品分别进行误差校正。
|
图 5 三个特殊年份内V6、GDA、MERGE与实测站点月降水MAE(a),Bias(b)时间变化序列图 Fig. 5 Time-series of MAE (a), Bias (b) between V6, GDA, MERGE and measured monthly precipitation for the typical three years |
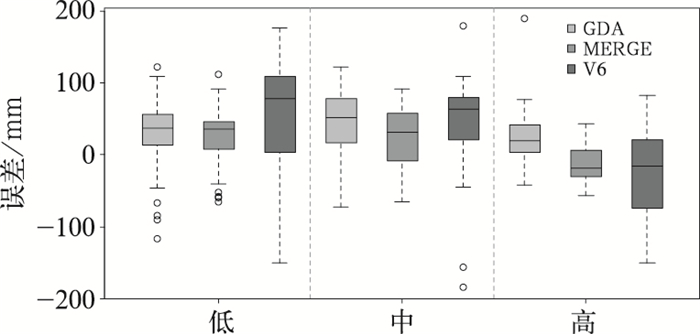
图 6是不同高程带内MERGE, GDA及V6与站点的误差分布图,V6的误差范围在低海拔地区较大(-200~200 mm),而经过校正后的MERGE(-60~90 mm)与GDA(-90~120 mm),不仅能有效降低原始TRMM产品的误差范围,且其平均误差更趋于0值,表明MERGE和GDA方法在低海拔地区的校正效果明显。然而,在中海拔地区,虽然MERGE(31 mm)与GDA(52 mm)的中位数较V6(63 mm)小,但它们对V6误差的改善情况较小,尤其是GDA(-70~120 mm)校正后的产品,与V6(-50~100 mm)相比,反而增加了其误差范围,表明该方法在中海拔地区的局限性。MERGE与GDA均能有效降低高海拔地区V6产品的误差,尤其是MERGE,表现出与气象站点最小的误差范围,表明即使在气象站点分布稀少的高海拔地区,通过MERGE校正方法也可以准确获取该区的降水信息。总体上,两种校正方法均能有效降低各高程带内误差,MERGE产品融合了GPM与站点的降水信息,在各高程带内均表现出良好的校正效果。
|
图 6 不同高程带内GDA,MERGE,V6与气象站点误差分布箱线图 Fig. 6 Boxplot of the error between GDA, MERGE, V6 and meteorological stations in different elevation zones |
(1) 由于山区地形复杂,降水受到下垫面和小地形气象因子的影响,常表现出较大的空间差异(Krajewski et al, 2003),降水在两个相邻的4 km×4 km的GEOS-12卫星像元间可能会表现出36.5%的降水差异(Harmsen et al, 2008)。然而,大多数对TRMM数据校正的方法,都忽略了这种尺度效应,只在原始分辨率下对其进行校正(Cheema and Bastiaanssen, 2012; 宇婧婧等, 2013; Jia et al, 2011; Wanders et al, 2015),如表 3所示。基于两套数据的空间差异,本文提出的MERGE方法能更精准地表达山区的降水分布(图 3, 图 4);即使在气象站点分布稀少的高海拔地区,通过MERGE方法也可以准确获取该区的降水信息(图 6)。
|
|
表 3 水文-气象研究中常用的误差校正方法 Table 3 Bias correction techniques commonly used in hydrometeorological studies |
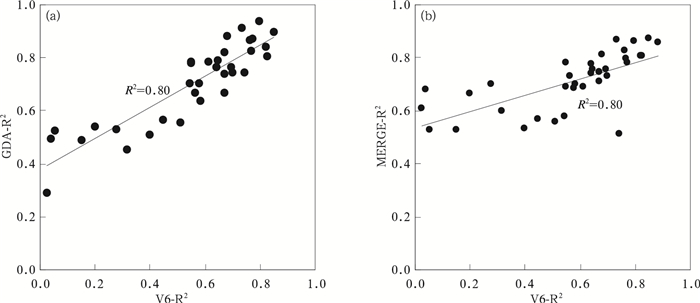
(2) Cheema and Bastiaanssen (2012)认为校正后产品的精度取决于原始TRMM数据的精度,但由于降水时间尺度问题没有进行深入探讨。本文利用V6、MERGE、GDA的月降水数据同站点数据的R2值来探讨原始TRMM数据精度对校正结果的影响。如图 7所示,GDA的精度与V6精度具有很强的相关性(R2=0.80),表明GDA方法对原始TRMM产品依赖性较强,继承了大部分V6的误差。相对于GDA,MERGE的精度与V6精度的相关性较弱(R2=0.47),结合上文三套产品在年、月尺度上的分析结果,表明即使在原始TRMM数据表现不佳的情况下,MERGE方法也能有效降低其误差。
|
图 7 V6精度分别与GDA(a)精度和MERGE(b)精度的散点图 (注:V6-R2、MERGE-R2、GDA-R2分别是V6、MERGE、GDA同站点数据的R2值) Fig. 7 The scatter plots of accuracy between V6 and GDA (a), MERGE (b) (Note: V6-R2, MERGE-R2, GDA-R2 are the R2 value between V6, MERGE, GDA and measured stations, respectively) |
(3) GPM作为新一代的降水观测卫星,搭载了先进的GMI与DPR,提供高时空分辨率的降水数据,相对于TMPA 3B42V7,GPM与站点观测数据相当,误差较小(Tang et al, 2016)。但是其数据的时间序列较短(2014年3月至2016年3月),且与当地的实际降水仍存在一定的误差。而本文仅使用两年的GPM降水数据(2014年3月至2016年3月)来校正TRMM,由于降水分布时空差异较大,尤其在某些年份(月份),降水的不确定性更大,因此,随着后续更多GPM产品的发布,有必要选取更长时间序列的GPM数据,对特定年份(月份)的TRMM数据进行误差校正。
4 结论本文提出的基于GPM和站点数据对TRMM降水产品进行校正的方法,并与广泛使用的GDA方法进行对比,通过天山山区40个气象站点进行交叉验证,结果表明:
(1) 经MERGE与GDA方法校正后的降水产品,增大了V6降水量的变化范围,在空间上表现出同V6一致降水格局,且MERGE方法还能去除部分异常点,起到平滑的效果。在三个典型年份,MERGE与GDA均能明显改善降水的误差,但在降水较少的2010年,GDA与MERGE的校正效果一般。
(2) MERGE与GDA的校正效果在不同月份存在很大差异,即在降水较多的雨季(4—10月)误差较大(MAE>3 mm),而在干季(11月至次年3月)误差较小(MAE < 3 mm);相对GDA,MERGE在低、高海拔区能显著降低V6的误差范围,对准确获取气象站点分布稀少的高海拔地区的降水具有重要意义。
(3) 相对于GDA(R2=0.80),MERGE(R2=0.47)的精度对原始TRMM产品的依赖性较小,即使在原始TRMM数据表现不佳的局部区域,也能有效降低其误差。
由于气象站点在高海拔山区分布稀少,可能会影响校正的结果;且山区的地形起伏变化大,可以在后续的研究中引入地形因子(高程、坡度、坡向)来对TRMM产品进行校正。另外,开发新的卫星产品校正算法对水文、气象和生态研究都有重要意义。
成璐, 沈润平, 师春香, 等, 2014. CMORPH和TRMM 3B42降水估计产品的评估检验[J]. 气象, 40(11): 1372-1379. DOI:10.7519/j.issn.1000-0526.2014.11.010 |
范彬彬, 罗格平, 张弛, 等, 2013. 新疆夏季降水时空分布的适用性评估[J]. 地理研究, 32(9). |
李瑞雪, 2010. 中国天山山区气候变化的时空分布特征[D]. 兰州: 西北师范大学.
|
骆三, 苗峻峰, 牛涛, 等, 2011. TRMM测雨产品3B42与台站资料在中国区域的对比分析[J]. 气象, 37(9): 1081-1090. DOI:10.7519/j.issn.1000-0526.2011.09.004 |
隋玉正, 崔林丽, 史军, 等, 2016. 一种多源全球海洋降水资料融合方法[J]. 热带海洋学报, 35(2): 50-56. DOI:10.11978/2015037 |
唐国强, 万玮, 曾子悦, 等, 2015. 全球降水测量(GPM)计划及其最新进展综述[J]. 遥感技术与应用, 30(4): 607-615. |
宇婧婧, 沈艳, 潘旸, 等, 2013. 概率密度匹配法对中国区域卫星降水资料的改进[J]. 应用气象学报, 24(5): 544-553. DOI:10.11898/1001-7313.20130504 |
张涛, 李宝林, 何元庆, 等, 2015. 基于TRMM订正数据的横断山区降水时空分布特征[J]. 自然资源学报, 30(2): 260-270. DOI:10.11849/zrzyxb.2015.02.009 |
张正勇, 何新林, 刘琳, 等, 2015. 中国天山山区降水空间分布模拟及成因分析[J]. 水科学进展, 26(4): 500-508. |
周胜男, 罗亚丽, 汪会, 2015. 青藏高原、中国东部及北美副热带地区夏季降水系统发生频次的TRMM资料分析[J]. 气象, 41(1): 1-16. |
Ceccherini G, Ameztoy I, Hernández C P R, et al, 2015. High-resolution precipitation datasets in South America and West Africa based on satellite-derived rainfall, enhanced vegetation index and digital elevation model[J]. Remote Sens, 7(5): 6454-6488. DOI:10.3390/rs70506454 |
Cheema M J M, Bastiaanssen W G M, 2012. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin[J]. Int J Remote Sens, 33(8): 2603-2627. DOI:10.1080/01431161.2011.617397 |
Condom T, Rau P, Espinoza J C, 2011. Correction of TRMM 3B43 monthly precipitation data over the mountainous areas of Peru during the period1998-. 2007[J]. Hydrol Process, 25(12): 1924-1933. DOI:10.1002/hyp.7949 |
Duan Z, Bastiaanssen W G M, 2013. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling-calibration procedure[J]. Remote Sens Environ, 131: 1-13. DOI:10.1016/j.rse.2012.12.002 |
Fang J, Du J, Xu W, et al, 2013. Spatial downscaling of TRMM precipitation data based on the orographical effect and meteorological conditions in a mountainous area[J]. Adv Water Resour, 61: 42-50. DOI:10.1016/j.advwatres.2013.08.011 |
Harmsen E W, Mesa S E G, Cabassa E, et al, 2008. Satellite sub-pixel rainfall variability[J]. Int J Syst Appl Eng Dev, 2(3): 91-100. |
Huang C C, Zheng X G, Tait A, et al, 2014. On using smoothing spline and residual correction to fuse rain gauge observations and remote sensing data[J]. J Hydrol, 508: 410-417. DOI:10.1016/j.jhydrol.2013.11.022 |
Huffman G J, Bolvin D T, Nelkin E J, 2015. Day 1 for the integrated multi-satellite retrievals for GPM (IMERG) data sets. NASA Goddard Space Flight Center and Science System Application.
|
Ji X, Chen Y F, 2012. Characterizing spatial patterns of precipitation based on corrected TRMM 3B43 data over the mid Tianshan Mountains of China[J]. J Mt Sci, 9(5): 628-645. DOI:10.1007/s11629-012-2283-z |
Jia S F, Zhu W B, Lü A F, et al, 2011. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China[J]. Remote Sens Environ, 115(12): 3069-3079. DOI:10.1016/j.rse.2011.06.009 |
Joyce R J, Janowiak J E, Arkin P A, et al, 2004. CMORPH:a method that produces global precipitation estimates from passive microwave and Infrared data at high spatial and temporal resolution[J]. J Hydrometeor, 5(3): 487-503. DOI:10.1175/1525-7541(2004)005<0487:CAMTPG>2.0.CO;2 |
Krajewski W F, Ciach G J, Habib E, 2003. An analysis of small-scale rainfall variability in different climatic regimes[J]. Hydrol Sci, 48(2): 151-162. DOI:10.1623/hysj.48.2.151.44694 |
Mantas V M, Liu Z, Caro C, et al, 2015. Validation of TRMM multi-satellite precipitation analysis (TMPA) products in the Peruvian Andes[J]. Atmos Res, 163: 132-145. DOI:10.1016/j.atmosres.2014.11.012 |
Ning S W, Ishidaira H, Udmale P, et al, 2015. Remote sensing based analysis of recent variations in water resources and vegetation of a semi-arid region[J]. Water, 7(11): 6039-6055. DOI:10.3390/w7116039 |
Tang G Q, Zeng Z Y, Long D, et al, 2016. Statistical and hydrological comparisons between TRMM and GPM Level-3 products over a midlatitude basin:is Day-1 IMERG a good successor for TMPA 3B42V7?[J]. J Hydrometeor, 17(1): 121-137. DOI:10.1175/JHM-D-15-0059.1 |
Vila D A, de Goncalves L G G, Toll D L, et al, 2009. Statistical evaluation of combined daily gauge observations and rainfall satellite estimates over continental South America[J]. J Hydrometeor, 10(2): 533-542. DOI:10.1175/2008JHM1048.1 |
Wanders N, Pan M, Wood E F, 2015. Correction of real-time satellite precipitation with multi-sensor satellite observations of land surface variables[J]. Remote Sens Environ, 160: 206-221. DOI:10.1016/j.rse.2015.01.016 |
Willmott C J, Robeson S M, Matsuura K, et al. Assessment of three dimensionless measures of model performance[J]. Environ Modell Soft, 73(c): 167-174.
|
Xu S G, Wu C Y, Wang L, et al, 2015. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics[J]. Remote Sens Environ, 162: 119-140. DOI:10.1016/j.rse.2015.02.024 |
 2018, Vol. 44
2018, Vol. 44 
