2. 中国科学院生态与地理研究所,荒漠与绿洲生态国家重点实验室,乌鲁木齐 830011;
3. 中国科学院大学,北京 100049
2. State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011;
3. University of Chinese Academy of Sciences, Beijing 100049
全球区域一体化同化预报系统(Global/Regional Assimilation and Prediction System,GRAPES)是在中华人民共和国科学技术部和中国气象局共同支持下我国自主发展的新一代数值预报系统。自2009年3月以来其先后完成以改进优化模式物理过程、三维变分同化、同化和模式协同为代表的三个重要阶段(何光鑫等,2011;王德立等,2013;王金成等,2014;郝民等,2014;庄照荣等,2014;姜晓飞等,2015;石荣光等,2015;沈学顺等,2017)。建立了水平分辨率为0.25°×0.25°、垂直方向为60层的全球预报系统GRAPES-GFS 2.0版本,已于2015年底通过了预报能力综合评估,2016年初正式投入业务化运行。
随着数值预报模式的持续发展,从短时临近、短期、中期和延伸期的各个范围和空间尺度越来越精细,预报能力也稳步提高,数值模式在预报业务中的角色日益重要。然而,由于观测、物理过程和网格分辨率等限制,数值预报仍存在误差,那么模式检验则成为“如何在数值模式预报的基础上突出预报员价值”的重要前提。目前,数值模式检验的研究主要集中在两个方面:一是针对模式进行定量化统计检验,二是模式天气学检验,即通过以预报员思路为基础从天气过程发展的环流形式、主要影响系统以及物理条件等方面主观分析和评估模式对不同天气过程的预报性能,虽然这种方法具有一定主观性,但还是能够提供统计检验方法所不能提供的信息,可有效帮助模式开发和研究人员及业务预报人员发现模式偏差特征和找出存在的问题(Kain et al, 2003;2008;毛冬艳等,2014)。
目前针对GRAPES-GFS模式的统计方法检验已经开展了大量工作,为模式研发人员提供了有效的改进依据。王德立等(2013)对GRAPES-GFS模式积云对流参数化方案性能进行评估并提出垂直速度方程和出流层改进方案。胡江林等(2007)研究了模式动力框架的长期积分特征,检验了其积分结果的可用性、收敛性和稳定性,证明了其作为气候研究大气框架的可行性,为改进模式动力框架提供了线索和依据。康岚等(2009)则检验分析了西南地区2 m温度预报偏差发现随着预报时效延长,温度预报误差并未明显增加,并总结了2 m温度预报在西南地区的时空偏差特征。庄照荣等(2014)用不同分辨率的模式预报差异估计了GRAPES-GFS模式的误差,发现模式误差随着分辨率降低和时效的延长而线性增加的趋势。刘艳等(2016)则对最新升级三维变分同化系统进行检验,发现与欧洲中期天气预报中心(ECMWF)和美国国家环境预报中心(NCEP)分析场差异主要来源于GRAPES同化系统中探空、地面报、掩星和飞机观测,以及地形因素导致的偏差的地理分布差异。此外朱红芳等(2007)、徐国强等(2008)、杨学胜等(2009)、陈炯等(2017)还分别从物理过程优化、初始场条件、辐射方案、边界层方案等方面对GRAPES-GFS模式数值预报的影响开展了检验,为模式的继续发展改进提供了依据。
随着2016年初GRAPES-GFS模式在全国正式业务化应用,预报员急需从天气学角度了解其对于各种天气过程的预报性能特点和偏差倾向,从而更好实现其业务预报应用。然而针对GRAPES-GFS模式天气学检验特征的梳理总结较为缺乏,尚难以为预报员提供足够参考。2011年以来,国家气象中心天气预报室开始承担GRAPES-GFS试验和业务模式的天气学检验工作,2015年依托建设搭建完善的THREDDS系统建立多模式数据服务器(http://thredds.cma.gov.cn/thredds/catalog.html),开展GRAPES数值模式产品天气学检验技术的业务化开发,并在2016年初GRAPES-GFS模式正式业务化运行之际完善建立了GRAPES-GFS模式天气学检验业务,正式建立了针对业务应用的日常预报性能常态化检验反馈机制。
据此本文将采用天气学检验方法,梳理总结业务GRAPES-GFS模式在2013—2016年不同季节、不同区域及不同尺度影响系统的暴雨过程预报特征,结合对比国家气象中心全球谱模式T639L60(T639模式)和欧洲中期天气预报中心确定性预报模式(EC模式)预报结果,从主观角度尝试总结其预报性能优势和系统性偏差特征,以期促进充分挖掘数值模式附加值并反馈推进其发展。
1 方法与资料采用主观天气学检验方法,对2013—2016年共38次主要的暴雨过程(北方暴雨6次,南方暴雨20次,热带扰动或者台风降水12次),从短期(模式84 h预报时效内)降水预报效果出发,结合对比EC模式和T639模式降水预报,并进一步对降水系统的相关形势预报或物理量进行主观检验,梳理总结GRAPES-GFS模式预报性能优势和偏差特征。其中对于降水预报的检验,采用观测散点图与模式多时效预报填色图直接叠加对比的方法,实现降水强度、分布形态、预报稳定性的主观直接对比。对于风场和高度场的检验,为直观对比检验槽、脊、切变线、气旋等系统位置强度位置差异,将风场和高度场实况分析场与预报场进行直接叠加对比。对于部分物理量场的水平和垂直分布检验,由于分布较为复杂,则将观测分析场和GRAPES-GFS模式预报场分别绘制对比,被检验的物理量包括相当位温、风速、水平散度和比湿等。另外对地面站点降水观测和预报进行统计分析,对比观测和降水各量级站点数差异,以及TS评分(唐文苑等,2017)情况。
被检验预报数据采用2016年4月业务化运行以来的GRAPES-GFS模式实时预报数据及2013年9月至2015年9月回算预报数据,被检验时效为84 h内(即短期时效)预报场数据。GRAPES-GFS模式业务运行参数设置如表 1。
|
|
表 1 GRAPES-GFS系统主要运行参数设置 Table 1 Parameters of GRAPES-GFS model |
降水实况资料采用了国家气象中心定量降水预报业务评分中使用的中国区域2513地面站逐日08时至次日08时24 h累积降水观测。采用EC模式和T639模式20时起报的12~36、36~60、60~84 h地面24 h累积降水预报数据进行降水预报的对比。大气要素场实况则采用了逐6 h NCEP等压面分析场数据,分辨率为0.5°×0.5°,垂直层次为27层。
2 GRAPES-GFS模式预报检验特征 2.1 短期降水预报性能检验 2.1.1 短期时效内降水预报稳定性特征短期时效内,从诸如东移高空槽、东北冷涡、西南涡、副热带高压边缘切变线、登陆台风系统等多种类型天气系统造成的降水过程看来(表 2),GRAPES-GFS模式对雨带位置、形态、稳定性等方面预报较好,整体较T639模式有一定优势。并且随时效临近雨区调整方向的一致性也优于T639模式,能够为预报员订正预报提供更多信息。
|
|
表 2 具有2.1.1节中描述特征的个例汇总 Table 2 Examples sharing the same characteristics described in 2.1.1 |
例如2016年6月19—20日长江流域降水过程,12~36 h时效(图 1a,1d,1g),GRAPES-GFS模式与T639模式预报相近,对于江汉暴雨到大暴雨降水预报较准,但对于长江下游沿岸大雨以上量级降水则预报略偏北。36~60 h时效(图 1b,1e,1g),T639模式在长江中下游预报则出现了较多漏报,GRAPES-GFS模式对于雨带的形态位置预报较为稳定,整体与12~36 h预报接近,位置略偏北。截至60~84 h时效(图 1c,1f,1i),T639模式未能预报出沿长江中下游的暴雨雨带,出现了较大面积漏报,对于长江沿岸的强降水几乎没有体现,GRAPES-GFS模式则预报雨带位置偏北,但强度和形态则与实况接近。从各时效的雨带预报调整来看,GRAPES-GFS模式预报随着时效临近,雨带位置误差缩小,雨强则与实况接近,并未出现明显的南北摆动,因此GRAPES-GFS模式预报更具有指示性意义。
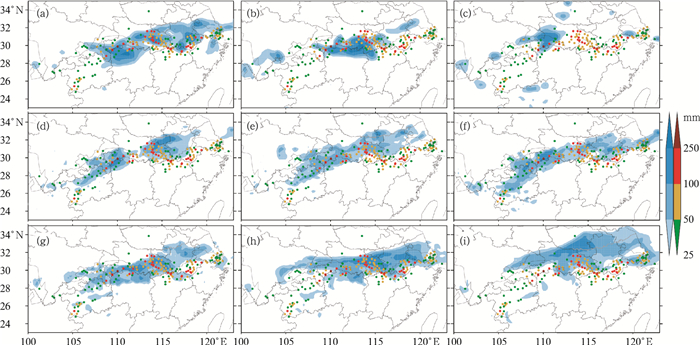
|
图 1 2016年6月19日08时至20日08时12~36 h(a, d, g), 36~60 h(b, e, h), 60~84 h(c, f, i)时效预报24 h累积降水检验(a~c) T639模式, (d~f) EC模式, (g~i) GRAPES-GFS模式 (填色为模式预报,彩色点为实况站点观测) Fig. 1 Verification of 24 h accumulated precipitation of 12-36 h (a, d, g), 36-60 h (b, e, h), 60-84 h (c, f, i) from 08:00 BT 19 to 08:00 BT 20 June 2016 (a-c) T639 model, (d-f) EC model, (g-i) GRAPES-GFS model (Shaded area: model forecast; colour dots: observation) |
另外,对于登陆后台风降水的预报,GRAPES-GFS模式同样体现出较好的预报稳定性,如对于2016年第17号台风鲇鱼登陆前后降水的预报,GRAPES-GFS模式对江南中东部地区和江淮大部降水预报均表现出了较好的稳定性和落区准确性,较T639模式有较明显优势,特别在登陆次日,台风系统与北侧高空槽系统相互作用明显,系统正处于由正压台风系统向副热带斜压系统转换阶段,GRAPES-GFS模式预报表现出令人满意的结果。从该日的预报检验来看(图 2),GRAPES-GFS各时效预报对于江淮地区弓状雨带的形态、位置、强度均与实况较T639模式有较好的表现,60~84 h时效预报雨带位置和雨带形态仍与实况较为接近,表现出较好的预报稳定性和准确性。EC模式则随着预报时效的临近(图 2d,2e,2f),雨带位置偏北和降水强度偏弱的误差缩小,对于雨带形态的预报同样较好。T639模式预报则较不稳定(图 2a,2b,2c),在36~60和60~84 h时效预报较实况偏弱较多,60~84 h则整体与实况雨带形态差异较大,出现了较多漏报。可见,短期时效内,GRAPES-GFS模式对登陆中国大陆台风所产生的降水预报较T639有一定优势,主要表现在台风降水强度、范围、形态等方面。但受限于较长时效的台风路径预报能力,GRAPES-GFS模式对于尚远离大陆的台风系统在较长时效下大陆降水预报稳定性仍较EC模式有一定不足(徐道生等,2014)。

|
图 2 同图 1,但为2016年9月29日08时至30日08时 Fig. 2 Same as Fig. 1, but from 08:00 BT 29 to 08:00 BT 30 September 2016 |
从以上主观天气学检验的角度,GRAPES-GFS模式短期降水预报较T639模式能够提供更有效的预报参考信息,有利于预报员在决定大范围雨带落区和强度时进行参考和释用。而从客观统计检验的角度,对于表 2中所列的天气过程的暴雨预报动态TS评分(图 3),GRAPES-GFS模式各时效预报均较T639模式TS评分较高,且随着时效的延长,TS评分较T639模式降低较小,客观上也表明了GRAPES-GFS模式降水预报较T639模式更加稳定。
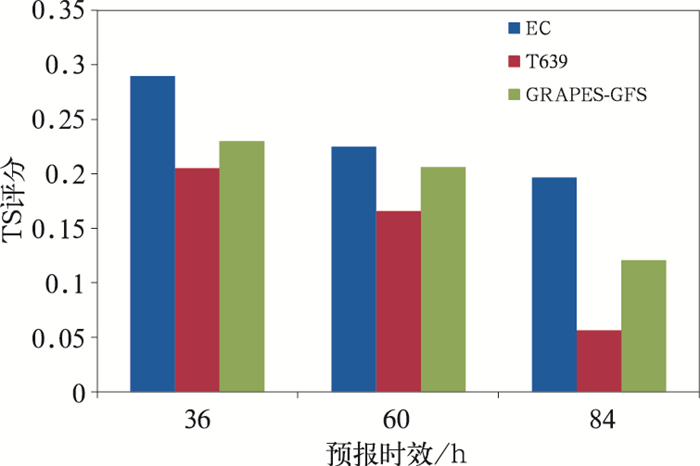
|
图 3 表 2中所列天气过程EC、T639和GRAPES-GFS模式12~36、36~60、60~84 h时效暴雨预报(24 h累积降水>50 mm)动态TS评分 Fig. 3 Dynamical TS score of EC, T639 and GRAPES-GFS models 12-36 h, 36-60 h, and 60-84 h forecast rainfall events showed in Table 2 |
对于部分对流性较强、斜压性相对弱的暴雨天气过程,GRAPES-GFS模式短期时效内预报雨带位置趋于偏北,或者对主雨带南侧暖区的强降水预报不足(表 3)。如2016年3月21日华南中北部暴雨过程(图略),GRAPES-GFS模式虽然对雨带的形态和强度预报与实况接近,但雨带位置预报位于江南地区中南部,较实况偏北约100~200 km。
|
|
表 3 具有2.1.2节中描述特征的个例汇总 Table 3 Examples sharing the same characteristics described in 2.1.2 |
2016年6月30日至7月5日,我国长江中下游地区出现持续性强降水,过程具有对流性较强、降水强度大、持续时间长的特征。对此次天气过程的12~36 h时效累积降水预报的检验可见(图 4a),虽然对实况雨带的准东西向分布特征和雨强预报较为准确,但是GRAPES-GFS模式对于强降水带的预报有偏北误差,实况雨带出现在长江流域沿岸,而模式预报则出现在了江淮中部。然而,预报性能相对优秀的EC模式预报同样出现了类似的偏差特征(图 4c),对主雨带位置的预报较实况偏北。究其原因,一方面从大尺度系统角度,可能是由于模式对雨带南侧偏南气流预报偏强(图略),大尺度锋区被强迫北推,导致降水预报偏北。另一方面,则可能受中尺度预报能力的影响。从地面2 m温度的预报检验来看(图略),GRAPES-GFS模式预报的降水系统下部冷池强度较实况偏弱,温度偏高,由于全球预报模式网格距未及对流可分辨尺度,对于对流性降水中所产生的诸如云中的水凝物蒸发冷却和拖曳作用产生的大气冷却下沉作用预报不足,从而形成宏观角度的冷空气预报偏弱,锋区位置预报偏北,一定程度上导致了模式对降水预报的偏北。又或者由于对较小尺度触发因素(如小地形、冷池等)的预报能力有限,使得对主降水系统南侧低空急流中对流触发的预报不足,从而一定程度上产生了全球预报模式对于此类降水预报偏北的误差特征(Arakawa and Schubert, 1974; Johnson and Wang, 2013; 肖玉华等,2013;王德立等,2013;姜晓飞等,2015;符娇兰和代刊,2016)。对比采用对流可分辨级别分辨率的GRAPES-Meso 3 km模式的降水预报检验可见(图 4b),其降水预报位置与实况更为接近,并无明显预报偏北特征,从侧面反映了模式中尺度过程预报能力对与降水预报准确性的重要作用。

|
图 4 2016年6月30日08时至7月5日08时累积降水检验
(a)GRAPES-GFS模式12~36 h预报,(b)同时效的3 km分辨率GRAPES区域数值预报业务系统(GRAPES-Meso 3 km)模式预报,(c)EC模式预报 (图注同图 1) Fig. 4 Verification of accumulated precipitation from 08:00 BT 30 June to 08:00 BT 5 July 2016 (a) GRAPES-GFS model 12-36 h forecast, (b) GRAPES-Meso 3 km model, (c) EC model (illustration same as Fig. 1) |
从降水站点观测与预报散点图统计来看(图 5a),GRAPES-GFS模式对于小量级预报有一定的过报和空报情况,而对于约50 mm以上量级降水预报则有偏弱的情况。从分量级站点降水预报和观测统计来看(图 5b),对于大雨以下(< 25 mm)量级降水,GRAPES-GFS模式预报站点数偏多,而对于暴雨(>50 mm)以上量级降水预报,GRAPES-GFS模式则明显较实况预报的站点数偏少,整体上GRAPES-GFS模式预报表现出小量级降水预报空报较多而大量级降水预报偏弱明显。类似特征在诸如EC模式和T639模式预报也有出现(张宏芳等,2014),属全球模式预报偏差的共同特征。而对于GRAPES-GFS模式,在中高层波动不明显而低层天气系统主导作用的天气过程中降水预报偏弱的特征则较为明显(表 4)。

|
图 5 2016年汛期(4月1日至10月31日)站点降水观测和预报统计
(a)GRAPES-GFS站点降水预报与观测散点图 (黑色实线和公式为观测和预报线性拟合结果,虚线为最理想状态线性拟合结果), (b)各量级降水的站点个数的对数统计 Fig. 5 Rainfall observation and forecast statistics from 1 April to 31 October 2016 (a) scatter plot of rainfall observation and GRAPES-GFS model forecast (Solid black line is the linear fit result, dashed line is the ideal linear fit result); (b) logrithmic statistics of the number of stations under every magitude of precipitation |
|
|
表 4 具有2.1.3节中描述特征的个例汇总 Table 4 Examples sharing the same characteristics described in 2.1.3 |
如2016年4月2日的一次长江中下游的大到暴雨降水过程,实况中高空500 hPa等高线较平直,没有明显的高空槽影响(图 6c),而低层850 hPa则受一准东西向切变线影响(图 6b),实况700和850 hPa相当位温密集带位于江淮地区以北(图 7),GRAPES-GFS模式24 h预报对以上天气系统特征均与实况较为一致。然而对于降水的预报,虽然GRAPES-GFS模式对雨带准东西向分布与实况接近,但雨强明显较实况偏弱,且雨区强中心较分散。

|
图 6 2016年(a)4月3日08时36 h时效累积降水检验(图注同图 1);(b)GRAPES-GFS模式4月2日20时24 h时效850 hPa高度场和风场检验及(c)500 hPa高度场和风场检验 (黑线为GRAPES-GFS模式24 h时效预报,蓝线为NCEP分析场;单位:dagpm) Fig. 6 Verification of (a) 36 h accumulated precipitation (shaded) and observation (colour dots) at 08:00 BT 3 April, (b) GRAPES-GFS 24 h at 850 hPa, wind and geopotential height forecast, (c) 500 hPa geopotential height and wind at 20:00 BT 2 April 2016 (Black lines and wind barbs are GRAPES-GFS 24 h forecast while the blue ones are observation; unit: dagpm) |
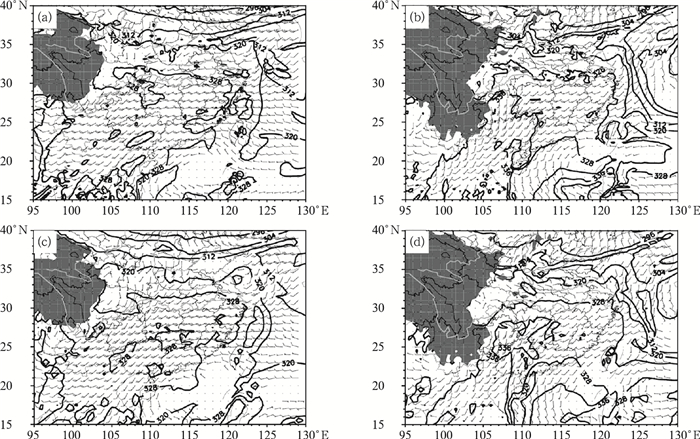
|
图 7 2016年4月2日20时24 h时效GRAPES-GFS模式(a,c)700 hPa、(b,d)850 hPa相当位温场(单位:K)和风场检验(a, b)GRAPES-GFS预报,(c, d)NCEP分析场 Fig. 7 GRAPES-GFS 24 h forcast θe (unit: K) and wind at 700 hPa (a, c) and 850 hPa (b, d) at 20:00 BT 2 April 2016 (a, b) GRAPES-GFS forecast, (c, d) NCEP analysis |
从出现这类降水预报误差的天气过程(表 4)实况分析来看,在类似以上高空波动较弱,低层扰动系统活跃的降水过程中,实况降水系统均具有一定的对流性质。模式误差产生的原因则可能是受限于全球模式较粗的网格分辨率,在高空波动条件相对较弱的背景下,对于低层物理过程预报能力依赖性更高,而对这些物理过程描述的方案与网格分辨率有着较大的联系,如边界层方案和云物理方案、辐射方案等(王德立等,2013;刘羽等,2013;姜晓飞,2015),因此对于此类弱高空波动影响过程,预报员在业务应用中可参考分辨率更高的区域数值模式预报酌情进行订正。
2.2 物理量和天气系统预报偏差检验特征 2.2.1 低层大气湿度预报检验特征对于大型雨带南侧的暖湿空气输送带中的水汽预报,GRAPES-GFS模式预报湿度趋于偏大,相当位温也较实况偏大,整体表现为能量输送偏大,低层高能高湿层偏厚,但降水预报并未出现明显过报。
图 8表示一次江南地区暴雨过程,从图中低层比湿场来看,冷式切变线南侧的偏南气流中,GRAPES-GFS模式预报比湿普遍大于18 g· kg-1,较实况偏大约2 g·kg-1(图 8b,8c),而沿118°E垂直剖面检验可见(图 8d,8e),GRAPES-GFS模式预报的锋区附近的(相当位温密集带)大气低层比湿16 g·kg-1以上的厚度明显厚于实况,高度可达850 hPa,对应位置的低层相当位温也较实况偏高,850 hPa等压面位置相当位温超过了332 K,而从实况来看则未及该数值。从表 5中的个例来看,GRAPES-GFS模式对切变线南侧预报均有湿偏差特征,相当位温数值偏大,表现为大气低层能量预报偏强,相当位温也较实况偏大,能量输送偏强,低层高能高湿层偏厚,然而从降水预报结果来看,在此类湿偏差背景下,GRAPES-GFS模式预报的降水强度并未出现明显偏强现象(图 8a),预报员在业务应用中可把握好此规律,而模式开发者在进行后续物理过程调试时,也要注意模式目前所具有的此种特性。
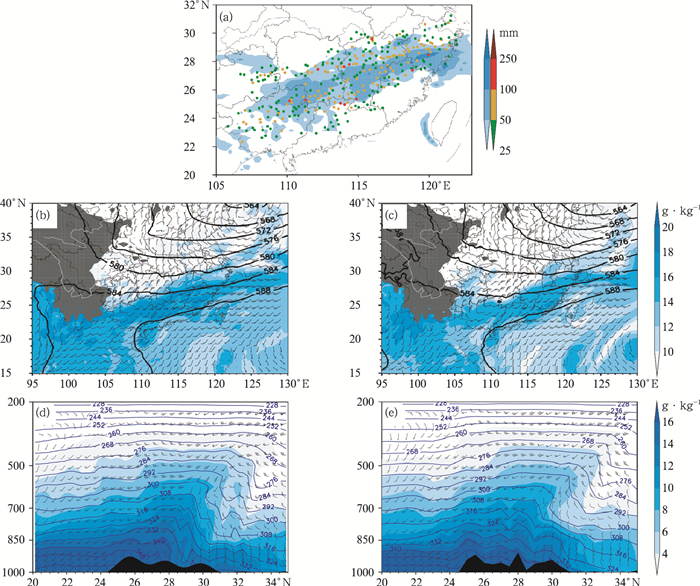
|
图 8 2016年6月16日08时24 h累积降水检验(a,填色为12~36 h时效的24 h累积降水,散点为观测的24 h累积降水)及15日20时24 h时效天气形势检验(b~e) (b)GRAPES-GFS模式24 h小时预报(等值线为500 hPa高度场,单位:dapgm;风标为850 hPa风场,填色为850 hPa比湿场),(c)同图 8b,但为NCEP-GFS模式分析场,(d)GRAPES-GFS模式24 h预报沿118°E垂直剖面(等值线为相当位温,单位:K;风标为水平风场,填色为比湿场),(e)同图 8d,但为NCEP-GFS模式分析场 Fig. 8 Verification of 24 h accumulated precipitation at 08:00 BT 16 June and weather background at 20:00 BT 15 June 2016 (b-e) (a) GRAPES-GFS 12-36 h forecast 24 h accumulated precipitation (shaded) and observation (colour dots), (b) GRAPES-GFS 24 h forecast (contour: 500 hPa geopotential height, unit: dagpm, wind barbs: 850 hPa wind, colored: specific humidity), (c) same as Fig. 8b, but for NCEP-GFS model analysis, (d) vertical cross-section of GRAPES-GFS 24 h forecast along 118°E (contour: equivalent temperature, unit: K, wind barbs: horizontal wind, colored: specific humidity), (e) same as Fig. 8d, but for NCEP-GFS model analysis |
|
|
表 5 具有2.2.1节中描述特征的个例汇总 Table 5 Examples sharing the same characteristics described in 2.2.1 |
GRAPES-GFS模式对副热带地区低涡系统预报趋于偏强,具体表现为对低涡中心的等高线预报偏低或者槽偏深,低涡附近辐合偏强,急流风速偏大。如图 9天气过程,对于西南涡旋系统的预报较实况偏强明显,850 hPa(图 9b)在四川盆地上空出现了140 dagpm闭合线,而实况中并未出现该闭合线,500 hPa低涡预报同样偏强(图 9e,9f),出现了580 dagpm闭合曲线,而实况则仅为一高空槽形态;与高度场预报偏差相伴随,在850 hPa(图 9b,9c)低涡外围环流低空急流中也出现了过报,GRAPES-GFS模式预报最大超过了21 m·s-1,而实况中仅超过15 m·s-1,并且涡旋东南象限的低层水平散度场较实况偏强明显(图 9e,9f),整体上GRAPES-GFS模式对于此次天气过程涡旋系统较实况更加深厚、强盛,对动力场的预报较实况偏强。
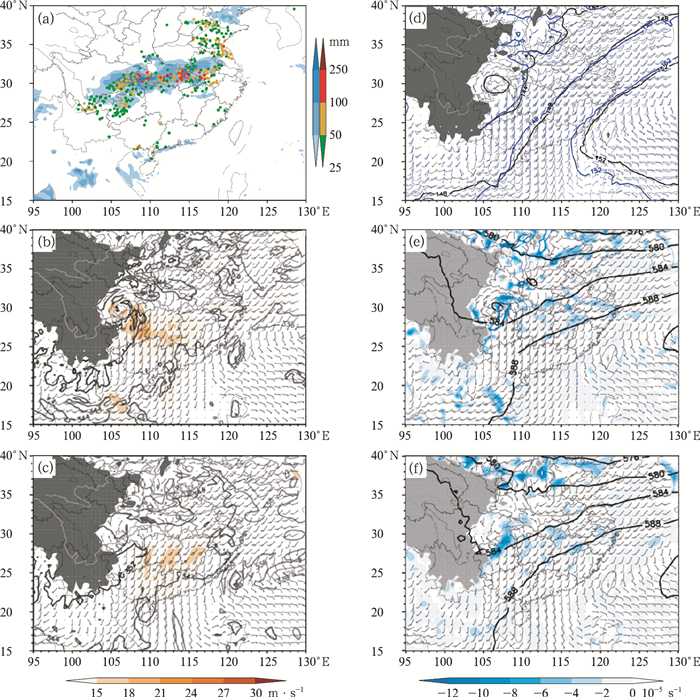
|
图 9 2016年7月1日08时24 h累积降水检验(a,填色为GRAPES-GFS模式12~36 h时效预报的24 h累积降水,散点为观测的24 h累积降水)和6月30日20时天气形势检验(b-f) (b)GRAPES-GFS模式24 h预报(等值线为850 hPa相当位温,单位:K,风标为850 hPa风场;填色为风速),(c)同图 9b,但为NCEP-GFS模式分析杨,(d)GRAPS-GFS模式850 hPa天气形势24 h时效预报检验(黑色等值线为高度场预报,蓝色等值线为NCEP分析场,单位:dagpm;黑色风标为水平风场预报,蓝色风标为NCEP-GFS模式分析场),(e)同图 9b(等值线为500 hPa高度场,单位:dagpm;填色为850 hPa散度场),(f)同图 9e,但为NCEP-GFS模式分析场 Fig. 9 Verification of 24 h accumulated precipitation at 08:00 BT July 1 (a) and weather background at 20:00 BT June 30 2016 (b-f) (a) GRAPES-GFS 12-36 h forecast 24 h accumulated precipitation (shaded) and observation (scatter points), (b) GRAPES-GFS 24 h forecast (contour: 850 hPa equivalent temperature, unit: K; wind barbs: 850 hPa wind, shaded: wind speed), (c) same as Fig. 9b, but for NCEP-GFS model analysis, (d) GRAPES-GFS 24 h 850 hPa weather background forecast verification (black contour: geopotential height forecast, unit: dagpm; black wind barb: wind forecast, blue bar: NCEP-GFS analysis), (e) same as Fig. 9b (contours: 500 hPa geopotential height, unit: dagpm; shaded: 850 hPa divergence), (f) same as Fig. 9e, but for NCEP-GFS model analysis |
具有与以上相同偏差特征的个例如表 6,表现为对低涡中心的等高线预报偏低或者槽偏深,低涡附近辐合偏强,急流风速偏大,低涡系统较实况偏深厚,这表明GRAPES-GFS模式在预报该类天气过程中对于大气动力场的抬升作用偏强,然而从降水预报检验来看,模式降水预报并未出现过报情况(图 9a),这一特点同样值得预报员和模式开发者注意。
|
|
表 6 具有2.2.2节中描述特征的个例汇总 Table 6 Examples sharing the same characteristics described in 2.2.2 |
本研究采用天气学检验方法,依靠预报员主观分析,通过对2013—2016年GRAPES-GFS模式实时预报和回算的38次暴雨过程的降水和天气系统检验,梳理总结出了以下模式预报性能优势和系统性偏差特征,供业务预报和模式研发人员参考应用,以期充分利用数值模式附加值并推进其发展。
对于短期时效降水预报,GRAPES-GFS模式对雨带位置、形态和雨带随时效临近调整趋势一致性等方面均较T639模式有一定优势。但对于部分对流性较强、斜压性相对较弱的暴雨过程,GRAPES-GFS模式短期时效内预报雨带位置趋于偏北,或者对主雨带南侧的强降水预报不足,预报员可相应向南订正雨带。此外对于高空波动较弱而低层天气系统活跃并具有一定对流性的天气过程,GRAPES-GFS模式预报降水趋于偏弱,预报员可结合具有更高分辨率的中尺度模式进行订正应用。
而对于天气系统和高空物理量预报,在降水预报大致正确的情况下,GRAPES-GFS模式预报出现湿度场和副热带低涡系统偏强的系统性偏差特征。具体表现为模式对大型雨带南侧的暖湿空气输送带中的湿度预报偏大,相当位温也较实况偏高,低层高能高湿层偏厚,急流风速偏强,偏南暖湿气流能量输送偏强,对低涡中心的高度场预报偏小或高空槽偏深,低涡附近辐合偏强,整体呈现出热力场和动力场预报偏强的特征。然而在以上偏差背景下,GRAPES-GFS模式降水预报并无明显过报出现,这类天气系统偏差与降水预报的对应关系十分值得预报员和模式开发者的注意和进一步探讨。
总结以上检验结论,GRAPES-GFS模式预报所具有的偏差特征的重要原因或为模式网格分辨率的限制。GRAPES-GFS模式水平分辨率为0.25°,而微物理、边界层和辐射等物理过程的预报方案对网格分辨率水平有较大的依赖性,因而在尚未达到对流可分辨的模式网格分辨率级别上,模式对于多种物理过程预报会产生偏差,如对不稳定能量释放所产生的大气对流运动预报会偏弱,对降水系统内部冷却和拖曳作用所导致的干冷空气下沉堆积估计不足(郭云云等,2015;聂皓浩等,2016;宫宇,2013;宫宇和罗亚丽,2014),对尺度较小的地形或冷池的对流激发作用难以体现(Luo et al, 2014),从而导致了对各种物理过程依赖性较大的过程预报偏差,如对流性降水较强过程的雨带位置预报偏北,弱高空波动背景下降水预报偏弱的偏差特征。
而从相反的角度出发,GRAPES-GFS模式又或可通过增强大气动力强迫作用,增大大气不稳定能量输送,以减少由于全球预报模式降水相关物理方案的“先天不足”所导致的强降水预报不足的情况。如2.2.1和2.2.2节中检验发现的GRAPES-GFS模式对大气湿度场和副热带低涡预报的系统性偏差特征与降水预报的对应关系,或可以理解为此类动力和大气湿热力条件的过报现象正是数值预报模式大气动力热力场对于物理方案不足的一种自动适应调整,预报员在业务应用中可参考此类偏差特征加以相应的调整释用。未来随着计算能力的提升而带来的模式分辨率的提升,更加全面完善的物理过程方案得以应用,GRAPES-GFS模式预报能力会得到更加长足的发展。
本研究对GRAPES-GFS模式系统性天气学检验特征进行了一定梳理总结,一方面为业务预报人员对其更好的运用提供了一定认识背景;另一方面则为模式开发者从现象层面发现模式预报偏差倾向,从而进行有针对性的改进模式提供了依据。但目前该文章的研究内容主要是对于偏差现象层面的总结、讨论和解释,未来对于产生偏差特征的更深层次模式内部过程机理的探讨尚需要结合更多数值试验进行更深入研究。
陈炯, 马占山, 苏勇, 2017. 适用于GRAPES模式C-P边界层方案的设计和实现[J]. 应用气象学报, 28(1): 52-61. |
符娇兰, 代刊, 2016. 基于CRA空间检验技术的西南地区东部强降水EC模式预报误差分析[J]. 气象, 42(12): 1456-1464. DOI:10.7519/j.issn.1000-0526.2016.12.003 |
宫宇, 2013.梅雨锋前线状中尺度对流系统的观测及模拟研究[D].北京: 中国气象科学研究院. http://cdmd.cnki.com.cn/Article/CDMD-85101-1013212472.htm
|
宫宇, 罗亚丽, 2014. 梅雨锋前线状中尺度对流系统成熟阶段的空气垂直运动分析[J]. 热带气象学报, 30(4): 687-699. DOI:10.3969/j.issn.1004-4965.2014.04.009 |
郭云云, 邓莲堂, 范广洲, 等, 2015. GRAPES中尺度模式中不同积云参数化方案预报性能对比研究[J]. 气象, 41(8): 932-941. |
郝民, 田伟红, 龚建东, 2014. L波段秒级探空资料在GRAPES同化系统中的应用研究[J]. 气象, 40(2): 158-165. |
何光鑫, 李刚, 张华, 2011. GRAPES-3DVar高阶递归滤波方案及其初步试验[J]. 气象学报, 69(6): 1001-1008. |
胡江林, 沈学顺, 张红亮, 等, 2007. GRAPES模式动力框架的长期积分特征[J]. 应用气象学报, 18(3): 276-284. DOI:10.3969/j.issn.1001-7313.2007.03.003 |
姜晓飞, 刘奇俊, 马占山, 2015. GRAPES全球模式浅对流过程和边界层云对低云预报的影响研究[J]. 气象, 41(8): 921-931. |
康岚, 冯汉中, 屠妮妮, 等, 2009. GRAPES模式预报西南地区夏季2m温度的检验评估[J]. 高原山地气象研究, 29(2): 26-32, 40. DOI:10.3969/j.issn.1674-2184.2009.02.004 |
刘艳, 薛纪善, 张林, 等, 2016. GRAPES全球三维变分同化系统的检验与诊断[J]. 应用气象学报, 27(1): 1-15. |
刘羽, 杨学胜, 孙健, 2013.在GRAPES模式中引入夹卷过程的影响试验[C]//创新驱动发展提高气象灾害防御能力——S10大气物理学与大气环境.南京: 中国气象学会: 215-220. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=RDQX201302004&dbname=CJFD&dbcode=CJFQ
|
毛冬艳, 朱文剑, 樊利强, 等, 2014. GRAPES_MESO V3.3模式强天气预报性能的初步检验[J]. 气象, 40(12): 1429-1438. DOI:10.7519/j.issn.1000-0526.2014.12.001 |
聂皓浩, 刘奇俊, 马占山, 2016. 高分辨率GRAPES模式中云微物理方案对强降水的模拟和诊断研究[J]. 气象, 42(12): 1431-1444. DOI:10.7519/j.issn.1000-0526.2016.12.001 |
沈学顺, 苏勇, 胡江林, 等, 2017. GRAPES_GFS全球中期预报系统的研发和业务化[J]. 应用气象学报, 28(1): 1-10. |
石荣光, 刘奇俊, 马占山, 2015. 利用GRAPES模式研究气溶胶对云和降水过程的影响[J]. 气象, 41(3): 272-285. |
唐文苑, 周庆亮, 刘鑫华, 等, 2017. 国家级强对流天气分类预报检验分析[J]. 气象, 43(1): 67-76. |
王德立, 徐国强, 贾丽红, 2013. GRAPES的积云对流参数化方案性能评估及其改进试验[J]. 气象, 39(2): 166-179. |
王金成, 庄照荣, 韩威, 等, 2014. GRAPES全球变分同化背景误差协方差的改进及对分析预报的影响:背景误差协方差三维结构的估计[J]. 气象学报, 72(1): 62-78. |
肖玉华, 康岚, 徐琳娜, 等, 2013. 西南区域中尺度数值模式预报性能及其与天气过程关系初探[J]. 气象, 39(10): 1257-1264. DOI:10.7519/j.issn.1000-0526.2013.10.003 |
徐道生, 陈子通, 戴光丰, 等, 2014. 对流参数化方案的改进对GRAPES模式台风预报的影响研究[J]. 热带气象学报, 30(2): 210-218. DOI:10.3969/j.issn.1004-4965.2014.02.002 |
徐国强, 陈德辉, 薛纪善, 等, 2008. GRAPES物理过程的优化试验及程序结构设计[J]. 科学通报, 53(20): 2428-2434. DOI:10.3321/j.issn:0023-074X.2008.20.006 |
杨学胜, 沈元芳, 徐国强, 2009. 辐射方案对GRAPES全球模式的影响[J]. 大气科学, 33(3): 593-599. DOI:10.3878/j.issn.1006-9895.2009.03.16 |
张宏芳, 潘留杰, 杨新, 2014. ECMWF、日本高分辨率模式降水预报能力的对比分析[J]. 气象, 40(4): 424-432. DOI:10.3969/j.issn.1671-1742.2014.04.016 |
朱红芳, 王东勇, 管兆勇, 等, 2007. 不同初始场条件对GRAPES模式数值预报的影响[J]. 气象学报, 65(4): 493-502. DOI:10.3321/j.issn:0577-6619.2007.04.003 |
庄照荣, 薛纪善, 陆慧娟, 等, 2014. 全球GRAPES等压面三维变分分析预报循环系统及试验[J]. 高原气象, 33(3): 666-674. |
Alpert J C, 2004.Sub-grid scale mountain blocking at NCEP[C]. http://www.emc.ncep.noaa.gov/gmb/wd23ja/presentations/mb_16confNWP_P2.4/mbnwp8b.pdf
|
Arakawa A, Schubert W H, 1974. Interaction of a cumulus cloud ensemble with the large-scale environment, Part Ⅰ[J]. J Atmos Sci, 31(3): 674-701. DOI:10.1175/1520-0469(1974)031<0674:IOACCE>2.0.CO;2 |
Johnson A, Wang Xuguang, 2013. Object-based evaluation of a storm-scale ensemble during the 2009 NOAA Hazardous Weather Testbed Spring Experiment[J]. Mon Wea Rev, 141(3): 1079-1098. DOI:10.1175/MWR-D-12-00140.1 |
Kain J S, Baldwin M E, Janish P R, et al, 2008. Subjective verification of numerical models as a component of a broader interaction between research and operations[J]. Wea Forecasting, 18(5): 847-860. |
Kain J S, Janish P R, Weiss S J, et al, 2003. Collaboration between forecasters and research scientists at the NSSL and SPC:the spring program[J]. Bull Amer Meteor Soc, 84(12): 1797-1806. DOI:10.1175/BAMS-84-12-1797 |
Kim Y J, Arakawa A, 1995. Improvement of orographic gravity wave parameterization using a mesoscale gravity wave model[J]. J Atmos Sci, 52(11): 1875-1902. DOI:10.1175/1520-0469(1995)052<1875:IOOGWP>2.0.CO;2 |
Lott F, Miller M J, 1997. A new subgrid-scale orographic drag parametrization:Its formulation and testing[J]. Quar J Roy Meteor Soc, 123(537): 101-127. DOI:10.1002/(ISSN)1477-870X |
Luo Yali, Gong Yu, Zhang Dalin, 2014. Initiation and organizational modes of an extreme-rain-producing mesoscale convective system along a Mei-Yu front in East China[J]. Mon Wea Rev, 142(1): 203-221. DOI:10.1175/MWR-D-13-00111.1 |
 2018, Vol. 44
2018, Vol. 44 
