2. 重庆市气象科学研究所,重庆 401147
2. Chongqing Institute of Meteorology and Science, Chongqing 401147
对称不稳定是空气在垂直方向对流稳定、水平方向惯性稳定时,具有的一种倾斜方向的大气不稳定特征,是倾斜对流发展的必要条件。对称不稳定也可以表述为等相当位温面上的惯性不稳定或等绝对角动量面上的对流不稳定(Emanuel,1983)。在干空气、湿空气及饱和湿空气中存在的对称不稳定分别称为干对称不稳定、位势对称不稳定及条件性对称不稳定,其中,位势对称不稳定及条件性对称不稳定统称为湿对称不稳定(费建芳等,2009)。
湿对称不稳定广泛存在于不同季节的各类降水现象中。Byrd(1989)统计了冬季美国南部平原的27次异常降水事件发现,超过80%的带状降水满足条件性对称不稳定条件,60%的非带状降水中也出现了条件性对称不稳定条件。Reuter and Aktary(1995)分析了加拿大Alberta中部1990—1991年的1460个探空资料,认为冬季44%的探空分析表明是湿对称不稳定的,春季、秋季和夏季分别为20%、26%和3%。
湿对称不稳定可以解释锋区带状降水产生和发展的机制(Bennetts and Hoskins, 1979;Bennetts and Sharp, 1982)。理想实验对比(Fischer and Lalaurette, 1995a;1995b)表明,无锋生及湿对称不稳定释放的数值模拟过程不足以解释观测结果,且垂直速度的增长也弱于有锋生及湿对称不稳定释放的模拟过程。湿对称不稳定常出现在副热带气旋的暖锋附近,及对流层中层长波槽前的强而湿的西南气流区域。垂直方向表现为水平风速随高度增加,风向随高度顺转,大气斜压性强且处于近似饱和或湿绝热递减率状态(Wiesmueller and Zubrick, 1998)。Schultz and Schumacher(1999)总结了锋生与湿对称不稳定的关系,认为锋区带状降水的形成是锋生及倾斜对流共同释放湿对称不稳定性产生的结果。由于湿对称不稳定的释放需要克服湍流扩散作用及外部对流不稳定产生的补偿下沉气流,因此,锋生强迫作用对湿对称不稳定的释放非常必要。许多锋区带状的暴雨(周玉淑等,2003;王宗敏等,2014;张芳华等,2014;刘璐等,2015;王晨曦等,2018;李瑞萍等,2019)和暴雪天气(Snook,1992;Moore and Lambert, 1993;王建中和丁一汇,1995;盛春岩和杨晓霞,2002),均与锋面抬升作用下湿对称不稳定性的释放相联系。
然而,锋生强迫效应除了释放湿对称不稳定性外,与湿对称不稳定的形成是否有联系?本文拟通过数值模拟资料诊断分析2016年6月27日20时至28日20时(北京时,下同)发生在重庆、贵州及湖南等地的一次大暴雨过程,探讨暴雨过程中湿对称不稳定的演变特征及其与锋生作用之间可能存在的关系。
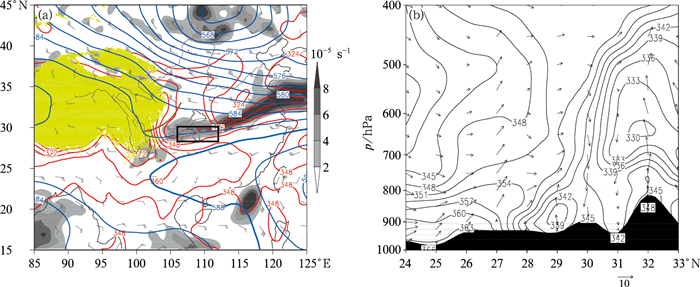
1 天气过程及数值模拟验证 1.1 天气过程2016年6月27日20时,500 hPa副热带高压控制100°E以东的长江以南地区,高原槽东移至四川盆地西部,700 hPa切变线位于四川宜宾以东的长江沿线地区,850 hPa相当位温(θe)锋区位于贵州北部至湖南北部一带(图 1a)。在高原槽及副热带高压之间,地面锋区到达28°N附近,暖湿舌位于倾斜锋区的前部,西南气流携暖湿空气沿着准纬向的锋区倾斜向上爬升,形成锋前上升、锋后下沉的锋区次级环流(图 1b)。在稳定的切变线及锋区抬升作用下,6月27日20时至28日20时,重庆、贵州及湖南等地的降水显著发展,雨带呈准纬向分布,24 h累积最大降雨出现在酉阳县花田站,达210.8 mm,其中28日05—08时连续出现19,32.3,33.7,19.7 mm的强降雨,如图 2a所示。按暴雨过程中雨团的组织与发展特征,强降水可分为两个阶段:第一阶段自27日20时开始,重庆西南部有一中尺度雨团发展东移,28日00时移至湖南地区北部;第二阶段自28日00时左右开始,为暴雨过程的主要降雨时段,重庆南部有多个中尺度雨团同时发展,并逐渐与湖南地区北部的雨团联接,至02时组织成重庆南部、贵州北部至湖南地区北部的近千千米的纬向雨带。雨带缓慢南移,28日02—08时为纬向雨带的主要降雨时段,之后降雨逐渐减弱,至17时雨带移出重庆。此次大暴雨过程是重庆地区夏季的一次典型的纬向锋面暴雨过程,强降雨致重庆南部的綦江流域出现了自1998年以来的最高水位,引发綦江、彭水、酉阳等多地出现暴雨洪涝灾害。通过诊断分析进一步了解此次暴雨发生发展的动热力特征,将有助于加强对此类暴雨的分析和预报能力。
|
图 1 2016年6月27日20时(a)500 hPa位势高度(蓝色等值线,单位:dagpm)、500 hPa风场(风向杆)、700 hPa涡度(灰度阴影)及850 hPa相当位温θe(红线,单位:K) (黄色阴影代表青藏高原,黑色方框代表研究的强降水区域,棕色粗实线为500 hPa槽线),(b)风(矢线,由V与W×10合成,单位:m·s-1)与相当位温θe(黑线,单位:K)沿109°E的剖面图(阴影为地形) Fig. 1 (a) The 500 hPa geopotential height (blue contours, unit: dagpm), 500 hPa wind (wind barb), 700 hPa vorticity (grey shadows), and 850 hPa equivalent potential temperature θe (red lines, unit: K) (Yellow area represents Tibetan Plateau, black box represents studied heavy rainfall area, brown thick solid line represents 500 hPa trough), (b) vertical cross-section of wind (vector, formatted by V and W×10, unit: m·s-1) and equivalent potential temperature θe (black lines, unit: K) along 109°E at 20:00 BT 27 June 2016 (Shadow represents terrain) |
|
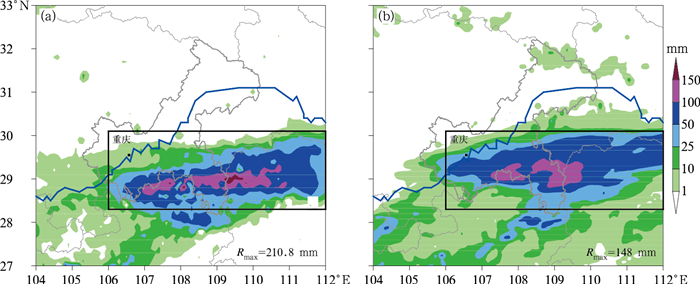
图 2 2016年6月27日20时至28日20时累积的(a)观测降水及(b)模拟结果 (黑色方框同图 1;Rmax代表最大累积降水量;蓝线代表长江,下同) Fig. 2 2 (a) Observed and (b) simulated precipitation from 20:00 BT 27 to 20:00 BT 28 June 2016 (The black box is same as Fig. 1; Rmax denotes the maximum accumulated rainfall; blue line denotes the Yangtze River, the same below) |
采用非静力中尺度数值模式WRF V3.9.1对此次暴雨过程进行了数值模拟,模拟时间从6月27日08时开始,积分36 h至28日20时,积分步长为2 min,spin-up时间约12 h。模拟使用双重嵌套方案,水平范围以34.5°N、104.5°E为中心,D01格距为27 km,网格数为201×161,D02格距为9 km,网格数为289×217,垂直方向分51层。积云对流参数化采用BMJ方案,微物理过程采用Goddard方案,长波和短波辐射均采用RRTMG方案,行星边界层处理采用MYJ方案,陆面过程采用Noah方案。初始场及侧边界条件为1°×1°分辨率的NCEP/NCAR间隔6 h的再分析资料,模拟结果的输出时间间隔为1 h。
图 2b为第二层嵌套方案模拟的6月27日20时至28日20时的累积降水,对比观测结果(图 2a)可见,模拟的雨带位置、走向与范围均和观测较一致,均呈纬向分布于重庆南部至湖南地区北部一带,雨带中心也较为一致,只是模拟的最大降雨量偏小,为148 mm,而观测的最大降雨量为210.8 mm。
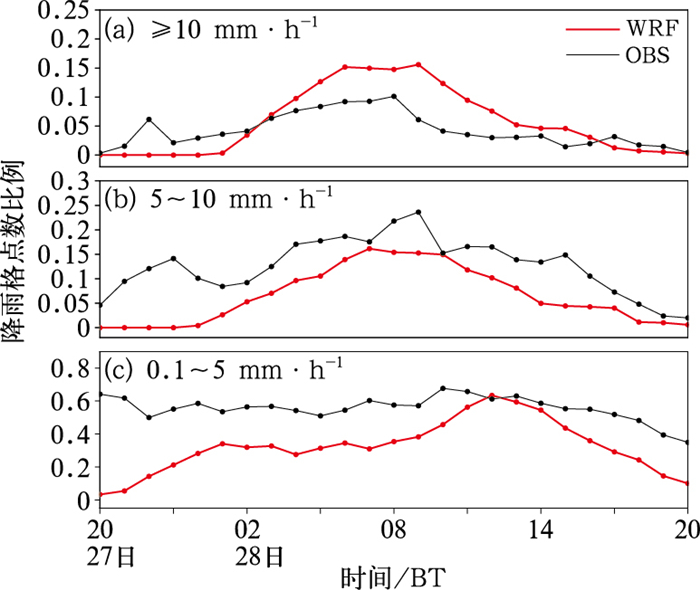
为了反映不同强度降雨的模拟效果,结合了Luo et al(2014)的方法,将雨强分为3个等级:强降雨(≥10 mm·h-1)、中等降雨(5~10 mm·h-1)及弱降雨(0.1~5 mm·h-1)。分析所选区域内(图 2中黑色方框)各等级雨强的格点数比例的演变,以反映不同强度降雨模拟的区域大小,如图 3所示。在暴雨过程的第一阶段(6月27日20时至28日00时),观测的强降雨(图 3a)及中等降雨(图 3b)均出现短时峰值,但模拟结果仅出现小范围的弱降雨(图 3c),强度与范围较观测均显著偏小,表明对第一阶段的单一中尺度雨团的模拟效果较差。而在暴雨过程的第二阶段(6月28日00—17时),即暴雨过程的主要降雨时段,模拟与观测结果在强降雨、中等降雨及弱降雨的变化趋势上均较为一致。降雨范围的模拟有一定偏差,模拟的强降雨范围较观测略偏大,而中等及弱降雨范围略偏小。但总体来看,主要降雨时段内的模拟结果与观测较为接近,可以使用模拟资料来分析暴雨发生、发展的过程及原因。因此,下文的诊断分析是基于第二层嵌套方案的模拟结果,经双线性插值至0.25°×0.25°网格上得到的数据进行。
|
图 3 2016年6月27日20时至28日20时强降水区域(图 2中黑色长方形区域) (a)雨强≥10 mm·s-1、(b)雨强5~10 mm·s-1及(c)雨强0.1~5 mm·s-1的格点数比例随时间的演变 Fig. 3 Temporal evolution of grid points proportion with (a) rainfall rate ≥ 10 mm·s-1, (b) rainfall rate between 5-10 mm·s-1, and (c) rainfall rate between 0.1-5 mm·s-1 in heavy rainfall area (the black rectangle area in Fig. 2) from 20:00 BT 27 to 20:00 BT 28 2016 |
吴国雄等(1995)证明,在满足静力近似,并假定垂直速度的水平变化远小于水平速度的垂直切变时,p坐标系中湿位涡MPV可分解为垂直分量MPV1和水平分量MPV2,其表达式见式(1)。
| $ \begin{array}{l}{M P V 1=-g\left[f+\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\right] \frac{\partial \theta_\text{e}}{\partial p}} \\ {M P V 2=g\left(\frac{\partial v}{\partial p} \frac{\partial \theta_\text{e}}{\partial x}-\frac{\partial u}{\partial p} \frac{\partial \theta_\text{e}}{\partial y}\right)}\end{array} $ | (1) |
可见,湿位涡的垂直分量MPV1受垂直方向的绝对涡度及对流稳定度影响,水平分量MPV2(湿斜压项),受垂直风切变和水平方向的相当位温梯度影响。
Schultz and Schumacher(1999)、费建芳等(2009)指出,在大气为惯性稳定和对流性稳定的情况下,以地转风计算的湿位涡为负值时(MPVg < 0),则存在湿对称不稳定性(moist symmetric instability, MSI)。此判据适用于与推导条件相同的二维坐标下(章丽娜等,2018)。惯性稳定的条件可由绝对地转涡度>0判定,即ζg+f>0,ζg为地转涡度,f为地转参数。对流稳定的条件为∂θe/∂p < 0。在实际分析时,由于中尺度模式模拟的地转风常包含更多的噪音,常使用ζ来代替ζg,MPV来代替MPVg(王宗敏等,2014)。本文采用上述方法,当∂θe/∂p < 0,f+ζ>0时,若湿位涡MPV < 0,则判断为对称不稳定,即通过计算在满足惯性稳定及对流稳定时,湿位涡的演变来表征湿对称不稳定的演变特征。
锋生效应与湿对称不稳定之间的联系密切,锋生强度可通过锋生函数进行诊断分析,包含水汽因子的湿锋生函数F可写为如下形式(Chen et al,2007;张芳华等,2014):
| $ \begin{aligned} F=& \frac{\mathrm{d}}{\mathrm{d} t}\left|\nabla \theta_{\mathrm{e}}\right|=F_{1}+F_{2}+F_{3} \\ F_{1}=&-\frac{1}{2\left|\nabla \theta_{\mathrm{e}}\right|}\left[\left(\frac{\partial \theta_{\mathrm{e}}}{\partial x} \frac{\partial \theta_{\mathrm{e}}}{\partial x}-\frac{\partial \theta_{\mathrm{e}}}{\partial y} \frac{\partial \theta_{\mathrm{e}}}{\partial y}\right)\left(\frac{\partial u}{\partial x}-\right.\right.\\ &\left.\left.\frac{\partial v}{\partial y}\right)+2 \frac{\partial \theta_{\mathrm{e}}}{\partial x} \frac{\partial \theta_{\mathrm{e}}}{\partial y}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right]\\ F_{2} &=-\frac{1}{2}\left|\nabla \theta_{\mathrm{e}}\right|\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) \\ F_{3} &=-\frac{1}{\left|\nabla \theta_{\mathrm{e}}\right|} \frac{\partial \theta_{\mathrm{e}}}{\partial p}\left(\frac{\partial \theta_{\mathrm{e}}}{\partial x} \frac{\partial \omega}{\partial x}+\frac{\partial \theta_{\mathrm{e}}}{\partial y} \frac{\partial \omega}{\partial y}\right) \end{aligned} $ | (2) |
式中,F1为变形项,F2为辐合项,F3为垂直项。当F>0时锋生,F < 0时锋消。
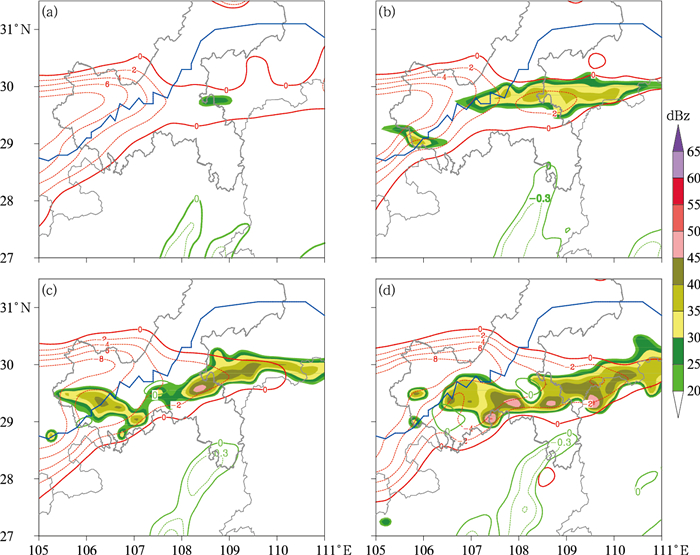
3 纬向雨带的湿对称不稳定特征图 4为750 hPa上对流稳定度、惯性稳定度及基本反射率的水平分布。可以看出,在6月27日22时(图 4a),重庆及周边大部地区f+ζ>0,满足惯性稳定条件。∂θe/∂p < 0的对流稳定区位于重庆西部至两湖交界地区,其中西段范围较宽广,东段呈较窄的带状分布。降雨回波开始在这一对流稳定且惯性稳定的区域内生成。28日00时(图 4b),迅速发展成为纬向带状的强降雨回波带。02时(图 4c)及04时(图 4d),纬向雨带继续发展,强降雨回波基本维持在对流稳定且惯性稳定的区域内,但纬向雨带断裂处出现小范围的惯性不稳定区域。可见,在纬向雨带生成及迅速发展的过程中,纬向雨带所在区域不仅在垂直方向上是对流稳定的,而且在水平方向上是惯性稳定的,不利于纬向雨带的迅速发展。
|
图 4 模拟的2016年6月27—28日750 hPa上的负∂θe/∂p(红色虚线,单位:10-4 K·Pa-1)、负绝对涡度(绿色虚线,单位:10-4 s-1)以及反射率因子(彩色阴影) (a)27日22时,(b)28日00时,(c)28日02时,(d)28日04时 Fig. 4 Simulated 750 hPa negative ∂θe/∂p (red dashed lines, unit: 10-4 K·Pa-1), negative absolute vorticity (green dashed lines, unit: 10-4 s-1), and reflectivity (color shadows) during 27 to 28 June 2016 (a) 22:00 BT 27, (b) 00:00 BT 28, (c) 02:00 BT 28, (d) 04:00 BT 28 |
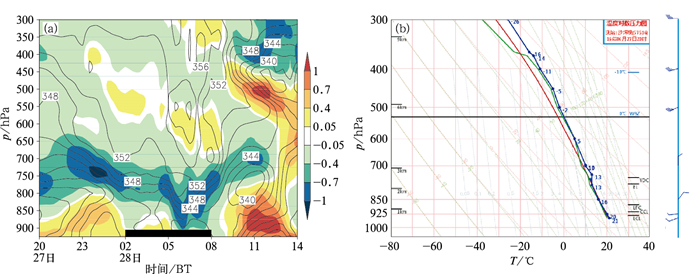
为了更清晰地了解此次暴雨过程中对流稳定性的分布及演变,图 5a给出了沙坪坝站6月27日20时至28日14时模拟的θe及∂θe/∂p的时间高度分布。27日20时至28日02时,沙坪坝站上空800~650 hPa维持显著的对流稳定层结,而800 hPa以下存在一定的对流不稳定性。对比27日20时的探空曲线(图 5b),777 hPa以下为对流不稳定层结,自由对流高度为877 hPa,CAPE为7.3 J·kg-1,观测的低空弱不稳定性层结较模拟结果略为深厚。可见,模拟结果较好地再现了低空弱对流不稳定和800 hPa以上对流稳定的层结特征,但对第一阶段中尺度雨团的模拟结果并不理想,而对第二阶段的纬向雨带模拟较接近实况。结合图 4a可知,27日22时回波开始在重庆东部发展,其所在位置的模式地面在900 hPa高度附近,对流不稳定层结非常浅薄,降雨回波主要在稳定层结中发展。同时图 5a表明,主要降雨时段内,即28日02时以后,对流稳定层结迅速向下扩展,低空对流不稳定层结基本消失,至28日08时以后才再次出现低空对流不稳定层结,纬向雨带主要在对流稳定性层结中发生发展,因此下文将探讨纬向雨带在倾斜方向上的不稳定性。
|
图 5 2016年6月27日20时至28日14时沙坪坝站(a)模拟的θe(黑线,单位:K)及∂θe/∂p(彩色阴影,单位:10-3 K·Pa-1)的时间高度分布(黑色长条代表强降雨时段),(b)27日20时观测T-logp图 Fig. 5 (a) Simulated time-height distribution of θe (black line, unit: K) and ∂θe/∂p (color shadows, unit: 10-3 K·Pa-1) from 20:00 BT 27 to 14:00 BT 28 June 2016 (black strip: period of heavy rainfall), (b) observed T-logp of Shapingba Station at 20:00 BT 27 June 2016 |
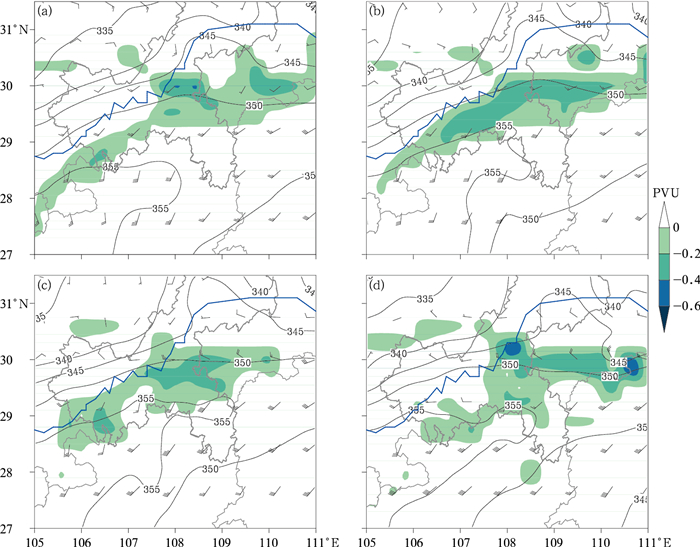
当湿空气在垂直方向对流稳定、水平方向惯性稳定时,可能发展倾斜方向的湿对称不稳定性。Wiesmueller and Zubrick(1998)对一次暴雪天气的诊断分析显示,观测到的增强雪带与湿对称不稳定区的位置几乎一致。图 6给出了750 hPa上的湿对称不稳定、相当位温及风的水平分布。可以看出,27日22时(图 6a),750 hPa上锋区的相当位温密集带位于29°~30°N附近,呈准纬向分布,贵州西北部至重庆南部地区为低空锋区南侧的西南暖湿气流控制,带状的湿对称不稳定区位于锋区南侧及西南暖湿气流北端。28日00时(图 6b),湿对称不稳定带有所扩展和增强。02时(图 6c)至04时(图 6d),湿对称不稳定带向重庆东部及两湖交界地区收缩。在低空锋区与湿对称不稳定的演变过程中,对比图 4中纬向雨带的演变可以发现,纬向雨带与湿对称不稳定的分布具有密切联系,湿对称不稳定区及纬向雨带始终位于低空锋区南侧的西南暖湿气流中,湿对称不稳定与纬向雨带的分布较为一致,纬向雨带生成于湿对称不稳定区中,并在其中发展。
|
图 6 模拟的2016年6月27—28日750 hPa湿对称不稳定区(彩色阴影)、风场(风向杆)及相当位温(黑线,单位:K) (a)27日22时,(b)28日00时,(c)28日02时,(d)28日04时 Fig. 6 Simulated distribution of 750 hPa moist symmetric instability (color shadows), wind (wind barb) and θe (black line, unit: K) during 27 to 28 June 2016 (a) 22:00 BT 27, (b) 00:00 BT 28, (c) 02:00 BT 28, (d) 04:00 BT 28 |
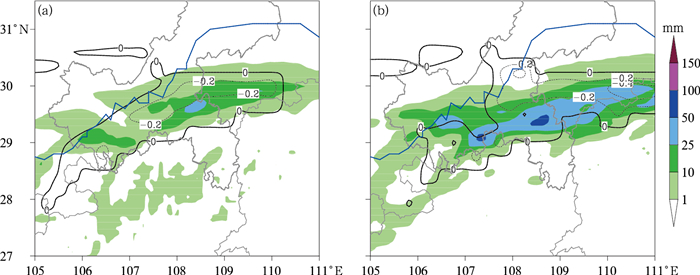
3 h累积降雨与对应时段平均的湿对称不稳定的水平分布可以进一步体现低空湿对称不稳定与纬向雨带之间的关系,如图 7所示。27日22时,弱降雨开始在湿对称不稳定区域内出现,23时至28日02时(图 7a),纬向雨带逐渐生成,3 h累积达10 mm以上的降雨基本位于湿对称不稳定区内。28日02—05时(图 7b),湿对称不稳定区域扩展,重庆南部至两湖交界地区出现宽广的湿对称不稳定区,纬向雨带也显著发展,雨带中心3 h累积降雨达50 mm以上,且25 mm以上的累积降雨仍基本维持在湿对称不稳定区内。
|
图 7 模拟的2016年6月(a)27日23时至28日02时,(b)28日02—05时的750 hPa平均的湿对称不稳定区(黑虚线,单位:PVU)以及累积降雨(彩色阴影) Fig. 7 Simulated distribution of 750 hPa average moist symmetric instability (black dashed lines, unit: PVU) and accumulated precipitation (color shadows) from (a) 23:00 BT 27 to 02:00 BT 28 June, (b) 02:00 BT to 05:00 BT 28 June 2016 |
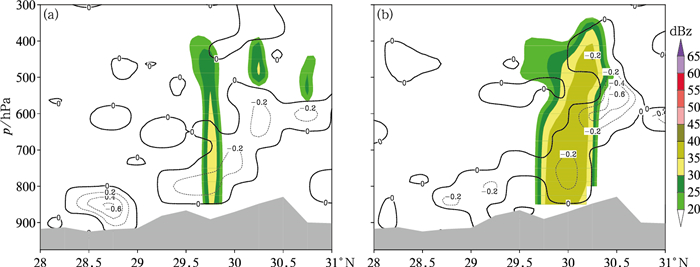
王晨曦等(2018)指出,发展旺盛的条件性对称不稳定主要活跃在对流层低层。图 8给出沿109°E对湿对称不稳定及基本反射率所做的垂直剖面,剖面基本垂直于雨带走向。图 8a显示,27日23时,湿对称不稳定区自南向北逐渐从地面倾斜向上延伸至对流层中层600 hPa附近,降雨回波垂直分布于29.5°~30°N的低空湿对称不稳定区域。图 8b显示,28日01时,湿对称不稳定条件倾斜向上发展,达到500 hPa以上,降雨回波带较27日23时显著变宽,位于29.5°~30.5°N,随高度增加略向北倾斜。回波带仍与低空湿对称不稳定区相联系。湿对称不稳定与降雨回波的垂直剖面表明,暴雨期间湿对称不稳定自南向北呈倾斜形态,降雨的形成及增强与低空湿对称不稳定区相联系。
|
图 8 模拟的2016年6月(a)27日23时及(b)28日01时湿对称不稳定(黑虚线,单位:PVU)及反射率因子(彩色阴影)的沿109°E垂直剖面 (灰色阴影代表地形) Fig. 8 Simulated vertical cross sections of moist symmetric instability (black dashed lines, unit: PVU), and reflectivity (color shadows) along 109°E at (a) 23:00 BT 27 and (b) 01:00 BT 28 June 2016 (Grey shadow represents terrain) |
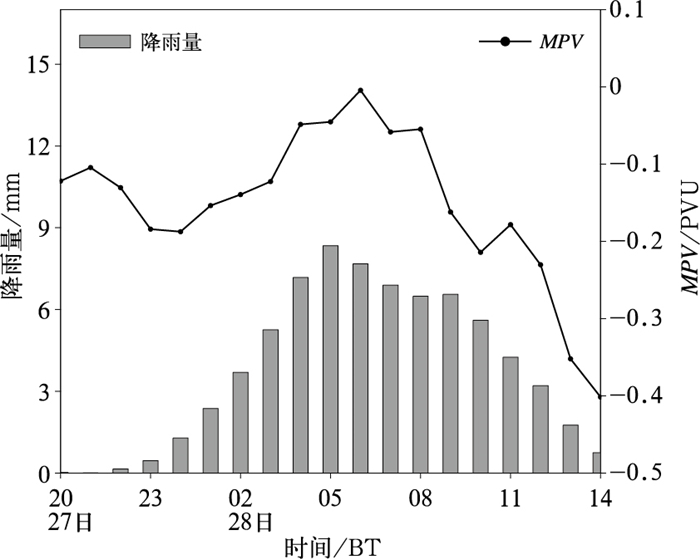
为了探讨降雨与湿对称不稳定性演变之间的关系,并避免单个站点的偶然性,给出750 hPa上29°~30°N、107°~110°E区域内平均的降雨量及MPV的逐小时变化,如图 9所示。由于该区域基本满足对流稳定及惯性稳定条件,MPV的演变可以表征湿对称不稳定的演变特征。图中显示,在纬向雨带形成前,27日21时至28日00时,平均的MPV呈现负值增长,湿对称不稳定逐渐增强,在28日00时以后,纬向雨带形成并发展,在降雨的作用下,28日00—06时湿对称不稳定缓慢释放减弱。07时以后,随着纬向雨带的减弱,低空对流稳定度减小并逐渐转为对流不稳定,不再满足湿对称不稳定条件。可见,在纬向雨带出现前,湿对称不稳定逐渐积累增强,在纬向雨带生成后,湿对称不稳定维持并缓慢释放减弱,为纬向雨带的持续发展提供了有利的动力条件。
|
图 9 模拟的2016年6月27日20时至28日14时平均降雨及750 hPa MPV的逐小时演变 Fig. 9 Simulated hourly evolution of average precipitation and 750 hPa MPV from 20:00 BT 27 to 14:00 BT 28 June 2016 |
对流层低层的锋生不仅有利于对称不稳定能量的释放(王宗敏等,2014),且锋生效应增强后,降水产生的潜热释放有利于条件对称不稳定性和锋生次级环流的发展(张芳华等,2014)。在此次暴雨过程中,纬向雨带的持续发展增强与湿对称不稳定的存在和持续有关,但湿对称不稳定的产生和维持机制是什么?下文试图从纬向锋生效应的角度对此进行分析。
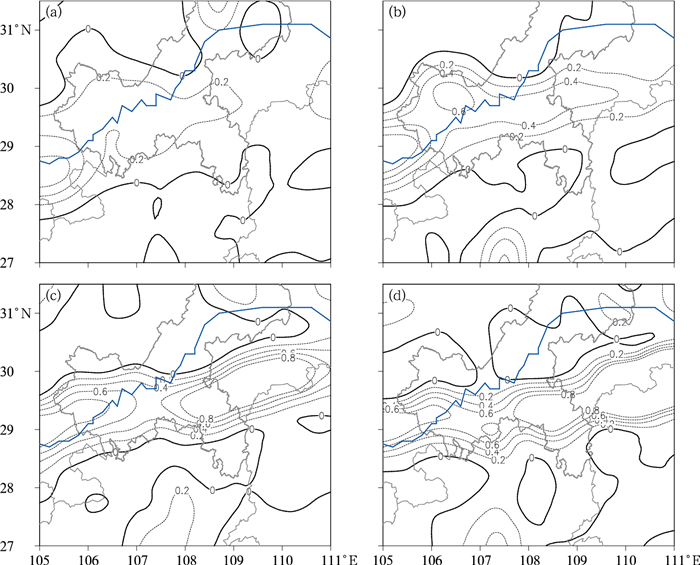
图 10为暴雨期间750 hPa上正锋生函数的水平分布。图中显示,6月27日22时至28日04时,重庆南部地区维持准纬向的正锋生函数,锋生函数逐渐增大,表明重庆南部地区的低空纬向锋生逐渐增强。对比图 4与图 6中回波带及湿对称不稳定区的分布可以发现,同时刻的锋生带、纬向雨带及湿对称不稳定区的位置近乎一致,均位于锋区南侧的西南气流中,西南气流在锋区向上滑行,锋生效应加强了锋前湿对称不稳定性的释放和纬向雨带的形成。
|
图 10 模拟的2016年6月27—28日750 hPa正锋生函数
(黑虚线,单位:10-8 K·m-1·s-1)
(a)27日22时,(b)28日00时,(c)28日02时,(d)28日04时 Fig. 10 Simulated 750 hPa positive frontogenesis function value during 27 to 28 June 2016 (black dashed lines, unit: 10-8 K·m-1·s-1) (a) 22:00 BT 27, (b) 00:00 BT 28, (c) 02:00 BT 28, (d) 04:00 BT 28 |
孙力等(2015)指出,湿位涡 < 0的主要负贡献来源于湿斜压项。由锋生函数与湿位涡的表达式可知,锋生函数与湿位涡的湿斜压项均与水平相当位温梯度相联系。由于锋区及其附近的θe等值线呈准纬向分布,在理想条件下,∂θe/∂x
3 h平均的湿对称不稳定与锋生函数的水平分布可以较为清楚地反映两者间的关系(图 11)。27日20—23时(图 11a),纬向的弱锋生位于重庆地区南部,锋生区域内分布着带状不均匀的湿对称不稳定区。27日23时至28日02时(图 11b),随着锋生效应的增强,锋生区域内的湿对称不稳定范围同样有所扩展,且带状特征更加明显。

|
图 11 模拟的2016年6月27—28日750 hPa上3 h平均的湿对称不稳定(彩色阴影)与正锋生函数(黑虚线,单位:10-8 K·m-1·s-1)的水平分布
(a)27日20—23时,(b)27日23时至28日02时 Fig. 11 Simulated distribution of 750 hPa 3 h average moist symmetric instability (color shadows, unit: PVU) and positive frontogenesis function value
(black dashed lines, unit: 10-8 K·m-1·s-1)
(a) from 20:00 BT to 23:00 BT 27, (b) from 23:00 BT 27 to 02:00 BT 28 June 2016 |
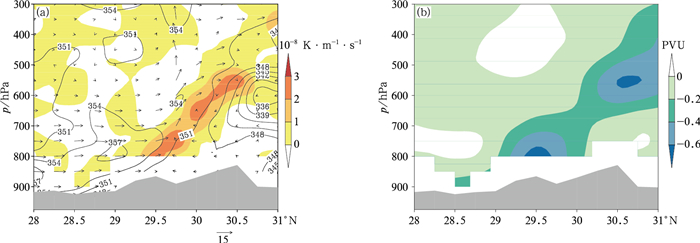
28日02时湿对称不稳定区109°E附近的平均风呈现准西风特征,偏南风分量较弱(图 1,图 6),沿109°E作相当位温、锋生函数及MPV2的垂直剖面,剖面基本垂直于环境的平均风,如图 12所示。锋区θe密集带的南侧,由于低空急流及低空辐合的增强,沿着倾斜锋区有斜升气流及显著的锋生效应存在,斜升气流与锋区北侧的下沉气流形成了倾斜的锋区次级环流(图 12a)。锋生位置对应着较强的湿位涡负水平分量MPV2(图 12b),并因此在锋区南侧29.5°N附近的对流层低层和30.5°N附近的对流层中层分别形成两处显著的湿对称不稳定区域,降雨主要发生在锋区南侧的29.5°N附近的低空湿对称不稳定区(图略)。可见,纬向锋生、湿对称不稳定及纬向雨带的联系主要体现在对流层低层,这可能与低层常满足风速随高度增加,且降雨的发展离不开低层水汽条件有关。
|
图 12 模拟的2016年6月28日02时(a)锋生函数(彩色阴影)、θe(黑色等值线,单位:K)及风(矢线,由V与W×10合成,单位:m·s-1),(b)MPV2(彩色阴影)沿109°E的垂直剖面 (灰色阴影代表地形) Fig. 12 Simulated vertical cross-sections of (a) frontogenesis function (color shadows), θe (black lines, unit: K) and wind (vector, formatted by V and W×10, unit: m·s-1), (b) MPV2 (color shadows) along 109°E at 02:00 BT 28 June 2016 (Grey shadow represents terrain) |
为进一步说明纬向锋生与湿位涡水平分量MPV2的联系,图 13给出了29°~30°N、107°~110°E区域内800 hPa上平均的锋生函数各项及湿斜压项随时间的变化。27日20时至28日03时,锋生函数的辐合项和变形项显著增强,导致锋生效应迅速增强,对比图 13中MPV2的演变可知,这一阶段伴随着MPV2的负值增长。28日03时以后,随着锋生效应的减弱,MPV2也由负值增长转为负值减弱。结合前述分析可见,纬向锋生效应的增强,引起MPV2的负值增长,有利于纬向雨带形成前湿对称不稳定的增强及形成后湿对称不稳定的维持,从而有利于纬向雨带的生成及持续发展。纬向锋生效应增强引起MPV2的负值增长,可能是此次暴雨过程中湿对称不稳定条件增强及维持的重要机制,也是纬向雨带生成并持续发展的重要成因。

|
图 13 模拟的2016年6月27—28日800 hPa平均的锋生函数(单位:10-8 K·m-1·s-1)及其变形项(单位:10-8 K·m-1·s-1)、辐合项(单位:10-8 K·m-1·s-1)、垂直项(单位:10-8 K·m-1·s-1)及湿斜压项MPV2(单位:PVU)的时间演变 Fig. 13 Simulated temporal evolution of 800 hPa average frontogenesis function value (unit: 10-8 K·m-1·s-1) and its deformation part (unit: 10-8 K·m-1·s-1), divergence part (unit: 10-8 K·m-1·s-1), vertical part (unit: 10-8 K·m-1·s-1) and MPV2 (unit: PVU) during 27 to 28 June 2016 |
此次暴雨天气发生在副热带高压北侧及500 hPa高原槽前的切变锋区内,锋区及雨带均呈准纬向分布于重庆、贵州及湖南等地。暴雨分为两个阶段,其中与纬向雨带对应的第二阶段为暴雨的主要降雨时段。本文通过对暴雨过程中纬向雨带的数值模拟及其湿对称不稳定特征的诊断分析,得出如下主要结论:
(1) 纬向雨带所在区域对流稳定且惯性稳定,但存在倾斜方向的湿对称不稳定性。纬向雨带形成前,低空湿对称不稳定逐渐增强;形成后,低空湿对称不稳定缓慢释放减弱,但仍维持了较长时间; 湿对称不稳定的持续释放为纬向雨带的持续发展提供了有利的动力条件。
(2) 锋生与湿位涡的关系表明,在纬向锋条件下,锋生效应的增强可能导致低空湿位涡水平分量MPV2的负值增长,有利于对流稳定且惯性稳定区域内湿位涡的负值增强,从而有利于纬向雨带形成前湿对称不稳定的增强及纬向雨带形成后湿对称不稳定的维持。在纬向锋生的作用下,纬向雨带、低空湿对称不稳定与纬向锋生的分布近乎一致,均位于低空锋区南侧的西南暖湿气流中。锋生效应增强,引起湿位涡水平分量MPV2的负值增长,促进湿对称不稳定的增强及维持,可能是此次暴雨过程中纬向雨带生成及持续发展的重要机制。
本文仅是在纬向锋面条件下,通过个例的模拟与诊断对暴雨过程中湿对称不稳定条件的特征及其与锋生效应的关系作了初步分析,模拟结果虽然再现了纬向雨带的湿对称不稳定特征及演变,但较观测仍有一定误差,如模式对于暴雨过程前期的低空弱对流不稳定性及可能与其有关的第一阶段的中尺度雨团的模拟结果不够理想,对于暴雨过程中可能存在的对流不稳定向对称不稳定转化的过程仍需做进一步的分析。并且,在实际的锋生过程中,锋面走向及锋生效应的分布多种多样,锋生与湿对称不稳定的关系实际上非常复杂,锋生在湿对称不稳定条件产生及释放中的作用仍有待于更多的研究。
费建芳, 伍荣生, 宋金杰, 等, 2009. 对称不稳定理论的天气分析与预报应用研究进展[J]. 南京大学学报(自然科学版), 45(3): 323-333. Fei J F, Wu R S, Song J J, et al, 2009. Advances in synoptic analysis and application of symmetric instability theory[J]. J Nanjing Univ (Nat Sci), 45(3): 323-333 (in Chinese). DOI:10.3321/j.issn:0469-5097.2009.03.001
|
李瑞萍, 王秀明, 夏扬, 等, 2019. 一次夏季冷锋后暴雨的形成机制探析[J]. 气象, 45(1): 50-60. Li R P, Wang X M, Xia Y, et al, 2019. Study on formation mechanism of a summer cold sector torrential rainfall[J]. Meteor Mon, 45(1): 50-60 (in Chinese).
|
刘璐, 冉令坤, 周玉淑, 等, 2015. 北京"7.21"暴雨的不稳定性及其触发机制分析[J]. 大气科学, 39(3): 583-595. Liu L, Ran L K, Zhou Y S, et al, 2015. Analysis on the instability and trigger mechanism of torrential rainfall event in Beijing on 21 July 2012[J]. Chin J Atmos Sci, 39(3): 583-595 (in Chinese).
|
盛春岩, 杨晓霞, 2002. 一次罕见的山东暴雪天气的对称不稳定分析[J]. 气象, 28(3): 33-37. Sheng C Y, Yang X X, 2002. Symmetry instability analysis of an unusual storm snow in Shandong Pro-vince[J]. Meteor Mon, 28(3): 33-37 (in Chinese).
|
孙力, 董伟, 药明, 等, 2015. 1215号"布拉万"台风暴雨及降水非对称性分布的成因分析[J]. 气象学报, 73(1): 36-49. Sun L, Dong W, Yao M, et al, 2015. A diagnostic analysis of the causes of the torrential rain and precipitation asymmetric distribution of Typhoon Bolaven (2012)[J]. Acta Meteor Sin, 73(1): 36-49 (in Chinese). DOI:10.3969/j.issn.1005-0582.2015.01.008
|
王晨曦, 邓莲堂, 范广洲, 等, 2018. 一次华北锋面带状降水过程中的对流-对称不稳定诊断分析[J]. 气象, 44(12): 1518-1528. Wang C X, Deng L T, Fan G Z, et al, 2018. Diagnostic analysis of convective symmetric instability during a banded precipitation process in north China[J]. Meteor Mon, 44(12): 1518-1528 (in Chinese). DOI:10.7519/j.issn.10000526.2018.12.002
|
王建中, 丁一汇, 1995. 一次华北强降雪过程的湿对称不稳定性研究[J]. 气象学报, 53(4): 451-460. Wang J Z, Ding Y H, 1995. Research of moist symmetric instability in a strong snowfall in North China[J]. Acta Meteor Sin, 53(4): 451-460 (in Chinese). DOI:10.3321/j.issn:0577-6619.1995.04.003
|
王宗敏, 丁一汇, 张迎新, 等, 2014. 副高外围对流雨带中的对流-对称不稳定及锋生的诊断分析[J]. 大气科学, 38(1): 133-145. Wang Z M, Ding Y H, Zhang Y X, et al, 2014. Analysis of convective-symmetric instabilities and frontogenesis in a convective rain band on the northwest Edge of WPSH[J]. Chin J Atmos Sci, 38(1): 133-145 (in Chinese).
|
吴国雄, 蔡雅萍, 唐晓菁, 1995. 湿位涡和倾斜涡度发展[J]. 气象学报, 53(4): 387-405. Wu G X, Cai Y P, Tang X J, 1995. Moist potential vorticity and slantwise vorticity development[J]. Acta Meteor Sin, 53(4): 387-405 (in Chinese). DOI:10.3321/j.issn:0577-6619.1995.04.007
|
张芳华, 陈涛, 杨舒楠, 等, 2014. 一次冬季暴雨过程中的锋生和条件对称不稳定分析[J]. 气象, 40(9): 1048-1057. Zhang F H, Chen T, Yang S N, et al, 2014. Diagnosis of the frontogenesis and CSI features during a torrential rainfall event in winter[J]. Meteor Mon, 40(9): 1048-1057 (in Chinese).
|
章丽娜, 周小刚, 夏扬, 2018. 关于业务上应用条件对称不稳定相关问题的讨论[J]. 气象学报, 76(5): 824-832. Zhang L N, Zhou X G, Xia Y, 2018. A discussion on conditional symmetric instability in operational application[J]. Acta Meteor Sin, 76(5): 824-832 (in Chinese).
|
周玉淑, 邓国, 黄仪虹, 2003. 长江流域一次暴雨过程中的不稳定条件分析[J]. 气象学报, 61(3): 323-333. Zhou Y S, Deng G, Huang Y H, 2003. Analysis on instability condition during a torrential rain over Yangtze River Basin[J]. Acta Meteor Sin, 61(3): 323-333 (in Chinese).
|
Bennetts D A, Hoskins B J, 1979. Conditional symmetric instability-a possible explanation for frontal rainbands[J]. Quart J Roy Meteor Soc, 105(446): 945-962. DOI:10.1002/qj.49710544615
|
Bennetts D A, Sharp J C, 1982. The relevance of conditional symme-tric instability to the prediction of mesoscale frontal rainbands[J]. Quart J Roy Meteor Soc, 108(457): 595-602. DOI:10.1002/qj.49710845707
|
Byrd G P, 1989. A composite analysis of winter season overrunning precipitation bands over the southern plains of the United States[J]. J Atmos Sci, 46(8): 1119-1132. DOI:10.1175/1520-0469(1989)046<1119:ACAOWS>2.0.CO;2
|
Chen G T J, Wang C C, Wang A H, 2007. A case study of subtropical frontogenesis during a blocking event[J]. Mon Wea Rev, 135(7): 2588-2609. DOI:10.1175/MWR3412.1
|
Emanuel K A, 1983. On assessing local conditional symmetric instability from atmospheric soundings[J]. Mon Wea Rev, 111(10): 2016-2033. DOI:10.1175/1520-0493(1983)111<2016:OALCSI>2.0.CO;2
|
Fischer C, Lalaurette F, 1995a. Meso-β-scale circulations in realistic fronts.Ⅰ:steady basic state[J]. Quart J Roy Meteor Soc, 121(526): 1255-1283. DOI:10.1002/qj.49712152605
|
Fischer C, Lalaurette F, 1995b. Meso-β-scale circulations in realistic fronts.Ⅱ:frontogenetically forced basic states[J]. Quart J Roy Meteor Soc, 121(526): 1285-1321. DOI:10.1002/qj.49712152606
|
Luo Y L, Gong Y, Zhang D L, 2014. Initiation and organizational modes of an extreme-rain-producing mesoscale convective system along a Mei-Yu front in East China[J]. Mon Wea Rev, 142(1): 203-221. DOI:10.1175/MWR-D-13-00111.1
|
Moore J T, Lambert T E, 1993. The use of equivalent potential vorticity to diagnose regions of conditional symmetric instability[J]. Wea Forecasting, 8(3): 301-308. DOI:10.1175/1520-0434(1993)008<0301:TUOEPV>2.0.CO;2
|
Reuter G W, Aktary N, 1995. Convective and symmetric instabilities and their effects on precipitation: Seasonal variations in central Alberta during 1990 and 1991[J]. Mon Wea Rev, 123(1): 153-162. DOI:10.1175/1520-0493(1995)123<0153:CASIAT>2.0.CO;2
|
Schultz D M, Schumacher P N, 1999. The use and misuse of conditional symmetric instability[J]. Mon Wea Rev, 127(12): 2709-2732. DOI:10.1175/1520-0493(1999)127<2709:TUAMOC>2.0.CO;2
|
Snook J S, 1992. Current techniques for real-time evaluation of conditional symmetric instability[J]. Wea Forecasting, 7(3): 430-439. DOI:10.1175/1520-0434(1992)007<0430:CTFRTE>2.0.CO;2
|
Wiesmueller J L, Zubrick S M, 1998. Evaluation and application of conditional symmetric instability, equivalent potential vorticity, and frontogenetic forcing in an operational forecast environment[J]. Wea Forecasting, 13(1): 84-101. DOI:10.1175/1520-0434(1998)013<0084:EAAOCS>2.0.CO;2
|
 2019, Vol. 45
2019, Vol. 45 