下垫面热状况的变化直接引起大气环流变化,是天气系统发生发展的重要驱动。青藏高原(以下简称高原)是世界上海拔最高的高原,其地表直接加热对流层中部,在春、夏季成为一个强大的热源(Flohn,1957;1960;叶笃正等,1979;季国良等,1989)。Tao and Ding(1981),Wu and Zhang(1998),赵平和陈隆勋(2001),段安民和吴国雄(2003),段安民等(2003;2018),Duan and Wu(2005),徐祥德和陈联寿(2006),Duan et al(2013),徐士琦和李栋梁(2016),吴国雄等(2018)和徐祥德等(2014)研究表明高原大气热源对于亚洲夏季风的建立和维持具有重要调控作用,与东亚大气环流关系密切(单幸等,2019;于涵等,2019),甚至对整个北半球天气气候变化有显著影响。
精确计算大气热源一直是个难点,主要在于计算方法和所用资料引起的偏差(王同美等,2011;田雨润等,2017)。王美蓉等(2012)指出精确计算高原热源的变化趋势仍很困难,特别是利用再分析资料估算存在很大不确定性。Duan et al (2014)分析了高原热源趋势估算的不确定因素,提出估算存在偏差主要是因为高原站点缺乏且分布不均、无热通量观测资料和卫星辐射资料差异明显,而再分析资料存在的问题是模式偏差较大。罗小青和徐建军(2019)研究了高原大气热源的年代际变化特征及其不确定性因素,认为计算方法和资料均会导致结果的不确定性。
高原大气热源不仅有明显的长期变化趋势,其年际和季节内变化特征同样十分显著,且对高原局地及中国东部地区气候变化有重要影响(Chen and Li, 1985;黄荣辉,1985;赵平和陈隆勋,2001;王跃男等,2009;Wang et al,2013;段安民等,2018)。由于高原站点资料稀缺,学者们广泛使用多套再分析资料计算高原热源并开展研究,然而不同再分析资料估算出的高原热源是否较为一致?是否能合理表征高原的热状况?在研究高原热源不同尺度(长期趋势、年际和季节内)时,不同再分析资料的适用性是否又有所不同?本文旨在分析观测和再分析资料计算所得高原热源存在的偏差,并探究不同再分析资料针对热源不同尺度变率时的适用性问题,为研究高原热源变率选择资料方面提供理论参考,为“高原气象学”课程教学提供理论支撑,为选修该课程的学生开阔视野、提升兴趣。
1 数据 1.1 站点观测和卫星辐射资料(1) 中国气象局提供的高原中东部71个测站1979—2014年一日4次常规观测资料,包括地表温度(Ts)、2 m空气温度(Ta)、10 m风速(V10),及同期日平均降水量,所有资料均经过质量控制。
(2) NASA/GEWEX地表辐射收支(surface radiation budget,SRB;https://eosweb.larc.nasa.gov/project/srb/srb_table;Gupta et al,2011)逐日辐射资料(以下简称SRB),包括地表和大气层顶长波和短波辐射参数,水平分辨率为1°×1°,时间段为1984—2007年。
(3) 国际卫星云气候计划P(International Sa-tellite Cloud Climatology Project,ISCC,https://isccp.giss.nasa.gov/products/products.html;Rossow and Schiffer, 1999)全球卫星辐射资料(以下简称ISCCP),包括大气层顶和地面辐射所有分量,水平分辨率为280 km等面积网格,时间分辨率为3 h,时间段取1984—2009年。
1.2 再分析资料(1) NCEP/NCAR(https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.html;Kalnay et al,1996)逐日再分析资料Ⅰ(以下简称NCEP1),采用当时最为先进的全球资料同化系统和数据库,采用三维变分同化技术获取的一套完整的1948年至今的同化资料集。空间分辨率为2.5°×2.5°,本文所取再分析资料时段均为1979—2014年(下同)。
(2) NCEP-DOE(美国气象环境预报中心/美国能源部合作,NCEP/Department of Energy,https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis2.gaussian.html;Kanamitsu et al,2002)逐日再分析资料Ⅱ(以下简称NECP2),是NCEP/NCAR再分析Ⅰ的改进版本。所采用的数值预报模式和观测系统与NCEP/NCAR大体相同,但增加了对陆地降水的同化,在近地表温度和洋面辐射通量等方面有明显改进。空间分辨率为全球高斯格点192×94,资料时间段为1979年起始至今。
(3) ERA-Interim(https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/)6 h再分析资料(以下简称ERAI),该资料同化系统是具有12 h分析窗口的4维变分分析系统(Dee et al,2011)。该资料于2011年释放,是目前适用广泛且适用性较好的再分析资料,空间分辨率约为80 km,垂直方向上一共从地表到0.1 hPa有60层数据,资料起始于1979年。
(4) JRA-55(Japanese 55-year Reanalysis or JRA55;https://jra.kishou.go.jp/JRA-55/index_en.html#jra-55)再分析资料,是日本气象厅使用更加复杂的资料同化系统开展的第二个再分析项目(Kobayashi et al,2015; Harada et al,2016),也是最新释放的一套再分析数据集。该资料覆盖了自1958年以来的55年时间,该时间段正是常规无线电观测开始在全球观测的时间段。JRA55解决了其前身JRA-25的很多缺陷,因此JRA55项目产生了一套高质量的气候数据集。
2 大气热源计算方法大气热源/汇反映了空气柱的热量收支情况(叶笃正等,1979),目前对其计算主要有两种方法,即正算法和倒算法,计算过程所需变量有所不同,通常正算法基于观测资料得以计算,而倒算法应用于再分析资料更为便利。
2.1 正算法大气热源(E)正算法的计算公式为
| $ E=SHF+LH+NRF $ | (1) |
式中,SHF(sensible heat flux)代表地表感热通量,LH(latent heat)是通过降水凝结释放的潜热,NRF(net radiation flux)代表的是空气柱的净辐射通量,单位:W·m-2。
式(1)中感热通量的计算较为复杂,也蕴含更多不确定性,目前其计算多采用总体动力学公式:
| $ S H F=c_{p} \rho C_{\mathrm{DH}} V_{10}\left(T_{\mathrm{s}}-T_{\mathrm{a}}\right) $ | (2) |
式中:ρ是空气密度,取0.8 kg·m-3;cp=1005 J·kg-1·K-1,是常压下干空气的定压比热;CDH指热量拖曳系数。
潜热释放由降水资料计算得来:
| $ L H=P_{r} L_{w} \rho_{0} $ | (3) |
式中:Pr为降水量,单位:mm;ρ0为水的密度,取1.0 kg·m-3;Lw=2.5×106 J·kg-1,是凝结潜热系数。
大气柱净辐射通量的计算公式:
| $ \begin{aligned} N R F=& R_{\infty}-R_{0}=\left(S_{\infty}^{\downarrow}-S_{\infty}^{\uparrow}\right)-\left(S_{0}^{\downarrow}-S_{0}^{\uparrow}\right)-\\ &\left(F_{0}^{\downarrow}-F_{0}^{\uparrow}\right)-F_{\infty} \end{aligned} $ | (4) |
式中,R0和R∞表示地表和大气层顶的净辐射通量,S和F则分别为短波和长波辐射通量,下标∞和0分别代表大气层顶和地表,↑和↓则分别为向上和向下的通量输送。
2.2 倒算法倒算法最先由Yanai et al(1973)提出,计算方法如下:
| $ Q_{1}=c_{p}\left[\frac{\partial T}{\partial t}+\boldsymbol{V} \cdot \nabla T+\left(\frac{p}{p_{0}}\right)^{k} \omega \frac{\partial \theta}{\partial p}\right] $ | (5) |
| $ <Q_{1}>=\frac{1}{g} \int_{p_{{\rm s}}}^{p_{0}} Q_{1} {\rm d} p $ | (6) |
式中:Q1为各层大气视热源,单位:K·d-1;而<Q1>则为整层垂直积分大气视热源,单位:W·m-2;T是温度;V是水平风速;p0是1000 hPa大气压;ps为地表气压;k=R/cp;R=8.314 J·mol-1·K-1,为气体常数;ω为p坐标系的垂直速度,单位:Pa·s-1;θ是位温,单位:K。
3 两种方法的计算偏差分析 3.1 正算法偏差分析采用正算法计算大气热源,需要计算地表感热通量、潜热释放及辐射通量这三个分量,而这三者的计算过程均存在偏差。对感热通量而言,首先其计算公式中拖曳系数是个动态系数,随地表粗糙度不同而变化(李国平等,2000),因此不同测站拖曳系数大小不同,但为方便计算,通常取其平均值代入计算,这会影响感热通量的计算精确性。不同学者对拖曳系数均值的取值从3.3×10-3~8×10-3大小不一(Chen et al,1985;叶笃正等,1979;Li et al,1996;李国平等,2000),但陈隆勋和朱乾根(1991),Li and Yanai(1996),Duan and Wu(2008)研究认为在高原中东部地区拖曳系数取平均值4×10-3较为合理,也是本文计算的取值。此外,阳坤等(2010),Duan et al(2018)也考虑了拖曳系数的日变化进而给出了高原大气热源的结算结果,与将拖曳系数取为平均值的结果相比而言,考虑了拖曳系数日变化之后,高原热源的变化趋势仍旧呈减弱趋势,但变化幅度有所减弱,可见拖曳系数的取值不影响热源的定性分析结果,但定量上会有影响,是造成感热计算结果存在不确定性的另一原因。
事实上,资料的观测时制同样会影响感热通量的估算。高原地表感热有较大的日变化,中午时极强,夜晚则基本为负值(王美蓉等,2012),因此若用日平均资料依据式(2)来计算感热,则势必造成计算结果不准确。王美蓉等(2012)采用一日4次站点观测资料分别计算出4个时次的高原地表感热通量,再做日平均计算,则正是考虑了感热的复杂日变化,很大程度上减少了计算误差。
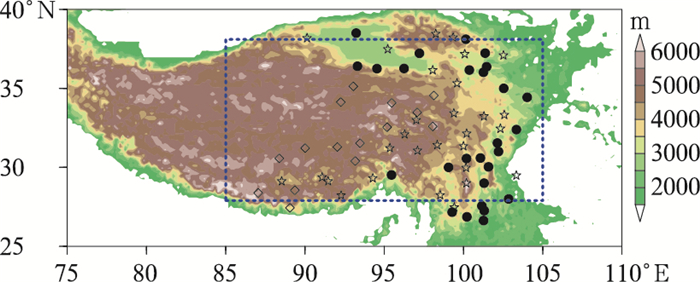
虽然正算法通常使用观测资料算得大气热源,增加了计算结果的可信度,但是不能忽视观测资料本身的缺点。站点空间分布不均是一个方面(图 1),尤其是对于高海拔的高原地区,其中东部地区的测站所在海拔高度差异很大,西部更是仅有寥寥几个测站,因此准确计算高原全区的大气热源是一个挑战。对于使用站点降水计算得到的凝结潜热释放则存在同样的问题。
|
图 1 高原中东部71个气象站点的海拔高度(阴影)及位置 [实心圆点、五角星及棱形方块分别代表海拔高度位于2000~3000,3000~4000和4000~5000 m的站点,方框则给出了再分析资料计算所得高原热源的区域平均范围(28°~38°N、85°~105°E)] Fig. 1 Terrain height (shading) and locations of 71 observation stations over the Tibetan Plateau (TP) [Solid circles, stars and blocks indicate the stations with elevations at 2000-3000, 3000-4000, and 4000-5000 m, respectively; boxed area represents the regional average domain (28°-38°N, 85°-105°E) of heating calculated by reanalysis datasets] |
高原大气柱的净辐射通量由卫星观测资料计算而来,不同辐射(ISCCP和SRB)卫星资料也存在很大差异,其计算所得净通量自然有所不同(王美蓉等,2012),这从辐射分量上增加了大气热源的计算偏差。
3.2 倒算法偏差分析通过倒算法计算大气热源通常依赖于再分析资料,而不同再分析资料之间差异非常明显,在不同地区的适用性也有所不同,尤其对于像高原这种高海拔、地形复杂地区,对再分析资料的选择更需慎重。何冬燕等(2013)发现相较NCEP1和NCEP2,ERAI的地温资料在高原地区的适用性最好。胡梦玲等(2015)考察了7套再分析资料的位势高度场和风场在高原地区的表现,指出ERAI和NCEP1在位势高度的变化趋势上表现较好,而JRA55和ERAI的位势高度资料与探空资料相关最好。不同再分析资料之间的主要差异体现在同化资料及同化方案不尽相同,且不同模式物理过程不同程度的偏差均会导致最终资料产品的差异性。
4 观测与再分析资料结果比较高原地区观测资料匮乏,尤其是西部地区,因此再分析资料被广泛用于计算高原大气热源并分析其变化特征。但多套再分析资料的各自适用性如何,特别是针对不同尺度的热源变率进行研究时,多套再分析资料的适用性可能有所不同,因此,接下来将高原中东部地区71个测站(图 1)和4套再分析资料(NCEP1,NCEP2,ERAI和JRA55,图 1方框区域平均)计算所得大气热源进行多尺度比较。
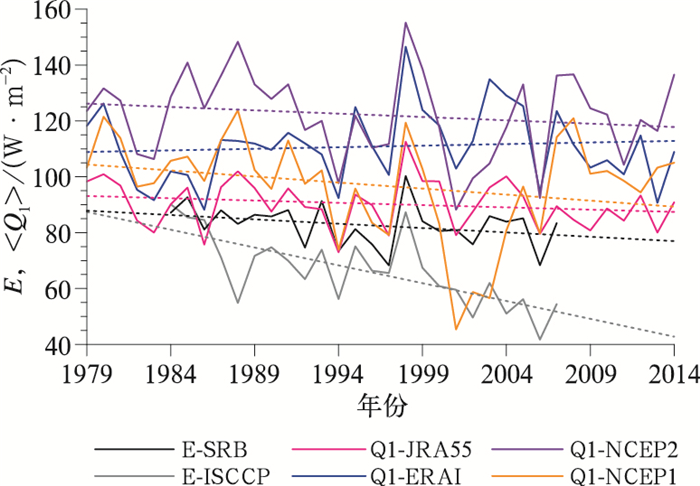
4.1 长期趋势根据1984—2007年站点观测(E-SRB和E-ISCCP)和1979—2014年4套再分析资料(<Q1>-NCEP1,<Q1>-NCEP2,<Q1>-ERAI和<Q1>-JRA55)计算所得高原中东部大气热源的时间演变序列,图 2给出了6套资料得到的夏季高原大气热源年际变化。从图中可以看出,6套资料所得热源结果总体较为相似,但差异也十分明显。E-ISCCP热源结果偏小,与E-SRB变化幅度有一定差距,说明所用两套卫星辐射资料存在差异,使得计算所得大气热源存在很大不确定性。而<Q1>-NCEP2和<Q1>-ERAI结果则明显偏高,<Q1>-NCEP1结果十分不稳定,相较而言,<Q1>-JRA55与E-SRB的一致性最好。
|
图 2 站点观测(1984—2007年)和4套再分析资料(1979—2014年)计算所得夏季高原中东部大气热源时间演变序列 (E-SRB和E-ISCCP分别表示用SRB和ISCCP卫星资料计算辐射通量部分) Fig. 2 Time series of the atmospheric heat source in summer seasons over the central and eastern TP calculated by observations (1984-2007) and four reanalysis datasets (1979-2014) (E-SRB and E-ISCCP indicate the net radiation flux computed by SRB and ISCCP satellite datasets, respectively) |
相关系数(表 1)同样印证了E-SRB较E-ISCCP更为可靠,与所有再分析资料结果的相关性均十分显著。NCEP2作为NCEP1的资料进化版本,二者相关密切,但<Q1>-NCEP2与E-SRB,<Q1>-ERAI及<Q1>-JRA55相关系数均更高(0.71,0.45和0.66)。<Q1>-ERAI和<Q1>-JRA55相关性更好,相关系数达0.83,表明最新释放的两套再分析资料计算所得高原热源具有较高一致性,也是目前广泛使用的再分析数据。
|
|
表 1 站点观测(1984—2007年)和4套再分析资料(1979—2014年)计算所得高原中东部大气热源的相关系数 Table 1 Correlation coefficients among the atmospheric heat sources over the central and eastern TP calculated by observations (1984-2007) and four reanalysis datasets (1979-2014) |
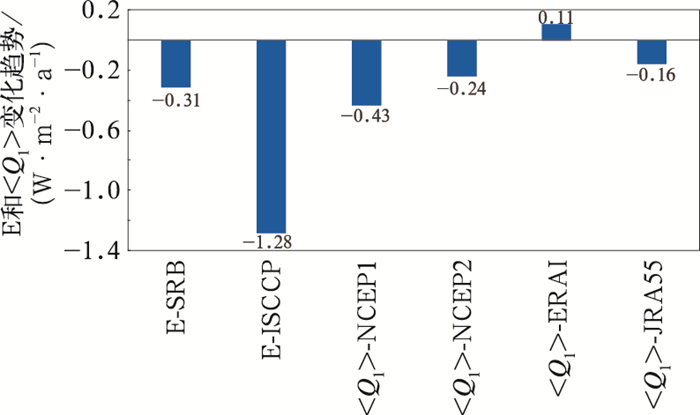
图 2显示出6组大气热源序列均表现为明显的长期趋势,具体的线性趋势如图 3所示,可见除<Q1>-ERAI表现为微弱的上升趋势之外,其余序列均显示高原大气热源呈持续减弱趋势,且<Q1>-NCEP2和<Q1>-JRA55与观测E-SRB最为接近,而E-ISCCP减弱趋势最强,与其他热源资料差异明显。
|
图 3 6套资料计算所得夏季高原大气热源变化趋势 Fig. 3 Trends in the atmospheric heat source in summer over the TP calculated by six datasets |
为获取年际尺度变率,对上述6组热源序列进行去除线性趋势处理,结果显示6组热源数据的年际变化均十分接近(图略)。需要注意的是<Q1>-NCEP1和<Q1>-NCEP2的变化幅度在1999年之前与观测较为贴合,之后则偏差相对较大;<Q1>-ERAI与<Q1>-JRA55的年际变率总体来说与观测更为相似。
由表 2给出的6组数据在年际变率的相关系数可知,E-SRB更能代表高原热源变化特征,且其与<Q1>-ERAI和<Q1>-JRA55的相关系数分别达0.68和0.72,通过了0.05显著性水平检验,两套再分析资料计算所得热源的年际变率相关则更好,达0.86。
4.3 季节内尺度为进一步确定再分析资料计算所得夏季高原热源资料在季节内尺度上的适用,首先分析其各自功率谱(图略),发现再分析资料与观测类似,高原大气热源的季节内显著周期均为10~20 d和7~9 d,其中主导周期为10~20 d。
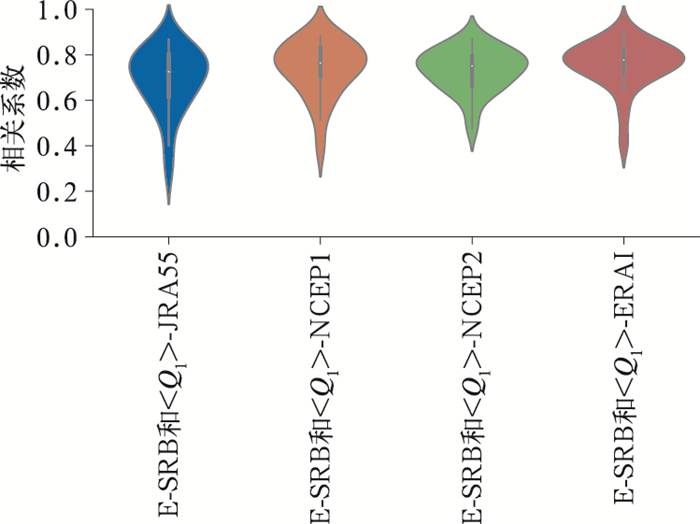
此外,计算了1984—2007年E-SRB分别与4套再分析资料的逐年夏季热源序列的相关系数的多年平均,结果相差不大,分别为0.69,0.74,0.73和0.76,均通过了0.05显著性水平检验,这表明在研究季节内振荡时间尺度的热源变率时,4套再分析资料在高原地区均有较好适用性。图 4给出了多年相关系数的分布情况,由图可见,4组数据的中位数基本在0.7上下,E-SRB与<Q1>-JRA55的平均相关系数略微偏低则主要归因于确实有部分年份的相关系数在0.4以下,而高相关系数分布较多的年份主要体现在<Q1>-NCEP2及<Q1>-ERAI两组数据。
|
图 4 984—2007年E-SRB与4套再分析资料计算所得大气热源季节内相关系数 Fig. 4 Distributions of correlation coefficients between the E-SRB and<Q1> calculated by reanalysis datasets over the TP during 1984-2007 |
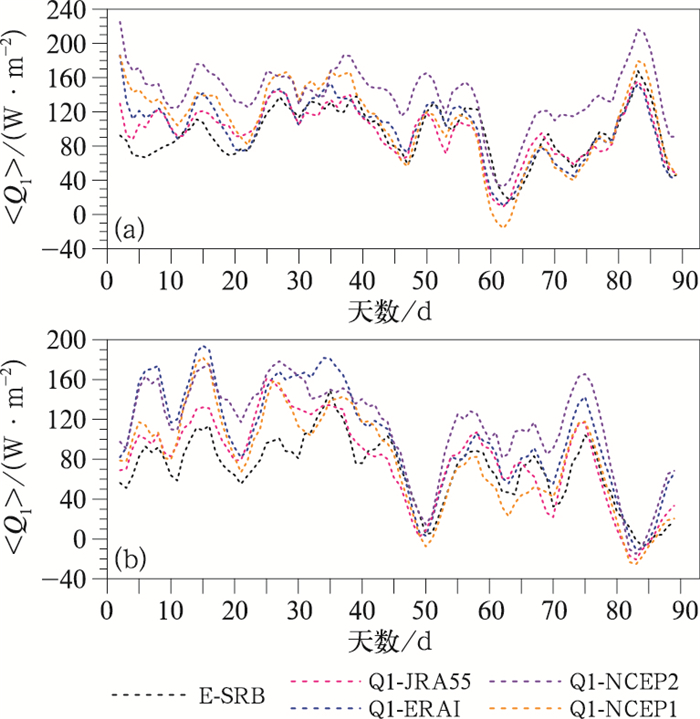
为更直观地展示4套再分析资料在分析高原热源的季节内变化时的适用性,图 5给出了1985年和1997年夏季4套再分析资料计算所得大气热源和观测结果的演变曲线。可见,整体而言4套再分析资料计算所得热源与观测热源的变化均较为一致,在高原均有较好的适用性,说明了在季节内尺度上,4套再分析资料的差别不大,均可用来在高原地区开展研究。
|
图 5 1985年(a)和1997年(b)夏季观测(黑色)和再分析资料(彩色)计算所得大气热源的演变序列 Fig. 5 Time series of the atmospheric heat source over the TP calculated by observations (black) and reanalysis datasets (colorful) in 1985 (a) and 1997 (b) |
文中详细介绍了大气热源的计算方法,以及因计算过程所使用到的资料数据不同,存在的计算偏差。正算法的偏差主要可归因于拖曳系数取值大小不一、资料观测时制不同和空间分布不均匀,以及辐射资料的不确定性;倒算法则由于不同再分析资料的巨大差异性而使得计算结果不尽相同。
再分析资料计算所得大气热源在高原的适用性分析,则发现在长期趋势上,再分析结果<Q1>-JRA55与观测结果E-SRB一致性最好;在年际尺度上,<Q1>-ERAI与<Q1>-JRA55的年际变率总体与观测十分相似;而在季节内尺度上,多套再分析资料均可很好地刻画出夏季高原热源的季节内变化周期,在高原均有较好的适用性。
精确估算大气热源一直以来都是一个挑战,也是高原气象中一个十分重要的知识点和关键点,对其从计算方法、计算偏差及多尺度结果等多方面进行详细介绍和分析均十分必要,为青年学者和研究生全面深入探究高原热源变率选择资料时提供可靠参考。“高原气象学”课程涵盖了高原气候变化特征及其气候效应,科学研究的最新成果对于课程建设和支撑及课程大纲的修订均至关重要,可使学生更系统地了解高原天气和气候学意义,以及相关主要科学问题的最新研究进展。
陈隆勋, 朱乾根, 1991. 东亚季风[M]. 北京: 气象出版社: 362. Chen L X, Zhu Q G, 1991. East Asian Monsoon[M].
Beijing: China Meteorological Press: 362 (in Chinese).
|
段安民, 刘屹岷, 吴国雄, 2003. 4~6月青藏高原热状况与盛夏东亚降水和大气环流的异常[J]. 中国科学D辑:地球科学, 33(10): 997-1004. |
Duan A M, Liu Y M, Wu G X, 2005. Heating status of the Tibetan Plateau from April to June and rainfall and atmospheric circulation anomaly over East Asia in midsummer[J]. Sci China SerD:Earth Sci, 48(2): 250-257.
|
段安民, 吴国雄, 2003. 7月青藏高原大气热源空间型及其与东亚大气环流和降水的相关研究[J]. 气象学报, 61(4): 447-456. Duan A M, Wu G X, 2003. The main spatial heating patterns over the Tibetan Plateau in July and the corresponding distributions of circulation and precipitation over eastern Asia[J]. Acta Meteor Sin, 61(4): 447-456 (in Chinese).
|
段安民, 肖志祥, 王子谦, 2018. 青藏高原冬春积雪和地表热源影响亚洲夏季风的研究进展[J]. 大气科学, 42(4): 755-766. Duan A M, Xiao Z X, Wang Z Q, 2018. Impacts of the Tibetan Plateau winter/spring snow depth and surface heat source on Asian summer monsoon:a review[J]. Chin J Atmos Sci, 42(4): 755-766 (in Chinese).
|
何冬燕, 田红, 邓伟涛, 2013. 三种再分析地表温度资料在青藏高原区域的适用性分析[J]. 大气科学学报, 36(4): 458-465. He D Y, Tian H, Deng W T, 2013. Applicability analysis of three reana-lysis surface temperature data over the Tibetan Plateau[J]. Trans Atmos Sci, 36(4): 458-465 (in Chinese).
|
胡梦玲, 游庆龙, 林厚博, 2015. 青藏高原地区多套位势高度和风场再分析资料的对比分析[J]. 冰川冻土, 37(5): 1229-1244. Hu M L, You Q L, Lin H B, 2015. Comparative analyses of geopotential height and wind field from multiple reanalysis data over the Tibetan Plateau[J]. J Glaciol Geocryol, 37(5): 1229-1244 (in Chinese).
|
黄荣辉, 1985. 夏季青藏高原上空热源异常对北半球大气环流异常的作用[J]. 气象学报, 43(2): 208-220. Huang R H, 1985. The influence of the heat source anomaly over Tibetan Plateau on the Northern Hemispheric circulation anomalies[J]. Acta Meteor Sin, 43(2): 208-220 (in Chinese).
|
季国良, 钟强, 沈志宝, 1989. 青藏高原地面热源观测研究的进展[J]. 高原气象, 8(2): 127-132. Ji G L, Zhong Q, Shen Z B, 1989. Advances in observation and research of the surface heat source over the Qinghai-Xizang Plateau[J]. Plateau Meteor, 8(2): 127-132 (in Chinese).
|
李国平, 段廷扬, 巩远发, 2000. 青藏高原西部地区的总体输送系数和地面通量[J]. 科学通报, 45(8): 865-869. Li G P, Duan T Y, Gong Y F, 2000. The bulk transfer coefficients and surface fluxes on the western Tibetan Plateau[J]. Chin Sci Bull, 45(13): 1221-1226 (in Chinese).
|
罗小青, 徐建军, 2019. 青藏高原大气热源及其估算的不确定性因素[J]. 气候变化研究进展, 15(1): 33-40. Luo X Q, Xu J J, 2019. Estimate of atmospheric heat source over Tibetan Plateau and its uncertainties[J]. Climate Change Res, 15(1): 33-40 (in Chinese).
|
单幸, 周顺武, 王美蓉, 等, 2019. 青藏高原大气热力异常对西风急流的影响[J]. 气象科学, 39(2): 206-213. Shan X, Zhou S W, Wang M R, et al, 2019. Influence of atmospheric heat anomaly over the Tibetan Plateau on the westerly jet[J]. J Meteor Sci, 39(2): 206-213 (in Chinese).
|
田雨润, 李国平, 刘云丰, 2017. 三种再分析资料计算青藏高原大气热源的比较[J]. 沙漠与绿洲气象, 11(4): 1-8. Tian Y R, Li G P, Liu Y F, 2017. Comparison of the atmospheric heat sources over the Tibetan Plateau computed by three reanalysis data sets[J]. Desert Oasis Meteor, 11(4): 1-8 (in Chinese).
|
王美蓉, 周顺武, 段安民, 2012. 近30年青藏高原中东部大气热源变化趋势:观测与再分析资料对比[J]. 科学通报, 57(2): 178-188. Wang M R, Zhou S W, Duan A M, 2012. Trend in the atmospheric heat source over the central and eastern Tibetan Plateau during recent decades:comparison of observations and reanalysis data[J]. Chin Sci Bull, 57(2): 178-188 (in Chinese).
|
王同美, 吴国雄, 应明, 2011. NCEP/NCAR(Ⅰ、Ⅱ)和ERA40再分析加热资料比较[J]. 中山大学学报(自然科学报), 50(5): 128-134. Wang T M, Wu G X, Ying M, 2011. Comparison of diabatic heating data from NCEP/NCAR (Ⅰ, Ⅱ) and ERA40[J]. Acta Sci Natur Univer Sunyatseni, 50(5): 128-134 (in Chinese).
|
王跃男, 陈隆勋, 何金海, 等, 2009. 夏季青藏高原热源低频振荡对我国东部降水的影响[J]. 应用气象学报, 20(4): 419-427. Wang Y N, Chen L X, He J H, et al, 2009. Effect of summer heat source low-frequency oscillation over the Tibetan Plateau on precipitation in eastern China[J]. J Appl Meteor Sci, 20(4): 419-427 (in Chinese).
|
吴国雄, 刘屹岷, 何编, 等, 2018. 青藏高原感热气泵影响亚洲夏季风的机制[J]. 大气科学, 42(3): 488-504. Wu G X, Liu Y M, He B, et al, 2018. Review of the impact of the Tibetan Plateau sensible heat driven air-pump on the Asian summer monsoon[J]. Chin J Atmos Sci, 42(3): 488-504 (in Chinese).
|
徐士琦, 李栋梁, 2016. 东北地区春季首场透雨的变化特征及与青藏高原地面加热场强度的关系[J]. 气象, 42(3): 271-279. Xu S Q, Li D L, 2016. Characteristics of the first soaking rain in Northeast China and its response to surface heat source over the Tibetan Plateau[J]. Meteor Mon, 42(3): 271-279 (in Chinese).
|
徐祥德, 陈联寿, 2006. 青藏高原大气科学试验研究进展[J]. 应用气象学报, 17(6): 756-772. Xu X D, Chen L S, 2006. Advances of the study on Tibetan Plateau experiment of atmospheric sciences[J]. J Appl Meteor Sci, 17(6): 756-772 (in Chinese).
|
徐祥德, 王寅钧, 赵天良, 等, 2014. 高原东南缘大气近地层湍能特征与边界层动力、热力结构相关特征[J]. 气象, 40(10): 1165-1173. Xu X D, Wang Y J, Zhao T L, et al, 2014. Relationship between turbulent energy in the near surface layer and atmosphe-ric boundary layer thermodynamic structure over the southeas-tern side of Tibetan Plateau[J]. Meteor Mon, 40(10): 1165-1173 (in Chinese).
|
阳坤, 郭晓峰, 武炳义, 2010. 青藏高原地表感热通量的近期变化趋势[J]. 中国科学:地球科学, 40(7): 923-932. |
Yang K, Guo X F, Wu B Y, 2011. Recent trends in surface sensible heat flux on the Tibetan Plateau[J]. Sci China Earth Sci, 54(1): 19-28.
|
叶笃正, 高由禧, 周明煜, 等, 1979. 青藏高原气象学[M]. 北京: 科学出版社: 278. Ye D Z, Gao Y X, Zhou M Y, et al, 1979. Tibetan Plateau Meteorology[M].
Beijing: Science Press: 278 (in Chinese).
|
于涵, 张杰, 刘诗梦, 2019. 青藏高原地表非绝热加热模态及其与中国北方环流异常的联系[J]. 高原气象, 38(2): 237-252. Yu H, Zhang J, Liu S M, 2019. Surface diabatic heating mode of the Qinghai-Tibetan Plateau and its relationship with the anomalous circulation in northern China[J]. Plateau Meteor, 38(2): 237-252 (in Chinese).
|
赵平, 陈隆勋, 2001. 35年来青藏高原大气热源气候特征及其与中国降水的关系[J]. 中国科学D辑:地球科学, 44(4): 327-332. Zhao P, Chen L X, 2001. Climatic features of atmospheric heat source/sink over the Qinghai-Xizang Plateau in 35 years and its relation to rainfall in China[J]. Sci Chin Series D:Earth Sci, 44(9): 858-864 (in Chinese).
|
Chen L X, Li W L, 1985. The atmospheric heat budget in summer over Asia monsoon area[J]. Adv Atmos Sci, 2(4): 487-497.
|
Chen L X, Reiter E R, Feng Z Q, 1985. The atmospheric heat source over the Tibetan Plateau:May-August 1979[J]. Mon Wea Rev, 113(10): 1771-1790.
|
Dee D P, Uppala S M, Simmons A J, et al, 2011. The ERA-Interim reanalysis:configuration and performance of the data assimilation system[J]. Quart J Roy Meteor Soc, 137(656): 553-597.
|
Duan A M, Wu G X, 2005. Role of the Tibetan Plateau thermal for-cing in the summer climate patterns over subtropical Asia[J]. Climate Dyn, 24(7-8): 793-807.
|
Duan A M, Wu G X, 2008. Weakening trend in the atmospheric heat source over the Tibetan Plateau during recent decades.Part Ⅰ:observations[J]. J Climate, 21(13): 3149-3164.
|
Duan A M, Wang M R, Lei Y H, et al, 2013. Trends in summer rainfall over China associated with the Tibetan Pla-teau sensible heat source during 1980-2008[J]. J Climate, 26(1): 261-275.
|
Duan A M, Wang M R, Xiao Z X, 2014. Uncertainties in quantitatively estimating the atmospheric heat source over the Tibetan Pla-teau[J]. Atmos Oceanic Sci Lett, 7(1): 28-33.
|
Duan A M, Liu S F, Zhao Y, et al, 2018. Atmospheric heat source/sink dataset over the Tibetan Plateau based on satellite and routine meteorological observations[J]. Big Earth Data, 2(2): 179-189.
|
Flohn H, 1957. Large-scale aspects of the "summer monsoon" in South and East Asia[J]. J Meteor Soc Jpn Ser Ⅱ, 35A: 180-186.
|
Flohn H, 1960.Recent Investigations on the Mechanism of the "Summer Monsoon" of Southern and Eastern Asia[M]//Delhi N.Monsoons of the World.India: Hindu Union Press: 75-88.
|
Gupta S K, Stackhouse P W Jr, Cox S J, et al, 2011.The NASA/GEWEX surface radiation budget release 3.0: 24.5-year dataset[OL/Z].GEWEX News, 21(1): 10-12.
|
Harada Y, Kamahori H, Kobayashi C, et al, 2016. The JRA-55 reana-lysis:representation of atmospheric circulation and climate variability[J]. J Meteor Soc Jpn Ser Ⅱ, 94(3): 269-302.
|
Kalnay E, Kanamitsu M, Kistler R, et al, 1996. The NCEP/NCAR 40-year reanalysis project[J]. Bull Amer Meteor Soc, 77(3): 437-472.
|
Kanamitsu M, Ebisuzaki W, Woollen J, et al, 2002. NCEP-DOE AMIP-Ⅱ reanalysis (R-2)[J]. Bull Amer Meteor Soc, 83(11): 1631-1644.
|
Kobayashi S, Ota Y, Harada Y, et al, 2015. The JRA-55 reanalysis:general specifications and basic characteristics[J]. J Meteor Soc Jpn Ser Ⅱ, 93(1): 5-48.
|
Li C F, Yanai M, 1996. The onset and interannual variability of the Asian Summer Monsoon in relation to land-sea thermal contrast[J]. J Climate, 9(2): 358-375.
|
Li G P, Duan T Y, Wan J, et al, 1996. Determination of the drag coefficient over the Tibetan Plateau[J]. Adv Atmos Sci, 13(4): 511-518.
|
Rossow W B, Schiffer R A, 1999. Advances in understanding clouds from ISCCP[J]. Bull Amer Meteor Soc, 80(11): 2261-2288.
|
Tao S Y, Ding Y H, 1981. Observational evidence of the influence of the Qinghai-Xizang (Tibet) Plateau on the occurrence of heavy rain and severe convective storms in China[J]. Bull Amer Me-teor Soc, 62(1): 23-30.
|
Wang Z Q, Duan A M, Wu G X, 2013. Time-lagged impact of spring sensible heat over the Tibetan Plateau on the summer rainfall anomaly in East China:case studies using the WRF model[J]. Climate Dyn, 42(11/12): 2885-2898.
|
Wu G X, Zhang Y S, 1998. Tibetan Plateau forcing and the timing of the monsoon onset over South Asia and the South China Sea[J]. Mon Wea Rev, 126(4): 913-927.
|
Yanai M, Esbensen S, Chu J H, 1973. Determination of bulk properties of tropical cloud clusters from large-scale heat and moisture budget[J]. J Atmos Sci, 30(4): 611-627.
|
 2019, Vol. 45
2019, Vol. 45 