2. 国网浙江省电力公司,杭州 310007;
3. 浙江省气象网络信息中心,杭州 310008
2. State Grid Zhejiang Electric Power Company, Hangzhou 310007;
3. Zhejiang Meteorological Network Information Center, Hangzhou 310008
自然风的形成机理十分复杂,其主要成因是大气环流、季风环流和局地环流共同作用的结果。与温度、湿度、气压等常规气象要素具有较强的时间连续性不同,自然风速受到地形、纬度、海拔、昼夜和季节等多种因素的影响,表现出很强的间歇性和随机性,因此风速预报一直是常规天气预报中的难题之一。同时,风能作为一种清洁、可再生、储量巨大的能源(柳艳香等,2008),其最直接的效用是应用于风力发电(余江等,2015),精准的风速预报是风电开发中的关键技术。针对风速预报,研究提高预报精准度以及可靠的预报算法,具有重要的学术价值和工程学实用意义(姚日升等,2016;张颖超等,2016;王丙兰等,2017)。
目前,对于风速的预测方法主要以数值天气预报法和统计方法为主。数值天气预报法考虑了较多动力过程,预报时效长,但是其预报精度会随预报时效的增加而降低。现阶段WRF模式受物理参数化方案不完善、地形不够精确、分辨率低等因素的影响,导致其风速预报结果相对观测差异较大(龚强等, 2006;朱智慧和黄宁立,2012)。统计方法是一类根据历史数据序列间的数学规律进行预报的方法。主要包括:时间序列法(Box et al, 1976; Bossanyi, 1985)、持续法(Alexiadis et al, 1998)、空间相关法(Barbounis et al, 2006)、人工神经网络法(Mabel and Fernandez, 2008)等。持续法精准度较高、算法简单且不需要大量的建模数据,但其预报时效较短。人工神经网络具有分布式存储、并行处理与容错性等特征,对于复杂问题的求解十分有效。但其存在收敛速度慢、训练数据庞大、隐节点的选取缺乏理论指导等缺点。空间相关法和时间序列法预报效果都不错,但计算过程需要大量原始数据。
除此以外,偏最小二乘回归被誉为第二代统计回归方法(Wold, 1966)。近年来,因其应用上的便捷性、出色的预测能力以及能实现多种数据分析方法的综合应用,在金融、化学、生物等众多领域得到广泛应用(李刚等,2012;胡美娟等,2015)。气象问题研究方面,舒守娟等(2007)应用该方法对中国区域降水分布进行估算;宋金杰等(2011)提出了基于该方法的热带气旋强度统计预报方法;经过评估检验都得到了不错的预测效果。
事实上,不论是数值天气预报法还是各类统计方法,都各有其特点和预报长处,但由于风的形成机理的复杂性和强随机性,使得单一方法的应用效果受到了限制。因此本文拟使用模式预报风速数据,结合偏最小二乘回归方法对预报风速进行订正,以期提高预报数据的精准率。
1 资料和方法 1.1 资料来源浙江省中尺度区域模式系统(以下简称ZJWARMS)于2012年5月投入业务试运行。该系统基于WRF模式和ADAS同化系统,每日发布08和20时两次预报。每次预报可提供浙江省(25°~32°N、116°~124°E)72 h预报时效、1 h时间分辨率、3 km空间分辨率数值预报产品。选取模式资料:2 m温度、地表气压、2 m湿度、10 m经/纬向风速作为建模自变量。浙江境内及邻近区域自动站(含常规地面站)共计956站逐时观测数据(所选站点见图 4),选取资料:空气温度、本站气压、相对湿度、2 min平均风速作为建模因变量。研究时间段:浙江省2013—2016年冬季(12月至次年2月)共计12个月。
ZJWARMS模式资料来自于浙江省气象科学研究所自主备份。自动站资料来源于浙江省气象信息中心,资料入库保存时都经过了人工核查,并在实际研究中对数据的均一性、完整度等做了初步质量控制。
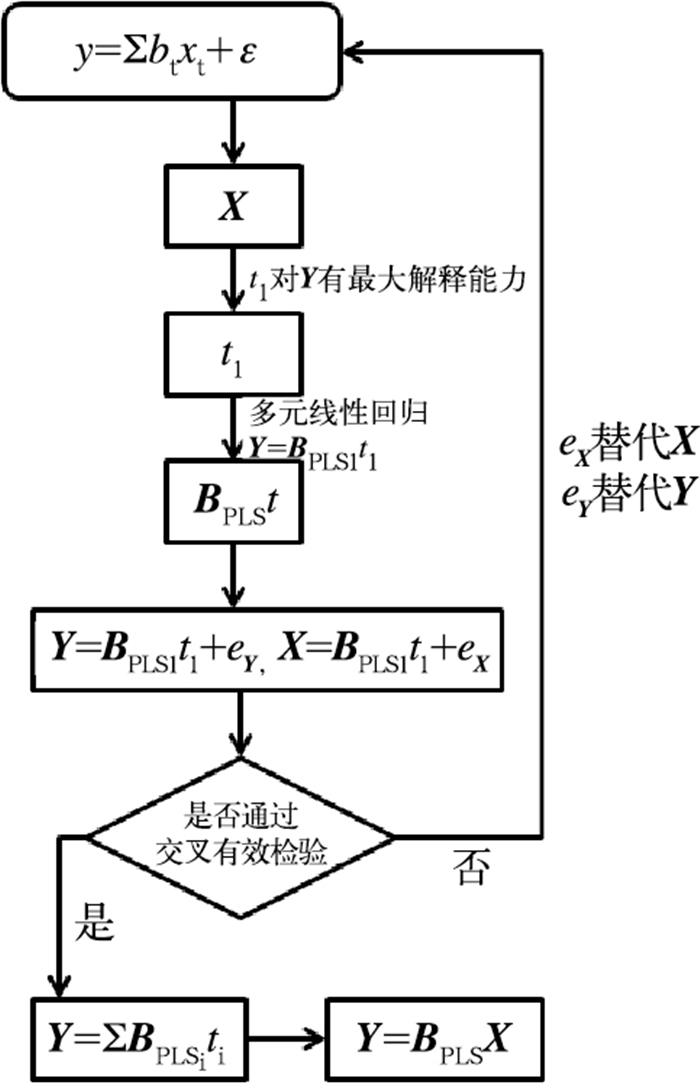
1.2 偏最小二乘回归算法及应用偏最小二乘回归算法是一种数学优化技术,在统计学上可实现多因变量对多自变量建模,实际应用中能较好地解决许多以往用普通多元回归无法解决的问题, 如风速订正中自变量之间的多重相关性问题、历史观测偶有缺失问题等。图 1是偏最小二乘回归建模的流程。与常规建模方案不同的是,偏最小二乘回归首先从自变量向量X中提取第一有效成分t1,它既是自变量的线性组合,又能最大程度的携带中的数据变异,假设因变量向量Y=BPLS1t1+eY,经过交叉有效性检验,若方程没有达到满意的精度,则利用X和Y被t1解释后的残余信息eX和eY进行第二轮成分提取,直到达到满意精度,最终再还原成关于原始变量的回归方程Y=BPLSX。
|
图 1 偏最小二乘回归建模流程 Fig. 1 Modeling flow of partial least square regression |
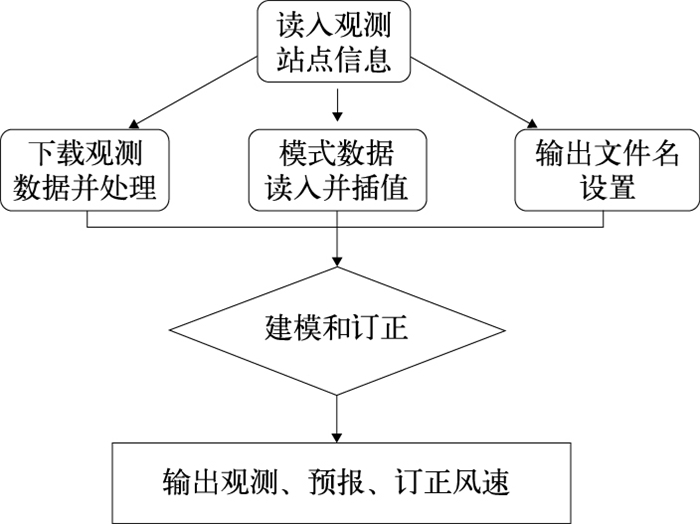
利用业务化的ZJWARMS预报产品与956站逐时观测数据(风速、温度、气压、相对湿度),本研究开发完成基于偏最小二乘回归方法的风速订正预报模型。具体的计算方法如下:首先将历史模式预报数据作为自变量,同时刻观测数据作为因变量,建立模型并获取参数;再将建模参数带入需订正的预报时刻,算出风速的“观测值”,即所谓的风速订正值。图 2为风速订正业务的基本框架。
|
图 2 风速订正业务的基本框架 Fig. 2 Basic framework of wind speed correction |
同时刻建模:每次预报有1~72 h累计72个时次预报值。建模时采用同时次预报值与对应的观测值建模,即每天的预报要建立72个订正模型,除此以外00时刻模式预报的分析场也经过该订正模型质控。建模样本956个,取订正前10 d的预报值和观测值建模。
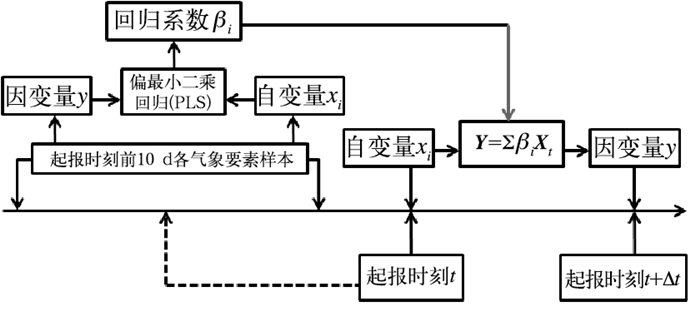
对于起报时刻为t的预报风速,其在未来t+Δt的风速订正结果流程说明见图 3。首先按照上述建模方案选取历史样本,并计算相应的自变量xi和因变量y,然后用偏最小二乘回归算法得到每个自变量的回归系数βi,最后利用起报时刻t的自变量X,得到在未来时刻t+Δt的风速订正结果Y。
|
图 3 风速订正建模和订正核心工作流程 Fig. 3 Wind speed correction modeling and core workflow |
风速订正后的评估研究用到以下统计参数。其中vi为某类风速第i个测算值。voi为第i个风速观测值,vmi和vci分别为第i个模式预报值和风速订正值。
平均风速:
| $ \overline{v}=\frac{1}{n} \sum\limits_{i=1}^{n} v_{i} $ | (1) |
模式绝对误差:
| $ \Delta v_{m}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|v_{m_{i}}-v_{o_{i}}\right| $ | (2) |
订正绝对误差:
| $ \Delta v_{c}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|v_{c_{i}}-v_{o_{i}}\right| $ | (3) |
模式相对误差:
| $ {r_m} = \frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{v_{{m_i}}} - {v_{{o_i}}}} \right)}^2}} } }}{{\frac{1}{n}\sum\limits_{i = 1}^n {{v_{{o_i}}}} }} \times 100\% $ | (4) |
订正相对误差:
| $ {r_c} = \frac{{\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{v_{{c_i}}} - {v_{{o_i}}}} \right)}^2}} } }}{{\frac{1}{n}\sum\limits_{i = 1}^n {{v_{{o_i}}}} }} \times 100\% $ | (5) |
订正结果相对模式改善百分比:
| $ P M=\frac{\Delta v_{c_{i}}-\Delta v_{m_{i}}}{\Delta v_{m_{i}}} \times 100 \% $ | (6) |
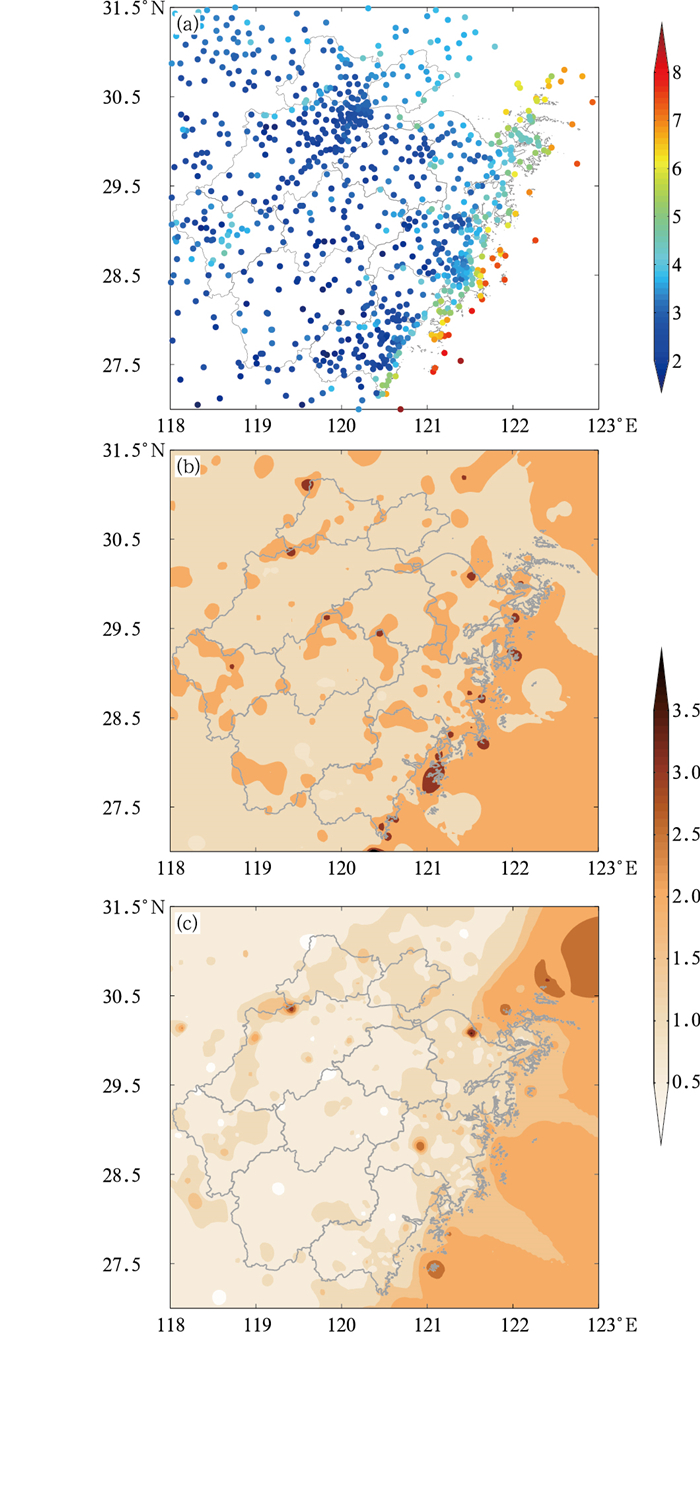
如图 4a所示,陆地上浙江冬季近地面风速基本在2~4 m·s-1。沿海地区自动站布点密集,但依然可看出风速分布几乎与海岸线平行,自西向东逐渐增大。海上近地面风速超过7 m·s-1。预报风速绝对误差空间分布(图 4b)显示,陆地上绝对误差约为1.5 m·s-1,部分地区超过2 m·s-1,极少数地区出现3 m·s-1以上的绝对误差。沿海及海上大部分地区风速绝对误差都超过2 m·s-1,其中邻海的洋面及部分岛屿超过3 m·s-1。经订正后风速绝对误差如图 4c所示,在浙中到浙西的大部分地区绝对误差都小于1 m·s-1,订正后的风速相对模式预报风速绝对误差明显降低。浙东沿海地区风速绝对误差约1~1.5 m·s-1,杭州湾以东洋面订正后绝对误差约2.5 m·s-1,相对预报风速该地区订正效果不明显,其他洋面订正后风速绝对误差约2 m·s-1,略好于预报风速绝对误差。
|
图 4 浙江省冬季自动气象站近地面风速均值空间分布(a)、预报风速绝对误差空间分布(b)以及订正风速绝对误差(c)(单位:m·s-1) Fig. 4 Spatial distributions of the mean wind speed observed by AWSs (a), the absolute error of forecasting wind speed (b) and the absolute error of corrected wind speed (c) in winter in Zhejiang Province (unit: m·s-1) |
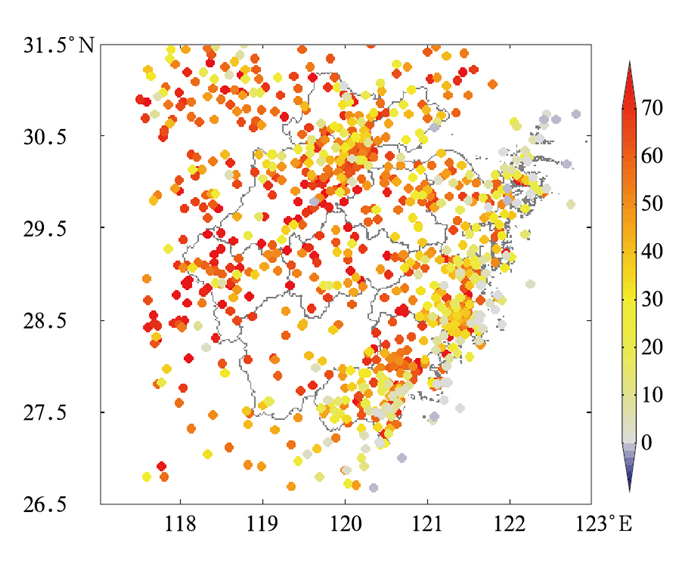
根据式(6)计算得研究时间段内各站点风速订正改善情况百分比,其结果见图 5。
|
图 5 站点风速订正效果改善百分比(单位:%) Fig. 5 The improvement percentage of corrected wind speed at each station (unit: %) |
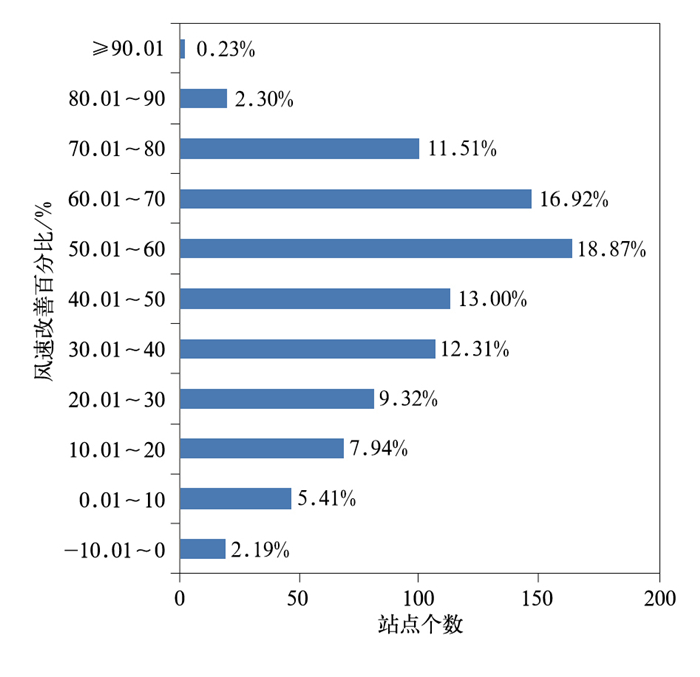
如图 5所示,所选956个站分布均匀,且多数站点风速订正后有改善。陆地上的站点订正效果明显优于沿海及海上。特别是浙北地区,虽然站点较为密集,但该区整体订正后风速改善百分比超过50%;沿海地区站点订正后改善效果稍逊于内陆,风速改善百分比在20%~30%;海上站点整体改善效果较小,以10%以内的风速改善为主;其中舟山以东洋面及温州东南部洋面上的几个站点改善效果为负,这可能是因为海上部分站点观测资料不稳定以及海陆间局地地形差异所造成。统计结果显示所有站点中有改善的站点占97.81%,其中改善百分比超过50%的站点占总站点数的49%。图 6为所有站点改善比例区间分布。由图可见,风速改善百分比 < 0的站点较少,-10.01%~0%的站点仅占2.19%。订正风速改善百分比分布最多的三个区间分别是50.01%~60%、60.01%~70%和40.01%~50%,分别占总百分数的18.87%、16.92%和13.00%。可见,绝大多数站点经订正后风速改善效果明显。
|
图 6 站点风速改善百分比区间分布 (每个横向柱条右侧的百分数为该区间内站点数占总站点数的百分比) Fig. 6 The interval distribution of wind speed improvement percentage (Percentage of each lateral column on the right is for total station number in this range) |
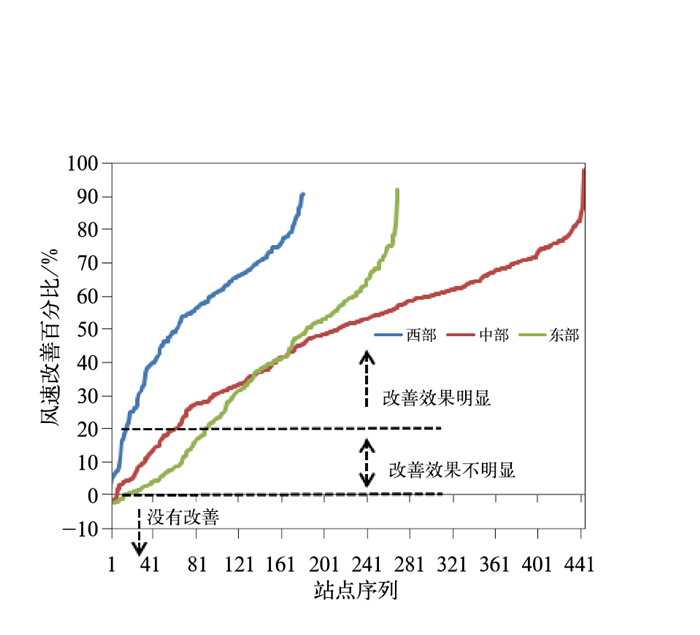
由于内陆和沿海地区风速订正差异明显,将浙江省划分为西部(117°~119°E)、中部(119°~121°E, 不包含119°和121°E)和东部(121°~123°E)分别考察三个区域内站点风速订正后的改善效果。图 7为不同区域内站点风速订正改善比例序列图,图中三个区域内站点的改善百分比按照从小到大排列。在此定义改善百分比等于0作为改善与否的分界线;改善百分比等于20%作为改善效果明显与否的分界线(如图 7中黑色虚线所示)。如图可知西部内陆地区风速订正效果最好(蓝线),该地区所有站点订正后改善百分比都大于0,即所有站点都有所改善,其中多数站点改善效果明显,改善效果不明显的站点仅15个,改善明显站点占91.7%。中部地区包含的站点数最多(红线),该地区有极个别站点订正后没有改善,经核查发现这些站点主要分布在温州东南海域。改善效果不明显的站点有55个,改善明显站点占86.5%,主要仍位于温州地区。东部地区(绿线)相对中西部地区没有改善的站点最多,主要位于舟山、宁波和台州的海域,改善效果不明显的站点数也是最多的,共76个,改善明显站点占67%,主要分布在沿海各市。
|
图 7 不同区域风速订正改善比例序列 Fig. 7 Sequence diagram of wind speed improvement percentage in different areas |
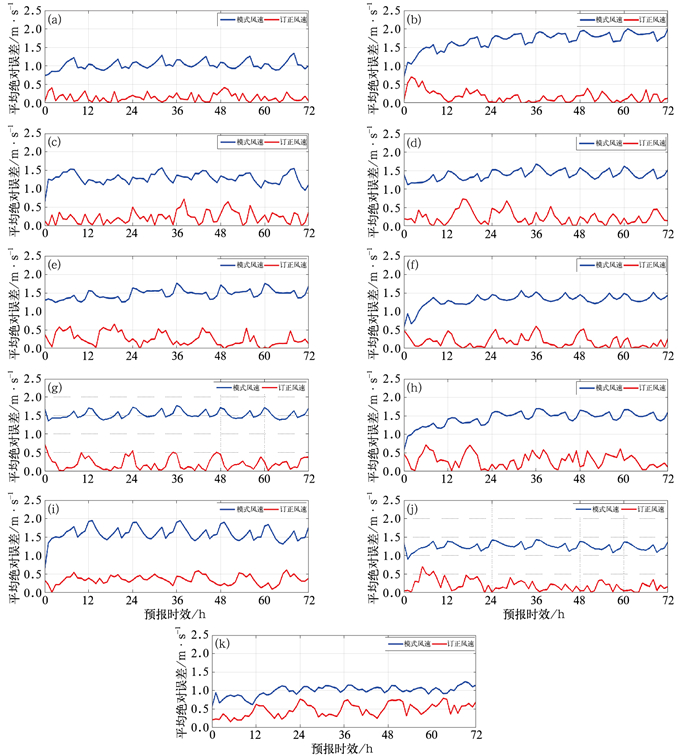
浙江省虽然面积不大,但是地形差异显著。杭嘉湖一带与绍兴、宁波地区以平原为主,地势平坦;金华、衢州地区为金衢盆地;浙东为低山丘陵;浙西南又以山地为主,丽水市海拔1000 m以上的山峰有3573座。通过图 7的分析可知各地区风速订正后的改善效果参差不齐,因此拟将冬季风速订正结果分11个地级市进行评估,重点分析订正前后风速绝对误差0~72 h的时序差异(0~72 h特指00时刻分析场和1~72 h预报场,下同)。图 8为浙江各市订正前后0~72 h预报及订正风速绝对误差时序图。由图 8可见,各市0~72 h预报时效内订正后风速均有明显改进。图 8k(舟山)订正后风速绝对误差减小不足0.5 m·s-1;图 8c,8g,8i,8j订正后0~72 h风速绝对误差整体减小了1 m·s-1以上;其他地区订正后风速绝对误差减小范围在0.5~1 m·s-1。不少站点0时刻订正效果不明显,主要是因为0时刻模式同化了观测资料后本身质量较高。表 1给出了各市风速订正效果统计参数。由表 1可见,预报风速相对观测整体偏大,订正风速拉近了与观测风速的距离,但相对观测仍略微偏大。除舟山外各市预报相对误差均大于50%,其中衢州地区甚至超过100%;订正后除衢州相对误差降至48.26%外,其他大部分地级市低于20%。风速改善百分比各市表现均不错,除舟山地区为49.9%,其他各地区风速改善比例均超过50%。
|
图 8 浙江省各市0~72 h风速绝对误差时序图 (a)杭州,(b)宁波,(c)温州,(d)绍兴,(e)湖州,(f)嘉兴,(g)金华,(h)衢州,(i)台州,(j)丽水,(k)舟山 Fig. 8 Absolute error sequence chart of wind speed over 0-72 h in every city of Zhejiang Province (a) Hangzhou, (b) Ningbo, (c) Wenzhou, (d) Shaoxing, (e) Huzhou, (f) Jiaxing, (g) Jinhua, (h) Quzhou, (i) Taizhou, (j) Lishui, (k) Zhoushan |
|
|
表 1 浙江各市风速订正效果统计参数 Table 1 Statistical parameters of wind speed correction of Zhejiang Province |
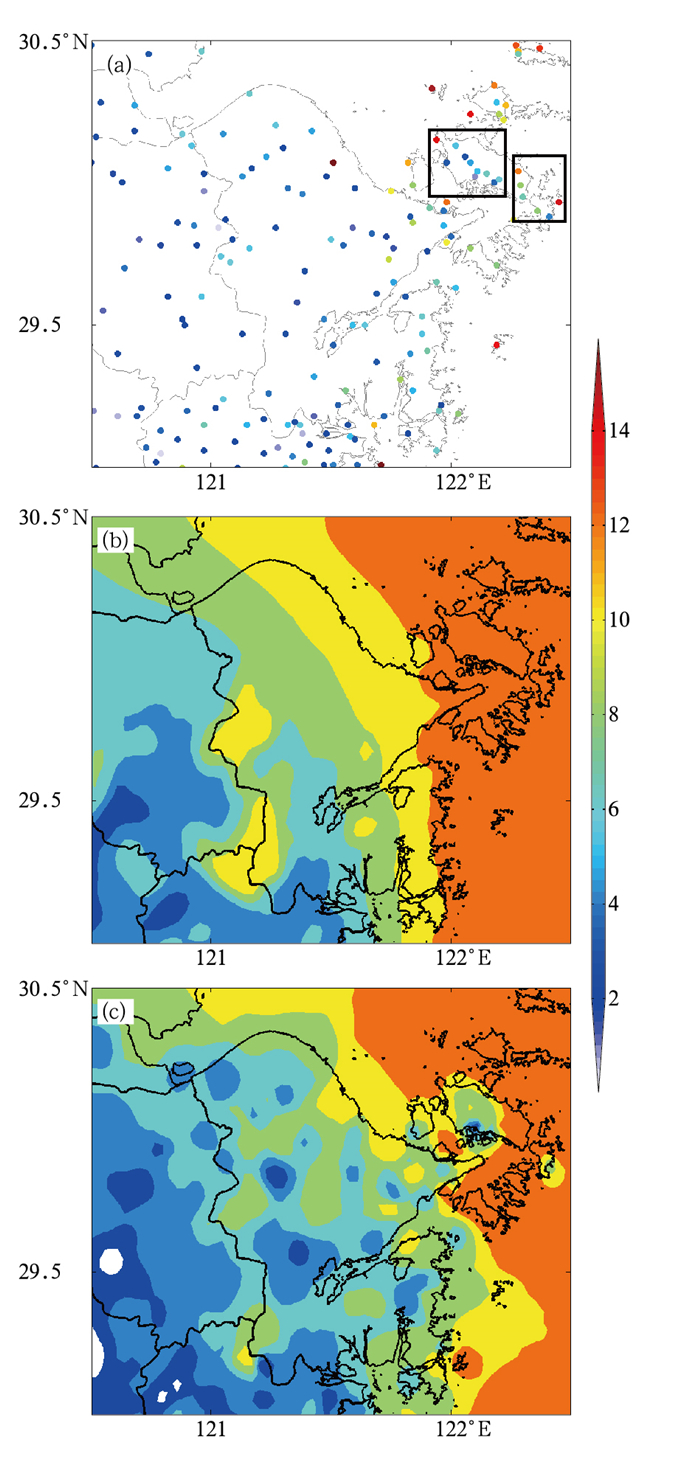
选取2017年1月20日发生在浙江东北沿海的冬季大风过程。图 9为2017年1月20日08时宁波和舟山本岛地区近地面风速观测、预报、订正空间分布。如图 9a所示宁波地区近地面观测风速约4~6 m·s-1,风速分布特征不明显;图 9b中宁波地区预报风速呈由东向西逐渐减小趋势,近海地区风速为10~12 m·s-1,内陆地区为8~10 m·s-1。可见预报风速明显偏大。图 9c中订正后宁波地区近地面风速以4~6 m·s-1为主,相对预报风速有显著改善。舟山本岛地区一共16个观测站点(图 9a),其中东南角的58572白沙站和西北角的K9627马目社区站,观测风速约为14 m·s-1,预报和订正风速在这两个站点都>12 m·s-1;预报风速与观测差异不大,其他站点订正后风速有显著改善。
|
图 9 2017年1月20日08时宁波市舟山本岛地区(a)站点观测近地面风速,(b)预报近地面风速以及(c)订正后近地面风速(单位:m·s-1) Fig. 9 Observation of near-surface wind speed (a), forecasted wind speed (b) and corrected wind speed (c) in Ningbo and Zhoushan Area at 08:00 BT 20 January 2017 (unit: m·s-1) |
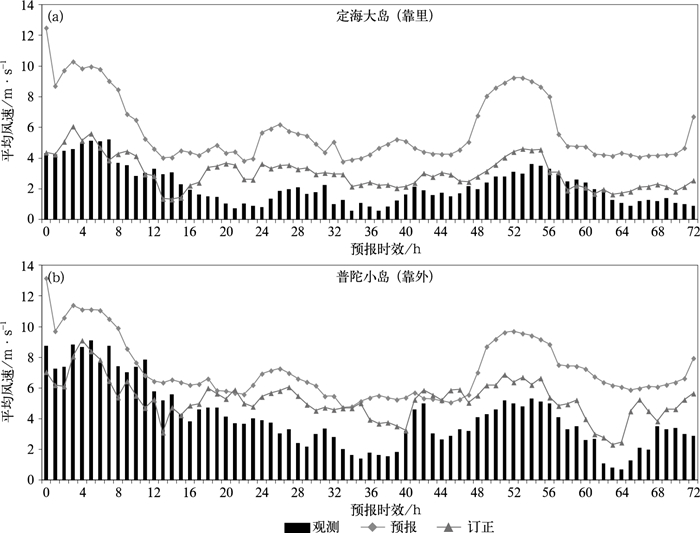
为计算订正后风速的改善效果,将所有观测站点分为普陀小岛(图 9a右边黑框中6站)和定海大岛(图 9a左边黑框中10站),除58572站和K9627站观测风速>12 m·s-1外,其他站点多数风速维持在4~8 m·s-1,其中近海站点以6~8 m·s-1为主,近岸站点以4~6 m·s-1为主。将两个黑框中的所有站点0~72 h过程观测、预报和订正风速求均值后可得图 10。
|
图 10 2017年1月20日定海大岛(a)和普陀小岛(b)过程风速时序图 Fig. 10 Process wind speed sequence diagram of the 20 January 2017 case (a) nearshore stations, (b) offshore stations |
如图 10所示,定海大岛站点(靠里)观测风速相对普陀小岛站点(靠外)整体偏小,这是由于海陆交界处地面摩擦造成的风速衰减所致,而这种风速衰减特征在预报风速中没有显著体现,因此两个区域的预报风速量级及其0~72 h变化趋势都比较接近,导致靠里站点预报风速明显偏大。靠外站点经过订正后的风速相对预报0~72 h变化趋势依然类似,但风速量级明显减小,与观测风速更接近。靠外站点虽然已选用不同的自变量组合,订正后整体效果不如近岸站点明显,主要表现在0~12 h订正后部分时次风速相对预报偏小,虽然订正前预报风速相对观测偏大,但由于偏大值在可接受范围内,所以导致订正效果不如靠里站点明显。同时也说明当预报风速跟观测差异较大时,经该方法订正后的近地面风速效果更好。
4 结论及讨论利用偏最小二乘回归技术,对2013—2016年冬季浙江省ZJWARMS预报近地面风速进行订正和评估,得到以下结论:
(1) 整体而言,订正后的风速相对模式预报风速绝对误差明显降低。通过定量分析可知西部地区整体改善效果最好,其中效果明显站点占91.7%;中部地区改善效果明显站点占86.5%;东部沿海地区改善效果略差,其中有明显改善的站点占67%。舟山以东洋面及温州东南部洋面上的几个站点改善效果为负值,这可能是因为海上部分站点观测资料不稳定以及海陆间局地地形差异所造成。
(2) 选取2017年1月20日浙江东北沿海大风过程,分析订正前后预报风速的具体表现。该天气过程,宁波地区预报风速整体偏大,订正后的预报风速明显减小,与观测站点风速分布基本相似。将舟山本岛分为定海大岛(10站)和普陀小岛(6站)两个区域,分别讨论订正前后该区域内站点过程风速0~72 h的时序特征,发现订正后的风速与观测风速更为接近,在近岸站点中表现尤为明显,订正后的结果具有显著参考价值。
本文的风速订正技术基于偏最小二乘回归技术,可有效改善因自变量间的多重相关性(如风速和气压),观测资料偶有缺失等问题。但如图 5所见,并非所有站点订正后都有改善。气象站风速大小与观测场周边环境关系非常密切,956个自动站观测环境如何,有多少个站能代表模式3 km范围的下垫面状况和风况?这需要在今后的研究中首先将所有站点的预报风速进行评估,重点订正预报风速偏差大的站点,才能有效提高风速订正的效率。
龚强, 袁国恩, 张云秋, 等, 2006. MM5模式在风能资源普查中的应用试验[J]. 资源科学, 28(1): 145-150. Gong Q, Yuan G E, Zhang Y Q, et al, 2006. Application of MM5 Model in wind energy resources survey[J]. Resources Sci, 28(1): 145-150 (in Chinese). DOI:10.3321/j.issn:1007-7588.2006.01.023 |
胡美娟, 周年兴, 李在军, 等, 2015. 南京市三维生态足迹测算及驱动因子[J]. 地理与地理信息科学, 31(1): 91-95. Hu M J, Zhou N X, Li Z J, et al, 2015. Calculation and driving factor analysis of three-dimensional ecological footprint in Nanjing City[J]. Geogra Geo-Informa Sci, 31(1): 91-95 (in Chinese). DOI:10.3969/j.issn.1672-0504.2015.01.019 |
李刚, 熊婵, 赵丽英, 等, 2012. 基于多维漫反射光谱技术的复杂混合溶液成分检测[J]. 光谱学与光谱分析, 32(2): 491-495. Li G, Xiong C, Zhao L Y, et al, 2012. Component analysis of complex mixed solution based on multidimensional diffuse reflectance spectroscopy[J]. Spectroscopy and Spectral Analysis, 32(2): 491-495 (in Chinese). DOI:10.3964/j.issn.1000-0593(2012)02-0491-05 |
柳艳香, 陶树旺, 张秀芝, 2008. 风能预报方法研究进展[J]. 气候变化研究进展, 4(4): 209-214. Liu Y X, Tao S W, Zhang X Z, 2008. Review on methods of wind power forecasting[J]. Adv Climate Change Res, 4(4): 209-214 (in Chinese). DOI:10.3969/j.issn.1673-1719.2008.04.003 |
舒守娟, 王元, 熊安元, 2007. 中国区域地理、地形因子对降水分布影响的估算和分析[J]. 地球物理学报, 50(6): 1703-1712. Shu S J, Wang Y, Xiong A Y, 2007. Estimation and analysis for geographic and orographic influences on precipitation distribution in China[J]. Chin J Geophy, 50(6): 1703-1712 (in Chinese). DOI:10.3321/j.issn:0001-5733.2007.06.010 |
宋金杰, 王元, 陈佩燕, 等, 2011. 基于偏最小二乘回归理论的西北太平洋热带气旋强度统计预报方法[J]. 气象学报, 69(5): 745-756. Song J J, Wang Y, Chen P Y, et al, 2011. A statistical prediction scheme of tropical cyclone intensity over the western North Pacific based on the partial square regression[J]. Acta Meteor Sin, 69(5): 745-756 (in Chinese). DOI:10.3969/j.issn.1004-4965.2011.05.017 |
王丙兰, 宋丽莉, 袁春红, 等, 2017. 河南电网输电线路舞动的气象要素指标研究[J]. 气象, 43(1): 108-114. Wang B L, Song L L, Yuan C H, et al, 2017. Study of meteorological indices for transmission line galloping in Henan power grid[J]. Meteor Mon, 43(1): 108-114 (in Chinese). DOI:10.3969/j.issn.1673-503X.2017.01.015 |
姚日升, 涂小萍, 蒋璐璐, 等, 2016. 浙江近海冬季大风风速推算和ASCAT风速订正方法探讨[J]. 气象, 42(5): 621-627. Yao R S, Tu X P, Jiang L L, et al, 2016. Analysis on methods about the winter offshore gale speed estimation and ASCAT wind correction in Zhejiang[J]. Meteor Mon, 42(5): 621-627 (in Chinese). |
余江, 江志红, 俞卫, 等, 2015. 风电场风速数值预报的误差分析及订正[J]. 气象科学, 35(5): 587-592. Yu J, Jiang Z H, Yu W, et al, 2015. Error analysis and correction of wind speed numerical forecast at wind farm[J]. J Meteor Sci, 35(5): 587-592 (in Chinese). |
张颖超, 肖寅, 邓华, 2016. 基于ELM的风电场短期风速订正技术研究[J]. 气象, 42(4): 466-471. Zhang Y C, Xiao Y, Deng H, 2016. Modification technology research of short-term wind speed in wind farm based on ELM method[J]. Meteor Mon, 42(4): 466-471 (in Chinese). |
朱智慧, 黄宁立, 2012. 上海沿海WRF模式风速预报的检验和释用[J]. 大气科学研究与应用, (2): 69-76. Zhu Z H, Huang N L, 2012. Verification and application of wind speed forecast in Shanghai coastal area by the WRF Model[J]. Atmos Sci Res Appl, (2): 69-76 (in Chinese). |
Alexiadis M C, Fotopoulos P S, Sahsamanoglou H S, et al, 1998. Short-term forecasting of wind speed and related electrical power[J]. Solar Energy, 63(1): 61-68.
|
Barbounis T G, Theoharis J B, Alexiadis M C, et al, 2006. Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE Trans Energy Conv, 21(1): 273-284. DOI:10.1109/TEC.2005.847954
|
Bossanyi E A, 1985. Short-term wind prediction using Kalman filters[J]. Wind Eng, 9(1): 1-8.
|
Box G E P, Jenkins G M, Reinsel G C, 1976.Time Series Analysis: Forecasting and Control[M].New York: John Wiley and Sons.
|
Mabel M C, Fernandez E, 2008. Analysis of wind power generation and prediction using ANN:a case study[J]. Renew Energy, 33(5): 986-992. DOI:10.1016/j.renene.2007.06.013
|
Wold H, 1966.Estimation of principal components and related models by iterative least squares[M]//Krishnaiaah P R.Multivariate Analysi.New York: Academic Press: 391-420.
|
 2019, Vol. 45
2019, Vol. 45 