2. 江苏省气象台,南京 210008;
3. 北京城市气象研究院,北京 100089;
4. 国防科技大学气象海洋学院,南京 211101
2. Jiangsu Meteorological Observatory, Nanjing 210008;
3. Institute of Urban Meteorology, CMA, Beijing 100089;
4. Institute of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101
暴雨是江苏省夏季最常见的一种灾害性天气。数值预报的迅速发展为这类灾害性天气的预报提供了有效工具,但目前的模式预报效果并不完美,对暴雨落区和强度预报依然是难点。陶诗言(1977)曾指出暴雨多产生在中尺度扰动中,是多种尺度天气系统相互作用的结果,这中间包含一系列复杂的非线性物理过程,在数值模式中无法得到精确的描述。此外,受数值模式初始条件误差、模式误差和非线性大气运动混沌特性的影响,单一的数值预报仍存在较大的不确定性(Leith,1974;丑纪范,2002)。
集合预报是针对数值预报不确定性问题发展起来的新一代随机动力概率预报技术,它既能给出单一的最佳可能预报,也能定量估计天气预报的可靠性,同时可以提供概率预报产品,是研究暴雨这一类小概率极端性天气事件的发展方向(Toth and Kalnay, 1993;Molteni et al, 1996)。集合预报技术在最近十多年来得到迅速的发展与推广应用。现代天气业务发展指导意见明确提出以集合数值预报为依托,提高降水、灾害性天气和其他极端天气的概率预报水平(陈静等,2002;2005)。国家气象中心从2007年开始,不断积累着在定量降水预报(QPF)、中期预报、台风海洋预报和强对流预报等业务中的集合预报产品应用技术和经验(邓国等,2010;杜钧和陈静,2010;陈涛等,2017;代刊等,2018;刘琳等,2018;王毅等,2018)。
不少研究已指出集合预报在暴雨等灾害性天气的预报中有重要作用(刘家峻等,2010;李俊等,2007;王晨稀,2005;黄红艳等,2016;高守亭等,2018)。杜钧和李俊(2014)从暴雨集合预报系统的建立、集合预报方法、集合预报后处理及对暴雨的订正、应用集合预报研究天气系统发展机理和指导目标观测四个方面总结了集合预报方法在暴雨研究和预报中的应用。杜钧等(2014)利用集合预报以及和气候资料相结合的“集合异常预报法”对2012年北京7月21日特大暴雨事件的分析发现“集合异常预报法”可以提供比单一模式预报更可靠和更准确的信息。王亚男和智协飞(2012)分析了欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)、日本气象厅、美国国家环境预报中心和英国气象局四个全球集合预报系统对中国区域暴雨的预报效果发现,集合暴雨概率预报对暴雨预报具有较好的指示意义,但存在系统性偏小问题。因此,多种集合强降水预报订正方法被提出,如“融合法”“融合-概率匹配法”(陈博宇等,2015)、“频率匹配法”(李俊等,2014;2015;周迪等,2015)、“集合动力因子法”(高守亭等,2013)、“贝叶斯集合降水概率”(韩焱红等,2013;张宇彤等,2016)等,这些后处理方法在特定的区域或研究个例中均最大可能地减少了集合预报的系统误差,提高了暴雨的预报技巧。随着集合预报的业务运行,许多研究工作将集合预报在我国不同地区的应用效果进行了检验,这些检验结果也有助于预报员对当地常用的集合预报系统各预报产品对不同量级降水的预报性能有了更深入的了解,帮助预报员在海量信息中更快地选取有用的产品(陈力强等,2005;赵琳娜等,2010;范苏丹等,2015;包慧濛等,2015;斯琴等,2016)。
目前江苏省对于集合预报的研究和业务使用还处于初步阶段,集合预报的业务应用,尤其在灾害性天气预报方面的应用还需要进一步深入和持续的研究。在日常业务中,集合预报产品的使用率较低,其原因归根于不少预报员对集合预报的概念、系统构架、产品解读和如何应用都缺乏清晰的认识,各集合预报产品及其集合成员的预报性能如何,预报员们目前也并没有一个初步的意识。鉴于此,本文将着眼于暴雨这一灾害性天气,收集大样本暴雨预报事件,分析现有的各集合预报产品及其客观释用产品对暴雨的预报能力,综合评估集合预报系统对江苏夏季暴雨的预报效果,探讨暴雨的可预报性问题,为预报员更直接、快速地选取有效的模式预报参考产品,订正预报结果提供参考依据。
1 资料与方法 1.1 资料(1) 降水实况资料为2011—2015年6—8月江苏省70个基本站24 h(20时至次日20时)降水数据。
(2) 降水集合预报数据取自TIGGE(THORPEX Interactive Grand Global Ensemble)数据集ECMWF的集合预报数据,该数据共有51个成员,包括1个控制预报成员和50个集合扰动预报成员,空间分辨率为0.5°×0.5°,起报时间为每日08时。
(3) 在进行暴雨预报检验时,同时加以分析了2011—2015年6—8月的ECMWF确定性降水数值预报产品的预报能力,其空间分辨率为0.5°×0.5°。
1.2 检验方法 1.2.1 降水预报常用检验方法TS评分:
| $ \mathit{TS}\text{=}\frac{\mathit{ }{{\mathit{N}}_{\mathit{A}}}}{{{\mathit{N}}_{\mathit{A}}}\mathit{+}{{\mathit{N}}_{\mathit{B}}}\mathit{+}{{\mathit{N}}_{\mathit{C}}}}\times 100\text{ }\!\!%\!\!\text{ } $ | (1) |
漏报率:
| $ {{\mathit{P}}_{\mathit{O}}}\text{= }\frac{{{\mathit{N}}_{\mathit{C}}}}{{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{C}}}}\times 100\text{ }\!\!%\!\!\text{ } $ | (2) |
空报率:
| $ {{\mathit{F}}_{\mathit{AR}}}\text{= }\frac{{{\mathit{N}}_{\mathit{B}}}}{{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{B}}}}\times 100\text{ }\!\!%\!\!\text{ } $ | (3) |
预报偏差:
| $ {{\mathit{B}}_{\mathit{S}}}\text{= }\frac{{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{B}}}}{{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{C}}}}\times 100\text{ }\!\!%\!\!\text{ } $ | (4) |
公平成功指数:
| $ \mathit{ETS}\text{= }\frac{{{\mathit{N}}_{\mathit{A}}}}{{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{B}}}\text{+}{{\mathit{N}}_{\mathit{C}}}\text{-}\mathit{r}}\times 100\text{ }\!\!%\!\!\text{ } $ | (5) |
| $ \mathit{r}\text{= }\frac{\text{(}{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{B}}}\text{)(}{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{C}}}\text{)}}{\text{(}{{\mathit{N}}_{\mathit{A}}}\text{+}{{\mathit{N}}_{\mathit{B}}}\mathit{+}{{\mathit{N}}_{\mathit{C}}}\text{+}{{\mathit{N}}_{\mathit{D}}}\text{)}}\times 100\text{ }\!\!%\!\!\text{ } $ | (6) |
式中,NA为暴雨预报正确站(次)数,NB为暴雨空报站(次)数,NC为暴雨漏报确站(次)数, ND为未预报暴雨且无暴雨发生的站(次)数。
1.2.2 暴雨预报准确率检验办法根据各预报检验站(次)预报雨量和实况雨量,对比量级的误差,计算逐站的预报评分,并统计得出预报责任区内的暴雨预报准确率评分。
对于某区域,暴雨预报准确率(heavy rainfall score,HRSc)计算公式如下:
| $ \mathit{HRSc}\text{=}\frac{\sum{{{S}_{i}}}}{{{\mathit{N}}_{\mathit{F}}}\text{+}{{\mathit{N}}_{\mathit{C}}}} $ | (7) |
式中, i为达到检验标准的预报站(次)数,Si为各预报检验站(次)的预报评分,NF为预报总站(次)数,NC为漏报站(次)数。各站(次)暴雨预报准确率评分Si计算见表 1。
|
|
表 1 逐站(次)暴雨预报梯级递减评分表 Table 1 Score standard for different heavy rainfall thresholds for each station(time) |
对于A站暴雨预报得分的评定细则如下:
(1) A站预报暴雨以下级别(<50.0 mm),且A本站的实况为暴雨以下级别(<50.0 mm),则A站不评分,不计入预报总站(次)数NF;
(2) A站预报暴雨及以上级别(≥50.0 mm),且A站预报量级大于本站实况量级,则NF加1;
(3) A站预报大雨及以上级别(≥25.0 mm),A站实况为暴雨及以上级别(≥50.0 mm),且A站预报量级小于或等于本站实况量级,则直接按照暴雨预报梯级递减评分表对A站进行评分,NF加1;
(4) A站预报大雨以下级别(<25.0 mm),且A站实况为暴雨及以上级别(≥50.0 mm),则A站记暴雨漏报,得分为0,则NC加1。
1.3 插值方法利用距离平方加权平均法将模式格点产品插值到江苏省70个基本站站点上。
1.4 暴雨样本统计2011—2015年江苏省70个站6—8月某一日至少有1个站发生暴雨,则计为1个暴雨日,5年内共有150个实际暴雨日,分别为44、28、26、20、32 d,7月累计最多(64 d),8月为55 d。在各类产品的检验总样本中包含实际暴雨日和完全空报情形,即检验总样本大于或等于实际暴雨日。
1.5 预报时效选取研究所取集合预报数据均为每日08时起报,业务上由于资料获取时间受限,在制作20时至次日20时预报时参考的最新预报时间为08时;通常,随着预报时效的延长,模式预报能力降低;且本研究的重点是评估各集合统计量和后处理技术的暴雨预报能力,故综合考虑,重点对每日08时起报的未来12~36 h的24 h暴雨预报的落区进行检验。
2 集合预报产品效果分析 2.1 EC集合预报系统子成员和EC集合平均产品对江苏暴雨事件预报能力评估ECMWF(以下简称EC)集合预报系统共有51个成员:1个控制性试验CF和50个敏感性试验PF。从51个成员输出场中可以得到一系列的基本产品,包括集合平均、集合离散度、天气要素概率图、分位数、面条图、邮票图和单站集合预报。针对暴雨这一江苏省常见的灾害性天气,可以参考哪些集合预报产品?利用怎样的集合预报产品可以为预报员提供更方便直接、更客观准确的暴雨预报参考?
初步计算了EC集合预报系统所有成员对江苏暴雨的TS评分(图略)。针对同一暴雨事件,不同成员的预报TS评分差异较大,有的成员评分为0,也有的达到95分以上的。平均而言,对于2011—2015年夏季暴雨预报,EC集合预报系统各成员平均TS评分5.21%,最高不高于7.00%,ETS不高于9.00%,HRSc不超过17%,漏报率和空报率均比较高,最低的漏报率也高于88%,最低的空报率高于50%,漏报现象尤为突出。
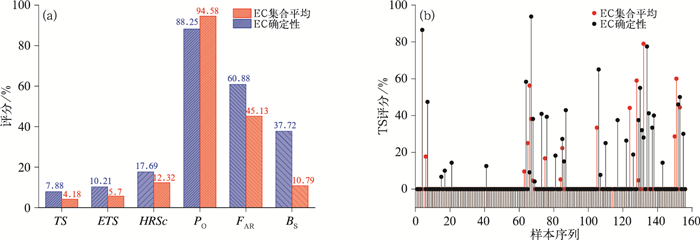
集合平均是集合预报的最初级产品,是各集合成员简单的数学平均,提供的也是确定性预报(Lorenz, 1963)。图 1给出了EC集合平均预报和EC确定性预报暴雨预报的TS评分,可见对于未来12~36 h暴雨预报,EC确定性预报的TS、ETS、HRSc各项预报评分均明显高于EC集合平均(图 1a),其中仅8个样本EC集合平均评分高于EC确定性预报,有25个样本EC集合平均评分低于EC确定性预报(图 1b);EC集合平均产品表现出更高的漏报率,高达94.58%,但集合平均的空报率和预报偏差有所降低。由上述分析可知,EC集合平均产品并非江苏省暴雨预报参考的有效工具,其预报效果不如EC确定性预报和部分原始集合成员,因此不少后处理技术相继被提出来订正集合平均预报值(李俊等,2014;陈博宇等,2015)。
|
图 1 EC集合平均与EC确定性预报各项指标平均评分(a),样本序列EC集合平均与EC确定性预报暴雨预报TS评分(b) Fig. 1 Multiple evaluation scores of ECMWF ensemble-mean forecast and deterministic forecast (a), threat scores (TS) of each samples of ECMWF ensemble-mean forecast and deterministic forecast (b) |
EC集合预报系统在预报暴雨这类灾害性天气事件上是否具有一定预报能力?或者说,EC集合预报系统对江苏暴雨的预报评分能否有所提高?针对150个暴雨预报事件,挑选出EC集合系统51个成员中预报评分最高的成员构成一个最优预报组合,计算该最优组合的平均预报评分,平均TS评分高达22.29%,明显高于EC集合平均和EC确定性预报,其中72个暴雨预报样本最优预报组合评分高于EC确定性预报,76个暴雨预报样本最优预报组合评分高于EC平均;仅4个暴雨预报样本最优预报组合评分低于EC确定性预报;共有57个暴雨预报样本的集合平均TS评分为0,而最优组合的评分高于0,42个暴雨预报样本EC确定性预报TS评分为0,而最优组合的评分高于0。可见,如果每次过程能挑选出最优预报成员的话,EC集合预报系统对江苏省暴雨的预报能力会有很大提高,即“真相”很可能藏在集合预报成员的多种可能性当中,也间接表明集合预报具有较大的应用潜力。
2.2 EC集合预报多种统计量和后处理技术在江苏省暴雨预报中的的应用集合预报具有多成员的特点,其提供的信息量非常丰富,多个成员的降水产品经过统计学算法可以获得集合平均、不同百分位数的统计量产品,对这些统计量产品再使用多元数据的一些数学算法,如融合方法、概率匹配方法、概率预报方法等,又可以获得新的产品。结合江苏省实际暴雨预报个例,探讨各统计量产品的优势和不足,评估各产品对暴雨的预报能力,为预报员在利用集合预报系统进行预报暴雨快速选择合适的集合预报产品、订正预报结果提供参考依据。
2.2.1 集合分位数类似集合平均,最大值、90%分位数、75%分位数和中位数也是集合预报系统中常用的简单的具有单一预报值的统计量产品。集合分位数值对应51个集合成员的百分位数值:P%分位数值即第P百分位数,它对应这样一个值,使得至少有P%的集合成员值小于或等于这个值,且至少有(100-P)%的集合成员值大于这个值。最大值即为100%分位数,中位数即为50%分位数。
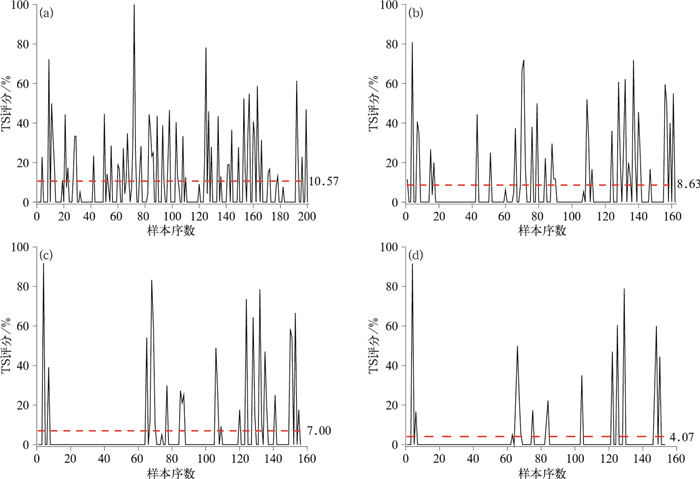
通过对2011—2015年夏季暴雨预报样本的检验(图 2和表 2),可以看出:(1)最大值产品平均TS评分最高,达到10.57%,高于EC确定性产品和EC集合平均产品对暴雨的预报;(2)其他分位值产品平均TS评分低于最大值,随着分位数的减少,评分显著降低,90%和75%分位数产品的预报效果均优于EC集合平均,75%以下分位数的预报平均均低于EC确定性,中位值对暴雨的预报评分与EC集合平均相当,对暴雨几乎没有预报效果;(3)结合漏报率和空报率,最大值由于较低的漏报率(漏报率为60.94%,明显低于EC确定性88.25%和EC集合平均94.58%),故TS评分最高,却同时出现了较高的空报率(85.35%明显高于EC确定性60.88%和EC集合平均45.13%)。同样的,随着分位数的减少,漏报率增加,空报率降低,漏报率和空报率呈现线性反相关;(4)虽然最大值产品平均TS评分最高,但细致分析具体个例可以发现,由于最大值产品存在明显的空报,也会使得一些样本预报评分不如其他产品,例如2011年6月18日暴雨,75%分位数产品TS评分最高为91.89%,而最大值仅为72.34%。
|
图 2 EC集合分位数产品的暴雨预报TS评分曲线 (a)最大值,(b)90%分位数,(c)75%分位数,(d)中位数(红色虚线为平均TS评分) Fig. 2 TS of ensemble percentile products of ECMWF for heavy rainfall (a) maximum value, (b) the 90th percentile value, (c) the 75th percentile value, (d) the 50th percentile value (Red dashed line denotes the average TS) |
|
|
表 2 EC集合系统各分位数预报产品和EC集合平均与EC确定性预报的暴雨预报平均漏报率和空报率 Table 2 The missing forecast rate and false forecast rate of each ensemble percentile product and ECMWF ensemble-mean forecast and deterministic forecast for heavy rainfall |
由此可见,最大值产品对暴雨预报评分的显著提高主要归功于明显降低了暴雨漏报率,但一定程度上带来了不少空报。因此,今后还需进一步研发一个既能补漏又能消空的集合预报后处理方法,这样才能真正提高EC集合系统对暴雨的预报能力,为预报员提供更有效的参考。
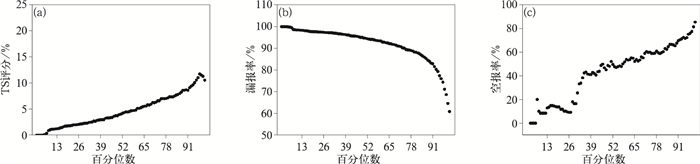
2.2.2 最优百分位集合预报产品集中最常规的百分位值产品为固定百分位值:0(即为最小值)、10、50、75、90、100(即为最大值)百分位产品。现将固定百分位值转变为动态百分位值,根据2011—2015年历史同期模式预报和站点观测资料,计算了101个百分位值的TS评分{0,1,2,3,…,97,98,99,100}。针对暴雨量级以上的降水预报,由图 3可以看出,85以下百分位值的平均TS评分已经低于EC确定性(平均评分为7.88%),51以下百分位值评分低于EC集合平均(平均评分为4.18%),对暴雨预报基本无效果改进;随着百分位数的增加,TS评分总体增加(非线性),评分最高的对应97百分位值,为11.75%,较最大值(10.57)也有所提高,第98、99和100分位值(即最大值)又低于了97百分位值。由图 3b、3c可见,随着百分位数的增加,尤其是大于80%百分位数时,漏报率显著减小。在漏报率减少的同时,空报率显著上升。漏报率减少使得评分提高,空报率上升又降低了评分,是否存在一种平衡,使得预报评分达到最高值?所以通过这5年历史预报资料的检验,计算动态百分位值的TS评分,可以寻找到针对暴雨预报的最优百分位值,那么针对2011—2015年夏季暴雨预报,EC集合预报的最优百分位值为97%。
|
图 3 EC集合预报动态百分位产品的暴雨预报评分曲线
(a)TS评分,(b)漏报率,(c)空报率 (横坐标为第i个百分位数,i=0,1,2,3,…,97,98,99,100) Fig. 3 Evalution of each ensemble percentile of (from the 0th to the 100th percentile) products for heavy rainfall (a) TS, (b) missing forecast rate and (c) false forecast rate |
由此可见,最优百分位值方法对EC确定性预报、集合平均、最大值产品均有所改进,其思想在于当漏报率减少,伴随空报率增加时,寻找到一个平衡点使得预报评分最高,但该最优百分位值可随季节、预报时效、历史资料时段的变化而变化,不具有确定性。因此,预报员在参考最优百分位产品时,需结合历史同时统计结果确定最优百分位值。
2.2.3 融合、概率匹配、融合—概率匹配、概率匹配—融合预报产品国家气象中心基于多种统计量的融合技术,在不同降水量级上采用最优评分集合统计量的叠加产品作为新的集合预报确定性产品,称为融合(statistic fusing,FUSE)产品(Ebert, 2001; 陈博宇等, 2015)。此外,概率匹配集合平均法(probability marched ensemble mean,PM)也是常用的集合预报后处理技术(陈博宇等, 2015)。陈博宇等(2015)对2013年汛期EC集合统计量产品的降水预报检验发现,PM产品对大雨落区的调整有较稳定的表现,而对暴雨预报的把握则略显不足。融合产品侧重于对降水量级的调整。为此,结合PM和FUSE产品各自的特点,进一步提出了两种新的技术方案:概率匹配—融合(PM-FUSE)产品和融合—概率匹配(FUSE-PM)产品。两者的技术流程分别为:(1)PM-FUSE:在PM产品的基础上,按照FUSE产品的计算规则进行量级调整;(2)FUSE-PM:在计算得到FUSE产品后,采用PM平均的原理,将FUSE产品序列与集合平均序列按从大到小匹配,从而实现对融合产品降水落区位置调整的目的。
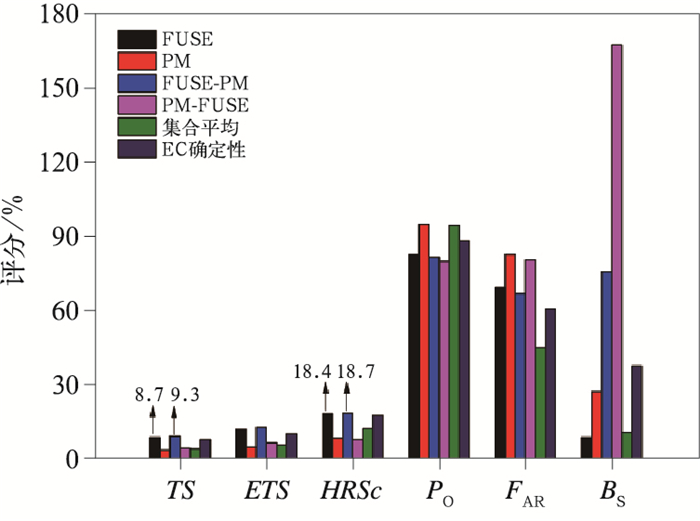
针对在江苏省暴雨预报上的应用,本研究同样拟检验这4种后处理技术对暴雨及以上量级降水的预报效果。图 4是FUSE、PM、FUSE-PM、PM-FUSE、集合平均和EC确定性预报产品各项指标平均评分对比。由图 4可见,FUSE产品相对集合平均产品来说,对强降水量级确有调整,其TS(8.7%)、ETS(12.0%)和HRSc(18.4%)评分均高于集合平均和确定性预报,尤其高于集合平均,但PM产品对暴雨预报效果不佳,TS评分仅为3.59%,订正后的效果不如集合平均,空报率和漏报率均显著增加,尤其是漏报率。两个新的方案FUSE-PM、PM-FUSE,对于暴雨预报,效果有提高的产品是FUSE-PM产品:TS(9.3%)、ETS(12.8%)和HRSc(18.7%)评分较FUSE产品有所提高,FUSE-PM产品在调整量级的基础再进行空间调整,漏报率和空报率均较FUSE产品有所下降,FUSE-PM改进方案是有效的。对比FUSE-PM产品和集合平均、EC确定性预报产品的PO和FAR,可以看到,FUSE-PM产品虽然较集合平均、EC确定性预报降低了漏报率,但同时空报率也有所提高,依然呈“跷跷板”现象。从降低漏报率角度看,PM-FUSE产品最明显,但该产品呈现出空报率高于漏报率的现象,故出现了较大的预报偏差Bs评分。综上所述,就江苏省暴雨量级降水预报而言,FUSE和FUSE-PM产品较PM、PM-FUSE、集合平均和EC确定性预报这4种预报产品更具参考价值。
|
图 4 FUSE、PM、FUSE-PM、PM-FUSE、集合平均和EC确定性预报产品各项指标平均评分对比 Fig. 4 Different evaluations of FUSE, PM, FUSE-PM, PM-FUSE, ensemble mean and deterministic forecast of ECMWF ensemble forecast |
在降水预报中,简单的集合平均由于平滑作用往往会放大小降水预报区而使得小量级降水预报偏大,也会缩小大降水预报区而使得大量级降水预报偏小。前文的分析也可知简单的集合平均对于暴雨量级的降水明显漏报。针对这一问题,Ebert(2001)提出了“频率匹配”的思路。基于这一思路,提出了利用实况降水频率订正集合成员降水预报系统偏差(简称“降水偏差订正”)的频率匹配法(Zhu and Luo, 2015;李俊等,2014; 2015;周迪等,2015),该方法的原理是假设降水预报频率与观测降水频率一致。具体实施方案可有两种,一种是通过两者频率的匹配获得降水预报的订正值,如李俊等(2014)通过简单的计数法(暴雨出现总站次/总站次)计算了预报和实况降水频率,通过多项式插值方法,订正预报降水频率,得到降水预报订正系数,进而用该订正系数乘以降水预报值,获得降水预报订正值。另一种是通过两者频率的匹配获取暴雨预报临界阈值,如观测降水量R=50 mm以上的频率为PO(R),与频率值PO(R)所对应的模式降水预报值记为Pf(R*)。假定预报降水频率与实况降水频率相同,即Pf(R*)=PO(R),则R*为针对暴雨量级降水的模式预报频率匹配订正值,当集合预报降水量大于R*时即预报该站点有暴雨。周迪等(2015)利用Gamma分布拟合观测与预报的降水累积概率分布。上述两种方案均可以有效订正模式降水预报的系统性误差,改进雨量预报。该方法计算中有两个关键过程,一是如何表征实况降水频率,二是如何反算出暴雨预报的临界阈值或预报降水订正值。
为深入理解该方法的设计原理,认知该方法在暴雨量级降水的预报能力,本研究参考第二种实施方案(周迪等,2015)将利用大数量暴雨样本检验该方法对江苏省暴雨的预报水平。具体计算步骤是(1)基于2011—2015年6—8月逐日降水集合平均预报和实况数据,计算江苏省70个站观测降水为50 mm时的Gamma分布累积概率PO(R=50);(2)令每个预报时效集合平均的暴雨预报阈值对应的累积概率值Pf(R*)=PO(R=50);(3)反算出Pf(R*)所对应的暴雨预报阈值。Gamma函数计算详见周迪等(2015)。江苏省70站各站Gamma分布α、β参数和集合平均暴雨预报阈值见表 3。经检验,集合平均经降水偏差频率订正后的平均TS评分为11.33%,明显高于EC集合平均和EC确定性预报,漏报率为78.73%,明显下降,空报率为66.65%,空报率有所增加,可见,基于降水偏差订正的频率匹配法对于集合平均的暴雨预报改进效果显著,有效降低了集合平均的漏报率。然而,该方法的订正效果会受到训练期样本的选择,在业务中该方法还需进一步结合长时间的样本序列滚动修正暴雨预报临界阈值。
|
|
表 3 江苏省70个站观测降水Gamma累积概率分布函数拟合参数和EC集合平均暴雨预报临界阈值表 Table 3 Parameters of Gamma cumulative probability curves for observed precipitation and the forecast threshold value of heavy rainfall for EC ensemble-mean forecast at 70 stations over Jiangsu Province |
概率是表达预报不确定性的一种方式,而集合预报是获得概率预报的一个有效途径(Krzysztofowicz, 1983;1999)。综合所有成员的预报结果可以获得未来某种天气现象发生的相对概率,与以往仅凭经验或用统计方法做出的概率预报相比,具有客观性和定量性。本研究拟分别用平均法、相关法进行短期集合降水概率预报试验。
(1) 平均法:每个成员在集合预报中的权重均等为1/N,N为集合成员数,若预报发生某量级降水的成员有M个,则未来发生该量级降水的概率P为M×1/N。
(2) 相关法:该方法在集合预报的基础上结合了统计的方法。根据积累的一定次数的集合预报结果和对应的降水实况统计各成员的预报与实况降水间的相关性,假设ri为第i个成员的预报与实况的相关系数, 该成员在集合预报中的权重则为
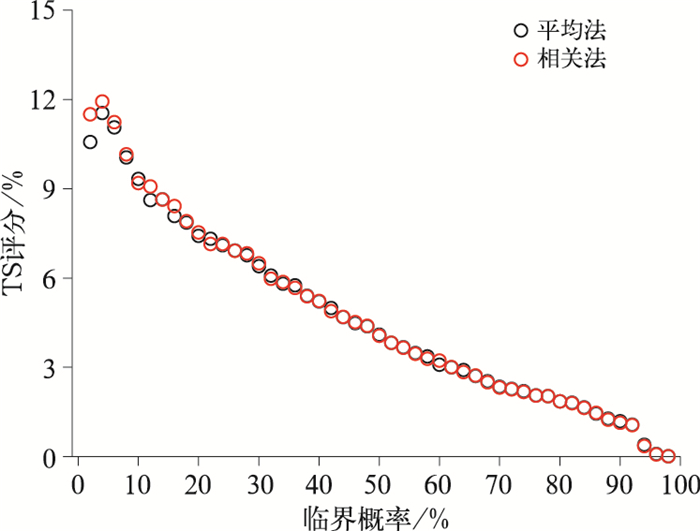
分别通过平均法和相关法生成集合概率预报产品,并对2011—2015年夏季暴雨预报进行历史回报检验。由图 5可以看出,(1)暴雨是一小概率事件,在小概率临界值时(该概率值高于临界值时,即预报有暴雨)对应的TS评分最高,平均法和相关法均在临界值为4%时,评分最高,分别为11.54%、11.93%,两种概率预报均高于EC确定性和EC集合平均预报。目前,相关法概率预报的TS评分最高,高于最优百分位法(TS=11.75%)。(2)随着概率临界值的增大,评分迅速减小,主要是由于漏报率的显著增大,如果达到较大概率值再去报暴雨的话,虽然消空了,但出现明显的漏报。(3)集合预报概率预报在预报暴雨这类小概率灾害性天气事件时,小的概率值就需要引起重视。(4)集合预报概率预报对暴雨落区的预报比单一的确定性预报和集合平均预报要更准确一些,具有较好的参考价值。
|
图 5 平均法、相关法生成的EC集合概率预报产品各临界概率值对应的暴雨预报TS评分 Fig. 5 TS of different critical probability values of probabilistic forecasting of EC ensemble system |
集合预报系统含有较多的成员,在进行极端天气预报时,往往会将多个成员的预报产品转化为极端天气的概率信息,而后进行预报和决策。极端天气预报指数(EFI)是较为常见的后处理方法。Laurette(2003)假设如果集合预报系统中的某一事件相对于“模式气候”为极端事件,则与之对应的实况天气相对于真实气候也为极端事件。基于这一假设,定义了EFI。通过积分加权的集合预报系统累计分布函数(CDF)和“模式气候”的CDF之差,定量地确定未来某一气象要素发生概率相对于“模式气候”概率的差异,这一差异越大,说明天气偏离气候态越大,则极端事件发生的概率越大,从而可以对极端天气事件进行预报和早期预警。EFI在极端天气的预报中得到了广泛的应用(夏凡和陈静,2012;董全等,2017;刘琳等,2013)。
暴雨是极端天气事件中极端降水天气。利用集合预报进行极端强降水预报原理可以简单概括为根据模式历史气候与集合预报各成员降水预报累积概率分布函数的连续差异大小以获取极端强降水是否发生的预报信息(Laurette, 2003)。具体算法是:
| $ \mathit{EFI}\text{=}\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{1}{\frac{\mathit{p}\text{-}{{\mathit{F}}_{\mathit{f}\text{(}\mathit{p}\text{)}}}}{\sqrt{\mathit{p}\text{(1-}\mathit{p}\text{)}}}}\text{d}\mathit{p} $ | (8) |
式中,p为模式历史气候累积概率函数,将气候序列按升序排列,每一个百分位(0%,1%,2%,…,100%)都对应着一个概率阈值f(p),那么f(0)和f(1)分别对应气候序列中最小和最大值,依此类推,将Ff(p)定义为集合预报累积概率,而极端降水天气预报指数为各个百分位(0%,1%,2%,…,100%)上气候累积概率和集合预报累积概率之差的总和。
| $ \mathit{EFI}\text{=}\frac{2}{\text{ }\!\!\pi\!\!\text{ }}\sum\limits_{i=0}^{100}{\left(\frac{{{\mathit{p}}_{\mathit{i}}}\text{-}{{\mathit{F}}_{\mathit{f}\text{(}\mathit{p}\text{)}}}}{\sqrt{{{\mathit{p}}_{\mathit{i}}}\text{(1-}{{\mathit{p}}_{\mathit{i}}}\text{)}}} \right)}\times 0.01 $ | (9) |
式中pi=i/100(i=0, 1, 2, …, 100)。EFI的值在-1~1,越接近1,说明预报事件越偏向极端偏高情况,如极端强降水。EFI的值达到1(-1),说明EC集合预报的所有成员大于(小于)“模式气候”的最大(小)值。
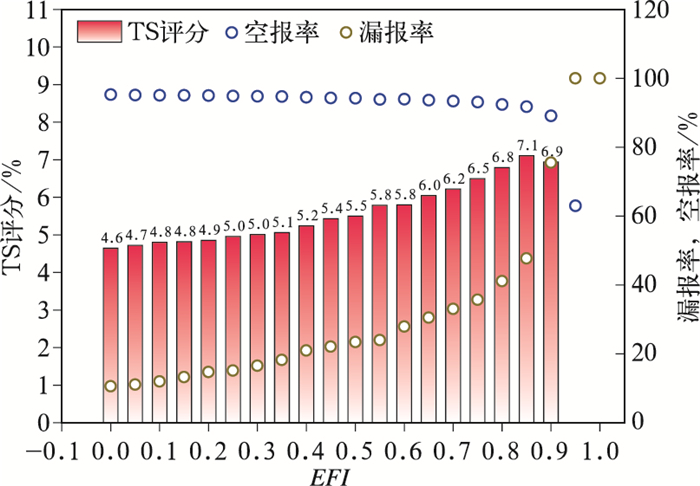
由于计算时段有限且资料数据量较大,本文选取2011—2015年5年EC集合预报数据的平均为模式气候态。当EFI高于多少(即阈值)则预报暴雨的发生呢?这个阈值在使用EFI产品进行预报暴雨时是最为关键的。通过间隔0.05确立阈值(从0开始)来分别检验预报效果(图 6)。由图可见,TS评分最高(7.1%)的EFI阈值为0.85,TS曲线总体呈现单峰型,当EFI阈值大于0.85时,漏报率显著增加,TS评分迅速下降至0。值得注意的是,EFI产品对暴雨的预报总体漏报率较低,空报率较高,在EFI指数取0时,TS评分4.6%也要高于集合平均。
|
图 6 EFI各临界值对应的TS评分、空报率和漏报率 Fig. 6 TS, missing forecast rate and false forecast rate of different critical values of EFI |
对罕见极端高影响天气,即使一个模式有能力来预报它,其数值预报也至少有以下两大难点:一是有多大把握所预报的天气确是极端事件?二是其具体的定时、定量、定点预报稳定可靠吗?杜钧等(2014)通过对2012年北京7月21日特大暴雨事件的分析显示,集合预报及其与气候资料相结合的“集合异常预报法”可以提供比单一模式预报更可靠和更准确的信息,从而有效地缓解上述两大难点来大大地提高重大灾害性天气的预报能力。集合异常预报法的具体步骤如下:通过计算标准化异常度(SA)把数值模式预报同气候资料相比较,判断所预报的事件是否是罕见的极端事件,一般其绝对值超过3(即同气候平均之差超过气候标准差3倍)往往为极端事件的表征(Grumm and Hart, 2001),并进一步与集合预报相结合,计算集合中每一个成员的SA就可导出某一等级的极端事件出现的概率大小或其预报的可信度。根据这一可信度来增加或减弱预报员对该预报的信心,可有效地提高对罕见极端高影响天气预报的可靠性。
本研究拟将该方法应用到EC集合预报中,基于SA输出两类产品,一类是集合平均的异常度:首先给定一个异常度临界值,当高于异常度临界值时,即预报暴雨。SA取值范围为0.1~5,每隔0.1设定临界值进行检验;另一类产品是集合异常度概率预报:将SA单独应用到各集合成员,然后集中起来计算概率(概率计算采用平均法)。同样,先给定一个概率临界值,当高于概率临界值时,即预报暴雨。概率值取值范围为0~100%,每隔2%设定临界值进行检验。早期研究把异常程度超过气候平均值3个标准差确定为异常的天气事件。为了结合江苏省暴雨事件,试验得到更高的预报评分,在集合异常度概率预报中,分别取1、2、3个标准差,即SA=1, 2, 3分别检验计算。
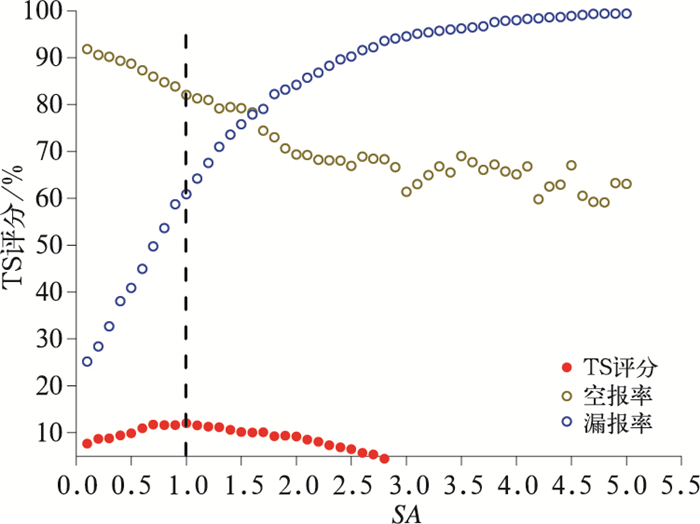
图 7是集合平均的异常度各临界异常度值对应的TS评分、空报率和漏报率。从图中可以看到,集合平均异常度预报的TS评分随着临界异常度值的增加总体呈现单峰型,在临界值取1个标准差时,评分最高为12.07%,也是目前几个方法中评分最高的后处理产品,此时的空报率(82.09%)高于漏报率(60.90%),临界值越低(高),空报率越高(低),漏报率越低(高),临界值不宜取得太高,当临界值超过3个标准差时,几乎全部漏报。
|
图 7 集合平均的异常度各临界异常度TS评分、空报率和漏报率 (黑色虚线为TS最高分对应的临界异常度) Fig. 7 TS, missing forecast rate and the false forecast rate of different standardized anomaly (SA) for ensemble mean (The black dashed line denotes the critical SA value associated with the top TS) |
图 8为集合异常预报法对江苏暴雨的预报效果检验:(1)随着异常度取值的增加(SA=1, 2, 3),TS最高分有所下降,当SA=1时,相应的最高评分是当临界概率取30%时,TS=11.79%。随着SA取值的增加,相应的最高评分值降低,最高评分对应的临界概率值也会下调。(2)最高评分值时均对应着空报率高于漏报率。与前几种后处理方法有明显不同,该方法有效降低了漏报率。鉴于此,能否将该方法与其他能有效降低空报率的方法结合,设计一种新的方案,既降低漏报率,又减小空报率呢?值得探讨。

|
图 8 基于不同集合异常度的概率预报各临界概率值的TS评分、空报率和漏报率 (a)SA=1,(b)SA=2,(c)SA=3 (黑色虚线为TS最高分对应的临界概率值) Fig. 8 TS, missing forecast rate and the false forecast rate of probabilistic forecasts based on different SA for each ensemble member (a) SA=1, (b) SA=2, (c) SA=3 (Black dashed line denotes the critical probabilistic value associated with the top TS) |
EFI考虑的是累积的“集合预报的概率分布”同“模式气候的概率分布”之差,其优点是直接用概率计算,其绝对值的大小不但反映了事件的异常度(与模式气候平均值的距离)也包含了预报的可信度(集合预报概率密度函数峰值分布的窄宽和高低)。杜钧和李俊(2014)指出EFI的缺点是易漏掉小概率事件:即当从集合预报中导出的概率很小而接近模式气候概率,其EFI值可能达不到预先设定的最小阈值而可能出现漏报现象;而“集合异常预报法”的空报率较为明显,所以两种方法各有利弊。若能在今后实际应用例子中对这两种方法进行具体比较也将是一项值得做的研究。
2.2.8 杜-周排序法为了订正集合平均降水预报量级偏低的问题,Du and Zhou(2011)提出了一种预估成员相对优劣的方法(称为“杜-周排序法”)来选取最佳成员或进行加权平均等。该方法的原理是:如果模式没有系统性的偏差,集合成员预报应该围绕在真值的周围,那么从理论上来说所有集合成员的平均应该是最靠近真值的,所以愈靠近集合平均的成员就应该愈准确。根据这一原理就可用成员与集合平均之间的相对距离来事先对一个集合预报预估其成员的相对优劣并计算出各成员的相对权重系数,用于计算加权集合平均和调整概率密度函数分布。“杜-周排序法”不同于其他方法的根本之处是它不需要知道每个成员过去的表现,而只依赖各成员的现时预报本身,是一种随时间、随空间和随气流而变的准动力学方法。
具体算法是:(1)计算各成员相对“真值”的偏差,第j个成员有量级偏差(
|
|
表 4 “杜-周排序法”试验方案 Table 4 Test setting of Du-Zhou Ranking Method |
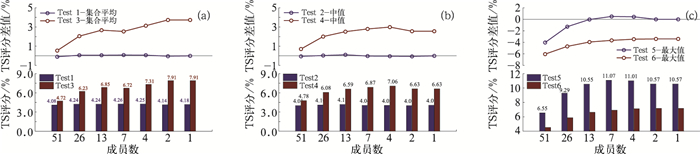
共设计了6个方案去检验加权平均改进效果(表 4)。方案Test 1和Test 3、方案Test 2和Test 4、方案Test 5和Test 6分别针对集合平均、集合中值、最大值分别考虑量级偏差和形态偏差。图 9a是Test 1和Test 3对集合平均的订正效果(TS评分),横坐标为加权平均集合成员数,例如26即为权重为前26名的加权平均,1为挑选出的最优成员。由图 9a可见,考虑量级偏差的加权平均改进效果不如考虑形态偏差的加权平均,Test 1方案TS评分与集合平均预报效果相当,甚至不如集合平均,存在明显的漏报率,空报率甚至较集合平均增加(图略);Test 3方案对集合平均预报有明显改进,随着优选成员数的减小,其改进效果总体提高,在最优成员和优选2名成员时TS评分提高最多。相应地,Test 3方案漏报率明显减小,最大减少6%~7%,而空报率有所增加(图略),可见考虑形态偏差的集合加权平均或者集合成员优选技术对集合平均产品的效果改进明显。对于中值产品的改进,同样的,Test 4方案效果优于Test 2,由图 9b可见,各成员数加权平均的TS评分均高于中值产品(4.07),最大评分出现在取前4名优选成员时,评分为7.06。相应的,改进后的漏报率下降较Test 2明显,空报率随着优选成员数的减小有所提高(图略)。值得关注的是,对于Test 4方案,将51个成员进行加权平均(即考虑各个成员的权重系数)则漏报率和空报率都有所下降,虽然两者下降得不明显,但可喜的是,确实存在一些方法可以通过同时降低空报率和漏报率来显著提高预报TS评分。由上述分析可知:(1)对于集合平均和集合中值,考虑形态偏差权重的改进方案能明显提高集合平均和集合中值对暴雨的预报效果;(2)“杜-周排序法”对集合平均和集合中值产品的暴雨预报效果有所改进,但提高的程度也是有限的,并非一种的全新的客观释用技术;(3)针对暴雨这类小概率事件,“杜-周排序法”中的“真值”值得商榷。(4)集合预报系统各成员与“真值”之间的形态偏差是否是决定各成员“优劣”的主要指标?也不尽然,当最大值作为“真值”参考时,经检验(图 9c),需要重点考虑量级偏差的权重,当取前7个优选成员时,改进方案中TS预报评分最高,为11.07,略高于最大值产品。
|
图 9 (a) Test 1和Test 3各成员数集合加权平均的TS评分及其与集合平均的TS评分差;(b)Test 2和Test 4各成员数集合加权平均的TS评分及其与中值的TS评分差;(c)Test 5和Test 6各成员数集合加权平均的TS评分及其与最大值的TS评分差 Fig. 9 (a) TS for different ensemble sizes of Test 1 and Test 3 and the TS difference from the ensemble mean forecast, (b) TS for different ensemble sizes of Test 2 and Test 4 and the TS difference from the median value forecast, (c) TS for different ensemble sizes of Test 5 and Test 6 and the TS difference from the maximums forecast |
本文利用2011—2015年6—8月TIGGE数据集ECMWF的集合降水预报数据和江苏省70个基本站逐日20时至次日20时24 h降水数据,系统检验和评估了EC确定性预报、EC集合各成员预报、集合预报多统计量及各类后处理释用技术对江苏省暴雨的预报性能(表 5)。结果表明:(1)EC集合预报不同成员预报技巧差异较大,其中最优成员组合的预报能力显著优于EC确定性预报,集合预报具有较大的应用潜力;作为集合预报的初级产品,集合平均产品预报存在明显的漏报率,近五年来对江苏省暴雨预报评分较低。对江苏省暴雨的预报水平不如EC确定性预报。(2)基于大数量暴雨预报样本和降水实况,检验多种集合预报统计量及各后处理释用技术,发现最大值、最优百分位、概率预报、降水偏差订正频率匹配法、集合异常预报法和杜-周排序法(最大值方法)的平均TS评分均超过10%,具有较高的评分。此外,90%分位数、融合、融合—概率匹配和杜-周排序法(集合平均/集合中值)的预报效果也均优于EC确定性预报。在强降水的预报上,大多数后处理计算的预报水平均较EC确定性预报和EC集合预报有明显提高;(3)中位值、概率匹配两种方法的TS评分均低于集合平均和EC确定性预报对江苏省暴雨的预报效果,这两种后处理技术在江苏省暴雨的预报上的参考价值相对较低。
|
|
表 5 EC集合预报各种后处理技术TS评分排序 Table 5 Sorting of TS for different post-processing techniques for EC ensemble forecast |
通过评估,可以在进行暴雨预报时,为预报员推送出性能相对较优的产品,帮助预报员更直接、快速地选取有效的模式预报参考产品,订正预报结果。通过本研究也可以看到,不同的后处理释用技术对原始预报改进的设计上有着不同的着眼点,例如:融合预报、最大值预报、杜-周排序法(最大值)考虑了对集合预报系统,尤其是对集合平均降水量级的调整;融合—概率匹配、杜-周排序法(集合平均Test 3)在于实现对降水落区位置调整;集合异常预报法和EFI强调了降水量级的极端性;杜-周排序法考虑了成员之间的相对优劣性,改进集合平均,进行加权平均;概率预报既可用作暴雨确定性预报,也反映了暴雨的不确定性,在用作暴雨确定性预报时,概率预报的平均TS评分明显高于降水量级的集合确定性产品,概率预报在江苏省暴雨预报上的应用应加以拓展、加大研究力度。降水偏差订正频率匹配法和集合异常预报法对集合平均预报的订正效果很大程度受到所选训练期样本的影响,在实际业务预报中,这类方法还需进一步结合长时间的观测样本序列滚动修正相关参数,进而订正预报。此外,大部分产品的改进重点为“补漏”,如最大值、融合、降水偏差订正频率匹配法、集合异常预报法和EFI等,漏报率和空报率大体呈现反相关关系,这些后处理技术“补漏”,也会同时带来较高的空报率,因此通常TS评分达到最高点时,似乎对应着一个漏报率和空报率的平衡。要想显著提高EC集合预报系统对江苏暴雨的预报准确率还有待深入研究出一个既“补漏”又“消空”的释用技术,才是“完美”的改进。
包慧濛, 郭达烽, 肖潇, 2015. ECMWF集合预报统计量在江西降水预报中的检验分析[J]. 气象与减灾研究, 38(3): 60-67. Bao H M, Guo D F, Xiao X, 2015. Validation of ECMWF ensemble forecast statistics in Jiangxi precipitation forecast[J]. Meteor Dis Reduct Res, 38(3): 60-67 (in Chinese). DOI:10.3969/j.issn.1007-9033.2015.03.008 |
陈博宇, 代刊, 郭云谦, 2015. 2013年汛期ECMWF集合统计量产品的降水预报检验与分析[J]. 暴雨灾害, 34(1): 64-73. Chen B Y, Dai K, Guo Y Q, 2015. Precipitation verification and analysis of ECMWF ensemble statistic products in 2013 flooding season[J]. Torr Rain Dis, 34(1): 64-73 (in Chinese). DOI:10.3969/j.issn.1004-9045.2015.01.009 |
陈静, 陈德辉, 颜宏, 2002. 集合数值预报发展与研究进展[J]. 应用气象学报, 13(4): 497-507. Chen J, Chen D H, Yan H, 2002. A brief review on the development of ensemble prediction system[J]. J Appl Meteor Sci, 13(4): 497-507 (in Chinese). DOI:10.3969/j.issn.1001-7313.2002.04.013 |
陈静, 薛纪善, 颜宏, 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究[J]. 大气科学, 29(5): 717-726. Chen J, Xue J S, Yan H, 2005. A new initial perturbation method of ensemble mesoscale heavy rain prediction[J]. Chin J Atmos Sci, 29(5): 717-726 (in Chinese). DOI:10.3878/j.issn.1006-9895.2005.05.05 |
陈力强, 周小珊, 杨森, 2005. 短期集合预报中定量降水预报集合方法初探[J]. 南京气象学院学报, 28(4): 543-548. Chen L Q, Zhou X S, Yang S, 2005. A quantitative precipitation forecasts method for short-range ensemble forecasting[J]. J Nanjing Inst Meteor, 28(4): 543-548 (in Chinese). DOI:10.3969/j.issn.1674-7097.2005.04.015 |
陈涛, 林建, 张芳华, 等, 2017. "16·7"华北极端强降水过程对流尺度集合模拟试验不确定性分析[J]. 气象, 43(5): 513-527. Chen T, Lin J, Zhang F H, et al, 2017. Uncertainty analysis on the July 2016 extreme precipitation event in North China using convection allowing ensemble simulation[J]. Meteor Mon, 43(5): 513-527 (in Chinese). |
丑纪范, 2002. 大气科学中的非线性与复杂性[M]. 北京: 气象出版社. Chou J F, 2002. Nonlinearity and Complexity in Atmospheric Science[M]. Beijing: China Meteorological Press (in Chinese). |
代刊, 朱跃建, 毕宝贵, 2018. 集合模式定量降水预报的统计后处理技术研究综述[J]. 气象学报, 76(4): 493-510. Dai K, Zhu Y J, Bi B G, 2018. The review of statistical post-process technologies for quantitative precipitation forecast of ensemble prediction system[J]. Acta Meteor Sin, 76(4): 493-510 (in Chinese). |
邓国, 龚建东, 邓莲堂, 等, 2010. 国家级区域集合预报系统研发和性能检验[J]. 应用气象学报, 21(5): 513-523. Deng G, Gong J D, Deng L T, et al, 2010. Development of mesoscale ensemble prediction system at national meteorological center[J]. J Appl Meteor Sci, 21(5): 513-523 (in Chinese). DOI:10.3969/j.issn.1001-7313.2010.05.001 |
董全, 代刊, 陶亦为, 等, 2017. 基于ECMWF集合预报的极端天气预报产品应用和检验[J]. 气象, 43(9): 1095-1109. Dong Q, Dai K, Tao Y W, et al, 2017. Application and verification of extreme weather forecast products of ECMWF ensemble prediction system[J]. Meteor Mon, 43(9): 1095-1109 (in Chinese). |
杜钧, 陈静, 2010. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 36(11): 1-11. Du J, Chen J, 2010. The corner stone in facilitating the transition from deterministic to probabilistic forecasts: ensemble forecasting and its impact on numerical weather prediction[J]. Meteor Mon, 36(11): 1-11 (in Chinese). DOI:10.7519/j.issn.1000-0526.2010.11.001 |
杜钧, Grumm R H, 邓国, 等, 2014. 预报异常极端高影响天气的"集合异常预报法":以北京2012年7月21日特大暴雨为例[J]. 大气科学, 38(4): 685-699. Du J, Grumm R H, Deng G, et al, 2014. Ensemble anomaly forecasting approach to predicting extreme weather demonstrated by extremely heavy rain event in Beijing[J]. Chin J Atmos Sci, 38(4): 685-699 (in Chinese). |
杜钧, 李俊, 2014. 集合预报方法在暴雨研究和预报中的应用[J]. 气象科技进展, 4(5): 6-20. Du J, Li J, 2014. Application of ensemble methodology to heavy-rain research and prediction[J]. Adv Meteor Sci Technol, 4(5): 6-20 (in Chinese). |
范苏丹, 盛春岩, 肖明静, 等, 2015. 多模式集合对山东省气象要素预报效果检验[J]. 气象与环境学报, 31(6): 68-77. Fan S D, Sheng C Y, Xiao M J, et al, 2015. Forecast effect verification of multi-model ensemble for meteorological elements in Shandong Pro-vince[J]. J Meteor Environ, 31(6): 68-77 (in Chinese). DOI:10.3969/j.issn.1673-503X.2015.06.009 |
高守亭, 冉令坤, 李娜, 等, 2013. 集合动力因子暴雨预报方法研究[J]. 暴雨灾害, 32(4): 289-302. Gao S T, Ran L K, Li N, et al, 2013. The "Ensemble Dynamic Factors" approach to predict rainstorm[J]. Torr Rain Dis, 32(4): 289-302 (in Chinese). DOI:10.3969/j.issn.1004-9045.2013.04.001 |
高守亭, 周玉淑, 冉令坤, 2018. 我国暴雨形成机理及预报方法研究进展[J]. 大气科学, 42(4): 833-846. Gao S T, Zhou Y S, Ran L K, 2018. A review on the formation mechanisms and forecast methods for torrential rain in China[J]. Chin J Atmos Sci, 42(4): 833-846 (in Chinese). |
韩焱红, 矫梅燕, 陈静, 等, 2013. 基于贝叶斯理论的集合降水概率预报方法研究[J]. 气象, 39(1): 1-10. Han Y H, Jiao M Y, Chen J, et al, 2013. Study on the method of rainfall ensemble probability forecast based on Bayesian theory and its preliminary experiments[J]. Meteor Mon, 39(1): 1-10 (in Chinese). |
黄红艳, 齐琳琳, 刘健文, 等, 2016. 多物理ETKF在暴雨集合预报中的初步应用[J]. 大气科学, 40(4): 657-668. Huang H Y, Qi L L, Liu J W, et al, 2016. Preliminary application of a multi-physical ensemble transform Kalman filter in precipitation ensemble prediction[J]. Chin J Atmos Sci, 40(4): 657-668 (in Chinese). |
李俊, 杜钧, 陈超君, 2014. 降水偏差订正的频率(或面积)匹配方法介绍和分析[J]. 气象, 40(5): 580-588. Li J, Du J, Chen C J, 2014. Introduction and analysis to frequency or area matching method applied to precipitation forecast bias correction[J]. Meteor Mon, 40(5): 580-588 (in Chinese). |
李俊, 杜钧, 陈超君, 2015. "频率匹配法"在集合降水预报中的应用研究[J]. 气象, 41(6): 674-684. Li J, Du J, Chen C J, 2015. Applications of "frequency-matching" method to ensemble precipita-tion forecasts[J]. Meteor Mon, 41(6): 674-684 (in Chinese). DOI:10.3969/j.issn.1000-6362.2015.06.003 |
李俊, 廖移山, 张兵, 等, 2007. 集合数值预报方法在山洪预报中的初步应用[J]. 高原气象, 26(4): 854-861. Li J, Liao Y S, Zhang B, et al, 2007. The preliminary application of ensemble prediction in flash flood forecasting[J]. Plateau Meteor, 26(4): 854-861 (in Chinese). |
刘家峻, 张立凤, 关吉平, 等, 2010. 集合预报产品在台风麦莎预报中的应用[J]. 气象, 36(5): 21-31. Liu J J, Zhang L F, Guan J P, et al, 2010. Application of ensemble prediction products to the forecast of Typhoon Masta[J]. Meteor Mon, 36(5): 21-31 (in Chinese). |
刘琳, 陈静, 程龙, 等, 2013. 基于集合预报的中国极端强降水预报方法研究[J]. 气象学报, 71(5): 853-866. Liu L, Chen J, Cheng L, et al, 2013. Study of the ensemble-based forecast of extremely heavy rainfalls in China:experiments for July 2011 cases[J]. Acta Meteor Sin, 71(5): 853-866 (in Chinese). |
刘琳, 陈静, 汪娇阳, 2018. 基于T639集合预报的持续性强降水中期客观预报技术研究[J]. 气象学报, 76(2): 228-240. Liu L, Chen J, Wang J Y, 2018. A study on medium-range objective weather forecast technology for persistent heavy rainfall events based on T639 ensemble forecast[J]. Acta Meteor Sin, 76(2): 228-240 (in Chinese). |
斯琴, 包福祥, 张旭, 2016. 基于EC集合预报产品的降水预报检验[J]. 中国农学通报, 32(7): 162-167. Si Q, Bao F X, Zhang X, 2016. Precipitation forecasting verification based on EC ensemble prediction products[J]. Chin Agric Sci Bull, 32(7): 162-167 (in Chinese). |
陶诗言, 1977. 有关暴雨分析预报的一些问题[J]. 大气科学, 1(1): 64-72. Tao S Y, 1977. Some aspects on the analysis and forecast of the heavy rainfall[J]. Chin J Atmos Sci, 1(1): 64-72 (in Chinese). |
王晨稀, 2005. 短期集合降水概率预报试验[J]. 应用气象学报, 16(1): 78-88. Wang C X, 2005. Experiments of short-range ensemble precipitation probability forecasts[J]. J Appl Meteor Sci, 16(1): 78-88 (in Chinese). DOI:10.3969/j.issn.1001-7313.2005.01.009 |
王亚男, 智协飞, 2012. 多模式降水集合预报的统计降尺度研究[J]. 暴雨灾害, 31(1): 1-7. Wang Y N, Zhi X F, 2012. Statistical downscaling of the precipitation multimodel ensemble forecast[J]. Torr Rain Dis, 31(1): 1-7 (in Chinese). DOI:10.3969/j.issn.1004-9045.2012.01.001 |
王毅, 马杰, 代刊, 2018. "7·20"华北强暴雨集合预报的中期预报转折和不确定性分析[J]. 气象, 44(1): 53-64. Wang Y, Ma J, Dai K, 2018. Ensemble-based analysis of medium-range forecast change and uncertainty for the 20 July 2016 severe heavy rainfall over North China[J]. Meteor Mon, 44(1): 53-64 (in Chinese). DOI:10.3969/j.issn.1007-6190.2018.01.012 |
夏凡, 陈静, 2012. 基于T213集合预报的极端天气预报指数及温度预报应用试验[J]. 气象, 38(12): 1492-1501. Xia F, Chen J, 2012. The research of extreme forecast index based on the T213 ensemble forecast and the experiment in predicting temperature[J]. Meteor Mon, 38(12): 1492-1501 (in Chinese). |
张宇彤, 矫梅燕, 陈静, 等, 2016. 基于贝叶斯方法的极端降水概率预报试验[J]. 气象, 42(7): 799-808. Zhang Y T, Jiao M Y, Chen J, et al, 2016. Probabilistic forecasting of extreme precipitation experiment based on Bayesian theory[J]. Meteor Mon, 42(7): 799-808 (in Chinese). |
赵琳娜, 吴昊, 田付友, 等, 2010. 基于TIGGE资料的流域概率性降水预报评估[J]. 气象, 36(7): 133-142. Zhao L N, Wu H, Tian F Y, et al, 2010. Assessment of probabilistic precipitation forecasts for the Huaihe basin using TIGGE data[J]. Meteor Mon, 36(7): 133-142 (in Chinese). |
周迪, 陈静, 陈朝平, 等, 2015. 暴雨集合预报-观测概率匹配订正法在四川盆地的应用研究[J]. 暴雨灾害, 34(2): 97-104. Zhou D, Chen J, Chen C P, et al, 2015. Application research on heavy rainfall calibration based on ensemble forecast vs.observed precipitation probability matching method in the Sichuan Basin[J]. Torr Rain Dis, 34(2): 97-104 (in Chinese). DOI:10.3969/j.issn.1004-9045.2015.02.001 |
Du J, Zhou B B, 2011. A dynamical performance-ranking method for predicting individual ensemble member performance and its application to ensemble averaging[J]. Mon Wea Rev, 139(10): 3284-3303. DOI:10.1175/MWR-D-10-05007.1
|
Ebert E E, 2001. Ability of a poor man's ensemble to predict the probability and distribution of precipitation[J]. Mon Wea Rev, 129(10): 2461-2480.
|
Grumm R H, Hart R, 2001. Standardized anomalies applied to significant cold season weather events:preliminary findings[J]. Wea Forecasting, 16(6): 736-754.
|
Krzysztofowicz R, 1983. Why should a forecaster and a decision ma-ker use Bayes Theorem[J]. Water Resour Res, 19(2): 327-336. DOI:10.1029/WR019i002p00327
|
Krzysztofowicz R, 1999. Point-to-area rescaling of probabilistic quantitative precipitation forecasts[J]. J Appl Meteor, 38(6): 786-796.
|
Laurette F, 2003. Early detection of abnormal weather conditions using a probabilistic extreme forecast index[J]. Quart J Roy Meteor Soc, 129(594): 3037-3057. DOI:10.1256/qj.02.152
|
Leith C E, 1974. Theoretical skill of Monte Carlo forecasts[J]. Mon Wea Rev, 102(6): 409-418.
|
Lorenz E N, 1963. Deterministic nonperiodic flow[J]. J Atmos Sci, 20(2): 130-141.
|
Molteni F, Buizza R, Palmer T N, et al, 1996. The ECMWF ensemble prediction system:methodology and validation[J]. Quart J Roy Meteor Soc, 122(529): 73-119. DOI:10.1002/qj.49712252905
|
Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC:the generation of perturbations[J]. Bull Amer Meteor Soc, 74(12): 2317-2330.
|
Zhu Y J, Luo Y, 2015. Precipitation calibration based on the frequency -matching method[J]. Wea Forecasting, 30(5): 1109-1124. DOI:10.1175/WAF-D-13-00049.1
|
 2019, Vol. 45
2019, Vol. 45 
