水汽是产生降水的必要条件也是引发暴雨的重要因素,大气可降水量(precipitable water vapor, PWV)被认为是衡量大气水汽条件以及判断强对流天气的重要指标(丁金才等,2004;陈淑琴等,2018;徐道生等,2016)。已有学者利用GPS、微波辐射计和MODIS反演以及气象探空数据累加、地面水汽压推算等方法计算得到PWV,并针对PWV与降水关系进行深入研究(Li et al, 2013; 向玉春等,2009)。通过对国内外研究进行总结发现,基于PWV的降水预报研究主要可以概括为两个方向:一是利用PWV在降水前的变化率来预报降水(Benevides et al, 2015; Cao et al, 2016; Shoji, 2013);二是建立PWV降水阈值,通过观察PWV是否达到该阈值判断是否产生降水(Shi et al,2015;曹云昌等,2005;敖雪等,2011)。研究表明降水前一段时间内,PWV会有一定的跃增,其高值阶段往往对应着较高的降水概率,即当PWV达到某一阈值时出现降水的可能性较大(郝丽萍等,2013;李国翠等,2008),该值称为PWV降水阈值(threshold of PWV, PWVt)。降水预报中阈值定得过高,会降低预报的准确率,阈值过低,虽然会提高准确率,但同时会增加空报率(Yao et al,2017),因此准确计算PWVt对提高降水临近预报精度具有重要意义。近年来,尽管许多学者针对不同地区和季节的PWVt进行了分析,并在降水预报中取得了较好的应用效果(李青春等, 2007; 党张利等, 2015; 叶其欣等, 2008),但研究表明PWVt与季节、地域和天气类型密切相关(万蓉和郑国光,2008),不同地区和季节具有较大差异。因此,只代表特定季节和地区的固定PWVt在实际应用中将会受到一定限制,而且以往的统计结果缺少充分物理解释以及统计检验。因此,本研究旨在提供“动态”PWVt的计算方法,为PWV与降水关系研究提供理论依据和新的思路。
大气中水汽必须达到一定层次的饱和才能成云致雨,因此本文引入整层大气饱和水汽含量(preci-pitable water vapor saturation, PWVsat)概念,PWVsat表示整个气柱容纳水汽的上限。Chamberlin and Bally(1995),Chamberlin and Grossman(2002)利用大气各层单位面积饱和水汽压进行累加的方法计算得到PWVsat,但该方法依赖各层大气中的实际温度,因此在应用中存在一定的不便。本文在一定条件基础上推导出多元大气条件不依赖各层温度的PWVsat计算公式,发现PWVsat仅为地面温度ts的函数。基于相同的思路,利用2015年5月至2016年10月辽宁地区36个站PWV数据与ts进行了拟合,建立了“动态”PWVt计算方法,并验证了该方法在降水预报中的适用性。
1 资料与方法 1.1 数据介绍GPS探测PWV是根据GPS卫星发射的信号穿过大气层产生的延迟与气象条件的关系得到的,其测量结果与辽宁地区的探空具有较好的一致性(杨磊等,2016)。本研究主要利用2015年5月至2016年10月辽宁地区36个GPS观测站测得的PWV数据以及对应的地面温度(ts)和降水量资料进行分析,其时间分辨率均为1 h。为了剔除较弱以及持续时间较短的降水过程,筛选出1 h降水量超过1 mm并持续3 h以上共1122个样本进行研究。EC再分析资料由欧洲中期天气预报中心提供,时间分辨率为6 h,空间分辨率为0.125°×0.125°。探空数据为2017年7月至2019年3月沈阳站(54342)数据,探测时间为每日的08时和20时。
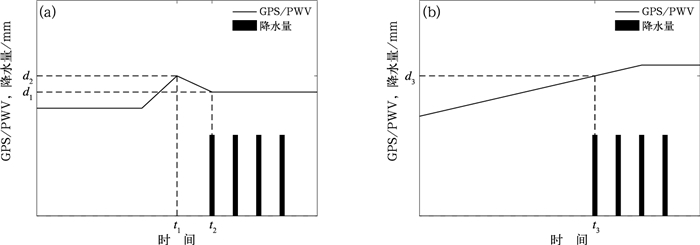
1.2 PWVt的选取大多研究者将降水开始时刻对应的PWV值定为PWVt,这种定义较为粗糙。本研究将降水前PWV的变化类型分为两类(图 1),根据两类的特点对PWVt的取值进行定义。如图 1a所示,t1为PWV峰值出现时刻,此时PWV为d2,t2为降水出现时刻,此时PWV为d1,虽然产生降水的时刻对应的PWV为d1,但是本文没有将d1作为PWVt,考虑到水汽成为雨滴需要一个转化过程,一般降水开始后PWV值开始下降,说明一部分水汽已经转化成为云滴或者雨滴,因此将降水前的峰值d2确定为该降水过程的PWVt。如图 1b所示二型为PWV在降水前持续上升,当上升到t3时到达d3,地面出现降水,在此期间没有峰值出现,将d3确定为该过程的PWVt。
|
图 1 一型(a)和二型(b)PWV变化示意图 Fig. 1 Variations of PWV by time Type 1 (a), Type 2 (b) |
通过对PWV和降水量等资料进行研究发现:降水前PWV至少有一次跃增,一般跃增到某一阈值后将出现降水;当降水结束后PWV迅速下降,同时降水时刻与PWV高值区对应较好。这与其他学者研究的结论基本一致(杨磊等,2016;刘晶和杨莲梅,2017)。本文利用1122个降水样本资料分别得到各降水过程的PWVt,其中最小值为8.2 mm,最大值为73 mm,由此可见,辽宁地区PWVt差异很大,由此说明“固定”的PWVt值不具有普适性,因此,为了找到较为准确计算PWVt的方法,本文引入整层大气饱和水汽含量概念。
2.1 整层大气饱和水汽含量公式推导PWV为大气可降水量,是整层水汽密度的积分量,见式(1)。PWVsat表示整层大气在饱和状态下可容纳的最大水汽量,是整层饱和水汽密度的积分量,见式(2)。
| $ P W V=\int_{0}^{\infty} \rho_{\mathrm{v}} \mathrm{d} z $ | (1) |
| $ P W V_{\mathrm{sat}}=\int_{0}^{\infty} \rho_{\mathrm{vs}} \mathrm{d} z $ | (2) |
式中,ρv和ρvs分别为水汽密度和饱和水汽密度(单位:kg·m-3),z为高度。ρvs=εes/RdT,es为饱和水汽压,根据修正的Tetens公式可知,es=6.112exp[17.67t/(t+243.5)](Bolton, 1980),当-30℃≤t≤30℃时,ρvs可以近似为4.97×10-3eαt(R2=0.9985),式中α=0.0612,多元大气对流层中t(z)=ts-γz,γ为温度递减率,有
| $ P W V_{\mathrm{sat}}=\int_{0}^{\infty} 4.97 \times 10^{-3} \mathrm{e}^{α\left(t_{{\rm s}}-\gamma z\right)} \mathrm{d} z $ | (3) |
| $ P W V_{\mathrm{sat}}=\frac{81.24 \times 10^{-3}}{\gamma} \mathrm{e}^{0.0612 t_{\mathrm{s}}} $ | (4) |
在对流层中γ一般为4~7℃·km-1,因此整层大气饱和水汽含量为
| $ P W V_{\text {sat }}=(11.6 \sim 20.3) \mathrm{e}^{0.0612 t_{\rm s}} $ | (5) |
若γ取6.5℃·km-1,有:
| $ P W V_{\mathrm{sat}}=12.49 \mathrm{e}^{0.0612 t_{\mathrm{s}}} $ | (6) |
由式(5)和式(6)可以看出PWVsat是ts的函数。由于多元大气对流层的大气温度随高度递减,气温垂直梯度变化较小,而且水汽主要集中在大气底层,所以ts对PWVsat具有较好的指示作用。大气中水汽必须达到一定层次的饱和才能成云致雨,因此PWVsat是PWVt的极大值。由于ts影响着PWVsat,因此推断ts与PWVt也可能存在一定的相关性。
2.2 拟合分析为了验证上文结论,根据本文1.2节PWVt的选取规则,从2015年5月至2016年10月辽宁地区36个GPS观测站测得的PWV数据以及对应的ts和降水量资料中筛选出1122个降水样本,利用样本的PWVt和ts进行拟合研究(见图 2)。如图 2所示,PWVt与ts拟合结果较好,R2为0.82,拟合公式为:

|
图 2 2015年5月至2016年10月辽宁地区1122个降水样本PWVt和ts的拟合曲线 Fig. 2 Fitting curve of PWVt and 2 m temperature of 1122 precipitation samples in Liaoning Province from May 2015 to October 2016 |
| $ P W V_{t}=a \mathrm{e}^{b t_s} $ | (7) |
式中,a为12.188,b为0.0604。
表 1给出了辽宁地区36个站的拟合参数,R2均大于0.6,总体拟合结果较好,超过0.8的站到达28个,占总数的78%,最大达0.92(抚顺站)。36个站参数a的值主要集中在10~14,b主要集中在0.06左右,这与式(5)较为一致,说明PWVt与PWVsat密切相关,同时表明ts是影响PWVt的重要因子,本文尝试利用ts建立起计算PWVt的新方法。
|
|
表 1 辽宁地区36个站PWVt与温度拟合公式参数 Table 1 Parameters in fitting of PWVt and 2 m temperature for 36 stations in Liaoning Province |
为了进一步讨论PWVsat与PWVt关系,选取2017年7月至2019年3月沈阳站956个探空样本,利用式(2)、式(6)和式(7),分别计算得到理论PWVsat、推导PWVsat和PWVt并进行统计分析。理论PWVsat与推导PWVsat的相关系数、平均偏差和均方差分别为0.9612、3.42 mm和6.33 mm,理论PWVsat与PWVt的相关系数、平均偏差和均方差分别为0.9613、4.47 mm和6.51 mm。由此可见,理论PWVsat与推导PWVsat和PWVt均具有较好的相关关系,但也存在一定偏差。本文认为理论PWVsat与推导PWVsat偏差可能是由多元大气温度廓线模型与实际大气廓线的差异带来的,而理论PWVsat与PWVt的偏差可能是由于实际降水过程中并不需要整层大气全部饱和,大气达到一定层次的饱和就可能成云致雨,理论PWVsat与PWVt的平均偏差大于0也可证明这一点。
2.4 拟合结果的影响因素为了探究大气稳定度条件对PWVt的影响,利用EC再分析资料中850 hPa和500 hPa的假相当位温之差(Δθse850-500)判断对流层中低层的对流稳定度(周雪松等,2014),其值大于(小于)0则认为对流不稳定(稳定),对所有样本进行分类。图 3为大气稳定和不稳定条件下的拟合结果,稳定条件R2为0.84,不稳定条件R2为0.74,由此可见稳定天气类型的拟合结果优于不稳定天气类型。在大气不稳定条件下,天气系统发展速度相对较快、单位时间内水汽凝结释放的潜热较大,影响高低空温度配置,而本文采用多元大气温度廓线模型计算得到的PWVt,这与实际大气廓线的差异带来的误差可能是稳定天气类型的拟合结果优于不稳定天气类型的原因。

|
图 3 大气稳定条件(a)和不稳定条件(b)PWVt和ts的拟合曲线 Fig. 3 Fitting curve of PWVt and 2 m temperature under convective stability (a) and unstability (b) |
对不同天气系统影响下,PWVt拟合结果的差异进行研究。研究期间,500 hPa影响辽宁省降水过程的天气系统分为西风槽和冷涡两类,所占比例分别为76%和24%。两类天气类型的拟合结果见图 4,西风槽类天气型R2为0.85,冷涡天气类型R2仅为0.42。冷涡天气类型一般具有对流不稳定等特征(张立祥和李泽椿,2009),这可能是拟合结果较差的一个原因。另外一个原因可能是辽宁地区冷涡天气类型常出现在夏季(孙力等,1994),该期间ts较高,而且样本温度分布较为集中,因此样本温度变化范围较小,如由图 6b所示,冷涡天气类型温度在10~22℃,区间范围12℃左右,而西风槽天气类型温度区间范围在20℃左右,较小的温度区间影响了拟合的效果。

|
图 4 西风槽(a)和冷涡(b)天气类型PWVt和ts的拟合曲线 Fig. 4 Fitting curve of PWVt and 2 m temperature under westerly trough pattern (a) and cold cyclone pattern (b) |
为验证本文的计算方法在全省临近降水预报中的可靠性,对降水预报的正确率、漏报率和空报率进行统计检验,方法如下:
正确率=(a+d)/(a+b+c+d)×100%
漏报率=b/(a+b+c+d)×100%
空报率=c/(a+b+c+d)×100%
式中,a,b,c,d分别表示正确肯定、漏报、空报和正确否定的次数。当预报有雨,若实况降水量R>0.0 mm,评定为正确肯定,若实况无雨则评定为空报;当预报为无雨,若实况无雨评定为正确否定,若实况降水量R> 0.0 mm,评定为漏报。
筛选出2015年5月至2016年10月辽宁地区36个站1 h降水、ts和PWV数据完整的共计201539时次,其中降水总时次为13510,根据检验方法统计得出a, b, c, d分别为8834,4676,8044,179985,因此正确率为93.69%,漏报率为2.32%,空报率为3.99%。虽然正确率较高,但漏报和空报次数也较高,其中一方面因为本研究给出的拟合参数对于西风槽稳定性降水结果较好,但用于检验的数据没有进行稳定度以及天气系统区分,另一方面,统计检验利用的是1 h数据进行判断,由于PWV达到PWVt时未来3 h内将出现降水,按上文统计原则会将未来几个时次算为空报,这会增大漏报和空报次数。若预报出降水3 h内出现降水就算正确肯定,而期间时次不算空报,按此原则计得出a, b, c, d分别为11157,3500,5721,172911。本文研究给出PWVt计算方法在临近降水预报方面有一定的参考价值,但必须结合天气形势和其他气象资料以及具体降水特征进行综合分析和判断。
3 个例分析为验证结论的可靠性和普适性,选取2017年5月22—23日辽宁地区一次降水过程进行个例分析,详细介绍PWVt在临近降水预报中的应用。
3.1 天气形势本次降水过程是由500 hPa西风槽配合地面冷锋东移共同影响所致,辽宁西部首先出现降水,之后降水落区逐渐东移(图略),属于西风槽影响下的稳定性降水。
3.2 降水预报本次降水过程共筛选出46个同时具有完整PWV和地面观测资料的站,其中36个具有拟合参数的站用表 1参数计算,其余10个用式(7)进行计算。分析所用的PWV、ts和降水量数据的时间分辨率均为1 h。为了方便叙述,本文将定义一个变量S,S为实际PWV与PWVt之差,反映PWV超出其降水阈值部分的大小。
以建昌和法库为例,图 5给出了两地PWV、ts、PWVt和降水量的演变,如果实际观测PWV值达到或超过PWVt即S>0,未来3 h内将有可能产生降水。如图 5a所示,建昌地区在整个降水过程温度变化不大,22日03时PWVt为27.3 mm,而当时实测PWV为14.2 mm,S < 0,之后PWV不断跃增,在22日08时,PWV跃增到29.5 mm,PWVt为27.8 mm,S为1.7mm,但此时没有降水,而当22日10时,也就是过去2 h之后PWV跃增到32.5 mm,PWVt下降到为26.3 mm,S为6.2 mm,此时地面出现降水,在整个降水持续过程中,S均大于0,由此可见,建昌站在该次过程中利用S可以提前2 h预报出降水,同时发现降水时段位于S>0的范围内。如图 5b所示,法库站ts在降水前有一个增大过程,增大到降水前2 h开始下降,对应的PWVt也是同样的变化过程,但不管PWVt如何变化,PWV增大到PWVt时开始出现降水,PWV降至PWVt以下时降水结束,整个降水时间段同样位于S>0的区间内。46个站中没有出现S>0而没有出现降水或者S < 0而出现降水的时间段,说明在此次降水预报中准确率较高。由此可见PWVt可以较好地应用到降水预报中,而且PWVt不仅可以预报降水开始时间,同时也可以作为判断降水是否持续的参考指标。

|
图 5 2017年5月22—23日建昌(a)和法库(b) PWV、ts、PWVt和降水量的演变 Fig. 5 Variations of PWV, 2 m temperature, PWVt and precipitation at Jianchang Station (a) and Faku Station (b) in 22-23 May 2017 |
由于PWVt与PWVsat密切相关,因此PWVsat和PWVt可以衡量大气容纳水汽的能力,该能力与ts相关,S表示超出大气容纳水汽部分的大小,由此推断S的大小与降水量可能存在一定对应关系。为了验证这一推断,下文对S与降水量的关系进行初步研究。
首先以新民和法库为例进行讨论,统计发现降水期间这两站S与降水量具有较好的相关性,因此分别对新民和法库两站的S和降水量进行拟合研究(图 6)。如图 6a所示,新民站的S与降水量的拟合很好,R2高达0.99,得到的拟合曲线成指数分布,法库站拟合曲线(图 6b),R2为0.86。但根据该方法对本次过程的46个站分别进行拟合研究,发现拟合结果并不十分理想,有16个站R2>0.6,占总站的35%。不同R2大小的站点分布见图 7,发现各类站分布较为集中,而且呈阶梯状分布,其中拟合结果较好(R2 < 0.6)的站集中在辽河平原一带,而拟合结果较差(R2 < 0.3)的站分布在辽东山区一带,由此推断地形可能是影响拟合结果的因素之一。

|
图 6 2017年5月22—23日新民(a)和法库(b)S和降水量的拟合曲线 Fig. 6 Fitting curve of S and precipitation at Xinmin Station (a) and Faku Station (b) in 22-23 May 2017 |

|
图 7 2017年5月22—23日辽宁地区各站拟合结果 Fig. 7 Distribution of fitting results at different stations in Liaoning Province in 22-23 May 2017 |
由于降水过程十分复杂,除了受水汽条件、动力条件和云滴增长条件影响外,同时还受地形等多方面因素的共同影响,这都可能是导致部分站拟合结果不理想的原因。而部分站S与降水量具有较好的相关性,说明S在一定程度上影响着降水量,是产生降水的重要条件,但其转化成降水的比例除了温度还受多种因子影响,探寻其他影响因子需要将来的进一步研究。
4 结论与讨论(1) PWVt是PWV与降水关系研究的纽带,为了找到影响PWVt的影响因子,建立PWVt的计算公式,本文引入整层大气饱和水汽含量(PWVsat)概念,并推导出多元大气条件下PWVsat计算公式,即PWVsat=12.49e0.0612ts,说明ts影响着PWVsat,由于PWVsat和PWVt表示的含义较为类似,因此推断ts可能是PWVt的一个影响因子。
(2) 将PWVt与ts进行拟合,发现两者具有较好的拟合关系,说明ts对PWVt具有一定指示作用,西峰槽类型和稳定性天气系统拟合的结果较好。
(3) PWVt的拟合公式与PWVsat推导公式较为一致,说明PWVt与PWVsat密切相关,两者可以衡量大气容纳水汽的能力,该能力与ts有关。
(4) 对该方法计算的PWVt在降水预报中的准确性进行统计检验,准确率、漏报率和空报率分别为93.69%、2.32%和3.99%,说明PWVt在降水预报中具有一定的应用价值。
(5) 通过一次降水个例进行应用分析,定义变量S为实际PWV与PWVt之差,根据本文方法计算的PWVt可以较好预报降水,大部分站降水时间段位于S>0的范围内,由此说明PWVt不仅可以预报降水,也可以作为判断降水是否持续的参考指标。部分站S与降水量具有较好的相关性,S大小影响着降水量,说明S是产生降水的重要条件,但其转换率除了ts外还受多种因子影响,探寻其他影响因子需要将来的进一步研究。
本文研究给出PWVt计算方法对于西风槽稳定性降水预报具有一定的参考价值,但必须结合天气形势和其他气象资料以及具体降水特征进行综合分析和研判。由于降水过程十分复杂,除了水汽条件外还有动力条件和云滴增长条件,因此,希望通过接下来的研究,找出更多影响PWVt以及S转化为降水比例的因素,以期为降水临近预报等方面提供更准确参考。
致谢:感谢胡志晋老师对本研究给予的建议和指导。
敖雪, 王振会, 徐桂荣, 等, 2011. 地基微波辐射计资料在降水分析中的应用[J]. 暴雨灾害, 30(4): 358-365. Ao X, Wang Z H, Xu G R, et al, 2011. Apply of ground-based microwave radiometer observation in precipitation events[J]. Torr Rain Dis, 30(4): 358-365 (in Chinese). DOI:10.3969/j.issn.1004-9045.2011.04.012
|
曹云昌, 方宗义, 夏青, 2005. GPS遥感的大气可降水量与局地降水关系的初步分析[J]. 应用气象学报, 16(1): 54-59. Cao Y C, Fang Z Y, Xia Q, 2005. Relationship between GPS precipitable water vapor and precipitation[J]. J Appl Meteor Sci, 16(1): 54-59 (in Chinese). DOI:10.3969/j.issn.1001-7313.2005.01.006
|
陈淑琴, 徐燚, 曹宗元, 等, 2018. 冷空气和热带低压共同作用下的一次暴雨预报失败原因分析[J]. 气象, 44(1): 142-150. Chen S Q, Xu Y, Cao Z Y, et al, 2018. Results of a failure forecast about a rainstorm caused by cold air and tropical low pressure[J]. Me-teor Mon, 44(1): 142-150 (in Chinese).
|
党张利, 张京朋, 曲宗希, 等, 2015. 微波辐射计观测数据在降水预报中的应用[J]. 干旱气象, 33(2): 340-343. Dang Z L, Zhang J P, Qu Z X, et al, 2015. The application of microwave radiometer observation data on precipitation forecast[J]. J Arid Meteor, 33(2): 340-343 (in Chinese).
|
丁金才, 黄炎, 叶其欣, 等, 2004. 2002年台风Ramasun影响华东沿海期间可降水量的GPS观测和分析[J]. 大气科学, 28(4): 613-624. Ding J C, Huang Y, Ye Q X, et al, 2004. GPS observation and analysis of precipitable water vapor during typhoon Ramasun in 2002 influencing east China Coast[J]. Chin J Atmos Sci, 28(4): 613-624 (in Chinese). DOI:10.3878/j.issn.1006-9895.2004.04.13
|
郝丽萍, 邓佳, 李国平, 等, 2013. 一次西南涡持续暴雨的GPS大气水汽总量特征[J]. 应用气象学报, 24(2): 230-239. Hao L P, Deng J, Li G P, et al, 2013. Characteristics of GPS vapor in a persistent heavy rainfall related to southwest vortex[J]. J Appl Me-teor Sci, 24(2): 230-239 (in Chinese). DOI:10.3969/j.issn.1001-7313.2013.02.011
|
李国翠, 李国平, 连志鸾, 等, 2008. 不同云系降水过程中GPS可降水量的特征—华北地区典型个例分析[J]. 高原气象, 27(5): 1066-1073. Li G C, Li G P, Lian Z L, et al, 2008. Features of precipitable water vapor by GPS in different cloudform precipitation-analyses on some typical cases in North China[J]. Plateau Meteor, 27(5): 1066-1073 (in Chinese).
|
李青春, 张朝林, 楚艳丽, 等, 2007. GPS遥感大气可降水量在暴雨天气过程分析中的应用[J]. 气象, 33(6): 51-58. Li Q C, Zhang C L, Chu Y L, et al, 2007. Applications of precipitable water vapor monitored by ground-based GPS to analyzing heavy rain event[J]. Meteor Mon, 33(6): 51-58 (in Chinese).
|
刘晶, 杨莲梅, 2017. 一次中亚低涡造成的天山北坡暴雨GPS大气水汽总量演变特征[J]. 气象, 43(6): 724-734. Liu J, Yang L M, 2017. Development features of GPS atmospheric precipitable water vapor in heavy rainfall caused by Central Asia vortex on the north slope of Tianshan Mountain[J]. Meteor Mon, 43(6): 724-734 (in Chinese).
|
孙力, 郑秀雅, 王琪, 1994. 东北冷涡的时空分布特征及其与东亚大型环流系统之间的关系[J]. 应用气象学报, 5(3): 297-303. Sun L, Zheng X Y, Wang Q, 1994. The climatological characteristics of northeast cold vortex in China[J]. Quart J Appl Meteor, 5(3): 297-303 (in Chinese).
|
万蓉, 郑国光, 2008. 地基GPS在暴雨预报中的应用进展[J]. 气象科学, 28(6): 697-702. Wan R, Zheng G G, 2008. Advances in the application of ground based GPS data to rainstorm forecast and nowcasting[J]. Sci Meteor Sin, 28(6): 697-702 (in Chinese). DOI:10.3969/j.issn.1009-0827.2008.06.019
|
向玉春, 陈正洪, 徐桂荣, 等, 2009. 三种大气可降水量推算方法结果的比较分析[J]. 气象, 35(11): 48-54. Xiang Y C, Chen Z H, Xu G R, et al, 2009. A comparison and analysis of the results of three methods for the calculation of water vapor resources[J]. Meteor Mon, 35(11): 48-54 (in Chinese). DOI:10.7519/j.issn.1000-0526.2009.11.006
|
徐道生, 张艳霞, 陈子通, 等, 2016. 不同水汽分析场对一次华南前汛期暴雨预报的影响分析[J]. 热带气象学报, 32(2): 155-162. Xu D S, Zhang Y X, Chen Z T, et al, 2016. Influence of different moisture analysis field to the forecast of precipitation during the pre-flood season in South China[J]. J Trop Meteor, 32(2): 155-162 (in Chinese).
|
杨磊, 蒋大凯, 王瀛, 等, 2016. 辽宁省汛期GPS大气可降水量的特征分析[J]. 干旱气象, 34(1): 82-87. Yang L, Jiang D K, Wang Y, et al, 2016. Analysis of atmospheric precipitable water vapor characteristics during flood season in Liaoning Province based on GPS remote sensing data[J]. J Arid Meteor, 34(1): 82-87 (in Chinese).
|
叶其欣, 杨露华, 丁金才, 等, 2008. GPS/PWV资料在强对流天气系统中的特征分析[J]. 暴雨灾害, 27(2): 141-148. Ye Q X, Yang L H, Ding J C, et al, 2008. Application of GPS/PWV data to forecast strong convection weather in Shanghai[J]. Torr Rain Dis, 27(2): 141-148 (in Chinese).
|
张立祥, 李泽椿, 2009. 东北冷涡研究概述[J]. 气候与环境研究, 14(2): 218-228. Zhang L X, Li Z C, 2009. A summary of research on cold vortex over Northeast China[J]. Climatic Environ Res, 14(2): 218-228 (in Chinese).
|
周雪松, 吴炜, 孙兴池, 2014. 山东暴雨天气学预报指标的统计特征分析[J]. 气象, 40(6): 744-753. Zhou X S, Wu W, Sun X C, 2014. Statistics on physical indicators of rainstorms in Shandong Pro-vince[J]. Meteor Mon, 40(6): 744-753 (in Chinese).
|
Benevides P, Catalao J, Miranda P M A, 2015. On the inclusion of GPS precipitable water vapour in the nowcasting of rainfall[J]. Nat Hazards Earth Syst Sci, 15(12): 2605-2616. DOI:10.5194/nhess-15-2605-2015
|
Bolton D, 1980. The computation of equivalent potential temperature[J]. Mon Wea Rev, 108(7): 1046-1053. DOI:10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.CO;2
|
Cao Y J, Guo H, Liao R W, et al, 2016. Analysis of water vapor cha-racteristics of regional rainfall around Poyang Lake using ground-based GPS observations[J]. Acta Geodaet Geophys, 51(3): 467-479. DOI:10.1007/s40328-015-0137-1
|
Chamberlin R A, Bally J, 1995. The observed relationship between the South Pole 225-GHz atmospheric opacity and the water vapor column density[J]. Int J Infrared Millim Waves, 16(5): 907-920. DOI:10.1007/BF02066665
|
Chamberlin R A, Grossman E N, 2012. The wintertime South Pole tropospheric water vapor column:comparisons of radiosonde and recent terahertz radiometry, use of the saturated column as a proxy measurement, and inference of decadal trends[J]. J Geophys Res:Atmos, 117(D13): D13111.
|
Li Z H, Muller J P, Cross P, 2013. Comparison of precipitable water vapor derived from radiosonde, GPS, and moderate-resolution imaging Spectroradiometer measurements[J]. J Geophys Res:Atmos, 108(D20): ACH 10.
|
Shi J B, Xu C Q, Guo J M, et al, 2015. Real-time GPS precise point positioning-based precipitable water vapor estimation for rainfall monitoring and forecasting[J]. IEEE Trans Geosci Remote Sens, 53(6): 3452-3459. DOI:10.1109/TGRS.2014.2377041
|
Shoji Y, 2013. Retrieval of water vapor inhomogeneity using the Ja-panese nationwide GPS array and its potential for prediction of convective precipitation[J]. J Meteor Soc Jpn Ser II, 91(1): 43-62. DOI:10.2151/jmsj.2013-103
|
Yao Y B, Shan L L, Zhao Q Z, 2017. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application[J]. Sci Rep, 7(1): 12465. DOI:10.1038/s41598-017-12593-z
|
 2020, Vol. 46
2020, Vol. 46 