随着数值预报技术的不断改进,近年来台风路径预报误差不断减小,但是台风强度数值预报的改进却并不明显(Rappaport et al, 2009;Lei et al, 2016;麻素红等,2018)。一个重要原因在于台风的路径主要受大尺度环境风场的控制(Wang and Wu, 2004),而通过模式改进、资料同化(Qu and Heming, 2002;Kamineni et al, 2006)等手段,模式对大尺度流场的预报水平已经得到了有效的提升。台风强度的变化则主要依赖于大尺度环境动力和热力场、低层边界条件(海洋热容量以及陆面过程)以及内核结构。如果要对台风内核区的对流运动进行精确的模拟,就必须通过提高模式分辨率来减少次网格物理过程参数化过程带来的不确定性(Davis et al, 2010;Xue et al, 2013)。
Li et al(2008)使用网格距为2 km的MM5模式对台风Rananim(2004)进行模拟,发现模式能比较准确地模拟出台风内核区的垂直风切变特征和眼墙附近非对称分布的对流。Hall et al(2013)利用ARPS模式对台风Morakot(2009)进行模拟,对3 km和15 km两种分辨率的模拟结果进行比较,发现提高分辨率可以更为准确地模拟出台风眼墙附近涡旋罗斯贝波结构特征。在实际业务方面,近年来人们也相应地开发了很多高分辨率台风模式预报系统,并取得了较好的预报效果。Goldenberg et al(2015)基于HWRF模式建立了最高分辨率为3 km的业务台风预报系统,测试结果表明它对于台风强度的预报有了明显的改进。Hazelton et al(2018)利用GFDL的fvGFS模式也建立了一个高分辨率台风预报系统,同样发现它对于强度预报有明显的改进,特别是对台风快速加强过程中结构演变特征的预报。在台风预报改进计划中,Gall et al(2013)提出了通过建立3 km分辨率的业务模式来加强台风强度预报水平的设想。最近Magnusson et al(2019)对ECMWF的台风业务预报进行了总结,认为水平分辨率不足导致模式无法准确预报强台风内核区的气压陡降过程,从而进一步影响了对台风强度的预报效果。
由广州热带海洋气象研究所开发并业务运行的南海台风模式(Tropical Regional Assimilation Model for the South China Sea,TRAMS),其2.0版本在路径预报方面具有较好的表现,但是在强度预报方面仍然存在明显的不足,特别是在超强台风的加强过程方面(Chen et al, 2014)。为了改善TRAMS模式对台风强度预报的性能,我们将TRAMS模式的水平分辨率从原来的18 km提高到9 km,并对动力框架和物理过程进行相应的调整和优化,形成了TRAMS 3.0升级版本。第三节中我们将分别对优化的具体内容和评估结果进行论述。
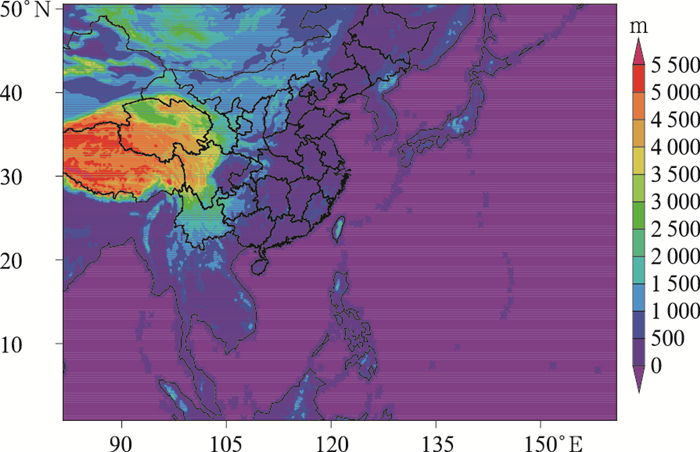
1 南海台风模式概况南海台风模式TRAMS模式是基于GRAPES[Global/Regional Assimilation and Prediction System,(薛纪善和陈德辉,2008)]区域模式版本开发而成,其主要用途是为华南沿海地区提供南海区域的台风业务数值预报产品,该模式范围如图 1所示。目前TRAMS模式业务版本的水平分辨率为18 km,垂直方向采用65层地形追随坐标,模式层顶高度为31 km。使用的物理过程方案包括:WSM6微物理过程、SAS对流参数化、MRF边界层参数化、SLAB陆面过程、SFCLAY近地层方案和RRTMG长短波辐射方案。该模式以ECMWF全球模式提供的分辨率为0.09°的分析场和预报场分别生成初始场和侧边界条件,每天运行两次(分别于00时和12时启动,世界时,下同),每次向前积分168 h。
|
图 1 TRAMS模式的范围 (图中填色表示地形高度) Fig. 1 The domain of TRAMS model (Colored area means height of terrain) |
如引言所述,提高模式分辨率对改进台风强度预报具有重要意义。基于双向移动嵌套技术,HWRF模式(Hurricane Weather Research and Forecasting model)可以在台风区域实现2 km水平分辨率的业务预报(Biswas et al, 2018)。目前国内很多业务台风模式主要基于GRAPES模式,由于GRAPES区域模式还不具备移动嵌套功能,无法实现将分辨率在台风发生区域提高到对流尺度,因此大多业务台风模式的分辨率仍然在10 km左右(麻素红, 2019;许晓林等,2019)。提高TRAMS模式的分辨率会引起计算量的较大幅度增长。根据现有的计算机条件和实际业务时效需求,我们将TRAMS模式的水平分辨率从18 km提高到9 km。
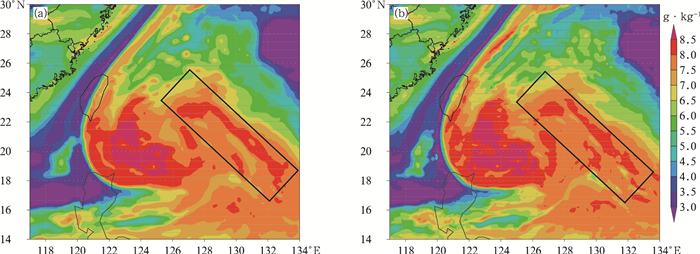
分别利用水平网格距为18 km和9 km的TRAMS模式模拟2017年超强台风天鸽(起报时间为2017年8月20日00时),并对600 hPa比湿场的24 h预报结果(图 2)进行比较。可以看出提高模式水平分辨率以后,粗网格的平滑滤波作用得到了有效抑制,湿度场的细节特征变得更为明显。以位于台风中心右侧的螺旋云带为例(在图 2中以黑色长方形标注),可以看出提高分辨率以后(图 2b),云带侧边界附近具有更加明显的小尺度变化特征,特别是在云带的西北端出现了断裂的现象,而这些特征在18 km分辨率模拟结果(图 2a)中是无法体现的。以上结果说明提高模式分辨率可以更加细致地描述台风内核区附近的对流过程,而这对于准确模拟台风强度变化是非常必要的(Yu et al, 2017)。
|
图 2 2017年8月20日00时起报18 km(a)、9 km(b)水平分辨率下台风天鸽600 hPa比湿场的24 h预报结果 (黑色长方形为台风中心右侧的螺旋云带) Fig. 2 The 24 h forecast of specific humidity at 600 hPa for Typhoon Hato under different horizontal resolutions of 18 km (a) and 9 km (b) (Black rectangle represents spiral cloud band of typhoon center on the right. Initiated at 0000 UTC 20 August 2017) |
静态参考大气方案的设计对于半隐式半拉格朗日模式动力框架的计算精度有重要影响(杨兆礼和陈子通,2014)。陈子通等(2016)将TRAMS模式中的等温参考大气(一维)推广为三维参考大气,新方案通过引入参考大气的水平变化使之更加接近实际大气,避免了因模式扰动量级偏大而导致的计算不稳定问题。
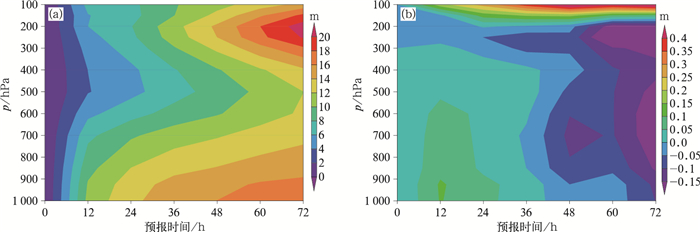
在原三维参考大气方案中,参考大气的水平变化项被纳入非线性项中,这种做法会导致非线性项量级大于线性项,从而降低时间离散过程的计算精度。苏勇等(2018)将参考大气水平变化项移入线性项,使得该方案的计算精度和稳定性得到进一步改善。将该项技术引入到TRAMS 3.0模式中,并选取2018年9月(每天00时起报,一共进行30次预报)进行批量测试,发现新方案对于提高模式计算精度确实会有一定程度的改进(图 3),图中的预报误差由2018年9月期间模式区域范围内平均后得到。
|
图 3 2018年9月月平均位势高度预报场均方根误差时间-气压剖面
(a)原三维参考大气方案,(b)改进方案和原方案的差异(改进方案减去原方案)
Fig. 3 Time-pressure cross sections of averaged RMSE for geopotential height in September 2018
(a)original 3-dimension reference atmosphere, (b) difference between original and revised scheme (revised scheme minus original scheme) |
在模式物理过程中,对流参数化方案对于水平网格距的变化非常敏感,因此在提高模式水平分辨率的同时必须考虑对流参数化方案的尺度自适应(Han et al, 2017;Huang et al, 2018)。TRAMS 3.0模式中积云参数化方案的改进主要包括以下两个方面:
(1) 在早期的SAS对流参数化方案中(Pan and Wu, 1995),通常都假设次网格积云的面积相对于模式网格面积来说是可以忽略不计的(即积云覆盖比σu远远小于1)。当模式分辨率进入到灰色尺度(网格距介于1~10 km)时这种假设已经不再适用,必须考虑对流参数化的尺度自适应过程,避免它的过度调整引起的网格稳定化问题(徐道生等,2015)。改进后的SAS方案引入了尺度识别技术,使之更加适用于灰色尺度分辨率的模式:
| $ {M_{\rm{B}}} = {\left({1 - {\sigma _{\rm{u}}}} \right)^2}{M_{{\rm{BE}}}} $ | (1) |
式中:MBE是基于σu远远小于1的假设而诊断得到的云底质量通量,MB则是考虑了σu的影响之后云底质量通量。上式中积云覆盖比是按照如下方法估算的:
| $ \begin{array}{l} {\sigma _{\rm{u}}} = \frac{{3.14R_{\rm{c}}^2}}{{{A_{{\rm{grid}}}}}}\\ {R_{\rm{c}}} = \frac{{0.2}}{{{\varepsilon _0}}} \end{array} $ | (2) |
式中:Agrid表示网格面积,Rc表示对流上升气流的半径,ε0表示上升气流的侧面卷入率。
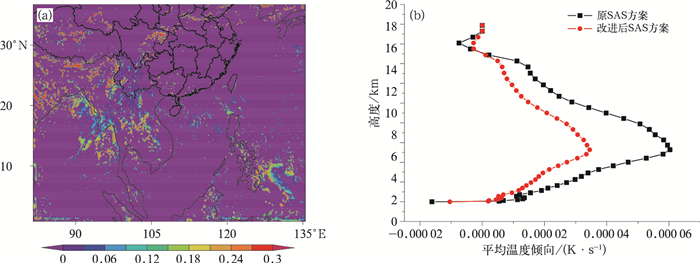
在9 km分辨率下利用改进后的SAS对流参数化方案进行单步预报(起报时间为2017年8月21日12时),可以发现在很多地区积云覆盖比达到了0.2~0.3(图 4a)。从温度倾向反馈来看,考虑尺度自适应技术之后SAS方案的加热率明显减弱了(图 4b),这基本符合公式(1)的理论预期。
|
图 4 2017年8月21日12时起报的SAS对流参数化方案的单步预报诊断结果 (a)积云覆盖比,(b)区域平均温度倾向廓线 Fig. 4 Single step prediction of revised SAS convection scheme initialized at 1200 UTC 21 August 2017 (a) cumulus fractional area, (b) profile of area averaged temperature tendency |
(2) 在原SAS方案中,气块上升过程中雨水转化率d0是不随高度变化的常数(0.002 m-1),这与三维云模式的模拟结果是不一致的,另外对于气溶胶的影响也未加以考虑。在新方案中考虑了零度层以上降水转化率随高度逐渐减少的趋势,以及气溶胶浓度对降水转换率的影响(Han et al, 2016):
| $ {d_0} = a\exp \left[ {b\left({T - {T_0}} \right)} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{当}}T \le {T_0}{\rm{时}} $ | (3) |
| $ {d_0} = a{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{当}}T > {T_0}{\rm{时}} $ | (4) |
式中:
近地层方案主要用于诊断不同下垫面附近的摩擦速度和交换系数,为地表感热通量、潜热通量和动量通量的计算提供准备,该方案对于台风边界层过程的预报具有重要影响。在TRAMS 3.0模式中近地层方案修改内容主要包括以下两个方面:
(1) 原方案中海洋下垫面粗糙度z0的计算公式为:
| $ {z_0} = {z_{{\rm{ch}}}}\frac{{{u^2}_*}}{g} + 0.00001 $ | (5) |
式中:zch为Charnock参数(Charnock,1955),u*表示摩擦速度,g为重力加速度。根据近年来的海洋观测资料(Zhao et al, 2015; Bi et al, 2015),新方案对粗糙度和摩擦速度的拟合系数对zch值进行了订正(从原来的0.015 6修改为0.018 5),并通过一个与u*成反比的调整项来修正洋面风速极小情况下的粗糙度估算偏差,其具体形式为:
| $ {z_0} = {z_{{\rm{ch}}}}\frac{{{u^2}_*}}{g} + 0.11\frac{{0.000015}}{{{u_*}}} $ | (6) |
(2) 在原方案中,对流速度Vc的计算公式为:
| $ \left\{ \begin{array}{l} {V_{\rm{c}}} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{对于稳定层结}}\\ {V_{\rm{c}}} = 2\sqrt {\left({{\theta _{\rm{g}}} - {\theta _{\rm{a}}}} \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{对于中性和不稳定层结}} \end{array} \right. $ | (7) |
式中:θg为地表湿位温,θa为近地层内(位于模式第一层高度上)的湿位温。为了减少静风条件下Vc对摩擦速度和粗糙度的贡献,新方案将Vc缩小为原来的一半,即:
| $ \left\{ \begin{array}{l} {V_{\rm{c}}} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{对于稳定层结}}\\ {V_{\rm{c}}} = \sqrt {\left({{\theta _{\rm{g}}} - {\theta _{\rm{a}}}} \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{对于中性和不稳定层结}} \end{array} \right. $ | (8) |
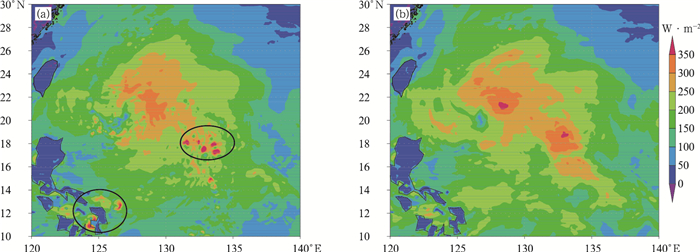
分别利用修改前后的近地层参数化方案对台风天鸽进行模拟,并对海表面的潜热通量以及海平面气压进行比较(图 5)。在台风中心附近新方案(图 5b)模拟的潜热通量要稍强于原方案(图 5a),其值达到了350 W·m-2以上。在远离台风眼的地区,原方案模拟的潜热出现了一些大于350 W·m-2的孤立中心(见图 5a中椭圆形标识),而在新方案模拟结果中这种小范围强蒸发中心消失了,这可能与新方案减小低风速区的洋面粗糙度后导致海表面蒸发变少有关。
|
图 5 2017年8月20日00时起报的台风天鸽第12 h的海表潜热通量模拟结果 (a)原方案,(b)改进方案 Fig. 5 The 12 h simulated sea surface latent heat flux of Typhoon Hato initiated from 0000 UTC 20 August 2017 (a) original scheme, (b) revised scheme |
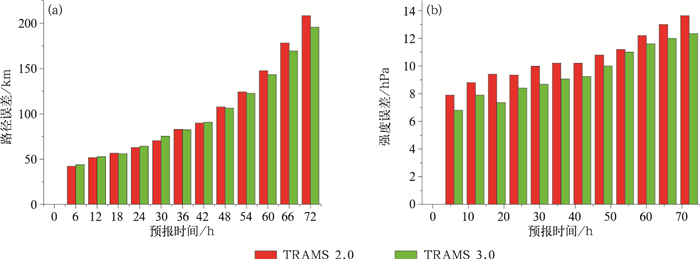
利用TRAMS 3.0模式对2107年模式范围内的所有台风过程(共有163个样本)进行预报和评估。从评估结果(图 6)来看,TRAMS 3.0模式对48 h以后的路径预报有明显改进,72 h的平均路径误差减少了13.6 km,改进幅度约为7.0%(图 6a)。强度误差的改进在各个时次均能达到1.2 hPa左右,改进幅度约为10.5%(图 6b)。
|
图 6 2017年台风预报的TRAMS模式平均路径误差(a)和强度误差(b) Fig. 6 Average track error (a) and intensity error (b) for typhoon forecasts in 2017 |
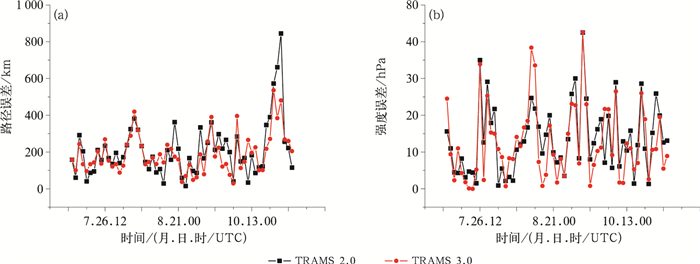
从台风路径预报误差随时间的变化曲线(图 7a)可以看到,TRAMS 2.0模式在10月中下旬的(对应的是1724号台风兰恩)误差最大值达到了800 km左右,而TRAMS 3.0模式对该台风的改进效果最为明显,其最大误差下降到约500 km左右。对于强度预报误差,其改进幅度随时间的分布相对比较均匀(图 7b),大部分样本的强度预报误差都有不同程度的减小。但是需要指出的是,TRAMS 3.0模式仍然有不少样本的强度预报误差大于TRAMS 2.0模式,其中最明显的8月3日台风奥鹿(1705号)的预报。其原因一方面与TRAMS 3.0模式中一些仍然存在的固有缺陷有关(例如没有考虑预报过程中海表温度的时间变化),另外即使将模式分辨率提高到9 km,次网格对流参数化过程仍然对模式预报有较强的影响,而该过程存在较大的不确定性,容易导致某些台风个例的强度预报出现误差变大的现象。
|
图 7 TRAMS模式2017年台风72 h路径预报误差(a)和强度预报误差(b)的时间变化 Fig. 7 Time series of track error (a) and intensity error (b) for 72 h forecast of typhoon in 2017 |
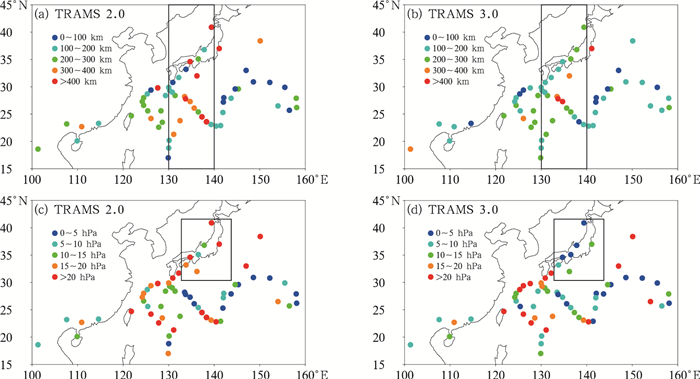
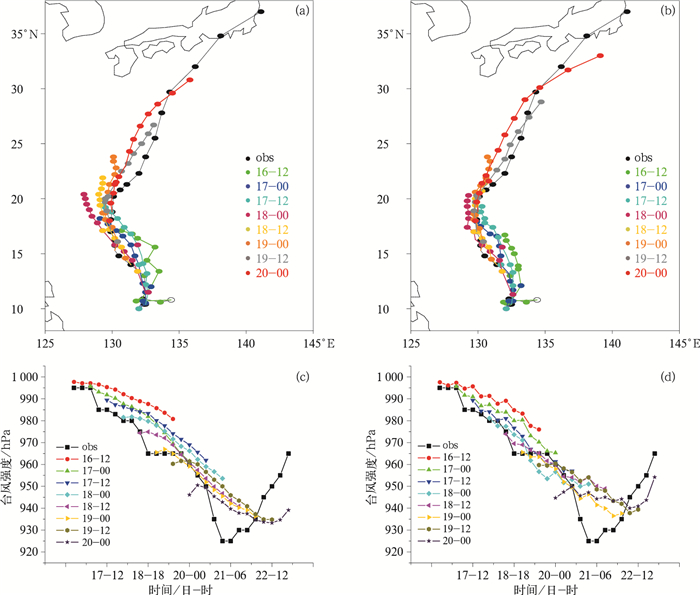
进一步对72 h预报误差的空间分布特征进行比较。从图 8a可以看到,TRAMS 2.0模式的路径预报误差主要集中分布在130°~140°E,TRAMS 3.0模式对台风路径的改进也主要体现在这些区域(图 8b)。TRAMS 2.0模式的台风强度误差空间分布并没有表现出明显的规律特征(图 8c),而TRAMS 3.0模式对于日本岛附近区域(图 8d黑色方框)的强度预报改进效果最为明显。选择该区域的典型个例台风兰恩进行多时次预报,发现TRAMS 2.0模式模式的预报存在前期路径偏东,后期移速偏慢的现象(图 9a),TRAMS 3.0模式可以有效地改善这种偏差(图 9b)。对于“兰恩”的强度预报,TRAMS 3.0模式也有明显改进(图 9c,9d)。以10月16日12时启动的(图 9c,9d中红色线)预报结果为例,TRAMS 2.0模式的72 h中心最低气压预报值为980.8 hPa,明显比实况(965.0 hPa)偏弱,而TRAMS 3.0模式的预报值达到了976 hPa,更为接近实际观测。
|
图 8 TRAMS模式2017年台风72 h路径预报误差(a,b)和强度预报误差(c,d)的空间分布 Fig. 8 Spatial distributions of typhoon track error (a, b) and intensity error (c, d) for 72 h forecasts of typhoon in 2017 |
|
图 9 台风兰恩的TRAMS 2.0模式(a, c)和TRAMS 3.0模式(b, d)路径(a, b)和强度(c, d)多时次预报对比 (“obs”表示实际观测,不同颜色表示不同的预报起报时间) Fig. 9 Multi-time track (a, b) and intensity (c, d) forecasts comparisons of Typhoon Lan (1724) by TRAMS 2.0 (a, c) and TRAMS 3.0 (b, d) ("obs" means the real observation, and the initial time for every forecast was denoted by different colors) |
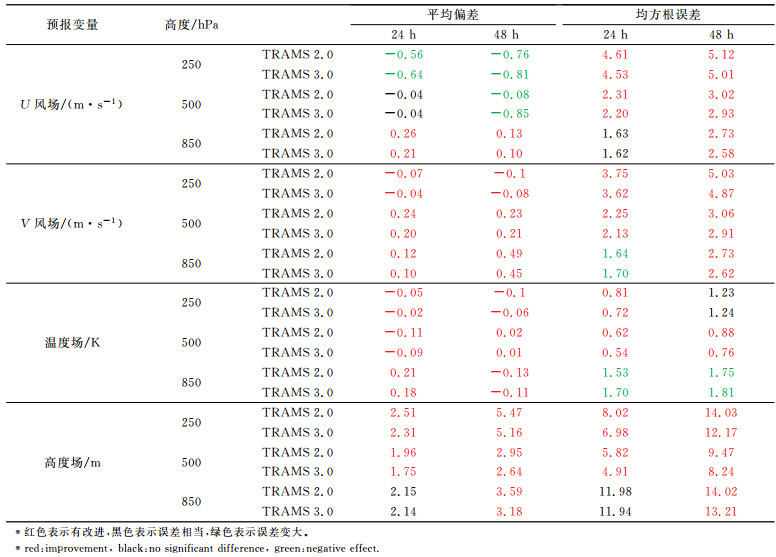
为了更加全面地评估技术升级对模式预报性能的影响,进一步对高空气象要素预报场也进行了检验(表 1)。评估时间从2017年1月1日00时开始至12月31日12时结束(其中每天00时和12时启动预报,一共730个样本)。从均方根误差可以看到,除了850 hPa的温度场以外,TRAMS 3.0模式对高空要素的预报效果均有不同程度的改进。对于平均偏差,除250 hPa和500 hPa高度上的U风场以外,其他大部分要素也都有改善。
|
|
表 1 TRAMS 2.0和TRAMS 3.0预报误差评分卡 Table 1 Score card of forecast error for TRAMS 2.0 and TRAMS 3.0 |
南海台风预报一直都是TRAMS模式预报业务中的重点关注对象,下面进一步评估模式升级对于南海台风路径和强度预报的影响。选取2017年期间影响南海附近区域的15个典型台风个例(表 2),分别对每一项技术更新的影响进行测试。试验设计如表 3所示。
|
|
表 2 2017-2018年期间影响南海的15个台风个例 Table 2 Fifteen typhoons influencing the South China Sea during 2017-2018 |
|
|
表 3 试验方案 Table 3 Experimental scheme |
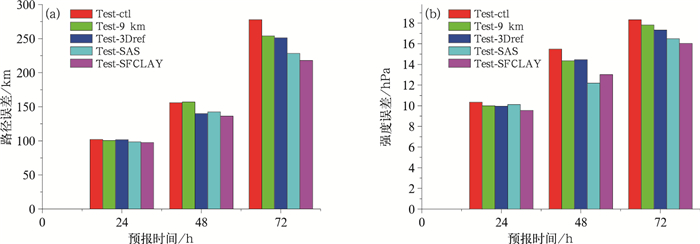
利用所选的15个南海台风个例,分别评估模式分辨率、三维参考大气、对流参数化方案和近地层方案的改进对台风预报误差的影响,其结果如图 10所示。从台风路径误差来看,48 h预报误差的减少主要来自于三维参考大气的改进(Test-3Dref,减少幅度约为16 km)。72 h预报误差的减少主要由提高分辨率(Test-9 km)和更新对流参数化方案(Test-SAS)贡献,减少幅度分别约为24 km和23 km,而近地层方案(Test-SFCLAY)引起的误差改进约为10 km。Test-SAS对于48 h台风强度预报的改进最为明显(最低气压误差减少约2.3 hPa),其次是Test-9 km(误差减少1.1 hPa)。对于72 h强度预报误差,各项模式技术改进的贡献大体接近(每项技术对最低气压误差的改进幅度都在0.5 hPa左右)。
|
图 10 不同试验方案的15个南海台风平均(a)路径误差和(b)强度误差结果 Fig. 10 Average track error (a) and intensity error (b) for 15 typhoon cases of different experiment schemes at the South China Sea |
总的来说,TRAMS 3.0模式中分辨率的提高和对流参数化的改进对于提高南海台风预报效果贡献最大。
5 结论与讨论在业务版本TRAMS 2.0模式的基础上,从模式分辨率、动力框架、物理过程三个方面进行了相应的技术更新,形成了升级版本TRAMS 3.0模式。评估结果表明TRAMS 3.0模式对台风路径和强度的预报均有显著改善,同时对高空气象要素的预报误差也有系统性的减少。在TRAMS 3.0模式的各项技术更新中,模式分辨率和对流参数化方案的修改对于台风预报效果的改进贡献最大。从2019年7月开始,TRAMS 3.0模式正式替换原来的TRAMS 2.0模式投入业务应用,目前该模式版本仍然在业务运行。
总的来说,TRAMS 3.0模式对台风强度预报有较为明显的改进,但是仍然有不少样本出现误差变大的现象(参考图 7b)。这可能是因为TRAMS 3.0模式的分辨率属于典型的“灰色地带”(即网格距介于1~10 km的模式),在这种尺度下如何正确地使用对流参数化目前仍然存在很大的争议(Arakawa and Wu, 2013;赵晨阳和徐国强,2020),
本文通过积云覆盖比因子进行尺度识别的方法对于台风内部对流过程的前期预报可能还存在一定的不足。为了减少这种次网格对流参数化引起的台风强度预报不确定性,在下一步的模式版本升级计划中我们准备将TRAMS模式的水平分辨率进一步提高到3 km左右。
目前TRAMS 3.0模式对于超强台风的强度预报仍然存在明显的偏弱现象,这说明该模式仍然有很大的进一步改进空间。很多研究表明模式垂直分辨率(Zhang et al,2015),台风初始化(瞿安祥等,2016;许晓林等,2019)以及海气耦合过程(刘磊等,2017)对于改进台风强度预报具有较好的改进效果,这些方面也将是我们下一步升级过程中的重点。对于台风暴雨过程的预报效果,也是检验数值预报模式性能的重要指标(漆梁波和徐珺, 2018;王新敏和栗晗,2020),在以后TRAMS模式版本升级过程中,这方面的评估也需要加以完善。
陈子通, 戴光丰, 钟水新, 等, 2016. 中国南海台风模式(TRAMS-v20)技术特点及其预报性能[J]. 热带气象学报, 32(6): 831-840. Chen Z T, Dai G F, Zhong S X, et al, 2016. Technical features and prediction performance of typhoon model for the South China Sea[J]. J Trop Meteor, 32(6): 831-840 (in Chinese).
|
刘磊, 费建芳, 马占宏, 等, 2017. 区域台风-海洋耦合模式的构建及应用研究[J]. 大气科学, 41(1): 178-188. Liu L, Fei J F, Ma Z H, et al, 2017. Construction and application of a regional typhoon-ocean coupled model[J]. Chin J Atmos Sci, 41(1): 178-188 (in Chinese).
|
麻素红, 2019. 涡旋强度调整半径对2016年第18号热带气旋路径预报的影响[J]. 气象学报, 77(4): 662-673. Ma S H, 2019. Impact of radius of TC intensity correction on No.1618 TC track prediction[J]. Acta Meteor Sin, 77(4): 662-673 (in Chinese).
|
麻素红, 张进, 沈学顺, 等, 2018. 2016年GRAPES_TYM改进及对台风预报影响[J]. 应用气象学报, 29(3): 257-269. Ma S H, Zhang J, Shen X S, et al, 2018. The upgrade of GRAPES_TYM in 2016 and its impacts on tropical cyclone prediction[J]. J Appl Meteor Sci, 29(3): 257-269 (in Chinese).
|
漆梁波, 徐珺, 2018. 豫北"7·9"特大暴雨的短期预报分析和反思[J]. 气象, 44(1): 1-14. Qi L B, Xu J, 2018. Rethink on short-range forecast of the 9 July severe rainstorm in Northern Henan[J]. Meteor Mon, 44(1): 1-14 (in Chinese).
|
瞿安祥, 麻素红, 张进, 2016. T639全球模式的台风初始化方案升级试验[J]. 气象, 42(6): 664-673. Qu A X, Ma S H, Zhang J, 2016. Updated experiments of tropical cyclone initialization in global model T639[J]. Meteor Mon, 42(6): 664-673 (in Chinese).
|
苏勇, 沈学顺, 陈子通, 等, 2018. GRAPES_GFS中三维参考大气的研究:理论设计和理想试验[J]. 气象学报, 76(2): 241-254. Su Y, Shen X S, Chen Z T, et al, 2018. A study on the three-dimensional reference atmosphere in GRAPES_GFS:theoretical design and ideal test[J]. Acta Meteor Sin, 76(2): 241-254 (in Chinese).
|
王新敏, 栗晗, 2020. 多数值模式对台风暴雨过程预报的空间检验评估[J]. 气象, 46(6): 753-764. Wang X M, Li H, 2020. Spatial verification evaluation of typhoon rainstorm by multiple numerical models[J]. Meteor Mon, 46(6): 753-764 (in Chinese).
|
徐道生, 张艳霞, 王刚, 等, 2015. Meso-SAS对流参数化方案的改进及其在9 km分辨率模式中的应用[J]. 热带气象学报, 31(5): 608-618. Xu D S, Zhang Y X, Wang G, et al, 2015. Improvement of Meso-SAS cumulus parameterization scheme and its application in a model of 9 km resolution[J]. J Trop Meteor, 31(5): 608-618 (in Chinese).
|
许晓林, Liu Q F, 陈葆德, 等, 2019. GRAPES-TCM台风模式的新涡旋初始化方案——原理和实施[J]. 大气科学, 43(5): 975-989. Xu X L, Liu Q F, Chen B D, et al, 2019. Vortex initialization scheme in GRAPES-TCM model:technical description and implementation[J]. Chin J Atmos Sci, 43(5): 975-989 (in Chinese).
|
薛纪善, 陈德辉, 2008. 数值预报系统GRAPES的科学设计与应用[M]. 北京: 科学出版社. Xue J S, Chen D H, 2008. The Scientific Design and Application of GRAPES Numerical Weather Prediction System[M].
Beijing: Science Press (in Chinese).
|
杨兆礼, 陈子通, 2014. 区域模式参考大气扰动量算法的预报试验[J]. 热带气象学报, 30(6): 1107-1112. Yang Z L, Chen Z T, 2014. The forecasting experiment with a reference atmosphere disturbance algorithm of Guangdong regional model[J]. J Trop Meteor, 30(6): 1107-1112 (in Chinese).
|
赵晨阳, 徐国强, 2020. 尺度适应的对流参数化方案对一次华南飑线模拟的影响[J]. 大气科学, 44(2): 297-314. Zhao C Y, Xu G Q, 2020. The impact of scale-aware cumulus parameterization scheme on the numerical simulation of a squall line in South China[J]. Chin J Atmos Sci, 44(2): 297-314 (in Chinese).
|
Arakawa A, Wu C M, 2013. A unified representation of deep moist convection in numerical modeling of the atmosphere Part Ⅰ[J]. J Atmos Sci, 70(7): 1977-1992.
|
Bi X Y, Gao Z Q, Liu Y G, et al, 2015. Observed drag coefficients in high winds in the near offshore of the South China Sea[J]. J Geophys Res, 120(13): 6444-6459.
|
Biswas M K, Bernardet L, Abarca S, et al, 2018.Hurricane Weather Research and Forecasting (HWRF) model: 2017 scientific documentation[R].NCAR/TN-544+STR.(Available online at http://www.dtcenter.org/sites/default/files/community-code/hwrf/docs/scientific_documents/HWRFv3.9a_ScientificDoc.pdf).
|
Charnock H, 1955. Wind stress on a water surface[J]. Quart J Roy Meteor Soc, 81(350): 639-640.
|
Chen Z T, Zhang C Z, Huang Y Y, et al, 2014. Track of super typhoon Haiyan predicted by a typhoon model for the South China Sea[J]. J Meteor Res, 28(4): 510-523.
|
Davis C, Wang W, Dudhia J, et al, 2010. Does increased horizontal resolution improve hurricane wind forecasts?[J]. Wea Forecasting, 25(6): 1826-1841.
|
Gall R, Franklin J, Marks F, et al, 2013. The hurricane forecast improvement project[J]. Bull Amer Meteor Soc, 94(3): 329-343.
|
Goldenberg S B, Gopalakrishnan S G, Tallapragada V, et al, 2015. The 2012 triply nested, high-resolution operational version of the hurricane weather research and forecasting model (HWRF):track and intensity forecast verifications[J]. Wea Forecasting, 30(3): 710-729.
|
Hall J D, Xue M, Ran L K, et al, 2013. High-resolution modeling of Typhoon Morakot (2009):vortex rossby waves and their role in extreme precipitation over Taiwan[J]. J Atmos Sci, 70(1): 163-186.
|
Han J Y, Hong S Y, Lim K S S, et al, 2016. Sensitivity of a cumulus parameterization scheme to precipitation production representation and its impact on a heavy rain event over Korea[J]. Mon Wea Rev, 144(6): 2125-2135.
|
Han J L, Wang W G, Kwon Y C, et al, 2017. Updates in the NCEP GFS cumulus convection schemes with scale and aerosol awareness[J]. Wea Forecasting, 32(5): 2005-2017.
|
Hazelton A T, Bender M, Morin M, et al, 2018. 2017 Atlantic hurricane forecasts from a high-resolution version of the GFDL fv-GFS model:evaluation of track, intensity, and structure[J]. Wea Forecasting, 33(5): 1317-1337.
|
Huang W, Bao J W, Zhang X, et al, 2018. Comparison of the vertical distributions of cloud properties from idealized extratropical deep convection simulations using various horizontal resolutions[J]. Mon Wea Rev, 146(3): 833-851.
|
Kamineni R, Krishnamurti T N, Pattnaik S, et al, 2006. Impact of CAMEX-4 datasets for hurricane forecasts using a global model[J]. J Atmos Sci, 63(1): 151-174.
|
Lei X T, Yu H, Chen G M, et al, 2016. WMO typhoon landfall forecast demonstration project (WMO-TLFDP) progress and future plans[J]. Trop Cyclone Res Rev, 5(S1): 72-84.
|
Li Q Q, Duan Y H, Yu H, et al, 2008. A high-resolution simulation of Typhoon Rananim (2004) with MM5 Part Ⅰ:Model verification, Inner-core shear, and asymmetric convection[J]. Mon Wea Rev, 136(7): 2488-2506.
|
Magnusson L, Bidlot J R, Bonavita M, et al, 2019. ECMWF activities for improved hurricane forecasts[J]. Bull Amer Meteor Soc, 100(3): 445-458.
|
Pan H L, Wu W S, 1995.Implementing a mass flux convection parameterization package for the NMC medium-range forecast model[R].Washington, DC: NCEP: 40.
|
Qu X B, Heming J, 2002. The impact of dropsonde data on forecasts of Hurricane Debby by the Meteorological Office Unified Model[J]. Adv Atmos Sci, 19(6): 1029-1044.
|
Rappaport E N, Franklin J L, Avila L A, et al, 2009. Advances and challenges at the National Hurricane Center[J]. Wea Forecasting, 24(2): 395-419.
|
Wang Y, Wu C C, 2004. Current understanding of tropical cyclone structure and intensity changes—a review[J]. Meteor Atmos Phys, 87(4): 257-278.
|
Xue M, Schleif J, Kong F Y, et al, 2013. Track and intensity forecasting of hurricanes:impact of convection-permitting resolution and global ensemble kalman filter analysis on 2010 Atlantic season forecasts[J]. Wea Forecasting, 28(6): 1366-1384.
|
Yu Z F, Wang Y Q, Xu H M, et al, 2017. On the relationship between intensity and rainfall distribution in tropical cyclones making landfall over China[J]. J Appl Meteor Climatol, 56(10): 2883-2901.
|
Zhang D L, Zhu L, Zhang X J, et al, 2015. Sensitivity of idealized hurricane intensity and structures under varying background flows and initial vortex intensities to different vertical resolutions in HWRF[J]. Mon Wea Rev, 143(3): 914-932.
|
Zhao Z K, Liu C X, Li Q, et al, 2015. Typhoon air-sea drag coefficient in coastal regions[J]. J Geophys Res, 120(2): 716-727.
|
 2020, Vol. 46
2020, Vol. 46