引言

短时强降水是一种生消迅速、局地性强、致灾程度高的灾害性天气，对其的预报、预警一直是气象业务工作中的重点和难点。短时强降水的短时临近预报方法主要包括实况外推、统计预报、数值模式等。基于雷达回波与卫星图像的实况外推在0~1 h的临近预报中相当有效，如交叉相关法和单体质心法等，通过提取风暴移动特征来实现路径预报，然而由于缺乏对强对流系统发生、发展和消亡的物理机制描述，随着时效增加，实况外推的预报能力迅速降低(Wilson et al, 2010; 郑永光等，2013)。统计预报方法基于历史资料获得统计关系或经验阈值，利用探空资料等对强对流天气的发生潜势进行预报，如配料法、指数法、消空法、套叠法等，然而受限于高空观测的时空分辨率，统计预报结果的时空分辨率较低且以定性为主(张小玲等，2018)。数值模式在动力与物理过程描述上虽仍存在一些不足，但其对强对流系统活动的刻画在原理上优于实况外推方法，在时空分辨率上优于统计预报方法(陈葆德等，2013)。利用基于数据同化技术，包含详细热动力和微物理过程的中小尺度数值模式，可提高对强对流天气发生、发展的预报能力(Wilson and Mueller, 1993；陈明轩等，2004)。

随着高性能计算的迅速发展，数值预报模式的分辨率逐渐提高，高分辨率数值模式本身存在的诸多"不完美"可以藉由合适的后处理技术得以"完善"。英国的NIMROD系统(Nowcasting and Initialisation for Modelling Using Regional Observation Data System)、美国的NIWOT系统、香港天文台的SWIRLS(Short-Range Warnings of Intense Rainstorm of Localized System)系统以及中国自主研发的GRAPES-SWIFT(Global-Regional Assimilation Prediction System: Severe Weather Integrated Forecast Tools)系统通过赋予外推与模式预报在不同时效上以不同权重来进行短时临近降水预报(王秀明等，2015)；上海中心气象台通过尺度分解，利用雷达外推和区域高分辨率数值模式预报，实现目标订正及权重融合，建立了0~6 h短时临近精细化客观预报定量降水融合产品(储海等，2017)。基于实况检验的统计预报融合也是业务预报常用的订正方法，用以对模式预报的系统性偏差进行订正，在短时临近时效内效果尤为显著。Qi et al(2014)基于ECMWF的热带气旋路径集合预报，通过评估集合成员在短时效内的预报误差，优选出误差较小的若干成员进行算术平均，其在短时临近时效内(12 h)的预报效果优于加权平均。此外，一些学者还提出了基于实况的模式降水预报订正技术。如Johnson and Wang(2012)利用邻域法和目标向检验对高分辨率模式降水概率预报进行订正，仅用邻域法的概率预测在午后对流高发时段预报技巧差，而目标向订正通常能提高技巧。Zhu et al(2002)、Zhu and Luo(2015)和代刊等(2018)则应用频率匹配方法，通过假设降水预报频率与观测频率分布一致，对定量降水预报进行订正，虽然在极端事件和干偏差消除方面具有局限性，但对降水强度误差控制方面具有明显的积极作用。吴启树等(2017)的评分最优化订正算法，在不改变雨带预报位置和形态的前提下，对各级降水预报进行订正，在业务应用中取得良好表现。

短时强降水事件不确定性大，概率预报而非确定性预报能够更好地面向不同用户提供决策基础(杜钧和邓国，2010)。陈朝平等(2010)和祁海霞等(2020)先后利用贝叶斯概率理论，采用历史观测资料对集合概率预报进行订正，提高了原始集合预报的技巧。唐文苑和郑永光(2019)利用滞后集合预报方法构建多个成员，利用最优评分得到逐小时降水订正预报，显著提高了模式对强降水位置、形态和量级的预报水平。黄威和牛若芸(2017)利用SVM多模式集成预报提高了中期暴雨预报准确率，其优势主要体现在对强降水中心分布的范围和强度的预报更接近实况。他们的结果都表明，基于单一模式集合预报或多模式集成预报，通过实况检验和频率订正，可以得到更为可靠的概率预报。Liguori and Rico-Ramirez(2012)评估了雷达与模式融合预报，随着降水强度和模式分辨率的增加，概率融合预报相对于确定性预报的优势更为明显，定量降水概率预报是预报业务发展的大趋势。本文分"两步走"，利用四个业务高分辨率区域模式降水预报构建集成预报，先应用分位数频率匹配法，对多模式小时降水预报进行订正；同时基于上游关键区域的实时检验评分结果，调整各模式动态权重，从而得到订正的逐小时降水概率预报，以探讨多模式动态集成技术在短时强降水概率预报中的应用前景。

1 数据与方法 1.1 数据

经过多年引进吸收与自主研发，国家气象中心和多个区域气象中心均建立了区域高分辨率数值预报业务系统。选取2018年4—8月每日08时起报的欧洲中期天气预报中心高分辨全球模式(ECMWF-IFS)的500、700和850 hPa风场作为背景流场(用于确认与动态权重相关的上游关键区，详见下文)，同期各时次起报的四个业务高分辨率区域模式作为多模式成员，即GRAPES-Meso、RMAPS、SMS-WARMS(以下简称WARMS)、GRAPES-MARS(以下简称MARS), 各模式性能详见表 1。

降水实况格点数据采用国家气象信息中心下发的智能网格实况融合降水分析数据(CMPA-FRT)，时间分辨率为1 h，空间分辨率为0.05°×0.05°，空间范围为0°~60°N、70°~145°E，采用空间模糊检验时，以0.2°(约20 km)半径为模糊窗区取实况最大值，计在0.1°×0.1°网格上；频率匹配时，则采用跳点取值取到0.1°×0.1°网格。王在文等(2016)指出，虽然降水评分与模式或实况水平分辨率有关，但对于中雨以上量级的降水，模式水平分辨率的改变对评分的影响趋势不明显。故预报数据采用线性插值方法统一插值到0.1°×0.1°网格上，研究范围为20°~40°N、100°~125°E。

1.2 订正方法

分位数频率匹配法是一种基于实况的模式预报订正方法，假设区域内模式预报降水相对大小具有参考意义，只在具体降水量上存在偏差；则仅将降水预报频率分布订正为观测频率，便可以消除模式预报降水各量级频率分布的系统性偏差(图 1a)。实际计算方法如下：以一段时间内模式预报逐小时降水分布(大小)的各百分位数与实况降水分布(大小)的对应百分位数进行匹配，模式预报降水与实况降水的各百分位数均采用降序排列，在上述对应的两组百分位数之间建立分段线性关系：

$ R = a{R_m} + b $

(1)

式中：R为订正结果，R_m为订正前模式输出结果, a、b分别表示斜率与截距，由模式预报与实况计算得到a、b，并逐日随滑动步长更新。在本文中，滑动步长选取起算时间过去20 d，在保证样本量的同时，也避免了不同季节降水性质差异以及数值模式版本变化引入的新误差，后续进行预报集成时采用经过匹配订正的预报结果。

根据业务实践，当雷暴自身的传播效应对雷暴整体移动影响不大时，雷暴移动大致受大气各层平均风场的引导，受此启发，由平均引导流确定上游关键区域。以ECMWF-IFS当日08时起报的未来0~30 h的850、700和500 hPa 3个特征层平均风矢，插值得到逐小时的平均风场，采用溯源方法反推各点3 h前的上游位置，考虑模式预报偏差、移动速度与引导气流的关系，以上游位置为中心，3 h移动路程为半边长确定的上游敏感区域的大小，该区域最大程度涵盖了待研究格点3 h前的上游区域信息(图 1b)。检验该敏感区内模式预报与实况降水，检验方法为TS(threat score)评分，检验阈值为5 mm·(3 h)^-1，以评分作为赋权依据。

确定初始预报时刻不同模式的权重

$ {Q_i} = \frac{{TS_i^2}}{{\mathop \sum \limits_i^n TS_i^2}} $

(2)

式中：在n个模式中，Q_i为第i个模式的初始权重系数，TS_i为第i个模式的TS评分，TS_i²类似于决定系数，这是对不同模式预报上游区域检验结果的奖惩，"好"模式的预报信息尽可能被保留，而"差"模式所占权重很低；至6 h以后上游信息的价值降低，恢复为等权重平均，中间时次权重由初始权重与最终权重线性插值得来。至此，每个待预报点都获得了基于上游检验的多个模式的权重系数集。

在降水预报集成概率的计算中，由于短时强降水时空尺度较小，为了减少模式由落区偏差和时间偏差造成的双重惩罚，利用时空邻域法对概率进行平滑。首先设定不同的阈值(V)，对时空邻域内模式预报降水超过阈值的格点进行计数，预报降水率(R)超过V(例如5 mm·h^-1)则该格点I记为1，其余则记为0，那么第i个模式待预报点超过设定阈值的概率为P_i。

$ I = \left\{ {\begin{array}{*{20}{l}} 1 & {R \ge V}\\ 0 & {R ＜ V} \end{array}} \right. $

(3)

$ {P_i} = \frac{1}{N}{\left({\sum\limits_{t = - 1}^1 {\sum\limits_{l = - 2}^2 {\sum\limits_{m = - 2}^2 {I_{l, m}^t} } } } \right)_i} $

(4)

式中：l为空间邻域纬向方向的格点，m为空间邻域经向方向的格点，t为时间邻域，N为时空邻域格点总数。

从而，由模式定量降水概率(P_i)与对应模式权重系数(Q_i)乘积之和确定动态权重调整后格点短时强降水的概率(P)：

$ P = \mathop \sum \limits_i ({Q_i}{P_i}) $

(5)

1.3 检验方法

对订正结果进行检验以验证该方法的预报效果，由于订正是基于高分辨率模式展开的，在某个格点上依然存在预报发生而实况未发生或预报未发生而实况发生的双重惩罚，故采取空间上的模糊检验(李佰平等，2016)。本文采用的模糊半径为0.2°，对每日08时起报的预报时效为6~30 h逐小时降水预报进行订正和检验，除TS评分、探测效率(probability of detection, POD)、空报率(false alarm ratio, FAR)等常规评分以外，还采用Bias比较预报与观测的频率偏差，ETS(equitable threat score)、HK(Hanssen and Kuipers discriminant)评分排除气候频率的干扰，对预报进行综合评估，采用BS(Brier score)评分和可靠性图解验证概率预报的准确度。

根据表 2中预报和观测的关系，可以得到如下各检验评分的具体计算公式：

$ TS = \frac{H}{{H + M + F}} $

(6)

$ POD = \frac{H}{{H + M}} $

(7)

$ FAR = \frac{F}{{H + F}} $

(8)

$ Bias{\rm{ }} = \frac{{H + F}}{{H + M}} $

(9)

$ ETS = \frac{{H - \frac{{(H + M)(H + F)}}{{H + M + F + C}}}}{{H + M + F - \frac{{(H + M)(H + F)}}{{H + M + F + C}}}} $

(10)

$ HK = \frac{H}{{H + M}} - \frac{F}{{F + C}} $

(11)

$ BS = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left({{p_i} - {o_i}} \right)}^2}} $

(12)

式中：p_i为预报概率，o_i为观测概率(事件发生记1，未发生记0)，N为格点总数，i为格点序号。

2 结果与分析

根据第一节介绍的降水概率预报集成思路，设计了动态权重多模式短时强降水概率预报流程：利用起算时间过去20 d历史数据进行分位数频率匹配订正，输出处理完毕的模式预报数据；基于上游关键区的检验结果，采用动态权重订正得到定量降水概率预报。利用2018年4—8月研究区域逐小时降水预报与实况进行训练和检验，检验分位数频率匹配订正和动态权重集成的效果。

2.1 分位数频率匹配订正效果分析

由于初始场误差的存在以及物理框架和参数化方案的不完善，模式输出结果存在随机性和系统性误差，需要通过一些方法进行订正，频率订正技术是其中一种被广泛使用的技术(李俊等，2015)。利用观测降水的频率分布校正预报降水，既改进降水预报的落区，也能改进降水预报的量级。利用第一节介绍的分位数频率匹配法对2018年7月各模式预报结果进行订正，结果如下。图 2a~2e显示了实况降水分析数据与模式预报各量级降水率的频率分布。可以看出，实况降水率大致呈现γ分布，弱降水事件的频率要比强降水事件大得多，随着降水率的增大，事件发生频率迅速降低；模式预报降水率的频率分布虽也呈γ分布，但各模式之间以及模式与实况分析之间频率分布并不一致，如MARS与RMAPS的降水频率直方图显得"瘦长"，表现出低估降水的倾向，二者频率峰值较实况更高，且频率随降水率增大更快地下降；与之相比，GRAPES-Meso和WARMS在小量级降水预报的频率偏低，随降水率增大频率降低较缓，其中WARMS对10 mm·h^-1以上降水预报频率较实况偏高，存在整体上对降水的高估。

图 2f~2i显示了模式订正前后降水率的对应关系，斜率接近1则表明该模式预报降水率的频率分布与实况接近，订正前后区别不大，斜率大(小)于1则表明模式预报降水偏大(小)。研究发现，GRAPES-Meso的斜率接近1，表明其预报降水与实况降水的频率分布较为接近，但对中等以上降水(3~30 mm·h^-1)的预报存在低估；RMAPS斜率更小，表明其低估程度更大，10 mm·h^-1预报降水对应的实况达到20 mm·h^-1, 在日常预报实践中可将模式预报量级适当提高以减少漏报；WARMS斜率接近1.5，表明该模式对各量级降水预报均存在高估，即系统性的湿偏差，偏高幅度约为50%，在业务应用中要适度调低WARMS的预报量级以减少假警(空报)；MARS预报降水较实况呈现明显低估，存在明显的干偏差，10 mm·h^-1的预报降水与实况30 mm·h^-1相匹配，表明其对大量级降水的预报不足，参考价值低。一般地，全球模式在小量级降水上存在湿偏差，而在大量级降水中存在干偏差。

为了预报灾害性天气，高分辨率模式通常会选用适应本地天气背景的参数化方案，也就不可避免地带来新的系统性偏差，在应用时必须考虑最大程度消除这些系统性偏差，频率匹配就是消除系统性偏差的一种直接手段。

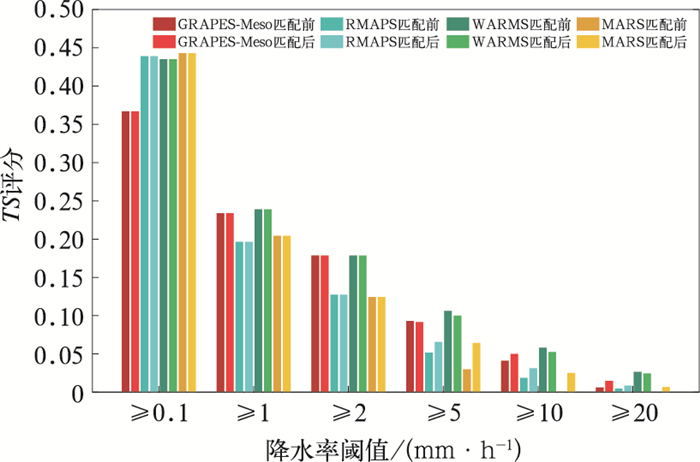
频率匹配法利用集合成员或实况降水，针对模式降水频率分布存在的系统性偏差进行订正，常用的频率匹配方法一般在各雨量量级上对预报进行订正，本文采用的分位数频率匹配法在各百分位将模式预报降水率的频率分布订正至实况频率，较一般按量级订正结果更加连续，也为之后的进一步处理提供便利。对匹配订正前后各家模式预报进行检验(图 3)，在进行匹配订正之前，若以0.1 mm·h^-1作为晴雨预报分界的阈值，则RMAPS、WARMS、MARS的TS评分均达到0.44左右，GRAPES-Meso稍逊，也有0.37，高分辨率数值模式对晴雨的预报能力整体相差不大；WARMS在大量级降水预报效果更好，其中≥5 mm·h^-1和≥10 mm·h^-1的TS分别为0.11和0.058，比第二名GRAPES-Meso分别高出8%和30%，对≥20 mm·h^-1(业务规定的短时强降水标准)降水预报也具有一定的预报能力，与此同时，GRAPES-Meso、RMAPS和MARS等三家模式对≥20 mm·h^-1降水的预报能力则略显不足。经过匹配订正后，多数模式的TS评分有所改善或持平，具体表现为：5 mm·h^-1以下降水的TS评分在订正前后变化不大，表明分位数频率匹配法对中等降水(1~5 mm·h^-1)预报准确率的提高并不明显；而在强降水(≥5 mm·h^-1)的订正上则有明显正效果，如MARS模式，由于该模式的降水预报具有明显的干偏差，其对10 mm·h^-1以上的降水几乎无预报能力，通过分位数频率匹配，其对10 mm·h^-1以上降水的预报能力显著提高，表明该方法对强降水具有明显订正作用，除WARMS以外，分位数频率匹配对其他三家模式均表现为正效果，降水越强改善效果越明显，将"降水低估"模式的预报降水量向上订正，能够有效提高其命中率，进而提高降水的TS评分；匹配前后WARMS的TS评分略有下降，表明匹配在消除假警的同时也使漏报率提高，但整体上分位数频率匹配对高分辨率模式降水订正具有正效果。

2.2 动态权重定量降水概率预报

高分辨率模式能够模拟与风暴发展、维持相关的中尺度特征，但降水预报落区往往与实际存在较大偏差(Ebert，2008)。怎样在保证信息有效性的同时保存高分辨率模式中对流发生发展的描述？将实况信息与模式信息相融合，利用上游关键区的检验结果来进行多模式集成，赋予"好"的模式成员以更大的权重；采用概率预报而非平均，突出小概率事件，可望达到更合理的集成结果。利用第一节介绍的敏感区域确定方法，对上游降水落区预报与实况分析匹配程度较高的成员，赋予较大的权重，反之则赋予较小的权重，起到锐化和消空的效果。该方法能做到及时滚动，不断把新的实况信息与模式预报信息进行融合，目标针对性强、计算量小。计算动态权重定量降水概率预报，并对未经订正的原始概率(未经匹配和动态权重调整等权重集成)、匹配后计算的概率预报(匹配订正后进行等权重集成)以及匹配与动态权重相结合得到的概率预报进行检验和比较。表 3的结果表明，与原始概率(未经频率匹配采用等权集成)相比，频率匹配方法能够提高预报的POD，POD从36.65%提高到37.64%，但由于其预报事件发生的频数增加，FAR不降反升，Bias达到255.67%，表示预报频率显著高于观测频率，预报发生较多空报的情况。而采用频率匹配和动态权重相结合的方法，虽然损失了一些POD，但是经过上游检验消空作用，FAR得到有效控制，Bias降低至166%，空报偏多的情况得到明显缓解。TS评分由11.77%提高至12.88%，相当于获得9.4%的正技巧，BS评分从7.67%降低至5.74%，与实况的偏差明显降低，显示出动态权重匹配方法较原始概率具有更好的预报效果。

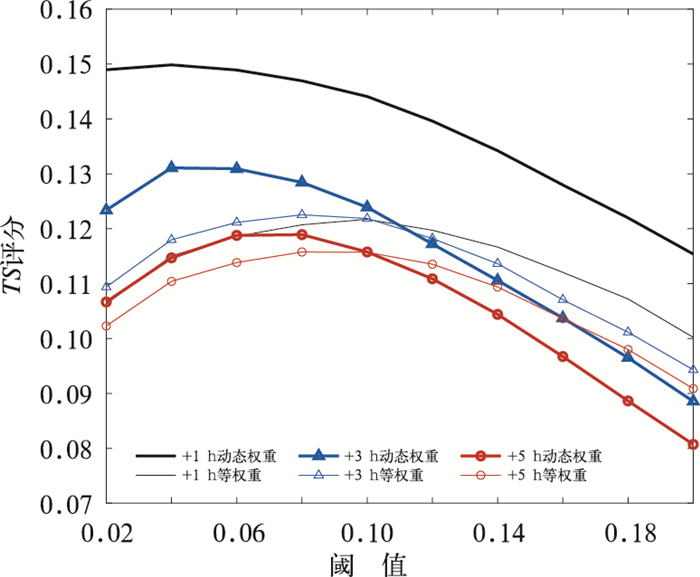
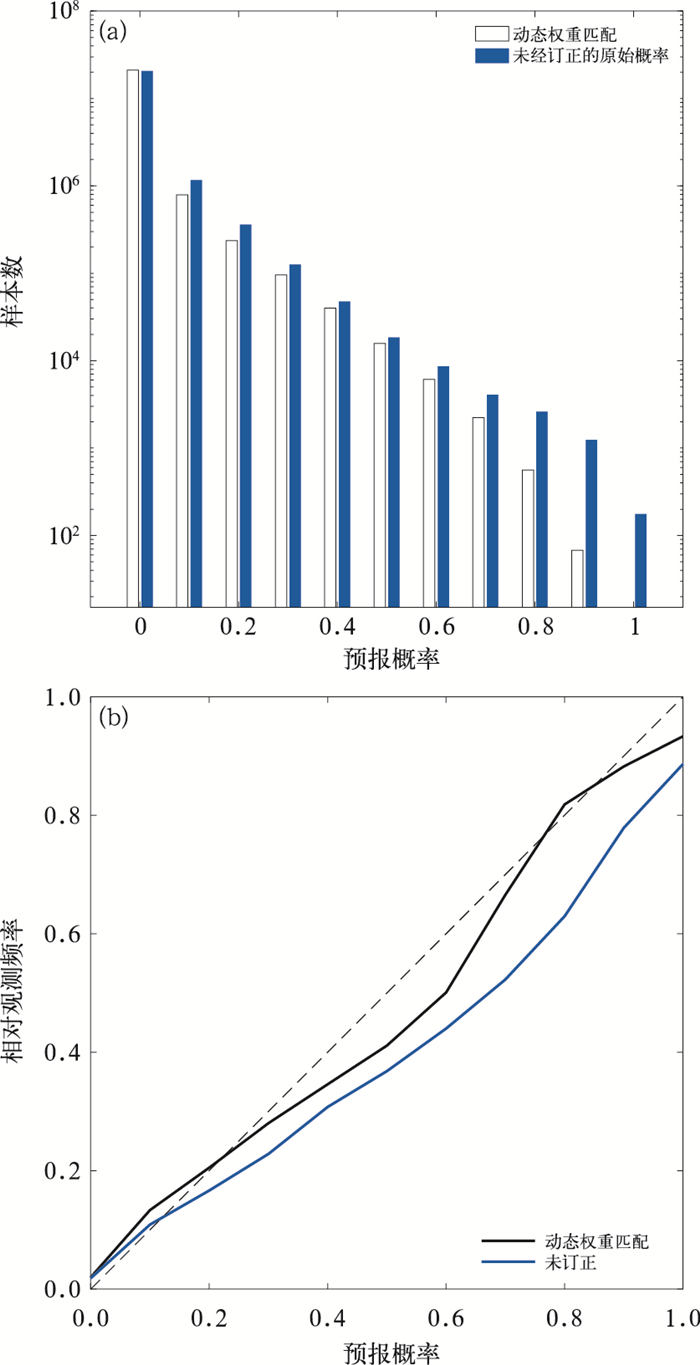
集成概率计算每6 h进行一次，各模式在定量降水概率预报中的权重会在6 h后变为等权，上游信息随预报时效是逐渐衰减的，通过比较不同预报时效的预报，可以研究上游敏感区检验在订正中的作用。图 4的结果表明，1 h预报时效评分总是高于3 h和5 h预报时效，预报效果随着预报时效的增加而降低。这是因为在临近时效内，上游实况信息在动态权重分配上占有很大的比重，上游信息的加入有效改善了降水预报，随着时效的增加，上游信息对权重的影响逐渐下降，相当于等权平均，预报的效果也逐渐变差。比较动态权重(粗线)与等权重(细线)评分变化可以发现，在1 h和3 h时效上，动态权重较等权集成好，而在5 h时效上，订正前后的准确率变化不大，甚至动态权重TS评分还略有降低；这都表明在较短时效内，上游敏感区的实况信息在订正中起到正效果，随着时效变长，实况信息的作用逐渐减弱，模式预报信息作用加大。利用可靠性图解来检验订正的效果(图 5)，一个理想的概率预报结果，落在某预报概率区间上的相对观测频率应该等于预报概率，亦即落在图 5b中灰色虚线所示对角线上，高于对角线表示预报概率偏低，低于对角线则表示过度预报，图 5a则显示了概率预报在各个区间上的样本数，样本数分布应为期望与气候频率一致的偏态分布; 由于5 mm·h^-1以上降水频率仅为2.8%，为小概率事件；样本数主要集中在0~5%的预报概率区间内，随着预报概率的增大，样本个数显著下降。从图解曲线上可知，无论原始预报还是订正后的预报，仅在0.2以下预报概率阈值区间内高于对角线，而在大值区间内位于对角线以下，表明总体上都存在对事件的预报过度，原始概率尤甚；同时两线的斜率均接近于1，表明都具有一定的预报意义，其中动态权重概率预报的可靠性曲线更接近对角线，表示其可靠性趋于理想，反映了订正的正效果。

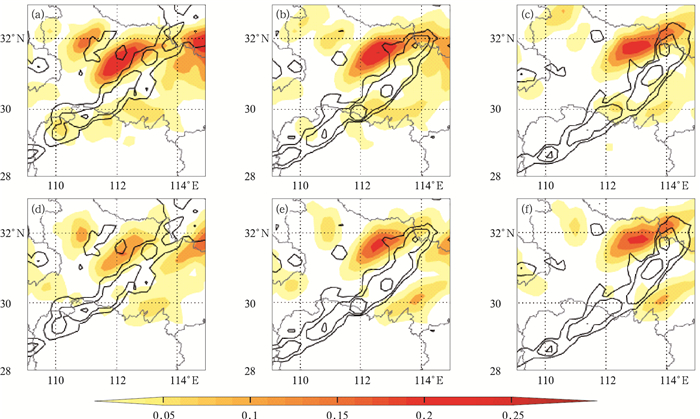
为进一步比较动态权重集成与等权集成对短时强降水事件的预报效果，选取2018年5月6日发生在湖北中东部到湖南北部的一次降水天气过程进行具体分析。5月6日18—20时(北京时)一次飑线过程在湖南西北部至湖北中部造成较大范围的短时强降水天气，中心最大小时降水量达到20 mm以上(图 6)，等权集成预报(图 6d~6f)显示湖北中东部大部为强降水概率大值区，湖南北部强降水概率几乎为0。表明多数模式能够报出湖北中部的强降水过程，但预报落区较实况明显偏西，湖南西北部的强降水明显漏报(图略)，个别模式即使报出了该强降水事件，但在等权重处理下，对于其量级估计不足。利用分位数频率匹配法使GRAPES-Meso、RMAPS、WARMS对该区域降水量级预报向上订正，通过6日14—17时已经发生在湖北中部的强降水实况，挑选出WARMS、GRAPES-Meso等与上游实况相接近的"好"模式赋予较高的权重，故采用实况与模式融合的动态权重概率预报不仅预报出湖北中部的强降水，还预报出湖南北部出现短时强降水的可能性(图 6a~6c)，但由于模式对于系统传播机制刻画的缺陷，其预报主体位置依然偏西，对于模式一致预报的湖北中部强降水天气过程，未能很好地消空，说明该方法对模式一致性误差订正能力还较为有限。频率匹配和动态权重集成相结合的方法对疑难短时强降水天气过程具有一定把握能力，预报员可以根据上述预报信息对短时临近预报进行适当调整。

3 结论与讨论

利用2018年4—8月格点降水分析资料和四个高分辨率区域模式降水预报资料，应用分位数频率匹配法，对模式1 h降水预报分别订正；并基于上游关键区域的检验评分结果，设计动态权重多模式短时临近定量降水概率预报方法，研究了多模式集成技术在短时强降水概率预报中的应用。得到以下结论：

(1) 不同模式预报的降水率频率分布与实况之间存在差别，GRAPES-Meso与RMAPS预报在中等到强降水率区间上略有低估；MARS预报降水较实况明显低估，WARMS对各量级降水预报均存在高估，在业务应用上可作适当调整。

(2) 利用分位数频率匹配法订正模式预报降水，对降水落区和量级预报均有不同程度的订正效果，除WARMS以外，"频率匹配"对其他三家模式均表现为正效果，降水越强改善效果越明显。

(3) 基于上游敏感区域降水实况与模式预报的匹配程度，分配模式动态权重的方法，能够有效提高定量降水概率预报的预报准确性。改进效果与预报时效有关，时效越短，上游实况信息在提高预报能力上的作用越大。各类评分显示基于实况检验的动态权重多模式降水概率预报产品较等权集成具有更高的预报准确率，短时强降水个例也显示，动态权重多模式短时强降水概率预报能较好地预报短时强降水事件的可能。

外推、统计与模式的融合是提高降水预报准确率的有效方式。需要说明的是，由于资料有限，本文仅对2018年暖季若干月的降水预报进行订正和检验，其结果具有一定局限性；检验方法也较为单一，未来通过长时间的训练和检验以及多种检验方法(目标检验等)的应用可以得到更好的评估。除了降水落区和量级，降水中心雨量极值也是业务预报中的关注重点，未来考虑其他方法将降水中心进一步突出。此外，上游敏感区的设定也是根据预报员经验选取的，仅考虑环境风场引导或在此基础上的角度偏转，其位置、大小的合理性还未经过严格的考证，但将系统的发展与引导加以分解，高分辨率模式和全球模式分别提供对流生消发展信息和对流引导信息不失为一种将复杂问题简单化的方法。总之，高分辨率区域模式订正方法的研究方兴未艾，高分辨率模式在业务预报中的实际应用价值还需要被进一步挖掘(Mass et al，2002；漆梁波，2015)，本文的订正和检验方法不够丰富，有待在预报实践中进一步总结和提升。