2. 广州市气象台,广州 511430;
3. 广东省气象台,广州 510060;
4. 中山大学广东省气候变化与自然灾害研究重点实验室,珠海 519082
2. Guangzhou Meteorological Observatory, Guangzhou 511430;
3. Guangdong Meteorological Observatory, Guangzhou 510060;
4. Guangdong Key Laboratory for Climate Change and Natural Disaster Studies, Sun Yat-Sen University, Zhuhai 519082
近30年来,随着中国城市化进程加快,极端强降水有向超大城市群集中并增强的趋势(Liang and Ding, 2017;唐永兰等,2019),受强热岛效应影响,珠三角城市群短时突发的极端小时降水事件显著增加(Wu et al,2019)。例如,2017年5月7日广州出现突发性极端强降水过程,小时降水量达到184.4 mm,日降水量为542.7 mm,均打破了60年纪录(伍志方等,2018;Zhang et al, 2019a)。2020年5月22日广州市的小时降水量超过200 mm,再次突破历史极值,此次过程造成了4人死亡,公交、地铁、动车停运,经济损失非常严重。城市内涝问题已经成为威胁超大城市人民生命财产安全的主要自然灾害之一。
目前数值天气预报仍存在较大的不确定性(穆穆等,2011;Du and Chen, 2018),尤其在弱天气强迫形势下,局地性、突发性的短时强降水的预报水平仍难以满足社会及公众的期许(伍志方等,2018; 王璐和沈学顺,2019)。因此,加强对强对流天气系统的跟踪和降水的定量观测以提高短时临近预测预警能力尤为重要,天气雷达在其中发挥了最重要的作用。目前中国业务上应用于降水探测的新一代S波段多普勒天气雷达采用VCP21体扫模式,该模式共有9个仰角,耗时约6 min(朱丹等,2018)。然而中小尺度灾害性强对流天气的监测预警对雷达的硬件指标有了更高的需求,S波段业务天气雷达难以精确探测中小尺度灾害性天气系统的内部涡旋动力结构,时效性难以满足生命史只有数十分钟的龙卷、中气旋等强天气的要求(Zhang et al,2019b)。同时,S波段雷达探测范围较广,间距较远,对近地面1 km的观测能力也明显不足,低层存在雷达探测盲区。
利用电子扫描的相控阵雷达(phase array radar,PAR)由于具有快速转换波束指向的能力,被美国国家雷达技术委员会推荐作为美国下一代雷达发展的方向(Weber et al,2007)。大量的观测和数值模拟试验表明,PAR观测显著增加了强天气的预警提前量(Bluestein et al,2010;Newman and Heinselman, 2012;French et al,2014;Kuster et al,2015)、提高了模式预报准确率(Yussouf and Stensrud, 2010)和减小定量降水估测的累积误差(Anagnostou and Krajewski, 1999),在城市内涝和流域洪峰预测服务中发挥重要作用。
为了完善和发展天气雷达布局,填充新一代多普勒天气雷达网的观测盲区,中国气象局部署在粤港澳大湾区开展X波段双偏振相控阵天气雷达(X-band dual-polarization phased array radar, XPAR)协同观测业务试验,对云、雨滴、冰雹等水成物的微物理过程开展更加精细化的识别和跟踪,并增强低空尤其是行星边界层观测的能力(McLaughlin et al,2009)。目前粤港澳大湾区已有15部XPAR投入了试运行,由于其时空分辨率更高的优势,XPAR在强天气中能快速把握细致的对流结构及生消发展趋势(程元慧等,2020; 傅佩玲等,2020)。
由于华南区域强对流天气频发,X波段雷达的回波衰减率是C波段或S波段雷达的7~10倍(Park et al,2005a),雨滴衰减问题对XPAR的业务应用造成较大程度的干扰,严重影响其推广应用。早期的Hitschfeld-Bordan算法不适用于X波段雷达(Hitschfeld and Bordan, 1954),而Hildebrand(1978)的逐步订正法所适用的反射率因子最大不能超过60 dBz,具有地域局限性。随着双偏振雷达的发展,借助偏振量帮助衰减订正取得了更好的效果(Aydin et al,1989;Meneghini et al,1989;Gorgucci et al,1996;Carey et al,2000)。由于差分传播相移率(KDP)不会受到衰减及雷达标定的影响,并与衰减率(AH)和差分衰减率(ADP)存在线性关系(α=AH/KDP,β=ADP/KDP),为基于KDP方法来订正反射率因子和差分反射率因子提供了思路,并得到更稳定的订正效果(Bringi et al,1990)。但是由于大雨滴的α和β值是小到中雨滴的2~4倍,如果使用固定系数,会导致较大的订正误差,Carey et al(2000)、Ryzhkov(2007)、Gu et al(2011)和Vulpiani et al(2008)利用偏振量区分雨滴大小,发展了变系数订正法,订正效果有所改善。
为了克服迭代算法的不稳定性,借鉴TRMM(tropical rainfall measurement mission)星载测雨雷达中的降水廓线算法,Testud et al(2000)提出了ZPHI算法,将差分传播相移(ϕDP)作为衰减订正的外部约束,适用于S、C和X波段雷达。Bringi et al(2001)把系数的变化考虑进去,提出了改良版的ZPHI法,称为自适应算法。Park et al(2005b)验证了自适应算法在X波段雷达上应用的优越性。毕永恒等(2012)结合中层大气与X波段雷达的特点,改进了自适应约束算法。Gou et al(2019)补充了三个约束条件,以适应实际业务运算速度的需求。ZPHI算法还可以分段进行,但是全路径的ZPHI法可减少ϕDP数据质量问题引起的订正误差,效果最佳(王晗等,2018)。本文利用双偏振参量的自适应约束性质,对数据进行有效的质量控制,联合XPAR雷达试验网和CINRAD双偏振天气雷达网观测,对比分析衰减订正前后的数据,试图改进衰减订正效果,增强XPAR的业务适用性。
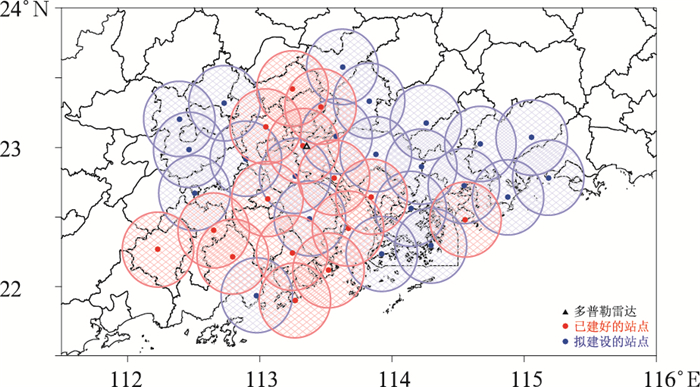
1 数据 1.1 相控阵雷达资料粤港澳大湾区相控阵天气雷达试验网由37部XPAR组成,覆盖珠三角地区9个市,其中15部XPAR已投入试运行(图 1),其方位分辨率为0.9°,距离库长为30 m。XPAR采用双偏振模式,垂直方向使用相控阵电子扫描,其扫描方式为:先在固定方位角进行17层仰角无间隙垂直扫描,然后切换方位角,再次垂直扫描,最低仰角为0.9°,波束垂直宽度为1.8°。在该扫描方式下,雷达转速不需太快,机械转动以及形成波束指标的稳定性大大提高,既减少了仰角切换所带来的数据污染,又获得无时间延时的距离高度显示(RHI)数据(程元慧等,2020)。
|
图 1 粤港澳大湾区X波段双偏振相控阵雷达(XPAR)布网规划图 (红色点和圈为已建好的站点及覆盖范围,蓝色点和圈为拟建设站点及覆盖范围,黑色三角形为广州S波段多普勒雷达的位置) Fig. 1 The X-band dual-polarization phased array radar network distribution in the Guangdong-Hong Kong-Macao Greater Bay Area (The red dots and circles represent the established sites and their coverage, while the blue dots and circles denote the planned sites and its coverage, black triangle is the position of S-band Doppler radar in Guangzhou |
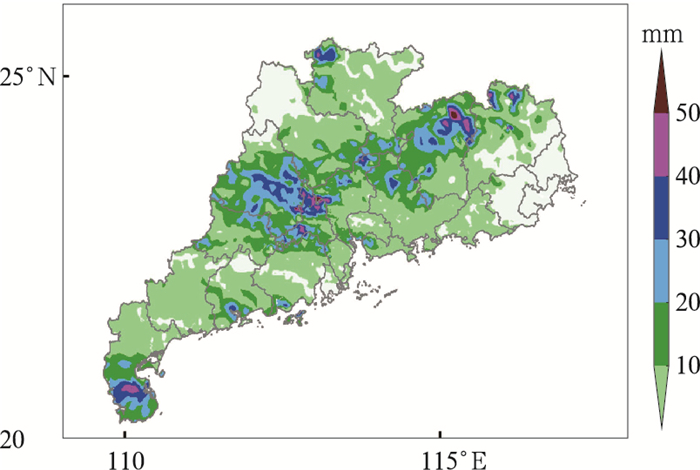
本文以2019年9月2日一次局地强降水为例进行研究。当天,广东省位于北高南低的环流背景下,2日05时热带低压的中心位于海南省万宁市偏东方约85 km的海面上,其后向西偏南方向移动,强度变化不大,受到热带低压影响,午后雷雨云团自东南向西北方向移动,给珠三角地区带来了明显的降水。最大6 h降水量(14—20时)出现在广州市西部和佛山市东北部地区(图 2),位于两市三部相控阵雷达观测范围内。
|
图 2 2019年9月2日14—20时广东省6 h累积降水量 Fig. 2 Accumulated precipitation in Guangdong Province from 14:00 BT to 20:00 BT 2 September 2019 |
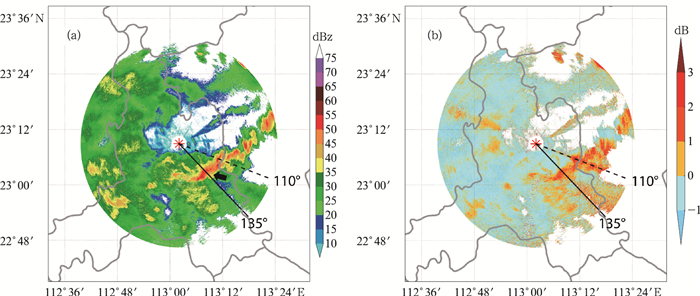
以2019年9月2日15:57佛山雷达观测的原始反射率因子和差分反射率因子分布为例,雷达东南方向降水回波最大强度超过50 dBz(图 3a),差分反射率因子达到2 dB及以上(图 3b)。135°方位角上,从雷达中心沿着径向向外,反射率因子出现了锐降的现象,强回波的远侧出现了开口朝向外的V型结构(箭头所指之处),110°方位角上强回波远侧出现了反射率因子梯度较大的现象,可见雷达信号穿过强降水回波中心后出现了信号衰减。
|
图 3 2019年9月2日15:57佛山雷达1.8°仰角未经衰减订正的反射率因子(a)和差分反射率因子(b)分布 (黑色直线指示135°,虚线指示110°方位角;下同) Fig. 3 Reflectivity factor (a) and differential reflectivity (b) at 1.8° elevation without attenuation correction observed by the Foshan XPAR at 15:57 BT 2 September 2019 (Black solid and dotted lines indicate 135° and 110° azimuths respectively, the same below) |
就差分反射率因子分布而言(图 3b),在靠近雷达的弱降水区域,差分反射率因子均为负值。沿着径向向外,差分反射率因子正负值相间的噪点现象加剧。110°方位角上的差分反射率因子普遍较大,约为1~3 dB,该区域以水滴粒子分布为主。135°方位角强降水中心的差分反射率因子达到1 dB及以上,经过强回波中心有所减小,在反射率因子V型结构所对应的区域,差分反射率因子的值大致为0~1 dB。继续沿着径向向外,间或有些负值分布,并且噪声比周边显著,反映了差分反射率因子探测存在小幅衰减及不稳定问题。但是由于差分反射率因子的值较小,从平面分布上,其衰减的绝对值与反射率因子相比显著偏小。
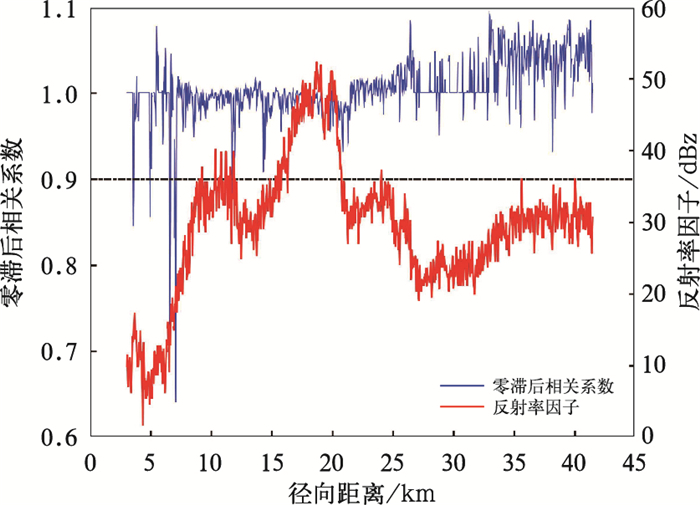
沿着图 3中135°径向方向(黑色直线)绘出反射率因子及相关系数(CC)的原始基数据径向分布(图 4)。CC普遍高于0.9,均有降水。距离雷达8 km以内,CC的振荡较明显,主要由弱降水与非气象回波的混合相态引起的。20 km附近,CC维持在0.9~1.0。沿着径向向外至19~20 km附近,反射率因子振荡上升达到极大值50 dBz,接着断崖式下降至32 dBz,这种变化是由于受到电磁波信号经过强降水云团后衰减的影响。
|
图 4 2019年9月2日15:57佛山雷达1.8°仰角上135°方位角的反射率因子和零滞后相关系数的径向分布 Fig. 4 Radial distribution of reflectivity factor and correlation coefficient at 135° azimuth at 1.8° elevation of the Foshan Radar at 15:57 BT 2 September 2019 |
天气雷达受到硬件的影响,首先要对雷达数据进行噪声过滤,去除原始反射率因子、差分反射率因子和相关系数中孤立的点或者线造成的数据污染,根据式(1)进行处理(黄朝盈,2019):
| $ P_{I}=N / N_{\text {TOTAL }} $ | (1) |
式中:I为基数据中给定的距离库,N是以I为中心的5×5的窗口中存在有效数值的总库数;NTOTAL为窗口包含的总库数,等于25,PI为有效雷达库个数所占的百分比,当PI < 55%时,像素点I就被当作非气象回波剔除。
2.1.2 确定降水回波初始差分传播相移ϕDP(0)差分传播相移(ϕDP)容易受到雷达系统噪声、地物回波、气象目标特性的影响,出现高低起伏的附加相位移。因此,在应用ϕDP之前应先找到初始相位ϕDP(0)(肖艳姣等,2012):从径向第1个距离库开始,沿着径向向外滑动,计算连续30个距离库的ϕDP的标准差σ,当σ < 5且CC>0.7的连续距离库达到10个,则为一段连续的降水回波起始点,用这10个距离库的ϕDP均值表示初始相位的大小ϕDP(0),并标记每个初始相位所在的径向位置。
2.1.3 ϕDP退折叠在双发双收的工作模式下,ϕDP取值范围是0~360°,当ϕDP高于360°时,会发生与多普勒速度类似的相位折叠问题,X波段雷达尤其容易超过不模糊范围(肖艳姣等,2012),因此需要对ϕDP进行去折叠处理。需注意的是,在探测到非气象回波的方向上,ϕDP的脉动较大,但不属于折叠现象,因此在开展去折叠之前要限制CC>0.9以消除非降水回波的影响。
此外,斜率以及相邻距离库的标准差均能表现ϕDP脉动情况,较大的斜率和标准差可能是由于地物杂波引起的。因此基于斜率和标准差的概率分布情况,限制取值范围,有助于抑制杂波的影响。沿起始距离库径向向外滑动10个距离库计算标准差(σ),取5个距离库做线性拟合计算斜率(a),根据概率分布可确定其取值范围为[-20, 20],σ为[0, 6],只有符合以上阈值条件的数据才应用于分析及退折叠运算。具体步骤如下:(1)取初始差分相位ϕDP(0)作为退折叠的初始参考值R;(2)沿径向逐个距离库向外滑动,利用a更新参考值R=R+aΔr,其中Δr为雷达分辨率,取Δr=30 m;(3)比较R和当前距离库的ϕDP,当R-ϕDP>80°时,则认为ϕDP发生了折叠,需进行去折叠处理:ϕDP=ϕDP+360°;(4)将去折叠后的ϕDP值调整到[0, 180],则退折叠过程结束(Wang and Chandrasekar, 2009;肖艳姣等,2012)。
2.1.4 小波分析方法滤波ϕDP的径向廓线常常存在起伏现象,在应用之前需完成预处理工作,使ϕDP数据更加平滑和连续,并保留有效的气象信息。常用的预处理方法包括滑动平均、中值滤波、卡尔曼滤波等(何宇翔等,2009;曹俊武等,2011;魏庆等,2016)。但是当电磁波通过的是雷暴群时,云体边缘的ϕDP会产生异常或者不连续值,大振幅杂波经滤波控制变成小振幅波动,但未能完全被滤除。胡志群等(2014)和魏庆等(2016)使用了小波分析方法,能够有效剔除噪声,提高ϕDP的连续性、平滑度,且保存了气象回波的有效信息。
本研究采用小波分析方法对数据加以处理,共包括三步。(1)信号分解, 利用小波函数对ϕDP数据进行五层分解,每层均可以分解成为低频和高频分量,分别用CA1,CA2,CA3,CA4,CA5和CD1,CD2,CD3,CD4,CD5来表示,数字越小,代表的频率相对越高。(2)信号去噪,主要针对高频分量去噪处理。CD1频率最高,将其系数设为0可将其信号删除;接着对CD2,CD3和CD4做中值滤波,降低噪音;CD5保留原信号。(3)信号重构,增加系数处理的第一至第五层高频信号和小波分解第五层低频信号重构成新的ϕDP数列。
2.2 自适应约束算法自适应约束算法是在Testud et al (2000)提出的ZPHI法上改良而得。以下第一、二、四步骤为ZPHI法的核心内容,第三步为Bringi et al(2001)提出的改良步骤,执行了ϕDP-ZDR联合约束条件,综合两者可形成对反射率因子和差分反射率因子进行衰减订正的算法(Bringi and Chandrasekar, 2010)。
第一步:非均匀路径上,反射率(Zh)和衰减率(AH)之间存在幂指数关系,即:AH(r)=a[Zh(r)]b,以r0作为固定参考距离,r为距离变量,经过公式转换,径向上AH(r)可用固定参考距离上AH(r0)、反射率测量值Zh(r0)及Zh(r)表示,如式(2)所示:
| $ \left\{\begin{array}{l} A_{\mathrm{H}}(r)=A_{\mathrm{H}}\left(r_{0}\right)\left\{\frac{\left[Z_{\mathrm{h}}(r)\right]^{b}}{\left[Z_{\mathrm{h}}\left(r_{0}\right)\right]^{b}-A_{\mathrm{H}}\left(r_{0}\right) I\left(r_{0}, r\right)}\right\} \\ I\left(r_{0}, r\right)=0.46 b \int_{r_{0}}^{r}\left[Z_{\mathrm{h}}(x)\right]^{b} \mathrm{~d} x \end{array}\right. $ | (2) |
第二步:假设AH与KDP的线性关系与已知的α参数有关,即:AH(r)=αKDP(r)。另外,定义离开降雨单体以外的距离为rm,而ϕDP(rm)是差分相位最后的稳定值,以这个值作为约束条件,可得到:
| $ A_{\mathrm{H}}(r)=\frac{\left[Z_{\mathrm{h}}\left(r_{0}\right)\right]^{b}\left[10^{0.1 b \alpha \Delta\phi_{\mathrm{DP}}\left(r_{0} \cdot r_{\mathrm{m}}\right)}-1\right]}{I\left(r_{0}, r_{\mathrm{m}}\right)+\left[10^{0.1 b_{\alpha} \Delta \phi_{\mathrm{DP}}\left(r_{0} \cdot r_{\mathrm{m}}\right)}-1\right] I\left(r, r_{\mathrm{m}}\right)} $ | (3) |
第三步:对于给定的频率,b为0.8。α与温度及假设的雨滴轴比和直径之间的关系有关,但ZPHI法的缺陷在于将α设为常数,Bringi et al(2001)把系数α的变化考虑进去,通过训练得到最佳系数α,提出自适应算法。本文采用自适应算法对经过预处理的XPAR数据进行本地化试验,寻找最优的α值。
依据AH(r)=αKDP(r),径向距离[r0,rm]内重构的ϕDPrconstructed(r,α)有
| $ \phi_{\mathrm{DP}}^{\text {reconstructed }}(r, \alpha)=2 \int_{r_{0}}^{r_{\mathrm{m}}} \frac{A_{\mathrm{H}}(x, \alpha)}{\alpha} \mathrm{d} x $ | (4) |
取α值的范围是[0.025, 0.575],以0.025为间隔反复计算ϕDPreconstructed(r,α),并计算ϕDPreconstructed(r,α)与测量值ϕDP之间的绝对差值eϕ,当eϕ值最小,则该α为最优值αopt:
| $ e_{\dot{\phi}}=\int_{r_{0}}^{r_{\mathrm{m}}}\left|\phi_{\mathrm{DP}}^{\text {reconstructed }}(x, \alpha)-\phi_{\mathrm{DP}}(x)\right| \mathrm{d} x $ | (5) |
第四步:利用前三个步骤,对每个方位角都可以求得一个最优αopt,如果每个方位角αopt均不同,对反射率校正之后,其结果在方位角之间会出现较大的数据不连续现象。固然可采用平滑或者滤波的方式对校正后的数据进行处理,但会平滑高分辨率雷达的细节信息,因此取所有方位角的平均值作为该体扫订正所需的αoptmean,求得r0和rm之间的任意位置上的比衰减AH(r,αoptmean)之后,可以用式(6)对反射率因子Z′H进行校正:
| $ Z_{\mathrm{H}}^{\prime}(r)=10 \log _{10}\left[Z_{\mathrm{h}}(r)\right]+2 \int_{r_{0}}^{r} A_{\mathrm{H}}\left(x, \alpha_{\mathrm{opt}}^{\mathrm{mean}}\right) \mathrm{d} x $ | (6) |
第五步:Park et al(2005a;2005b)根据散射仿真实验得到了反射率因子(ZH)和差分反射率因子(ZDR)在三种雨滴分布情况下的平均关系:
| $ Z_{\mathrm{DR}}= \begin{cases}0 & Z_{\mathrm{H}} \leqslant 10 \mathrm{dBz} \\ 0.051 Z_{\mathrm{H}}-0.486 & 10<Z_{\mathrm{H}} \leqslant 55 \mathrm{dBz} \\ 2.3 & Z_{\mathrm{H}}>55 \mathrm{dBz}\end{cases} $ | (7) |
式中:ZH的单位是dBz,而ZDR的单位是dB。
与反射率因子的订正相似,差分反射率因子的订正也需差分衰减率ADP(r)参与。在自适应约束算法中,
| $ Z_{\mathrm{DR}}^{\prime}(r)=Z_{\mathrm{DR}}(r)+2 \frac{\gamma}{\alpha_{\mathrm{ogg}}^{\mathrm{mean}}} \int_{r_{\mathrm{o}}}^{r} A_{\mathrm{H}}(x) \mathrm{d} x $ | (8) |
电磁波经过一段距离,差分反射率因子测量值和根据式(7)求得理论值的变化幅度分别为ΔZDR1和ΔZDR2,两者理应相同。但是由于存在衰减作用,两者存在差值为ADP1。自适应约束算法通过循环不同的γ,根据式(8)订正差分反射率因子,当
由于降水单体相对周边雷达方位和距离均有差异,受到雨滴衰减影响的程度也有区别。一个合理的方案针对不同雷达订正后的结果应该具有高度一致性。因此本文针对相邻雷达的共同覆盖面积,从一致性角度去检验衰减订正方法的准确性,称其为X-X检验。另外,除非在湿雹区,S波段雷达基本不存在雨区衰减(Chandrasekar et al,2006),因此以S波段雷达的观测资料为真值,并与衰减前后的XPAR的数据比对,可检验衰减订正的准确程度,称为X-S检验。
为了更客观地以格点对格点的方式比对衰减订正效果,需将相邻天气雷达资料订正到同一个坐标系下。本文选定佛山雷达作为参考站点C,将广州S波段多普勒双偏振雷达A及X波段相控阵雷达B的观测数据插值到C的坐标系上,需进行两个步骤:(1)将三部雷达的观测资料均转换到经纬度坐标上(李明凤等,2018);(2)利用距离权重法将A和B插值到C的格点上:以A为例,从低层向上逐层抬仰角,比对经纬度信息,从A逐个仰角层次上找到距离最近的点A0,并计算A0的海拔高度HA0与C(i, j)格点的海拔高度HC,找到HC上下两层的高度,并利用距离权重法进行插值,将两者的高度插值到一致(王晗等,2018)。
定量评估指标包括相对偏差(relative bias,RB)、均方根误差(root mean squared error,RMSE)、分数标准偏差(fractional standard error,FSE)和相关系数(related coefficient,R)等。RB用以评价不同雷达之间参量的总体偏差趋向,能够消除局地个别数据的影响,取值范围是[-1,1],越接近于0,则误差越小。RMSE反映偏差的总体水平,其数值越小则越准确。FSE反映单个变量造成的偏差程度,其值越小,偏差越小。R衡量的是观测数据之间的一致性,取值范围同RB,但绝对值越大,估测效果越好(黄嘉佑和李庆祥,2015;肖柳斯等,2019;Zhang et al,2019a)。
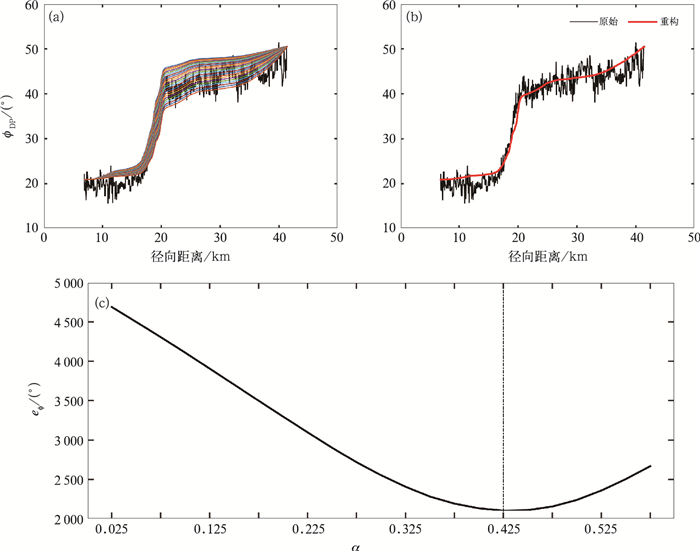
3 衰减订正效果分析 3.1 径向订正效果评估利用自适应算法进行衰减订正,首先对反射率因子进行订正,关键在于选择最优的α值,选定α值的范围在[0.025, 0.575],以0.025为间隔,共有23个α值,反复测试重构ϕDP,得到23个重构ϕDP值(如图 5a),这23条重构ϕDP线均在测量线(黑线)附近,各有偏离。利用式(5)计算测量和重构的ϕDP之间的误差eϕ,当α为0.425的时候,eϕ最小(图 5c)。如图 5b所示,重构得到的ϕDP(红色)在17~22 km范围内增长最快,与观测线大致重合,较为可信,22 km之外观测线起伏较大,重构的ϕDP大致位于观测的中值线上,可信度仍然较高。由图 5可见,重构之后的ϕDP可反映原始差分传播相移的变化趋势,光滑程度更高,可选用0.425作为α的最优系数进行衰减订正。
|
图 5 23个α值重构的ϕDP和测量的ϕDP(a), αopt重构的ϕDP和测量的ϕDP(b), 以及重构误差随α值的变化(c) Fig. 5 Reconstructed ϕDP lines with 23 α values and observed ϕDP (a), reconstructed ϕDP lines with αopt (b), and reconstruction error variation with α (c) |
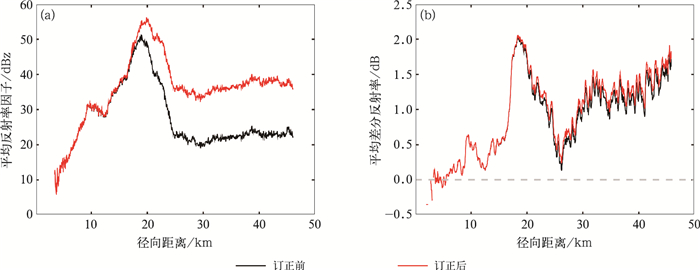
1.8°仰角上126°~135°方位角订正前后的平均反射率因子和差分反射率因子的效果如图 6所示。沿着径向向外,在反射率因子达到35 dBz之前,订正前后的曲线几乎重合,订正前后结果几乎没有差异,而在35~50 dBz,订正后的反射率因子略有增大,当电磁波穿越强降水区域(超过50 dBz)之后,反射率因子有明显的调整。在20 km附近,测量的反射率因子极大值约为52 dBz,订正后的值可达到58 dBz,订正幅度达6 dB。继续沿着径向向外,订正后的反射率因子梯度值大幅减小,5 km的减幅从30 dBz订正为20 dBz。25 km向外订正的反射率因子约为35 dBz,并略有上升趋势(图 6a)。
|
图 6 2019年9月2日15:57衰减订正前后的平均反射率因子(a)和平均差分反射率(b) Fig. 6 Comparison of mean reflectivity factor (a) and mean differential reflectivity (b) before and after attenuation correction at 15:57 BT 2 September 2019 |
在靠近雷达的弱降水区,差分反射率因子普遍为负值,因此根据初始差分反射率因子的分布规律,将差分反射率因子整体提高了0.8 dB,以使得近雷达的弱降水区域的差分反射率因子维持在0 dB的理论值附近,有效约束了差分反射率因子的负值。其后再展开衰减订正。图 6b显示,电磁波经过强降水回波(距离雷达20 km)之前,几乎无衰减;而在强回波之后,订正前后的线条能够区分出来,但是差异不是很明显。结合图 6a可见,在27 km处,订正后的反射率因子约为33 dBz,强度小,对应的差分反射率因子也接近谷值,约为0.3 dB。但是继续沿着径向向外,差分反射率因子显著增大,与反射率因子的增长幅度和趋势关系不匹配。而本方法由于受到反射率因子的约束,订正后的差分反射率因子并没有因为其测量增幅而出现过度订正的情况。
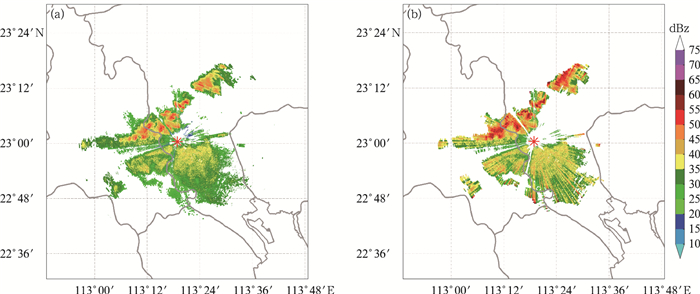
3.2 X-X对比结果广州XPAR探测到的反射率因子分布显示(图 7a),线性对流位于雷达的西北象限。由于广州XPAR遮挡较多,西北方向上的对流未能形成连贯的线状形式,仍能大致反映其东北—西南走向分布的态势,最大反射率因子在50~55 dBz,分布形势与佛山XPAR观测结果(图 3a)相似。但是对流强度偏弱,尤其是佛山境内的强回波带的组织形式不完整,以单体对流为主。图 7a中第二象限上的回波强度达到35 dBz,在相同位置上,佛山雷达测量的强度在30 dBz以下(图 3a)。即是说,在不同的位置上,两雷达观测的强度具有一定程度上的差异。究其原因,两部雷达的电磁波从不同方向穿越强降水云团,雨区造成的衰减强度不同,从而产生了观测误差不一致。
|
图 7 2019年9月2日15:57广州XPAR站1.8°仰角未经订正(a)和完成自适应算法衰减订正(b)的反射率因子 (图中红色标记指示广州XPAR的位置) Fig. 7 Reflectivity factor before (a) and after (b) self-consistent attenuation correction at 1.8° elevation of Guangzhou XPAR at 15:57 BT 2 September 2019 (The red mark denotes the location of Guangzhou XPAR) |
采用自适应算法对广州XPAR进行订正,利用各个方位角的观测数据,求得广州最优系数αoptmean=0.308 0。经过衰减订正的回波强度显著增加(图 7b),线性对流最大值可达到60~65 dBz。尤其是第四象限上佛山区域的反射率因子强中心区连成线,线状对流特征较订正前明显,组织性结构更清晰,体现出衰减订正算法的有效性。
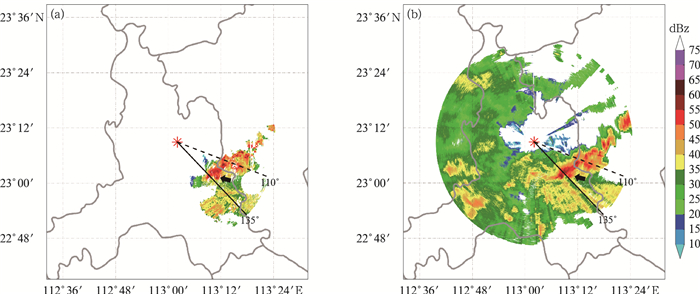
为了提高比对的客观性,本文将经过衰减订正的广州XPAR观测资料插值到佛山XPAR第二个仰角的坐标系上。由于两部XPAR的共同覆盖范围仅限于佛山XPAR第二象限,并且受到广州XPAR静锥区和部分遮挡的影响,数据连续性不是很理想(如图 8a)。但是图 8a仍然能够抓住对流主体,其形态与佛山雷达的观测(图 8b)分布相似,强度也相仿。箭头所指的强回波均能被订正至55 dBz以上,110°方位角上的回波也明显体现出订正增强的效果。110°~135°方位角上的回波形态分布较一致。以上结果表明将衰减订正算法应用于相邻的两部XPAR,订正后的反射率因子具有较高的一致性。
|
图 8 2019年9月2日15:57经过衰减订正及插值的广州(a) 和佛山(b)X波段相控阵1.8°仰角的反射率因子 (图中红色标记指示佛山XPAR的位置,下同,箭头指示衰减显著的位置) Fig. 8 Reflectivity factor at 1.8° elevation after self-consistent attenuation correction and interpolation of Guangzhou (a) and Foshan (b) XPAR at 15:57 BT 2 September 2019 (Red mark denotes the location of Foshan XPAR, the same below; arrow indicates where the attenuation is significant) |
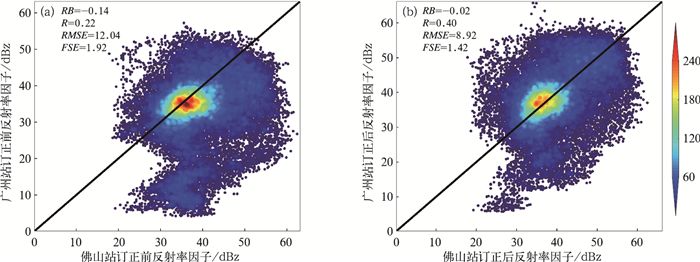
佛山站和广州站的散点分布显示,订正前(图 9a)散点偏心于佛山站,RB为-0.14,RMSE为12.04,FSE为1.92,R为0.22,即佛山站的原始探测数据总体偏高于广州站。经过衰减订正(图 9b)后,对角线两侧的散点分布更均匀,密度中心位于对角线上。订正后的RB为-0.02,佛山站的数值仍略高于广州站数据,但是两个站点的资料一致性增强。其他定量统计结果也佐证了一致性显著增强的观点,例如RMSE和FSE都显著减小,分别为8.92和1.42,R显著增加达到0.40,订正效果显著。由此可见,从数据的一致性说明了采用恰当的衰减订正算法进行数据订正的必要性,这不仅仅增强了单个XPAR资料应用的可靠性,也为多雷达组网所要求的数据质量均一性打下了基础。
|
图 9 2019年9月2日15:57广州与佛山X波段相控阵订正前(a)、后(b)的反射率因子散点图 (色标指示以0.5 dBz半径为圆的格点密度) Fig. 9 Scatter plot of reflectivity factor of Foshan and Guangzhou XPAR before (a) and after (b) self-consistent attenuation correction and interpolation at 15:57 BT 2 September 2019 (Color area denotes the density of data within a radius of 0.5 dBz) |
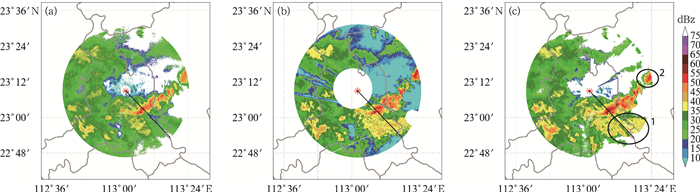
对所有方位角的αopt取平均求得αoptmean=0.3281,将该平均值代入求得所有方位角上衰减订正后的反射率因子,订正效果如图 10c所示。订正后反射率因子的分布结构形态与订正前(图 10a)相似,最强的回波中心位于佛山XPAR的西南方向上,呈现为东北—西南走向的线状对流形态,强度最大的对流单体位于雷达135°附近,其值可超过55 dBz,经过订正后,强对流单体远侧的反射率因子显著增强,从之前的35 dBz以下(绿色)订正为35 dBz以上(图 10c,黑色圆圈1)。雷达东北偏东方向上(黑色圆圈2)是电磁波经过了较长一段的无降水区域方到达的相对独立单体,经过衰减订正后,这个单体的中心强度增强幅度可达5 dBz。
|
图 10 2019年9月2日15:57佛山X波段相控阵雷达原始观测(a)、经过坐标匹配的广州S波段双偏振雷达(b),利用自适应算法衰减订正佛山X波段相控阵雷达的反射率因子(c) Fig. 10 Reflectivity factor observed by Foshan XPAR (a), reflectivity factor of Guangzhou S-band Doppler radar after coordinate matching (b) and reflectivity factor of Foshan XPAR after self-consistent attenuation correction and interpolation (c) at 15:57 BT 2 September 2019 |
为了更直观对比S波段和XPAR数据的差异,在数据处理时已将S波段雷达观测数据插值到佛山XPAR的坐标系上(图 10b)。XPAR的观测分辨率更高,观测所得的反射率因子强度结构分布更为细致,体现了XPAR的高精度观测的优势。与S波段雷达探测数据的分布形态相比,订正前的线状对流强度较弱;订正后显著增强,与S波段雷达的强度相当,局部较强。在线性对流东南侧,即雷达电磁波径向通过强对流单体的远端,订正后的反射率因子强度和分布均与S波段雷达探测数据的分布更为接近。在雷达观测的其他象限,本文所使用的衰减订正算法对远距离的探测都能表现出较为理想的订正效果。因此,从反射率因子的平面分布来看,本文所使用的衰减订正算法对粤港澳大湾区统一使用的XPAR探测数据有较好订正效果,具有较高的本地适用性。
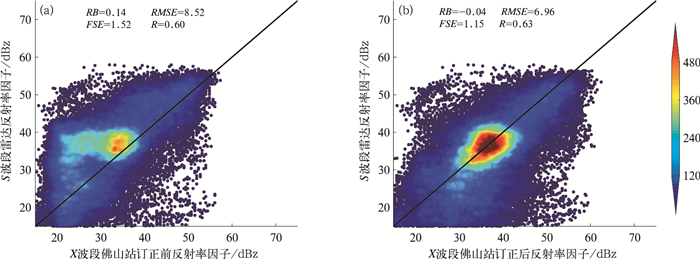
选择佛山XPAR的90°~180°方位角上(也就是强回波所在区间)订正前后的反射率因子进行散点分析(图 11)。订正前,XPAR散点密度最高的区间均在30~40 dBz,与S波段雷达相似,但是两者的散点分布偏离对角线,位于对角线上方。XPAR存在一个较弱的次中心位于20~30 dBz(图 11a)。散点图上,单位面积格点数超过240的中心区如平行于X轴的“蝌蚪”状,横亘在对角线上方,横向跨度可达20 dBz,以S波段雷达作为参考,XPAR的探测结果明显低估了反射率因子的强度。定量评估的统计量表明,RB为0.14,RMSE为8.52,FSE为1.52,反映了X波段低估了反射率因子的事实。相关系数R值为0.60,通过了0.01的显著性水平检验,表明两个雷达观测具有较好的正相关关系。经过衰减订正后,对角线两侧的散点分布较订正前均匀,密度中心量级增加,并分布在对角线上。经过订正后的统计量RB、RMSE、FSE和R分别为-0.04、6.96、1.15和0.63,XPAR订正后的数据略微高估了反射率因子,但是估测偏差幅度减小,相关性有所增加。以上定量结果均意味着经过衰减订正后的XPAR的反射率因子准确率提升,本算法具有较好的本地适用性。
|
图 11 2019年9月2日15:57 S波段多普勒雷达与佛山X波段相控阵雷达90°~180°方位角上订正前(a)、订正后(b)高于15 dBz的反射率因子散点图 (色标指示以0.5 dBz半径为圆的格点密度) Fig. 11 Scatter plot of reflectivity factor (> 15 dBz) before (a) and after (b) self-consistent attenuation correction between interpolation of Guangzhou S-band Doppler Radar and Foshan XPAR at 15:57 BT 2 September 2019 (Color area denotes the density of grids within a radius of 0.5 dBz) |
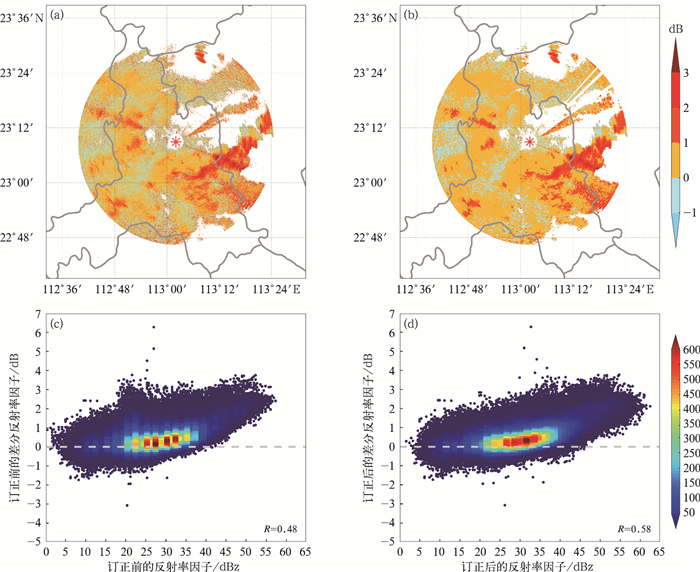
低仰角观测的反射率因子小于10 dBz时,差分反射率因子理论值应为0 dB(何宇翔等,2009),因此本文在开展衰减订正前,基于反射率因子与差分反射率因子的统计关系,将差分反射率因子整体增加0.8 dB,差分反射率因子的负值得到有效约束,但是噪点明显(图 12a)。后续开展的差分反射率因子衰减订正效果如图 12b所示,噪点现象得到抑制,图中可辨识独立的回波单体分布特征,订正幅度不是很明显。
|
图 12 2019年9月2日15:57佛山XPAR1.8°仰角上订正前(a, c)、后(b, d)差分反射率平面分布(a,b) 和反射率因子与差分反射率因子的散点图(c,d) (色标指示0.5 dBz×0.05 dB矩形的格点密度) Fig. 12 Distribution of differential reflectivity (a, b) and scatter plot between differential reflectivity and reflectivity factor (c, d) at 15:57 BT 2 September 2019 (a, c) before attenuation correction, (b, d) after attenuation correction (Color area denotes the density of grids within a 0.5 dBz×0.05 dB rectangle in Figs. 12c, 12d) |
由于差分反射率因子值反映的是雨滴大小,大雨滴的差分反射率因子有所增大,而通常而言大粒子的反射率因子较大,两者具有一定的相关性。散点分布图(图 12c)显示订正前差分反射率因子和反射率因子之间存在正相关关系,相关系数为0.48。反射率因子小于15 dBz时,差分反射率因子相对均匀地分布在0 dB上下;反射率因子在15~40 dBz时,差分反射率因子主要集中在0~1 dB,大致呈现曲线相关关系,其中在20~25 dBz区间上,差分反射率因子出现凸起现象,可能是由于数据抖动导致的;当反射率因子超过40 dBz,差分反射率因子随反射率因子增大而增加的幅度有所增大。
经衰减订正之后(图 12d),散点分布更为集中,差分反射率因子和反射率因子之间的正相关关系更显著,相关系数增加至0.58,并且20~25 dBz区间上没有了凸起的数据分布,异常数据现象得到抑制。反射率因子在15~40 dBz时,单位面积上的格点数量较订正前显著增加,差分反射率因子更集中于0~1 dB,该区间内主要为小水滴。
4 结论本文针对X波段双偏振相控阵雷达的雨滴衰减问题进行订正算法研究,利用自适应约束算法对佛山相控阵雷达的反射率因子和差分反射率因子进行质量控制,并将订正前后的数据与S波段多普勒雷达及相邻的广州X波段相控阵雷达数据对比评估。检验结果表明,X波段相控阵雷达所得的反射率因子强度结构分布更为细致,体现了其高精度观测的优势。沿着径向向外,在强降水中心远离雷达的一侧,回波强度明显增强,反射率因子梯度值明显减小。图形分析及定量评分结果均表明: 订正后的反射率因子与S波段雷达的观测分布强度相当,局部更强;与相邻X波段相控阵雷达的订正值分布均较为一致,自适应约束衰减订正算法对反射率因子有较好订正效果,具有较高的本地适用性。差分反射率因子也得到了一定程度的订正,有效约束了负值,径向分布表明在强降水回波远侧有微弱的订正幅度。但是由于差分反射率因子的量值分布范围较小,增幅在平面图的对比上不如反射率因子的订正效果明显。订正后的反射率因子和差分反射率因子的正相关关系显著增强,相关系数由订正前的0.48增长到订正后的0.58。
以上的评估效果可见,自适应衰减订正方法能够基于不同的雷达及降水目标物自适应调整关系系数,较好地解决了X波段双偏振相控阵雷达的雨滴衰减问题,具有较好的可移植性和本地适应性。本研究可为粤港澳大湾区X波段双偏振相控阵雷达网资料推广应用和产品开发提供前期数据质量保障,有助于增强高分辨率雷达对强对流天气系统的追踪和定量降水估测能力,以及提高国家重要大城市群的短时临近天气预测和预警能力。
致谢:感谢广东纳睿雷达科技股份有限公司地对本研究评估工作的支持。
毕永恒, 刘锦丽, 段树, 等, 2012. X波段双线偏振气象雷达反射率的衰减订正[J]. 大气科学, 36(3): 495-506. Bi Y H, Liu J L, Duan S, et al, 2012. Attenuation correction of reflectivity for X-band dual-polarization radar[J]. Chin J Atmos Sci, 36(3): 495-506 (in Chinese).
|
曹俊武, 胡志群, 陈晓辉, 等, 2011. 影响双线偏振雷达相位探测精度的分析[J]. 高原气象, 30(3): 817-822. Cao J W, Hu Z Q, Chen X H, et al, 2011. Accuracy analysis of dual-linear polarization signal-process measurement[J]. Plateau Meteor, 30(3): 817-822 (in Chinese).
|
程元慧, 傅佩玲, 胡东明, 等, 2020. 广州相控阵天气雷达组网方案设计及其观测试验[J]. 气象, 46(6): 823-836. Cheng Y H, Fu P L, Hu D M, et al, 2020. The Guangzhou phased-array radar networking scheme set-up and observation test[J]. Meteor Mon, 46(6): 823-836 (in Chinese).
|
傅佩玲, 胡东明, 黄浩, 等, 2020. 台风山竹(1822)龙卷的双极化相控阵雷达特征[J]. 应用气象学报, 31(6): 706-718. Fu P L, Hu D M, Huang H, et al, 2020. Observation of a tornado event in outside-region of Typhoon Mangkhut by X-band polarimetric phased array radar in 2018[J]. J Appl Meteor Sci, 31(6): 706-718 (in Chinese).
|
何宇翔, 吕达仁, 肖辉, 2009. X波段双线极化雷达差分反射率的衰减订正[J]. 高原气象, 28(3): 607-616. He Y X, Lyu D R, Xiao H, 2009. Attenuation correction of radar differential reflectivity for X-band dual polarization radar[J]. Plateau Meteor, 28(3): 607-616 (in Chinese).
|
胡志群, 刘黎平, 吴林林, 2014. C波段偏振雷达几种系统误差标定方法对比分析[J]. 高原气象, 33(1): 221-231. Hu Z Q, Liu L P, Wu L L, 2014. Comparison among several system biases calibration methods on C-band polarimetric radar[J]. Plateau Meteor, 33(1): 221-231 (in Chinese).
|
黄朝盈, 2019. 双偏振天气雷达定量降水估计关键技术研究[D]. 南宁: 南宁师范大学. Huang Z Y, 2019. Study on key technologies of quantitative precipitation estimation with dual polarimetric weather radar[D]. Nanning: Nanning Normal University(in Chinese).
|
黄嘉佑, 李庆祥, 2015. 气象数据统计分析方法[M]. 北京: 气象出版社: 28-47. Huang J Y, Li Q X, 2015. Statistical Analysis Methods of Meteorological Data[M].
Beijing: China Meteorological Press: 28-47 (in Chinese).
|
李明凤, 闵超, 张阿思, 等, 2018. 基于SRTM数据的广东新一代天气雷达覆盖研究[J]. 地球信息科学学报, 20(8): 1201-1208. Li M F, Min C, Zhang A S, et al, 2018. Analysis of CINRAD coverage in Guangdong Province based on SRTM data[J]. J Geo-Info Sci, 20(8): 1201-1208 (in Chinese).
|
穆穆, 陈博宇, 周菲凡, 等, 2011. 气象预报的方法与不确定性[J]. 气象, 37(1): 1-13. Mu M, Chen B Y, Zhou F F, et al, 2011. Methods and uncertainties of meteorological forecast[J]. Meteor Mon, 37(1): 1-13 (in Chinese).
|
唐永兰, 徐桂荣, 于晓晶, 2019. 近49 a中国30°N带不同地形下大城市与其郊区的降水特征[J]. 暴雨灾害, 38(4): 354-363. Tang Y L, Xu G R, Yu X J, 2019. Precipitation characteristics in large cities and their suburbs under different terrains in 30°N zone of China in recent 49 years[J]. Torr Rain Dis, 38(4): 354-363 (in Chinese). DOI:10.3969/j.issn.1004-9045.2019.04.008
|
王晗, 刘黎平, 张扬, 2018. X波段双线偏振雷达不同衰减订正法对比分析[J]. 气象科技, 46(1): 1-9, 15. Wang H, Liu L P, Zhang Y, 2018. Comparison of different attenuation correction methods using X-band dual polarimetric radar[J]. Meteor Sci Technol, 46(1): 1-9, 15 (in Chinese).
|
王璐, 沈学顺, 2019. 对流尺度集合预报与模式不确定性研究进展[J]. 气象, 45(8): 1158-1168. Wang L, Shen X S, 2019. Review on the representation of model uncertainty in convection-allowing ensemble prediction system[J]. Meteor Mon, 45(8): 1158-1168 (in Chinese).
|
魏庆, 胡志群, 刘黎平, 等, 2016. C波段偏振雷达数据预处理及在降水估计中的应用[J]. 高原气象, 35(1): 231-243. Wei Q, Hu Z Q, Liu L P, et al, 2016. C-band polarization radar data preprocessing and its application to rainfall estimation[J]. Plateau Meteor, 35(1): 231-243 (in Chinese).
|
伍志方, 蔡景就, 林良勋, 等, 2018. 2017年广州"5·7"暖区特大暴雨的中尺度系统和可预报性[J]. 气象, 44(4): 485-499. Wu Z F, Cai J J, Lin L X, et al, 2018. Analysis of mesoscale systems and predictability of the torrential rain process in Guangzhou on 7 May 2017[J]. Meteor Mon, 44(4): 485-499 (in Chinese).
|
肖柳斯, 张阿思, 闵超, 等, 2019. GPM卫星降水产品在台风极端降水过程的误差评估[J]. 高原气象, 38(5): 993-1003. Xiao L S, Zhang A S, Min C, et al, 2019. Evaluation of GPM satellite-based precipitation estimates during three tropical-related extreme rainfall events[J]. Plateau Meteor, 38(5): 993-1003 (in Chinese).
|
肖艳姣, 王斌, 陈晓辉, 等, 2012. 移动X波段双线偏振多普勒天气雷达差分相位数据质量控制[J]. 高原气象, 31(1): 223-230. Xiao Y J, Wang B, Chen X H, et al, 2012. Differential phase data quality control of mobile X-band dual-polarimetric Doppler weather radar[J]. Plateau Meteor, 31(1): 223-230 (in Chinese).
|
朱丹, 谷军霞, 师春季, 等, 2018. 新一代天气雷达布网设计的有效覆盖和地形遮挡分析[J]. 气象, 44(11): 1434-1444. Zhu D, Gu J X, Shi C J, et al, 2018. Analysis of effective coverage and terrain blockage for next generation radar network design[J]. Meteor Mon, 44(11): 1434-1444 (in Chinese).
|
Anagnostou E N, Krajewski W F, 1999. Real-time radar rainfall estimation.Part Ⅱ: case study[J]. J Atmos Ocean Technol, 16(2): 198-205. DOI:10.1175/1520-0426(1999)016<0198:RTRREP>2.0.CO;2
|
Aydin K, Zhao Y, Seliga T A, 1989. Rain-induced attenuation effects on C-band dual-polarization meteorological radars[J]. IEEE Trans Geosci Remote Sens, 27(1): 57-66. DOI:10.1109/36.20275
|
Bluestein H B, French M M, Popstefanija I, et al, 2010. A mobile, phased-array Doppler radar for the study of severe convective storms[J]. Bull Amer Meteor Soc, 91(5): 579-600. DOI:10.1175/2009BAMS2914.1
|
Bringi V N, Chandrasekar V, 2010. 偏振多普勒天气雷达原理和应用[M]. 李忱, 张越, 译. 北京: 气象出版社. Bringi V N, Chandrasekar V, 2010. Polarimetric Doppler Weather Radar: Principles and Applications[M]. Li C, Zhang Y, trans. Beijing: China Meteorological Press(in Chinese).
|
Bringi V N, Chandrasekar V, Balakrishnan N, et al, 1990. An examination of propagation effects in rainfall on radar measurements at microwave frequencies[J]. J Atmos Ocean Technol, 7(6): 829-840. DOI:10.1175/1520-0426(1990)007<0829:AEOPEI>2.0.CO;2
|
Bringi V N, Keenan T D, Chandrasekar V, 2001. Correcting C-band radar reflectivity and differential reflectivity data for rain attenuation: a self-consistent method with constraints[J]. IEEE Trans Geosci Remote Sens, 39(9): 1906-1915. DOI:10.1109/36.951081
|
Carey L D, Rutledge S A, Ahijevych D A, et al, 2000. Correcting propagation effects in C-band polarimetric radar observations of tropical convection using differential propagation phase[J]. J Appl Meteor, 39(9): 1405-1433. DOI:10.1175/1520-0450(2000)039<1405:CPEICB>2.0.CO;2
|
Chandrasekar V, Lim S, Gorgucci E, 2006. Simulation of X-band rainfall observations from S-band radar data[J]. J Atmos Ocean Technol, 23(9): 1195-1205. DOI:10.1175/JTECH1909.1
|
Du Y, Chen G X, 2018. Heavy rainfall associated with double low-level jets over Southern China.Part Ⅰ : Ensemble-based analysis[J]. Mon Wea Rev, 146(11): 3827-3844. DOI:10.1175/MWR-D-18-0101.1
|
French M M, Bluestein H B, PopStefanija I, et al, 2014. Mobile, phased-array, Doppler radar observations of tornadoes at X band[J]. Mon Wea Rev, 142(3): 1010-1036. DOI:10.1175/MWR-D-13-00101.1
|
Gorgucci E, Scarchilli G, Chandrasekar V, 1996. Operational monitoring of rainfall over the arno river basin using dual-polarized radar and rain gauges[J]. J Appl Meteor, 35(8): 1221-1230. DOI:10.1175/1520-0450(1996)035<1221:OMOROT>2.0.CO;2
|
Gou Y B, Chen H N, Zheng J F, 2019. An improved self-consistent approach to attenuation correction for C-band polarimetric radar measurements and its impact on quantitative precipitation estimation[J]. Atmos Res, 226: 32-48. DOI:10.1016/j.atmosres.2019.03.006
|
Gu J Y, Ryzhkov A, Zhang P, et al, 2011. Polarimetric attenuation correction in heavy rain at C band[J]. J Appl Meteor Climatol, 50(1): 39-58. DOI:10.1175/2010JAMC2258.1
|
Hildebrand P H, 1978. Iterative correction for attenuation of 5cm radar in rain[J]. J Appl Meteor, 17(4): 508-514. DOI:10.1175/1520-0450(1978)017<0508:ICFAOC>2.0.CO;2
|
Hitschfeld W, Bordan J, 1954. Errors inherent in the radar measurement of rainfall at attenuating wavelengths[J]. J Meteor, 11(1): 58-67. DOI:10.1175/1520-0469(1954)011<0058:EIITRM>2.0.CO;2
|
Kuster C M, Heinselman P L, Austin M, 2015. 31 may 2013 El Reno tornadoes: advantages of rapid-scan phased-array radar data from a warning forecaster's perspective[J]. Wea Forecasting, 30(4): 933-956. DOI:10.1175/WAF-D-14-00142.1
|
Liang P, Ding Y H, 2017. The long-term variation of extreme heavy precipitation and its link to urbanization effects in shanghai during 1916-2014[J]. Adv Atmos Sci, 34(3): 321-334. DOI:10.1007/s00376-016-6120-0
|
McLaughlin D J, Pepyne D, Chandrasekar V, et al, 2009. Short-wavelength technology and the potential for distributed networks of small radar systems[J]. Bull Amer Meteor Soc, 90(12): 1797-1818. DOI:10.1175/2009BAMS2507.1
|
Meneghini R, Nakamura K, Ulbrich C W, et al, 1989. Experimental tests of methods for the measurement of rainfall rate using an airborne dual-wavelength radar[J]. J Atmos Ocean Technol, 6(4): 637-651. DOI:10.1175/1520-0426(1989)006<0637:ETOMFT>2.0.CO;2
|
Newman J F, Heinselman P L, 2012. Evolution of a quasi-linear convective system sampled by phased array radar[J]. Mon Wea Rev, 140(11): 3467-3486. DOI:10.1175/MWR-D-12-00003.1
|
Park S G, Bringi V N, Chandrasekar V, et al, 2005a. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band.Part Ⅰ: theoretical and empirical basis[J]. J Atmos Ocean Technol, 22(11): 1621-1632. DOI:10.1175/JTECH1803.1
|
Park S G, Maki M, Iwanami K, et al, 2005b. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band.Part Ⅱ: evaluation and application[J]. J Atmos Ocean Technol, 22(11): 1633-1655. DOI:10.1175/JTECH1804.1
|
Ryzhkov A V, 2007. The impact of beam broadening on the quality of radar polarimetric data[J]. J Atmos Ocean Technol, 24(5): 729-744. DOI:10.1175/JTECH2003.1
|
Testud J, Le Bouar E, Obligis E, et al, 2000. The rain profiling algorithm applied to polarimetric weather radar[J]. J Atmos Ocean Technol, 17(3): 332-356. DOI:10.1175/1520-0426(2000)017<0332:TRPAAT>2.0.CO;2
|
Vulpiani G, Tabary P, Parent Du Chatelet J, et al, 2008. Comparison of advanced radar polarimetric techniques for operational attenuation correction at C band[J]. J Atmos Ocean Technol, 25(7): 1118-1135. DOI:10.1175/2007JTECHA936.1
|
Wang Y T, Chandrasekar V, 2009. Algorithm for estimation of the specific differential phase[J]. J Atmos Ocean Technol, 26(12): 2565-2578. DOI:10.1175/2009JTECHA1358.1
|
Weber M E, Cho J Y N, Herd J S, et al, 2007. The next-generation multimission U.S.surveillance radar network[J]. Bull Amer Meteor Soc, 88(11): 1739-1752. DOI:10.1175/BAMS-88-11-1739
|
Wu M W, Luo Y L, Chen F, et al, 2019. Observed link of extreme hourly precipitation changes to urbanization over coastal South China[J]. J Appl Meteor Climatol, 58(8): 1799-1819. DOI:10.1175/JAMC-D-18-0284.1
|
Yussouf N, Stensrud D J, 2010. Impact of phased-array radar observations over a short assimilation period: observing system simulation experiments using an ensemble Kalman filter[J]. Mon Wea Rev, 138(2): 517-538. DOI:10.1175/2009MWR2925.1
|
Zhang A S, Xiao L S, Min C, et al, 2019a. Evaluation of latest GPM-era high-resolution satellite precipitation products during the May 2017 Guangdong extreme rainfall event[J]. Atmos Res, 216: 76-85. DOI:10.1016/j.atmosres.2018.09.018
|
Zhang G F, Mahale V N, Putnam B J, et al, 2019b. Current status and future challenges of weather radar polarimetry: bridging the gap between radar meteorology/hydrology/engineering and numerical weather prediction[J]. Adv Atmos Sci, 36(6): 571-588. DOI:10.1007/s00376-019-8172-4
|
 2021, Vol. 47
2021, Vol. 47 
