2. 天津市气象科学研究所, 天津 300074;
3. 国网天津市电力公司, 天津 300010;
4. 天津市气候中心, 天津 300074
2. Tianjin Institute of Meteorological Science, Tianjin 300074;
3. State Grid Tianjin Electric Power Company, Tianjin 300010;
4. Tianjin Climate Center, Tianjin 300074
电能作为重要能源之一,是工业生产、交通运输及日常生活的基本保障,电力需求的变化可能对城市安全、未来温室气体的减排要求、区域及全球的能源政策产生一定影响。对电力需求的准确预测,不仅能够有效地指导电力调控,帮助电力企业节约发电成本,还对未来能源供应的规划和经济评估具有重要意义(Scapin et al, 2016;Wang and Bielicki, 2018)。很多学者利用气象因子与用电量之间的关系展开预测分析(胡江林等, 2002;Mirasgedis et al, 2006;Apadula et al, 2012;尹炤寅等, 2017;刘俊等, 2019;李海英等, 2020;乔黎伟等, 2020),由于用电量与气象因子之间呈非线性变化,研究中往往通过建立分段模型来分析气象因子对用电量的影响,并基于此实现对电力需求的预测。因此,深入理解用电量和气象因子之间的非线性关系对于提升电力需求的预测效果具有重要意义。在以往研究中,不同学者利用多种方法分析了气温和用电量之间的非线性特征(Moral-Carcedo and Vicéns-Otero, 2005;Bessec and Fouquau, 2008;Lee and Chiu, 2011)。其中度日值作为能源预测中的常用方法,被用于探究其与用电量之间的关系(Al-Zayer and Al-Ibrahim, 1996),并以此建立了气温和用电量之间的“V”型分段模型,即设置一个气温阈值,当室外气温低于气温阈值时,电能主要用于加热,而气温高于气温阈值时,则转换为冷却。通过气温阈值将用电量与气温之间的关系区分为加热区和冷却区,从而直接通过气温变化判断电力需求,并得到了广泛应用(Al-Zayer and Al-Ibrahim, 1996;石玉恒等, 2019)。在“V”型分段方法中,气温阈值选用18.3℃。Moral-Carcedo and Vicéns-Otero (2005)在研究中发现,分段后的气温阈值实际上是一个温度区间,并由此引入平滑过渡方法,假设在该温度区间内,用电量随气温的改变没有明显变化,则定义为舒适区,从而形成了气温和用电量的“U”型分段模型。Wang and Bielicki(2018)在逐时用电量研究中也发现,气温与用电量中大约有7℃范围的舒适区。利用度日值的分段能够将用电量与气温的非线性关系转为线性进行分析,在“V”型或“U”型分段方法的实际应用中发现,根据用电量与气温在不同区域的关系,还可进一步分为线性对称、线性不对称及非线性模型(Hekkenberg et al, 2009;Bessec and Fouquau, 2008;Gupta, 2012;罗慧等, 2016)。
以往的研究中,利用分段回归、门限回归、平滑转换模型等多种方法来确定气温阈值(Moral-Carcedo and Vicéns-Otero, 2005;Deschênes and Greenstone, 2011;Wang and Bielicki, 2018),但大部分研究仅根据气温和用电量的关系展开分析,而未考虑其他气象要素对气温阈值的影响。Hekkenberg et al(2009)指出用电量与气温之间的分段阈值会随体感温度等要素发生偏移;Wang and Bielicki(2018)也在研究中提出,相对湿度和辐射会对气温阈值的范围产生一定影响。然而,目前针对用电量分段方法的研究中,还未考虑相对湿度,这可能是导致舒适区产生一定偏差的主要因素,特别是在湿度高低差异较大时,气温阈值的范围会与平均状态相差较多,从而影响最终的用电量预测结果。
本文综合考虑了气温和相对湿度两个气象因子,研究其对用电量分段的影响,通过分析不同相对湿度范围下,用电量与气温的拟合曲线,利用曲线斜率判断气温随相对湿度变化的阈值,建立综合考虑温湿度的电力分段方法,以期提升用电量分段的科学性与准确性,为精准预测电力需求提供科学依据。
1 数据与方法 1.1 数据本文数据包括电力数据和气象数据。电力数据为国网天津市电力公司提供的2014—2018年逐日用电量。气象数据为2014—2018年天津市城市气候监测站的逐时气温和相对湿度,均处理为日平均值。为减小特殊日期用电量波动对研究结果的影响,本文剔除了节假日期间的数据,主要包括元旦、农历小年至元宵节、清明节、劳动节、端午节、中秋节和国庆节,每年约40余天。
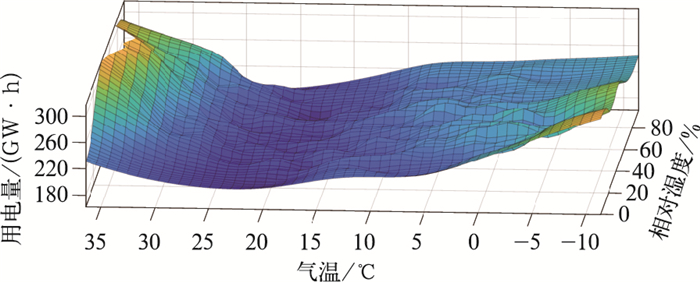
对用电量与气象因子之间响应特征的初步分析(图 1)表明:日用电量与气温和相对湿度之间呈现明显的非线性关系,随着气温的降低,用电量先减少后增加,且减少与增加区域呈现非对称的特点,这与以往研究中“U”型、“V”型的非对称性相一致。同时发现,在不同相对湿度条件下,用电量和气温的变化特征存在差异。用电量对气温的低敏感区(舒适区)会随相对湿度的变化发生明显偏移;当相对湿度较小时,舒适区的气温区间较大,且气温阈值偏高,当相对湿度较大时,舒适区的气温区间减小,且随着相对湿度的增加,气温阈值向低温一侧有明显偏移。可见,舒适区受温度和相对湿度的共同影响,因此分段方法需要同时引入气温和相对湿度这两个气象要素。
|
图 1 2014—2018年天津日用电量与气温和相对湿度之间的三维关系分布 Fig. 1 Distribution of three-dimensional relationship between daily electricity load and temperature and relative humidity in Tianjin during 2014-2018 |
Scapin et al (2016)的研究结果表明,用电量预测模型主要受周期性变化和气象条件变化两部分影响,而用电量随气象条件的变化表现为线性和非线性特征,Brown et al(2016)认为线性不对称模型在评估多种气象条件对用电量的影响及人为控制变量方面存在明显优势,故文中以此模型来确定分段阈值。具体公式如下所示:
| $ D=\sum\limits_{i=0}^{m} \alpha_{i} t^{i}+\sum\limits_{j=1}^{4} \beta_{j} I_{j}+\sum\limits_{k=1}^{n} \gamma_{k} V_{k}+\varepsilon $ | (1) |
式中:D表示日用电量;等式右端前两项均代表周期性变化的影响,第一项是用电量随时间的变化,主要代表经济形势和消费习惯的长期变化对电力需求的影响,采用二阶函数表示(更高阶拟合效果提升极小),即m=2,α为系数,t为时间;第二项代表周周期的用电量变化,相关研究表明(Pardo et al, 2002;Moral-Carcedo and Vicéns-Otero, 2005),周二至周五用电量比较接近,周一次之,周末最少,因此本文通过控制虚拟变量I的取值(I1、I2、I3、I4分别代表周一、周六、周日及周二至周五四个时段,对应时段取1,其他时段为0),仅选取周二至周五的数据进行分析,以排除其他时段系数β选取不当造成的偏差;等式右端第三项表示气象条件影响下的用电量变化,选取气温和相对湿度作为预测因子,即n=2,V1代表平均气温,V2代表平均相对湿度,γ为系数;右端第四项ε为残差项。
由式(1)可知,在日用电量D中减去第一项长期趋势变化,排除第二项周周期影响,第三项和第四项的和即可代表用电量受气象条件的影响程度,如式(2)所示。本文通过分析DF(去除时间趋势项的用电量)与气象条件之间的关系,得到对应的用电量分段方法。
| $ D F=\sum\limits_{k=1}^{n} \gamma_{k} V_{k}+\varepsilon $ | (2) |
Hansen(1999)在求取分段阈值的研究中以残差平方和的最小化为条件来确定阈值,本文采用类似的均方根误差(RMSE)的最小化来选取最优气温阈值,该模型也被广泛用于评估各类模型预测效果(吴琼等, 2020;任永建等, 2020;张天航等, 2020),具体计算公式为:
| $ R M S E=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}} $ | (3) |
除RMSE外,由于平均绝对百分误差(MAPE)可以捕捉预测绝对误差与实际载荷之间的比例关系,因此在负荷和用电量预测中被更广泛采用(Barman et al, 2018)。具体计算公式为:
| $ M A P E=\frac{100 \%}{n} \sum\limits_{i=1}^{n}\left|\frac{y_{i}-\widehat{y}_{i}}{y_{i}}\right| $ | (4) |
式中:y和
文中分段建立不同相对湿度下气温和用电量的非线性拟合曲线,利用曲线斜率确定气温阈值,由此得到相对湿度和气温阈值的对应矩阵,并拟合得到基于温湿度的用电量分段曲线。具体计算方法如下:
首先,选取相对湿度范围为P(分别为20%~25%,25%~30%, …, 70%~75%,75%~80%,相对湿度低于20%或高于80%的样本少,所以不予考虑)的所有样本,该样本中的用电量和气温数据经归一化处理为数组(Tj,Dj),两者之间的非线性拟合方程如式(5)所示(由于二次拟合公式的R2超过0.98,故不再取更高阶):
| $ D_{j}=a T_{j}{ }^{2}+b T_{j}+c $ | (5) |
式中:T代表气温;D代表日总用电量;j代表样本编号;a, b为系数;c为常数。
计算拟合曲线上每点j的斜率为k,代表用电量随气温的变化幅度,用下式表示:
| $ k_{j}=\frac{\Delta D}{\Delta T}=\frac{D_{j}-D_{j-1}}{T_{j}-T_{j-1}} $ | (6) |
假设冷却区与舒适区的临界点为m,加热区与舒适区的临界点为n。斜率分别为km和kn。舒适区作为用电量与气象因子的低敏感区域,其上下限点(m, n)应具备两个特点,日总用电量较小(计算中取1/3),且日总用电量随气温变化幅度较小,基于以上两点,推得上下限临界值的公式如下所示:
| $ D_{m}<\frac{1}{3} \text { & } D_{n}<\frac{1}{3} $ | (7) |
由此得到,在相对湿度范围为P,斜率取km和kn时,冷却区与舒适区对应的临界气温为Tm,加热区与舒适区对应的临界气温为Tn。当km=kn=0时,电量分段呈现“V”型分布。当km≠0或kn≠0时,Tm至Tn温度区间则对应舒适区,用电量分段则呈现“U”型分布。
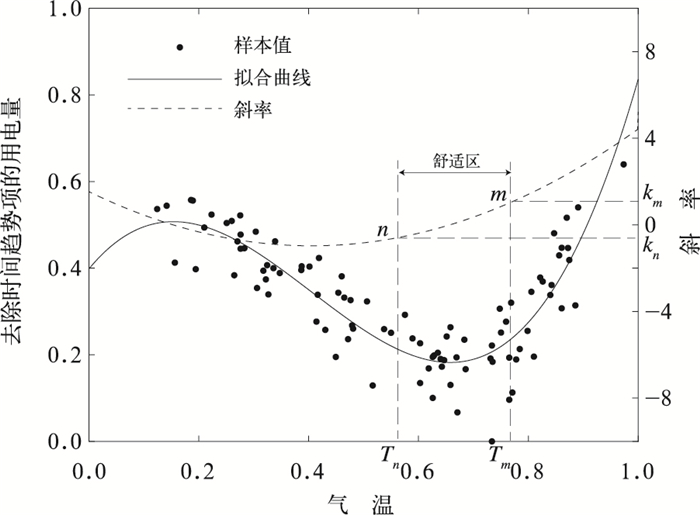
图 2给出相对湿度P取55%~60%时,用电量和气温的拟合曲线及对应舒适区范围的示意图。根据拟合曲线斜率的变化情况,选取最佳斜率km和kn。对应的m, n即为归一化后冷却区与舒适区、加热区与舒适区的分段节点,计算得到对应的Tm和Tn即分别为上、下限气温阈值,两点之间的范围为舒适区。
|
图 2 相对湿度为55%~60%时气温和用电量归一化数据的非线性拟合及分段示意图 Fig. 2 Nonlinear fitting and segmental diagram of normalized temperature and electricity load in the range of 55%-60% relative humidity |
按照式(5)~(7),可确定每个相对湿度范围内的邻近点气温T(m,P,km)和T(n,P,kn),即得到一个包括气温T、相对湿度RH(P)、斜率k值、冷却或加热临界点m或n的四维数组(为计算方便,相对湿度取P的中值,如当P为20%~25%,RH取为22.5%),从而建立冷却区与舒适区、加热区与舒适区邻近点的温湿度数组为(Tm,km, RHm,km, Tn,kn, RHn,kn),并分别建立对应的线性拟合方程(8)和(9)。
| $ T_{m, k_{m}} =\omega_{m, k_{m}} R H_{m, k_{m}}+\theta_{m, k_{m}} $ | (8) |
| $ T_{n, k_{n}} =\omega_{n, k_{n}} R H_{n, k_{n}}+\theta_{n, k_{n}} $ | (9) |
拟合曲线对应的均方差误差分别为Qm和Qn,公式如下所示:
| $ Q_{m, k_{m}}=\sqrt{\sum\limits_{i=1}^{8}\left(T_{m, k_{m}, i}-\omega_{m, k_{m}} R H_{m, k_{m}, i}-\theta_{m, k_{m}}\right)^{2}} $ | (10) |
| $ Q_{n, k_{n}}=\sqrt{\sum\limits_{i=1}^{8}\left(T_{n, k_{n}, i}-\omega_{n, k_{n}} R H_{n, k_{n}, i}-\theta_{n, k_{n}}\right)^{2}} $ | (11) |
通过取Qm,km值的极小值,解得系数ωm,km,ωn,kn值,同理求得常数θm,km,θn,kn值,得到气温阈值和相对湿度的拟合曲线。表 1以km=1.0,kn=0.8为例,给出不同相对湿度下,Tm和Tn的变化情况。
|
|
表 1 km=1.0, kn=0.8时,不同相对湿度范围内的用电量分段的气温阈值 Table 1 Temperature thresholds for electricity load segments during different relative humidity when km=1.0, kn=0.8 |
根据表 1得到相对湿度范围和上下限气温阈值的拟合曲线及舒适区变化如图 3所示,可以看出,随着相对湿度的增大,Tm逐渐下降,Tn则变化不大,舒适区范围逐渐缩小,其范围变窄主要因为Tm的波动明显大于Tn,说明二者对相对湿度的敏感度存在差异。这是由于当相对湿度增加时,人体对高温的承受度下降,因此体感气温会随之上升,特别是在高湿的天气条件下,Tm会明显下降,进而影响用电量,这与实际经验相一致;而对于Tn,其受相对湿度的影响较小,这表明加热区和舒适区之间的气温边界随相对湿度的变化并不明显。说明该方法应当更有利于对Tm阈值的改进。

|
图 3 km=1.0, kn=0.8时,用电量分段的温湿度拟合曲线 Fig. 3 Fitting curve of temperature and RH by different electricity load segments when km=1.0, kn=0.8 |
由上文可知,不同相对湿度下,用电量和气温拟合曲线斜率k的取值将直接决定临界点m, n的位置,并通过改变Tm和Tn,最终影响分段曲线的变化,为了能够更加精准地捕捉到RH在用电量分段中的影响,利用上文中所述方法,以Δk=0.1为步长,计算不同k值下的拟合结果,并通过选取RMSE最小值,确定最优取值为:km=1.0,kn=0.8,表 2给出气温阈值与RH的分段关系模型。
|
|
表 2 基于温湿度的日用电量分段模型——以天津为例 Table 2 Segmental model of daily electricity load based on temperature and humidity in Tianjin |
为了检验该模型引入相对湿度后的计算效果,本文选择常用的18.3℃为气温阈值的“V”型分段模型和采用门限回归模型(TR)计算的“U”型分段模型与文中分段方法进行对比。
门限回归模型在经济学分析中有很好的应用(Hansen, 1999),Moral-Carcedo and Vicéns-Otero (2005)研究表明,该方法也同样适用于研究用电量随气温变化的阈值,其中双阈值一元线性回归模型的计算公式为:
| $ D F= \begin{cases}\mu_{1}+\omega_{1} T+\varepsilon & T<n \\ \mu_{2}+\omega_{2} T+\varepsilon & m>T \geqslant n \\ \mu_{3}+\omega_{3} T+\varepsilon & T \geqslant m\end{cases} $ | (12) |
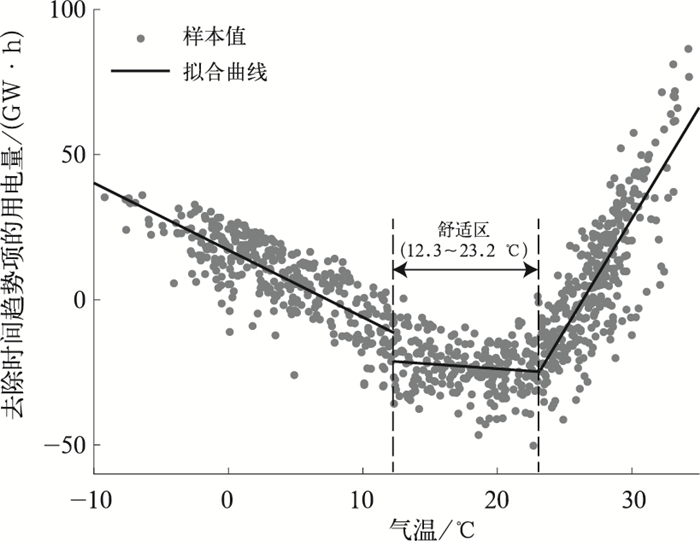
式中:DF代表去除时间趋势的日用电量,与式(2)中DF意义一致;T为平均气温;μ和ω为回归系数;ε是残差;m和n即为门限值,也即“U”型分段模型中的气温阈值。利用TR模型计算得到的舒适区气温阈值为23.2℃和12.3℃,如图 4所示。
|
图 4 基于TR模型的天津地区气温和用电量的拟合分布曲线 Fig. 4 Fitting curve of temperature and electricity load in Tianjin based on threshold regression model |
在以往研究对用电量与气温关系曲线的分析中,模型的不同会造成一定差异,为了提升评估的科学性和准确性,文中采用线性和非线性两种预测方法进行评估。
3.2.1 线性模型下的预测效果检验表 3给出基于式(1)的线性预测方法下的评估结果,可以看出,“U”型分段方法的预测效果整体优于“V”型。与不考虑相对湿度的传统“V”型相比,考虑相对湿度的“V”型分段方法(km=kn=0)能够将RMSE减小0.36 GW·h,MAPE减小0.141%。同样,在“U”型分段方法中,考虑相对湿度的日用电量预测效果均优于传统分段方法。其中基于温湿度日用电量分段模型(km=1.0,kn=0.8)的预测效果最好,与18.3℃的“V”型分段方法相比,日用电量预测的RMSE和MAPE分别减小1.562 GW·h和0.546%,较TR模型计算的“U”型分段方法相比,RMSE和MAPE分别减小0.253 GW·h和0.112%。
|
|
表 3 基于公式(1)的各类分段方法下日用电量预测效果对比 Table 3 Comparison of daily electricity load forecasting result by different segmentation methods based on Eq.(1) |
前文发现,Tm阈值对相对湿度更为敏感,因此表 3中给出舒适区与冷却区过渡范围内用电量的预测效果,对应分段曲线m在P为20%~80%时的气温阈值区间,选取气温在21.1~26.2℃的样本进行计算,相应值在括号中给出,可以看出,引入相对湿度后的RMSE和MAPE值分别减小了0.759 GW·h和0.215%,提升效果更加明显。
3.2.2 非线性模型下的预测效果检验文中确定分段方法时采用的线性不对称模型,一般来说,该模型比非线性模型的预测效果差,因此对应表 3中MAPE明显偏大。为了检验文中分段方法在非线性模型下适用能力,修改式(1)为:
| $ D=\sum\limits_{i=0}^{m} \alpha_{i} t^{i}+\sum\limits_{j=1}^{4} \beta_{j} I_{j}+\sum\limits_{k=1}^{n} \gamma_{k} V_{k}+\sum\limits_{g=1}^{2} \omega_{g} L_{g} D_{t-1}+\varepsilon $ | (13) |
式中:右侧前两项与式(1)意义一致;右侧第三项n取为3;V1代表度日值TP;V2代表度日值的平方值(TP)2;V3代表相对湿度;度日值的计算方法见式(14);由于用电量受到用电惯性及建筑热惯性的影响(Scapin et al, 2016),用第四项代表该效应,其中Dt-1代表预测日前一日用电量,对于周间的用电量差异,同样利用虚拟变量,L1和L2在预测周一和周二至周五时分别为1,其他时段为0,系数分别取为ω1和ω2。
| $ \begin{gathered} T P=\left(T-\bar{T}_{m}\right) \theta\left(T>\bar{T}_{m}\right)+\left(\bar{T}_{n}-T\right) \times \\ \theta\left(\bar{T}_{n}>T\right)+T \theta\left(\bar{T}_{m} \geqslant T \geqslant \bar{T}_{n}\right) \end{gathered} $ | (14) |
式中: Tm和Tn分别对应表 2中的阈值气温;θ为一个指标函数,当括号里的公式成立时取为1,否则为0。
非线性模型对比预测结果(表 4)表明,考虑相对湿度的用电量分段方法同样提升了非线性模型中的预测效果,与传统的“U”型分段模型相比,RMSE和MAPE值分别减小了0.316 GW·h和0.101%,针对舒适区和冷却区过渡区域的预测效果也有明显提升,RMSE和MAPE值分别减小了0.647 GW·h和0.209%。
|
|
表 4 基于式(12)各类分段方法下日用电量预测效果对比 Table 4 Comparison of daily electricity load forecasting result by different segmentation methods based on Eq.(12) |
综上看出,基于温湿度的日用电量分段方法的预测效果在线性和非线性模型中均有明显提升,这主要由于对数据实现了更为科学的分类,正确的分区提升了样本准确性,同时去除以往错误归入舒适区或冷却区的样本值对预测曲线的影响,从而提升了整体预测的准确性。
4 结论与讨论本文通过分析用电量和气象因子之间的非线性关系,提出了基于温湿度的日用电量分段新方法。并到如下结论:
(1) 日用电量对气温和相对湿度均表现出高敏感性,随着相对湿度的变化,用电量和气温之间的低敏感区范围(即舒适区)会发生明显偏移,并在冷却区与舒适区之间表现更为显著。
(2) 分析舒适区的气温阈值发现,随着相对湿度增大,Tm向低温一侧偏移,Tn则变化不大,因此舒适区范围会随相对湿度增大而变窄。
(3) 对预测效果评估结果显示,线性模型中,预测效果较传统“V”型和“U”型均有所提升,针对舒适区和冷却区过渡区,RMSE和MAPE值分别减小了0.759 GW·h和0.215%;非线性模型中同样表现出了较好的提升效果,RMSE和MAPE值分别减小了0.647 GW·h和0.209%,不同模型的预测效果均有提升且效果稳定,表明新方法在提升对气象敏感的电力需求预测的准确性上具有显著意义。
文中对临界斜率最优解的选取及对比均以天津地区为例,因此实际应用中会随着地区气候特点、居住环境的不同而有所差异。同时,Tn对相对湿度敏感较低,因此在实际业务中,Tn的计算可以仅考虑气温。
胡江林, 陈正洪, 洪斌, 等, 2002. 华中电网日负荷与气象因子的关系[J]. 气象, 28(3): 14-18, 37. Hu J L, Chen Z H, Hong B, et al, 2002. A relationship between daily electric loads and meteorological elements in central China[J]. Meteor Mon, 28(3): 14-18, 37 (in Chinese).
|
李海英, 杨冰芳, 孙伟卿, 2020. 基于即时学习差异化建模的用电量预测方法[J]. 电力系统及其自动化学报, 32(3): 14-19. Li H Y, Yang B F, Sun W Q, 2020. Lazy learning based diversity models for electricity consumption forecasting[J]. Proc the CSU-EPSA, 32(3): 14-19 (in Chinese).
|
刘俊, 赵宏炎, 刘嘉诚, 等, 2019. 基于协整-格兰杰因果检验和季节分解的中期负荷预测[J]. 电力系统自动化, 43(1): 72-80. Liu J, Zhao H Y, Liu J C, et al, 2019. Medium-term load forecasting based on cointegration-granger causality test and seasonal decomposition[J]. Automa Elec Power Sys, 43(1): 72-80 (in Chinese).
|
罗慧, 徐军昶, 肖波, 等, 2016. 气象因子对西安城市用电量的影响研究及中长期系统化预测[J]. 气象, 42(1): 54-60. Luo H, Xu J C, Xiao B, et al, 2016. Study on the impact of weather on electricity consumption in Xi'an and its application to mid-long term prediction[J]. Meteor Mon, 42(1): 54-60 (in Chinese).
|
乔黎伟, 王静怡, 郭炜, 等, 2020. 基于随机森林算法的中短期用电量预测[J]. 电力科学与技术学报, 35(2): 150-156. Qiao L W, Wang J Y, Guo W, et al, 2020. Medium and short-term electricity demand prediction based on random forests algorithm[J]. J Elec Power Sci Tech, 35(2): 150-156 (in Chinese).
|
任永建, 熊守权, 洪国平, 等, 2020. 气象因子对夏季最大电力负荷的敏感性分析[J]. 气象, 46(9): 1245-1253. Ren Y J, Xiong S Q, Hong G P, et al, 2020. Sensitivity analysis of meteorological factors to summer maximum power load[J]. Meteor Mon, 46(9): 1245-1253 (in Chinese).
|
石玉恒, 赵娜, 王凌, 等, 2019. 北京地区日最大电力负荷预测模型初探[J]. 中国电力, 52(8): 157-163. Shi Y H, Zhao N, Wang L, et al, 2019. Study on forecasting model of maximum daily power load in Beijing Area[J]. Elec Power, 52(8): 157-163 (in Chinese).
|
吴琼, 窦芳丽, 郭杨, 等, 2020. FY-3C微波成像仪海上大气可降水产品质量检验[J]. 气象, 46(1): 73-79. Wu Q, Dou F L, Guo Y, et al, 2020. Validation of FY-3C MWRI total precipitable water products[J]. Meteor Mon, 46(1): 73-79 (in Chinese).
|
尹炤寅, 范进进, 陈幼姣, 等, 2017. 体感温度对夏季气象负荷率变化的影响研究——以湖北省黄石市为例[J]. 气象, 43(5): 620-627. Yin Z Y, Fan J J, Chen Y J, et al, 2017. Impact of sensible temperature on summer weather—sensitive power load rate in Huangshi City[J]. Meteor Mon, 43(5): 620-627 (in Chinese).
|
张天航, 迟茜元, 张碧辉, 等, 2020. 全国网格化多模式集成空气质量预报的初步建立[J]. 气象, 46(3): 381-392. Zhang T H, Chi X Y, Zhang B H, et al, 2020. Development of gridding multi-model ensemble air quality forecast in China[J]. Meteor Mon, 46(3): 381-392 (in Chinese).
|
Al-Zayer J, Al-Ibrahim A A, 1996. Modelling the impact of temperature on electricity consumption in the eastern province of Saudi Arabia[J]. J Forecasting, 15(2): 97-106.
|
Apadula F, Bassini A, Elli A, et al, 2012. Relationships between meteorological variables and monthly electricity demand[J]. Applied Energy, 98: 346-356.
|
Barman M, Dev Choudhury N B, Sutradhar S, 2018. A regional hybrid GOA-SVM model based on similar day approach for short-term load forecasting in Assam, India[J]. Energy, 145: 710-720.
|
Bessec M, Fouquau J, 2008. The non-linear link between electricity consumption and temperature in Europe: a threshold panel approach[J]. Energy Economics, 30(5): 2705-2721.
|
Brown M A, Cox M, Staver B, et al, 2016. Modeling climate-driven changes in U.S.buildings energy demand[J]. Climatic Change, 134(1/2): 29-44.
|
Deschênes O, Greenstone M, 2011. Climate change, mortality, and adaptation: evidence from annual fluctuations in weather in the US[J]. Amer Economic J: Appl Economics, 3(4): 152-185.
|
Gupta E, 2012. Global warming and electricity demand in the rapidly growing city of Delhi: a semi-parametric variable coefficient approach[J]. Energy Economics, 34(5): 1407-1421.
|
Hansen B E, 1999. Threshold effects in non-dynamic panels: Estimation, testing, and inference[J]. J Econometrics, 93(2): 345-368.
|
Hekkenberg M, Moll H C, Uiterkamp A J M S, 2009. Dynamic temperature dependence patterns in future energy demand models in the context of climate change[J]. Energy, 34(11): 1797-1806.
|
Lee C C, Chiu Y B, 2011. Electricity demand elasticities and temperature: evidence from panel smooth transition regression with instrumental variable approach[J]. Energy Economics, 33(5): 896-902.
|
Mirasgedis S, Sarafidis Y, Georgopoulou E, et al, 2006. Models for mid-term electricity demand forecasting incorporating weather influences[J]. Energy, 31(2): 208-227.
|
Moral-Carcedo J, Vicéns-Otero J, 2005. Modelling the non-linear response of Spanish electricity demand to temperature variations[J]. Energy Economics, 27(3): 477-494.
|
Pardo A, Meneu V, Valor E, 2002. Temperature and seasonality influences on Spanish electricity load[J]. Energy Economics, 24(1): 55-70.
|
Scapin S, Apadula F, Brunetti M, et al, 2016. High-resolution tempera- ture fields to evaluate the response of Italian electricity demand to meteorological variables: an example of climate service for the energy sector[J]. Theor Appl Climat, 125(3): 729-742.
|
Wang Y P, Bielicki J M, 2018. Acclimation and the response of hourly electricity loads to meteorological variables[J]. Energy, 142: 473-485.
|
 2021, Vol. 47
2021, Vol. 47 