我国西部山地地区位于青藏高原东部,既受不同尺度天气系统相互作用,也受复杂地形的影响,发生的突发性山地暴雨也是我国主要自然灾害之一,预报难度非常大(彭贵康等,1994;宇如聪等,1994;肖递祥等,2012;高珩洲和李国平,2020;张芳丽等,2020)。西部山地暴雨的影响系统具有非线性特征,再加上观测资料和模式固有的误差,单一确定性预报存在一定局限性,因此采用集合预报技术是解决西部山地暴雨预报不确定性的一种有效途径。
集合预报系统的预报不确定性来源包括初始条件误差、边界条件误差和模式误差。初值扰动可以体现由观测及模式分析场存在的误差所造成的不确定性,其研究开始较早也更加成熟,代表性方案包括奇异向量法(Molteni et al,1996;Ehrendorfer and Tribbia, 1997)、增长模繁殖法(Toth and Kalnay, 1993;1997)、集合变换卡尔曼滤波(Bishop et al,2001;Wang and Bishop, 2003)和条件非线性最优扰动(Mu and Zhang, 2006)等。区域模式侧边界扰动方法通常考虑由全球集合预报动力降尺度为区域集合提供边界条件(张涵斌等,2017;范宇恩等,2019)。仅采用初值扰动方法的集合预报普遍存在离散度偏小的问题,因此考虑模式不确定性的扰动技术也是集合预报研究的一个重点方向。模式扰动代表性方案主要有以下3种:(1)多模式扰动方案,即利用组合多个不同模式描述模式动力过程及物理过程的不确定性(Krishnamurti et al,1999);(2)多物理参数方案,即利用不同的物理参数化方案表达物理过程的不确定性(Houtekamer et al, 1996);(3)随机物理扰动方案,即通过在模式物理参数化过程加入随机扰动综合考虑次网格物理过程的不确定性。与多模式或多物理场集合不同,随机物理扰动方案使用具有相同物理参数化的单一模式实现集合成员具有同等可能性的预报结果(Romine et al,2014)。近年来,模式随机物理扰动已成为集合预报系统扰动技术研究的重要方向之一(杜钧和李俊,2014)。随机物理扰动方案又可以分为随机动能后向散射方案(stochastic kinetic energy backscatter scheme,SKEBS;Shutts,2005;Berner et al,2009;2011;2015;Duda et al,2016;张涵斌等,2019)、随机物理倾向扰动方案(stochastically perturbed parametrization tendencies,SPPT;Buizza et al,1999;Palmer et al,2009)和随机参数扰动方案(Bowler et al,2008; Hacker et al,2011; 徐致真等,2019;陈雨潇等,2020)。
SPPT作为一种模式随机物理扰动方法,最早应用在全球集合预报系统中。Buizza et al(1999)在欧洲中心集合预报系统中总物理参数化过程倾向上引入乘性噪声扰动,设计了随机物理倾向扰动方案(BMP方案,由Buizza、Miller和Palmer三人名字首字母命名,其为最初的SPPT;Buizza et al,1999)。该方案基于以下概念,即物理参数化强迫中的随机误差在不同的参数化模块之间是一致的,并且在与有组织对流方案相关的空间和时间尺度上具有一定的一致性。而且该方案假设参数化倾向越大,随机误差分量越大。但是,BMP方案使用空间和时间分段常数的随机数。对于最初的实现来说这是一个方便的选择。然而,在随机数发生变化的地方和时间,扰动存在不连续性,这在某种程度上是不符合物理实际的。于是Palmer et al(2009)提出了改进SPPT方案,用单变量扰动替换BMP方案中的多变量扰动,在时间和空间上更为连续,使扰动在物理方案中保持一致性,具有一定的物理意义,有效抑制由不同变量扰动引起能量不匹配而导致计算崩溃现象,尤其是温度场和湿度场的扰动。任志杰等(2011)和谭宁等(2013)在我国T213集合预报系统开展扰动物理倾向方案的应用研究,发现加入物理过程随机扰动后,对模式预报变量可产生较明显的影响。李晓莉等(2019)、陈静和李晓莉(2020)在GRAPES全球集合预报系统(GRAPES_GEPS)中引入了SPPT方案,可有效提高在南北半球和热带地区等压面要素预报的集合离散度,同时减小集合平均误差。
随机物理扰动方法也越来越多地应用到区域模式当中(张涵斌等,2017;孔凡铀,2018;王璐和沈学顺,2019)。法国气象局的对流尺度集合预报系统AROME-EPS(Bouttier et al,2012)在2.5 km的水平分辨率下,增加了SPPT方案作为模式扰动,可以显著改进概率预报的性能,尤其是在集合可靠性和离散度技巧一致性方面。个例研究结果表明,随机物理方法不仅会增加整体离散度,而且有助于将高离散度区域平滑到更大范围区域。尽管整体设计缺少地面扰动,但通过模式中的物理过程相互作用,SPPT对低层物理量场也会有重要的最终影响。GRAPES区域集合预报系统(GRAPES_MEPS)引入了SPPT方案,开展不同随机场扰动幅度和时间尺度参数敏感性的集合预报试验,并确定适用于GRAPES_MEPS的SPPT方案中随机扰动场的优化参数设置,即采用较大随机扰动幅度([0.2,1.8],均值为1),及6 h去相关时间尺度的随机型,表明SPPT方案在一定程度上可提高系统的预报技巧,降低系统的漏报率(袁月等,2016)。Berner et al(2015)将SPPT方案引入WRF模式中,并在45 km网格间距下测试SKEB和SPPT,发现这些模式误差方案在整个大气中都是有益的,尤其是在地表附近。Romine et al(2014)基于SKEB、PLBC(侧边界扰动)和SPPT利用3 km水平分辨率WRF模式对美国中部开展1个月的30个集合成员预报试验。SPPT试验对于大多数变量的集合离散度增长最大,其次是SKEB和PLBC试验。其中SPPT试验的随机数选择中尺度天气过程的经验参数(去相关空间尺度为150 km, 去相关时间尺度经验性由6 h减少为1 h和格点标准差为0.35)。与同一模式较粗分辨率的试验相比,水平网格间距为3 km时,SPPT的影响要大得多。特别是在该研究中,SPPT模拟的离散度和均方根误差明显大于SKEB模拟,与Berner et al(2015)发现的情况正好相反。为了使模式误差方案适应云分辨率,对方案进行调整可能是造成某些差异的原因。李俊等(2015)对KF对流参数化方案和YSU边界层参数化方案进行随机扰动试验,研究发现随机物理产生的离散度比初值扰动和多物理方案偏小,其离散度贡献主要集中在较小尺度上,未考虑随机扰动场在空间和时间上的关联性可能成为限制离散度增长的一个原因。蔡沅辰等(2017)利用3 km水平分辨率(内层区域)的WRF模式,针对安徽一次暴雨过程调整SPPT方案的随机扰动场的时空尺度达到最优配置,改善预报效果,并提出将SPPT和SKEB组合构建的混合扰动方案。闵锦忠等(2018)基于4 km水平分辨率(内层区域)的WRF模式选取江淮流域一次强降水过程探讨SPPT在风暴尺度集合预报中的影响。研究发现造成降水主要天气系统的维持时间对去相关时间参数的选取有较大影响,去相关空间尺度的选取与天气过程中的大尺度信息、中小尺度系统的活跃以及模式的空间分辨率有一定关系,且在一定范围内,扰动振幅越大集合预报系统设计越合理,这些为风暴尺度集合预报的改进提供参考。Qiao et al(2018)在ARPS模式中利用SPPT方法对微物理参数化方案的温度倾向(stochastically perturbed temperature tendency from microphysics method,SPTTM)进行扰动,开展理想超级单体的集合预报初步研究。其去相关空间尺度的选取基于研究对象约为50 km水平空间尺度,评估扰动尺度大于、相当于或小于50 km的影响。不同的标准差有助于确定最佳扰动振幅,过大的标准差可能导致不稳定,而过小的标准差可能不够。鉴于早期研究去相关时间尺度大于60 min会导致数值不稳定,所以试验选用30 min的去相关时间尺度。Lupo et al(2020)以美国及台湾地区三个中尺度暴雨事件为例,对3 km水平分辨率(内层区域)的WRF模式中SPPT和iSPPT(independent SPPT; Christensen et al, 2015; 2017)配置进行了敏感性研究,主要关注降水的集合均值和标准差以及预测技巧。研究发现,降水的标准差对扰动时间尺度和振幅尺度调整最为敏感。
自从Buizza et al(1999)引入SPPT以来,随机场的振幅、时间和空间尺度参数仍然是不完全了解的参数,随机扰动可能与流依赖有关(Leutbecher et al,2017),Bouttier et al(2012)进一步指出,SPPT参数配置应基于观测的天气条件。因此,SPPT方法的随机扰动场应当具有时间和空间变化特征,且其时、空尺度以及扰动振幅与模式配置和个例选取有一定关系。目前,国内已有SPPT研究多针对我国华北、长江中游、黄淮以及江淮流域降水,对我国西部复杂地形下的对流尺度集合预报研究较少。为此,基于SPPT利用WRF V3.9模式开展随机扰动场参数的敏感性试验,对2018年5月21—22日发生在四川盆地南部和东部一次强对流天气过程进行数值模拟,研究西部复杂地形条件下对流尺度集合预报中的扰动演变规律,为西部山地集合预报的模式扰动技术提供科学依据。
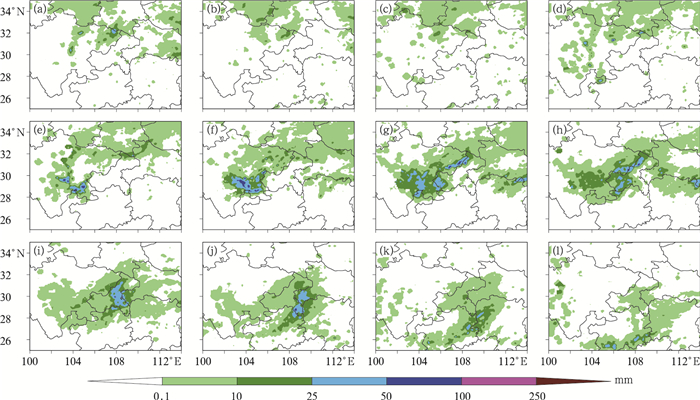
1 个例和模式介绍2018年5月21—22日在我国西部地区四川盆地的南部和东部受西南低涡移动的影响发生一次强降水过程。部分地区3 h累计降水可达到50 mm以上,降水区域直径不超过200 km(2°左右),是一次典型的突发性山地暴雨过程(张芳丽等,2020)。主要降水时段为2018年5月21日12时至22日12时(UTC,下同;图 1)。针对这次强降水过程,利用WRF V3.9模式开展SPPT方案的敏感性试验。模拟区域中心位于29.0°N、106.5°E,单层网格,水平分辨率为3 km,格点数为700×700,模拟的区域范围19.3°~38.6°N、95.4°~117.6°E(图略),垂直方向为51层,模式顶层气压为30 hPa,积分时间步长20 s。模拟试验的时间范围为2018年5月21日00时至22日12时,预报时效为36 h,其中12~36 h预报涵盖了观测的主要降水时间段。控制试验的主要物理参数化方案是Thompson graupel微物理方案、MYNN3边界层参数化方案、RRTMG长波和短波辐射方案、RUC陆面模式、无积云对流参数化方案。初始场和侧边界均由NCEP 0.5°×0.5°全球预报系统(GFS)数据提供。用到的对比检验降水观测数据是中国国家气象信息中心提供的0.1°×0.1°网格化逐时实况降水融合数据,温度、风场、湿度场实况数据为欧洲中心再分析ERA5数据,时间分辨率为逐小时,高空水平分辨率为0.25°×0.25°,地面水平分辨率为0.1°×0.1°。
|
图 1 2018年5月21日00时至22日12时逐3 h降水实况 (a)21日00—03时,(b)21日04—06时,(c)21日07—09时,(d)21日10—12时,(e)21日13—15时,(f)21日16—18时,(g)21日19—22时,(h)21日22时至22日00时,(i)22日01—03时,(j)22日04—06时,(k)22日07—09时,(l)22日10—12时 Fig. 1 The 3 h accumulated precipitation from 0000 UTC 21 to 1200 UTC 22 May 2018 (a) 0000-0300 UTC 21, (b) 0400-0600 UTC 21, (c) 0700-0900 UTC 21, (d) 1000-1200 UTC 21, (e) 1300-1500 UTC 21, (f) 1600-1800 UTC 21, (g) 1900-2200 UTC 21, (h) 2200 UTC 21 to 0000 UTC 22, (i) 0100-0300 UTC 22, (j) 0400-0900 UTC 22, (k) 0700-0900 UTC 22, (l) 1000-1200 UTC 22 |
SPPT方案在WRF中的实现与ECMWF实现(Palmer et al,2009)密切相关,但也有微小差异(Berner et al,2015)。该方案考虑了模式次网格尺度物理参数化过程的不确定性,对模式物理参数化方案的总倾向进行扰动,即模式在非绝热物理过程参数化方案计算结束后得到的总温度倾向项、风场倾向项、湿度倾向项上,乘以一个随机扰动场来表达次网格物理过程的不确定性(图 2)。SPPT方案应用在调用微物理参数化之前的物理参数化方案(辐射传输、边界层过程、积云对流、浅对流、火灾、四维资料同化张弛逼近法等)倾向ε之前。

|
图 2 SPPT方案在模式中实现示意图 Fig. 2 Illustration of of SPPT applied in model |
其数学模型基于用一个乘性噪声项来体现物理参数化方案的不确定性,线性扰动总的物理量参数化倾向(式1)。
| $ \frac{\partial x}{\partial t}=\frac{\partial x_{\mathrm{dyn}}}{\partial t}+(1+r) \frac{\partial x_{\text {param }}}{\partial t} \quad|r| \leqslant 1 $ | (1) |
式中: x∈(u, v, T, q),等式左边表示每个格点的总倾向,它包括了等式右边的运动方程数值离散化的“动力倾向”(∂xdyn/∂t)和物理参数化的“物理倾向”(∂xparam/∂t)。∂xparam/∂t用相同的单变量随机场r(x, y, t)扰动,确保了不同变量的相对变化与未扰动系统的相对变化成比例,并防止因产生重力波而进行的快速调整(Berner et al,2015)。r为满足高斯分布的随机数,平均值为0,标准偏差为η2,且具有一定的时空相关性r(x, y, t)。|r|≤1用来限制倾向扰动的绝对值在[0, 2|∂xparam/∂t|]。
在ECMWF中,随机扰动形态是具有不同时空特性的两个(或更多)独立随机扰动形态的总和。第一种随机扰动形态模拟全球“快速”演变天气尺度的不确定性,其水平相关空间长度尺度为500 km,相关时间尺度为6 h。第二种随机扰动形态代表缓慢演变的行星尺度误差,因此具有数千千米的相关空间长度尺度和1个月相关时间尺度。在WRF实现中,只使用一个表示中尺度不确定性(默认情况下)的随机扰动场。将式(1)的随机扰动场r(x, y, t)进行二维傅里叶展开:
| $ r(x, y, t)=\sum\limits_{k=-K / 2}^{K / 2} \sum\limits_{l=-L / 2}^{L / 2} r_{k, l}(t) \mathrm{e}^{2 \pi i(k x / X+l y / Y)} $ | (2) |
式中: k和l分别表示纬向x和经向y的波数,t表示积分时间,
| $ r_{k, l}(t+\Delta t)=(1-\alpha) r_{k, l}(t)+g_{k, l} \varepsilon_{k, l}(t) $ | (3) |
式中: 1-α是线性自回归参数,gk, l为依赖波数的扰动振幅,εk, l是一个同时满足均值〈εk, l(t)〉=0和方差〈εk, l(s)εm, n*(t)〉=δk, lδl, nδs, t复值高斯白噪声过程(*表示共轭)。
rk,l随时间变化特征由自回归参数控制,定义一个去相关时间参数(简称为时间尺度参数,下同)τ=Δt/α, 其中Δt为模式积分步长。gk,l是具有空间的自相关扰动振幅(Weaver and Courtier, 2001):
| $ g_{k, l}=F_{0} \mathrm{e}^{-4 \pi \kappa \rho_{k, l}^{2}} $ | (4) |
式中:
从SPPT方案的随机扰动场构造可以看出,其主要由三个参数确定:时间尺度(τ)、空间尺度(κ),以及每个格点标准差(η)。τ表示在τ所在范围的每个时段中每次积分步长间的随机扰动值具有相关性,在两个不同τ中随机扰动值不相关。τ值越大,随机扰动场随时间变化的频率越低,反之越高。κ表示在参数所在的每个空间范围内格点之间的随机扰动值均具有相关关系,在两个不同的κ范围中不相关,κ值越大,随机扰动场空间尺度越大,反之越小。η表示扰动振幅的大小,η值越大,扰动振幅越大,反之越小。
2.2 试验方案设计本文重点关注物理过程不确定性对预报结果的影响,故在方案设计中没有引入对初值和侧边界的扰动。蔡沅辰等(2017)对比了多组试验后得出空间尺度为60 km、时间尺度为3 h和格点标准差为0.5的配置在所分析个例中能获得更好的集合预报效果。闵锦忠等(2018)经过研究得出空间尺度为100 km、时间尺度为6 h和格点标准差为0.525的配置在所分析个例中对24 h降水预报技巧更高。本研究关注的个例发生在复杂地形地区,受多尺度天气影响,降水具有突发性、历时短、强度大的特点。模式水平分辨率为3 km,可分辨对流尺度系统。根据以往研究经验(Bouttier et al,2012;Romine et al,2014;蔡沅辰等,2017;闵锦忠等,2018),结合模式设置及个例特点,为研究SPPT方案中适用于西部山地复杂地形的对流尺度预报,针对随机扰动场的三个参数进行敏感性试验。考虑空间尺度为90 km和30 km,时间尺度为6 h和3 h,格点标准差为0.5和0.525,同时尽可能地避免其他参数的干扰,每组试验选用的物理过程和控制试验相同,通过改变SPPT方案中的随机种子生成8个集合成员(加控制试验共9个集合成员),且每组试验对应成员的随机种子相同,设计如表 1所示的五组试验。
|
|
表 1 试验方案设计 Table 1 Sensitivity experiment design |
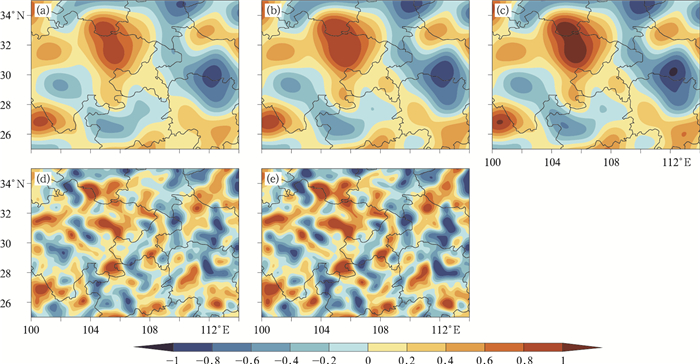
图 3给出表 1中五组试验对应的同一集合成员(以M01成员为例)在不同预报时间(以3 h为例)对应的随机扰动结构。如图所示,SPPTh90t6s0.5、SPPTh90t3s0.5和SPPTh90t3s0.525的随机扰动场空间分布特征非常接近,较明显的差别是扰动振幅的大小。SPPTh30t6s0.5和SPPTh30t3s0.5也有类似的特点。另外,扰动振幅的调整主要影响扰动的中心强度,对扰动结构和分布没有影响。与其他预报时效的随机扰动场对比,各试验的扰动场具有随时间变化的特征(图略)。随机扰动场在垂直方向上也保持不变(图略)。
|
图 3 SPPTh90t6s0.5(a)、SPPTh90t3s0.5(b)、SPPTh90t3s0.525(c)、SPPTh30t6s0.5(d)和SPPTh30t3s0.5(e)试验中集合成员1(M01)在预报3 h时的随机扰动场结构 Fig. 3 The random fields for 3 h lead time forecast of member 01 in the experiment SPPTh90t6s0.5 (a), SPPTh90t3s0.5 (b), SPPTh90t3s0.525 (c), SPPTh30t6s0.5 (d) and SPPTh30t3s0.5 (e) |
以下将从高空要素预报分析、近地面要素预报分析、扰动振幅的敏感性,以及降水集合平均、离群率及其概率预报等方面,对这次强降水过程中不同随机扰动场参数下SPPT方案的试验(表 1)结果进行对比评估。
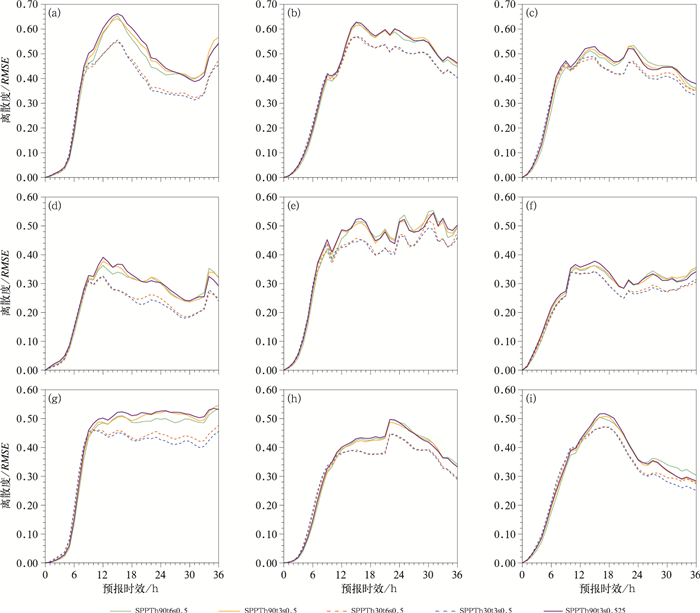
3.1 高空要素的预报分析图 4给出各组试验中不同层次(200、500和700 hPa)上的纬向风场(u)、温度场(T)、湿度场(q)的离散度和均方根误差(RMSE)随预报时效(0~36 h)的变化。整体来看,每组试验在各层次上不同高空要素的离散度在较短预报时效内快速增加达到饱和,之后逐渐减小,在积分的后期一般又开始增加。在200 hPa高度,水平风场积分到约18 h增速放缓,温度场在积分约15 h、湿度场在积分约12 h增速减慢,纬向风场达到饱和的时间晚于温度场和湿度场。500 hPa和700 hPa具有类似变化规律。

|
图 4 五组试验的u(a, b, c),T(d, e, f),q(g, h, i)的离散度和RMSE随预报时效的变化 (a,d,g)200 hPa,(b,e,h)500 hPa,(c,f,i)700 hPa Fig. 4 Changes of spreads and RMSEs of u (a, b, c), T (d, e, f), q (g, h, i) in 5 experiments with forecast lead time (a, d, g) 200 hPa, (b, e, h) 500 hPa, (c, f, i) 700 hPa |
以下具体分析不同试验间的离散度变化规律。此处先比较在相同格点标准差0.5的条件下,不同时间和空间尺度参数的试验(SPPTh90t6s0.5、SPPTh90t3s0.5、SPPTh30t6s0.5和SPPTh30t3s0.5) 结果,将在3.3节中讨论调整格点标准差SPPT-h90t6s0.525试验结果。从图 4可见,在积分约9 h之前,各组试验的风场、温度场和湿度场在不同气压层的离散度比较接近,空间尺度30 km的试验(SPPTh30t6s0.5和SPPTh30t3s0.5)略大于空间尺度90 km的试验(SPPTh90t6s0.5、SPPTh90t3s0.5)。在积分约9 h之后,空间尺度90 km的试验(SPPT-h90t6s0.5、SPPTh90t3s0.5)的风场、温度场和湿度场离散度迅速增大,明显大于空间尺度30 km的试验(SPPTh30t6s0.5和SPPTh30t3s0.5)。
时间尺度参数对离散度的影响没有空间尺度明显。空间尺度选择90 km,不同时间尺度的敏感性试验(SPPTh90t6s0.5和SPPTh90t3s0.5)在各个层次纬向风场、温度场、湿度场的离散度随时间的变化趋势较一致。积分前约12 h,两组试验在200 hPa风场离散度比较接近,SPPTh90t3s0.5略大于SPPTh90t6s0.5,之后,SPPTh90t3s0.5增加较快,到积分约24 h后,两者相差不大。温度场和湿度场离散度的变化与风场类似。随着气压增加到500 hPa,两组试验的离散度大小非常接近,尤其是风场和湿度场。到700 hPa,SPPTh90t3s0.5中的风场离散度在积分前20 h小于SPPTh90t6s0.5,之后大于SPPTh90t6s0.5,温度场和水汽场离散度变化与风场类似。空间尺度选择30 km,分析时间尺度分别为6 h和3 h的敏感性试验(SPPTh30t6s0.5和SPPTh30t3s0.5)的离散度。两组试验的风场、温度场、湿度场的离散度在各个气压层的变化趋势相同,与空间尺度90 km的试验类似。在积分的前期,时间尺度3 h的离散度接近或略大于时间尺度6 h的试验。在积分的中期和后期,时间尺度3 h的离散度接近或者小于时间尺度6 h的试验。在500 hPa气压层,两组试验的离散度变化曲线几乎重合,尤其是风场和湿度场。
从各组试验中不同层次上的纬向风场、温度场、湿度场集合平均的RMSE随预报时效的变化(图 4)来看,每组试验在各层次上不同高空要素的RMSE变化趋势非常一致。风场在200 hPa的RMSE大于500 hPa和700 hPa,温度场和湿度场在700 hPa的RMSE最大。与离散度相比,不管时间尺度和空间尺度的大小,各组试验的RMSE非常接近,尤其在积分的前期,大小几乎没有差别。到了积分的中期和后期,空间尺度90 km试验的RMSE整体上略大于空间尺度30 km试验。时间尺度参数6 h和3 h的试验对RMSE的影响较小。
一个好的集合预报系统具有合理的离散度,同时较为接近实际单模式预报的RMSE(张涵斌等,2017)。离散度过大会导致虚假预报,过小则会导致较多漏报。集合系统的扰动应当和可观测到的预报误差具有相当的增长率,集合成员间的离散度同集合平均的预报误差大体相当。因此,将预报误差考虑在内,用离散度与集合平均的RMSE的比值作为离散度技巧进一步来衡量集合预报的合理性(蔡沅辰等,2017;武天杰和闵锦忠,2020)。如果两者的比值趋近于理想值1,则该试验的离散度可以更好地度量预报误差的变化。如果两者比值大于1,则表示该试验出现过发散现象,反之则发散不够(蔡沅辰等,2017)。图 5是各组试验中不同层次上的纬向风场、温度场、湿度场离散度/RMSE随预报时效的变化。整体来看,离散度/RMSE小于1,即集合成员间的离散度较预报误差偏小,其随时间变化规律与离散度表现比较类似。扰动的空间尺度选择较大的90 km时,在积分前期(约0~9 h)时,风场在200 hPa的集合离散度/RMSE小于空间尺度30 km试验,之后增长速度很快,超过空间尺度30 km试验的离散度/RMSE,更接近于理想值1。其他要素在不同高度上的离散度/RMSE也有类似变化规律。时间尺度参数对离散度/RMSE的影响,也没有空间尺度明显。在积分的前期和中期,时间尺度3 h的离散度接近或略大于时间尺度6 h的试验。在积分的后期,时间尺度3 h的离散度接近或者小于时间尺度6 h的试验。在500 hPa气压层,两组试验的离散度变化曲线几乎重合,尤其是风场和湿度场。
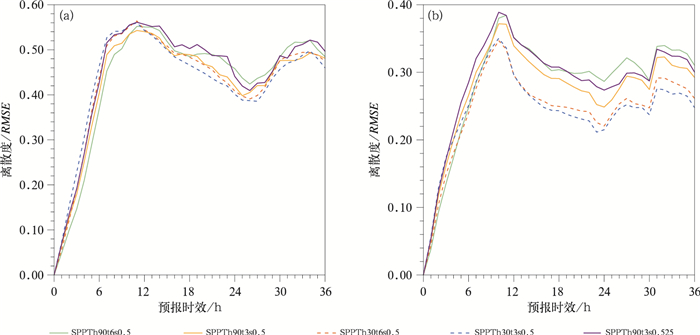
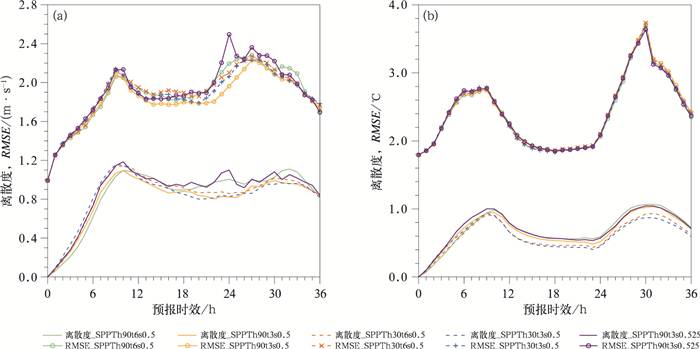
3.2 近地面要素的预报分析图 6给出各组试验中10 m纬向风和2 m温度的离散度和RMSE随预报时效变化。整体来看,近地面要素的离散度在积分前约9 h内快速增加达到饱和。具体分析不同空间尺度的试验可以发现,在积分约9 h之前,空间尺度30 km试验10 m纬向风的离散度大于空间尺度90 km的,之后,空间尺度30 km试验的离散度下降较快。2 m温度的离散度变化与10 m纬向风表现相似。分析不同时间尺度试验可以发现,在积分约9 h之前,时间尺度3 h试验10 m纬向风的离散度略大于时间尺度6 h试验,之后,时间尺度3 h试验的离散度下降较快。2 m温度的离散度变化与之类似。
|
图 6 五组试验的10 m纬向风(a)和2 m温度(b)的离散度和RMSE随预报时效的变化 Fig. 6 Changes of spreads and RMSEs of 10 m zonal wind (a) and 2 m temperature (b) in 5 experimerts with forecast lead time |
从各组试验中10 m纬向风和2 m温度的RMSE随预报时效变化(图 6)来看,每组试验10 m纬向风的RMSE变化比较一致。在积分前期约9 h,各组试验10 m纬向风的RMSE比较接近,空间尺度30 km试验的略大于空间尺度90 km,其中SPPTh30t3s0.5的RMSE最大,SPPTh90t6s0.5的RMSE最小。到了积分中期,SPPTh90t3s0.5的RMSE下降最快,SPPTh30t6s0.5降低速度最慢。到了积分约21 h,各试验的RMSE又开始增加,SPPTh90t6s0.5最大,SPPTh90t3s0.5最小。到了积分30 h,各试验RMSE又逐渐变小且越来越接近。2 m温度的RMSE试验之间相差很小。
图 7是各组试验中10 m纬向风和2 m温度的离散度/RMSE随预报时效的变化。整体来看,离散度/RMSE随时间变化与离散度表现比较类似。扰动的空间尺度选择90 km时,在积分约9 h之前,10 m纬向风的离散度/RMSE小于空间尺度30 km,之后,下降速度较空间尺度30 km慢,更接近于理想值1。在不同时间尺度条件下,时间尺度3 h在积分约9 h之前的离散度/RMSE更接近于1,之后,时间尺度6 h的试验更接近1。2 m温度的离散度/RMSE变化与之类似。
3.3 扰动振幅敏感性分析基于前面高空和地面要素的离散度分析,可知在格点标准差为0.5的情况下,随机扰动场的时间尺度参数为3 h、空间尺度参数为90 km时,水平风场、温度场和湿度场在各层的离散度较大,且离散度/RMSE更接近与理想值1,能更好地度量预报误差的变化。但同时发现,这个随机扰动配置虽然对近地面要素离散度相对于空间尺度30 km的试验有所改善,但是却不如时间尺度6 h、空间尺度90 km的试验的离散度大。Berner et al(2015)指出在保证计算稳定的前提下应使扰动振幅尽可能大。在前面试验格点标准差η=0.5的基础上,增加5%调整为0.525设计增加扰动振幅的试验,时间尺度选为3 h和空间尺度选为90 km,即试验SPPT-h90t3s0.5和SPPTh90t3s0.525,以此来研究不同扰动振幅对高空和近地面要素的影响。
从SPPTh90t3s0.5和SPPTh90t3s0.525试验的离散度随积分时间的变化(图 4)中可见,两组试验在各层次上的水平风场、温度场、湿度场离散度随时间变化趋势一致。在积分的前期和中期,SPPT-h90t3s0.525的离散度普遍大于前者,到积分后期,SPPTh90t3s0.525的离散度则接近或者略小于SPPTh90t3s0.5。两组试验高空要素的RMSE的变化(图 4)和大小也比较接近,离散度/RMSE的变化规律(图 5)与离散度类似。
从近地面要素离散度变化(图 6)来看,增加扰动振幅可以较好地改善整个积分时段的离散度。在积分前期,SPPTh90t3s0.525的10 m纬向风离散度接近于空间尺度30 km的,在积分中期和后期,离散度接近于时间尺度6 h的试验结果,大于SPPTh90t3s0.5。2 m温度的离散度也有类似的变化。增加扰动振幅的试验中近地面要素的RMSE(图 6)也有所增加,但离散度/RMSE(图 7)比SPPTh90t3s0.5更接近理想值1。
3.4 降水预报的检验降水是预报中最关注的一个要素。以下从集合平均降水、Talagrand分布和离群率及概率预报等多方面对这次降水过程的结果进行对比评估,分析不同时间尺度、空间尺度和格点标准差对降水预报结果的影响。
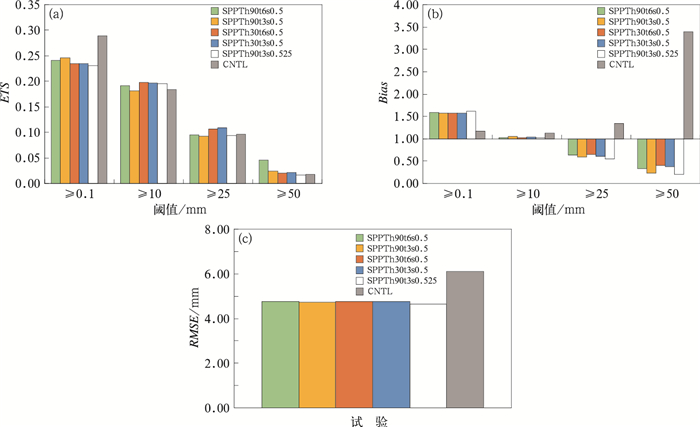
3.4.1 集合平均降水的检验图 8给出了3 h累积降水集合平均(等权重算术平均)在各量级(≥0.1 mm、≥10 mm、≥25 mm、≥50 mm)的ETS评分、偏差(Bias)评分和RMSE。ETS是一种确定性降水评分方法,分值越高预报技巧越高。在本次对流尺度的集合预报中,采用SPPT方案相对于控制试验可以提高预报技巧,3 h累积降水的集合平均在≥10 mm、≥25 mm和≥50 mm的降水等级的ETS评分接近或者高于控制试验。
|
图 8 3 h累积降水的ETS(a)、Bias(b)和RMSE(c) (CNTL为控制试验) Fig. 8 ETS (a), Bias (b) and RMSE (c) of 3 h accumulated precipitation (CNTL is the control experiment) |
空间尺度为90 km的集合平均降水在≥0.1 mm和≥50 mm上ETS评分好于空间尺度30 km的试验,在≥10 mm和≥25 mm低于空间尺度30 km的试验。空间尺度固定为90 km,不同时间尺度试验的ETS有较明显的差别,如SPPTh90t3s0.5在≥0.1 mm量级的ETS大于SPPTh90t6s0.5,在≥10 mm、≥25 mm和≥50 mm小于SPPTh90t6s0.5。但是对于空间尺度固定为30 km,不同时间尺度试验的ETS相差不大。扰动振幅的增加(SPPTh90t3s0.525) 改善了≥10 mm的ETS,但在≥0.1 mm和≥50 mm量级上ETS低于SPPTh90t3s0.5,在≥25 mm的ETS与SPPTh90t3s0.5相当。
Bias越接近1,模拟结果与实况越接近。从图 8b可以看到,各扰动试验在≥0.1 mm的Bias大于1,模拟存在湿偏差,对≥10 mm量级降水的Bias最接近1,对于≥25 mm和≥50 mm以上量级降水的Bias都小于1,模拟存在干偏差。时间尺度6 h或空间尺度30 km试验的Bias在≥10 mm、≥25 mm和≥50 mm量级上更接近1。增加扰动振幅(SPPT-h90t3s0.525)试验的Bias与SPPTh90t3s0.5相差不多,比SPPTh90t6s0.5偏干或偏湿程度略大一点。
RMSE可以用来衡量集合平均降水与实况之间的偏差。从图 8c来看,各组扰动试验的降水的RMSE相差不大,且都小于控制试验的结果,其中增加扰动振幅试验略微小于其他扰动试验。
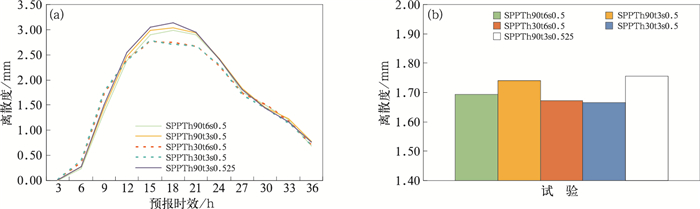
3.4.2 Talagrand分布和离群值检验首先,分析了不同扰动试验的降水离散度的情况。图 9是3 h累积降水的离散度随积分时间的变化及时间平均。从时间变化来看(图 9a),降水离散度随预报时间的延长先增加再减少。空间尺度参数对降水离散度的影响比时间尺度参数明显,尤其是在积分中期(12~36 h)。空间尺度90 km的试验在积分前期(0~12 h)降水离散度小于空间尺度30 km的试验结果。到了积分中期(12~36 h)空间尺度90 km试验的降水离散度增长很快,大于空间尺度30 km离散度,其中空间尺度90 km试验在积分18 h达到最大值,而空间尺度30 km在15 h达到最大值。到了积分约24 h之后,两种空间尺度试验离散度差别不大。不同时间尺度试验的降水离散度非常接近,只有当空间尺度固定为90 km时可以看出,时间尺度3 h试验的降水离散度在积分中期大于时间尺度6 h试验结果。此外,扰动振幅的增加,可以改善降水的离散度,特别是在积分中期,明显大于SPPTh90t3s0.5及其他扰动试验。从积分时间平均来看,SPPTh90t3s0.5和SPPTh90t3s0.525试验的降水离散度大于其他试验,且后者略大于前者。
|
图 9 3 h累积降水集合离散度随积分时间变化(a)和时间平均(b) Fig. 9 Temporal variations (a) and temporal averages (b) of 3 h accumulated precipitation for ensemble spread |
Talagrand分布直方图(Talagrand et al,1997;Hamill,2001)是检验离散度的方法之一,可以用来统计观测与集合预报成员的概率分布差异。概率均方差(谭燕和陈德辉,2007;李俊等,2020)是Talagrand频率分布与理想频率分布之间的均方差,也可以用来度量离散度适宜性。
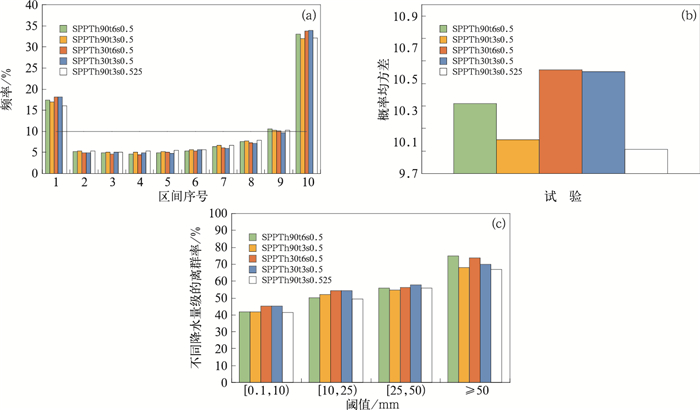
图 10a为各组试验3 h累积降水预报的Talagrand分布,其中横线为9个集合预报成员(含控制试验)的理想概率分布(10%)。从图中可见,模式的Talagrand分布与理想概率分布存在一定的差距,实况落在集合区间之外的频率偏大,特别是右端值明显偏大,呈现反“L”型分布,表明两组集合预报的离散度均偏小,并具有系统性的干偏差。
|
图 10 3 h累积降水的Talagrand分布(a)、概率均方差(b)和离群率(c) [图10a黑色横线为Talagrand分布的理想状态(10%)] Fig. 10 Talagrand (a), the root mean squared differences between the ranked-probability and expected-probability summed over all the categories in the Talagrand distribution (b) and outlier (c) of 3 h accumulated precipitation (Black horizontal line in Fig. 10a expresses ideal state of Talagrand distribution 10%) |
图 10b为各组试验的概率均方差。空间尺度90 km试验的概率均方差小于空间尺度30 km的试验,说明其离散度分布更接近理想状态。不同的时间尺度试验在空间尺度为30 km时,概率均方差差别不大,但在空间尺度为90 km时,时间尺度3 h的试验概率均方差小于6 h试验。增加扰动振幅也可以降低概率均方差。
图 10c进一步给出两组3 h累积降水集合平均在不同量级上的离群率。离群率用于检验集合预报降水的准确性,离群率越低,预报的准确性越高。按照观测值分成4个降水区间[0.1, 10)、[10, 25)、[25, 50)和≥50 mm,统计各等级的观测落在由各集合成员的预报区间外的平均概率(李俊等,2020)。如图所示,3 h累积降水的离群率随观测量级的增大而增大。SPPTh90t3s0.5的离群率在[0.1, 10)量级和SPPTh90t6s0.5相当,但小于SPPTh30t3s0.5,在[10, 25)量级上高于SPPTh90t6s0.5,但小于SPPTh30t3s0.5,在[25, 50)和≥50 mm低于SPPTh90t6s0.5和SPPTh-30t3s0.5。空间尺度为90 km试验的离群率整体上看小于空间尺度30 km试验,尤其在[0.1, 10)和[10, 25)量级。另外,增加扰动振幅(SPPTh90t3s0.525)相对于SPPTh90t3s0.5试验的离群率略有降低。
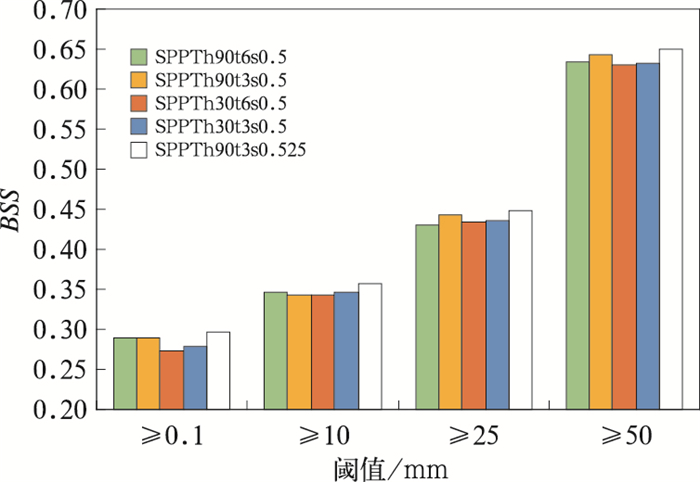
3.4.3 概率预报检验与确定性预报相比,集合预报的概率预报可以提供更多信息。降水概率预报的检验是集合预报效果检验的重要指标之一。Brier技巧评分(BSS)可表示概率预报对控制试验的改进程度(Brier,1950;Murphy,1993)。BSS>0,表示事件的概率预报有意义; 反之,则不如控制试验。BSS值越高,概率预报效果越好。图 11是3 h累积降水的BSS评分。从图中可见,BSS随降水阈值的提高而增加,表明概率预报效果随降水阈值增大而更加准确。空间尺度90 km试验的BSS在各降水量级上普遍大于空间尺度30 km试验。空间尺度固定为90 km时,分析不同时间尺度对降水的BSS影响。SPPTh90t6s0.5和SPPTh90t3s0.5在≥0.1 mm的BSS评分非常接近,SPPTh90t6s0.5在≥10 mm的BSS略高于SPPTh90t3s0.5,SPPTh90t6s0.5在≥25 mm和≥50 mm的BSS小于SPPTh90t3s0.5。当空间尺度固定为30 km时,时间尺度3 h试验略在各量级上的BSS略大于时间尺度6 h。增加扰动振幅对改进降水的BSS也有积极作用。总体来看,时间尺度为3 h、空间尺度为90 km和格点标准差为0.525的配置在各个量级降水上的概率技巧最高。
|
图 11 3 h累积降水BSS评分 Fig. 11 BSS score of 3 h accumulated precipitation |
针对2018年5月在四川盆地南部和东部发生的一次强降水天气过程,采用SPPT方法开展在复杂地形条件下对流尺度集合预报试验。从高空要素和近地面要素的预报分析、扰动振幅的敏感性、降水集合平均和离群率及其概率预报等方面,研究不同时间尺度、空间尺度和格点标准差生成的随机扰动场对本次过程的集合预报影响。结果表明:
(1) SPPT方案中空间尺度比时间尺度参数对离散度的影响更加明显。空间尺度为90 km试验在对不同高度(200、500和700 hPa)高空要素(纬向风场、温度场和湿度场)和近地面要素(10 m风和2 m温度)的离散度检验中总体上表现更为出色,尤其是在积分中期和后期,空间尺度为90 km试验的高空要素离散度大于空间尺度30 km的试验。在500 hPa高度,空间尺度相同试验的风场、温度场和湿度场的离散度相差较小。
(2) SPPT方案中时间尺度选择3 h试验的集合成员的整体离散度更大。时间尺度在积分的不同阶段对离散度的贡献不同,时间尺度3 h试验在积分的前期和中期对高空要素的离散度表现更好,到了积分后期,小于时间尺度6 h的试验。时间尺度3 h试验在积分的前期对近地面要素的离散度表现较好,到了积分中期和后期,小于时间尺度6 h的试验。
(3) 格点标准差由0.5增加到0.525计算仍然稳定。扰动振幅的提高有助于增加高空要素及近地面要素的离散度,尤其对近地面要素离散度改善较大,且离散度/RMSE更接近于1,能更好地度量预报误差的变化。
(4) 在降水预报检验中,SPPT方案试验的集合平均降水相对于控制试验可以提高预报技巧,3 h累积降水的集合平均在≥10 mm、≥25 mm和≥50 mm的降水等级的ETS评分接近或者高于控制试验。SPPT方案的空间尺度参数的选取比时间尺度对降水的离散度的影响更加明显,增加扰动振幅对离散度的增加也起到积极的作用。虽然在降水的集合平均确定性预报的表现中,参数的选取对各个量级降水的ETS评分各有高低,但是从BSS技巧评分来看,选取空间尺度为90 km、时间尺度为3 h和格点标准差为0.525的参数配置可以提高在各个量级降水上的概率预报技巧。
SPPT方案通过扰动次网格物理参数化的总倾向来表达模式的不确定性,总物理倾向与天气系统以及物理过程的描述密切相关,随机扰动形态的时空分布对总倾向的扰动产生影响。本研究的天气过程发生在我国西部地形复杂区域,物理参数化对天气系统的描述也具有不确定性,利用SPPT的随机物理扰动方案研究开展的五组敏感试验,分析其扰动变化规律,优选了随机扰动场的最优参数配置。虽然相对于其他参数配置,该参数组合在所分析的个例中可以提高3 h降水的概率预报技巧,增加离散度,但仍然偏小。从高空要素和地面要素的预报分析及降水预报的检验表明,随机扰动场对空间尺度参数调整比时间尺度和振幅参数更加敏感,与Lupo et al(2020)结论略有不同。这可能与影响系统、研究区域以及研究对象不同有关。蔡沅辰等(2017)和闵锦忠等(2018)的研究也表明,扰动参数的选取,可能与天气系统的尺度和维持时间相关,随机扰动的时空分布应与天气系统的时空演变相匹配,此外,模式的分辨率可能也是影响扰动参数的因素之一,有关确切的定量关系仍然是值得研究的课题,这也可能是不同研究中结论存在细节差异的原因。本研究与上述工作类似,均是基于个例得到的结论,还有待进行更多的试验加以验证,但这些工作表明,随机扰动参数的选取对集合预报系统的性能具有重要影响,也正因如此,在实际应用中,针对特定地域和预报对象,开展最优的扰动参数的试验是十分必要的。
此外,为了研究物理过程不确定性对预报结果的影响,本研究没有引入其他方案扰动,扰动能量总体偏小。后期,可增加初值扰动或者结合SKEB等随机物理扰动方案,采用多种技术的混合扰动方案,以获得更佳的集合预报效果,本工作也可为多种方案的混合运用提供科学依据。
蔡沅辰, 闵锦忠, 庄潇然, 2017. 不同随机物理扰动方案在一次暴雨集合预报中的对比研究[J]. 高原气象, 36(2): 407-423. Cai Y C, Min J Z, Zhuang X R, 2017. Comparison of different stochastic physics perturbation schemes on a storm-scale ensemble forecast in a heavy rain event[J]. Plateau Meteor, 36(2): 407-423 (in Chinese).
|
陈静, 李晓莉, 2020. GRAPES全球/区域集合预报系统10年发展回顾及展望[J]. 气象科技进展, 10(2): 9-18, 29. Chen J, Li X L, 2020. The review of 10 years development of the GRAPES global/regional ensemble prediction[J]. Adv Meteor Sci Technol, 10(2): 9-18, 29 (in Chinese). DOI:10.3969/j.issn.2095-1973.2020.02.003
|
陈雨潇, 徐致真, 陈静, 等, 2020. 随机参数扰动方法对中国冬季降水集合预报的影响[J]. 大气科学, 44(5): 984-996. Chen Y X, Xu Z Z, Chen J, et al, 2020. Influence of stochastically perturbed parameterization on ensemble forecasting of winter precipitation in China[J]. Chin Atmos Sci, 44(5): 984-996 (in Chinese).
|
杜钧, 李俊, 2014. 集合预报方法在暴雨研究和预报中的应用[J]. 气象科技进展, 4(5): 6-20. Du J, Li J, 2014. Application of ensemble methodology to heavy-rain research and prediction[J]. Adv Meteor Sci Technol, 4(5): 6-20 (in Chinese).
|
范宇恩, 陈静, 邓国, 等, 2019. GRAPES区域集合预报两种侧边界扰动方法对比试验[J]. 气象, 45(12): 1629-1641. Fan Y E, Chen J, Deng G, et al, 2019. Comparison of two lateral boundary perturbation methods in the regional ensemble prediction system of GRAPES[J]. Meteor Mon, 45(12): 1629-1641 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.12.001
|
高珩洲, 李国平, 2020. 黔东南地形影响局地突发性暴雨的中尺度天气分析与数值试验[J]. 高原气象, 39(2): 301-310. Gao H Z, Li G P, 2020. Mesoscale synoptic meteorology analysis and numerical experiment of local sudden rainstorm affected by topography in southeast part of Guizhou Province[J]. Plateau Meteor, 39(2): 301-310 (in Chinese).
|
孔凡铀, 2018. 雷暴尺度天气集合数值预报研究[J]. 气象科技进展, 8(3): 53-60. Kong F Y, 2018. A study of storm-scale ensemble forecast[J]. Adv Meteor Sci Technol, 8(3): 53-60 (in Chinese). DOI:10.3969/j.issn.2095-1973.2018.03.004
|
李俊, 杜钧, 刘羽, 2015. 北京"7.21"特大暴雨不同集合预报方案的对比试验[J]. 气象学报, 73(1): 50-71. Li J, Du J, Liu Y, 2015. A comparison of initial condition-, multi-physics-and stochastic physics-based ensembles in predicting Beijing 7.21 excessive storm rain event[J]. Acta Meteor Sin, 73(1): 50-71 (in Chinese).
|
李俊, 杜钧, 许建玉, 等, 2020. 一次特大暴雨过程高分辨率集合预报试验的检验和评估[J]. 暴雨灾害, 39(2): 176-184. Li J, Du J, Xu J Y, et al, 2020. The assessment and verification of high-resolution ensemble forecast for a heavy rainstorm[J]. Torr Rain Dis, 39(2): 176-184 (in Chinese). DOI:10.3969/j.issn.1004-9045.2020.02.008
|
李晓莉, 陈静, 刘永柱, 等, 2019. GRAPES全球集合预报初始条件及模式物理过程不确定性方法研究[J]. 大气科学学报, 42(3): 348-359. Li X L, Chen J, Liu Y Z, et al, 2019. Representations of initial uncertainty and model uncertainty of GRAPES global ensemble forecasting[J]. Trans Atmos Sci, 42(3): 348-359 (in Chinese).
|
闵锦忠, 刘畅, 王世璋, 等, 2018. 随机物理倾向扰动在风暴尺度集合预报中的影响研究[J]. 气象学报, 76(4): 590-604. Min J Z, Liu C, Wang S Z, et al, 2018. Impact of stochastically perturbed parameterization tendencies on storm-scale ensemble forecast[J]. Acta Meteor Sin, 76(4): 590-604 (in Chinese).
|
彭贵康, 柴复新, 曾庆存, 等, 1994. "雅安天漏"研究Ⅰ: 天气分析[J]. 大气科学, 18(4): 466-475. Peng G K, Chai F X, Zeng Q C, et al, 1994. Research on "Ya-An-Tian-Lou". Part Ⅰ: weather analysis[J]. Sci Atmos Sin, 18(4): 466-475 (in Chinese). DOI:10.3878/j.issn.1006-9895.1994.04.11
|
任志杰, 陈静, 田华, 2011. T213全球集合预报系统物理过程随机扰动方法研究[J]. 气象, 37(9): 1049-1059. Ren Z J, Chen J, Tian H, 2011. Research on T213 ensemble prediction system stochastic physics perturbation[J]. Meteor Mon, 37(9): 1049-1059 (in Chinese).
|
谭宁, 陈静, 田华, 2013. 两种模式随机扰动方案比较及扰动传播分析[J]. 气象, 39(5): 543-555. Tan N, Chen J, Tian H, 2013. Comparison between two global model stochastic perturbation schemes and analysis of perturbation propagation[J]. Meteor Mon, 39(5): 543-555 (in Chinese). DOI:10.3969/j.issn.1671-1742.2013.05.016
|
谭燕, 陈德辉, 2007. 基于非静力模式物理扰动的中尺度集合预报试验[J]. 应用气象学报, 18(3): 396-406. Tan Y, Chen D H, 2007. Meso-scale ensemble forecasts on physical perturbation using a non-hydrostatic model[J]. J Appl Meteor Sci, 18(3): 396-406 (in Chinese). DOI:10.3969/j.issn.1001-7313.2007.03.017
|
王璐, 沈学顺, 2019. 对流尺度集合预报与模式不确定性研究进展[J]. 气象, 45(8): 1158-1168. Wang L, Shen X S, 2019. Review on the representation of model uncertainty in convection-allowing ensemble prediction system[J]. Meteor Mon, 45(8): 1158-1168 (in Chinese).
|
武天杰, 闵锦忠, 2020. 随机辐射参数化过程扰动方案对温度预报的影响[J]. 热带气象学报, 36(4): 477-488. Wu T J, Min J Z, 2020. The impact of stochastically perturbed radiation parameterization tendencies scheme on temperature forecasting[J]. J Trop Meteor, 36(4): 477-488 (in Chinese).
|
肖递祥, 杨康权, 祁生秀, 2012. 2011年7月四川盆地两次突发性暴雨过程的对比分析[J]. 气象, 38(12): 1482-1491. Xiao D X, Yang K Q, Qi S X, 2012. Comparative analysis of two abrupt heavy rain processes in Sichuan Basin in July 2011[J]. Meteor Mon, 38(12): 1482-1491 (in Chinese).
|
徐致真, 陈静, 王勇, 等, 2019. 中尺度降水集合预报随机参数扰动方法敏感性试验[J]. 气象学报, 77(5): 849-868. Xu Z Z, Chen J, Wang Y, et al, 2019. Sensitivity experiments of a stochastically perturbed parameterizations (SPP) scheme for mesoscale precipitation ensemble prediction[J]. Acta Meteor Sin, 77(5): 849-868 (in Chinese).
|
宇如聪, 曾庆存, 彭贵康, 等, 1994. "雅安天漏"研究Ⅱ. 数值预报试验[J]. 大气科学, 18(5): 535-551. Yu R C, Zeng Q C, Peng G K, et al, 1994. Research on "Ya-An-Tian-Lou". Part Ⅱ: numerical trial-forecasting[J]. Sci Atmos Sin, 18(5): 535-551 (in Chinese). DOI:10.3878/j.issn.1006-9895.1994.05.04
|
袁月, 李晓莉, 陈静, 等, 2016. GRAPES区域集合预报系统模式不确定性的随机扰动技术研究[J]. 气象, 42(10): 1161-1175. Yuan Y, Li X L, Chen J, et al, 2016. Stochastic parameterization toward model uncertainty for the GRAPES mesoscale ensemble prediction system[J]. Meteor Mon, 42(10): 1161-1175 (in Chinese). DOI:10.7519/j.issn.1000-0526.2016.10.001
|
张芳丽, 李国平, 罗潇, 2020. 四川盆地东北部一次突发性暴雨事件的影响系统分析[J]. 高原气象, 39(2): 321-332. Zhang F L, Li G P, Luo X, 2020. Some influence factors of a sudden rainstorm event in northeast Sichuan Basin of China[J]. Plateau Meteor, 39(2): 321-332 (in Chinese).
|
张涵斌, 范水勇, 陈敏, 等, 2019. 区域集合预报基于SKEB和多物理过程的混合模式扰动方法研究[J]. 气象, 45(1): 17-28. Zhang H B, Fan S Y, Chen M, et al, 2019. Study on a synthetic model perturbation method based on SKEB and multi-physics for regional ensemble forecast[J]. Meteor Mon, 45(1): 17-28 (in Chinese).
|
张涵斌, 智协飞, 陈静, 等, 2017. 区域集合预报扰动方法研究进展综述[J]. 大气科学学报, 40(2): 145-157. Zhang H B, Zhi X F, Chen J, et al, 2017. Achievement of perturbation methods for regional ensemble forecast[J]. Trans Atmos Sci, 40(2): 145-157 (in Chinese).
|
Berner J, Fossell K R, Ha S Y, et al, 2015. Increasing the skill of probabilistic forecasts: understanding performance improvements from model-error representations[J]. Mon Wea Rev, 143(4): 1295-1320. DOI:10.1175/MWR-D-14-00091.1
|
Berner J, Ha S Y, Hacker J P, et al, 2011. Model uncertainty in a mesoscale ensemble prediction system: stochastic versus multiphysics representations[J]. Mon Wea Rev, 139(6): 1972-1995. DOI:10.1175/2010MWR3595.1
|
Berner J, Shutts G J, Leutbecher M, et al, 2009. A spectral stochastic kinetic energy backscatter scheme and its impact on flow-dependent predictability in the ECMWF ensemble prediction system[J]. J Atmos Sci, 66(3): 603-626. DOI:10.1175/2008JAS2677.1
|
Bishop C H, Etherton B J, Majumdar S J, 2001. Adaptive sampling with the ensemble transform Kalman filter.Part Ⅰ: theoretical aspects[J]. Mon Wea Rev, 129(3): 420-436. DOI:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2
|
Bouttier F, Vié B, Nuissier O, et al, 2012. Impact of stochastic physics in a convection-permitting ensemble[J]. Mon Wea Rev, 140(11): 3706-3721. DOI:10.1175/MWR-D-12-00031.1
|
Bowler N E, Arribas A, Mylne K, et al, 2008. The MOGREPS short-range ensemble prediction system[J]. Quart J Roy Meteor Soc, 134(632): 703-722. DOI:10.1002/qj.234
|
Brier G W, 1950. Verification of forecasts expressed in terms of probability[J]. Mon Wea Rev, 78(1): 1-3. DOI:10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2
|
Buizza R, Milleer M, Palmer T N, 1999. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system[J]. Quart J Roy Meteor Soc, 125(560): 2887-2908. DOI:10.1002/qj.49712556006
|
Christensen H M, Lock S J, Moroz I M, et al, 2017. Introducing independent patterns into the stochastically perturbed parametrization tendencies (SPPT) scheme[J]. Quart J Roy Meteor Soc, 143(706): 2168-2181. DOI:10.1002/qj.3075
|
Christensen H M, Moroz I M, Palmer T N, 2015. Stochastic and perturbed parameter representations of model uncertainty in convection parameterization[J]. J Atmos Sci, 72(6): 2525-2544. DOI:10.1175/JAS-D-14-0250.1
|
Duda J D, Wang X G, Kong F Y, et al, 2016. Impact of a stochastic kinetic energy backscatter scheme on warm season convection-allowing ensemble forecasts[J]. Mon Wea Rev, 144(5): 1887-1908. DOI:10.1175/MWR-D-15-0092.1
|
Ehrendorfer M, Tribbia J J, 1997. Optimal prediction of forecast error covariances through singular vectors[J]. J Atmos Sci, 54(2): 286-313. DOI:10.1175/1520-0469(1997)054<0286:OPOFEC>2.0.CO;2
|
Hacker J P, Snyder C, Ha S Y, et al, 2011. Linear and non-linear response to parameter variations in a mesoscale model[J]. Tellus A Dyn Meteor Oceanography, 63(3): 429-444. DOI:10.1111/j.1600-0870.2010.00505.x
|
Hamill T M, 2001. Interpretation of rank histograms for verifying ensemble forecasts[J]. Mon Wea Rev, 129(3): 550-560. DOI:10.1175/1520-0493(2001)129<0550:IORHFV>2.0.CO;2
|
Houtekamer P L, Lefaivre L, Derome J, et al, 1996. A system simulation approach to ensemble prediction[J]. Mon Wea Rev, 124(6): 1225-1242. DOI:10.1175/1520-0493(1996)124<1225:ASSATE>2.0.CO;2
|
Krishnamurti T N, Kishtawal C M, LaRow T E, et al, 1999. Improved weather and seasonal climate forecasts from multimodel superensemble[J]. Science, 285(5433): 1548-1550. DOI:10.1126/science.285.5433.1548
|
Leutbecher M, Lock S J, Ollinaho P, et al, 2017. Stochastic representations of model uncertainties at ECMWF: state of the art and future vision[J]. Quart J Roy Met Soc, 143(707): 2315-2339. DOI:10.1002/qj.3094
|
Lupo K M, Torn R D, Yang S C, 2020. Evaluation of stochastic perturbed parameterization tendencies on convective-permitting ensemble forecasts of heavy rainfall events in New York and Taiwan[J]. Wea Forecasting, 35(1): 5-24. DOI:10.1175/WAF-D-19-0064.1
|
Molteni F, Buizza R, Palmer T N, et al, 1996. The ECMWF ensemble prediction system: methodology and validation[J]. Quart J Roy Meteor Soc, 122(529): 73-119. DOI:10.1002/qj.49712252905
|
Mu M, Zhang Z Y, 2006. Conditional nonlinear optimal perturbations of a two-dimensional quasigeostrophic model[J]. J Atmos Sci, 63(6): 1587-1604. DOI:10.1175/JAS3703.1
|
Murphy A H, 1993. What is a good forecast? An essay on the nature of goodness in weather forecasting[J]. Wea Forecasting, 8(2): 281-293. DOI:10.1175/1520-0434(1993)008<0281:WIAGFA>2.0.CO;2
|
Palmer T N, Buizza R, Doblas-Reyes F, et al, 2009. Stochastic parameterization and model uncertainty[OL/J]. [2020-08-13]. Ecmwf Rd Tech Memo, 598. http//www. ecmwf. int/node/11577.
|
Qiao X S, Wang S Z, Min J Z, 2018. The impact of a stochastically perturbing microphysics scheme on an idealized supercell storm[J]. Mon Wea Rev, 146(1): 95-118. DOI:10.1175/MWR-D-17-0064.1
|
Romine G S, Schwartz C S, Berner J, et al, 2014. Representing forecast error in a convection-permitting ensemble system[J]. Mon Wea Rev, 142(12): 4519-4541. DOI:10.1175/MWR-D-14-00100.1
|
Shutts G, 2005. A kinetic energy backscatter algorithm for use in ensemble prediction systems[J]. Quart J Roy Meteor Soc, 131(612): 3079-3102. DOI:10.1256/qj.04.106
|
Talagrand O, Vautard R, Strauss B, 1997. Evaluation of probabilistic prediction systems[C]//Workshop on Predictability. Shinfield Park: ECMWF: 20-22.
|
Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC: the generation of perturbations[J]. Bull Amer Meteor Soc, 74(12): 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2
|
Toth Z, Kalnay E, 1997. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 125(12): 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2
|
Wang X G, Bishop C H, 2003. A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes[J]. J Atmos Sci, 60(9): 1140-1158. DOI:10.1175/1520-0469(2003)060<1140:ACOBAE>2.0.CO;2
|
Weaver A, Courtier P, 2001. Correlation modelling on the sphere using a generalized diffusion equation[J]. Quart J Roy Meteor Soc, 127(575): 1815-1846. DOI:10.1002/qj.49712757518
|
 2021, Vol. 47
2021, Vol. 47