引言

随着我国经济高速发展，公众及高敏感行业对暴雨等灾害天气的精准预报要求也越来越强烈。暴雨等灾害天气系统多是由多种尺度系统相互作用条件下产生，如导致暴雨产生的系统中，大尺度系统为暴雨提供了有利的环境条件，而中小尺度系统是造成暴雨的直接系统(陆汉城和杨国祥，2004)。采用数值模式预报暴雨等灾害天气系统，虽然动力与物理过程的描述存在着一定不足，但对暴雨等系统活动的精准预报具有一定的优势。提高暴雨等灾害天气数值预报能力可从两方面着手：一方面是提高模式分辨率，开发适合高分辨率模式的物理过程参数化方案和动力框架，增强模式预报精度；另一方面是改善模式初始条件，提高模式对中小尺度系统的刻画(Vendrasco et al，2016)。资料同化给数值模式提供一个更为精准的初值场(陈东升等，2004)，是改善数值模式预报技巧的一种有效手段，因而资料同化方案提供的初值需要在不破坏大尺度环流形势场的同时，尽可能多地引入中小尺度信息。当前，各主要业务数值预报中心，主要采用变分资料同化方案为模式提供初值(Lorenc，2003；Bannister，2008)。在变分资料同化中，滤波特点以及观测信息的传播方式均由背景误差协方差矩阵B决定，合理的B矩阵是做好变分同化的关键。背景误差协方差矩阵在资料同化系统中控制信息从观测位置向四周传播的方式，并决定了模式变量之间在动力上是否协调一致。因此，同化分析增量的空间结构和多变量关系结构取决于背景误差协方差的结构。

由于B是一个维数很高的矩阵，对其直接求逆不现实，在近似得到B^-1的研究中，许多科研人员通过变量变换对目标函数进行预调节，B矩阵在预调节中被分解为几个部分，其中水平背景场误差协方差由各向同性递归滤波表示。递归滤波法不需要显式构造B矩阵，可以显著减小计算开销和内存(李冬等，2011)。英国气象局第一次将递归滤波方法引入到区域预报模式(Purser and McQuigg, 1982)。目前，递归滤波被广泛应用在区域三维变分系统(Hayden and Purser, 1995；Purser et al，2003a；2003b)。递归滤波中特征尺度是一个重要参数，特征尺度越大滤波影响范围越大，对于观测信息较少的地区可以扩大观测信息的影响(Hayden and Purser, 1995)。但是，特征尺度过大，同化结果将趋于平滑，无法提取观测的短波信息；特征尺度过小，则不能准确地提取长波信息。何光鑫等(2011a；2011b)利用多元正态分布的可加性进行递归滤波拟合(Wilks，2006)，将不同特征尺度递归滤波进行拟合，拟合后的多尺度递归滤波在保持原有大尺度信息的基础上，清晰显示出了更多中小尺度的信息。吴洋等(2018)在保证原递归滤波器水平特征尺度流函数、势函数和非平衡质量场500 km和湿度场200 km基础上，依据统计结果进行多次线性拟合出3种水平特征尺度经验性结果，然后采用3种特征尺度递归滤波器在分析和预报中获得了更多的α中尺度信息，使得形势场及降水预报技巧明显改善。庄照荣和李兴良(2021)通过分析高斯模型和尺度叠加高斯模型的空间特征，及拉普拉斯算子和谱响应函数的特征，以原方案流函数、势函数和非平衡质量场水平特征尺度值为中心形成等差序列水平特征尺度组，研究了尺度叠加高斯相关模型的特征及其在三维变分同化系统中的应用效果。他们的工作主要研究了多尺度叠加对分析和预报影响，但如何客观地从背景误差协方差中提取和估计多种特征尺度长度的工作相对较少。庄照荣等(2018；2020)通过采用二维离散余弦转换(2D-DCT)(Denis et al，2002；郑永骏等，2008)，将全球T639模式和区域GRAPES模式分析增量进行谱分解，获得全球和区域模式产品不同尺度信息，然后将全球大尺度信息部分与区域中小尺度信息部分混合组成新分析增量，使得分析和降水预报明显改善。本文参考庄照荣等(2018；2020)二维离散余弦转换获得全球和区域模式产品不同尺度信息方式，采用二维离散余弦变换对格点背景误差进行波谱展开后，对背景误差按照尺度大小分为3部分进行尺度分离和水平相关尺度拟合，然后将拟合的随高度变化背景误差水平相关特征尺度在3 km中尺度天气数值预报系统CMA-MESO(原GRAPES区域中尺度数值预报系统GRAPES-MESO)进行个例和连续试验，并与业务试验系统进行对比分析。

2 方案设计

CMA-MESO 3 km系统采用三维变分同化方法(马旭林等，2009；薛纪善和陈德辉，2008)，目标函数J为：

$ \begin{gathered} J=\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{b}}\right)^{\mathrm{T}} \boldsymbol{B}^{-1}\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{b}}\right)+ \\ \frac{1}{2}\left[\boldsymbol{y}^{\mathrm{o}}-\boldsymbol{H}(\boldsymbol{x})\right]^{\mathrm{T}}(\boldsymbol{E}+\boldsymbol{F})^{-1}\left[\boldsymbol{y}^{\mathrm{o}}-\boldsymbol{H}(\boldsymbol{x})\right] \end{gathered} $

(1)

式中：x表示分析场，x_b为背景场，B为背景场误差协方差矩阵；y^o为观测向量；H是把大气状态投影到观测空间的观测算子；E为仪器观测误差协方差矩阵，F为代表性误差协方差矩阵。背景场误差协方差矩阵B、观测算子H、观测资料质量控制是三维变分同化三个核心问题，任何一个问题没处理好，提供的分析场就会影响数值结果。上述目标函数最小化过程涉及背景误差协方差矩阵B求逆。鉴于B是超大规模矩阵，直接求逆计算代价比较高，且有时无法求逆，导致极小化计算难以收敛，通过引入控制变量变换预处理则可以避免背景误差协方差矩阵求逆，设x-x_b=Uw，B=UU^T，目标泛函J写为如下形式：

$ J=\frac{1}{2} w^{\mathrm{T}} w+\frac{1}{2}(\boldsymbol{H} \boldsymbol{U} w+\boldsymbol{d})^{\mathrm{T}} \boldsymbol{R}^{-1}(\boldsymbol{H} \boldsymbol{U} w+\boldsymbol{d}) $

(2)

式中：w为新的极小化控制变量，d=H(x_b)-y^o为新息向量，R=E+F为观测误差协方差。预处理变换中将误差协方差矩阵U分裂为3个独立的矩阵U=U_pU_hU_v，U_p为物理变换算子，为不同分析变量之间的误差交叉协相关，控制着观测信息在不同变量之间的传播；U_v为误差垂直变换算子，由经验正交函数(EOF)方法实现；U_h为误差水平变换算子。现有业务系统一般均假设背景水平误差满足各向同性的高斯分布，U_h采用递归滤波实现该误差模型(薛纪善和陈德辉，2008；庄照荣等，2019)。CMA-MESO 3 km三维变分同化系统中，误差高斯分布函数定义为:

$ \boldsymbol{b}_{i, j}=\sigma_b^2 \exp \left[-\left(r_{i, j} / L\right)^2\right] $

(3)

式中：b_{i, j}是B的元素，r_{i, j}是格点i，j之间距离，σ_b²是背景场误差标准差，L是影响半径(即水平相关尺度)。本文背景误差采用的统计数据来自CMA-MESO 3 km系统模式预报产品，垂直51层，水平分辨率为3 km，区域覆盖范围为(17°~50°N、102°~135°E)。时间段为2018年6月2日至8月31日(共计180个预报样本)，采用Parrish and Derber (1992)的NMC方法计算背景误差(同一时刻24 h与12 h预报场差)相关结构。采用二维离散余弦变换(2D-DCT)方法对格点分布背景误差进行波谱展开和尺度分离。

对于一个N_i×N_j的二维变量场f(i, j)，2D-DCT的直接变换和反变换定义为：

$ \begin{aligned} & F(m, n)=\beta(m) \beta(n) \sum\limits_{i=0}^{i=N_i-1} \sum\limits_{j=0}^{j=N_j-1} f(i, j) \times \\ & \quad \cos \left[\pi m \frac{(i+1 / 2)}{N_i}\right] \cos \left[\pi n \frac{(i+1 / 2)}{N_j}\right] \end{aligned} $

(4)

$ \begin{aligned} & f(i, j)=\sum\limits_{m=0}^{m=N_i-1} \sum\limits_{n=0}^{n=N_j-1} \beta(m) \beta(n) F(m, n) \times \\ & \quad \cos \left[\pi m \frac{(i+1 / 2)}{N_i}\right] \cos \left[\pi n \frac{(i+1 / 2)}{N_j}\right] \end{aligned} $

(5)

其中

$ \beta(m)= \begin{cases}\sqrt{1 / N_i} & m=0 \\ \sqrt{2 / N_i} & m=1, 2, \cdots, N_i-1\end{cases} $

(6)

$ \beta(n)= \begin{cases}\sqrt{1 / N_j} & n=0 \\ \sqrt{2 / N_j} & n=1, 2, \cdots, N_j-1\end{cases} $

(7)

式中：f(i, j)为二维变量场在格点(i, j)的值，而F(m, n)为(m, n)维波数对应的谱系数。2D-DCT对一个N_i×N_j维的物理量场f(i, j)的正变换可以获得N_i×N_j维的谱数场F(m, n)。经过变换的每一个谱系数的位置，即二维波数(m, n)需要与单一波长L相联系，因此对于一个N_i×N_j的二维谱系数场，则有：

$ \lambda=\frac{2 \Delta}{\sqrt{\frac{m^2}{N_i^2}+\frac{n^2}{N_j^2}}} $

(8)

式中：Δ为模式格点分辨率。波长L与对应的二维波数k为:

$ k=\sqrt{m^2+n^2} $

(9)

结合天气系统尺度划分系统和3 km模式系统关注的天气系统，将背景误差按照以下3种尺度区间(≥500 km，100~500 km，≤100 km)进行分离。

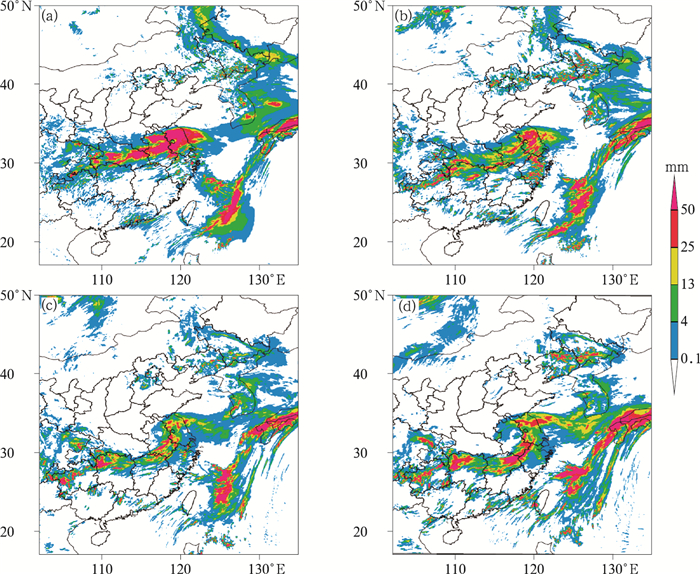
随机选取一个时次某层温度背景误差，从图 1可见，3种尺度背景误差分布特征及大值区与尺度分离前(图 1a)大体一致；≥500 km背景误差(图 1d)分布相对光滑，100~500 km区间背景误差(图 1c)多了些小扰动，分布不如≥500 km的背景误差光滑，小扰动少于≤100 km(图 1b)下尺度背景误差。3种尺度分离后的结果基本反映了3种尺度信息，说明尺度分离合理。

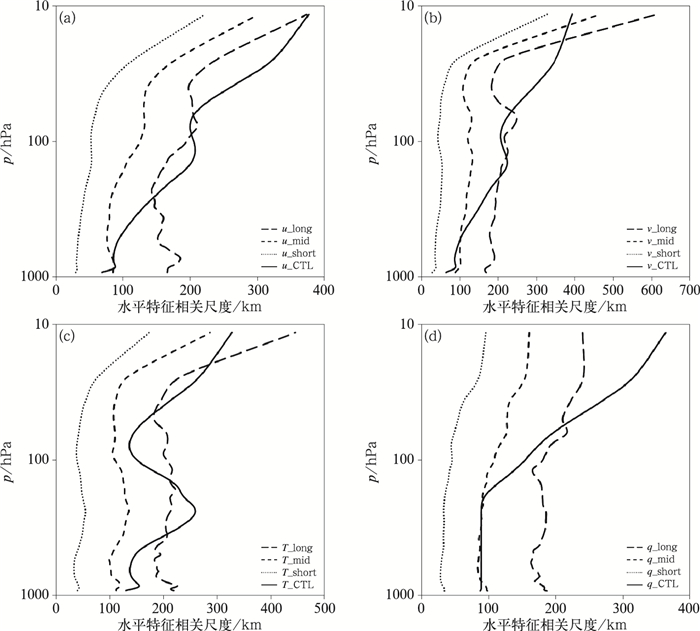
将背景误差尺度分离后3组样本进行水平特征相关尺度拟合，结果见图 2。由图 2可见，拟合的3种水平特征相关尺度随高度变化特征相似，水平特征尺度长度大小不同，低层水平特征尺度最大接近200 km，中间约为100 km，最小约为40 km。业务试验系统的水平特征相关尺度随高度变化特征与拟合的3种水平特征尺度不同，u、v风场高层、温度中层以及湿度高层差异较大，这可能与业务试验系统采用的背景误差样本量不同有关。在低层，业务试验系统单一水平特征尺度长度和3种水平特征尺度长度中间的长度接近。

3 CMA-MESO数值试验结果 3.1 CMA-MESO简介及试验方案

本文试验采用的是CMA-MESO 4.4版，模式系统水平分辨率为3 km，垂直不等间距51层，由于计算资源问题，试验范围为中国中东部区域(17°~36.8°N、102°~126.9°E)。采用的三维同化系统控制变量为u、v风场，地面气压p_s, 温度T和相对湿度RH。同化分析资料为探空报(u，v，T，RH)，地面报(p_s，RH)，船舶报(p_s，RH)，飞机报(u，v，T)，云导风，地基掩星反演可降水量(GPS/PW)，雷达速度方位显示反演风廓线(VAD风)，雷达径向风，风廓线雷达风，基于云分析系统(朱立娟等，2017)的雷达和卫星资料，松弛逼近方法(nudging)同化的地面自动站降水资料。试验为每3 h同化分析24 h预报，00时和12时(世界时，下同)包含一次冷启动和一次暖启动分析预报。采用美国国家环境预报中心(NCEP) 0.5°×0.5° FNL 6 h预报场做背景和侧边界条件资料，同化分析预报试验时段为2018年7月1—31日。

数值模拟试验分为2组：(1)CTL试验: 采用业务试验系统用水平特征相关尺度参与同化分析的控制试验；(2)MF试验：采用3种拟合水平特征相关尺度参与同化分析的敏感试验。

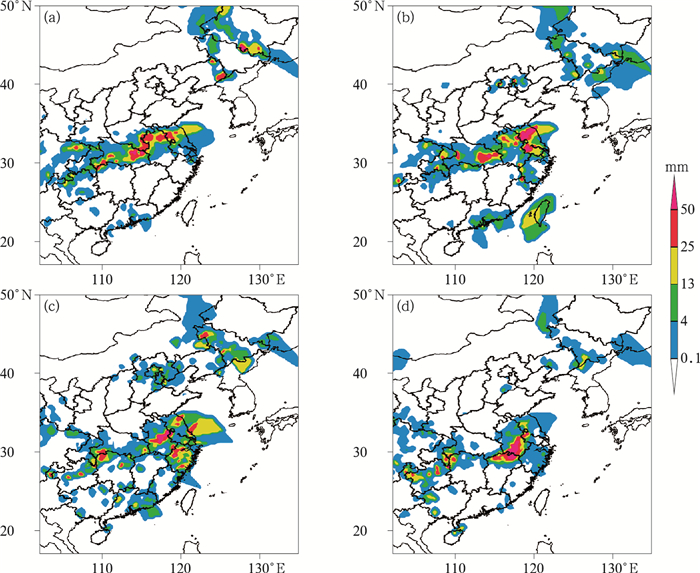
3.2 数值试验结果 3.2.1 个例试验

2018年7月4—7日在低空急流和江淮气旋的影响下，我国中东部大部地区出现较强降雨过程(张夕迪和孙军，2018)，河南东南部、安徽大部、湖北中东部、贵州中北部、重庆东部、湖南大部、江苏大部、江西中北部、广西北部、广东中北部出现暴雨，其中河南东部、安徽大部、江苏大部、江西北部、广西北部出现大暴雨，江西北部个别站点特大暴雨。图 3为7月5日00时至6日00时逐6 h降水实况，5日00—06时30°N上下有一条雨带，江苏、安徽、湖北等地降水量较大，然后降雨带逐步东移南压，12 h后强降水自北向南逐步移至江西省北部地区。北京地区在5日06—18时有降水发生。

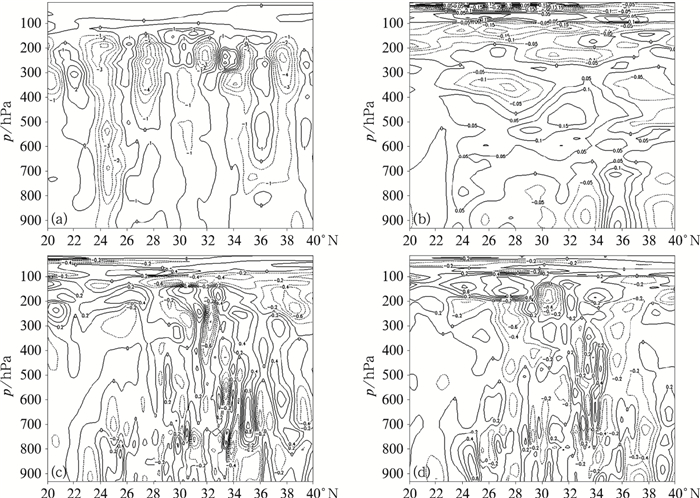
沿120°E对MF试验和CTL试验7月5日00时的湿度、温度和风场分析增量剖面进行对比分析发现(图 4)，两组试验的湿度、温度和风场分析增量差异较小，湿度分析增量差异不超过6%，风场分析增量差异不超过1.2 m·s^-1，温度分析增量差异不超过0.35℃。中低层(500 hPa以下), 主要降水区(26°~34°N)的相对湿度分析增量MF试验高于CTL试验，而700 hPa以下温度分析增量MF试验小于CTL试验，2组试验在29°~30°N及33°N附近u风场分析增量差为正偏差，在29°N附近和31°~32°N附近v风场分析增量为正偏差。

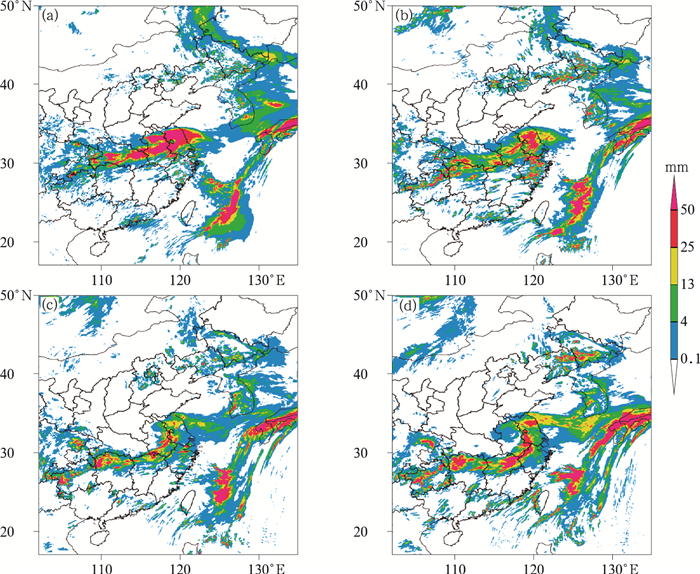
从逐6 h降水图来看(图 5，图 6)，MF试验和CTL试验都预报出了此次降水过程，降水分布较实况强度偏强，范围偏大。MF试验和CTL试验5日00—06时时段降水预报分布差异不明显, 江苏和安徽境内降水较实况偏强，06—12时和12—18时在江苏、安徽和湖北省区域降水预报逐渐出现细微差异，MF试验更接近实况。5日18时至6日00时预报雨带较实况略偏南，江苏北部地区预报偏大，MF试验效果略差。不同预报时段的降水分布结果显示，MF试验在北京地区的降水预报更接近实况。由此可见，MF试验和CTL试验的分析差异虽小，但对降水预报有影响，MF试验降水预报更接近实况。

3.2.2 连续试验

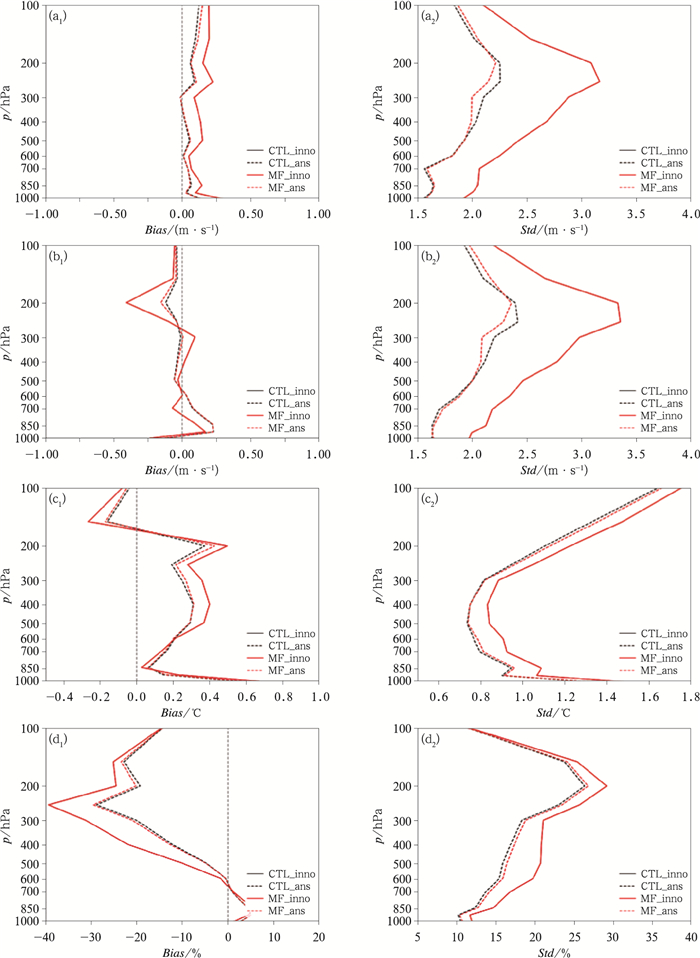
上文通过个例进行了MF试验和CTL试验结果分析，下面进行连续试验(2018年7月1—31日) 分析评估。用探空新息向量(inno, 背景减观测)和分析残差(ans，分析减观测)分析MF试验和CTL试验分析场差异。由2018年7月1—31日探空u、v风场、温度、相对湿度新息向量及分析残差偏差(Bias)和标准差(Std)廓线图(图 7)可见，00时冷启动，MF试验与CTL试验新息向量偏差和标准差廓线完全重合，说明两组试验初始条件是一致，即初始的背景场(FNL资料)和同化分析资料(包括探空资料)一致。2组试验分析残差廓线存在差异，u、v风场偏差和标准差在400~200 hPa相差较大，温度和湿度的偏差和标准差在低层相对较大。MF试验风场分析更接近探空观测，温度和湿度则稍微偏离探空观测。从相对湿度偏差和标准差来看，MF试验比CTL试验相对湿度更大(湿)。我国从2000年起应用L波段探空仪，采用的是碳湿敏元器件数字式电子探空仪，湿度观测资料偏干(郝民等，2018；唐南军等，2014)。因此，MF试验的湿度分析更接近实况。2组试验温度分析差异小，探空温度观测在低层与ERA再分析比存在一些正偏差(田伟红等，2019)，因此MF试验温度分析更接近ERA再分析。总体而言，MF试验分析风场和湿度更接近实况。

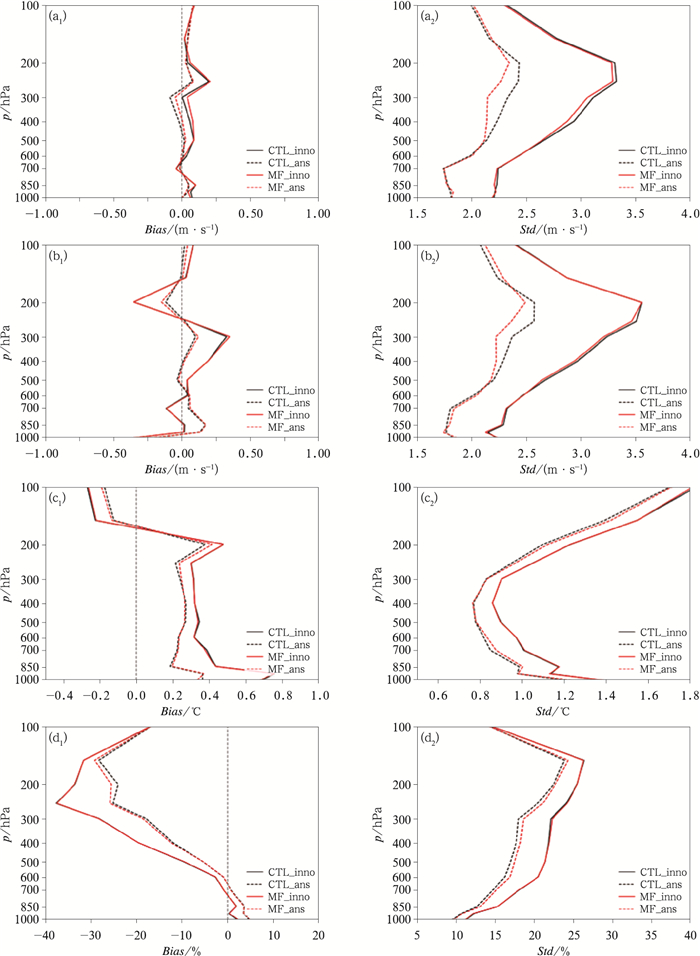
由2018年7月2—31日暖启动探空u、v风场、温度及相对湿度资料新息向量及分析残差廓线(图 8)可见，00时暖启动，MF试验与CTL试验的新息向量和分析残差偏差和标准差廓线都不重合，说明两组试验背景场和分析场都存在差异。MF试验和CTL试验每3 h同化一次观测资料并做3 h预报提供给下时次同化做背景场，暖启动同化分析的背景场是CMA-MESO模式系统3 h预报，冷启动时MF试验与CTL试验的分析已出现差异(图 7分析残差)，因此，多次同化循环暖启动时2组试验的背景场一定存在差异，虽然观测资料一致，暖启动时背景场不一致导致新息向量差廓线不重合。风场、温度场和湿度场新息向量的标准差MF试验较CTL试验略有减小，说明暖启动时MF试验背景更接近观测，即循环预报MF试验更接近观测。冷启动和暖启动2组试验分析残差廓线差异类似，400~200 hPa风场绝对误差相差较大，温度和湿度的均方差在低层更大。由此可见，暖启动MF试验分析的风场和湿度场更接近实况。

降水常采用TS(threat score)和Bias(bias score)分析(韦青等，2020)。TS值越大，Bias值越接近1，表示对降水的预报越准确。6 h降水量划分为小雨[0.1, 4) mm，中雨[4, 13) mm，大雨[13, 25) mm，暴雨[25, 60) mm和大暴雨(≥60 mm)5个量级。

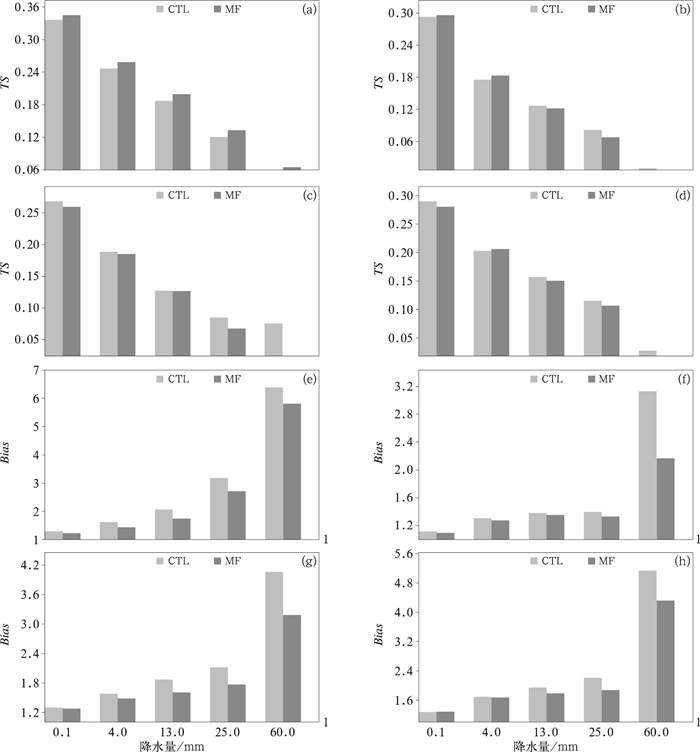
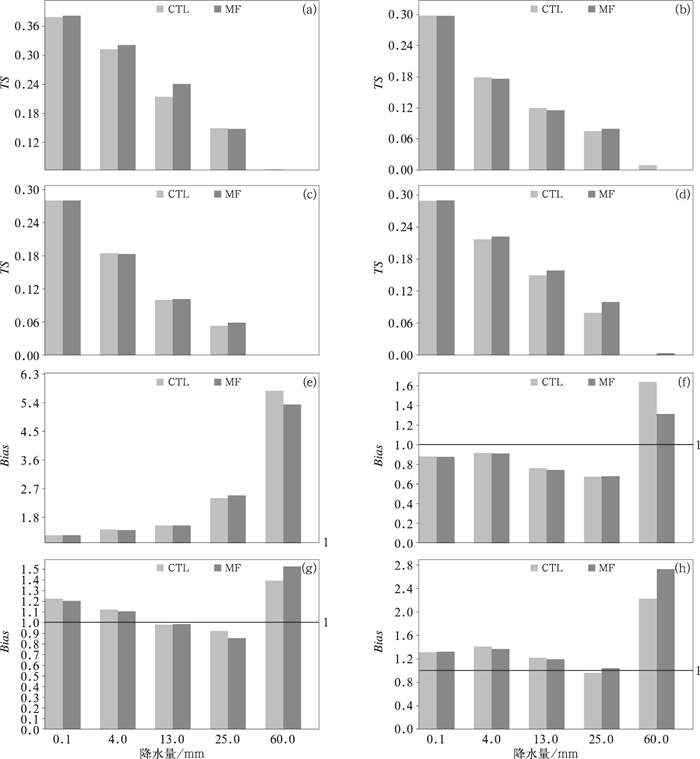
从00时冷、暖启动6 h降水检验TS评分(图 9、图 10)来看，00时冷启动MF试验对前6 h降水预报影响较大，各量级降水TS评分值明显提升，随着预报时效增加，对降水的影响逐渐减弱，TS评分值减小。MF试验每3 h同化都能更新一次分析场，不断改进模式的分析和预报效果(图 9显示冷启动结果前6 h基本为正贡献)，因而MF试验暖启动逐6 h降水TS评分检验基本表现为弱的正贡献(图 10，大部分量级降水TS评分在各时段都有所提高)。6 h降水检验偏差(图 9)则显示00时冷启动2组试验偏差差异明显，所有量级降水MF试验的偏差向1减小，而00时暖启动2组试验主要是大雨和暴雨的偏差(图 10)有差异，前12 h MF试验偏差更接近1，而后12 h则是CTL试验更接近1。结合背景和分析与探空资料的偏差和标准差以及冷暖启动的降水检验结果来看，MF试验能改进同化分析场和降水预报，但改进的幅度有限，维持的时间不是很长。这也许是背景误差做3种尺度分离时与模式的物理过程等结合不够紧密有关，需要进一步深入研究。

4 结论与讨论

本文通过对2018年6—8月的背景误差进行尺度分离，拟合出3种不同尺度的水平相关特征尺度在CMA-MESO 3Dvar系统中应用，与业务测试系统中单一水平特征相关尺度进行个例和连续试验对比分析，结果显示：

(1) 二维离散余弦变换尺度分离背景误差样本的3种水平特征相关尺度垂直结构相似，水平特征尺度的水平尺度相隔几十至几百千米。

(2) 3种水平特征相关尺度和单一水平特征相关尺度的湿度、温度和风场分析增量差异较小，湿度分析增量差异不超过6%，风场分析增量差异不超过1.2 m·s^-1，温度分析增量差异不超过0.35℃。3种水平特征相关尺度试验降水预报更接近实况。

(3) 3种水平特征相关尺度在CMA-MESO 3 km系统应用连续试验结果显示，3种拟合的水平特征相关尺度试验对u风、v风、湿度分析有明显正影响，分析更接近实况，对温度分析影响较小；对降水预报有改善，冷启动预报前6 h TS评分提高明显, 偏差减小向1靠近，暖启动24 h逐6 h降水预报TS评分值都有提升，Bias差异不大。