引言

台风是影响我国的主要热带天气系统之一，每年由台风引发的强降水及其次生灾害给我国, 尤其是沿海地区带来极大的经济损失和人员伤亡，因此如何准确预测台风降水也就成为气象学者关注的重要内容。相比于台风路径预报，台风降水预报的提升相对滞后，这是因为台风降水不仅与台风路径相关，而且还受到台风本体对流云带的分布结构、下垫面热动力特征以及大尺度外部环境流场等多个因素的制约(端义宏等，2020；喻自凤和余晖，2009；高栓柱, 2020；陈涛等, 2021)，表现出复杂的量级变化和分布形态，因此其预报复杂度也显著增加。

为了让预报员更好地利用模式降水预报产品，同时也为模式降水预报的改进提供客观参考依据，有必要运用新的检验技术对其开展更有效的评估，深入了解降水预报误差及其可能来源。以往的检验方法如ETS(equitable threat score)、POD(probability of detection)或FAR(false alarm ratio)等, 已在预报降水预报检验中得到了广泛应用，但这些方法是基于特定区域内“点对点”的评估技术，并非针对独立的降水对象，检验结果只能得到“预报是好或坏”的总体评价，无法反馈较全面的误差信息，也无法反映降水预报的误差来源。近年来，国际上一些气象学家开始尝试面向对象方法来开展目标检验研究。Ebert and McBride(2000)较早引入了一种针对定量降水预报并基于降水对象的CRA(contiguous rain area)检验方法，该方法可以将预报和观测对象间的误差分解为位移、总量和形态误差。Ebert and Gallus(2009)进一步分析了CRA方法的优缺点，而Moise and Delage(2011)则将旋转误差引入到CRA的误差分解中。Marchok et al(2007)使用一种新的方法来评估业务预报模式对于登陆美国台风的定量降水预报性能，该方法评估三个方面的降水预报技巧：降水形态、降水平均值和总量以及对于极端降水的预测。Wernli et al(2008)引入了一种新的定量降水检验方法SAL，它包含了降水场的三个不同分量：结构S、强度A和位置L，其中S反映了降水的分布特征，如降水范围、强度变化等，A反映了区域平均降水的偏差，L反映了降水中心的偏移量。在基于对象的降水检验过程中，对象匹配是关键，Davis et al(2006)的研究表明匹配能力与降水对象的尺度有关，或者说，可预报性相对较大的天气尺度系统的影响区域更大，也更容易匹配，而局地对流过程的影响范围更小，匹配难度增大。

尽管上述基于降水对象的检验方法的具体形式不同，但较传统检验方法而言，它们都能更全面、客观地描述降水误差。近年来，国内部分气象学者应用CRA空间检验评估方法分析降水预报的误差来源、降水落区偏差的空间分布及不同类型天气尺度系统对降水预报误差的可能影响(姜晓曼等，2014；符娇兰和代刊，2016；李晓兰和符娇兰，2021)。也有气象学者将CRA方法用于检验数值模式在登陆台风中的降水预报性能(Chen et al，2018；Yu et al，2020；王新敏和栗晗，2020；He et al，2022)，并得到了较传统降水检验方法更深入的预报误差来源和分布信息。

与西风带降水系统不同，台风作为热带天气系统，其降水分布与移动路径和自身结构有密切关系。为进一步探讨台风路径、结构等因素对台风降水预报的可能误差影响，针对台风降水的特点，本文将重点探讨以下两个问题：(1)路径误差对于降水位置误差的影响程度; (2)以台风移动路径为相对参考系的台风降水分布特征及预报误差。作为全球领先的欧洲中期天气预报中心(简称欧洲中心)高分辨率数值预报模式，其产品目前在我国各级气象部门得到了较广泛的应用。本文将利用CRA方法研究其产品对于2019年影响中国台风(王海平等, 2021)的降水预报误差及其可能来源，探讨其台风降水的预报能力，并供数值模式研发工作者、台风降水预报技术开发及业务人员作为参考。

1 数据与方法 1.1 欧洲中心确定性预报数据集

该数据集的地面层要素的水平分辨率为0.125°，高空层要素的水平分辨率为0.25°，0~72 h的时间间隔为3 h。本文对模式初始时次在台风登陆或靠近我国沿海前24 h至台风编报结束时段内(表 1)的0~6、0~24、24~48、48~72以及0~72 h降水预报数据进行检验分析。上述预报时段内如不包含观测或预报的台风编报信息，则该数据样本不计入降水检验中，以50 mm降水量级为例，各时段内对应的检验样本(CRA降水检验对象，详见1.4节)总数分别为44、45、38、27、42个。

1.2 卫星自动站融合的降水数据

本文中使用的观测降水数据来源于国家气象信息中心基于CMORPH(Climate Precipitation Center Morphing)卫星降水产品制作的卫星自动站融合降水数据。CMORPH降水产品可提供合理的降水分布，但也存在高估小量级降水和低估大量级降水的可能(Yu et al, 2009)，通过融合自动站降水数据可以提高中国区域内该降水产品的准确率。该降水融合数据的水平分辨率为0.1°，时间分辨率为1 h。

1.3 台风路径和强度的预报及观测数据

本文中使用的台风路径和强度预报数据来源于国家气象中心提供的基于欧洲中心确定性预报的诊断产品。台风观测路径来源于由中国气象局上海台风研究所提供的2019年台风最佳路径数据集，该数据集包含了3 h或6 h间隔的台风位置和强度信息。

1.4 CRA降水检验方法和步骤

(1) 确定降水对象：根据降水阈值P确定指定区域内的所有预报降水对象区域A_f(A_f中的格点降水值均大于等于P)和观测降水对象区域A_o(A_o中的格点降水值均大于等于P)，以及初始CRA降水检验区域CRA_origin=A_f∪A_o。

(2) 匹配降水对象：分别计算A_f和A_o的雨量中心位置C_f和C_o，并在C_o周边指定范围内搜寻A_f的最佳水平位移距离, 得到匹配区域A_f^′，使得新的CRA降水检验区域CRA_displacement=A_f^′∪CRA_origin内的预报和观测降水场的相关系数CORR_fo最大，且当CORR_fo=MAX_CORR时MSE_fo最小；在此基础上采用类似的方法搜寻A_f的最佳旋转角度Δθ, 并得到匹配区域A_f^″，新的CRA降水检验区域CRA_shifting=A_f^″∪CRA_origin，其中水平位移和旋转过程合称shifting。

(3) 误差分解：根据上述计算结果，将预报降水的均方误差MSE_total分解为位置误差MSE_displacement，旋转误差MSE_rotate，总量误差MSE_volume和形态误差MSE_pattern，每类误差的具体计算公式可参考Grams et al(2006)和Chen et al(2018)。下文将这几类误差依次分别简称为D、R、V、P。

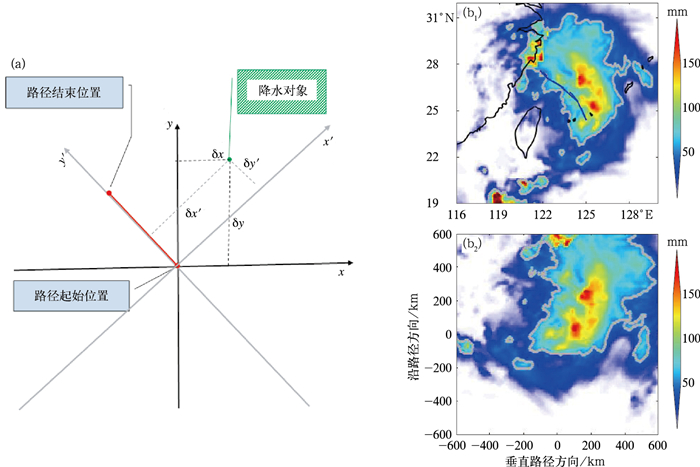
1.5 经纬度地理坐标系到台风移动路径相对坐标系的转换

通常降水检验分析使用经纬度地理坐标系，但在某些情况下也会采用相对台风移动路径的距离坐标系。如图 1a所示，xy地理坐标系的原点设在路径起始位置上，x和y方向分别对应原点处的纬向和经向，某个降水对象点的坐标为(δx, δy)，分别为该点到原点处的经纬度距离。而在x^′y^′的路径相对坐标系中，将y^′轴的方向设为路径的起止方向，则该降水对象点的坐标变为(δx^′, δy^′)，它们分别为该点到原点的最短球面距离在x^′和y^′轴上的投影(单位：km)。以台风Lekima为例，其登陆前24 h观测降水分布的坐标转换如图 1b所示。

1.6 台风降水非对称性和环境垂直风切变的计算

非对称性是台风降水分布的重要特征之一(Lonfat et al, 2004；Chen et al，2006；Yu et al，2015；黄燕燕等，2023)，同时这也是引起台风降水预报误差的一个主要因素。Boyd(2001)提出了一种基于Fourier级数的方法来定量计算降水的非对称性特征，其中降水的一阶非对称性空间结构M₁的具体算法是针对指定半径范围内(如500 km)围绕台风中心的宽度为10 km的所有圆环，计算每个圆环上的一阶系数：

$ a_1=\sum\limits_i\left(R_i \cos \theta_i\right), \quad b_1=\sum\limits_i\left(R_i \sin \theta_i\right) $

式中：R_i为圆环上的降水格点值，θ_i为该降水格点与台风移动方向之间的相位角，非对称性M₁的空间分布可以表示为：

$ M_1=\left(a_1 \cos \theta+b_1 \sin \theta\right) / R $

式中R为整个圆环的平均降水率。

本文还将计算所有台风在登陆或靠近沿海前后的垂直风切变强度及其变化，并基于此分析不同垂直风切变下降水非对称性的预报误差。需要注意的是，不同学者对于环境垂直风切变的定义存在一定的差异(Rogers et al，2003；Chen et al，2006；Kaplan et al，2010；Wingo and Cecil, 2010；Reasor et al，2013；Yu et al，2015)，本文采用Chen et al(2006)中的垂直风切变的定义，即距台风中心200~800 km的圆环区域内200 hPa和850 hPa之间的平均风矢量差。

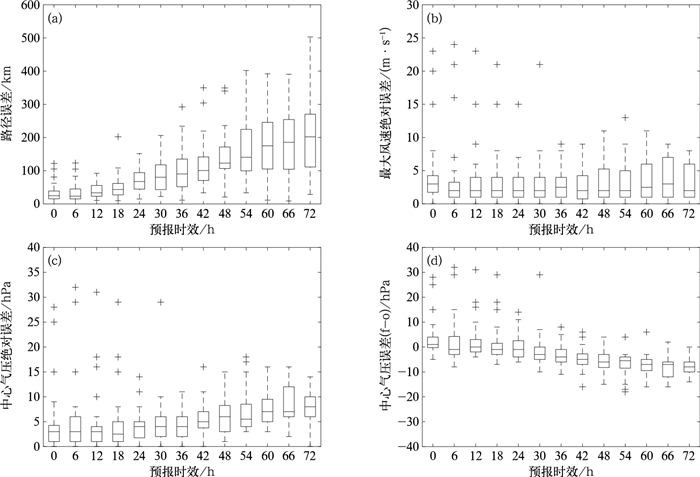
2 台风路径和强度预报误差分析

台风移动路径和强度是影响台风降水分布和总量的重要因素，本文首先分析这两项基本指标的预报误差。图 2是欧洲中心确定性预报对2019年影响中国台风(表 1)的0~72 h路径和强度误差的统计检验结果，下面主要以误差分布的50%分位值分析误差的变化趋势。0~6 h是模式积分的初始时段，该阶段反映了模式中初始同化方案的质量以及模式对于“spin-up”动力平衡过程的调整能力。可以看到6 h的台风路径和强度误差较初始时次(0 h)略有下降或基本保持不变，这表明模式在经过6 h积分以后就已表现出较好的动力平衡。12 h后路径误差和中心气压绝对误差均呈现出不同程度的增加趋势，而最大风速误差的变化则并不明显，其中24、48和72 h内大多数路径预报误差分别不超过100、200和300 km，中心气压差分别不大于5、10和15 hPa。随着预报时长的增加，预报和观测间的中心气压差逐渐减小为负值，这表明模式预报的中心气压要低于观测，且台风登陆或靠近沿海以后其预报强度要强于观测强度。此外也可以看到误差分布的异常值主要出现在24 h内，而这可能与个别起报时次的初始分析场与观测的偏离度较大有关。受资料所限，具体原因有待深入研究。

3 基于CRA方法的模式降水误差及其来源分析 3.1 降水误差比例的概率分布

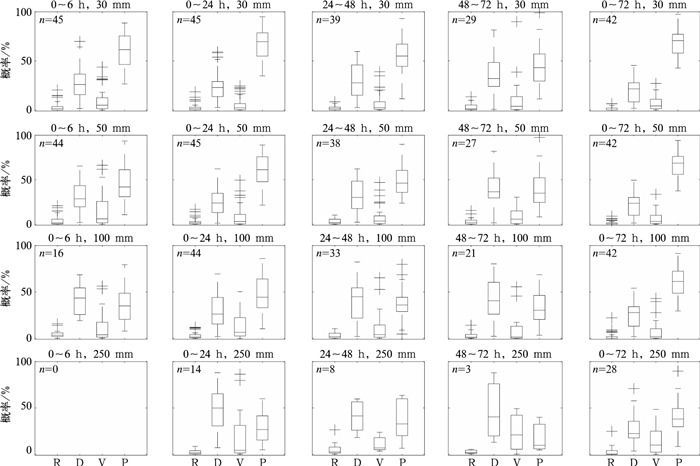
为了分析不同降水时段和降水量级下的预报误差来源，使用CRA方法对所有预报样本的降水误差进行分解，并计算不同误差来源的概率分布(图 3)。可以看到，对于6 h或24 h降水预报，总体而言各量级降水中主要误差均来自于位置误差和形态误差，旋转误差的比例最小。随着量级的增大，位置误差的比例上升，而形态误差则下降，这表明在小量级降水中，误差更多来源于降水的分布形态，而大量级降水中，落区上的偏差往往对降水预报造成较大影响。此外在大量级降水中，总量误差有所增长，这表明预报降水量级越大，其比例也有所加大。当降水量级为250 mm时，位置误差的比例明显要高于其他误差。对于48 h或72 h，误差比例的变化类似。从72 h累计降水的误差概率分布可以看到，位置误差和形态误差依然是降水误差的主要来源，但是与6 h或24 h降水不同的是，随着降水量级的增加，二者的比例变化并不明显，只是当降水量级为250 mm时，总量误差和形态误差则分别出现较明显的上升和下降变化。上述分析表明，位置误差和形态误差是预报降水的主要误差来源，而随着降水量级的增大，总量误差所占比例也有所增加。

3.2 降水对象偏移距离与台风路径误差的相关性

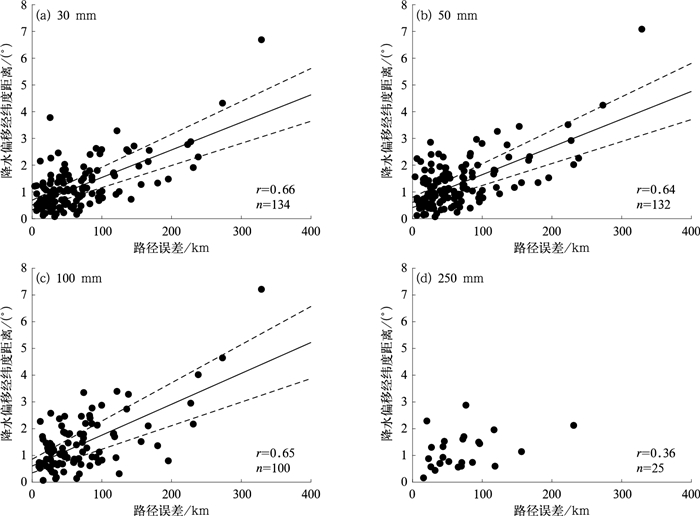
从各降水量级下不同预报时段的误差概率分布可以看到，随着预报时效的增加，位置误差的比例逐渐上升，这与台风路径误差的变化趋势相近，那么两者之间存在着怎样的关系？从CRA降水区域的偏移距离与对应降水时段内平均路径误差的散点分布(图 4)可以看到，当降水量级为30~100 mm时，降水区偏移距离与路径误差的相关系数为0.64~0.66，且通过置信度为95%的相关性检验，这说明两者间存在较高的相关性；而降水量级为250 mm的相关系数为0.36，没有通过95%的相关性检验，由于其样本数仅为25个，因此该结果在此仅作参考。通过对250 mm量级个例的具体分析(图略)可以发现，降水预报位置的偏差与模式降水结构分布的预报差异存在一定的关系。如台风Lekima中，对于48~72 h的降水预报，模式没有很好地反映出浙江沿海地形对于降水的显著增幅作用，反而对于台风移动路径附近降水存在量级过度预报的现象。

进一步分析位置误差的比例和平均路径误差的相关性可以发现(图略)，当降水量级为30、50、100 mm时，两者的相关系数分别为0.44、0.41和0.30，尽管较之前有所下降，但都通过了95%的相关性检验，表明两者还是显著相关的，而相关系数的下降与其他降水误差的引入有关。上述分析验证了在大多数情况下，台风路径误差与降水位置偏差之间存在显著相关性，这也解释了为何随着预报时间的增长，位置误差的比例也随之增加的原因。

3.3 降水对象事件的分类检验

在CRA降水检验中，检验的对象是由指定降水阈值构成的降水区域。通常预报员主要关注的是预报降水区域的位置和强度是否和观测相对应，但是检验的标准具有一定的主观性。

采用Ebert and McBride(2000)和Chen et al(2018)的分类统计方法检验不同降水量级和不同预报时段下降水对象的预报能力。检验标准如下：对于降水位置，设定其误差临界值为1.0°，按相近、远离进行分类；对于降水总量，设定其误差临界值为降水区域观测值的25%，按偏少、相近、偏多进行分类。

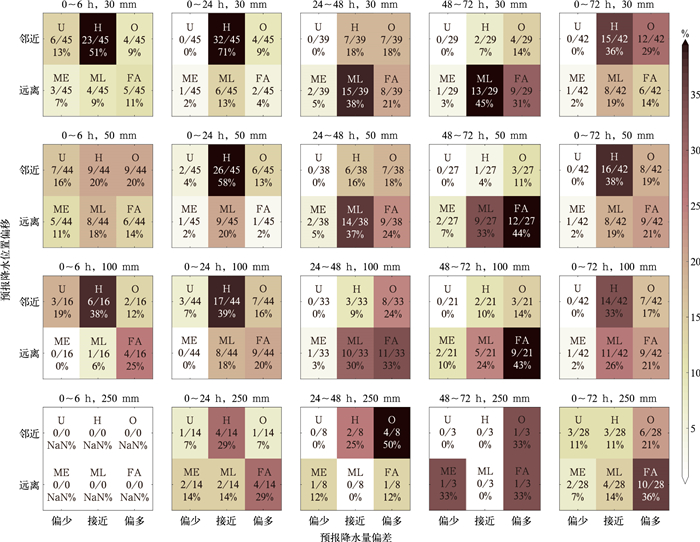
可以看到(图 5)对于所有量级的降水事件，随着预报时间的增加，命中率总体呈现出下降的趋势，6 h或24 h的命中率普遍要高于48 h或72 h，而这与随预报时间增大的降水位置偏移量有直接关系。此外还可以发现随着预报降水量级的增长，降水高估率和误报率总体呈现出增加的趋势，这也表明在预报较大量级降水时，模式预报降水量有偏多的倾向。降水漏报和低估事件的比例总体较低，只是在0~6 h降水时段和250 mm降水量级上的比例相对较高，前者与模式动力平衡过程有关，而后者表明模式对于降水极值的预报可能偏弱。对于0~72 h累计降水，30、50、100 mm降水的命中率变化不大，但当降水量为250 mm时，其位置偏移量和降水预报量均有不同程度的增大。

3.4 降水对象shifting前后的降水预报技巧及相关性比较

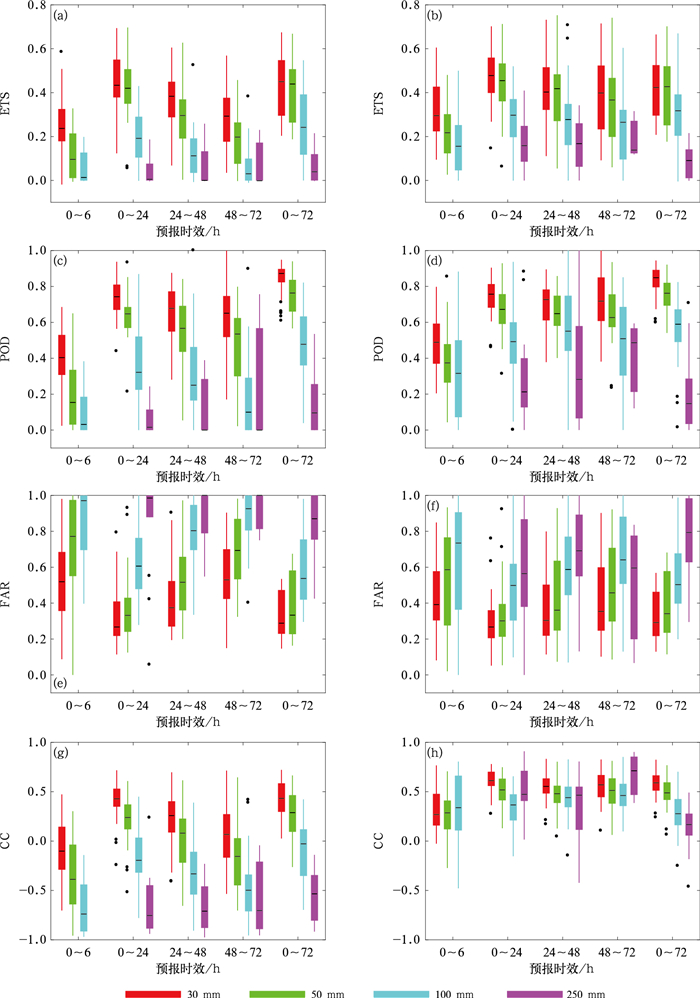
尽管传统的降水检验方法存在一定的不足，但是由于其在预报业务中的广泛应用，因而基于这些方法的降水评分仍具有一定的参考意义。黄伟等(2009)检验了上海台风研究所原GRAPES-TCM模式的早期版本对于2006年登陆热带气旋的降水预报性能，指出模式能较好地预报出登陆热带气旋的降水分布形态，但对暴雨以上级别降水，其Bias值明显偏大，ETS的平均得分不足0.05。He et al(2022)利用该模式的较新版本检验其对2019年超强台风Lekima的降水预报性能，结果表明72 h内0~24 h降水的平均ETS最高，其中30 mm降水的评分值接近0.4，100 mm降水为0.1，CRA shifting对大量级降水和较长时效的预报降水评分有较明显的改进。与此类似，本文分析欧洲中心全球模式在不同降水时段和量级下的降水预报性能及其经过CRA降水对象shifting后的变化，以样本的50%分位值作为参考值。可以看到(图 6a, 6b)，对于原始CRA降水区域，在所有6 h或24 h降水检验中，0~24 h的ETS评分是最高的，其中30 mm和50 mm均超过了0.4，而100 mm则接近0.2，尽管250 mm的评分几乎为0.0，但其也有近25%的个例评分达到0.1~0.2，这说明模式对于极端降水仍有一定的预报能力。0~6 h各量级降水的ETS评分明显偏低，这可能与模式处于“spin-up”动力调整阶段有关。对6 h或24 h的CRA降水区域进行shifting处理后可以发现，对于30 mm和50 mm量级降水，ETS的变化总体上并不明显，这与最初24 h内小量级降水的位置误差较小有关，但是对于100 mm以上的大量级降水，ETS还是有一定程度的提升。随着预报时间的增长，24 h降水的ETS评分出现不同程度的下降，对比移动匹配处理后相应的ETS评分可以发现，24~48 h和48~72 h的降水评分值明显上升，尤其是对于100 mm以上的大量级降水，这说明降水位置误差对降水评分具有显著影响。此外还可以看到0~72 h累计降水的ETS评分与0~24 h降水总体相当，其中100 mm以上降水评分甚至还略好于后者。而在相应的ETS shifting评分中，各量级上的降水评分值变化不明显，对于较长时段的累计降水而言，降水位置误差的影响较小。POD、FAR的评分结果及变化趋势与ETS类似(图 6c~6f)，在此不再赘述。预报和观测降水区域的相关性统计(CC)是CRA方法中计算预报降水位置误差的重要依据。从图 6g~6h可以看到，总体而言随着降水量级的增大，降水区域之间的相关性逐渐下降。除6 h降水以外，30 mm和50 mm的降水区域普遍为正相关，而100 mm以上降水区域普遍为负相关。经过CRA shifting处理后，各量级降水区域几乎都转为正相关，且除0~72 h降水以外，各量级降水区域的相关性较为接近。

3.5 台风路径修正对降水预报的影响

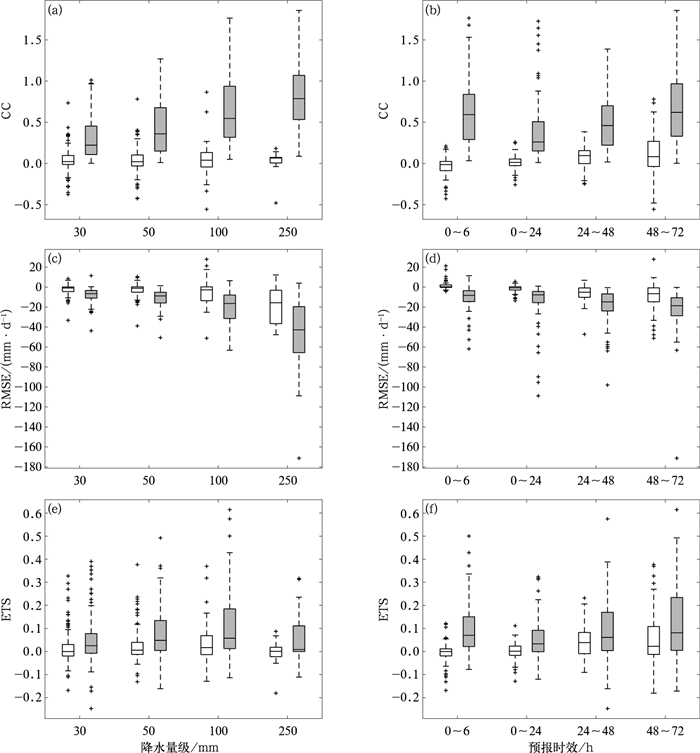
从3.2节的分析可以看到，CRA降水区域的偏移距离与对应降水时段内平均路径误差之间存在显著相关性，也就是说修正台风的路径误差有助于改进降水预报的位置误差。为了进一步研究不同降水量级或不同预报时段内的改进效果，本文首先对6 h间隔的模式降水预报进行最佳路径修正处理，即根据预报路径与最佳路径之间的位置偏移量来调整对应时段内的降水预报位置，然后与经CRA移动匹配后的模式预报降水进行对比分析(图 7)。可以看到，对于所有降水量级，模式降水在经过路径修正后，相关性(CC)提升的样本数要多于下降数，但与经CRA shifting后的模式降水相比并不显著(由于CRA shifting算法以寻找预报和观测降水对象间最大相关性为基础，因此其样本的相关性均大于0)。当降水量级为250 mm时，两者的差距达到最大，这也表明大量级降水下，路径误差与降水位置偏差间的相关性大大减小。均方根误差(RMSE)与CC类似，在经过路径修正后，大多数样本的RMSE都有所减小，但其改进没有CRA shifting算法显著，随着降水量级的增大，两者的差距也在逐渐增大。ETS的改进差异没有前两者明显，当降水量级为100 mm时，路径修正的改进量总体上最明显，极端改进值接近0.4，当降水量级为250 mm时，无论是路径修正还是CRA shifting，ETS的改进量均有所减小。从不同预报时段的改进量可以看到，24 h以内路径修正对降水的改进并不明显，CC、RMSE和ETS改进量的50%分位值接近0。24 h以后路径修正的改进量有较明显增加，但仍低于CRA shifting算法。上述分析表明，总体上路径修正可以减小模式降水误差，但主要对24 h以后的预报降水有一定的订正效果，且对于各量级的降水预报均有改进。此外还可以发现路径修正有时也未必会对降水预报产生正的改进效应，当然这类情况的比例相对较小。

4 台风登陆或靠近沿海前后降水分布的预报误差 4.1 台风降水概率分布的预报误差

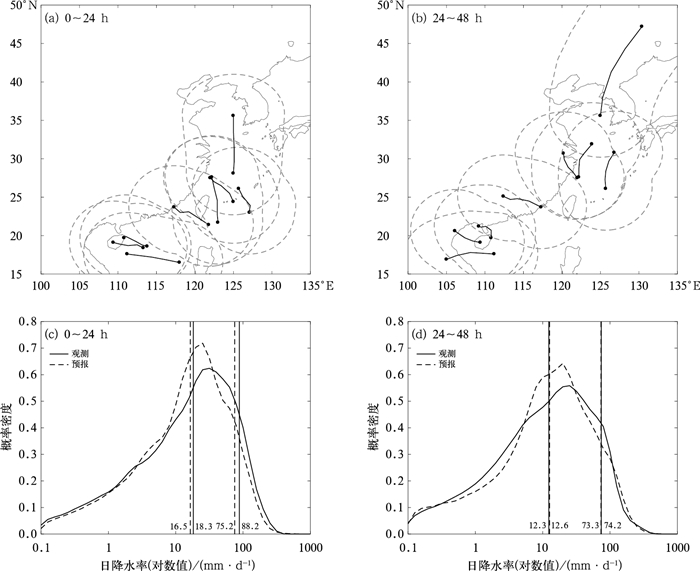
台风在登陆或靠近我国沿海前后，其下垫面环境以及大尺度环流场会产生较大的变化，这将对台风直接环流降水造成影响。为了研究该时段内观测及预报降水的变化特征，本文取初始时次与台风登陆或靠近沿海前24 h最接近的模式预报和对应时段的观测日降水量为研究对象，空间范围包括台风最佳路径或预报路径周边600 km内的格点区域(如 图 8a, 8b中虚线所示范围)，以模式的相对时次0~24 h代表台风登陆或靠近前的时段，24~48 h代表台风登陆或靠近后的时段。可以看到(图 8c, 8d)在台风登陆或靠近前(0~24 h)，预报的日降水率的概率密度分布形态与观测总体上较为一致，在10 mm以下的小量级雨段，两者非常接近，甚至出现重合。预报概率密度峰值和50%分位点的位置略偏于观测左侧，这也导致预报极值端或90%分位点降水量小于观测，或者说100 mm以上的强降水预报略偏弱。在台风登陆或靠近后(24~48 h)，预报和观测50%和90%分位点值几乎重合，这表明降水概率分布的预报误差进一步减小。总体而言，台风登陆或靠近沿海前后，模式预报的降水概率分布与观测较一致，只是对大量级降水，预报略偏弱。

4.2 台风径向降水分布的预报误差

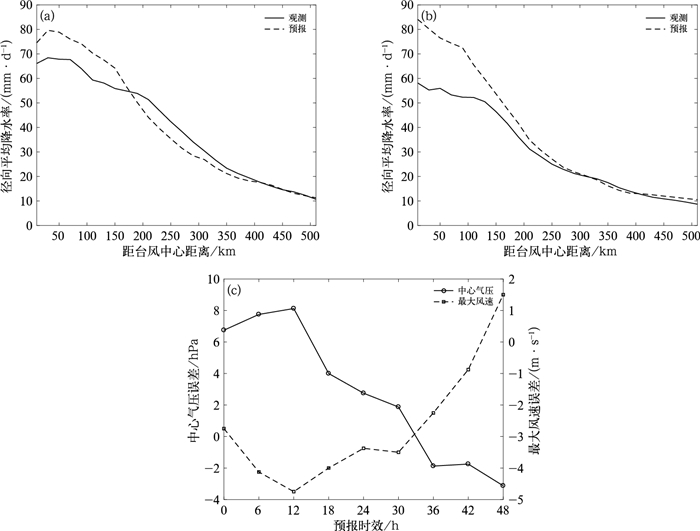
从前面的误差分析可以看到，位置误差是台风降水误差的主要来源之一，而位置误差与台风路径偏差又存在一定的相关性。为了深入研究台风降水的径向分布特征同时尽量减少由于台风路径偏差引入的降水误差，下面将以台风最佳或预报路径为相对坐标，对500 km范围内的台风降水做径向化处理。可以看到对于0~24 h(图 9a)，在距台风中心170 km以内的核心区域内，预报的平均降水率大于观测，两者的最大差异近10 mm·d^-1, 而200~400 km的台风核心区以外，预报的平均降水率则要小于观测。从图 9c可以看到，24 h以内预报台风的平均强度是要弱于观测的，最大差值在8 hPa或4 m·s^-1左右，这表明尽管模式预报的初始台风强度总体弱于观测值，然而其采用的物理方案却并没有使近台风中心附近的降水强度变小。24~48 h(图 9b)最大差异进一步加大超过20 mm·d^-1, 且范围扩大到距台风中心近300 km。此外，自台风核心区直到其外侧几乎都是预报降水强度大于观测，这应该与该时段内预报台风强度迅速接近或略强于观测有直接关系(图 9c)。总体而言，台风登陆或靠近沿海前后，其核心区内的预报平均降水强度明显大于观测，而在核心区以外，随着距离的增加两者的差异逐渐减小。

4.3 台风降水位置误差的水平分布特征

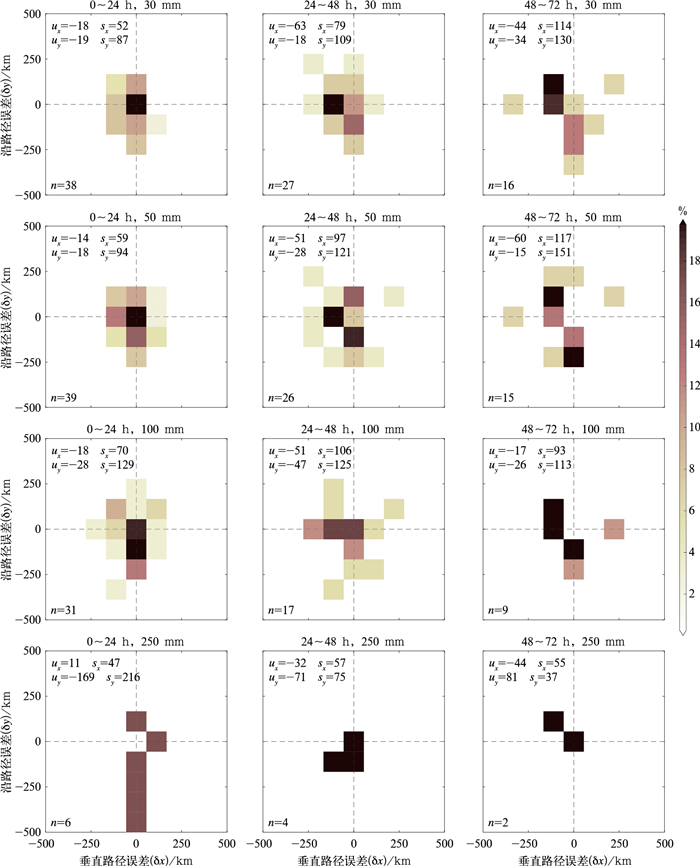
通过分析台风降水相对于台风中心的位置偏移，有助于了解其结构分布特征。下面以台风最佳或预报路径为相对坐标系，计算不同时次和不同量级下沿路径方向(along track)和垂直于路径方向(cross track)的降水对象位置预报误差分布(图 10)。其中along track误差定义为预报和观测降水对象在y方向的距离差, 正值表示预报降水对象超前于观测，负值表示预报滞后于观测；cross track误差定义为预报和观测对象偏离台风中心的绝对距离之差, 正值表示预报降水对象相比观测远离台风中心，负值表示预报更靠近台风中心。从图 10可以看到，多数情况下预报降水对象偏离台风中心的程度，或与观测相当，或小于观测，这表明预报降水对象总体上表现出较观测更靠近台风中心的倾向，预报的雨带结构比观测更加紧密。此外预报降水对象也略滞后于观测，尤其对于100 mm以上量级或72 h预报时效的降水，这说明观测雨带较预报位置更偏向于移动路径的前方。对于250 mm降水，由于统计样本数量明显偏少，因此其误差的分布形态并不完整，在此仅做个例参考。

4.4 台风非对称性降水的预报误差

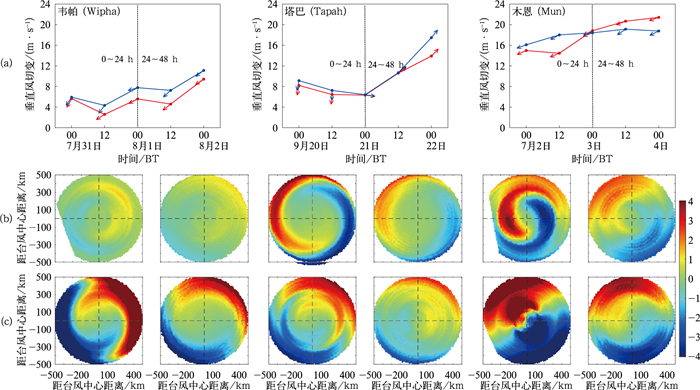
非对称性是台风降水的重要结构特征之一，它的产生与台风强度、台风本体移动以及环境场的垂直风切变等因素有关(Chen et al，2006；Yu et al，2015；2017)。本文以台风路径为相对坐标系，检验模式对于台风降水非对称性的预报能力。为了研究不同环境垂直风切变和不同下垫面下台风降水的非对称性预报特征，选择“Wipha”“Tapah”“Mun”进行对比研究(图 11a)。这三个台风，登陆或靠近沿海前(0~24 h)分别处于弱、中等和强的环境垂直风切变下，其中“Tapah”未登陆我国。可以看到在台风登陆或靠近沿海前(0~24 h，图 11b)，“Wipha”的降水非对称分布特征最弱，“Tapah”相对较强，且两者的最大非对称中心主要位于距离台风中心200 km以外的台风前进方向的两侧，“Mun”的最大非对称值与“Tapah”相近，但明显深入台风内核区。三个台风的环境垂直风切变预报强度和方向总体上与分析场接近，但预报降水的非对称特征却均弱于分析场，且最大非对称中心距离台风中心均较远。台风登陆或靠近沿海后(24~48 h，图 11c)，三个台风降水的非对称性特征进一步加强，“Mun”在台风核心区内也出现明显的非对称分布特征，这表明台风登陆以后，陆面进一步破坏台风的中心结构，然而这种特征在降水预报中并不显著。此外还可以看到，登陆或靠近我国沿海后(24~48 h)，尽管“Tapah”的垂直风切变较“Wipha”更明显，但是降水的非对称性特征却不如“Wipha”，这可能和“Tapah”并不是一个登陆台风有较大关系，其下垫面主体是摩擦作用相对较小的洋面。但在这样的环境下，预报降水的非对称性特征仍然偏弱。受台风样本限制，以上仅分析了三个代表性台风在不同垂直风切变和下垫面条件下模式的降水分布特征，总体而言，在台风登陆或靠近沿海地区前后，模式能较好地反映降水的非对称性分布特征及其变化，但在非对称性降水强度尤其是在台风登陆以后的预报上则明显偏弱。

5 结论

台风降水预报误差检验及分析，无论是对于预报员应用降水预报产品或是模式开发者改进台风降水的预报能力，均有重要意义。不同于传统的基于格点的降水检验方法，面向降水对象的CRA检验方法可以对降水误差进行分解，这有助于分析误差的主要来源。此外，台风降水的分布形态有其自身特点，对这些特征的预报误差检验也将有助于进一步了解模式的台风降水预报性能。本文的主要结论如下。

(1) 对于不同预报时段和降水量级，总体而言，主要误差均来自于位置误差D和形态误差P，旋转误差R的比例最小。在小量级降水中，误差更多来源于降水的分布形态，而大量级降水中，落区上的偏差往往对降水预报造成较大影响。预报降水量级越大，总量误差V的比例也有所加大，且预报降水量有偏多的倾向，但250 mm以上特大量级降水预报有时也偏弱。

(2) CRA降水区域偏移距离与路径误差的相关性检验表明，当降水量在30~100 mm时，两者存在显著相关；而对于250 mm以上的特大量级降水预报，其位置误差未必均由路径误差引起。尽管台风路径修正对于降水预报的改进逊于CRA shifting，但总体上也可以减小模式降水误差，主要对24 h以后的预报降水有一定的订正效果，且对于各量级的降水预报均有改进。

(3) 台风登陆或靠近沿海前后，其路径周边600 km范围内的日降水率的预报概率密度分布形态与观测总体上较为一致。台风登陆前，在台风核心区域内，预报的平均降水量大于观测，而在200~400 km的台风核心区以外地区，预报的平均降水量则要小于观测；当台风登陆后，台风核心区直到其外侧几乎都是预报降水强度大于观测，这与该时段内预报台风强度迅速接近或略强于观测有直接关系。

(4) 台风登陆或靠近沿海前后，预报降水较观测更靠近台风中心，且沿移动路径略滞后于观测，随着预报时效的增加，这种趋势更加明显。基于不同环境垂直风切变和下垫面的分类研究表明，预报和观测降水的非对称性分布形态总体较接近，但是预报的非对称性结构明显弱于观测，尤其是在台风登陆或靠近沿海后。台风登陆以后，台风内侧降水的非对称结构明显增强，但预报降水没有很好地反映出这种变化趋势。