2. 国家气象中心, 北京 100081;
3. 中国气象局地球系统数值预报中心, 北京 100081;
4. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081
2. National Meteorological Centre, Beijing 100081;
3. Center for Earth System Modeling and Prediction of CMA, Beijing 100081;
4. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
随着数值模式的不断发展和高性能计算机能力的提升,高分辨率的区域快速更新循环同化系统发展迅速,满足中小尺度灾害性天气预报需求。快速更新循环同化系统充分利用时空高频的观测资料来提高模式初始场质量,在短时临近预报上发挥重要作用。美国在1991年开始了快速更新同化预报技术的研究开发,并于1994年开始在NCEP(National Centers for Environmental Prediction)业务运行(rapid update cycle, RUC)(Benjamin et al, 2004),之后经过几次更新和升级,于2005年开始采用三维变分(3DVAR)技术(Benjamin et al, 2006),2012年建立了基于混合变分集合同化的快速更新系统(rapid refresh, RAP),2014年发展了高分辨率的3 km快速更新系统(high resolution rapid refresh, HRRR)(Benjamin et al, 2016)。2000年后中国气象业务部门陆续引进和发展适合本地区的RUC系统,尽管起步较晚,但发展却十分迅速(陈德辉等, 2008;薛纪善等,2008)。2007年北京快速更新数值模式系统(Beijing-Rapid Update Cycle, BJ-RUC)开始业务试运行,并成功应用于北京2008年奥运会和国庆60周年等大型活动的气象保障服务中,是北京气象台强对流天气短时临近预报的重要技术支撑系统(范水勇等, 2008)。2009年上海建立了基于ADAS(ARPS Data Assimilation System)同化系统和中尺度数值模式WRF(Weather Research and Forecasting Model)的快速更新同化预报系统(Shanghai Meteorological Bureau-WRF ADAS Rapid Refresh System, SMB-WARR),成功应用于2010年上海世博会气象服务保障(傅娜等, 2013)。广州基于CMA-MESO及三维变分同化发展了快速更新同化预报系统CMA-GD(陈子通等, 2010)。2009年武汉快速更新同化预报系统AREM-RUC(Advanced Regional Eta-coordinate Model-Rapid Update Cycle)投入业务应用(王叶红等, 2011)。
2010年,国家气象中心基于CMA-GD系统,采用模式面三维变分同化系统(Ma et al,2009)和CMA-MESO模式V3.0版本建立的全国区域15 km分辨率31层3 h循环的CMA-MESO进入准业务运行(徐枝芳等, 2013),2014年CMA-MESO水平分辨率升级到10 km、垂直分层为50层。随后,CMA-MESO不断升级改进提升要素场和降水预报(黄丽萍等, 2017),2015年建立了覆盖中国东部区域3 km水平分辨率的试验系统(许晨璐等, 2017)。2020年,CMA-MESO系统分辨率从10 km升级为3 km(庄照荣等, 2020),资料同化种类和资料量大幅增加,CMA-MESO系统在短时临近预报中发挥着越来越重要的作用。但面临的挑战也与日倶增,特别是高分辨率的数值天气预报应用于短时临近预报,如对流尺度的资料同化,物理过程构建等等,预报存在不可避免的误差。为了提高预报准确度,一方面可以通过加强资料同化技术改善初始场,优化模式物理过程参数化方案,改善模式对各类天气捕捉的精准度(王学忠等, 2003;托亚等,2003;盛春岩等,2006;薛谌彬等,2017);另一方面可以利用误差订正来改善数值预报产品的应用效果(王敏等, 2012;王丹等,2016;李佰平和智协飞,2012;赵滨和张博,2018)。国内学者在模式误差订正方面做了很多工作,如:马旭林等(2015)在卡尔曼滤波递减平均的一阶矩和二阶矩偏差订正方案基础上发展综合偏差订正方案,有效减小集合平均偏差;王婧等(2015)采用平均法、双权重平均法、滑动平均法和滑动双权重平均法对CMA-MESO 15 km系统2014年夏季2 m温度预报产品进行偏差订正,滑动双权重平均法订正取得了较好效果;薛谌彬等(2019)提出了结合滑动双权重平均订正法和空间误差逐步订正法的综合订正技术,并将该方法成功运用于江西省精细化气象要素客观预报业务系统;唐文苑和郑永光(2019)基于CMA-MESO 15 km系统2017年夏季逐小时降水预报,对时间滞后集合成员采用频率匹配订正法进行降水量级订正,提高了对强降水系统位置、形态及降水量级的预报水平;张玉涛等(2020)采用一阶自适应的卡尔曼滤波方法对CMA-MESO 3 km模式的2 m温度、2 m相对湿度和10 m风开展偏差订正,有效提高了这些产品在2018年平昌冬奥会气象服务中的预报能力。
本文通过对2020年12月至2021年2月CMA-MESO系统每日8个起报时间每3小时的2 m温度预报产品进行诊断。我国国土辽阔、地形复杂,地面2 m温度数据应用具有一定局地性。为了更好地分析CMA-MESO系统2 m温度预报的问题,依据订正前后标准差对比,本文对2 m温度预报效果存在明显差异的华北、华东、西南开展波谱分析,通过波谱分析来诊断模式系统不同尺度信息的捕捉能力与预报准确性的关系。庄照荣等(2018;2020)采用二维离散余弦转换(discrete cosine transform,2D-DCT),将全球T639模式和区域CMA-MESO模式分析增量进行谱分解,获得全球和区域模式产品中的不同尺度信息。二维离散余弦转换能较好分解模式预报的尺度信息,本文将采用该方法进行波谱分析。
1 资料和方法 1.1 资料选用2020年12月至2021年2月CMA-MESO系统每日00、03、06、09、12、15、18、21时(世界时,下同)共8个起报时间,每3小时一次2 m温度预报输出产品和全国地面观测2 m温度资料。由于12月1日21时起报的24 h预报产品对应观测时间为12月2日21时,为保证诊断分析时每个时刻的预报产品样本量一致,因此从每月3日开始诊断分析。CMA-MESO同化观测资料包括探空、地面报、船舶报、飞机报、云导风、雷达速度方位显示(VAD)反演风场和GPS(global positioning system)掩星反演可降水量(precipitable water vapor, GPS/PW),云分析使用了风云2G的亮温和云总量,以及雷达反射率资料。模式试验的水平分辨率为0.03°×0.03°,预报范围为15°~65°N、70°~145°E,覆盖了整个中国区域。由于观测站2 m温度存在少量缺失,对缺测率大于5%的观测站点进行了剔除,采用双线性插值法将2 m温度预报产品插值到观测站点,在站点进行诊断分析。
CMA-MESO系统每日00时和12时冷启动一次,每隔3小时一次资料同化和预报,冷启动预报时效为36 h,暖启动预报时效为30 h,一天8次提供快速更新中尺度数值预报的预报产品,为了保证诊断分析数据样本一致性,本文仅对前24 h预报产品做诊断分析。
1.2 诊断方法(1) 平均法(Mean):根据不同站点的观测增量Meankobs-b分别对其预报进行订正。
| $ \mathrm{Mean}_k^{\mathrm{obs}-\mathrm{b}}=\sum\limits_n T_{k, n}^{\mathrm{obs}}-T_{k, n}^{\mathrm{b}} $ | (1) |
| $ T_{k, n}^{\mathrm{b}, \mathrm{cal}}=T_{k, n}^{\mathrm{b}}+\mathrm{Mean}_k^{\mathrm{obs}-\mathrm{b}} $ | (2) |
式中:Tk, nobs为2 m温度观测值,Tk, nb为插值到站点的2 m温度预报值,Tk, nb, cal为订正后的2 m温度预报值,k为站点序号,n为观测时次。
(2) 双权重平均法(BMean):由观测增量Tk, nobs-Tk, nb的双权重平均分别对不同站点预报进行订正,该方法可以减少离群资料对平均值的影响。
| $ w_{k, n}^{\mathrm{obs}-\mathrm{b}}=\frac{\left(T_{k, n}^{\mathrm{obs}}-T_{k, n}^{\mathrm{b}}\right)-M_k^{\mathrm{obs}-\mathrm{b}}}{7.5 \mathrm{MAD}_k^{\mathrm{obs}-\mathrm{b}}} $ | (3) |
| $ \begin{aligned} & \operatorname{BMean}_k^{\mathrm{obs}-\mathrm{b}}=M_k^{\mathrm{obs}-\mathrm{b}}+ \\ & \frac{\sum\limits_n\left[\left(T_{k, n}^{\mathrm{obs}}-T_{k, n}^{\mathrm{b}}\right)-M_k^{\mathrm{obs}-\mathrm{b}}\right]\left[1-\left(w_{k, n}^{\mathrm{obs}-\mathrm{b}}\right)^2\right]^2}{\sum\limits_n\left[1-\left(w_{k, n}^{\mathrm{obs}-\mathrm{b}}\right)^2\right]^2} \end{aligned} $ | (4) |
| $ T_{k, n}^{\mathrm{b}, \mathrm{cal}}=T_{k, n}^{\mathrm{b}}+\mathrm{BMean}_k^{\text {obs-b }} $ | (5) |
式中:BMeankobs-b为第k个站点观测增量的双权重平均,Mkobs-b为第k个站点观测增量的中位数,MADkobs-b为对应的绝对离差中位数,即|(Tk, nobs-Tk, nb)-Mkobs-b|的中位数。权重wk, nobs-b>1时,取wk, nobs-b=1。
(3) 滑动双权重法:徐枝芳等(2013)指出2 m温度具有半日周期、日周期和15 d周期的变化特征,因此,本文采用前15 d的已知2 m温度预报值和站点实况资料,通过双权重方法计算出对应时次的订正量,对当前一天2 m温度预报场进行订正,以此类推,计算出2021年全国范围1月和华北地区2月订正后的预报场。
(4) 本文选用平均偏差(Bias)、均方根误差(RMSE)及标准差(Std)进行诊断分析。
平均误差:
| $ \operatorname{Bias}_{k, n}=T_{k, n}^{\mathrm{b}}-T_{k, n}^{\mathrm{obs}} $ | (6) |
均方根误差:
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N \times K} \sum\limits_{\substack{n=1 \\ k=1}}^{N, K}\left(T_{k, n}^{\mathrm{b}}-T_{k, n}^{\mathrm{obs}}\right)^2} $ | (7) |
标准差:
| $ \sigma _k^{{\rm{Bias }}} = \sqrt {\frac{{\sum\limits_{n = 1}^N {\left({{\mathop{\rm Bias}\nolimits} _{k, n}^{\rm{b}} - {{\left. {\overline {{\mathop{\rm Bias}\nolimits} _k^{\rm{b}}} } \right)}^2}} \right.} }}{N}} $ | (8) |
| $ \overline{\operatorname{Bias}_k^{\mathrm{b}}}=\frac{\sum\limits_{n=1}^N \operatorname{Bias}_{k, n}^{\mathrm{b}}}{N} $ | (9) |
| $ \sigma_k^{\mathrm{RMSE}}=\sqrt{\frac{\sum\limits_{n=1}^N\left(\operatorname{RMSE}_{k, n}^b-\overline{\operatorname{RMSE}_k^b}\right)^2}{N}} $ | (10) |
| $ \overline{\mathrm{RMSE}_k^{\mathrm{b}}}=\frac{\sum\limits_{n=1}^N \mathrm{RMSE}_{k, n}^{\mathrm{b}}}{N} $ | (11) |
式中:
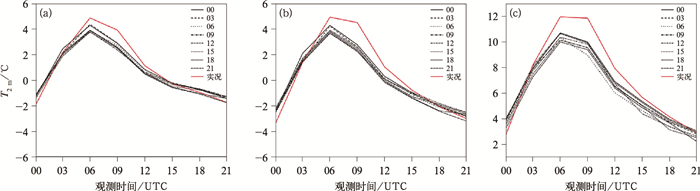
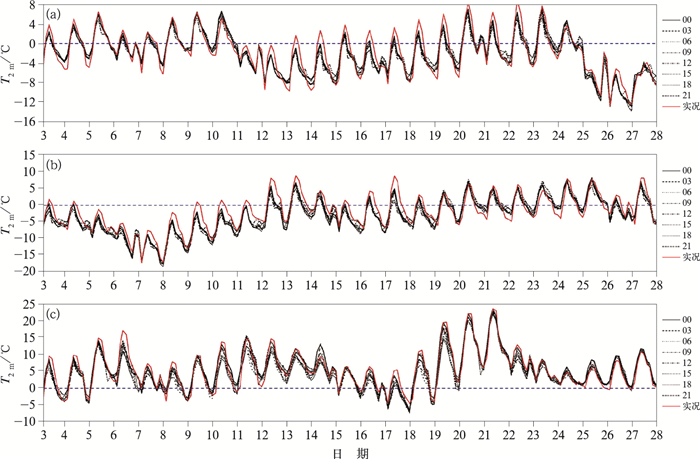
将不同起报时间、不同预报时效的预报与实况对比(图 1)可以看出,CMA-MESO系统可以较好地预报出2 m温度的日变化趋势。2020年12月至2021年2月总共出现2次最高温度低于0℃的过程:12月28—29日及1月7—10日。当出现温度明显大幅降低时,不同起报时间预报偏差变大,最大偏差可达到3℃。2月整体预报与实况的偏差较12月和1月偏大,2021年2月4—20日,由于模式参数调整,全国区域不同起报时间预报差异较大。1月预报与实况的偏差较12月偏大,每日06时和09时预报比实况更低,有时超过2℃,00时预报高于实况,整月温度波动变化幅度相对12月大,不同起报时间预报差异明显。
|
图 1 (a) 2020年12月, (b)2021年1月和(c)2月全国区域2 m温度实况与不同起报时间预报逐3 h变化 Fig. 1 The 3 h variation curves of observation and 2 m temperature prediction in China with different starting times in (a) December 2020, (b) January and (c) February 2021 |
将同一观测时间对应的8个起报时间2 m温度预报分别做月平均后与实况对比(图 2),每日最高温度出现在06时,最低温度出现在00时,模式对00—06时的升温过程预报效果好于06—21时的降温过程,每日00时预报比实况高1℃左右;06—15时预报比实况低;09时预报偏差值最大,12月为-2℃左右,1月为-3℃左右,2月为-2℃左右;12月和1月18时和21时预报与实况较接近,不同起报时间预报与实况的偏差值不超过0.5℃,2月偏差值稍大,在1℃左右。王婧等(2015)15 km系统夏季2 m温度结果显示09—12时不同起报时间预报结果相对集中,其他时间预报结果相对分散,且分散度远远大于3 km系统。这可能是由统计分析2 m温度季节差异造成的,也可能是模式系统及分辨率提升带来的影响。
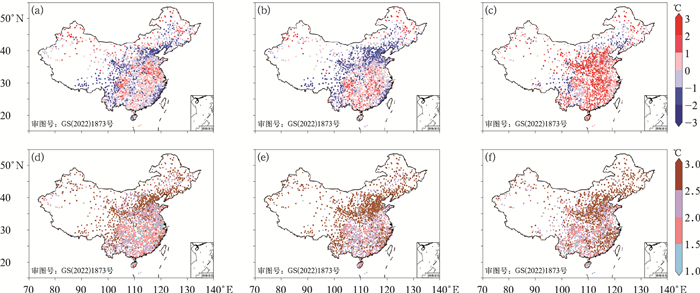
分别计算12月、1月和2月CMA-MESO系统不同起报时间的逐3 h预报与实况的平均误差和均方根误差,发现不同起报时间平均误差和均方根误差分布主要特征基本相似(图略),与总体平均误差和均方根误差分布基本一致(图 3)。12月京津冀地区、东三省大部分地区、西北地区、武夷山脉及西藏东部川西高原预报比实况低,青藏高原地区偏低幅度达到-3℃;内蒙古东北部、新疆地区、四川盆地及华南地区预报比实况高,天山附近正偏差超过3℃;华中地区模式预报相对好些,偏差较小,其值不超过1℃。1月偏差分布与12月略有不同,从华北至西北至西藏东部川西高原均呈现为模式预报偏低;黑龙江西北部及内蒙古东部、新疆北部及华中大部分地区为正偏差,大部分地区正偏差值在2℃内。两个月平均误差分布类似,负偏差大值地区主要在西藏东部川西高原、云贵高原、江南武夷山脉、华北地区;正偏差大值地区主要在东北、内蒙古东部、新疆地区;南疆地区两个月的偏差符号相反,12月为正偏差,偏差为2~3℃,1月为负偏差,偏差为-1℃左右;1月长三角地区的负偏差值要小于12月。12月和1月均方根误差分布大体相似,中部地区均方根误差较小,12月在1.5℃以下,1月在2.5℃以下。12月和1月华北西北至川西青藏东部地区及新疆天山山脉附近地区均方根误差相对较大,部分地区超过了3℃,与偏差大值区一致。2月偏差和均方根误差的大值区范围均有所扩大,华中地区偏差值明显变大;华南及西南大部分地区均方根误差较前两月明显增大;华北地区偏差值和均方根误差值均较前两月稍低,这可能是模式参数调整的影响。
|
图 3 (a,d)2020年12月, (b,e)2021年1月和(c,f)2月2 m温度预报的(a,b,c)Bias和(d,e,f)RMSE的全国分布 Fig. 3 National distribution of (a, b, c) Bias and (d, e, f) RMSE for 2 m temperature prediction in (a, d) December 2020, (b, e) January and (c, f) February 2021 |
CMA-MESO 3 km系统冬季2 m温度预报结果与王婧等(2015)CMA-MESO 15 km系统夏季2 m温度预报结果对比发现,两个季节平均误差和均方根误差大值地区分布类似,均分布在新疆大部分地区、西藏东部及川西高原、江南武夷山脉及华北地区。由此可见,这些地区模式系统的2 m温度预报还存在一些问题,需要改进。
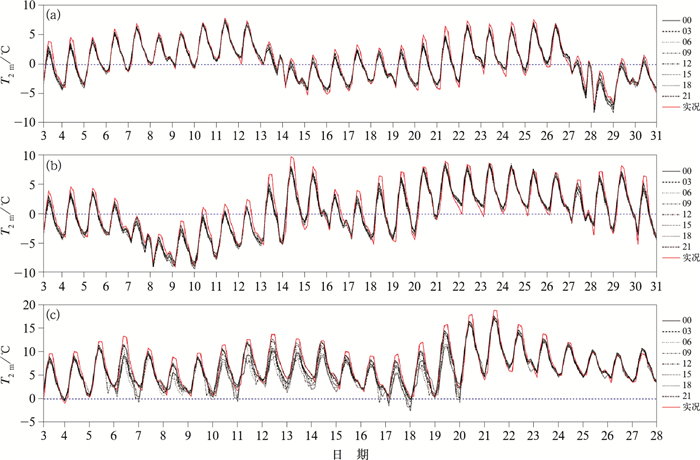
2.2 华北区域2 m温度特征分析冬季奥运会于2022年2月在北京及周边城市举办,选取该区域(以下简称华北地区,39°~45°N、112°~118°E)2020年12月至2021年2月CMA-MESO系统每日8个起报时间、同一起报时间24 h内间隔3 h的2 m温度预报产品进行分析。2020年12月与2021年1月,华北地区2 m温度变化特征(图 4)与全国基本一致,在相同时段出现2次最高温度低于0℃的过程,最高温度和最低温度差异略大于全国区域平均值。华北地区2021年2月2 m温度明显高于2020年12月和2021年1月,每日最高温度在0℃以上,预报的最高温度和最低温度差异及不同起报时间预报偏差较前两个月稍大,2021年2月16—20日有一次明显的升温过程,最高温度达到24℃,相较于前两个月出现的降温过程,升温过程的预报与实况间的差异更小一些。将华北地区8个起报时间、每3小时一次预报冬季2 m温度预报结果做3个月的平均(图 5),日平均变化趋势与全国基本一致,每日低温预报较好,高温预报较差,华北地区最高温度与最低温度间的差异比全国区域大,达10℃左右,不同起报时间预报差异更大,每日最高温度全国范围不同起报时间预报差异约为0.5℃,而华北地区接近1.5℃。

|
图 5 2020年12月至2021年2月华北地区2 m温度实况与不同起报时间预报日变化 Fig. 5 Daily variation of 2 m temperature observation and prediction in North China with different starting times from December 2020 to February 2021 |
由2020年12月至2021年2月全国区域2 m温度预报月变化(图 1)可知,2月预报由于参数的调整与12月和1月表现特征略有差异,1月总体温度变化趋势较12月波动大,且1月预报与实况的偏差更大,不同起报时间预报差异也更大,因此全国区域主要针对1月2 m温度预报展开订正诊断。采用双权重平均法和滑动双权重平均法对2021年1月全国区域不同起报时间、不同预报时效2 m温度预报进行订正。订正前(图 6a,6b),大部分预报与实况有一定的偏差,不同起报时间预报也存在差距,不同观测时间偏差大小也不一致,09时预报偏差最大,有的起报时间预报比实况偏低超过2℃,均方根误差超过2℃;滑动双权重平均法订正后结果(图 6c,6d)明显改善,预报与实况的偏差明显减小,偏差值不超过0.5℃,不同起报时间预报差距减到0.1℃内,均方根误差降至1℃内;1月统计权重系数的双权重平均法订正效果不如滑动双权重平均法,虽预报偏差和均方根误差均明显减少,但预报偏差和均方根误差数值都高于滑动双权重平均法。CMA-MESO系统2 m温度预报偏差订正后明显得到改善,说明大部分偏差为系统性偏差。两种订正方法中滑动双权重平均法订正效果更好,这可能是滑动双权重法考虑了模式系统对不同天气系统2 m温度预报能力。
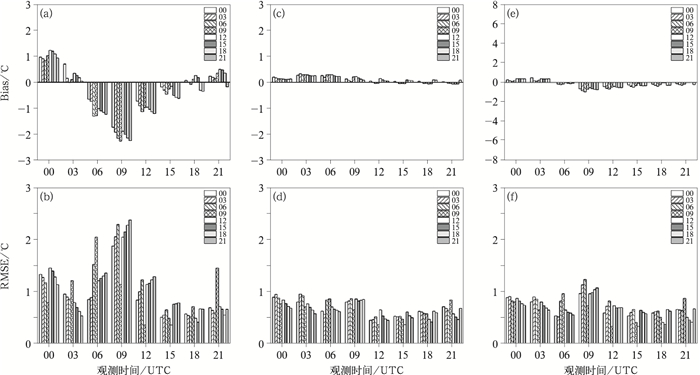
|
图 6 2021年1月不同起报时间全国区域订正前后2 m温度预报(a,c,e)Bias和(b,d,f)RMSE (a,b)订正前,(c,d)滑动双权重平均法,(e,f)1月双权重平均法 Fig. 6 (a, c, e) The Bias and (b, d, f) RMSE of 2 m temperature prediction before and after correction with different starting times in China in January 2021 (a, b) before revision, (c, d) moving-biweight average method, (e, f) January biweight average method |
对全国区域同一观测时间的不同起报时间预报取等权平均(图 7)。从图 7可见订正前后2 m温度预报与实况的日变化。订正前,00、03和21时预报高于实况,06—18时预报低于实况,09时预报偏差最大,超过2℃;两种订正方法订正后2 m温度预报更接近实况,滑动双权重平均法订正后预报略高于实况,1月双权重平均法订正后预报低于实况,1月权重系数订正09时预报后偏差在1℃左右,滑动双权重订正法订正后预报与实况几乎一致,订正效果很好。
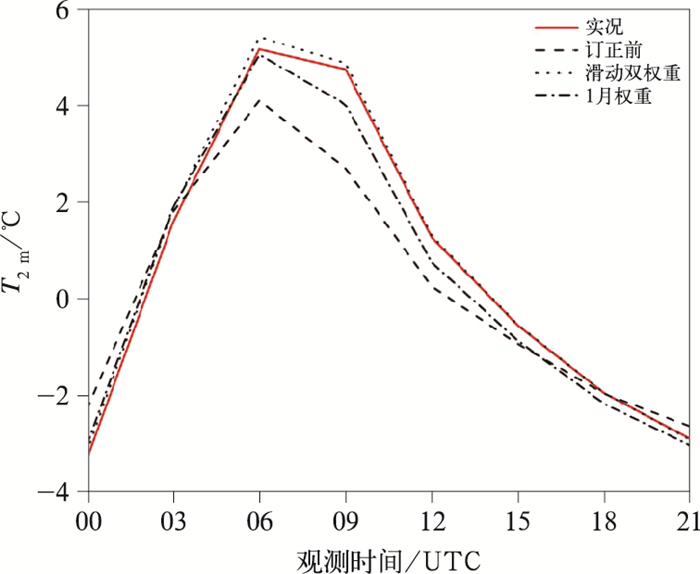
|
图 7 2021年1月全国区域订正前后2 m温度预报与实况的日变化曲线 Fig. 7 Daily variation of 2 m temperature observation and prediction before and after correction in China in January 2021 |
由于全国区域09时2 m温度预报偏差和均方根误差最大,下面对全国区域逐日09时预报做进一步分析(图 8)。如图 8所示,1月2 m温度预报为先降低后升高再降低直至平稳的趋势,两种订正方法订正后预报均与实况较为接近,滑动双权重法对于降温和升温过程预报的订正更为准确,1月双权重法对波动幅度较小的天气过程预报的订正效果更好。
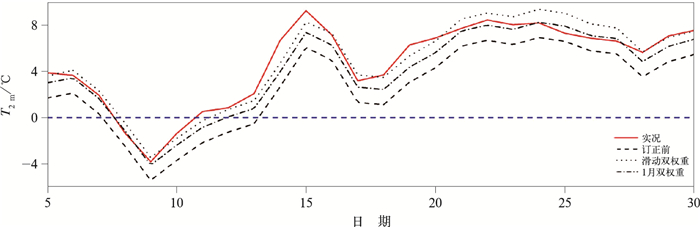
|
图 8 2021年1月逐日09时全国区域订正前后2 m温度预报与实况曲线 Fig. 8 Variation of 2 m temperature observation and prediction before and after the correction in China at 09 UTC January 2021 |
图 9为1月全国区域订正后2 m温度预报平均偏差和均方根误差分布。滑动双权重平均法(图 9a, 9c)订正后偏差值减小至1℃内,对订正前偏差较大的区域订正效果较好,均方根误差的订正效果与偏差相似,除极个别站点外,其余大值区均方根误差值降至2.5℃内。双权重平均法(图 9b, 9d)订正后,偏差值减小,均方根误差也相对降低,但对华北、西北地区的订正效果不如滑动双权重平均法。
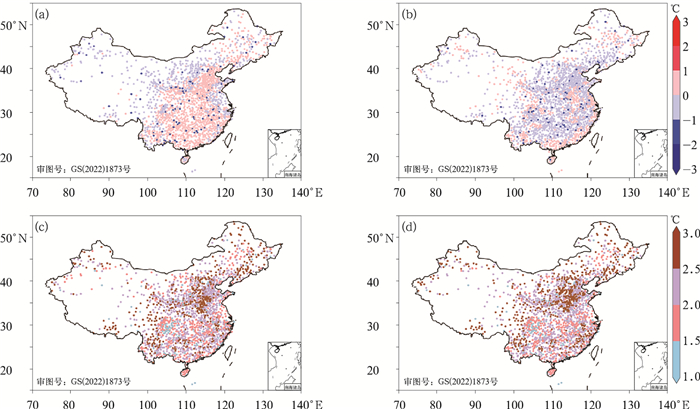
|
图 9 2021年1月订正后2 m温度预报(a,b)Bias和(c,d)RMSE的全国分布(a,c)滑动双权重平均法,(b,d)双权重平均法 Fig. 9 The national distribution of (a, b) Bias and (c, d) RMSE for the corrected 2 m temperature prediction in January 2021 (a, c) moving-biweight average method, (b, d) biweight average method |
由于09时不同起报时间预报均与实况相差较大,因此选择该观测时间研究不同站点间可预报性的差异。订正前(图 10a, 10b),华中和华南地区的标准差较小,大部分地区在0.5℃以下;黑河—腾冲一带附近区域、新疆北部天山一带、西藏东部的标准差均在0.8℃以上。均方根误差标准差的大值分布与偏差标准差的分布基本一致,低值地区范围明显扩大,部分华东地区标准差也在0.5℃以下。滑动双权重平均法(图 10c, 10d)订正后,除黄土高原及云贵高原小部分地区外,其余地区均在0.3℃以下,均方根误差的标准差也明显降低,除小部分西南地区及华北地区外,其余均降至0.3℃以下。1月双权重订正法(图 10e, 10f)订正后,全国范围不同成员间偏差的标准差有所降低,但华北地区和川西地区的标准差并未很好的进行改善,仍维持在0.7℃,其余地区降至0.4℃以下,均方根误差的标准差与偏差的标准差情况相似,与滑动双权重方法相比,该订正方法效果略显不足。
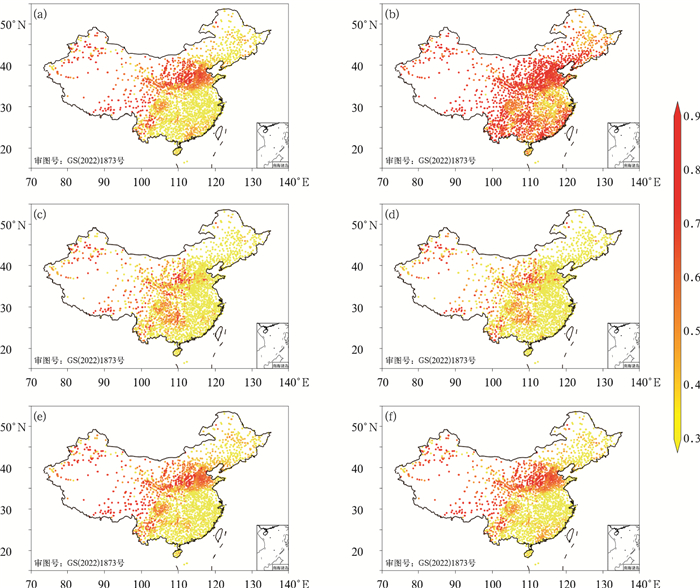
|
图 10 2021年1月09时订正前后2 m温度预报不同站点(a,c,e)Bias和(b,d,f)RMSE标准差全国分布(a,b)订正前,(c,d)滑动双权重平均法,(e,f)双权重平均法 Fig. 10 The national distribution of (a, c, e) Bias and (b, d, f) RMSE standard deviations for 2 m temperature prediction before and after correction at 09 UTC in January 2021 (a, b) before revision, (c, d) moving-biweight average method, (e, f) biweight average method |
选取订正前后标准差均较大的华北地区(39°~45°N、112°~118°E)、西南地区(25°~31°N、103°~109°E), 以及订正前标准差较大订正后明显减小的武夷山及周边地区(以下简称华东地区,25°~31°N、112°~118°E)这3个区域的1月逐日09时预报展开分析。华北地区订正前(图 11a)整体偏差较大,预报与实况最大偏差达到-8℃,订正后(图 11d)大部分预报偏差减到2℃内;西南地区订正前(图 11b)不同起报时间预报差异较大,订正后(图 11e)差异减小,预报偏差也减小;华东地区订正后不同起报时间预报差异减小。由于CMA-MESO系统一天冷启2次,因此00、03、06、09时起报和12、15、18、21时起报选取的大尺度背景不一致,华北地区订正前后12—21时起报的预报差异都较00—09时集中;西南地区订正后00—09时起报的预报较订正前更集中;华东地区订正后所有起报时间预报都更集中,预报效果在所选3个区域中最好。
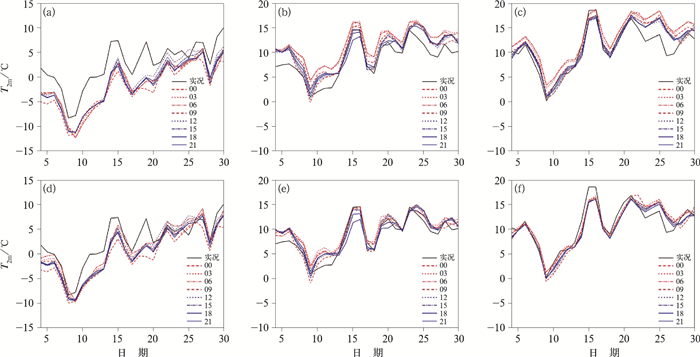
|
图 11 2021年1月逐日09时不同区域滑动双权重法(a,b,c)订正前,(d,e,f)订正后09时2 m温度预报与实况变化(a,d)华北地区,(b,e)西南地区,(c,f)华东地区 Fig. 11 Variation of 2 m temperature observation and prediction (a, b, c) before and (d, e, f) after correction by the moving-biweight average method in different regions at 09 UTC in January 2021 (a, d) North China, (b, e) Southwest China, (c, f) East China |
从华北地区1月滑动双权重平均法订正的2 m温度预报Bias和RMSE柱状图(图略)来看,华北地区订正效果与全国范围基本一致,即经过滑动双权重订正法订正后,预报与实况间的偏差和均方根误差均降低。选取2月(冬奥会举办时段:2月4—20日)华北地区滑动双权重法订正结果进行分析。订正前(图 12a, 12b),00时不同起报时间预报均为正偏差,06—12时预报均为负偏差,09时预报负偏差最大,大部分起报时间预报比实况偏低超过-2℃,均方根误差超过3℃。滑动双权重平均法订正后结果(图 12c, 12d)明显改善,预报与实况的偏差明显减小,除09时预报外,其余预报时间偏差值不超过0.5℃,均方根误差也得到改善,尤其对均方根误差的极大值有明显的订正效果。下节将依据这些结果,对华北地区2月09时和12时的预报平均进行谱分析。
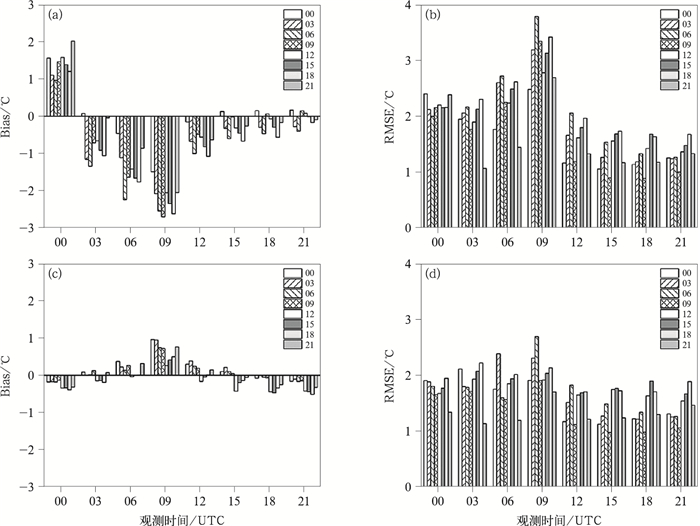
|
图 12 2021年2月华北地区不同起报时间预报订正前后2 m温度预报(a,c)Bias和(b,d)RMSE (a,b)订正前,(c,d)滑动双权重平均法 Fig. 12 (a, c) The Bias and (b, d) RMSE of 2 m temperature prediction before and after correction with different starting times in North China in February 2021 (a, b) before revision, (c, d) moving-biweight average method |
曾庆存(1979)指出动能谱的统计特性是大气的最基本规律之一, 数值模式和计算格式的优劣以及其预报效果的好坏, 与模式动能谱的统计特征与实际大气是否相符有密切关系。高分辨率区域模式的分析更注重天气系统的中小尺度部分, 为了诊断模式系统对不同天气尺度的捕捉能力, 本文采用了2D-DCT方法对有限区域2 m温度预报进行谱分解, 分析CMA-MESO系统中2 m温度预报与波长功率谱的关系。
选取1月9日和15日09时预报进行波谱能量分析。1月9日09时2 m温度为三个地区1月最低温度(图 11),15日不同起报时间预报差异较大。图 13为不同区域、不同起报时间的偏差和功率谱。由图可见,9日(图 13a)华北地区预报与实况偏差较大,不同起报时间预报偏差均超过了3℃,03时和06时起报偏差超过了4℃;西南地区09—18时起报预报比实况低,其他起报时间预报高,09时起报预报偏差最大;华东地区除15时起报预报较实况略微高外,其余起报时间预报比实况低,12—21时起报预报效果较好,均在0.2℃以下。15日(图 13b)三个区域的模式预报均比实况低,华北地区的偏差最大,09时起报预报偏差超过了6℃;西南地区除18时和21时起报外,其余起报时间预报均较为准确,偏差均在0.5℃内;华东地区不同起报时间预报差异较小,偏差均在2.5℃上下。所选三个区域的两个个例,华北区域预报效果最差,华北地区在大于600 km的α中尺度范围(200~2000 km)内功率谱明显较其余两个地区偏大,与预报误差偏大相对应;9日03时和06时及15日09时起报的2 m温度预报相较于其他起报时间预报,功率谱分布明显不同,15日09时功率谱能量在300~580 km范围明显较其他起报时间异常偏大,9日03时和06时在β中尺度范围(20~200 km)内均较其余起报时次小,该起报时间预报相对比其他起报时间预报偏差大。西南地区在9日00—06时大于600 km的α中尺度范围内功率谱能量比其他起报时间小,这些起报时间的预报明显为正偏差,09时起报的功率谱能量在大于600 km波长范围存在异常大值,对应明显大的负偏差,15日18时和21时在整个α中尺度范围内功率谱较其他起报时次明显偏高,对应这两个起报时间的预报偏差明显较大。华东地区9日00—06时在大于400 km的α中尺度范围内功率谱能量比其他起报时间大,12—21时起报功率谱分布较为一致,不同起报时间预报偏差小且差异也小,15日09时各个起报时间预报功率谱差异不明显,对应该区域预报差异也不大。
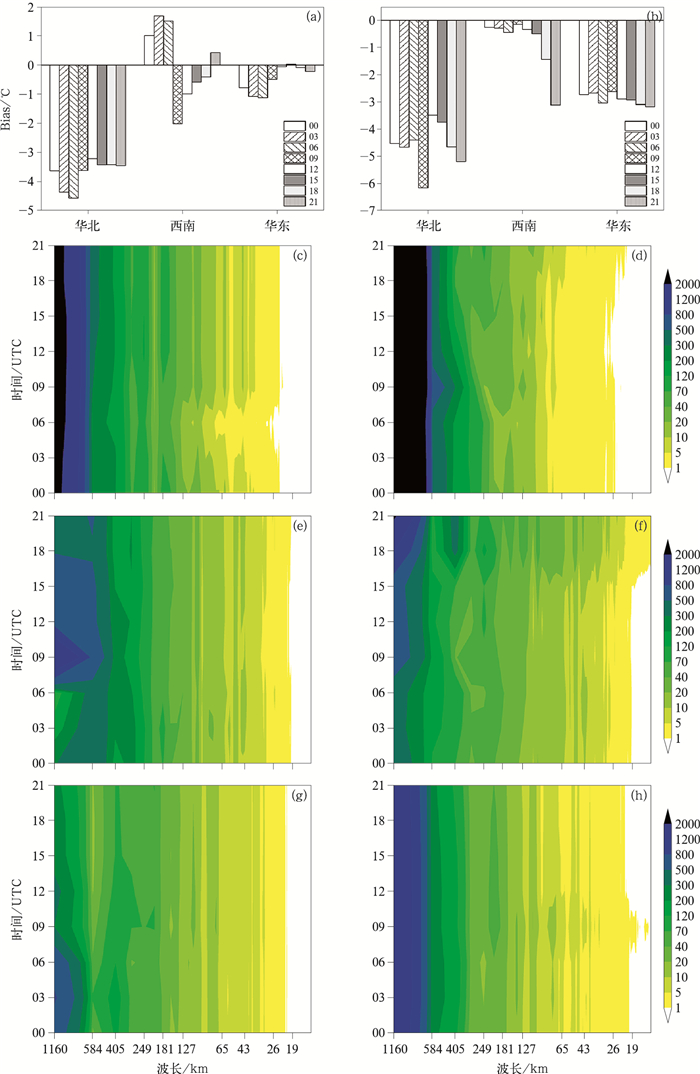
|
图 13 2021年1月(a,c,e,g)9日和(b,d,f,h)15日09时不同区域、不同起报时间2 m温度预报功率谱随波长变化(a,b)不同区域Bias,(c,d)华北地区,(e,f)西南地区,(g,h)华东地区 Fig. 13 Variation of power spectrum with wavelength of 2 m temperature prediction with different starting times in different regions at 09 UTC (a, c, e, g) 9 January and (b, d, f, h) 15 January 2021 (a, b) Bias of different regions, (c, d) North China, (e, f) Southwest China, (g, h) East China |
上述是针对三个不同区域的单日2 m温度功率谱分析,发现不同尺度上能量的差异能够较好地描述出同一观测时间,不同起报时间预报差异。针对华北地区,选取不同起报时间2月每日09时和12时预报分别做月平均,对其进行功率谱分析,由图 12可知09时各起报时间预报偏离实况最大,偏差超过了-2℃,相邻的12时各起报时间预报负偏差明显小于09时,偏差在-1℃内。图 14为09时和12时各起报时间预报对应的月平均功率谱,与单日功率谱类似,月平均功率谱能量同样随着尺度的增大而逐渐增多。从图 14可见,与1月单日功率谱能量相比,2月09时预报平均在α中尺度范围功率谱能量较1月15日明显偏低,在β中尺度范围差异不明显,2月平均预报偏差比1月9日略小,但明显小于1月15日的预报偏差。由此可见,2 m温度预报偏差的大小和2 m温度的不同尺度功率谱信息存在一定的对应关系。对2月09时和12时两个时间临近但偏差差异明显的预报时间进行对比,发现在大于200 km的α中尺度范围, 09时功率谱能量远高于12时,尤其是在1000 km以上的尺度范围,12时预报在12时左右,而09时预报除12时起报外其他起报时间预报功率谱值超过2000,对应的订正前12时起报预报偏差较小,这也许就是该起报时间预报订正效果更好的原因之一。

|
图 14 2021年2月(a)09时和(b)12时华北区域不同起报时间预报的2 m温度预报功率谱随波长变化 Fig. 14 Variation of power spectrum with wavelength of 2 m temperature prediction with different starting times in North China at (a) 09 UTC and (b) 12 UTC in February 2021 |
由此可见,无论是单日还是月平均功率谱,能量均随着尺度的增大逐渐增多。2 m温度预报偏差和2 m温度的不同尺度功率谱信息存在一定的对应关系,当2 m温度预报功率谱信息存在异常时,2 m温度预报就和实况偏差较大,当2 m温度预报不同尺度上功率谱信息分布相对均匀时,2 m温度预报就和实况比较接近。因此,当模式系统对各种尺度信息进行了准确捕捉时,预报就会更接近实况。随着模式分辨率的提升,局地气象要素的预报更需要关注中小尺度信息的捕捉能力。
5 结论与讨论本文通过对高分辨率CMA-MESO系统2020年12月至2021年2月每日8个起报时间每3小时预报的2 m温度预报产品进行诊断,分析了2 m温度预报效果以及与不同尺度信息谱能量关系,得到以下几点结论:
(1) CMA-MESO系统对不同地区、不同起报时间的2 m预报温度表现不一致。新疆西北部、四川盆地以、华中和华南部分地区模式比实况高,其他地区模式比实况低,华北至西北一带、川西及西藏东部等高海拔地区,比实况偏低超过2℃。每日8个预报时间表现为00时预报比实况高,06—15时预报比实况低,09时预报偏差最大,模式对00—06时的升温过程预报效果好于06—21时的降温过程。华北区域日变化趋势与全国相似,每日低温预报较好而高温预报较差,但其每日最高和最低温度差大于全国区域平均,华北地区2 m温度2月比12月和1月高,每日最高温度与最低温度间的差异及不同起报时间预报偏差更大。
(2) CMA-MESO系统2 m温度预报存在系统性偏差。双权重平均法和滑动双权重平均法订正后,不同起报时间2 m温度预报产品误差均有所减小,偏差较大地区订正效果更为明显,如华北至西北一带和西藏东部川西高原。两种方法订正后不同起报时间预报稳定度提高,各起报时间预报偏差减小。相比较而言,滑动双权重法对于降温和升温过程预报订正效果更好,双权重平均法对波动幅度较小的天气过程预报的订正效果较好。
(3) 功率谱能量随着尺度的增大逐渐增多,2 m温度预报偏差的大小和2 m温度的不同尺度功率谱信息存在一定的对应关系,当信息缺失或异常大值,则对应2 m温度预报与实况存在明显差异;当不同起报时间预报功率谱差异较小时,其预报的偏差也较为一致。华北地区2 m温度预报偏差最大,对应大于600 km功率谱值比西南和华东两个地区大很多,当某个起报时间预报功率谱分布明显异于其他起报时间时,其预报偏差与其他起报时间也存在明显差异。功率谱不仅能较好地描述单时次不同区域、不同预报成员间的功率谱差异,对于月平均预报同样有效。
(4) 波谱能量分析与CMA-MESO系统不同起报时间2 m温度预报效果有着很好的对应关系,下一步将借助功率谱分析开展多个预报间的时间滞后集合产品开发,更充分发挥CMA-MESO系统优势。
致谢:感谢郑永骏老师提供谱分解及功率谱程序。
陈德辉, 薛纪善, 杨学胜, 等, 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 53(20): 2396-2407. Chen D H, Xue J S, Yang X S, et al, 2008. New generation of multi-scale NWP system (GRAPES): general scientific design[J]. Chin Sci Bull, 53(20): 2396-2407 (in Chinese).
|
陈子通, 黄燕燕, 万齐林, 等, 2010. 快速更新循环同化预报系统的汛期试验与分析[J]. 热带气象学报, 26(1): 49-54. Chen Z T, Huang Y Y, Wan Q L, et al, 2010. Rapid updating cycle assimilation and forecasting system and its experiments and analysis in flood seasons[J]. J Trop Meteor, 26(1): 49-54 (in Chinese).
|
范水勇, 郭永润, 陈敏, 等, 2008. 高分辨率WRF三维变分同化在北京地区降水预报中的应用[J]. 高原气象, 27(6): 1181-1188. Fan S Y, Guo Y R, Chen M, et al, 2008. Application of WRF 3DVar to a high resolution model over Beijing Area[J]. Plateau Meteor, 27(6): 1181-1188 (in Chinese).
|
傅娜, 陈葆德, 谭燕, 等, 2013. 基于快速更新同化的滞后短时集合预报试验及检验[J]. 气象, 39(10): 1247-1256. Fu N, Chen B D, Tan Y, et al, 2013. Time-lag ensemble forecasting experiment and evaluation based on SMB-WARR[J]. Meteor Mon, 39(10): 1247-1256 (in Chinese).
|
黄丽萍, 陈德辉, 邓莲堂, 等, 2017. GRAPES_Meso V4.0主要技术改进和预报效果检验[J]. 应用气象学报, 28(1): 25-37. Huang L P, Chen D H, Deng L T, et al, 2017. Main technical improvements of GRAPES_Meso V4.0 and verification[J]. J Appl Meteor Sci, 28(1): 25-37 (in Chinese).
|
李佰平, 智协飞, 2012. ECMWF模式地面气温预报的四种误差订正方法的比较研究[J]. 气象, 38(8): 897-902. Li B P, Zhi X F, 2012. Comparative study of four correction schemes of the ECMWF surface temperature forecasts[J]. Meteor Mon, 38(8): 897-902 (in Chinese).
|
马旭林, 时洋, 和杰, 等, 2015. 基于卡尔曼滤波递减平均算法的集合预报综合偏差订正[J]. 气象学报, 73(5): 952-964. Ma X L, Shi Y, He J, et al, 2015. The combined descending averaging bias correction based on the Kalman filter for ensemble forecast[J]. Acta Meteor Sin, 73(5): 952-964 (in Chinese).
|
盛春岩, 薛德强, 雷霆, 等, 2006. 雷达资料同化与提高模式水平分辨率对短时预报影响的数值对比试验[J]. 气象学报, 64(3): 293-307. Sheng C Y, Xue D Q, Lei T, et al, 2006. Comparative experiments between effects of Doppler radar data assimilation and inceasing horizontal resolution on short-range prediction[J]. Acta Meteor Sin, 64(3): 293-307 (in Chinese).
|
唐文苑, 郑永光, 2019. 基于快速更新同化数值预报的小时降水量时间滞后集合订正技术[J]. 气象, 45(3): 305-317. Tang W Y, Zheng Y G, 2019. Improvement of hourly precipitation forecast using a time-lagged ensemble based on rapid refresh assimilation and forecast[J]. Meteor Mon, 45(3): 305-317 (in Chinese).
|
托亚, 梁海河, 马淑芬, 等, 2003. 用雷达观测资料改进MM5初始场的初步试验研究[J]. 南京气象学院学报, 26(5): 661-667. Tuo Y, Liang H H, Ma S F, et al, 2003. A preliminary research on improving MM5 initial fields using radar data[J]. J Nanjing Inst Meteor, 26(5): 661-667 (in Chinese).
|
王丹, 黄少妮, 高红燕, 等, 2016. 递减平均法对陕西SCMOC精细化温度预报的订正效果[J]. 干旱气象, 34(3): 575-583. Wang D, Huang S N, Gao H Y, et al, 2016. Analysis on errors of SCMOC refined guidance temperature prediction corrected by the decaying averaging method in Shaanxi Province[J]. J Arid Meteor, 34(3): 575-583 (in Chinese).
|
王婧, 徐枝芳, 范广洲, 等, 2015. GRAPES_RAFS系统2 m温度偏差订正方法研究[J]. 气象, 41(6): 719-726. Wang J, Xu Z F, Fan G Z, et al, 2015. Study on bias correction for the 2 m temperature forecast of GRAPES_RAFS[J]. Meteor Mon, 41(6): 719-726 (in Chinese).
|
王敏, 李晓莉, 范广洲, 等, 2012. 区域集合预报系统2 m温度预报的校准技术[J]. 应用气象学报, 23(4): 395-401. Wang M, Li X L, Fan G Z, et al, 2012. Calibrating 2 m temperature forecast for the regional ensemble prediction system at NMC[J]. J Appl Meteor Sci, 23(4): 395-401 (in Chinese).
|
王学忠, 沙文钰, 端义宏, 2003. 利用卫星云图变分同化初始场对热带气旋路径影响的数值试验[J]. 热带气象学报, 19(1): 107-112. Wang X Z, Sha W Y, Duan Y H, 2003. A numerical study of tropical cyclone forecasting based on satellite images variational assimilation initial field[J]. J Trop Meteor, 19(1): 107-112 (in Chinese).
|
王叶红, 彭菊香, 公颖, 等, 2011. AREM-RUC 3h快速更新同化预报系统的建立与实时预报对比检验[J]. 暴雨灾害, 30(4): 296-304. Wang Y H, Peng J X, Gong Y, et al, 2011. Establishment and real-time forecasting verification of AREM-RUC 3 h rapid update assimilation and forecast system[J]. Torr Rain Dis, 30(4): 296-304 (in Chinese).
|
许晨璐, 王建捷, 黄丽萍, 2017. 千米尺度分辨率下GRAPES-Meso4.0模式定量降水预报性能评估[J]. 气象学报, 75(6): 851-876. Xu C L, Wang J J, Huang L P, 2017. Evaluation on QPF of GRAPES-Meso4.0 model at convection-permitting resolution[J]. Acta Meteor Sin, 75(6): 851-876 (in Chinese).
|
徐枝芳, 郝民, 朱立娟, 等, 2013. GRAPES_RAFS系统研发[J]. 气象, 39(4): 466-477. Xu Z F, Hao M, Zhu L J, et al, 2013. On the research and development of GRAPES_RAFS[J]. Meteor Mon, 39(4): 466-477 (in Chinese).
|
薛谌彬, 陈娴, 吴俞, 等, 2017. 雷达资料同化在局地强对流预报中的应用[J]. 大气科学, 41(4): 673-690. Xue C B, Chen X, Wu Y, et al, 2017. Application of radar data assimilation in local severe convective weather forecast[J]. Chin J Atmos Sci, 41(4): 673-690 (in Chinese).
|
薛谌彬, 陈娴, 张瑛, 等, 2019. ECMWF高分辨率模式2 m温度预报误差订正方法研究[J]. 气象, 45(6): 831-842. Xue C B, Chen X, Zhang Y, et al, 2019. Bias correction method for the 2 m temperature forecast of ECMWF high resolution model[J]. Meteor Mon, 45(6): 831-842 (in Chinese).
|
薛纪善, 庄世宇, 朱国富, 等, 2008. GRAPES新一代全球/区域变分同化系统研究[J]. 科学通报, 53(20): 2408-2417. Xue J S, Zhuang S Y, Zhu G F, et al, 2008. Scientific design and preliminary results of three-dimensional variational data assimilation system of GRAPES[J]. Chin Sci Bull, 53(20): 2408-2417 (in Chinese).
|
曾庆存, 1979. 数值天气预报的数学物理基础, 第一卷[J]. 北京: 科学出版社: 329-337. Zeng Q C, 1979. The Physical-Mathematical Basis of Numerical Weather Prediction (I)[M]. Beijing: Science Press: 329-337(in Chinese).
|
张玉涛, 佟华, 孙健, 2020. 一种偏差订正方法在平昌冬奥会气象预报的应用[J]. 应用气象学报, 31(1): 27-41. Zhang Y T, Tong H, Sun J, 2020. Application of a bias correction method to meteorological forecast for the Pyeongchang Winter Olympic Games[J]. J Appl Meteor Sci, 31(1): 27-41 (in Chinese).
|
赵滨, 张博, 2018. 一种2 m温度误差订正方法在复杂地形区数值预报中的应用[J]. 大气科学学报, 41(5): 657-667. Zhao B, Zhang B, 2018. Application of a bias correction scheme for 2-meter temperature levels over complex terrain[J]. Trans Atmos Sci, 41(5): 657-667 (in Chinese).
|
庄照荣, 陈静, 黄丽萍, 等, 2018. 全球和区域分析的混合方案对区域预报的影响试验[J]. 气象, 44(12): 1509-1517. Zhuang Z R, Chen J, Huang L P, et al, 2018. Impact experiments for regional forecast using blending method of global and regional analyses[J]. Meteor Mon, 44(12): 1509-1517 (in Chinese).
|
庄照荣, 王瑞春, 李兴良, 2020. 全球大尺度信息在3 km GRAPES-RAFS系统中的应用[J]. 气象学报, 78(1): 33-47. Zhuang Z R, Wang R C, Li X L, 2020. Application of global large scale information to GRAEPS RAFS system[J]. Acta Meteor Sin, 78(1): 33-47 (in Chinese).
|
Benjamin S G, Dévényi D, Smirnova T, et al, 2006. From the 13-km RUC to the rapid refresh[J]. AMS Annual Meeting.
|
Benjamin S G, Dévényi D, Weygandt S S, et al, 2004. An hourly assimilation-forecast cycle: the RUC[J]. Mon Wea Rev, 132(2): 495-518.
|
Benjamin S G, Weygandt S S, Brown J M, et al, 2016. A North American hourly assimilation and model forecast cycle: the rapid refresh[J]. Mon Wea Rev, 144(4): 1669-1694.
|
Chen D H, Xue J S, Yang X S, et al, 2008. New generation of multi-scale NWP system (GRAPES): general scientific design[J]. Chin Sci Bull, 53(22): 3433-3445.
|
Ma X L, Zhuang Z R, Xue J S, et al, 2009. Developments of the three-dimensional variational data assimilation system for the nonhydrostatic GRAPES[J]. Acta Meteor Sin, 23(6): 725-737.
|
 2023, Vol. 49
2023, Vol. 49