2. 中国气象局公共气象服务中心, 北京 100081
2. CMA Public Meteorological Service Centre, Beijing 100081
气温对人们的日常生活影响无时不在,因而备受关注,是公众气象预报服务中最为重要的预报要素之一。近二十年来,数值模式产品在时空精细化程度、预报准确性等方面均取得了巨大进展,但迄今为止没有一个数值模式能够完美地呈现近地面的气象要素,包括气温的变化特征(Hoffman et al,2017)。因此,数值模式预报产品往往需要进行再加工处理。由此衍生了多种数值预报释用技术,在气温的客观预报研究中应用最为广泛。这些方法包括:模式输出统计方法(Glahn and Lowry, 1972;刘还珠等,2004)、直接模式输出方法(Stensrud and Skindlov, 1996)、神经网络方法(赵声蓉,2006;张亚刚等,2021)、多模式误差订正和集成(Woodcock and Engel, 2005;李佰平和智协飞,2012;郝翠等,2019;盛春岩等,2020),以及机器学习法(郭虎等,2008;任萍等,2020)等,使得气温预报效果得到显著提升。
在上述国内外精细化预报和客观模式订正方法研究中,对气象要素预报效果的检验是必不可少的环节。客观而全面的检验能反映预报产品的性能优劣,也能暴露释用技术的问题,进而推动问题的解决和技术的进步。2005年中国气象局下发了中短期天气预报质量检验办法,制定了一套气象预报产品质量检验评分标准,国家气象中心建立了“国家级天气预报检验分析系统”,对智能网格预报产品及其他相关模式预报产品和客观预报产品开展常规业务检验评估(韦青等,2020)。平均绝对误差(MAE)、均方根误差(RMSE)等传统的检验指标被广泛用于气温等连续变量的检验评估(Murphy and Winkler, 1987;Murphy, 1996)。但对实际预报业务和集成订正预报而言,常规检验标准虽然能够定量描述气温预报整体的误差和准确率,但针对性的误差分析、过程分析等仍然非常必要。
中国气象局公共服务中心的精细化多模式客观集成预报服务产品(refined multi-model objective consensus forecasting service products,以下简称OCF),一直广泛用于公众气象服务。多年来,OCF气温预报的平均效果已有常规检验佐证,但从集成订正技术改进的角度,以及从公众气象服务的关注点出发,都有对OCF气温预报进行针对性检验的需求。本文重点针对服务影响较大的OCF气温预报大误差日,及其中的典型特例——降温日开展检验分析,并主要与参与OCF集成的ECMWF、NCEP预报进行对比,以期发现模式气温预报和集成与订正的问题与规律,为OCF集成订正技术及其他客观数值预报释用方法评价提供参考。
1 精细化多模式客观集成预报服务产品简介国内外气象部门基于数值预报释用技术建立的客观预报业务系统,如美国的国家数字预报数据库(Glahn and Ruth, 2003)、德国基于优化集成预报方法提供的订正网格预报、澳大利亚的业务集成预报(Woodcock and Engel, 2005;Engel and Ebert, 2012)、奥地利气象局的无缝隙概率预报系统(Kann et al,2018)、中国气象局的智能网格预报(金荣花等,2019),等等。中国气象局公共气象服务中心于2012年建立了OCF相关业务,其运用不仅提高了预报准确率,而且为当今公众气象服务主流的基于位置的精细化天气预报服务提供了基础的技术支撑。下面简单介绍OCF的2 m气温的集成订正技术。
OCF气温集成预报模型中,用到包括ECMWF(时间分辨率为3 h,空间分辨率为0.125°)、NCEP(时间分辨率为6 h,空间分辨率为0.5°)、JMA(时间分辨率为3 h,空间分辨率为0.125°)、CMA_GFS(原GRAPES全球模式,时间分辨率为3 h,空间分辨率为0.25°)等数值预报模式2 m气温预报产品,以及地面2 m气温实时观测数据。OCF在建模过程中,采取对最近30天(即训练期设定为30天)多个模式的气温预报进行逐站点、逐时次滚动误差订正,动态计算权重,使集成预报结果随训练期内各模式预报效果的优劣而变化。
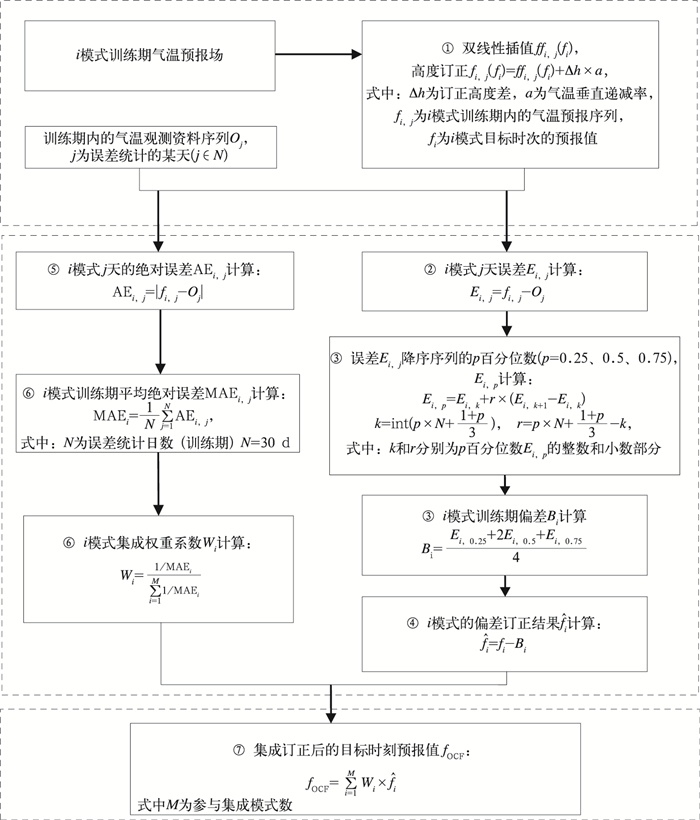
以20时(北京时,下同)起报的未来7 d逐3 h的OCF气温集成预报模型为例,具体步骤如下(图 1):
|
图 1 OCF气温集成预报模型数据和计算流程图 Fig. 1 Data and calculation flowchart of OCF consensus model's temperature forecast |
① 解析模式数据:读取各模式前30天08时起报,以及未来15~180 h时效的逐3 h气温预报场;应用双线性插值方法将各模式数据插值至所需的站点上;考虑模式高度与站点实际地形高度差,对气温进行高度误差订正。
解析后得到各模式训练期内(前30天08时起报)的气温预报序列,与对应时刻的实况观测数据,参与以下逐站点、逐目标时刻进行的集成订正步骤;解析后得到各模式未来15~180 h时效预报值作为各目标时次预报值。
② 预报误差计算:对各模式预报序列与对应时刻的实况观测数据相减,得到预报误差。
③ 模式预报偏差计算:按模式对②计算的预报误差排序,并应用百分位四分法计算各模式的预报偏差,算法具体参考Engel and Ebert(2007)、Hyndman and Fan(1996)。
④ 偏差订正:用目标时次预报值,减去③对应模式的预报偏差,得到偏差订正结果。
⑤ 模式绝对误差计算:对各模式预报序列求绝对误差均值,为模式绝对误差。
⑥ 集成权重系数计算:各模式绝对误差倒数,与所有模式绝对误差倒数之和的比,作为各模式的集成权重系数。
⑦ 集成订正结果:⑥得到的各模式权重系数与④得到的对应模式偏差订正结果相乘,得到最后的集成预报值。
2 检验方案 2.1 检验数据本文检验2020年6月1日至2021年5月31日(其中去除缺少各模式预报数据的12 d)OCF20时起报的24~168 h逐24 h(1~7 d时效),及参与集成的各模式相应时段的日最高气温和日最低气温预报。需要说明的是,本文所用数据取自OCF实际业务,CMA_GFS从2021年开始进入业务中,日本的JMA模式数据到2021年3月后停止提供,两个模式稳定进入OCF的为1~3 d时效的预报数据,因此检验时段内JMA和CMA_GFS不完整,不开展非常规检验。检验站点选取中国区域2401个国家级观测站,考虑预报和实况的更替及数据完整率、一致性等情况,最终得到实际检验站点1993个,以下所有检验如不做特别说明均包含中国区域所有1993个站点。
2.2 检验量和检验方法 2.2.1 常规检验公众接收到的气象预报信息以及评价,都是围绕所在地点的小范围开展的,OCF集成订正技术及输出产品也都是对应观测站点的,因此采用点对点的常规检验进行气温预报性能的评价。本文选取平均误差(E,公式见图 1)、均方根误差RMSE(公式详见郝翠等,2019)、气温预报准确率(绝对误差AE≤2℃的站次占总站次的比率,AE公式见图 1)作为常规检验指标,对OCF应用中最受公众关注的日最高气温和日最低气温预报进行讨论。
2.2.2 大误差检验本文从公众气象服务的效果和公众敏感度考虑,重点分析OCF气温预报中出现大范围大误差的天气。为便于讨论,大误差及相关气温变化的定义均以日最高气温和日最低温的平均值(以下简称高低温平均)作为判别指标:
(1) 大误差:根据公众气象服务经验,当气温预报AE>4℃时,公众会产生气温预报不准确的感受,因此对高低温平均求取AE,>4℃称为大误差;将区域内高低温平均的AE>4℃的站点占比率称为大误差率ER;将中国区域单日高低温平均大误差率ER≥20%定义为大误差日。
| $ \mathrm{ER}=N_{\mathrm{AE}>4} / N $ |
式中:NAE>4为AE>4℃的站点数,N为中国区域内的检验站点总数(本文为1993个站)。
(2) 气温变化:为探讨大误差日与气温变化的关系,对实况的高低温平均T求取其日变温ΔT作为气温变化的判断指标,ΔT≥4℃为明显升温,ΔT≤-4℃为明显降温,两者统称明显变温;单日明显升温站点比率≥20%作为升温日,单日明显降温站点比率≥20%为降温日,以上两者统称变温日。
| $ \begin{gathered} \bar{T}=\left(T_{\max }+T_{\min }\right) / 2 \\ \Delta \bar{T}=\bar{T}_i-\overline{T_{i-1}} \end{gathered} $ |
式中:T为高低温平均,Tmax为日最高气温,Tmin为日最低气温,i代表某日,
首先针对中国区域整个检验时段,统计OCF与主要参与集成的ECMWF、NCEP各预报时效的日最高、日最低气温的均方根误差(RMSE)和预报准确率,对比分析各预报在中国区域的整体预报性能。
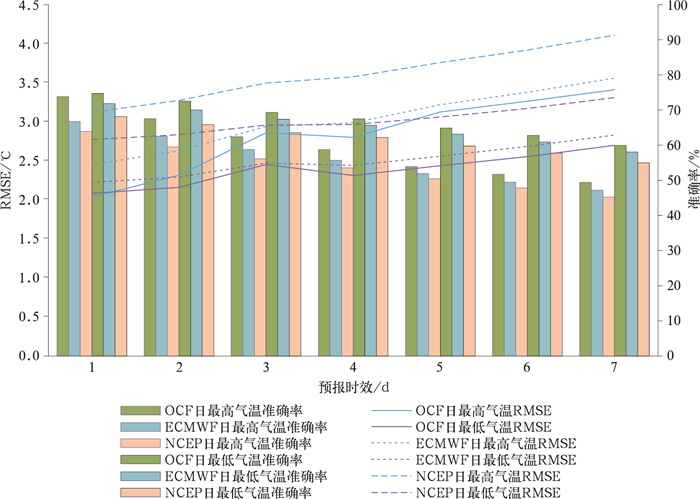
从1~7 d各预报时效的日最高气温、日最低气温均方根误差和预报准确率(图 2)来看,OCF预报效果最好、ECMWF次之、NCEP最差。其中,OCF日最高气温均方根误差为2.0~3.2℃,较ECMWF小0.2~0.8℃,较NCEP小1.1~1.5℃;OCF日最低气温均方根误差为2.0~2.6℃,较ECMWF小0.2~0.3℃、较NCEP小1.1~1.3℃。OCF日最高气温预报准确率为49%~74%,较ECMWF高1%~ 10%,较NCEP高4%~15%;OCF日最低气温预报准确率为60%~75%,较ECMWF高2%~5%,较NCEP高10%~13%。
|
图 2 2020年6月至2021年5月OCF、ECMWF和NCEP在不同预报时效日最高气温、日最低气温预报的RMSE和准确率 Fig. 2 RMSE and accuracies of daily maximum and minimum temperature forecasts in each forecasting period of OCF, ECMWF and NCEP from June 2020 to May 2021 |
OCF、ECMWF和NCEP的日最高气温和日最低气温均方根误差均随着预报时效的增长而增加。日最高气温预报的均方根误差明显大于日最低气温的,且日最高气温预报的均方根误差随时效增长的幅度较日最低气温明显。
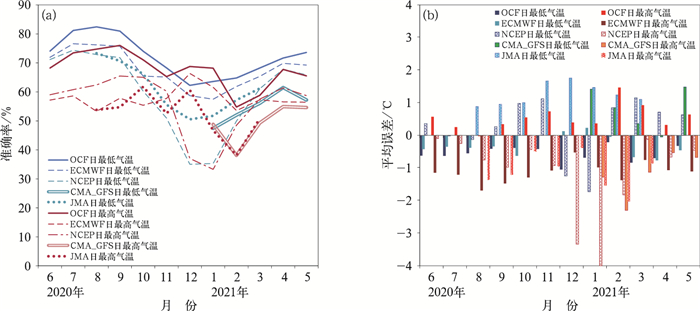
统计中国区域OCF和参与集成的各模式预报1~3 d短期时段(图 3)和4~7 d中期时段(图略)各月的准确率及平均误差,其中JMA和CMA_GFS仅参与1~3 d短期时段检验。OCF、ECMWF、NCEP短期时段和中期时段的准确率、平均误差月分布类似,只是短期时段准确率较中期时段高5%~15%左右,误差也是短期时段较中期时段低。
|
图 3 2020年6月至2021年5月各预报场1~3 d短期时段日最高、日最低气温的逐月(a)准确率,(b)平均误差 Fig. 3 Daily maximum and minimum temperature (a) accuracy and (b) average error in each month of each short-term forecasting feild from June 2020 to May 2021 |
分月来看,各预报的短期时段准确率(图 3a)优劣变化不同,ECMWF、NCEP均表现为夏季高冬季低的变化趋势,OCF也有同样的季节变化趋势,但始终优于各模式预报。OCF日最低气温、日最高气温短期时段各月平均准确率分别为72%、68%,中期时段准确率分别为64%、53%,仍是各预报中最高的;ECMWF次优,日最低气温、日最高气温短期时段各月平均准确率分别为68%、58%,中期时段准确率分别为61%、49%。
平均误差可以说明模式系统预报偏高(平均误差为正,简称正误差)或偏低(平均误差为负,简称负误差)的平均状况。从图 3b可以看出,ECMWF各月日最高、日最低气温都呈负误差,这种一致性的误差特征说明其气温预报偏低更多是系统性误差,存在进一步订正的空间;NCEP冬季时段预报的日最高、日最低气温都呈负误差,1月日最高气温的平均误差甚至达到-4℃以上,春、秋季检验时段的日最低气温多为正误差,日最高气温负误差相对较大,夏季日最低气温和日最高气温误差很小,说明其预报误差既有模式系统误差的影响,也有季节变化的影响;JMA和CMA_GFS在其各自检验时段内也有日最低气温正误差、最高气温负误差的特征。而OCF大部分月份的平均误差较模式预报明显减小,且呈现日最低气温负误差、日最高气温正误差,说明加入实况后的OCF气温集成订正的效果较好,拉开了气温变化的范围,也有效减小了误差。
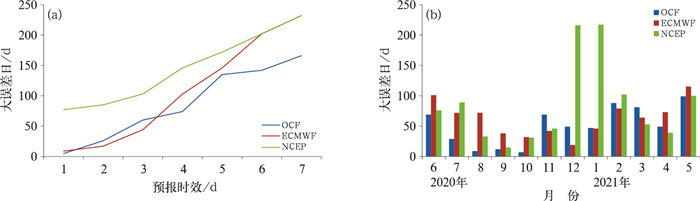
3.2 OCF大误差日对比分析 3.2.1 大误差日分布特征由于JMA和CMA_GFS数据不完整,以下检验及分析仅针对OCF、ECMWF和NCEP展开。根据前文的大误差日定义,统计检验时段内1~7 d时效各预报场高低温平均的大误差日总数,OCF为608 d,ECMWF为753 d,NCEP为1017 d,OCF大误差日数总体少于2个模式预报。OCF、ECMWF和NCEP的大误差日都随预报时效增长而增多(图 4a),NCEP的大误差日数明显高于其他两者。OCF和ECMWF各有优劣:1 d时效的大误差日,两者都小于10 d,OCF略少;2~3 d时效,OCF大误差日数较ECMWF多1/3左右;4~7 d时效OCF的大误差日较ECMWF少1/3左右。这说明,随着预报时效的延长,OCF集成订正有正效应,尤其在6~7 d时效效果更加明显;2~3 d时效OCF大误差日多于ECMWF,可能与OCF集成订正技术有关;另外由于1~3 d时效,JMA和CMA_GFS参与了OCF集成,而由图 3可见JMA和CMA_GFS的预报性能不如ECMWF,这可能也是导致OCF在2~3 d时效大误差日较ECMWF多的原因之一。
|
图 4 2020年6月至2021年5月OCF、ECMWF和NCEP (a)各预报时效大误差日总数, (b)各月大误差日总数 Fig. 4 Large error days of OCF, ECMWF, NCEP from June 2020 to May 2021 (a) in each forecasting period, (b) monthly distribution |
进一步分析大误差日的各月分布(图 4b)发现,9—10月OCF、ECMWF和NCEP的大误差日都比较少,均在40 d以下,2—3月、5—6月则均超过了50 d,NCEP冬季12—1月的预报缺陷非常明显。值得注意的是,5—10月期间,OCF的大误差日数大多少于ECMWF和NCEP,尤其7—10月期间,较ECMWF和NCEP少了70%以上,这体现了其优越的集成订正效果;但11—3月,OCF大误差日多于ECMWF,11—12月则较ECMWF偏多30 d左右。
总之,OCF大误差日总数少于ECMWF和NCEP,尤其在4 d以后预报时效、5—10月期间,大误差日较ECMWF和NCEP少,但2~3 d时效、11—3月则多于ECMWF。由此可见,OCF集成订正技术在气温相对稳定的5—10月具有很好的效果,而在降温多发、气温变化起伏较大的11—4月,则效果不佳,集成订正效果与气温变化的关系值得进一步探讨。
3.2.2 大误差日的气温变化特征分析为分析大误差日的气温变化特征,按前文气温变化相关定义,对OCF、ECMWF、NCEP在1~3 d时效各大误差日和检验时段内逐日实况,统计高低温平均的明显变温站点比率进行对比(图 5a, 5b)。由于4 d时效以上各预报的误差日超过了检验时段的1/3,气温变化特征与实况对比不明显,因此不开展讨论。
|
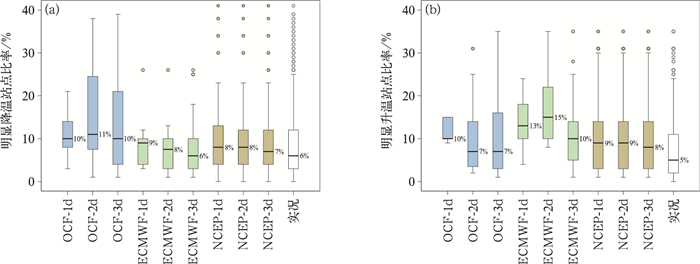
图 5 2020年6月至2021年5月OCF、ECMWF和NCEP 1~3 d时效大误差日及实况的(a)明显降温、(b)明显升温站点比率 注:箱体中横线及标注为中位数,“。”为离群值。 Fig. 5 (a) Obvious temperature-drop station rates and (b) obvious temperature-rise station rates of large error days in 1-3 d forecasting periods of OCF, ECMWF, NCEP and the observations from June 2020 to May 2021 |
分析发现OCF集成预报1~3 d时效大误差日中,降温站点比率较ECMWF和NCEP以及实况明显偏高,ECMWF和NCEP与实况相当;OCF在1 d时效、ECMWF在1~2 d时效大误差日中明显升温站点比率较实况明显偏高;相比之下OCF在1~3 d大误差日的降温特征较升温特征明显。
进一步统计各预报大误差日中的变温日(表 1),分析大误差日和变温日关系。根据2.2节中变温日的定义,统计得到中国区域检验时段实况有降温日39 d,升温日32 d。OCF大误差日中的降温日较升温日多,降温日占1~3 d时效大误差日的20%以上,较实况的降温日发生概率高了1倍左右,4~7 d中期时段大误差日涵盖了大部分的降温日;ECMWF 1~4 d大误差日中,升温日较降温日多,其大误差日中的降温日是各模式中最少的;NCEP大误差日中的降温日较升温日多,与OCF类似,其4~7 d中期时段大误差日涵盖了大部分的降温日。
|
|
表 1 2020年6月至2021年5月OCF、ECMWF和NCEP大误差日中的变温日统计(单位:d) Table 1 Statistics of temperature-change days in large error days of OCF, ECMWF, and NCEP from June 2020 to May 2021 (unit: d) |
总之,OCF大误差日的降温特征较升温明显,降温日占1~3 d时效大误差日20%以上,中期时段几乎所有的降温日都出现20%以上的大误差;而ECMWF在1~4 d时效预报更倾向于在升温日出现大误差;NCEP因大误差日多,大误差的气温变化特征不明显。可以说降温日是OCF气温集成预报大误差日的典型特例。
3.3 OCF在降温日中的预报性能对比分析 3.3.1 降温日与非降温日的预报性能差异对比中国区域内39 d降温日与其余的非降温日OCF、ECMWF、NCEP在1~7 d各时效预报的日最高气温、日最低气温的均方根误差平均值(表 2),来分析降温日中的预报效果。发现OCF与NCEP日最高气温、日最低气温,以及ECMWF的日最低气温均方根误差在降温日较非降温日都有所增长,ECMWF的日最高气温均方根误差在非降温日和降温日差异不大;OCF在降温日的日最低气温均方根误差仍小于ECMWF和NCEP,OCF集成订正的优势仍然明显,但OCF在降温日的日最高气温均方根误差略大于ECMWF模式0.03℃。
|
|
表 2 2020年6月至2021年5月降温日与非降温日的OCF、ECMWF和NCEP各预报时效RMSE平均(单位:℃) Table 2 The averaged RMSE of OCF, ECMWF, and NCEP in temperature-drop days and non-temperature-drop days from June 2020 to May 2021 (unit: ℃) |
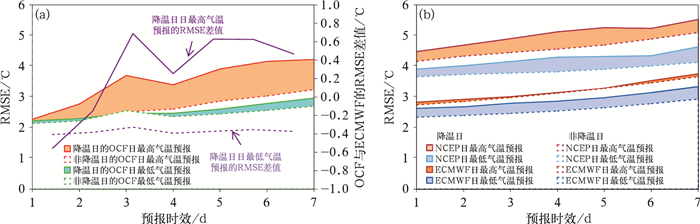
从1~7 d各时效降温日较非降温日的均方根误差增长幅度来看(图 6中以色块区域表示),日最低气温:NCEP最高(平均增长0.38℃),ECMWF次之(平均增长0.33℃),OCF最低(平均增长0.12℃);日最高气温:OCF最高(平均增长0.88℃),NCEP次之(平均增长0.43℃),ECMWF最低(平均增长0.24℃)。逐预报时效来看,OCF 1~4 d时效的日最低气温均方根误差增长不明显,5~7 d时效均方根误差增长幅度缓慢变大,日最高气温均方根误差增长明显,尤其2~3 d时效增长最快;而ECMWF日最高气温的均方根误差增长较为稳定,降温日和非降温日几乎没有变化,日最低气温的增长平稳;NCEP日最高、日最低气温的均方根误差增长幅度也都较为平稳。图 6a为降温日中OCF和表现较优的ECMWF的各预报时效均方根误差值,发现OCF各预报时效的日最低气温预报,以及1~2 d时效的最高气温均方根误差都小于ECMWF,但从3 d时效开始,OCF日最高气温的均方根误差大于后者。可见,OCF对降温日中的日最低气温和2 d时效内日最高气温预报有较好集成订正效果,但3 d以上时效的日最高气温均方根误差增长明显,且大于ECMWF,可以进行集成订正技术改进。
|
图 6 2020年6月至2021年5月降温日和非降温日各预报时效的(a)OCF的RMSE及降温日中OCF与ECMWF的RMSE差值, (b)ECMWF和NCEP的RMSE 注:色块部分表示各预报在降温日较非降温日的RMSE增长。 Fig. 6 (a) RMSE of OCF and the RMSE difference between OCF and ECMWF, (b) RMSE of ECMWF and NCEP in each forecasting period of temperature-drop days and non-temperature-drop days from June 2020 to May 2021 |
为分析降温日中的气温预报误差与气温变化的关系,将各降温日所有检验站点按照高低温平均日变温ΔT实况,进行变温区域划分:降温区域(ΔT≤-4℃)、升温区域(ΔT≥4℃)和变温幅度不大的弱变温区域(-4℃ < ΔT < 4℃)。各降温日都按变温区域对OCF、ECMWF、NCEP的1~3 d短期时段(图 7)、4~7 d中期时段(图略)日最高气温、日最低气温预报统计预报误差频率分布,并就准确率(AE≤2℃,即-2℃≤E≤2℃,图 7a, 7b中黄色区域)、负误差(E < -4℃,图 7a, 7b中蓝色区域)、正误差(E>4℃,图 7a, 7b中红色区域)等指标开展分析。
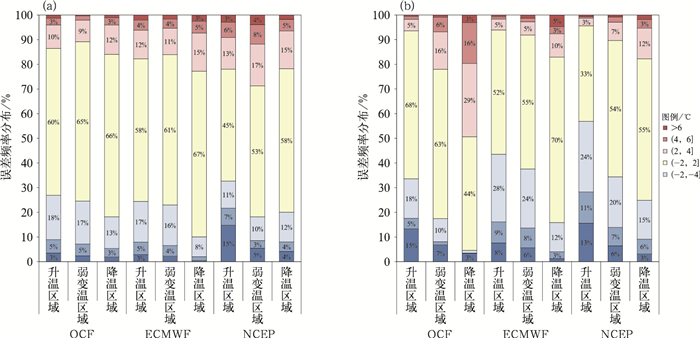
|
图 7 检验时段内降温日中各变温区域1~3 d短期时段OCF、ECMWF和NCEP气温预报误差频率分布 (a)日最低气温,(b)日最高气温 Fig. 7 Temperature forecast error frequency distributions of OCF, ECMWF and NCEP for 1-3 d forecasting periods in each temperature-change region of verified temperature-drop days (a) daily minimum temperature, (b) daily maximum temperature |
从降温日的1~3 d短期时段日最低气温预报在各变温区域的误差频率分布可见(图 7a),OCF、ECMWF、NCEP在各变温区域的误差分布特征类似:降温区域的气温预报准确率高于升温和弱变温区域,在升温和弱变温的负误差较多,即预报气温较实况偏低;OCF、ECMWF在降温区域正误差的比率增加,各模式在升温区域的负误差较降温和弱变温区域增加;各变温区域气温预报准确率最高的均是OCF。
OCF、ECMWF、NCEP日最高气温预报误差分布在各变温区域差异较大:各预报在升温区域的负误差都较降温和弱变温区域增加,降温区域的正误差较升温和弱变温区域增加,尤其OCF降温区域正误差比率明显增加,4℃以上误差比率平均达到了20%,而-4℃以下误差比率平均仅为3%,正误差倾向明显,即OCF日最高气温预报在降温区域预报偏高;OCF日最高气温的气温预报准确率在降温区域达68%,明显高于升温区域(44%),而ECMWF、NCEP的气温预报准确率在降温区域较高。各预报比较发现:升温区域气温预报准确率OCF(68%)高于ECMWF(52%)、NCEP(33%),降温区域气温预报准确率ECMWF(70%)、NCEP(55%)高于OCF(44%)。ECMWF、NCEP对日最高气温预报偏低4℃以上(负误差)的比率较OCF明显偏高约10%以上,说明OCF有效订正了ECMWF和NCEP在降温日中日最高气温预报偏低的误差倾向;但OCF在升温和弱变温区域正误差比率较ECMWF、NCEP明显偏高,说明在降温日的非降温区域,OCF对日最高气温的集成订正效果不佳,反而产生了预报偏高的误差倾向。
降温日4~7 d中期时段的各预报,较1~3 d短期时段的气温预报准确率降低,日最低气温和日最高气温的正误差都有增长,但负误差增长不明显。可见在中期时段的气温预报中,更体现出预报偏高的误差倾向;各预报各变温区域的误差特征分布与1~3 d短期时段类似,不再赘述。
总之,在降温日,OCF对各变温区域的日最低气温、非降温区域的日最高气温都具有集成订正效果;但其在降温区域日最高气温预报偏高,气温预报准确率较低,正误差明显增多。对各降温过程单独考察,发现OCF在降温区域日最高气温预报偏高的误差特征并非少数过程造成,且大部分过程的降温强度预报偏弱。OCF这一突出的误差分布特征与ECMWF和NCEP不同,说明误差并非参与集成的模式预报的影响,而是集成订正的方法问题;OCF有效订正了降温日中日最高气温偏低的误差,但同时也造成了降温区域的日最高气温正误差增多。
4 结论与讨论(1) 从常规检验来看,OCF气温集成预报及参与集成的各模式在中国区域各预报时效的气温预报性能,体现为:预报误差随预报时效增长而增大,日最低气温预报效果明显优于日最高气温的预报;在全部检验时段内OCF较ECMWF和NCEP总体上预报性能较优,尤其在1~2 d时效的日最高气温预报,其优势明显;分月来看OCF及各模式准确率大多夏季高冬季低,OCF气温集成预报拉开了气温变化范围,也有效减小了误差。
(2) 针对大误差日的分析发现:OCF大误差日总数少于ECMWF和NCEP,但2~3 d时效时段的大误差日多于ECMWF,在气温相对稳定的暮春到仲秋(5—10月)大误差日较少,而在降温多发、气温变化起伏较大的深秋到冬季(11—3月)大误差日甚至多于ECMWF。OCF大误差日的降温特征较升温明显,中期时段大部分降温日都出现20%以上的大误差,降温日是OCF大误差日的一种典型特例。
(3) 降温日和非降温日的对比检验揭示了OCF和ECMWF和NCEP在降温日的气温预报误差都有所增长,尤其是OCF在3 d时效以上的日最高气温预报的误差增长明显。对降温日划分变温区域分析气温预报误差分布发现,OCF对各变温区域的日最低气温、非降温区域的日最高气温都具有集成订正效果;但其在降温区域日最高气温预报偏高,准确率低于非降温区域,也低于参与集成的ECMWF和NCEP,正误差明显增多。
(4) 在降温过程中最高气温的变幅往往很大,易出现预报误差增大;降温区域预报偏高,升温区域预报偏低的误差特征是符合预报规律的。但OCF日最高气温预报在降温日的降温区域明显偏高,可理解为其有效订正了ECMWF和NCEP预报偏低的误差倾向,但同时也造成了在降温区域的正误差增多。这种误差主要是集成订正的方法问题,可作为OCF改进的方向之一。另外,这种误差或也与其他参与集成的模式预报效果差有关。针对降温日的日最高气温,采取调整训练周期、预报偏差指标、集成权重等方式来优化集成策略,或是进一步提高集成订正预报性能的道路之一。
(5) 在OCF气温预报整体预报性能较优的认识下,通过对大误差日、典型特例——降温日的研究,揭示了OCF集成订正技术的改进方向,说明针对性的检验更利于发现客观预报及集成订正方法的问题。
郭虎, 王建捷, 杨波, 等, 2008. 北京奥运演练精细化预报方法及其检验评估[J]. 气象, 34(6): 17-25. Guo H, Wang J J, Yang B, et al, 2008. Refined forecast techniques and related verification during 2007 Olympic drilling[J]. Meteor Mon, 34(6): 17-25 (in Chinese). DOI:10.3969/j.issn.1007-6190.2008.06.005
|
郝翠, 张迎新, 王在文, 等, 2019. 最优集合预报订正方法在客观温度预报中的应用[J]. 气象, 45(8): 1085-1092. Hao C, Zhang Y X, Wang Z W, et al, 2019. Application of analog ensemble rectifying method in objective temperature prediction[J]. Meteor Mon, 45(8): 1085-1092 (in Chinese).
|
金荣花, 代刊, 赵瑞霞, 等, 2019. 我国无缝隙精细化网格天气预报技术进展与挑战[J]. 气象, 45(4): 445-457. Jin R H, Dai K, Zhao R X, et al, 2019. Progress and challenge of seamless fine gridded weather forecasting technology in China[J]. Meteor Mon, 45(4): 445-457 (in Chinese).
|
李佰平, 智协飞, 2012. ECMWF模式地面气温预报的四种误差订正方法的比较研究[J]. 气象, 38(8): 897-902. Li B P, Zhi X F, 2012. Comparative study of four correction schemes of the ECMWF surface temperature forecasts[J]. Meteor Mon, 38(8): 897-902 (in Chinese).
|
刘还珠, 赵声蓉, 陆志善, 等, 2004. 国家气象中心气象要素的客观预报—MOS系统[J]. 应用气象学报, 15(2): 181-191. Liu H Z, Zhao S R, Lu Z S, et al, 2004. Objective element forecasts at NMC-a MOS system[J]. J Appl Meteor Sci, 15(2): 181-191 (in Chinese). DOI:10.3969/j.issn.1001-7313.2004.02.006
|
任萍, 陈明轩, 曹伟华, 等, 2020. 基于机器学习的复杂地形下短期数值天气预报误差分析与订正[J]. 气象学报, 78(6): 1002-1020. Ren P, Chen M X, Cao W H, et al, 2020. Error analysis and correction of short-term numerical weather prediction under complex terrain based on machine learning[J]. Acta Meteor Sin, 78(6): 1002-1020 (in Chinese).
|
盛春岩, 范苏丹, 荣艳敏, 等, 2020. 几种气温客观预报方法对比及最优集成预报研究[J]. 气象, 46(10): 1351-1361. Sheng C Y, Fan S D, Rong Y M, et al, 2020. Comparison of several objective methods and optimal consensus forecast study of temperature[J]. Meteor Mon, 46(10): 1351-1361 (in Chinese). DOI:10.7519/j.issn.1000-0526.2020.10.009
|
韦青, 代刊, 林建, 等, 2020. 2016—2018年全国智能网格降水及温度预报检验评估[J]. 气象, 46(10): 1272-1285. Wei Q, Dai K, Lin J, et al, 2020. Evaluation on the 2016-2018 fine gridded precipitation and temperature forecasting[J]. Meteor Mon, 46(10): 1272-1285 (in Chinese). DOI:10.7519/j.issn.1000-0526.2020.10.002
|
张亚刚, 杨银, 张成军, 等, 2021. 基于径向基函数神经网络温度预报订正方法及评估[J]. 热带气象学报, 37(1): 136-144. Zhang Y G, Yang Y, Zhang C J, et al, 2021. Temperature forecast correction method and evaluation based on radial basis function neural network[J]. J Tropical Meteor, 37(1): 136-144 (in Chinese). DOI:10.16032/j.issn.1004-4965.2021.013
|
赵声蓉, 2006. 多模式温度集成预报[J]. 应用气象学报, 17(1): 52-58. Zhao S R, 2006. Multi-model consensus forecast for temperature[J]. J Appl Meteor Sci, 17(1): 52-58 (in Chinese). DOI:10.3969/j.issn.1001-7313.2006.01.007
|
Engel C, Ebert E, 2007. Performance of hourly operational consensus forecasts (OCFs) in the Australian region[J]. Wea Forecasting, 22(6): 1345-1359. DOI:10.1175/2007WAF2006104.1
|
Engel C, Ebert E E, 2012. Gridded operational consensus forecasts of 2-m temperature over Australia[J]. Wea Forecasting, 27(2): 301-322. DOI:10.1175/WAF-D-11-00069.1
|
Glahn H R, Lowry D A, 1972. The use of model output statistics (MOS) in objective weather forecasting[J]. J Appl Meteor Climatol, 11(8): 1203-1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2
|
Glahn H R, Ruth D P, 2003. The new digital forecast database of the national weather service[J]. Bull Amer Meteor Soc, 84(2): 195-202. DOI:10.1175/BAMS-84-2-195
|
Hyndman R J, Fan Y, 1996. Sample quantiles in statistical packages[J]. Amer Statist, 50(4): 361-365.
|
Hoffman R R, LaDue D S, Mogil H M, et al, 2017. Minding the Weather: How Expert Forecasters Think[M].
Cambridge: The MIT Press.
|
Kann A, Wang Y, Atencia A, et al, 2018. Seamless probabilistic analysis and forecasting: from minutes to days ahead[C]//Proceeding of the 20th EGU General Assembly. Vienna: EGU: 7962.
|
Murphy A H, 1996. The finley affair: a signal event in the history of forecast verification[J]. Wea Forecasting, 11(1): 3-20. DOI:10.1175/1520-0434(1996)011<0003:TFAASE>2.0.CO;2
|
Murphy A H, Winkler R L, 1987. A general framework for forecast verification[J]. Mon Wea Rev, 155(7): 1330-1338.
|
Stensrud D J, Skindlov J A, 1996. Gridpoint predictions of high temperature from a mesoscale model[J]. Wea Forecasting, 11(1): 103-110. DOI:10.1175/1520-0434(1996)011<0103:GPOHTF>2.0.CO;2
|
Woodcock F, Engel C, 2005. Operational consensus forecasts[J]. Wea Forecasting, 20(1): 101-111. DOI:10.1175/WAF-831.1
|
 2023, Vol. 49
2023, Vol. 49 
