相比于雷达资料,静止卫星资料空间分辨率略低,但卫星云图观测范围广,云图中包含的天气系统空间尺度范围也广,包括锋面、台风、中尺度对流系统(MCS)、风暴等从几千米至数千千米(受卫星云图空间分辨率所限)的天气系统。不同天气系统一般伴随着不同空间尺度、不同稳定度的云系(陈渭民,2005),研究表明大气可预报性与天气系统时空尺度密切相关,尺度越小,误差增长率越大(闵锦忠和吴乃庚,2020),在外推预报中需给予重视(郑永光等,2015)。开展基于卫星资料的不同空间尺度云团的外推可预报时效研究,将进一步丰富卫星资料在短时临近预报业务中的应用。
外推预报常用于短时临近预报,在20世纪60—70年代就开发出针对雷达资料的“区域追踪”(area tracker)(Kessler,1966)和“单体追踪”(cell tracker)(Barclay and Wilk, 1970)这两种追踪算法。“区域追踪”法通过对不同时间雷达反射率图像求交叉相关,来确定回波移动的方向和速度(Rinehart and Garvey, 1978;Tuttle and Foote, 1990),代表性方法是TREC(tracking of radar echo with correlations)和光流法。Li et al(1995)在TREC的基础上提出了COTREC(continuity of TREC)算法。“单体追踪”法首先识别单个风暴,再求每个风暴质心的移动,代表性方法是SCIT(storm cell identification and tracking)(Johnson et al,1998)和TITAN(thunderstorm identification, tracking, analysis, and nowcasting)(Dixon and Wiener, 1993)等。经过不断的改进、扩展,这两种算法目前仍是临近预报业务系统中应用最为广泛的追踪算法(陈明轩等,2007;梁丰,2011;孙泓川等,2022;罗义等,2022)。基于雷达资料开展的雷暴、强对流系统和降水的短时临近预报研究结果表明,一般在0~2 h内雷达外推预报优于数值天气预报,第2~6小时融合雷达外推和数值天气预报效果更好,在6 h外使用数值天气预报结果(郑永光等,2010;俞小鼎等,2012)。
随着卫星资料的广泛应用,形成了基于静止卫星资料的类似SCIT的对流系统识别、追踪和外推预报技术和软件,比如RDT(rapid developing thunderstorms)(Lee et al,2020)和Cb-TRAM(cumulonim bus tracking and monitoring)(Zinner et al,2008)软件。基于GMS静止卫星红外资料,白洁等(1997)提出区域平滑滤波和阈值剔除相结合的强对流云团识别算法。刘年庆等(2013)利用慢特征分析方法对FY-2E云图中不同发展阶段的强对流云团进行识别和追踪。基于数字图像处理和模糊模式识别等技术,段炼和郭庚常(2016)实现风云卫星资料中MCS云团的自动识别与追踪。Chen et al(2019)基于日本葵花卫星资料详细研究了亚洲季风区MCS的发生频率和移动轨迹。此外,静止卫星资料在对流初生识别方面别具优势,对流初生外推预报也得到初步应用(Mecikalski and Bedka, 2006;郭巍等,2018;杨波等, 2021)。以上研究主要开展了MCS及对流初生的识别和追踪,对其他类型云系以及不同空间尺度云系的外推预报研究还很少。
基于雷达资料,Germann and Zawadzki(2002)分析了不同尺度降水系统的外推可预报性;Radhakrishna et al(2012)发现对于250 km以上尺度的降水系统外推预报时效可达2 h左右;Surcel et al(2015)发现β中尺度降水系统的外推预报时效也大约为2 h。故本文将基于FY-4卫星红外云图数据和光流法,分析研究整个云图和不同空间尺度云团(后续均指连接在一起的云)的外推可预报性,指导红外云图在短时临近预报业务中的应用。
1 方法和数据 1.1 光流法本文使用光流法开展云团目标追踪并做外推预报。光流法是由Gibson(1950)首先提出的,当被观测的目标和传感器之间有相对运动时,所观察到的亮度模式运动称之为光流。相比于拉格朗日持续性预报等线性外推方法,光流法基于最优化交叉相关系数实现目标追踪,可考虑目标的非线性变化(陈明轩等,2004),对于变化较快的天气过程,光流法具有一定的追踪优势(韩雷等,2008;吴剑坤等,2019),一直都在全球最先进的临近预报业务系统中起着非常重要的作用(Ayzel et al,2019)。
光流类似于刚体物体的速度矢量。速度矢量一般可用u、v两个分量来表达。假设该点在短时间内移动到新的位置,且在短时间内图像的灰度值保持不变,则可以建立随时间和位置变化的灰度值等量关系。进而采用泰勒公式展开,进行求解,得到光流约束方程(曹春燕等,2015)。由于该方程包含了u、v两个分量,方程的求解还需要一定的约束条件。约束条件的通常计算方法有由Lucas and Kanade(1981)和Horn and Schunck(1981)提出的LK局部约束方案和HS全局约束方案,本文使用HS全局约束方案。
主要计算步骤如下:
| $ J=J_{\mathrm{O}}+\alpha^2 J_{\mathrm{HS}} $ | (1) |
| $ J_{\mathrm{O}}=\iint\left(I_x u+I_y v+I_t\right)^2 \mathrm{~d} x \mathrm{~d} y $ | (2) |
| $ J_{\mathrm{HS}}=\iint\left[\left(\frac{\partial u}{\partial x}\right)^2+\left(\frac{\partial u}{\partial y}\right)^2+\left(\frac{\partial v}{\partial x}\right)^2+\left(\frac{\partial v}{\partial y}\right)^2\right] \mathrm{d} x \mathrm{~d} y $ | (3) |
式中:α为平滑系数;JO为灰度守恒项;JHS为平滑约束项;Ix、Iy和It分别给出了图像灰度的空间梯度和时间变率,可通过相邻的两幅图像的灰度值计算出来;(u, v)为光流。
采用变分方法和递归算法求解全局约束方程,可得(u, v)的递归解
| $ u^{(k+1)}=u^{(k)}-I_x \frac{I_x u^{(k)}+I_y v^{(k)}+I_t}{\alpha^2+I_x^2+I_y^2} $ | (4a) |
| $ v^{(k+1)}=v^{(k)}-I_y \frac{I_x u^{(k)}+I_y v^{(k)}+I_t}{\alpha^2+I_x^2+I_y^2} $ | (4b) |
式中:k是循环次数,u(0)和v(0)是光流的初始估计值,可以取为零。
在获取光流场的基础上,本文开展云图外推预报的方案是:首先计算t-Δt到t时刻的光流场(u, v),其次将光流场(u, v)作用于t时刻的云图(灰度图),得到t+Δt时刻的目标云图,其中Δt为外推时间长度。图像边缘数据使用平均值填充,且仅对边缘外区域进行结果统计检验。综上所述,从图像学角度实现了云团的外推预报。
1.2 云检测方法云检测的方法很多,主要分为阈值法、纹理分析法和统计学方法等三大类(刘紫涵和吴艳兰,2017)。从复杂度、普适性和效率等方面来看,每种方法各有优劣。针对红外通道,结合相关文献,本文采用阈值法原理设计一种简单方案开展云检测计算。
具体为:对固定区域来说,根据ISCCP算法(Rossow and Garder, 1993),假设观测辐射只来自晴空和云两种大气状况(郭洪涛等,2010),计算当前像元亮温值ΔBT12与7天内同时刻该卫星像元的最大亮温值(认为晴空状态)BTmax的差异。当这种差异ΔBT≥28 K时(张永宏等,2020),且当前亮温值BT12 < 240 K时,认为该像元被云覆盖。从原理分析,该算法简洁高效,对高、中、低云将有较好反映,对青藏高原等积雪地区也有较好效果;不足之处是对顶高特别低的低云和雾识别效果不佳,该方案优劣的定量分析还需进一步研究。
计算公式如下:
| $ \Delta \mathrm{BT}=\left|\mathrm{BT}_{\max }-\mathrm{BT}_{12}\right| $ | (5) |
如果BT12 < 240 K且ΔBT≥28 K,则认为存在云区。
1.3 数据本文使用卫星图像数据是我国新一代静止卫星FY-4的多通道扫描成像辐射计的L1级4 km空间分辨率数据,该数据是已经过质量检验、地理定位、辐射定标处理后得到的预处理产品。使用其第12通道(波长10.8 μm)数据,该通道卫星接收到的辐射主要与云、大气、地表的温度和发射率有关;对于一定厚度的云,收到的辐射主要与云的温度有关(云的温度越高,收到的辐射就越大;温度越低,辐射越小)。资料覆盖范围种类可为中国区和全圆盘,本文根据中国区的行列号信息将全圆盘数据也处理至中国区范围。
试验个例共12个,时间均为2020年,覆盖四季和四个典型时刻。具体是:1、5、9月的23日18:45(世界时,下同);2、6、10月的23日00:45;3、7、11月的23日06:45;4、8、12月的23日12:45。以2020年4月23日12:45个例为例,以该时刻为时间参考中心(即1.1节方案中的t时刻)开展个例试验,结合试验方案(详见第2.2节和2.3节),该个例使用到的临近时次卫星资料共63个文件。本研究共使用卫星图像文件756个(幅),使用人工逐幅检测方法对这些卫星资料进行了质量确认,其中因图像质量问题替换数据文件3个。
1.4 评价方法对照实测亮温或云区分布,对中国区采用光流法获得的外推预报亮温或云区采用平均绝对误差(MAE)、均方根误差(RMSE)和相关系数(R)等方法进行评价。其中,RMSE相比MAE对误差的异常值更加敏感,在外推过程中,O(实测亮温值)和S(预报亮温值)之间的位置预报偏差比O和S之间的强度预报偏差更易产生较大的异常值情况,所以,RMSE和MAE数值差的变化一定程度上说明了外推预报中位置偏差造成的影响大小。此外,一般认为|R| < 0.4为低度线性相关,0.4≤|R| < 0.7为显著性相关,0.7≤|R|≤1.0为高度线性相关。
2 试验和结果静止卫星资料相比雷达资料可包含更宽广空间尺度的天气系统,不同尺度云团的外推预报时效特征尚需进一步明确。本节我们首先将基于卫星资料测试光流法能否获取长时间的光流场信息,接着对比分析外推整个云图与仅外推所有云团的差异,最后给出不同空间尺度云团的外推准确率特征。
2.1 光流法和云团标识的初步检验(1) 光流法的性能检验
本节以间隔24 h的两张云图分别作为起始云图和目标云图,采用光流法获取它们间隔24 h的光流场,用光流场修正起始云图,检查其结果与目标云图的相似性,以此验证光流法的准确性和其应用于较长时间外推预报的可行性。以2020年4月23日12:45图像作为目标云图为例,结果如图 1所示,基于光流法获得的目标云图与输入的目标云图比较相似。在此个例中,相似性在哈萨克斯坦西北侧、青藏高原、孟加拉国、泰国、我国云南和贵州等地的云系分布中均有体现。可见,在较长时间尺度上,光流法也能获得一定精度的光流场。这种精度与预报对象的空间尺度有一定联系,在一定程度上可反映预报对象的可预报性。如果光流场中包含有较长时间的预报信息,则应可用于较长时间的外推预报,在2.2节和2.3节将研究云图和不同尺度云团中光流场预报信息的有效时长特征。

|
图 1 2020年4月23日12:45个例间隔24 h的光流法性能检验 (a)22日12:45输入的起始云图, (b)23日12:45输入的目标云图, (c)23日12:45输出的基于光流法获得的目标云图 Fig. 1 Test of optical flow method in 24 h interval of the example at 12:45 UTC 23 April 2020 (a) initial cloud image at 12:45 UTC 22, (b) target cloud image at 12:45 UTC 23, (c) result cloud image at 12:45 UTC 23 |
(2) 云检测和云团标识
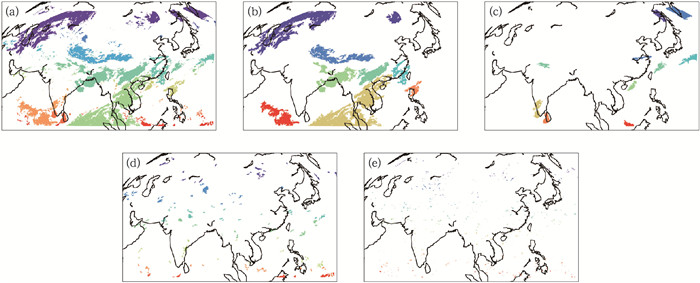
晴空和云团是云图主要组成,我们更关心云团的外推预报,故需对云图进行云检测和云团识别。图 2a是对图 1b中目标云图(2020年4月23日12:45图像)开展的云检测和云团识别结果。可见,云检测算法能够有效剔除青藏高原等寒冷地貌的影响,能够获得不同空间尺度的云团;云团识别采用了8连通区域识别算法,可识别出每个不同形状的云团,并可根据云团特征(比如面积、朝向、强度平均值等)进行云团的分类标记。
|
图 2 2020年4月23日12:45个例云检测与不同尺度云团(分辨率为4 km×4 km)标识 (a)所有云团, (b)>2000 km: 像元数>7500个, (c)200~2000 km:像元数2501~7500个, (d)20~200 km:像元数26~2500个, (e) < 20 km:像元数1~25个 Fig. 2 Distribution of cloud clusters (horizontal resolution: 4 km×4 km) with different scales of the example at 12:45 UTC 23 April 2020 (a) all cloud clusters, (b) >2000 km: >7500 pixels, (c) 200-2000 km: 2501-7500 pixels, (d) 20-200 km: 26-2500 pixels, (e) < 20 km: 1-25 pixels |
云图中包含不同空间尺度的云团,为分析不同尺度云团外推预报的准确率特征,根据Orlanski(1975)的天气系统尺度分类法,可将所有云团分为>2000 km、200~2000 km、20~200 km和 < 20 km等四档。对于大尺度云团,取其形状近似为条形;对于小尺度云团,取其形状近似为圆形。则云团由大到小所占的卫星像元(大小为4 km×4 km)点数分别近似为>7500个、2501~7500个、26~2500个和1~25个。图 2b~2e是同时刻不同尺度云团的水平分布。
2.2 云图和云团的外推试验 2.2.1 试验方案试验方案如表 1所示。对2020年12个个例分别按照表 1开展试验,然后进行检验结果的平均值统计。以2020年4月23日12:45个例为例,以该时刻为个例时间参考中心,获取该时刻之前5、10、30、60、120、240、360、720和1440 min的卫星图像,分别计算它们与时间参考中心卫星图像的光流场,并使用光流场对时间参考中心卫星图像进行修正,分别获得未来5、10、30、60、120、240、360、720和1440 min的外推预报卫星图像,最后计算与同时刻实测卫星图像的误差信息。其中,E系列试验对云图亮温进行外推预报;C系列试验对云检测结果(即云团)开展外推预报,其中像素有云标记为1,无云标记为0。通过试验,获取云图外推时效特征,对比分析云图亮温外推和0/1化云团外推之间的差异。
|
|
表 1 试验方案 Table 1 Experimental scheme |
(1) E系列试验结果分析
E系列试验所有样本的检验结果的平均值如表 2所示,分为对整个区域和仅对云区检验两类。
|
|
表 2 所有个例的E系列试验的检验结果的平均值 Table 2 Averaged values of verified results from E tests in all examples |
从对整个区域开展的检验结果可见,均方根误差随外推预报时长增加呈指数曲线增加,在第0.5、1、2和6小时亮温RMSE数值分别约为4、7、11和17 K,在第12小时后RMSE值趋于稳定,误差接近20 K。MAE与RMSE的数值具有类似的变化趋势,均反映了亮温预报的强度误差特征,不再赘述。
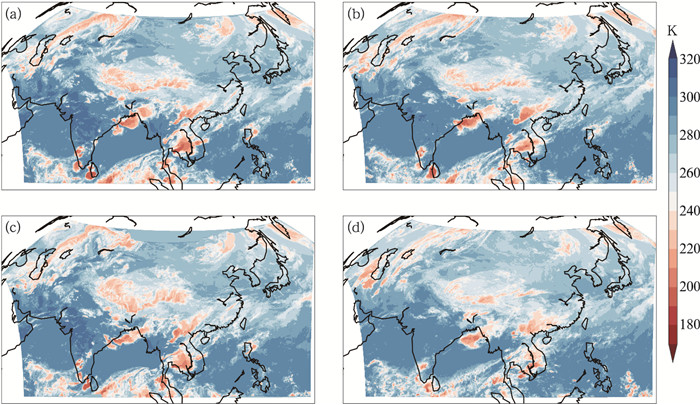
R反映了预报与实测亮温在形态分布上的相似性,其数值随外推预报时长增加呈指数曲线减少,在第0.5、1、2和6小时R数值分别约为0.97、0.93、0.86(高度线性相关)和0.66(显著性相关),在第12小时后R数值也趋于稳定,为0.5左右。图 3为2020年4月23日12:45个例中,2 h和6 h外推预报与实测的对比分布,可见2 h外推预报结果与实测云图比较一致,有较好效果;6 h外推预报结果与实测相比差异增大明显,但在主要云系分布上仍有一定参考性。
|
图 3 2020年4月23日12:45个例外推预报与实测云图分布 (a)2 h外推预报结果,(b)14:45实测云图,(c)6 h外推预报结果,(d)18:45实测云图 Fig. 3 Distributions of forecasted and observed cloud images of the example at 12:45 UTC 23 April 2020 (a) 2 h extrapolation forecast, (b) observation at 14:45 UTC, (c) 6 h extrapolation forecast, (d) observation at 18:45 UTC |
强度误差和相关系数后期趋于稳定,并不意味着外推预报仍有较好的效果,也可能是亮温分布的一种统计平衡状态。比如,当只关注云区预报时(云区检验),云区亮温误差数值在后期仍明显增加,说明预报效果继续变差。对12 h及以后的外推预报结果进行图像检验,发现此时预报结果已无更多参考意义。另外,云区亮温检验误差均比检验整个区域的误差数值要大,相关性也更弱一些,这主要由云区亮温数值变化范围大和云团位置预报偏差等因素引起。
在表 2的整个区域检验中,第24小时相比第12小时RMSE和MAE略有减小,是个似乎反常的地方。分析原因是由于亮温存在日变化,被外推云图亮温与检验时刻亮温的数值范围的差异随时间增大造成的,以第12小时误差最大,而相邻日期同时刻(第24小时)云图亮温数值范围却基本一致。故外推结果中既存在外推误差也存在因亮温日变化引入的误差,两者共同组成预报误差。进一步对00、06、12和18时的个例分别进行统计(表 2),发现06时预报结果的RMSE数值在12 h内远高于其他时刻的结果,说明此时段内亮温日变化相对剧烈,在外推预报中需加以特别关注,这是在雷达回波等外推预报中不需考虑的问题。
(2) C系列试验结果分析
鉴于亮温具有日变化特征而引入误差,故开展C系列试验,对云团进行外推预报,也从检验整个区域和只检验云区的角度衡量预报结果。
C系列试验所有样本的检验结果的平均值如表 3所示,RMSE、MAE和R的演变趋势与E系列试验一致,且云区检验的预报准确率同样低于整个区域的预报准确率。
|
|
表 3 所有个例的C系列试验的检验结果的平均值 Table 3 Averaged values of verified results from C tests in all examples |
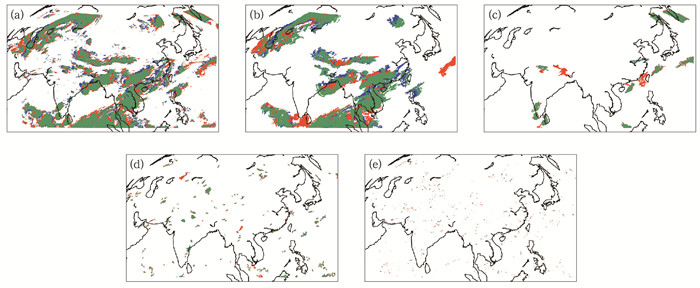
从检验整个区域看,R数值在第0.5、1、2和6小时分别为0.824、0.731、0.608和0.362。可见,外推预报结果与实测在1.5 h左右为高度线性相关,6 h左右低于显著性相关,即云团外推预报可用和可参考时效大约在1.5 h和6 h左右。图 5a是2020年4月23日12:45个例中对所有尺度云团开展2 h外推预报的结果分布,可见外推预报结果与实测有较好对应,能够反映中高纬度天气系统东移和低纬度天气系统西移的现象。
|
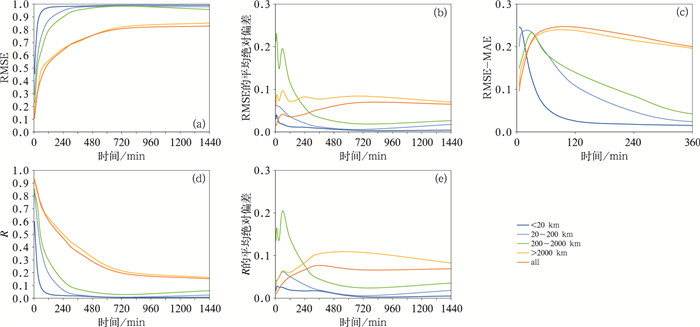
图 4 不同尺度云团(数值0/1)外推试验检验结果的平均值分布 (a)RMSE, (b)RMSE的平均绝对偏差, (c)RMSE-MAE, (d)R, (e)R的平均绝对偏差 Fig. 4 Averaged values of verified results from extrapolation tests of cloud clusters (data 0/1) with different scales (a) RMSE, (b) average deviation of RMSE, (c) RMSE-MAE, (d) R, (e) average deviation of R |
|
图 5 2020年4月23日12:45个例中不同尺度云团(数值0/1)的外推预报结果 (a)全部云团2 h外推对比,(b)>2000 km尺度云团4 h外推对比,(c)200~2000 km尺度云团30 min外推对比,(d)20~200 km尺度云团10 min外推对比,(e) < 20 km尺度云团5 min外推对比 注:蓝色代表该时刻实测云团分布;绿色代表外推一定时长后的预报结果;红色代表与外推预报结果时间一致的实测云团分布。 Fig. 5 Distributions of extrapolation forecast results of cloud clusters (data 0/1) with different scales of the example at 12:45 UTC 23 April 2020 (a) the 2 h extrapolation forecast of cloud clusters with all different scales, (b) the 4 h extrapolation forecast of cloud clusters with scale >2000 km, (c) the 30 min extrapolation forecast of cloud clusters with 200-2000 km scale, (d) the 10 min extrapolation forecast of cloud clusters with 20-200 km scale, (e) the 5 min extrapolation forecast of cloud clusters with scale < 20 km |
从只检验云区看,RMSE数值在第0.5、1、2和6小时分别为0.309、0.421、0.539和0.712。参考R分布特征,RMSE数值0.5和0.7具有较好分档指示意义。可认为,当RMSE≤0.5,外推预报结果可用;0.5 < RMSE≤0.7,外推预报结果有一定参考;RMSE>0.7,外推预报结果不可用。第2.3节,将进一步结合使用R和RMSE来确定不同尺度云团的外推预报可用时效。
此外,计算了云区中RMSE-MAE的数值。在0~1 h以内,云团面积变化不大,RMSE相比MAE数值增大明显,说明此时云区位置偏差导致的“有无”预报失误是其主要原因;在1~6 h中,云团位置偏差和云团面积变化是RMSE-MAE数值处于一个较大值的原因;6 h以后,RMSE和MAE数值均比较大,预报结果基本不可用,RMSE-MAE数值也趋于一个稳定状态。
综上所述,光流法可获得较长时间间隔的光流,且性能测试中有较好效果,但在云图或云团的实际外推预报过程中,由于预报对象位置、面积、强度等因素的复杂变化,可用和可参考光流信息分别为1.5 h和6 h左右。这与使用其他外推预报方法(俞小鼎等,2012)、机器学习(郭瀚阳等,2019;周康辉等,2021a)及其与数值预报产品相融合改进第0~6小时预报(周康辉等,2021b)等研究得到的时效结论基本一致。
2.3 不同尺度云团的外推试验在C系列试验的基础上,结合2.1节云团尺度分档标准(>2000 km、200~2000 km、20~200 km和 < 20 km等四档),进一步开展不同尺度云团外推预报准确率特征分析。
对所有样本的预报结果开展整个区域的R检验和有云区域的RMSE和MAE检验,不同尺度云团外推预报检验结果的平均值随时间的演变如图 4所示。另外,图 5是2020年4月23日12:45个例中不同尺度云团在一定外推时长下的预报结果。
图 4a为RMSE的统计结果,可见不同尺度云团外推预报的RMSE均随时间呈指数趋势增加;尺度越小,RMSE越大,且增长速度也越快,在更短时间内达到误差的稳定峰值状态,这说明尺度越小可预报性越低,可用时效越短;>2000 km尺度云团的误差曲线与外推“所有”云团的误差曲线比较一致,说明>2000 km尺度云团相比其他尺度云团,对“所有”云团外推预报有着至关重要的影响,外推“所有”云团预报主要体现了>2000 km尺度云团的外推预报特征。在2020年4月23日12:45个例的图 5a和5b的对比中,也可见>2000 km尺度云团对“所有”云团的外推预报效果起决定作用。
图 4b为RMSE的平均绝对偏差的统计结果,平均绝对偏差主要反映了本文12个样本相对RMSE平均值的偏差大小。图中可见大多数尺度云团的RMSE的平均绝对偏差数值约在0~0.1,而200~2000 km尺度的数值在前6 h内相比较大,可达0.23。图 5c是200~2000 km尺度云团的一次典型分布,相比其他尺度云团,该尺度云团云团数量相对较少,且在外推预报过程存在易向向其他相邻尺度转变的现象,使得不同样本间的RMSE数值存在较大差异。
MAE检验结果的变化趋势与RMSE的基本一致,故图 4c主要给出了RMSE-MAE数值的统计结果。除了 < 20 km尺度云团外,其他尺度云团的RMSE-MAE数值均为先增加后减小的趋势;峰值点出现的时间随云团尺度增加而依次增加,大约为5、20、32和100 min。云团位置预报偏差是RMSE-MAE快速增长的主要原因,在RMSE-MAE峰值点后,云团面积和位置预报偏差成为主要原因。RMSE-MAE峰值点出现时间的变化特征进一步表明云团尺度越小,生命史越短,面积形态变化也越明显,可用预报时效缩短。
图 4d为R的统计结果,其变化趋势与RMSE统计结果相反,云团尺度越小,R越小,且减小速度也越快,在更短时间内更易达到弱相关的稳定状态。值得注意的是,>2000 km尺度云团比“所有”尺度云团的R数值更大,外推预报可用时效明显提升,反映出大尺度云团物理属性比较稳定。从小到大,不同尺度云团和“所有”尺度云团R数值分别到达0.7(高度线性相关)和0.4(显著性相关)的时间约为0、16、32、68、72 min和16、56、76、360、308 min。与此类似,均方根误差数值(图 4a)分别为0.5和0.7的时间约为7、20、30、64、92 min和12、48、76、328、320 min。两种方法判别得到的可用和可参考预报时效结果比较接近。
图 4e为R的平均绝对偏差,其变化特征与图 4b相似,在前360 min内R或RMSE存在较大偏差,表明不同个例外推预报可用时效存在一定区别。以2020年4月23日12:45为例,图 5展示了不同尺度(由小到大)和“所有”尺度云团分别在第5、10、30、240和120分钟的外推预报结果,在以上时段内外推预报均有较好效果。
综合以上因素,选取R和RMSE判别时效长度的最大值作为参考值,结合偏差扰动的存在和便于业务使用的目的,给出不同尺度(由小到大)和“所有”尺度云团外推预报的可用时效和可参考时效分别是10、20、30、60、90 min和15、60、90、360、320 min。其中,200~2000 km尺度云团的外推预报可参考时效90 min与Surcel et al(2015)基于雷达资料获得的β中尺度降水系统的外推预报时效(约2 h)基本一致。
综上所述,本节给出了不同尺度云团详细的外推预报特征分析。可见,随着云团空间尺度增加,外推预报时效相应增加,这与不同尺度云团的物理属性演变特性、生命史长短等要素密切相关。
3 结论与展望 3.1 结论本文为研究云图和不同尺度云团的外推可预报性特征,设计了一种适应于FY-4卫星红外云图(10.8 μm)的云检测方法,结合区域识别算法,剥离出不同尺度的云团(数值0/1);使用具有HS全局约束方案的光流法,开展外推敏感试验。对2020年12个个例的不同时长的外推预报的检验结果进行平均值统计,得到以下结论:
(1) 在较长时间尺度上,光流法也能获得一定精度的光流场。但这种精度与预报对象的空间尺度有一定联系,在一定程度上可反映预报对象的可预报性。在云图外推预报中,试验表明可参考光流信息接近6 h。
(2) 外推预报准确率随着预报时长的增加而降低。对整幅亮温云图进行外推预报,在第0.5、1和6小时亮温的RMSE值约为4.4、7.1和16.7 K,这其中既包含外推预报误差,也包含亮温日变化带来的误差。对云检测结果进行外推预报,可消除亮温日变化的影响,云团位置预报偏差是外推预报在第0~1小时中的误差快速增长的主要原因,云团面积和位置的预报偏差是第1~6小时中误差的主要组成。
(3) 外推预报准确率随着云团空间尺度的减小而呈指数曲线降低。>2000 km、200~2000 km、20~200 km、< 20 km等尺度云团的可参考外推时长分别不超过6 h、1.5 h、1 h和15 min,可用外推时长与不同尺度云团的物理属性演变特性、生命史长短等要素密切相关。外推“所有”尺度云团的预报主要体现了>2000 km尺度云团的外推预报特征。
3.2 展望本文仅开展了光流法的基本应用,为测试获取预报时效特征,未在当前与过去时刻之间引入更多卫星图像。受光流法等传统方法局限,未能考虑云团生消演变等过程。这些因素对外推预报准确率会产生一定影响。
(1) 对流性云团和非对流性云团除了图像特征差异,还存在生命史长短、移动速度、发展强度等方面的差异,其可预报性不同,值得进一步研究。
(2) 机器学习(深度学习)相比传统方法具备一定对流系统生消演变的预报能力,与数值预报等多源产品相融合更能有效延长预报时效,值得进一步关注。
白洁, 王洪庆, 陶祖钰, 1997. GMS卫星红外云图强对流云团的识别与追踪[J]. 热带气象学报, 13(2): 158-167. Bai J, Wang H Q, Tao Z Y, 1997. Recognition and tracing of severe convective cloud from IR images of GMS[J]. J Trop Meteor, 13(2): 158-167 (in Chinese). DOI:10.16032/j.issn.1004-4965.1997.02.008
|
曹春燕, 陈元昭, 刘东华, 等, 2015. 光流法及其在临近预报中的应用[J]. 气象学报, 73(3): 471-480. Cao C Y, Chen Y Z, Liu D H, et al, 2015. The optical flow method and its application to nowcasting[J]. Acta Meteor Sin, 73(3): 471-480 (in Chinese).
|
陈明轩, 俞小鼎, 谭晓光, 等, 2004. 对流天气临近预报技术的发展与研究进展[J]. 应用气象学报, 15(6): 754-766. Chen M X, Yu X D, Tan X G, et al, 2004. A brief review on the development of nowcasting for convective storms[J]. J Appl Meteor Sci, 15(6): 754-766 (in Chinese). DOI:10.3969/j.issn.1001-7313.2004.06.015
|
陈明轩, 王迎春, 俞小鼎, 2007. 交叉相关外推算法的改进及其在对流临近预报中的应用[J]. 应用气象学报, 18(5): 690-701. Chen M X, Wang Y C, Yu X D, 2007. Improvement and application test of TREC algorithm for convective storm nowcast[J]. J Appl Meteor Sci, 18(5): 690-701 (in Chinese).
|
陈渭民, 2005. 卫星气象学[M]. 北京: 气象出版社: 238-397. Chen W M, 2005. Satellite Meteorology[M].
Beijing: China Meteorological Press: 238-397 (in Chinese).
|
段炼, 郭庚常, 2016. 风云卫星云图自动识别追踪MCS的方法[J]. 电子科技, 29(4): 116-119, 126. Duan L, Guo G C, 2016. Research on method for MCS automatic identification and tracking based on FY satellite cloud image[J]. Electron Sci Technol, 29(4): 116-119, 126 (in Chinese). DOI:10.16180/j.cnki.issn1007-7820.2016.04.030
|
郭瀚阳, 陈明轩, 韩雷, 等, 2019. 基于深度学习的强对流高分辨率临近预报试验[J]. 气象学报, 77(4): 715-727. Guo H Y, Chen M X, Han L, et al, 2019. High resolution nowcasting experiment of severe convections based on deep learning[J]. Acta Meteor Sin, 77(4): 715-727 (in Chinese).
|
郭洪涛, 王毅, 刘向培, 等, 2010. 卫星云图云检测的一种综合优化方法[J]. 解放军理工大学学报(自然科学版), 11(2): 221-227. Guo H T, Wang Y, Liu X P, et al, 2010. Integrated optimal method of cloud detection with meteorological satellite data[J]. J PLA Univ Sci Technol (Nat Sci Ed), 11(2): 221-227 (in Chinese).
|
郭巍, 崔林丽, 顾问, 等, 2018. 基于葵花8卫星的上海市夏季对流初生预报研究[J]. 气象, 44(9): 1229-1236. Guo W, Cui L L, Gu W, et al, 2018. Summer convective initiation forecasting in Shanghai based on Himawari-8 satellite[J]. Meteor Mon, 44(9): 1229-1236 (in Chinese).
|
韩雷, 王洪庆, 林隐静, 2008. 光流法在强对流天气临近预报中的应用[J]. 北京大学学报(自然科学版), 44(5): 751-755. Han L, Wang H Q, Lin Y J, 2008. Application of optical flow method to nowcasting convective weather[J]. Acta Sci Nat Univ Pekinensis, 44(5): 751-755 (in Chinese). DOI:10.3321/j.issn:0479-8023.2008.05.014
|
梁丰, 2011. 对流天气临近预报业务系统的新发展[J]. 沙漠与绿洲气象, 5(6): 1-6. Liang F, 2011. New development of convective weather nowcasting systems[J]. Desert Oasis Meteor, 5(6): 1-6 (in Chinese).
|
刘年庆, 郑媛媛, 蒋建莹, 等, 2013. 基于动态特征的强对流云团追踪[J]. 高原气象, 32(2): 556-563. Liu N Q, Zheng Y Y, Jiang J Y, et al, 2013. Severe convective cloud tracking based on dynamic features[J]. Plateau Meteor, 32(2): 556-563 (in Chinese).
|
刘紫涵, 吴艳兰, 2017. 遥感图像云检测方法研究进展[J]. 国土资源遥感, 29(4): 6-12. Liu Z H, Wu Y L, 2017. A review of cloud detection methods in remote sensing images[J]. Remote Sens Land Resour, 29(4): 6-12 (in Chinese).
|
罗义, 梁旭东, 王刚, 等, 2022. 自适应尺度的雷达回波交叉相关跟踪算法研究[J]. 气象, 48(3): 372-385. Luo Y, Liang X D, Wang G, et al, 2022. A study of the adaptive-scale tracking radar echoes by correlation method[J]. Meteor Mon, 48(3): 372-385 (in Chinese).
|
闵锦忠, 吴乃庚, 2020. 近二十年来暴雨和强对流可预报性研究进展[J]. 大气科学, 44(5): 1039-1056. Min J Z, Wu N G, 2020. Advances in atmospheric predictability of heavy rain and severe convection[J]. Chin J Atmos Sci, 44(5): 1039-1056 (in Chinese).
|
孙泓川, 吴海英, 曾明剑, 等, 2022. 结合中尺度模式物理约束的雷达回波临近外推预报方法研究[J]. 气象学报, 80(2): 257-268. Sun H C, Wu H Y, Zeng M J, et al, 2022. A study on radar echo extrapolation nowcasting method combined with physical constraints of mesoscale model[J]. Acta Meteor Sin, 80(2): 257-268 (in Chinese).
|
吴剑坤, 陈明轩, 秦睿, 等, 2019. 变分回波跟踪算法及其在对流临近预报中的应用试验[J]. 气象学报, 77(6): 999-1014. Wu J K, Chen M X, Qin R, et al, 2019. The variational echo tracking method and its application in convective storm nowcasting[J]. Acta Meteor Sin, 77(6): 999-1014 (in Chinese).
|
杨波, 蔡雪薇, 刘鑫华, 等, 2021. 中央气象台航空气象预报技术系统进展[J]. 气象科技进展, 11(3): 145-154. Yang B, Cai X W, Liu X H, et al, 2021. Progress on aviation meteorological forecast technology system of National Meteorological Centre[J]. Adv Meteor Sci Technol, 11(3): 145-154 (in Chinese).
|
俞小鼎, 周小刚, 王秀明, 2012. 雷暴与强对流临近天气预报技术进展[J]. 气象学报, 70(3): 311-337. Yu X D, Zhou X G, Wang X M, 2012. The advances in the nowcasting techniques on thunderstorms and severe convection[J]. Acta Meteor Sin, 70(3): 311-337 (in Chinese).
|
张永宏, 杨晨阳, 陶润喆, 等, 2020. 基于FY-4A数据的青藏高原多时相云检测方法[J]. 遥感技术与应用, 35(2): 389-398. Zhang Y H, Yang C Y, Tao R Z, et al, 2020. Multi-temporal cloud detection method for Qinghai-Tibet Plateau based with FY-4A data[J]. Remote Sens Technol Appl, 35(2): 389-398 (in Chinese).
|
郑永光, 张小玲, 周庆亮, 等, 2010. 强对流天气短时临近预报业务技术进展与挑战[J]. 气象, 36(7): 33-42. Zheng Y G, Zhang X L, Zhou Q L, et al, 2010. Review on severe convective weather short-term forecasting and nowcasting[J]. Meteor Mon, 36(7): 33-42 (in Chinese).
|
郑永光, 周康辉, 盛杰, 等, 2015. 强对流天气监测预报预警技术进展[J]. 应用气象学报, 26(6): 641-657. Zheng Y G, Zhou K H, Sheng J, et al, 2015. Advances in techniques of monitoring, forecasting and warning of severe convective weather[J]. J Appl Meteor Sci, 26(6): 641-657 (in Chinese).
|
周康辉, 郑永光, 韩雷, 等, 2021a. 机器学习在强对流监测预报中的应用进展[J]. 气象, 47(3): 274-289. Zhou K H, Zheng Y G, Han L, et al, 2021a. Advances in application of machine learning to severe convective weather monitoring and forecasting[J]. Meteor Mon, 47(3): 274-289 (in Chinese).
|
周康辉, 郑永光, 王婷波, 2021b. 利用深度学习融合NWP和多源观测数据的闪电落区短时预报方法[J]. 气象学报, 79(1): 1-14. Zhou K H, Zheng Y G, Wang T B, 2021b. Very short-range lightning forecasting with NWP and observation data: a deep learning approach[J]. Acta Meteor Sin, 79(1): 1-14 (in Chinese).
|
Ayzel G, Heistermann M, Winterrath T, 2019. Optical flow models as an open benchmark for radar-based precipitation nowcasting (rainymotion v0.1)[J]. Geosci Model Dev, 12(4): 1387-1402.
|
Barclay P A, Wilk K E, 1970. Severe thunderstorm radar echo motion and related weather events hazardous to aviation operations[R]. Norman, Oklahoma: National Severe Storms Laboratory: 10-21.
|
Chen D D, Guo J P, Yao D, et al, 2019. Mesoscale convective systems in the Asian monsoon region from advanced Himawari imager: algorithms and preliminary results[J]. J Geophys Res: Atmos, 124(4): 2210-2234.
|
Dixon M, Wiener G, 1993. TITAN: Thunderstorm identification, tracking, analysis, and nowcasting-a radar-based methodology[J]. J Atmos Oceanic Technol, 10(6): 785-797.
|
Germann U, Zawadzki I, 2002. Scale-dependence of the predictability of precipitation from continental radar images. Part Ⅰ: description of the methodology[J]. Mon Wea Rev, 130(12): 2859-2873.
|
Gibson J J, 1950. The Ecological Approach to Visual Perception[M].
Boston: Houghton Mifflin: 332.
|
Horn B K P, Schunck B G, 1981. Determining optical flow[J]. Artif Intell, 17(1-3): 185-203.
|
Johnson J T, MacKeen P L, Witt A, et al, 1998. The storm cell identification and tracking algorithm: an enhanced WSR-88D algorithm[J]. Wea Forecasting, 13(2): 263-276.
|
Kessler E, 1966. Computer program for calculating average lengths of weather radar echoes and pattern bandedness[J]. J Atmos Sci, 23(5): 569-574.
|
Lee J G, Min K H, Park H, et al, 2020. Improvement of the rapid-development thunderstorm (RDT) algorithm for use with the GK2A satellite[J]. Asia-Pacific J Atmos Sci, 56(2): 307-319. DOI:10.1007/s13143-020-00182-6
|
Li L, Schmid W, Joss J, 1995. Nowcasting of motion and growth of precipitation with radar over a complex orography[J]. J Appl Meteor, 34(6): 1286-1300.
|
Lucas B D, Kanade T, 1981. An iterative image registration technique with an application to stereo vision[C]//Proceedings of the 7th International Joint Conference on Artificial Intelligence. Vancouver: Morgan Kaufmann Publishers Inc. : 674-679.
|
Mecikalski J R, Bedka K M, 2006. Forecasting convective initiation by monitoring the evolution of moving cumulus in daytime GOES imagery[J]. Mon Wea Rev, 134(1): 49-78.
|
Orlanski I, 1975. A rational subdivision of scales for atmospheric process[J]. Bull AMS, 56(5): 527-530.
|
Radhakrishna B, Zawadzki I, Fabry F, 2012. Predictability of precipitation from continental radar images. Part Ⅴ: growth and decay[J]. J Atmos Sci, 69(11): 3336-3349.
|
Rinehart R E, Garvey E T, 1978. Three-dimensional storm motion detection by conventional weather radar[J]. Nature, 273(5660): 287-289.
|
Rossow W B, Garder L C, 1993. Cloud detection using satellite measurements of infrared and visible radiances for ISCCP[J]. J Climate, 6(12): 2341-2369.
|
Surcel M, Zawadzki I, Yau M K, 2015. A study on the scale dependence of the predictability of precipitation patterns[J]. J Atmos Sci, 72(1): 216-235.
|
Tuttle J D, Foote G B, 1990. Determination of the boundary layer airflow from a single Doppler radar[J]. J Atmos Oceanic Technol, 7(2): 218-232.
|
Zinner T, Mannstein H, Tafferner A, 2008. Cb-TRAM: Tracking and monitoring severe convection from onset over rapid development to mature phase using multi-channel Meteosat-8 SEVIRI data[J]. Meteor Atmos Phys, 101(3/4): 191-210.
|
 2023, Vol. 49
2023, Vol. 49 