2. 浙江省气象台,杭州 310017
2. Zhejiang Meteorological Observatory, Hangzhou 310017
作为水循环的重要组成部分,降水在全球水汽和能量平衡中起着重要的调节作用(李凤秀和朱业玉,2019;姜彤等,2020)。在全球变暖的背景下,极端降水事件的频数和强度呈上升趋势,降水时空分布也发生着变化(Groisman et al,1999;Goswami et al,2006;刘德地等,2009;高涛和谢立安,2014;Zhang and Zhou, 2019;姜彤等,2020;Li et al,2021)。在日尺度上,不同地区降水的日变化呈现明显的差异。美国中部和东南沿海降水峰值分别出现在夜间和下午(Kincer,1916)。日本东京暖季降水在午后呈现正异常(Fujibe et al,2009)。我国不同地区之间也存在降水日变化的差异(王婧羽等,2019;多典洛珠等,2020;苏锦兰等,2021),如原韦华等(2014)指出,我国西南、华南和中东部地区夏季降水分别在夜间、下午、清晨和午后达到峰值。
降水分布与地形关系密切(Katzfey,1995;Shafer et al,2006;王凌梓等,2018)。倪婷等(2018)发现,大别山区降水的大值区位于主峰的东南侧。复杂山区地形作用使降水产生增幅(董美莹等,2011)。特殊地形能对局地降水产生重要的影响,如发生在2015年7月22—24日鄂东北江汉平原河谷地区的局地短时强降水过程(李超等,2018)。赵勇等(2010)发现,天山南北两坡的极端降水均随地形高度增加而增多。然而在云贵高原东部,降水随海拔升高先增加之后再减少(周秋雪等,2019;郭晓芳等,2021)。除海拔之外,地形坡度和坡向同样影响着降水分布。如在天山山区,年降水量随坡度变化的关系呈现为抛物线状(张正勇等,2015)。在相同海拔高度上,天山北坡的极端降水多于南坡,且北坡最大降水所处的海拔高度低于南坡(赵勇等,2010)。鉴于这些因素对降水的影响,孙朋杰等(2021)利用多元线性回归方法,引入地理和地形因子(经度、纬度、海拔、坡度和坡向),建立了湖北省降水空间估算模型,结果与观测较为吻合。此外,迎风坡和背风坡降水的差异还与风向和风速有关(Smith,1979;傅抱璞,1992)。Johansson and Chen(2003)研究了地形和气象要素(风场)共同作用对瑞典降水的影响,发现迎风坡的降水随风速增强而增加,而背风坡的降水受地形和风场的影响较小,降水空间变化平缓。郭忆等(2013)利用能克服变量间共线性特征的偏最小二乘回归模型发现,地理、地形和风向等要素共同对长江中下游降水的空间分布产生重要的影响。
在复杂的多要素共同作用下,降水表现出非线性、不确定性和时空分布复杂的特征(彭昱忠等,2015)。因此,对降水的空间分布进行合理的估算具有一定难度和挑战性。空间异质性,也称空间非平稳性,是地理科学中衡量要素关系或结构在不同空间具有差异性的表征(Goodchild,2004)。普通线性回归(ordinary linear regression,OLR)模型作为确定各因素之间相关关系的基本方法,被学者广泛应用(Guan et al,2005;Jeong et al,2012;Wei et al,2015),但它只考虑因变量和自变量之间的线性或同质性关系,因此只能给出时空“平均的关系”。为了克服这个问题,地理加权回归(geographically weighted regression,GWR)模型被提出(Brunsdon et al,1998a;1998b)。该模型利用样本点间的空间距离衡量邻近关系,将地理位置融入回归参数,使得回归参数在不同空间位置有所不同,由此建立每个空间点的局部回归方程。利用该模型,Brunsdon et al(2001)发现,英国的降水与海拔的正相关性从东部向西—西北部增加。郭晓芳等(2021)和张铭明等(2021)也利用该模型研究了降水与海拔的关系。但是,当引入的影响因子较多且与因变量有复杂的非线性关系时,GWR模型并不能得到较好的拟合结果(Li et al,2019;杜震洪等,2020)。近年来,神经网络因有着对非线性关系的强拟合能力,在各领域中被广泛应用(何慧等,2007;葛彩莲,2011;董全等,2013;Moghadam,2017;Emamgholizadeh et al,2017;张烨方等,2021),并得到了比传统模型预测精度更高的结果(李永华等,2002;刘新等,2020)。为了结合不同模型的优势,吴森森(2018)进一步提出地理神经网络加权回归(geographically neural network weighted regression,GNNWR)模型。该模型利用神经网络的学习能力,将要素的空间异质性和要素间的复杂非线性特征同时加以考虑。在浙江近岸海域赤潮灾害时空分布(吴森森,2018)和中国PM2.5质量浓度空间分布(杜震洪等,2020)的建模中,GNNWR模型均表现出良好的性能并得到准确的结果。但对于复杂地形下的降水,如何考虑影响因子的空间异质性和非线性对降水空间分布的影响,目前尚没有充分的研究。
尽管目前观测资料日渐丰富,但仍存在站点分布不均、复杂地形区域站点偏少、特殊季节采样不能满足需求等问题。因此,对观测稀疏或缺失地区的降水进行科学准确的估算十分必要(周自江等,2022)。浙江省地处我国东南沿海,面向东海,具有典型的亚热带湿润季风气候。省内地形复杂多样,山区和丘陵约占全省总面积的75%,地势南高北低,且自西南向东北倾斜,气象站点分布不均且山区站点分布较少(图 1)。在湿润的亚洲夏季风和复杂地形的综合影响下,浙江省降水的空间分布差异较大。因此,对人口稠密、经济发达的浙江省来说,开展复杂地形下浙江省夏季主要时段降水空间估算及其影响因素的相关研究,有助于加深对降水空间变化及其影响因素等科学问题的理解,同时对浙江省水资源利用和防灾减灾具有重要的科学意义。
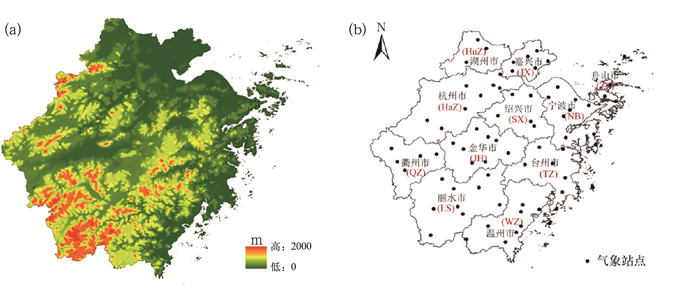
|
图 1 浙江省(a)海拔高度和(b)74个气象站的空间分布示意图 注:图 1b中,括号中的英文表示浙江省各行政区域的简称,下同。 Fig. 1 Spatial distributions of (a) terrain elevation and (b) the 74 meteorological stations in Zhejiang Province |
地形数据来自地理空间云网站的数字高程模型(digital elevation model,DEM)数据,分辨率为90 m×90 m(图 1a),从中可计算和提取地形的海拔、坡度和坡向信息。
用于建模的观测数据来自浙江省气象台提供的2014—2021年夏季全省74个气象站点的观测资料,包括站点、站号、位置及海拔、逐小时降水量、风速、风向和气温。图 1b是全省74个气象站点的分布情况。两个站点之间的平均距离约为27 km,但在西南至中部山区,以及西北部山区,气象站点的分布较为稀疏。
为了对建模揭示的降水过程进行验证,还用到美国国家环境预报中心(NCEP)每六小时一次、水平分辨率为0.25°×0.25°的FNL(final analysis)全球再分析资料。之所以使用该分辨率的资料,是为了和站点的平均距离相匹配;资料起始年为2015年,因此本文采用2015—2021年夏季的再分析资料进行相关结果的验证。
1.2 研究时段参考过去的做法,本文将北京时02—08时、08—14时、14—20时和20时至次日02时期间发生的累计降水分别定义为凌晨、早间、午后和晚间降水。为捕捉复杂地形和大气条件对降水的可能影响,同时为业务预报提供参考,本研究包含了2014—2021年8年间夏季的所有降水天数,包括与热带天气系统有关的极端强降水事件。从图 1b可以看出,74个气象站在全省的分布并不均匀。克里金插值法是目前应用最广泛的插值方法,它利用有限的观测数据,基于变异函数模型生成理想的空间格局(金芃霏和刘剑刚,2015)。通过将插值到站点的降水与站点直接观测的降水进行对比,发现插值后凌晨、早间、午后和晚间降水的平均相对误差仅为5.24 %,说明该插值方法是可靠的。利用此方法得到浙江夏季各时段降水的空间分布,如图 2所示。
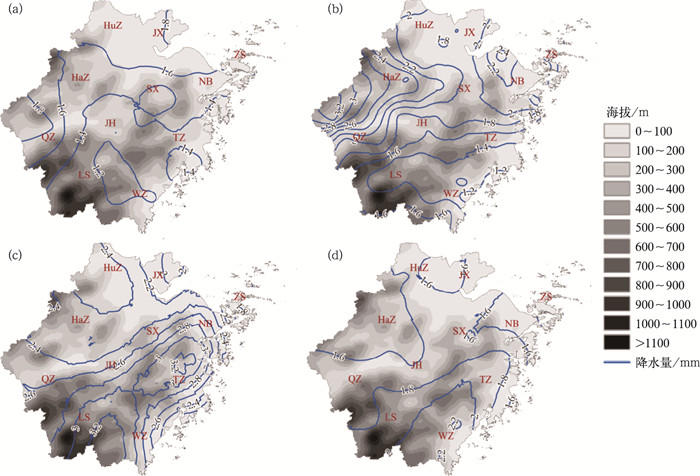
|
图 2 2014—2021年浙江省夏季不同时段降水(等值线)的空间分布 (a)凌晨,(b)早间,(c)午后,(d)晚间 Fig. 2 Spatial distributions of precipitation (contour) in different periods of summer from 2014 to 2021 in Zhejiang Province (a) wee hours, (b) morning, (c) afternoon, (d) evening |
表 1显示2014—2021年浙江省夏季日不同时段的降水概况。由表 1可知,无论是平均降水量还是最大降水量,午后时段均为最大,分别是2.51 mm和4.02 mm,大致为凌晨时段降水的2倍,这说明午后时段是浙江省夏季日降水最为集中的时段。宇如聪等(2014)研究发现,我国东南沿海地区的降水具有午后峰值的特征;李德帅(2016)指出,中国南方大部分地区的后汛期,降水峰值都出现在下午。本文的观测结果与过去的研究结果较为一致。
|
|
表 1 2014—2021年浙江省夏季日不同时段的降水(单位:mm) Table 1 Precipitation in different periods of summer days in Zhejiang Province from 2014 to 2021(unit: mm) |
由图 2可知,浙江省夏季日不同时段降水的空间分布存在差异。凌晨和早间降水整体呈现西多东少的空间分布格局(图 2a,2b),而午后和晚间降水则都表现为自西南向东北递减的趋势,主雨带明显(图 2c,2d)。比较午后和晚间降水可以发现,晚间降水的主雨带更弱且更偏向东南。从多方面来看,浙江省夏季降水主要发生在午后时段,故本文以浙江省夏季午后降水为研究对象,分析其空间变化特征,建立科学准确的降水估算模型,并进一步分析其降水的影响因素。
1.3 研究方法为了保证样本的充足和较小的插值误差,经过多次试验,本文从克里金插值结果中随机提取370个样本点。基于这些样本点,参照Shafer et al(2006)、舒守娟等(2005;2007)和Johansson and Chen(2003)研究,引入地理(经度、纬度)、地形(海拔、坡度、坡向)和气象要素(风向、风速),采用传统的线性回归和考虑空间权重的机器学习方法,建立浙江省夏季午后降水的估算模型。
由于本文建模考虑的因子较多,各因子之间可能存在多重共线性问题,使模型出现过拟合,故本文将370个样本点随机划分为三个数据集:训练数据集、验证数据集和测试数据集。其中,训练数据集主要用于训练和优化模型,验证数据集用于验证模型在经过训练之后是否被过拟合,测试数据集则用于评估模型的预测能力。本文按照15%的比例随机选取56个样本作为测试数据集,剩下的314个样本则包含了训练数据和验证数据。然后,采用十折交叉验证法,将这些数据进行十等分,轮流将其中一份作为测试集来测试模型,剩余九份则作为训练集来训练模型。按照这个方法,本文从剩余的314个样本中,随机选取32个样本(约10%)和282个样本(约90%)分别作为验证数据集和训练数据集。
1.3.1 普通线性回归(OLR)模型在OLR模型中,因变量和自变量的回归方程可表示为:
| $ y_i=\beta_0+\sum\limits_{k=1}^p \beta_k x_{i k}+\varepsilon_i \quad i=1, 2, \cdots, n $ | (1) |
式中:β0为常系数,下标k和i分别代表第k个自变量和第i个观测样本。βk为对应自变量xk的回归系数,εi为均值为零的样本i的误差项。
β的估计采用最小二乘法,故OLR模型系数的估计矩阵可表达为:
| $ \hat{\boldsymbol{\beta}}=\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{y} $ | (2) |
其中,
| $ \boldsymbol{y}=\left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array}\right], \quad \boldsymbol{X}=\left[\begin{array}{ccccc} 1 & x_{11} & x_{12} & \cdots & x_{1 k} \\ 1 & x_{21} & x_{22} & \cdots & x_{2 k} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & x_{n 1} & x_{n 2} & \cdots & x_{n k} \end{array}\right]_{n(k+1)} $ | (3) |
GWR模型(Brunsdon et al,1998a;1998b)考虑了样本点的空间位置及相互之间的距离,可定义为:
| $ \begin{gathered} y_i=\beta_0\left(u_i, v_i\right)+\sum\limits_{k=1}^p \beta_k\left(u_i, v_i\right) x_{i k}+\varepsilon_i \\ i=1, 2, \cdots, n \end{gathered} $ | (4) |
式中:(ui, vi)表示样本i的空间坐标,β0(ui, vi)是截距,βk(ui, vi)表示样本i第k个自变量的空间变化系数,与空间位置(ui, vi)有关。
因此,回归系数在不同空间位置上的估算矩阵可表示为:
| $ \hat{\boldsymbol{\beta}}\left(u_i, v_i\right)=\left[\boldsymbol{X}^{\mathrm{T}} \boldsymbol{W}\left(u_i, v_i\right) \boldsymbol{X}\right]^{-1} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{W}\left(u_i, v_i\right) \boldsymbol{y} $ | (5) |
式中,W (ui, vi)是(ui, vi)的空间权重矩阵,通常由空间核函数计算得到。
GWR模型的核函数包括固定型和适应型。固定型核函数是在给定带宽范围(即影响半径)内,寻找最优带宽值以得到最好的拟合结果,但当样本分布不均匀时效果会受到影响。故本文采用的是适应型Bi-square核函数,它是选取样本点i邻近点的最优值,此核函数可表示为:
| $ w_{i j}= \begin{cases}{\left[1-\left(d_{i j} / b_i\right)^2\right]^2} & d_{i j}<b_i \\ 0 & d_{i j} \geqslant b_i\end{cases} $ | (6) |
式中:bi表示点i到第q个邻近点的距离,所以适应型核函数需要估计的参数为q值,即带宽参数;dij表示位置i和j之间的距离,故wij指的是样本点j对样本点i的影响。可见,该模型利用空间权重核函数考虑了因子对降水影响的空间变化。
1.3.3 地理神经网络加权回归(GNNWR)模型GNNWR模型(吴森森,2018)利用神经网络考虑了回归关系在空间上的变化,其因变量和自变量的回归关系可表示为:
| $ \begin{gathered} y_i=w_0\left(u_i, v_i\right) \times \beta_0+\sum\limits_{k=1}^p w_k\left(u_i, v_i\right) \times \beta_k x_{i k}+\varepsilon_i \\ i=1, 2, \cdots, n \end{gathered} $ | (7) |
式中:w0(ui, vi)表示常系数的空间权重,wk(ui, vi)是样本i第k个自变量在(ui, vi)位置的空间权重,其余变量解释同式(1)、式(4)。
将OLR模型中的估计量
| $ \begin{aligned} \hat{y}\left(u_i, v_i\right) & =\sum\limits_{k=0}^p w_k\left(u_i, v_i\right) \times \hat{\beta}_k(\mathrm{OLR}) x_{i k} \\ & =\boldsymbol{x}_i^{\mathrm{T}} \boldsymbol{W}\left(u_i, v_i\right)\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{y} \end{aligned} $ | (8) |
式中:xi表示矩阵X第i行的向量。
为了更好地拟合空间权重和空间距离的关系,GNNWR模型设计了空间加权神经网络(spatial weighted neural network,SWNN),将目标点Pi与其他点的距离作为输入层,选取适当数量的隐含层(本文采用了3层隐含层,隐含层指的是输入层和输出层之间的层级,对输入数据特征进行抽象和划分),利用神经网络优越的拟合能力来寻找两者之间的最优关系(图 3),并输出空间权重矩阵,如下:
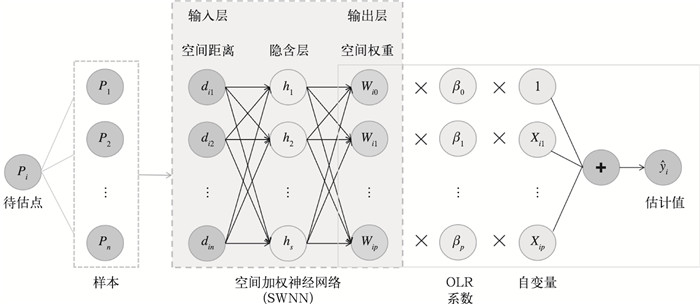
|
图 3 GNNWR模型的构建(改绘自Du et al,2020) Fig. 3 The construction of GNNWR model (revised from Du et al, 2020) |
| $ \boldsymbol{W}_i=\boldsymbol{W}\left(u_i, v_i\right)=\operatorname{SWNN}\left(\left[d_{i 1}, d_{i 2}, d_{i 3}, \cdots, d_{i n}\right]^{\mathrm{T}}\right) $ | (9) |
式中[di1, di2, di3, …, din]表示从点i到所有其他点的空间距离。
最后,将空间权重矩阵Wi与训练数据集得到的OLR回归系数
在评价模型性能方面,采用决定系数(R2)、均方根误差(RMSE)、平均绝对误差(MAE)和平均相对误差(MRE)这四个检验指标。R2表示自变量对因变量的解释程度,值越大说明拟合程度越好;RMSE用来衡量样本的离散程度,值越小说明模型效果越好;MAE和MRE分别指样本绝对误差和相对误差的平均值,值越小说明模型估计的误差越小。
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2}{\sum\limits_{i=1}^n\left(y_i-\bar{y}_i\right)^2} $ | (10) |
| $ \operatorname{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2}{n}} $ | (11) |
| $ \mathrm{MAE}=\frac{\sum\limits_{i=1}^n\left|y_i-\hat{y}_i\right|}{n} $ | (12) |
| $ \mathrm{MRE}=\frac{1}{n} \sum\limits_{i=1}^n\left|\frac{y_i-\hat{y}_i}{y_i}\right| \times 100 \% $ | (13) |
式中:yi表示观测值的平均值。
2 浙江省夏季午后降水的空间变化和估算 2.1 午后观测降水的空间分布基于2014—2021年浙江省74个气象站点的逐小时降水观测,计算得到浙江省夏季午后降水的平均值为2.51 mm,大部分地区的降水为1~4 mm。降水最多和最少的地区分别位于温州(WZ)泰顺和台州(TZ)大陈岛,分别为4.02 mm和1.17 mm。根据午后降水的空间分布(图 2c)可知,浙江省夏季午后降水表现为自西南向东北递减的趋势,在TZ和南部山区附近形成超过3 mm的降水区,这两个主要降水中心形成一条西南—东北走向的主雨带,且南部山区的东坡降水较强,东部沿海平原降水较弱。西南山区降水最多,北部平原降水最少,这和浙江省地势特征大体一致,说明地形对浙江省午后降水具有一定的影响。衢州(QZ)北部山区和杭州(HaZ)西部山区的海拔较高,降水却不显著,表明除了地形的影响,其他因素也影响了浙江省午后降水的空间分布。
从图 2c可以看出,随着纬度的增加,午后降水逐渐减少。由于降水多少和距离水汽源地的远近有关(Naoum and Tsanis, 2004),因此,对面朝东海的浙江省来说,午后降水在东西方向上分布不均也与经度有关。这些地理和地形因素如何在午后西南—东北走向的主雨带中发挥作用,将在以下进一步研究。
2.2 午后降水影响因素表 2给出了午后降水与各影响因子之间的相关性。由此可看出,午后降水与地理、地形、气象因素关系密切。地理因素(经度、纬度)与午后降水呈显著负相关,表明午后降水自西南向东北呈下降趋势。地形因子(海拔、坡度、坡向)与午后降水呈现正相关,尤其是海拔,相关性达到0.407,说明整体上浙江省海拔较高的地区,午后降水较多,这与图 2c中展现的一般特征基本一致。在所有因子中,风速与午后降水的相关性最高,为-0.521,这与以往揭示的风向、地形和地理因素影响的结果(舒守娟等,2005;2007;郭忆等,2013)不同,表明气象因素对降水的影响在不同地区表现不同。但表 2仅代表各因子和降水的全局线性关系,相关性较低的因子并不说明它们对午后局地降水的影响小或无影响。
|
|
表 2 2014—2021年浙江省夏季午后降水与各影响因子的相关性 Table 2 Correlations between the summer afternoon precipitation and various factors in Zhejiang Province from 2014 to 2021 |
基于74个气象站点的数据,利用OLR模型考虑上述影响因素估算午后降水,并将估算结果与观测降水进行比较。结果表明,相比于仅考虑地理因素,在加入地形和气象因素后,估算的午后降水绝对误差从0.459 mm减少到0.399 mm,相对误差从20.23 %减少到16.87 %,模型对午后降水空间分布的估算效果越来越好。仅考虑地理因素,估算的午后降水等值线接近直线,自西南向东北呈下降趋势(图 4a)。在加入地形因子后,中部地区降水等值线向东北倾斜,但与观测降水(图 4d)相比,等值线闭合中心的位置偏差较大,例如3 mm等值线(图 4b)。进一步引入气象因素后,东部降水的特征开始呈现,降水的空间分布更接近观测(图 4c)。这说明地理、地形和气象要素对浙江省夏季午后降水的空间分布均存在一定的影响。
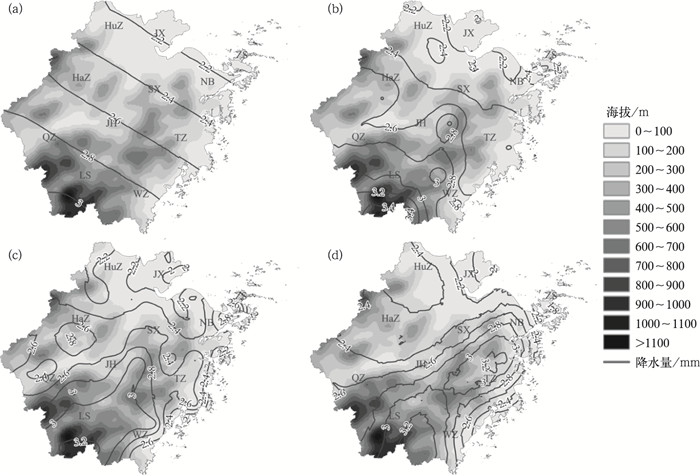
|
图 4 (a,b,c)OLR模型估算及(d)观测的2014—2021年浙江省夏季午后降水(等值线)空间分布 (a)仅引入地理因素,(b)同时引入地理和地形因素,(c)同时引入地理、地形和气象因素 Fig. 4 Spatial distributions of the summer afternoon precipitation (a-c) estimated by OLR model and (d) observation in Zhejiang Province from 2014 to 2021 (contour) (a) only with geographic factors, (b) with both the geographic and topographic factors, (c) with geographic, topographic and meteorological factors |
为了更好地估算具有空间异质性的浙江省夏季午后降水,不同于图 4用74个站点数据进行建模的做法,进一步基于上述随机提取的370个样本数据集,利用OLR模型和考虑空间异质性的GWR、GNNWR模型对午后降水进行估算,并利用R2、RMSE、MAE和MAPE指标评价和比较各模型的性能。
训练数据集和测试数据集的结果分别反映模型的拟合精度和预测精度。由表 3可知,相比于训练集的拟合精度,测试集的预测精度普遍下降,其中GWR模型下降幅度较大,OLR和GNNWR模型的差别较小。无论是训练集还是测试集,R2在OLR模型中都是最小的,RMSE、MAE和MAPE指标也为最大,超过GNNWR模型的四倍,这说明只考虑全局关系的OLR模型对浙江省夏季午后降水的拟合和预测精度非常有限。考虑空间异质性的GWR和GNNWR模型,两者拟合精度接近,但GNNWR模型的预测精度更高。GNNWR模型测试集的R2为0.975,明显高于GWR模型的0.840,且RMSE、MAE和MAPE指标都不到GWR模型指标的一半。这说明基于神经网络的、考虑要素空间异质性和因素间非线性关系的GNNWR模型,能够更好地估算浙江省夏季的午后降水。
|
|
表 3 OLR、GWR和GNNWR模型对2014—2021年浙江省夏季午后降水建模的性能比较 Table 3 Comparison of the performance of the OLR, GWR and GNNWR models for estimating the summer afternoon precipitation in Zhejiang Province from 2014 to 2021 |
图 5为OLR、GWR和GNNWR模型估算降水及观测降水的空间分布。从图 5a可以看出,OLR模型估算的午后降水与观测在空间分布上有相似之处,降水自西南向东北递减,但其覆盖面积、位置以及降水中心的大小与观测(图 5d)存在较大的差异,例如雨带整体更接近沿海且只延伸到中部山脉(TZ西南部),无北部降水中心(图 5a)。GWR(图 5b)和GNNWR(图 5c)模型估算的午后降水与观测降水的空间分布相似,雨带的覆盖范围和位置更准确,南、北两个降水中心都得到了体现,而且浙江省西北部和沿海地区午后降水的估算也更为准确,如湖州(HuZ)和HaZ北部的2.4 mm等值线分布。但在局部地区,GNNWR模型估算的午后降水比GWR模型更接近实况,如雨带北部3.2 mm的降水闭合区、嘉兴(JX)北部降水低于2 mm和舟山(ZS)北部降水低于1.8 mm等值线的特征在GNNWR模型中均有所体现,但在GWR模型中却没有显现。这说明基于神经网络的GNNWR模型能够抓住要素局部区域的变化特征,对复杂地形条件下降水的估算效果更好。

|
图 5 (a) OLR,(b)GWR,(c)GNNWR模型估算的2014—2021年浙江省夏季午后降水及(d)观测降水(等值线)的空间分布 Fig. 5 Spatial distributions of the summer afternoon precipitation in Zhejiang Province from 2014 to 2021 estimated by (a) OLR, (b) GWR, and (c) GNNWR models and (d) observation (contour) |
综上所述,对浙江省夏季午后降水的估算,考虑降水空间异质性的GWR和GNNWR模型在模型性能和估算降水的空间分布方面均优于OLR模型。而利用神经网络计算空间权重的GNNWR模型,由于同时处理了要素空间异质性和复杂的非线性问题,因此能够抓住要素的局部变化(如降水极值)特征,从而给出更准确的估算。
3 浙江省夏季午后降水的影响因素 3.1 不同因子对午后降水空间变化的影响虽然OLR、GWR和GNNWR模型都能给出不同因素对浙江省夏季午后降水的影响,但是OLR模型得到的是各因素对整个浙江省的“平均”影响,不随空间变化;而GWR和GNNWR模型能得到各因素在浙江省不同地区的不同影响,随空间发生变化。根据2.3节结果可知,GNNWR模型能更好地估算浙江省夏季午后降水,故本文基于GNNWR模型给出的影响因子权重,进一步分析各因素对浙江省各地夏季午后降水的影响。
权重的意义在于,它给出了某因子对降水的影响随空间变化的特点,正负权重分别表示该因子对降水的正负影响作用。从图 6a可以看出,海拔仅在北部降水中心表现为负权重,其余地方均为正权重。在主雨带区,正权重和负权重分别分布在南部和北部降水中心。这说明,在南部降水区,海拔越高,午后降水越大,这体现了地形对气流的抬升作用;对于北部降水区,大面积负权重分布在低海拔地区,显示地形抬升作用不显著。

|
图 6 GNNWR模型估算的2014—2021年浙江省夏季午后降水(等值线)和不同因子的空间权重(填色) (a)海拔,(b)坡度,(c)坡向,(d)风速,(e)风向(箭头) Fig. 6 Spatial distributions of summer afternoon precipitation (contour) in Zhejiang Province from 2014 to 2021 and weights (colored) for different factors estimated by the GNNWR model (a) altitude, (b) slope, (c) aspect, (d) wind speed, (e) wind direction (arrow) |
由图 6b可知,坡度在浙江省南部和西部地区表现为负面影响,在浙江省其他地区几乎是正面影响。南部和西部降水区,坡度权重与海拔权重相反,说明虽然高海拔有利于午后降水的产生,但陡峭地形却不利于降水的发展。而在TZ附近的北部降水中心,这种情况恰好相反,即海拔为负权重,坡度为正权重,这说明虽然该区域海拔对降水没有显著影响,但坡度有利于该地降水的产生。
坡向对浙江省大部分地区午后降水有正面影响,只对WZ东南缘地区有负面影响(图 6c)。由于西/南坡的坡向值较大,东/北坡坡向值较小,图 6c的分布模式表明,浙江省大部分地区西/南坡有利于上升运动和午后降水,而WZ东南缘地区则是东/北坡有利于上升运动和降水的发展。
风速权重空间分布(图 6d)的一个显著特征是,正权重和负权重区域分别位于雨带北部降水中心的东南部和西北部(正负权重的分界线非常接近北部降水中心)。由于正和负权重分别意味着强和弱风速有利于午后降水,所以北部降水中心的东南部风速越大越有利于降水,而西北部风速越小越有利于降水。浙江省夏季盛行东南季风(图 6e箭头),当东南部沿海地区风速较大而西北部地区风速较小时,将在地面发生气流的辐合。大量天气学观测和分析研究表明,水汽辐合是降水产生的本质原因。因此,该结果合理解释了北部降水中心的形成。
图 6e为风向的权重空间分布。在主雨带北部降水中心附近(TZ附近),南北两侧的权重相反,说明那里气流方向的影响是相反的,即南部(正权重)风向值越大,越有利于降水,北部(负权重)风向值越小越有利于降水。西/南风的风向值大,东/北风的风向值小,所以当西/南风和东/北风分别作用于北部降水中心的南侧和北侧时有利于该降水中心的产生,这体现了风向的辐合作用。从物理现象的角度来看,图 6d和6e的综合结果表明,气流辐合是午后北部降水中心形成的主要原因。由图 6e还可见,南部降水中心基本为正权重,表示风向越大(即西/南风)时,午后降水越多。结合图 6a,6c和6e,海拔、坡向和风向对南部降水中心都是正影响,即海拔越高、坡向和风向越大(即西/南坡或风)越有利于南部山区降水的产生。李占清和翁笃鸣(1987)和舒守娟等(2005;2007)指出,当风向与坡向一致时,即气流正对坡向吹时,气流在迎风坡上的垂直上升运动最强。因此,当南部降水中心坡向为西/南坡同时风向为西/南风时,地形抬升作用最显著,即地形对来自南方潮湿气流的抬升作用是南部降水中心形成的主要原因。同时,南部降水中心的东部沿海地区(图 6e中WZ以东)也存在类似于上述一正一反“偶极子”权重的影响模态,显示出风向辐合对东南部沿海降水的贡献作用。
3.2 午后降水影响因素的验证分析上述基于GNNWR模型的分析结果,显示出地形和气象要素(风速和风向)对浙江省夏季午后降水的综合影响。为了验证GNNWR模型结果的合理性,结合高分辨率NCEP再分析数据集作进一步分析。
由午后海平面气压减去日平均海平面气压的空间分布(图 7a)可知,正的气压扰动产生在海洋地区,负的大范围气压扰动位于浙江省和福建省内陆地区,由此形成了午后高压扰动(海洋)指向低压扰动(陆地)的气压梯度力。图 7b阴影是基于NCEP再分析数据得到的浙江省夏季午后地表温度的空间分布。高温和低温区分别位于浙江省及其周边陆地和东部海洋上,这与图 7a一致。因此,在气压梯度力和地转偏向力的共同作用下,出现由海洋吹向陆地的偏东/南风分量。它们叠加在大尺度夏季风背景上,起到加强偏东/南暖湿气流的作用,尤其是在海陆交界地带,这由图 7b中沿海更长的蓝色箭头得到了印证。
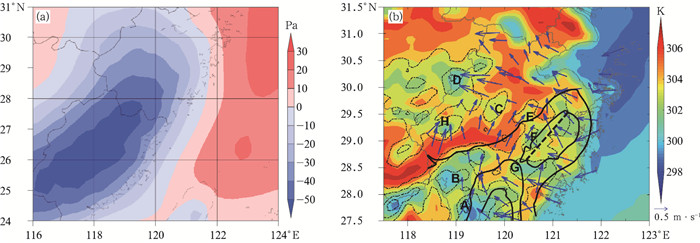
|
图 7 浙江省夏季午后(a)海平面气压扰动,(b)地表温度(填色)叠加地面扰动风场(蓝箭头:午后风减去日平均风)和观测降水(粗黑实线,单位:mm)的空间分布 注:图 7b中,粗黑虚线为地面辐合线,细黑虚线为地形等高线,主要山脉用大写字母A~G标注位置。 Fig. 7 Spatial distributions of (a) disturbance of mean sea level pressure, (b) surface temperature (colored) with disturbance wind field on ground (blue arrow: afternoon wind minus mean daily wind), and the observed precipitation (solid thick black contour, unit: mm) in Zhejiang Province in summer |
在浙江省内陆,温度和地形分布紧密相关。高温区主要位于较低海拔处,包括浙北平原和被B、G、C、H包围的中部盆地区域;低温区则主要位于较高海拔山区,尤其是西南山区(A、B)。在局地气压梯度力的驱动下,地表发生由高压扰动(低温)吹向低压扰动(高温)的弱偏西风分量,并与从海洋吹来的较强偏东/南风相汇合,在F附近形成了地面辐合线(粗黑虚线),促使北部降水中心的形成,这一发现验证了前述的分析结果。同样的辐合也有利于南部降水中心的形成。同时,南部山区迎风坡对东/南暖湿气流具有抬升作用,因此在A—G迎风坡上形成了较强的南部降水中心。这些结论与图 6中基于GNNWR模型的分析结果相一致,显示出该模型不但能够较准确地估算降水,而且在揭示降水主要物理过程方面也具有一定的参考意义。
4 结论和讨论浙江省地处我国东南沿海,地形复杂多样,山区和丘陵约占全省总面积的75%,气象站点分布不均且山区站点分布较少。基于浙江省气象站点的逐时观测资料,发现浙江省夏季日降水主要集中在午后时段。通过建立并比较三种估算模型(OLR、GWR和GNNWR模型),对复杂地形下浙江省夏季午后降水的空间估算及其影响因素进行研究,得到以下主要结论:
(1) 浙江省夏季午后降水整体呈现自西南向东北递减的分布特征,南部山区午后降水显著高于北部平原。从西南高山向东北至东部平原形成一西南—东北走向的降水主雨带,并存在南北两个主要降水中心。
(2) 考虑空间异质性的GWR和GNNWR模型在性能和估算降水空间分布方面都明显优于只考虑全局关系的普通线性回归(OLR)模型。其中,基于神经网络考虑空间异质性的GNNWR模型的预测精度是最高的,能准确估算复杂地形条件下午后降水整体和局部的空间分布特征,说明GNNWR模型在克服要素间复杂非线性关系和描述降水的空间异质性方面具有较好的效果。
(3) 基于GNNWR模型影响因子权重的空间分布和NCEP再分析资料的验证结果,发现地理、地形和气象要素共同对浙江省夏季午后降水的空间分布产生影响。气流辐合和地形抬升作用是浙江省夏季午后降水形成的主要因素,但具体物理过程还需要利用高分辨率数值模拟进一步验证。
将GNNWR模型用于复杂地形条件下降水空间分布的建模,是地理科学研究方法在大气科学研究中的一次尝试。本文的研究结果表明,基于神经网络的GNNWR模型在表征具有空间异质特性和非线性特征的气象要素时具有一定的优势,在强度和空间分布上均能对浙江省夏季午后降水给出较好的估算结果。然而,模型没有考虑要素的时间变化。后续将探索在GNNWR模型中进一步加入时间变量,如考虑降水的季节性和日变化等因素进行建模,以期为气象要素预报提供更多的参考。
董美莹, 陈联寿, 程正泉, 等, 2011. 地形影响热带气旋"泰利"降水增幅的数值研究[J]. 高原气象, 30(3): 700-710. Dong M Y, Chen L S, Cheng Z Q, et al, 2011. Numerical study of topography effect on rainfall reinforcement associated with tropical cyclone 'Talim'[J]. Plateau Meteor, 30(3): 700-710 (in Chinese).
|
董全, 黄小玉, 宗志平, 2013. 人工神经网络法和线性回归法对降水相态的预报效果对比[J]. 气象, 39(3): 324-332. Dong Q, Huang X Y, Zong Z P, 2013. Comparison of artificial nueral network and linear regression methods in forecasting precipitation types[J]. Meteor Mon, 39(3): 324-332 (in Chinese).
|
杜震洪, 吴森森, 王中一, 等, 2020. 基于地理神经网络加权回归的中国PM2.5浓度空间分布估算方法[J]. 地球信息科学学报, 22(1): 122-135. Du Z H, Wu S S, Wang Z Y, et al, 2020. Estimating ground-level PM2.5 concentrations across China using geographically neural network weighted regression[J]. J Geo-Inf Sci, 22(1): 122-135 (in Chinese).
|
多典洛珠, 周顺武, 宋倩倩, 等, 2020. 西藏拉萨汛期降水日变化特征[J]. 干旱气象, 38(1): 58-65. Duo D L Z, Zhou S W, Song Q Q, et al, 2020. Diurnal variation characteristic of precipitation during flood season in Lhasa of Tibet Autonomous Region[J]. J Arid Meteor, 38(1): 58-65 (in Chinese).
|
傅抱璞, 1992. 地形和海拔高度对降水的影响[J]. 地理学报, 47(4): 302-314. Fu B P, 1992. The effects of topography and elevation on precipitation[J]. Acta Geogr Sin, 47(4): 302-314 (in Chinese).
|
高涛, 谢立安, 2014. 近50年来中国极端降水趋势与物理成因研究综述[J]. 地球科学进展, 29(5): 577-589. Gao T, Xie L A, 2014. Study on progress of the trends and physical causes of extreme precipitation in China during the last 50 years[J]. Adv Earth Sci, 29(5): 577-589 (in Chinese).
|
葛彩莲, 2011. 西宁市降水量不同预报方法比较研究[D]. 杨凌: 西北农林科技大学, 89. Ge C L, 2011. Comparison and study of the different prediction methods about rainfall in Xining City[D]. Yangling: Northwest A&F University, 89(in Chinese).
|
郭晓芳, 李旭东, 程东亚, 2021. 云贵高原气温与降水空间分布特征及其影响因素[J]. 水土保持研究, 28(1): 159-163, 170. Guo X F, Li X D, Cheng D Y, 2021. Spatial distribution of temperature and precipitation and its influencing factors in the Yunnan-Guizhou Plateau[J]. Res Soil Water Conserv, 28(1): 159-163, 170 (in Chinese).
|
郭忆, 毕硕本, 张余庆, 等, 2013. 地理地形因子对长江中下游平原降水空间分布影响的估算和分析[J]. 科学技术与工程, 13(29): 8555-8560. Guo Y, Bi S B, Zhang Y Q, et al, 2013. Estimation and analysis for geographic and orographic influences on precipitation distribution on the Yangtze Plain, Middle and Lower[J]. Sci Technol Eng, 13(29): 8555-8560 (in Chinese). DOI:10.3969/j.issn.1671-1815.2013.29.002
|
何慧, 金龙, 覃志年, 等, 2007. 基于BP神经网络模型的广西月降水量降尺度预报[J]. 热带气象学报, 23(1): 72-77. He H, Jin L, Qin Z N, et al, 2007. Downscaling forecast for the monthly precipitation over Guangxi based on the BP neural network model[J]. J Trop Meteor, 23(1): 72-77 (in Chinese).
|
姜彤, 孙赫敏, 李修仓, 等, 2020. 气候变化对水文循环的影响[J]. 气象, 46(3): 289-300. Jiang T, Sun H M, Li X C, et al, 2020. Impact of climate change on water cycle[J]. Meteor Mon, 46(3): 289-300 (in Chinese).
|
金芃霏, 刘剑刚, 2015. 基于EOF的浙江省降水变化时空分析研究[J]. 环境科学与管理, 40(7): 40-45. Jin P F, Liu J G, 2015. Analysis on temporal and spatial precipitation changes based on EOF in Zhejiang Province[J]. Environ Sci Manage, 40(7): 40-45 (in Chinese).
|
李超, 崔春光, 蒋兴文, 等, 2018. 特殊地形对鄂东北一次局地强降水过程的作用机制分析[J]. 气象, 44(9): 1117-1135. Li C, Cui C G, Jiang X W, et al, 2018. Mechanism analysis of the effect of special topography in middle-lower reaches of Yangtze River on local severe precipitaion in Northeast Hubei[J]. Meteor Mon, 44(9): 1117-1135 (in Chinese).
|
李德帅, 2016. 基于逐小时资料的华南地区汛期降水时空变化特征及其成因研究[D]. 兰州: 兰州大学: 151. Li D S, 2016. Research on the spatiotemporal characteristics of hourly precipitation over South China during the warm season and its possible causes[D]. Lanzhou: Lanzhou University: 151(in Chinese).
|
李凤秀, 朱业玉, 2019. 1961-2017年郑州夏季降水日变化规律分析[J]. 河南科学, 37(6): 924-932. Li F X, Zhu Y Y, 2019. Precipitation diurnal variation in summer in Zhengzhou from 1961 to 2017[J]. Henan Sci, 37(6): 924-932 (in Chinese).
|
李永华, 刘德, 金龙, 2002. 基于BP神经网络的汛期降水预测模型研究[J]. 气象科学, 22(4): 461-467. Li Y H, Liu D, Jin L, 2002. Study on rainfall prediction model in rain season based on BP neural network[J]. Sci Meteor Sin, 22(4): 461-467 (in Chinese).
|
李占清, 翁笃鸣, 1987. 一个计算山地地形参数的计算机模式[J]. 地理学报, 42(3): 269-278. Li Z Q, Weng D M, 1987. A computer model to determine topographic parameters[J]. Acta Geogr Sin, 42(3): 269-278 (in Chinese).
|
刘德地, 李梅, 楼章华, 等, 2009. 近50年来浙江省降雨特性变化分析[J]. 自然资源学报, 24(11): 1973-1983. Liu D D, Li M, Lou Z H, et al, 2009. Analysis of precipitation characteristics variation in Zhejiang Province in the past 50 years[J]. J Nat Resour, 24(11): 1973-1983 (in Chinese).
|
刘新, 赵宁, 郭金运, 等, 2020. 基于LSTM神经网络的青藏高原月降水量预测[J]. 地球信息科学学报, 22(8): 1617-1629. Liu X, Zhao N, Guo J Y, et al, 2020. Prediction of monthly precipitation over the Tibetan Plateau based on LSTM neural network[J]. J Geo-Inf Sci, 22(8): 1617-1629 (in Chinese).
|
倪婷, 黄勇, 凌新锋, 等, 2018. 大别山区地形降水特征分析[J]. 气象科技, 46(3): 556-562. Ni T, Huang Y, Ling X F, et al, 2018. Characteristics of orographic precipitation in Dabie Mountain[J]. Meteor Sci Technol, 46(3): 556-562 (in Chinese).
|
彭昱忠, 王谦, 元昌安, 等, 2015. 数据挖掘技术在气象预报研究中的应用[J]. 干旱气象, 33(1): 19-27. Peng Y Z, Wang Q, Yuan C A, et al, 2015. Review of research on data mining in application of meteorological forecasting[J]. J Arid Meteor, 33(1): 19-27 (in Chinese).
|
舒守娟, 王元, 熊安元, 2007. 中国区域地理、地形因子对降水分布影响的估算和分析[J]. 地球物理学报, 50(6): 1703-1712. Shu S J, Wang Y, Xiong A Y, 2007. Estimation and analysis for geographic and orographic influences on precipitation distribution in China[J]. Chin J Geophys, 50(6): 1703-1712 (in Chinese).
|
舒守娟, 喻自凤, 王元, 等, 2005. 西藏地区复杂地形下的降水空间分布估算模型[J]. 地球物理学报, 48(3): 535-542. Shu S J, Yu Z F, Wang Y, et al, 2005. A statistic model for the spatial distribution of precipitation estimation over the Tibetan complex terrain[J]. Chin J Geophys, 48(3): 535-542 (in Chinese).
|
苏锦兰, 张万诚, 宋金梅, 等, 2021. 云南小时降水的时空分布变化研究[J]. 气象, 47(2): 133-142. Su J L, Zhang W C, Song J M, et al, 2021. Study on spatio-temporal distribution of hourly precipitation in Yunnan Province[J]. Meteor Mon, 47(2): 133-142 (in Chinese).
|
孙朋杰, 王必强, 陈正洪, 等, 2021. 湖北省复杂地形影响下降水精细化分布特征研究[J]. 湖北农业科学, 60(8): 74-80. Sun P J, Wang B Q, Chen Z H, et al, 2021. Study on the fine distribution characteristics of falling water affected by complex topography in Hubei Province[J]. Hubei Agric Sci, 60(8): 74-80 (in Chinese).
|
王婧羽, 李哲, 汪小康, 等, 2019. 河南省雨季短时强降水时空分布特征[J]. 暴雨灾害, 38(2): 152-160. Wang J Y, Li Z, Wang X K, et al, 2019. Temporal and spatial distribution characteristics of flash heavy rain in Henan during rainy season[J]. Torr Rain Dis, 38(2): 152-160 (in Chinese).
|
王凌梓, 苗峻峰, 韩芙蓉, 2018. 近10年中国地区地形对降水影响研究进展[J]. 气象科技, 46(1): 64-75. Wang L Z, Miao J F, Han F R, 2018. Overview of impact of topography on precipitation in China over last 10 years[J]. Meteor Sci Technol, 46(1): 64-75 (in Chinese).
|
吴森森, 2018. 地理时空神经网络加权回归理论与方法研究[D]. 杭州: 浙江大学: 171. Wu S S, 2018. The theory and method of geo- graphically and temporally neural network weighted regression[D]. Hangzhou: Zhejiang University: 171(in Chinese).
|
宇如聪, 李建, 陈昊明, 等, 2014. 中国大陆降水日变化研究进展[J]. 气象学报, 72(5): 948-968. Yu R C, Li J, Chen H M, et al, 2014. Progress in studies of the precipitation diurnal variation over contiguous China[J]. Acta Meteor Sin, 72(5): 948-968 (in Chinese).
|
原韦华, 宇如聪, 傅云飞, 2014. 中国东部夏季持续性降水日变化在淮河南北的差异分析[J]. 地球物理学报, 57(3): 752-759. Yuan W H, Yu R C, Fu Y F, 2014. Study of different diurnal variations of summer long-duration rainfall between the southern and northern parts of the Huai River[J]. Chin J Geophys, 57(3): 752-759 (in Chinese).
|
张铭明, 李建, 甘玉婷, 等, 2021. 基于GWR模型的中国中东部降水与海拔高度关系特征分析[J]. 暴雨灾害, 40(1): 1-11. Zhang M M, Li J, Gan Y T, et al, 2021. Analysis of the relationship between precipitation and altitude over central and eastern China based on the geographically weighted regression model[J]. Torr Rain Dis, 40(1): 1-11 (in Chinese).
|
张烨方, 冯真祯, 刘冰, 2021. 基于卷积神经网络的雷电临近预警模型[J]. 气象, 47(3): 373-380. Zhang Y F, Feng Z Z, Liu B, 2021. Lightning nowcasting early warning model based on convolutional neural network[J]. Meteor Mon, 47(3): 373-380 (in Chinese).
|
张正勇, 何新林, 刘琳, 等, 2015. 中国天山山区降水空间分布模拟及成因分析[J]. 水科学进展, 26(4): 500-508. Zhang Z Y, He X L, Liu L, et al, 2015. Spatial distribution of rainfall simulation and the cause analysis in China's Tianshan Mountains Area[J]. Adv Water Sci, 26(4): 500-508 (in Chinese).
|
赵勇, 邓学良, 李秦, 等, 2010. 天山地区夏季极端降水特征及气候变化[J]. 冰川冻土, 32(5): 927-934. Zhao Y, Deng X L, Li Q, et al, 2010. Characteristics of the extreme precipitation events in the Tianshan Mountains in relation to climate change[J]. J Glaciol Geocryol, 32(5): 927-934 (in Chinese).
|
周秋雪, 康岚, 蒋兴文, 等, 2019. 四川盆地边缘山地强降水与海拔的关系[J]. 气象, 45(6): 811-819. Zhou Q X, Kang L, Jiang X W, et al, 2019. Relationship between heavy rainfall and altitude in mountainous areas of Sichuan Basin[J]. Meteor Mon, 45(6): 811-819 (in Chinese).
|
周自江, 曹丽娟, 廖捷, 等, 2022. 水文气象信息概述: 观测、融合与再分析[J]. 气象, 48(3): 272-283. Zhou Z J, Cao L J, Liao J, et al, 2022. Overview of hydrometeorological information: obeservation, data fusion and reanalysis[J]. Meteor Mon, 48(3): 272-283 (in Chinese).
|
Brunsdon C, Fotheringham S, Charlton M, 1998a. Geographically weighted regression-modelling spatial non-stationarity[J]. J Roy Stat Soc Ser D Stat, 47(3): 431-443.
|
Brunsdon C, Fotheringham A S, Charlton M, 1998b. Spatial nonstationarity and autoregressive models[J]. Environ Plan A: Economy Space, 30(6): 957-973.
|
Brunsdon C, McClatchey J, Unwin D J, 2001. Spatial variations in the average rainfall-altitude relationship in Great Britain: an approach using geographically weighted regression[J]. Int J Climatol, 21(4): 455-466.
|
Du Z H, Wang Z Y, Wu S S, 2020. Geographically neural network weighted regression for the accurate estimation of spatial non- stationarity[J]. Int J Geogr Inf Sci, 34(7): 1353-1377.
|
Emamgholizadeh S, Shahsavani S, Eslami M A, 2017. Comparison of artificial neural networks, geographically weighted regression and Cokriging methods for predicting the spatial distribution of soil macronutrients (N, P, and K)[J]. Chin Geogr Sci, 27(5): 747-759.
|
Fujibe F, Togawa H, Sakata M, 2009. Long-term change and spatial anomaly of warm season afternoon precipitation in Tokyo[J]. SOLA, 5: 17-20.
|
Goodchild M F, 2004. The validity and usefulness of laws in geographic information science and geography[J]. Ann Assoc Am Geogr, 94(2): 300-303.
|
Goswami B N, Venugopal V, Sengupta D, et al, 2006. Increasing trend of extreme rain events over India in a warming environment[J]. Science, 314(5804): 1442-1445.
|
Groisman P Y, Karl T R, Easterling D R, et al, 1999. Changes in the probability of heavy precipitation: important indicators of climatic change[J]. Climatic Change, 42(1): 243-283.
|
Guan H D, Wilson J L, Makhnin O, 2005. Geostatistical mapping of mountain precipitation incorporating autosearched effects of terrain and climatic characteristics[J]. J Hydrometeorol, 6(6): 1018-1031.
|
Jeong D I, St-Hilaire A, Ouarda T B M J, et al, 2012. Comparison of transfer functions in statistical downscaling models for daily temperature and precipitation over Canada[J]. Stoch Environ Res Risk Assess, 26(5): 633-653.
|
Johansson B, Chen D L, 2003. The influence of wind and topography on precipitation distribution in Sweden: statistical analysis and modelling[J]. Int J Climatol, 23(12): 1523-1535.
|
Katzfey J J, 1995. Simulation of extreme New Zealand precipitation events.Part I: sensitivity to orography and resolution[J]. Mon Wea Rev, 123(3): 737-754.
|
Kincer J B, 1916. Daytime and nighttime precipitation and their economic significance[J]. Mon Wea Rev, 44(11): 628-633.
|
Li J M, Jin M J, Li H L, 2019. Exploring spatial influence of remotely sensed PM2.5 concentration using a developed deep convolutional neural network mode[J]. Int J Environ Res Public Health, 16(3): 454.
|
Li X, Zhang K, Gu P R, et al, 2021. Changes in precipitation extremes in the Yangtze River Basin during 1960-2019 and the association with global warming, ENSO, and local effects[J]. Sci Total Environ, 760: 144244.
|
Moghadam F M, 2017. Neural network-based approach for identification of meteorological factors affecting regional sea-level anomalies[J]. J Hydrol Eng, 22(3): 04016058.
|
Naoum S, Tsanis I K, 2004. Orographic precipitation modeling with multiple linear regression[J]. J Hydrol Eng, 9(2): 79-102.
|
Shafer J C, Steenburgh W J, Cox J A W, et al, 2006. Terrain influences on synoptic storm structure and mesoscale precipitation distribution during IPEX IOP3[J]. Mon Wea Rev, 134(2): 478-497.
|
Smith R B, 1979. The influence of mountains on the atmosphere[J]. Adv Geophys, 21: 87-230.
|
Wei S, Zhu Y Q, Huang S L, et al, 2015. Mapping the mean annual precipitation of China using local interpolation techniques[J]. Theor Appl Climatol, 119(1-2): 171-180.
|
Zhang W X, Zhou T J, 2019. Significant increases in extreme precipitation and the associations with global warming over the global land monsoon regions[J]. J Climate, 32(24): 8465-8488.
|
 2023, Vol. 49
2023, Vol. 49 
