2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081;
3. 中国气象局气象探测中心,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. CMA Meteorological Observation Centre, Beijing 100081
我国作为一个地域辽阔的国家,气象灾害频发。如龙卷、冰雹、暴雨等每年都会给我国带来几十亿的经济损失(刘彤和闫天池,2011;郑永光等,2021;周晓敏等,2023),因此灾害预警越来越受到人们的重视。而在这些强天气过程中,风场、温度场和气压场对中小尺度灾害性天气的研究和监测预警具有重要的意义和作用(孟智勇等,2019),尤其是近地面的风场对强对流天气的形成和维持起着至关重要的作用(Mueller et al,2003)。因多普勒天气雷达具有较高的时间和空间分辨率,所以通过多普勒天气雷达进行三维风场反演是获取中小尺度天气系统三维风场结构的一个重要方式。
Lhermitte and Atlas(1961)在假设风场分布均匀或呈线性变化、风场分布不随时间变化的前提条件下,利用径向速度反演平均风速和平均风向,即速度方位显示法(VAD)。Caton(1963)、Browning and Wexler(1968)、周小刚等(2015)、朱立娟等(2012)应用VAD方法,结合地面观测资料对反演的平均风速和风向进行定标。但是利用VAD方法做风场反演时,其准确性较差,并且空间分辨率不高,因此不能很好表示中小尺度天气系统的风场结构(李华宏等,2012;王蕙莹等,2021)。为了提高风场反演的准确性,Armijo(1968)首次提出了利用两部多普勒雷达联立观测进行风场反演,并且阐述反演基本原理和方法。随之而来的是运用双多普勒雷达进行风场反演时出现的一系列数据质量问题,刘黎平等(2003)从回波强度、径向速度等方面分析了出现误差的主要原因,并发现两部雷达进行风场反演时径向速度夹角在40°~140°范围最适合。庄薇等(2006)通过双多普勒雷达反演风场,发现飑线系统存在低层辐合和高层辐散的结构。黄勤等(2020)采用动态地球坐标系下双多普勒雷达风场反演方法,对2017年榆林地区一次强暴雨过程的三维风场进行分析,发现此次暴雨过程中偏南气流由增强到减弱、切变线由东北转向东南方向移动以及雷暴单体内部上升气流发生由增强到减弱的变化。
1990年以来变分方法开始应用于风场反演。Shao et al(2004)利用三维变分方法(3D-Var),对一次梅雨锋中大雨天气过程的风场进行了分析,发现此次强降水主要落在切变线南段,切变线主要盛行偏南气流,随着切变线的移动,降水强度也相应减弱。Qiu et al(2006)运用变分方法及单雷达数据,根据是否存在背景场,对比了二者在梅雨锋中的风场配置。Potvin et al(2012)在进行风场反演时,对垂直风场反演施加涡度方程,达到改进风场反演效果的作用。
在三维风场反演时,降水粒子下落末速度(Wt)的估算一直都是重要问题。雷达观测和反演的速度包含了空气本身的运动速度和Wt,准确估计Wt是正确反演空气垂直运动的关键。前人在进行风场反演之时,通过回波强度(ZH)来估算Wt,采用传统的ZH-Wt法,即认为Wt与ZH存在函数关系,如王艳春等(2016)在对比三维变分方法反演风场的效果时,对于Wt的剔除考虑的就是ZH-Wt关系。随着近几年双偏振雷达的布网,利用双偏振参量估计Wt的研究受到重视。值得注意的是,ZH-Wt关系为一个统计关系,会随降水类型等发生变化出现明显的变化,从而造成对Wt的估计存在较大误差, 因此不同地区存在不同的ZH-Wt关系。
本文利用前人提出的3D-Var方法对2019年春季华南地区的一次飑线过程进行三维风场反演,分析此次天气过程中三维风场的分布,利用雨滴谱数据建立双偏振量与Wt的关系,替代传统的ZH-Wt关系,对比改进前后获取的三维风场差异。
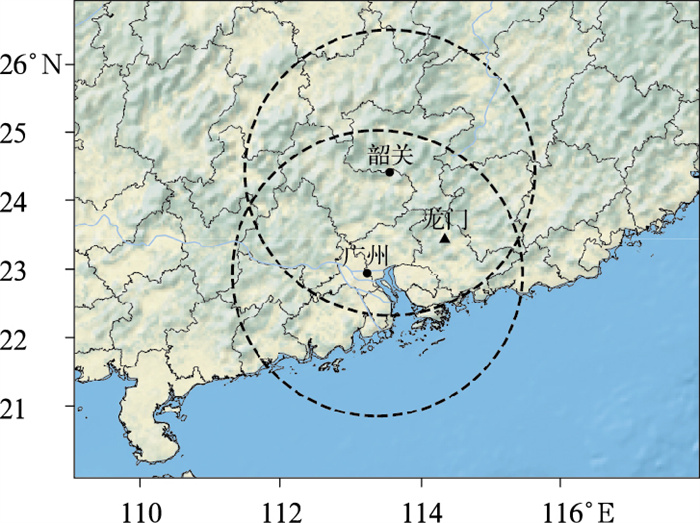
1 设备、资料和方法 1.1 设备和资料本文所使用的雷达资料包含一部新一代S波段双偏振雷达(简称S-POL)和一部天气雷达(简称CINRAD/SA),位置如图 1所示,分别位于广州和韶关。其中广州的S-POL自从2016年5月升级以来,在原雷达基数据之上新增加了一系列双偏振参量,陈超等(2018)、肖柳斯等(2021)和胡明东等(2019)都对其数据做了检验,认为所得观测资料可靠性较高,不存在明显的质量问题,可以直接使用。韶关的CINRAD/SA经过不断改进,资料可信,对于双偏振参量资料应用,以广州双偏振雷达为主。两部天气雷达的距离为163 km,位于风场反演的合适区域。雨滴谱仪位置位于广东龙门,与广州和韶关两部雷达的距离分别是94 km和138 km。以下分别对三种设备及资料做详细介绍。
|
图 1 观测仪器的位置分布 注:虚线距离圈是两部雷达的230km扫描距离,•:双偏振雷达所处的位置,▲:雨滴谱仪所处的位置。 Fig. 1 Location distribution of observation instruments |
(1) 广州S波段双偏振雷达(S-POL)(表 1)。该雷达采用双发双收的发射和接收形式,具有一个水平极化通道和垂直极化通道,通过这两个极化通道,可以得到差分相移率(KDP)、差分相位(ΦDP)和差分反射率(ZDR)等,其扫描仰角共9层,从0.5°到19.5°变化。
|
|
表 1 广州S-POL雷达和韶关CINRAD/SA雷达信息及参数 Table 1 Information and parameters of Guangzhou S-POL Radar and Shaoguan CINRAD/SA Radar |
(2) 韶关天气雷达(CINRAD/SA)(表 1)。该雷达参数与广州S-POL雷达相比,只有一个水平极化通道,但其他参数与广州S-POL的基本一致。
(3) 龙门激光雨滴谱仪(表 2)。激光雨滴谱是通过消光原理来获取降水粒子的设备,其工作原理是通过发射激光,当有降水粒子通过时激光被遮挡,从而电信号将发生变化,进而得到降水粒子在直径和速度通道中的分布。本文采用华创风云集团生产的激光雨滴谱仪,有32个粒子通道和32个速度通道。
|
|
表 2 龙门激光雨滴谱仪信息及参数 Table 2 Longmen's raindrop spectrometer information and parameters of Longmen raindrop spectrometer |
基于雨滴谱数据对于双偏振参量的反演方法主要步骤包括:
(1) 对雨滴谱数据进行质量控制:将降水强度小于0.5 mm·h-1和粒子总数小于50的数据剔除(Tokay et al, 2013; Jaffrain and Berne, 2011; 吴林林, 2014)。为了预防因雨滴飞溅、多个雨滴重叠和昆虫等产生的非正常数据,参照Jaffrain and Berne(2011)的处理方法,将出现下述状况的雨滴粒子也舍去。
| $ \left|v(D)_{\mathrm{M}}-v(D)_{\mathrm{T}}\right|>0.6 v(D)_{\mathrm{T}} \mid $ | (1) |
式中:v(D)M(单位:m·s-1)表示雨滴谱仪实测粒子末速度,v(D)T是由Jaffrain在实验室观测建立的粒子末速度模型。v(D)T具体计算见式(2),D(单位:m)代表对应雨滴的直径。
| $ \begin{gathered} v(D)_{\mathrm{T}}=-0.1021+4.932 D- \\ 0.9551 D^2+0.07934 D^3-0.002362 D^4 \end{gathered} $ | (2) |
(2) 利用质量控制后的雨滴谱数据进行双偏振参量和Wt反演,其公式如下:
| $ N\left(D_i\right)=\sum\limits_{i=1}^{32} \frac{A_{i j}}{V_j T S \Delta D_i} $ | (3) |
式中:雨滴数密度N(Di)表示直径通道Di在单位体积分布的粒子个数,Di(1≤i≤32)和Vj(1≤j≤32)分别表示为雨滴谱仪在各个通道对应的粒子直径和速度,Aij为落到对应的直径通道Di和速度通道Vj的粒子个数。T和S分别表示采样周期(60 s)和采样面积(0.0054 m2)。
| $ Z_{\mathrm{H}, \mathrm{V}}=\frac{\lambda^4}{\pi^5|U|^2} \sum\limits_{i=1}^{32} \sigma_{\mathrm{H}, \mathrm{V}}\left(D_i\right) N\left(D_i\right) \Delta D_i $ | (4) |
| $ U=\frac{m^2-1}{m^2+2} $ | (5) |
式中: ZH, V(单位:dBz)分别是雷达观测到的水平和垂直方向的回波强度;λ(单位:mm)是雷达波长,σH, V(单位:mm2)是发射的水平和垂直偏振波雨滴的后向散射截面;π为圆周率;U为常数,计算见式(5),其中m为水的折射率。
| $ Z_{\mathrm{DR}}=10 \lg \left(\frac{Z_{\mathrm{H}}}{Z_{\mathrm{V}}}\right) $ | (6) |
式中: ZDR(单位:dB)为差分反射率,其计算为在波束体积内水平通道回波强度ZH和垂直通道回波强度ZV之比。
| $ K_{\mathrm{DP}}=\frac{180 \lambda}{\pi} \sum\limits_{i=1}^{32}\left[f_{\mathrm{H}}\left(D_i\right)-f_{\mathrm{V}}\left(D_i\right)\right] N\left(D_i\right) N\left(D_i\right) \Delta D_i $ | (7) |
式中: KDP(单位:°·km-1)为差分相移率,fH、fV表示的是前向散射函数的实部。
| $ W_{\mathrm{t}}=\frac{\sum\limits_{i=1}^{32} \sigma_{\mathrm{H}}\left(D_i\right) V_i N\left(D_i\right) \Delta D_i}{\sum\limits_{i=1}^{32} \sigma_{\mathrm{H}}\left(D_i\right) N\left(D_i\right) \Delta D_i} $ | (8) |
式中: Wt(单位:m·s-1)为降水粒子的下落末速度,σH(单位:mm2)是发射的水平偏振波雨滴的后向散射截面,Vi为雨滴谱仪在各个通道对应的速度。
散射特征参数是由Barder and Yeh(1975)提出的扩展边界法计算得到。因不同波长的雷达对应的散射参数是不相同的,所以同一雨滴谱计算得到的双偏振参量有一定差别。雨滴的轴比关系是由Pruppacher and Beard(1971)经过试验得到的。张扬(2019)已经对雨滴谱反演的双偏振参量的准确性做了对比分析,其中ZH、ZDR、KDP的系统偏差分别为2.94 dBz、-0.01 dB、0.10°·km-1。虽然有一点偏差,但是考虑雷达和雨滴谱仪在观测时都存在着一些偏差,认为该结果能在一定程度上说明根据雨滴谱计算的双偏振参量与实际观测基本一致。
1.2.2 风场反演方法简介风场反演方法参考是Potvin et al(2012)提出的三维变分反演风场方法,具体步骤为:(1)采用Helmus and Collis(2016)发布的Py-ART/Region-base方案对雷达径向速度进行速度模糊判断,若存在速度模糊则进行退模糊纠正; (2)极坐标下的雷达径向速度数据转换到笛卡尔直角坐标系中,空间分辨率为1 km;(3)对插值后的数据运用3D-Var进行反演。其中3D-Var反演风场的主要步骤:记直角坐标系中的每个点存在三个方向的风分量(u,v,w),求解目标泛函数J取极小值时的u,v,w,即为该点的风场。
| $ J_{(u, v, w)}=J_0+J_{\mathrm{M}}+J_{\mathrm{V}}+J_{\mathrm{S}} $ | (9) |
式中: 各项分别为:观测约束项(JO)、质量守恒约束项(JM)、垂直涡度方程约束项(JV)和光滑约束项(JS)。
影响Wt估算的主要因子是观测约束项(JO),因此对其项进行单独说明。
| $ J_{\mathrm{O}}=\sum\limits_{i, j, k} W_{\mathrm{O} 1}\left(v_{r 1}^{\mathrm{obs}}-v_{r 1}\right)^2+\sum\limits_{i, j, k} W_{\mathrm{O} 2}\left(v_{\mathrm{r} 2}^{\mathrm{obs}}-v_{\mathrm{r} 2}\right)^2 $ | (10) |
式中: vr1obs和vr2obs分别代表的是第一部雷达和第二部雷达观测的速度,WO1和WO2代表对应两部雷达权重。而vr计算见下式:
| $ v_{\mathrm{r}}=x u+y v+z\left(w-\left|W_{\mathrm{t}}\right|\right) $ | (11) |
式中: x, y, z为直角坐标系中每个点距离雷达站点的水平距离和垂直距离。
1.2.3 降水粒子下落末速度的估算原方法中对于Wt估算分为两部分,一部分为固态粒子下落末速度的估算,另一部分为液态降水粒子下落末速度的估算,固态降水粒子下落末速度的估算方法是利用Shapiro et al(1995)得到的经验公式[式(12)],而对于液态降水粒子下落末速度的估算是利用Foote and Du Toit(1969)统计得到的经验公式[式(13)],现在对于液态降水粒子下落末速度的估算由雨滴谱反演拟合得到,见式(14)。对于液态粒子和固态粒子的区分方法为:在0℃层以下回波强度大于60 dBz为固态粒子,小于60 dBz为液态粒子,0℃层以上全为固态粒子。
原来的固态降水粒子下落末速度估算:
| $ W_{\mathrm{tS}}=3.088 \times Z_{\mathrm{H}}^{0.0957} \times\left(\rho_0 / \rho\right)^{0.4} $ | (12) |
原来的液态降水粒子下落末速度估算:
| $ W_{\mathrm{tL}}=2.6 \times Z_{\mathrm{H}}^{0.107} \times\left(\rho_0 / \rho\right)^{0.4} $ | (13) |
现在的液态降水粒子下落末速度估算:
| $ W_{\mathrm{t}}=\left(1.15 \times Z_{\mathrm{DR}}+0.44\right) \times\left(\rho_0 / \rho\right)^{0.4} $ | (14) |
式中:ρ0/ρ0.4为Foote and Du Toit(1969)订正Wt随高度的变化。其中ρ0为地面标准空气密度, ρ0=1.0 kg·m-3,而ρ=1.0e-ZH/H,ZH(单位:dBz)为回波强度,H(单位:m)为离地高度。
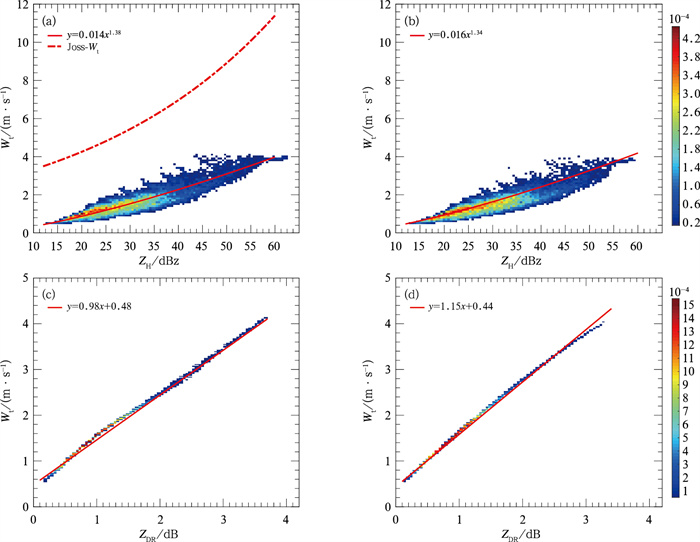
2 基于激光雨滴谱仪反演的双偏振参量与降水粒子下落末速度关系基于激光雨滴谱仪反演Wt的准确性,将雨滴谱反演得到的Wt当作真实值。为了得到双偏振参量与Wt的关系,选择龙门2019年和2020年4—10月的雨滴谱仪观测数据,对其进行质量控制,经过质量控制后,样本量由原来的508899个变成了26733个,利用质量控制后的雨滴谱数据进行S和X波段雷达的双偏振参量和Wt反演,建立二者的关系,如图 2。
|
图 2 雨滴谱模拟的双偏振参量(a, b)ZH, (c, d)ZDR和降水粒子下落末速度(Wt)的二维概率密度分布(a,c)X波段,(b,d)S波段 注:填色为各个区间的双偏振参量个数占总个数的千分比,红色实线为拟合的双偏振参量(ZH, ZDR)与Wt的关系,红色虚线为原方法中ZH与Wt关系。 Fig. 2 Two dimensional probability density distribution map of dual-polarization quantity (a, b) ZH, (c, d) ZDR and final falling velocity (Wt) of precipitation particles simulated by raindrop spectrum (a, c) X-band, (b, d) S-band |
图 2为雨滴谱模拟的双偏振参量和Wt的二维概率密度分布,表 3为拟合函数值与实际值的误差,因KDP的拟合效果过差,因此未做展示。从图 2和表 3可见:通过雨滴谱反演的Wt集中在0.4~3.6 m· s-1,反演的ZH、ZDR分别集中在17~35 dBz、0.4~1.4 dB。对于拟合的ZH、ZDR与Wt的函数形式为幂函数和一次函数的形式,随着Wt增大,ZH和ZDR也增大。原因是ZH和ZDR越大,代表其降水粒子平均直径越大,故对应Wt越大。对比ZDR-Wt关系与ZH-Wt关系,ZDR-Wt关系更好,原因是:Wt主要与粒子大小有关,与绝对的数密度无关,而ZDR也有这个特性,因此二者的拟合效果较好。且拟合的ZH-Wt函数关系,与Ulbrich and Chilson(1994)利用地面雨滴谱仪数据得到的ZH-Wt关系近似。对比Joss(1970)统计的ZH-Wt关系,其系数相较于现在ZH-Wt关系的系数偏大,原因是:Joss(1970)统计时所利用的数据为强天气过程数据,其粒子直径较大,因此系数也偏大。为了确定通过ZH与ZDR拟合Wt谁更准确,表 3统计了拟合函数值与实际值的误差。由表可见,通过双偏振参量ZDR估算Wt的效果最好。
|
|
表 3 拟合函数的各个数学量统计 Table 3 Statistics of various mathematical quantities of the fitting function |
为了分析此次飑线过程的风场结构以及对比通过不同双偏振参量估算的Wt在风场反演结果上的差异,选择华南地区2019年4月20日的一次飑线过程进行风场反演试验,此次飑线过程在20日09—15时(北京时,下同),共持续6 h。在风场反演试验中利用到第1节统计出的S波段ZDR估算Wt的公式,将其应用在0℃以下液态降水粒子区间内。
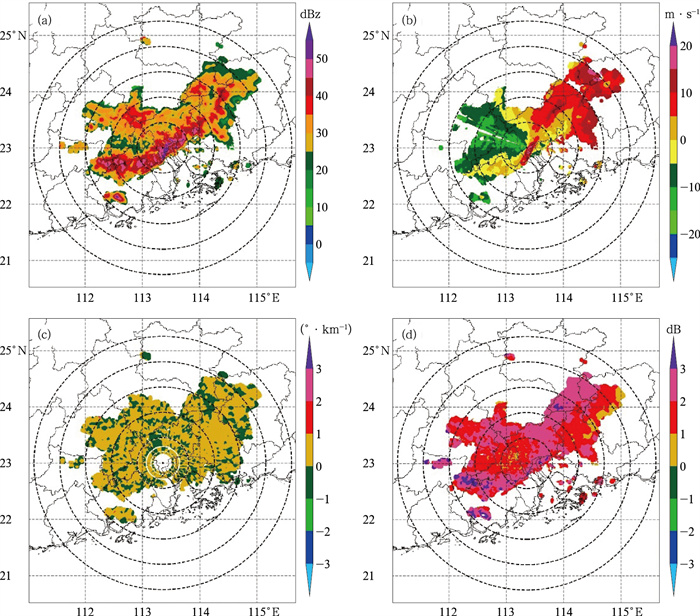
3.1 天气状况分析利用广州S-POL当天12时的观测数据,做了1 km高度上双偏振参量的分布。如图 3可见, 反演区域(150 km×150 km)没有明显的数据质量问题。从图 3a雷达回波可见,图中出现明显的代表飑线的弓状回波结构,弓状回波后部存在着层状云系结构,回波的最强值达到了57 dBz。由图 3b可见,此次飑线过程在低层主要是西北风,最大风速可达±10 m· s-1。图 3c和3d是双偏振参量(KDP,ZDR)的分布,KDP和ZDR基本上都是正值,说明这次飑线过程主要为液态降水过程,在低层不用考虑固态降水粒子。
|
图 3 2019年4月20日12时广州雷达1 km高度上(a)ZH,(b)V,(c)KDP,(d)ZDR的分布 注:每一个黑色虚线圆圈为50 km的观测范围。 Fig. 3 Distributions of (a) ZH, (b) V, (c) KDP, (d) ZDR at 1 km height of Guangzhou Radar at 12:00 BT 20 April 2019 |
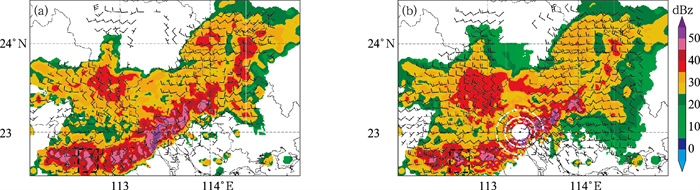
为了分析此次强飑线过程的风场结构,采用了广州S-POL和韶关CINRAD/SA在此次飑线过程中的观测数据。运用3D-Var反演12时的风场结构,其中对于Wt的估算利用的是前文统计的ZDR反演Wt公式,反演的空间范围是以广州S-POL位置为中心,周围150 km、高度20 km的区域,图 4为反演的1 km和4 km高度上水平风场。
|
图 4 2019年4月20日12时三维变分方法反演的(a)1 km和(b)4 km高度水平风场(风羽)和回波强度(填色) 注:矩形虚线方框为图 5选择的强回波区域。 Fig. 4 The (a) 1 km and (b) 4 km height horizontal wind field (barb) and echo intensity (colored) retrieved by the three-dimensional variational method at 12:00 BT 20 April 2019 |
由图 4可见,因雷达仰角的配置情况其在靠近雷达位置处上空会出现空值区域。从水平风场可见:此次飑线从西北方向发展,该过程的主要风系结构为飑线前部的弓状回波区域,为西南风,风速一般为2~4 m·s-1。在飑线后部的层状云系内主要为西北风,其风速较弓状回波区域内的风速偏大,为4~6 m·s-1。对比图 4a和4b,可见风速随着高度在增加,是因为随着高度增加,风所受阻力减少。此次飑线系统的气流结构呈现准二维特征,与Chong et al(1987)和Wang et al(1990)揭示的飑线结构基本类似。此次飑线过程在水平风场存在一个辐合区和一个辐散区,其中辐散区域是飑线后部层状云系中还未完全消散的强对流单体,范围约为50 km×50 km,风场的配置为一个未闭合的反气旋性结构,使得之前形成的强对流单体开始消散,转换为层状云系。辐合区域是在飑线前部的弓状回波区域内,风场的配置为:后部层状云系主要是西北风, 弓状回波区域内是西南风,其风速比层状云系的西北风要小,使其将后部吹来的西南风切断,从而在飑线前部形成水汽的堆积,造成辐合。从风场的结构来分析回波结构,层状云系中较均匀的风速是回波形成的主要原因。飑线前部风场的辐合造成前部的强回波区域,而飑线后层状云区域内存在辐散区域,也使以前存在的强对流单体开始消散,但是还没有完全消散,因此通过两部雷达反演的水平风场具有合理性。
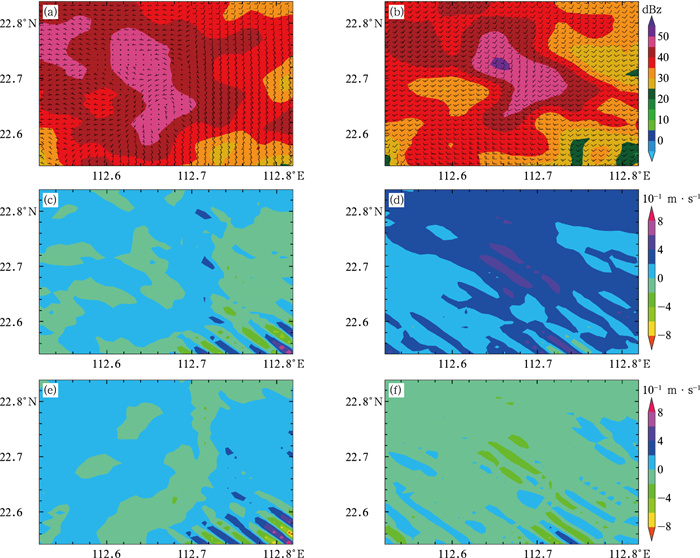
为了探究飑线前部弓状回波区域内风场的结构和现在方法反演的水平风场与原方法反演的水平风场差异,分别利用现在的方法和原来的方法对弓状回波区域进行风场反演,并两者反演结果相减。图 5是反演的弓状回波区域内1 km和4 km上水平风场Δu、Δv的分布。由图 5可见,强对流单体中心的回波强度随着高度的增加而变强,在4 km的高度上达到最强(54 dBz),是因为对流单体主要为上升气流,水汽上升凝结,在中部达到最大,但是单体的范围随着高度的增加在减少,周围较弱的上升气流发展达不到其高度,因此范围相对低层较小。分析1 km和4 km强对流单体的风场,在1 km上强对流单体的右侧为偏南风,单体左侧北部是西风,风速较右侧的小。单体南侧的风为西南风,有一个不明显的气旋性结构,因此在1 km高度上强对流单体辐合明显。在4 km高度上的风场结构相较于近地面简单,4 km上的风场配置主要是一个闭合的气旋结构,从而形成辐合结构。将现在(ZDR方法)与原来的方法相减,得到Δu、Δv的分布,整体来看水平风场变化集中在±1 m·s-1的范围,Δu是正值,即现有方法反演的u比原来方法反演的偏大,Δv大部分是负值,即现在方法反演的v较原方法反演的偏小。对比不同高度上Δu、Δv,其值在4 km高度上比1 km高度上大,其原因是ZDR在4 km高度上较1 km高度上的大。
|
图 5 2019年4月20日12时三维变分方法反演的(a,c,e)1 km和(b,d,f)4 km高度上(a, b)回波强度(填色)叠加水平风速(风羽), (c, d)Δu, (e, f)Δv的分布 注:Δu,Δv为现在方法反演的风速减去原方法反演的风速。 Fig. 5 (a, b) Echo intensity (colored) superimposed by horizantal wind speed (barb), (c, d) Δu, and (e, f) Δv at (a, c, e) 1 km and (b, d, f) 4 km heights retrieved by the three-dimensional variational method at 12:00 BT 20 April 2019 |
为了探究此次飑线过程的垂直风场分布和利用现在方法反演出的垂直风场与原方法之差,对此次飑线过程的风场反演结果在22.74° N和112.77° E方向做剖面,且与分析水平风场一致将现在方法反演的w和原方法反演的w进行相减,从而得到此次飑线过程的垂直风场和Δw分布(图 6)。由图 6可见,此次飑线过程发展高度最高达到10 km。其原因为: 从图 6a来看在112.7°E左侧是西风,右侧是东风,因此在低层形成辐合,从而出现较强的上升气流;从图 6b来看风场结构是随高度增加的逆时针环流,在高层辐散、低层辐合,在23.0°N出现明显的上升气流。分析其垂直风场的可行性发现,在强回波区域内有低层辐合的风场,输入暖湿气流,形成强回波区域,而高层区域呈辐散气流,使回波减弱,因此风场对比强回波区域分布具有合理性。对比Δu、Δv的变化,Δw的变化小得多,其主要集中在±0.15 m·s-1范围,沿112.77°E方向上的变化较沿着22.74°N方向上变化程度大,强回波区域内Δw变化较弱回波区域的变化更大。

|
图 6 2019年4月20日12时三维变分方法反演的(a, c)沿22.74°N方向, (b, d)沿112.77°E方向的(a, b)回波强度(填色)叠加垂直风速(风羽), (c, d)Δw的垂直剖面 注:Δw为现在方法反演的垂直风速减去原方法反演的垂直风速。 Fig. 6 (a, b) Echo intensity (colored) superimposed by vertical wind speed (barb) and (c, d) vertical profile of Δw along (a, c) 22.74°N and (b, d) 112.77°E retrieved by the three dimensional variational method at 12:00 BT 20 April 2019 |
为了分析此次飑线过程w和Δw的整体分布,利用两种方法反演出的垂直风场结果,统计了现在方法反演的w在各个区间上分布,对比分析两种方法反演的w的差异(图 7和表 4)。
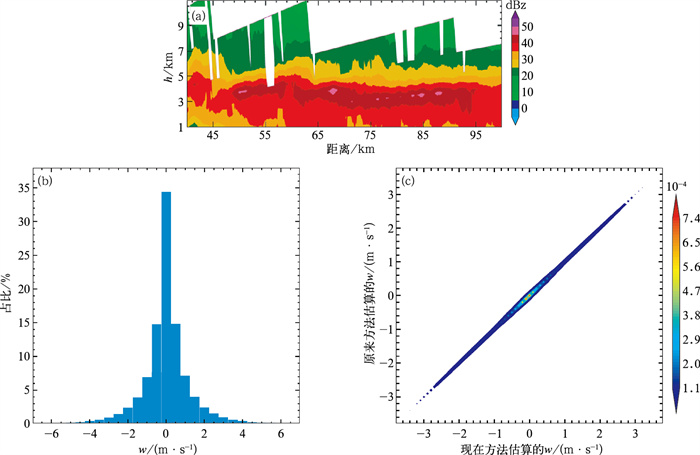
|
图 7 (a) 广州雷达回波强度的RHI图, (b)现在方法计算的w在各个区间分布, (c)现在方法估算的垂直速度和原方法估算的垂直速度的二维概率密度分布 注:图c中填色为各个区间的垂直速度占总数的比例。 Fig. 7 (a) RHI diagram of Guangzhou Radar echo intensity, (b) distribution of w in each interval calculated by the current method, (c) two-dimensional probability density distribution diagram of vertical velocity estimated by the current method and the vertical velocity estimated by the original method |
|
|
表 4 w,Δw在不同高度上的统计量 Table 4 The statistics of w and Δw at different heights |
由图 7可见, 此次飑线过程0°层高度在4.5 km。w的主要区间在±4 m·s-1,占比达到90.8%,在±0.25 m·s-1这个区间所占的比例最大,达到了34.4%。研究发现w满足了高斯正态分布,在正负速度两边呈现一个均匀的对称分布,原因是反演风场时,质量连续项的存在使得整体反演的上升运动和下沉运动都相对应地存在。对比现在方法得出的w与原方法反演的w,其在±1 m·s-1这个区间差异偏大。对比Wt与Δw,两者相差很大,因为w中对Wt的剔除并不是简单地将其减掉,还要考虑计算后的其他项对w的影响,不同项的权重也将会影响w最终结果。由表 4对不同高度w分布的第5%和第95%分位数等统计可见,在1 km高度上的w要比2~4 km高度上的w要小,原因之一是在接近地面时,风场易受到地形、地面粗糙度的影响,从而使风场相对于对流层的小;另一个原因是在进行垂直速度反演时,假设在地面边界上存在w=0的
边界条件。分析不同高度上Δw的变化,见表 4,并对比吴瑞娇等(2019)统计的江淮地区飑线过程的垂直风场结果,发现反演的垂直速度整体上较偏小。其主要有两个原因:一是因为分辨率插值时是插值成1 km×1 km×1 km的数据,插值对应有平滑作用,最大值变小,使最大下沉和上升速度变小;二是因为反演时从地面开始向上积分,但实际情况是随着离雷达站的位置越远,其观测到的最低高度越高,因此误差越大,会出现速度被估算过小的情况。
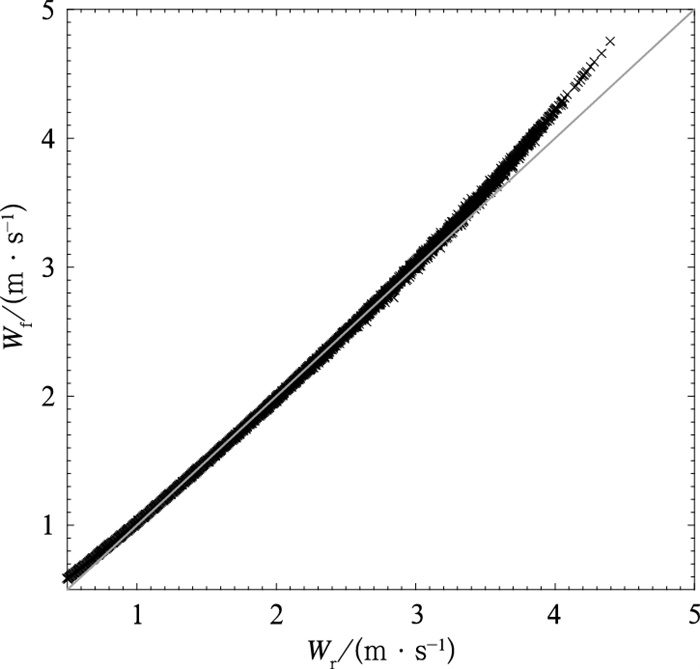
4 讨论为了分析S-POL对于ZDR的不同测量精度对于Wt的不同影响和利用ZDR估算Wt和真实Wt的差异,利用前文ZDR估算Wt的公式计算的降水粒子下落末速度(Wr)和实际的降水粒子下落末速度(Wf),做了Wr和Wf的散点图。从图 8可见:Wt在3.8 m·s-1以下时,Wr和Wf二者基本上一致,但在3.8 m·s-1以上时,Wr比Wf偏大。统计不同ZDR精度对应的Δw发现:ΔZDR为0.001 dB和0.01 dB时,Δw分别是在0.000518 m·s-1、0.0017 m·s-1,而随着ΔZDR增加到0.1 dB和1 dB时,Δw分别达到了0.0525 m·s-1、0.4726 m·s-1。而双偏振雷达ZDR的精度误差在±0.1 dB范围,对于Δw误差已经很小,因此精度是满足的。
|
图 8 利用ZDR拟合的粒子下落末速度(Wr)和实际的粒子下落末速度(Wf)对比散点图 注:实线代表二者相等。 Fig. 8 The scatter plot of the comparison between the particle final falling velocity fitted by ZDR (Wr) and the actual particle final falling velocity (Wf) |
为了探究Wt对垂直速度反演的影响,本文利用广东雨滴谱数据,计算得到了Wt与双偏振参量的关系,将其应用于广州和韶关的S波段天气雷达组成的双多普勒雷达的风场反演中,对2019年4月华南地区一次飑线过程的风场进行了反演,分析了Wt的估算对风场反演的影响,讨论了用双偏振参量估算Wt的效果,初步得到以下结论:
(1) 利用双偏振参量估算Wt,对于ZH和ZDR估算,函数形式分别是幂函数和一次函数。S和X波段二者都是利用ZDR估算的Wt比ZH估算Wt的效果更好,原因是Wt主要与粒子大小有关,与绝对的数密度无关,而ZDR也有这个特性,因此利用ZDR估算Wt的效果更好。
(2) 在此次飑线过程的三维风场反演中,对比用原方法估算的Wt和用现有方法估算的Wt得到的反演结果,水平风场的变化集中在±1 m·s-1,Δu主要是正值,而Δv绝大部分是负值,在4 km上变化较1 km上的变化要大得多,在1 km高度上强回波区的变化较弱回波区的变化大,而在4 km高度上结果却是相反的。在垂直风场上变化主要集中在±0.15 m·s-1,相较于水平风场来说其变化小很多,是因为w主要集中在±2 m·s-1的范围,相较于u、v来说本身上要小,因此其变化量较小。Δw低层的变化较高层的变化同Δu、Δv的结果是一致的,低层的变化比高层的小得多,原因之一是接近地面时,风场易受地形、地面粗糙度的影响,从而使风场相对于对流层的风场小;另外一个原因是在进行垂直速度反演时,假设了在地面边界上w=0的边界条件。
(3) 此次飑线过程主要从西北向东南发展,由回波图(图略)可以看到在广州地区存在一个明显的弓状回波区域,其后存在层状云系。飑线后部层状云系中的主要风系以西风和西北风为主,飑线前部是西南风,因此使后面层状云的西风和西北风被切断,从而形成飑线前部的辐合区域。垂直风场的变化是强回波区域低层辐合和高层辐散。结合风场与回波的配置,风场结构满足了回波强度的分布,因此利用双偏振参量估算的降水粒子下落末速度应用在垂直速度上具有合理性。
应当说明的是,利用雨滴谱仪反演降水粒子下落末速度仅仅是对液态降水粒子,因此其关系只能够应用于0℃层以下的液态水区间,双偏振参量估算冰晶粒子下落末速度的方法仍然需要探究,风场反演中不仅要考虑垂直速度的粒子下落末速度,还要考虑下边界上w=0的条件,使研究更贴近实际情况。
陈超, 胡志群, 胡胜, 等, 2018. 广州S波段双偏振雷达数据质量初步分析[J]. 热带气象学报, 34(1): 59-67. Chen C, Hu Z Q, Hu S, et al, 2018. Preliminary analysis of data quality of Guangzhou S-band polarimetric weather radar[J]. J Trop Meteor, 34(1): 59-67 (in Chinese). DOI:10.16032/j.issn.1004-4965.2018.01.006
|
胡东明, 张羽, 傅佩玲, 等, 2019. 广州S波段双线偏振天气雷达双通道一致性测试及分析[J]. 气象科技, 47(3): 373-379. Hu D M, Zhang Y, Fu P L, et al, 2019. Dual-channel consistency analysis of S-band dual-polarimetric radar[J]. Meteor Sci Technol, 47(3): 373-379 (in Chinese). DOI:10.19517/j.1671-6345.20180259
|
黄勤, 黄鑫, 李亚丽, 2020. 陕西榆林地区一次暴雨过程三维风场结构演变特征[J]. 干旱气象, 38(5): 747-754. Huang Q, Huang X, Li Y L, 2020. Evolution characteristics of three-dimensional structure of wind field during a heavy rainfall in Yulin of Shaanxi[J]. J Arid Meteor, 38(5): 747-754 (in Chinese).
|
李华宏, 曹杰, 杞明辉, 等, 2012. 雷达风廓线反演在云南强降水预报中的应用[J]. 高原气象, 31(6): 1739-1745. Li H H, Cao J, Qi M H, et al, 2012. Application of vertical wind profile from Dopplerradar to the forecast of heavy precipitation in Yunnan[J]. PlateauMeteor, 31(6): 1739-1745 (in Chinese).
|
刘黎平, 张沛源, 梁海河, 等, 2003. 双多普勒雷达风场反演误差和资料的质量控制[J]. 应用气象学报, 14(1): 17-29. Liu L P, Zhang P Y, Liang H H, et al, 2003. Error estimation in wind fields derived from dual-Doppler radar and data quality control[J]. J Appl Meteor Sci, 14(1): 17-29 (in Chinese). DOI:10.3969/j.issn.1001-7313.2003.01.003
|
刘彤, 闫天池, 2011. 我国的主要气象灾害及其经济损失[J]. 自然灾害学报, 20(2): 90-95. Liu T, Yan T C, 2011. Main meteorological disasters in China and their economic losses[J]. J Nat Dis, 20(2): 90-95 (in Chinese). DOI:10.13577/j.jnd.2011.0214
|
孟智勇, 张福青, 罗德海, 等, 2019. 新中国成立70年来的中国大气科学研究: 天气篇[J]. 中国科学: 地球科学, 49(12): 1875-1918. Meng Z Y, Zhang F Q, Luo D Q, et al, 2019. Review of Chinese atmospheric science research over the past 70 years: synoptic meteorology[J]. Sci China Earth Sci, 49(12): 1875-1918 (in Chinese).
|
王蕙莹, 周自江, 廖捷, 等, 2021. 面向CRA的中国风廓线雷达小时产品质量控制算法与评估[J]. 气象, 47(5): 573-585. Wang H Y, Zhou Z J, Liao J, et al, 2021. A quality control algorithm and evaluation of hourly data of China's wind profilers for CRA[J]. Meteor Mon, 47(5): 573-585 (in Chinese).
|
王艳春, 王红艳, 刘黎平, 2016. 三维变分方法反演风场的效果检验[J]. 高原气象, 35(4): 1087-1101. Wang Y C, Wang H Y, Liu L P, 2016. Performance evaluation of three-dimensional variation assimilation retrieval of wind field[J]. Plateau Meteor, 35(4): 1087-1101 (in Chinese).
|
吴林林, 2014. 利用雨滴谱对移动双偏振雷达进行质量控制及降水估测[D]. 南京: 南京信息工程大学. Wu L L, 2014. Application study of mobile C-band dual-polarization radar quality control and QPE using raindrop size distribution[D]. Nanjing: Nanjing University of Information Science & Technology(in Chinese).
|
吴瑞姣, 陶玮, 周昆, 等, 2019. 江淮灾害性大风飑线的特征分析[J]. 气象, 45(2): 155-165. Wu R J, Tao W, Zhou K, et al, 2019. General features of squall lines with disastrous gale in the Yangtze-Huaihe Area[J]. Meteor Mon, 45(2): 155-165 (in Chinese).
|
肖柳斯, 胡东明, 陈生, 等, 2021. X波段双偏振相控阵雷达的衰减订正算法研究[J]. 气象, 47(6): 703-716. Xiao L S, Hu D M, Chen S, et al, 2021. Study on attenuation correction algorithm of X-band dual-polarization phased array radar[J]. Meteor Mon, 47(6): 703-716 (in Chinese).
|
张扬, 2019. 业务双偏振雷达网与自动站联合定量降水估测方法及效果分析研究[D]. 北京: 中国气象科学研究院. Zhang Y, 2019. Study on the quantitative precipitation estimation algorithm utilized with the operational dual-polarization radar network and automatic stations and its effect analysis[D]. Beijing: Chinese Academy of Meteorological Sciences(in Chinese).
|
郑永光, 刘菲凡, 张恒进, 2021. 中国龙卷研究进展[J]. 气象, 47(11): 1319-1335. Zheng Y G, Liu F F, Zhang H J, 2021. Advances in tornado research in China[J]. Meteor Mon, 47(11): 1319-1335 (in Chinese). DOI:10.7519/j.issn.1000-0526.2021.11.002
|
周小刚, 费海燕, 王秀明, 2015. 基于多普勒雷达VAD算法的业务应用讨论[J]. 气象, 41(1): 113-120. Zhou X G, Fei H Y, Wang X M, 2015. Operational application discussion based on Doppler radar VAD algorithm[J]. Meteor Mon, 41(1): 113-120 (in Chinese).
|
周晓敏, 田付友, 郑永光, 等, 2023. 中国短时强降雨对暴雨的贡献特征[J]. 气象, 49(3): 267-278. Zhou X M, Tian F Y, Zheng Y G, et al, 2023. Contribution of short-duration heavy rainfall to rainstorm in China[J]. Meteor Mon, 49(3): 267-278 (in Chinese).
|
朱立娟, 龚建东, 李泽椿, 等, 2012. 利用地面观测资料参考标定雷达VAD资料气压高度方法研究[J]. 气象, 38(2): 250-256. Zhu L J, Gong J D, Li Z C, et al, 2012. Preliminary study on pressure estimation of radar VAD data based on surface observations[J]. Meteor Mon, 38(2): 250-256 (in Chinese).
|
庄薇, 刘黎平, 王楠, 2006. 新疆地区一次对流性降水的三维中尺度风场研究[J]. 应用气象学报, 17(4): 444-451. Zhuang W, Liu L P, Wang N, 2006. Study on three-dimensional wind fields of mesoscale convective systems in Xinjiang[J]. J Appl Meteor Sci, 17(4): 444-451 (in Chinese).
|
Armijo L, 1969. A theory for the determination of wind and precipitation velocities with Doppler radars[J]. J Atmos, 26(3): 570-573.
|
Barber P, Yeh C, 1975. Scattering of electromagnetic waves by arbitrarily shaped dielectric bodies[J]. Appl Opt, 14(12): 2864-2872.
|
Browning K A, Wexler R, 1968. The determination of kinematic properties of awind field using Doppler radar[J]. J Appl Meteor, 7(1): 105-113.
|
Canton P, 1963. The measurement of wind and convergence by Doppler radar[C]//Proceedings of the 10th Weather Radar Conference. Washington: Amer Meteor Soc: 965.
|
Chong M, Amayenc P, Scialom G, et al, 1987. A tropical squall line observed during the COPT 81 experiment in West Africa. Part 1: kinematic structure inferred from dual-Doppler radar data[J]. Mon Weather Rev, 115(3): 670-694.
|
Foote G B, Du Toit P S, 1969. Terminal velocity of raindrops aloft[J]. J Appl Meteor Climatol, 8(2): 249-253.
|
Helmus J J, Collis S M, 2016. The Python ARM Radar Toolkit (Py-ART), a library for working with weather radar data in the Python programming language[J]. J Open Research Software, 4: e25.
|
Jaffrain J, Berne A, 2011. Experimental quantification of the sampling uncertainty associated with measurements from PARSIVEL disdrometers[J]. J Hydrometeorol, 12(3): 352-370.
|
Joss J, 1970. Terminal velocity of raindrops aloft[J]. J Appl Meteor, 8(2): 249-253.
|
Lhermitte R M, Atlas D, 1961. Precipitation motion by pulse Doppler[C]//Proceedings of the 9th Weather Radar Conference. Kansas City.
|
Meng Z Y, Zhang F Q, Luo D Q, et al, 2019. Review of Chinese atmospheric science research over the past 70 years: synoptic meteorology[J]. Sci China Earth Sci, 62(12): 1946-1991.
|
Mueller C, Saxen T, Roberts R, et al, 2003. NCAR auto-nowcast system[J]. Wea Forecast, 18(4): 545-561.
|
Potvin C K, Shapiro A, Xue M, 2012. Impact of a vertical vorticity constraint in variational dual-Doppler wind analysis: tests with real and simulated supercell data[J]. J Atmos Ocean Technol, 29(1): 32-49.
|
Pruppacher H R, Beard K V, 1971. A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air[J]. Quart J Roy Meteor Soc, 97(411): 133-134.
|
Qiu C J, Shao A M, Liu S, et al, 2006. A two-step variational method for three-dimensional wind retrieval from single Doppler radar[J]. Meteor Atmos Phys, 91(1/2/3/4): 1-8.
|
Shao A M, Qiu C J, Li L P, 2004. Kinematic structure of a heavy rain event from dual-Doppler radar observations[J]. Adv Atmos Sci, 21(4): 609-616.
|
Shapiro A, Ellis S, Shaw J, 1995. Single-Doppler velocity retrievals with phoenix Ⅱ data: clear air and microburst wind retrievals in the planetary boundary layer[J]. J Atmos Sci, 52(9): 1265-1287.
|
Tokay A, Petersen W A, Gatlin P, et al, 2013. Comparison of raindrop size distribution measurements by collocated disdrometers[J]. J Atmos Ocean Technol, 30(8): 1672-1690.
|
Ulbrich C W, Chilson P B, 1994. Effects of variations in precipitation size distribution and fallspeed law parameters on relations between mean Doppler fallspeed and reflectivity factor[J]. J Atmos Ocean Technol, 11(6): 1656-1663.
|
Wang T C C, Lin Y J, Shen H, et al, 1990. Characteristics of a subtropical squall line determined from TAMEX dual-Doppler data. Part Ⅰ: kinematic structure[J]. J Atmos Sci, 47(20): 2357-2381.
|
 2023, Vol. 49
2023, Vol. 49 
