引言

内蒙古地区是影响我国东部天气气候系统的上游地区之一，该地区气象观测资料对本地和下游天气预报、气候预测都非常重要。然而，内蒙古地区幅员辽阔、东西跨度大，地形较为复杂，综合气象观测站点稀疏，建设和维护难度较大。其探空站平均站网间距为354.4 km(12个探空站)，地面站平均站网间距为46.1 km(119个国家站、589个遴选区域站)，距世界气象组织(World Meteorological Organization, WMO)观测系统能力分析与评审(observing systems capability analysis and review, OSCAR)对观测系统不同领域的指标要求还存在较大的差距。而站网布局设计首先要建立在对现有观测进行评估的基础上。本文主要从数值模式的角度探讨内蒙古区域数值预报对现有探空和地面观测资料的敏感性。

观测与预报互动试验目前主要包括观测系统试验(Observing System Experiments, OSEs)、观测系统模拟试验(Observing System Simulation Experiments, OSSEs)、基于伴随的预报对观测敏感性(Forecast Sensitivity to Observations, FSO)试验。OSEs主要采用加入/剔除某一类、不同时空分辨率观测资料的方法来评估现有观测系统(王平等，2017)；OSSEs采用参考大气构造模拟观测资料来确定观测敏感区，客观评估新增观测(王瑞文等，2023)；FSO试验则提供了一种有效方法去定量确定对某一天气过程有着重要影响的初始扰动或物理因子。其中OSEs与OSSEs要定位到某一类或某一个地区观测需要开展非常大量的对比试验和诊断评估计算；而FSO试验通过一次模拟试验就可以提供关于所有同化观测对选定的短期预报误差度量影响的更详细信息。

FSO方法描述了一种基于伴随的过程来评估数值天气预报中观测对短期预报误差的影响。该方法的基础理论最初由Baker and Daley(2000)提出，其使用一个简化的资料同化系统的伴随来直接确定预报对观测和背景场的敏感性。随后，Doerenbecher and Bergot(2001)基于该理论针对锋面和大西洋风暴路径试验(Fronts and Atlantic Storm-Track EXperiment, FASTEX)一个目标个例的详细结果，评估了特定敏感区下投式探空仪对风暴预报的影响。Fourrié et al(2002)则针对FASTEX期间的十个个例，讨论了同化泰罗斯业务垂直探测器(television infrared observation satellite operational vertical sounder, TOVS)观测的敏感性。Langland and Baker(2004)基于美国海军全球大气预报系统(Navy Operational Global Atmospheric Prediction System, NOGAPS)/美国海军研究实验室(Naval Research Laboratory, NRL)大气变分资料同化系统(Atmospheric Variational Data Assimilation System, NAVDAS)及其伴随版本，选择24 h和30 h全球干总能量(Zou et al, 1997)预报误差二阶函数的差值作为代价函数，评估了2002年6月和12月期间数值天气预报中观测对短期预报误差的影响，并论证了观测对短期天气预报误差的大部分(75%)影响可以用“干”观测(气温、风和高度)和预报模式中的准线性过程来解释。次年，Langland(2005)又针对性地讨论了2003年冬季北大西洋地区常规观测与卫星观测对短期预报的作用。随后，为了进一步提升精度，Errico(2007)重新推导了Langland and Baker(2004)伴随理论框架中预报误差切线性近似的表达式，明确地给出了其度量的三阶特征，认为其相较于一阶近似能得到更为可靠的结果。Gelaro et al(2007)则基于美国国家航空和宇宙航行局(National Aeronautics and Space Administration, NASA)戈达德地球观测系统(Goddard Earth Observing System, GEOS)大气资料同化系统的伴随版本，研究了观测影响的基于伴随的各阶近似。同时，Trémolet(2007)给出了高阶近似能产生相对准确估计的原因，进一步验证了更高阶的近似导致相对准确的估计。Zhu and Gelaro(2008)讨论了格点统计插值(gridpoint statistical interpolation, GSI)分析方案的切线性和伴随版本的发展，并开展了观测敏感性试验，在观测敏感性的大小、观测类型和分布以及周边观测密度等方面得到了与Baker and Daley(2000)一致的结论。Gelaro and Zhu(2009)基于NASA GEOS-5大气资料同化系统的正向和伴随版本，将基于伴随的FSO试验的观测影响估计与标准OSEs试验的结果进行了比较。结果表明，尽管两种方法在观测影响的测量上存在重要的潜在差异，但在主要观测系统对24 h预报误差干总能量减小的总体影响上提供了一致的估计。Cardinali(2009)首次在一个12 h 4D-Var同化系统中使用FSO方法作为诊断工具监测短期预报中的观测性能。Gelaro et al(2010)依托全球观测系统研究与可预报性试验(The Observing System Research and Predictability Experiment, THORPEX)量化和比较了NOGAPS、NASA GEOS-5和加拿大环境部全球确定性预报系统(Global Deterministic Prediction System, GDPS)等三个全球业务预报系统中的观测影响。Auligné et al(2011;2013)基于WRF/WRFPLUS/WRFDA框架开发了相应的WRFDA-FSO诊断工具。Joo et al(2013)基于英国气象局数值天气预报系统中开发的基于伴随的FSO方法，评估了观测对24 h预报误差减小的影响，并指出MetOp-A数据的影响是任何单个卫星平台中最大的(约占全球预报误差减小总影响的25%)。Jung et al(2013)则首次在有限区域模式框架内全面评估了基于伴随的观测对WRF系统的影响和对误差协方差参数的敏感性，基于WRFDA-FSO诊断工具对2008年台风季东亚和西北太平洋地区观测对预报的效果进行了评估。Lorenc and Marriott(2014)提出了一种在英国气象局全球4D-Var同化系统中计算观测影响的基于伴随的方法，其试验结果同Cardinali(2009)和Gelaro et al(2010)的结果非常类似。Zhang et al(2015)通过2010年1月和6月分别执行两周长度的FSO试验评估了对流层气象数据报告(tropospheric airborne meteorological data reporting, TAMDAR)对美国大陆24 h预报误差减小的影响。Mallick et al(2017)基于印度国家中期天气预报中心(National Centre for Medium Range Weather Forecasting, NCMRWF)全球统一模式(unified model, NCUM)，研究了不同卫星反演风观测对短期24 h预报的影响，并发现FSO方法在不良观测的质量控制和确定观测的相对影响上十分有效。Kim et al(2017)基于WRFDA-FSO诊断工具定量地评估了卫星反演的增强大气运动矢量对东亚地区数值天气预报的影响。

我国已有的评估观测对模式预报影响的研究多采用OSEs和OSSEs方法，而采用基于伴随的FSO方法的研究还处于探索和实践阶段。其中王曼等(2015)基于WRFDA-FSO诊断工具，统计分析了2009年和2010年5—10月青藏高原东侧常规地面和高空观测对WRF模式预报误差的贡献。韩峰等(2018)基于WRFDA-FSO诊断工具，针对2015年2月12—16日发生在东亚的一次预报过度的温带气旋开展了观测影响研究。王佳(2019)采用基于伴随的FSO方法，评估了2018年7—8月国家级地面自动站、探空和风廓线雷达(wind profile radar, WPRD)观测对华东地区12 h预报的影响，并初步讨论了台风预报对观测的敏感性。唐兆康(2021)采用基于伴随的FSO方法，开展了WPRD和地基微波辐射计(microwave radiometer, MWR)观测对WRF模式12 h预报的影响试验，分析了风温湿观测对模式预报的贡献。

以内蒙古睿图预报系统为核心的内蒙古数值预报业务系统，近年来通过技术引进和自主研发，根据本地气候特点和特色气象服务需求，持续开展数值预报研发和应用，推进数值预报业务集约化发展，解决本地精细化预报需求。目前，内蒙古睿图预报系统在初始场中同化常规探空和地面观测。当数值天气预报模式从分析场积分得到预报时，并不是所有同化进分析场的观测都能改善预报。因此，有必要定量地评估特定观测对预报的影响，以提供有关观测系统影响的相关信息。本文基于内蒙古睿图预报系统的低分辨率版本和WRFDA-FSO诊断工具，评估现有探空和地面观测对内蒙古睿图预报系统预报的影响，为改善内蒙古区域数值预报技巧确定相关敏感区，并对在最需要的地区进行最有用的观测提供决策参考。同时，分析对预报误差减小起负贡献作用次数偏多的站点及其分布，为该地区的站点布局的进一步加强和调整提供参考；并开展观测资料的质量控制及不确定性分析(王丹等，2020; 2022)等工作。该工作具有较高的理论意义和实际应用价值，同时目前也备受关注。

1 基于伴随的FSO算法与WRFDA-FSO诊断工具简介 1.1 基于伴随的FSO算法

Langland and Baker(2004)给出了基于伴随的预报误差减小估计δe_a^b表达式的推导过程。Auligné et al(2011)在开发WRFDA-FSO诊断工具时将预报误差度量明确为干总能量，以综合考量预报场中水平风场、位温和气压与大气参考状态的误差。观测敏感性的计算是一个涉及预报模式伴随和同化系统伴随的两步过程。

虽然背景场预报误差e_b和分析场预报误差e_a是由初始条件和预报模式的不确定共同引起的，但预报误差之间的差异(Δe_a^b=e_a-e_b)可以被认为是仅仅由于观测的同化所致。Δe_a^b被称之为预报误差减小或观测影响，可以将其写成

$ \begin{gathered} \Delta e_{\mathrm{a}}^{\mathrm{b}}=e_{\mathrm{a}}-e_{\mathrm{b}}=\left\langle\left(\boldsymbol{x}_{\mathrm{a}}^{\mathrm{f}}-\boldsymbol{x}_{\mathrm{b}}^{\mathrm{f}}\right), \right. \\ \left.\left[\boldsymbol{C}\left(\boldsymbol{x}_{\mathrm{b}}^{\mathrm{f}}-\boldsymbol{x}^{\mathrm{t}}\right)+\boldsymbol{C}\left(\boldsymbol{x}_{\mathrm{a}}^{\mathrm{f}}-\boldsymbol{x}^{\mathrm{t}}\right)\right]\right\rangle= \\ \left\langle\left(\boldsymbol{x}_{\mathrm{a}}^{\mathrm{f}}-\boldsymbol{x}_{\mathrm{b}}^{\mathrm{f}}\right), \left(\frac{\partial F_{\mathrm{b}}}{\partial \boldsymbol{x}_{\mathrm{b}}^{\mathrm{f}}}+\frac{\partial F_{\mathrm{a}}}{\partial \boldsymbol{x}_{\mathrm{a}}^{\mathrm{f}}}\right)\right\rangle \end{gathered} $

(1)

式中：x_b^f和x_a^f分别为以背景场x_b和分析场x_a为初始条件的短期预报，x^t为大气参考状态，C为代表干总能量的能量加权系数矩阵。括号〈, 〉代表向量的欧式内积，〈x, y〉=∑x_iy_i。F=e/2为预报准确度代价函数，相应的一阶导数∂F/∂x为预报准确度梯度，将作为两次伴随积分的初始条件。

敏感性计算的第一步是使用预报模式的伴随，分别沿着x_b→x_b^f和x_a→x_a^f两条预报轨迹将它们映射回初始时刻。则可以将预报误差减小估计为

$ \begin{gathered} \delta e_{\mathrm{a}}^{\mathrm{b}}=\left\langle\left(\boldsymbol{x}_{\mathrm{a}}-\boldsymbol{x}_{\mathrm{b}}\right), \left(\boldsymbol{L}^{\mathrm{T}} \frac{\partial F_{\mathrm{b}}}{\partial \boldsymbol{x}_{\mathrm{b}}^{\mathrm{f}}}+\boldsymbol{L}^{\mathrm{T}} \frac{\partial F_{\mathrm{a}}}{\partial \boldsymbol{x}_{\mathrm{a}}^{\mathrm{f}}}\right)\right\rangle= \\ \left\langle\left(\boldsymbol{x}_{\mathrm{a}}-\boldsymbol{x}_{\mathrm{b}}\right), \left(\frac{\partial F_{\mathrm{b}}}{\partial \boldsymbol{x}_{\mathrm{b}}}+\frac{\partial F_{\mathrm{a}}}{\partial \boldsymbol{x}_{\mathrm{a}}}\right)\right\rangle \end{gathered} $

(2)

式中：L^T为代表预报模式伴随的算子。

敏感性计算的第二步是使用同化系统的伴随，将初始条件敏感性梯度从网格空间扩展到观测空间。则式(2)可进一步改写为

$ \begin{gathered} \delta e_{\mathrm{a}}^{\mathrm{b}}=\left\langle\boldsymbol{K}\left(\boldsymbol{y}-\boldsymbol{H} \boldsymbol{x}_{\mathrm{b}}\right), \left(\frac{\partial F_{\mathrm{b}}}{\partial \boldsymbol{x}_{\mathrm{b}}}+\frac{\partial F_{\mathrm{a}}}{\partial \boldsymbol{x}_{\mathrm{a}}}\right)\right\rangle= \\ \left\langle\left(\boldsymbol{y}-\boldsymbol{H} \boldsymbol{x}_{\mathrm{b}}\right), \boldsymbol{K}^{\mathrm{T}}\left(\frac{\partial F_{\mathrm{b}}}{\partial \boldsymbol{x}_{\mathrm{b}}}+\frac{\partial F_{\mathrm{a}}}{\partial \boldsymbol{x}_{\mathrm{a}}}\right)\right\rangle= \\ \left\langle\left(\boldsymbol{y}-\boldsymbol{H} \boldsymbol{x}_{\mathrm{b}}\right), \frac{\partial F_{\mathrm{a}}^{\mathrm{b}}}{\partial \boldsymbol{y}}\right\rangle \end{gathered} $

(3)

式中：K为卡尔曼增益矩阵，y为观测向量，H将x_b投影到观测空间中。

使用式(3)，可以将观测影响划分为任何单个观测或感兴趣的观测分组所作出的贡献。当δe_a^b为负时，e_a < e_b，即观测的同化减小了预报误差，观测对预报起正贡献作用；当δe_a^b为正时，e_a>e_b，即观测的同化增大了预报误差，观测对预报起负贡献作用。

1.2 WRFDA-FSO诊断工具简介

WRFDA-FSO诊断工具由WRF非线性模式及其切线性伴随模式WRFPLUS和WRFDA同化系统及其伴随模块组成。包含1次分析同化、2次非线性预报模式积分、2次切线性伴随模式积分、1次伴随分析同化，计算代价约为普通单次模式预报的10~15倍。图 1为预报对观测敏感性试验流程示意图。

2 资料简介与试验设计 2.1 观测资料

试验的观测资料主要由中国高空秒级数据和中国地面逐小时全要素数据组成，来自气象大数据云平台“天擎”(China Meteorological Administration Data as a Service, CMADaaS)。试验中将中国高空秒级数据稀释为分钟级观测输入同化系统；试验中选取模式区域内的国家级地面自动站和内蒙古自治区境内的区域级地面自动站观测。

两种观测类型对应的站点数量和观测影响评估相关观测变量如表 1所示。观测资料的前处理包括将资料格式转换为WRFDA同化系统所需的LITTLE_R格式以及运行质量控制程序。

2.2 模式设置

本研究采用的WRF非线性模式及其前处理系统的版本为WRF-4.1.3与WPS-4.1，WRFPLUS切线性伴随模式的版本为WRFPLUS-4.1.2，WRFDA同化系统及其伴随模块的版本为WRFDA-4.1.3。模式区域以43.5°N、106.7°E为中心，覆盖了我国北方大部分地区(图 2)，并将全域作为计算预报准确度的目标区域。模式水平分辨率为12 km，水平格点数为241个×208个，垂直层数为50层，模式层顶气压为50 hPa，积分时间步长为72 s。模拟过程中采用的各参数化方案如表 2所示，其中WRFPLUS切线性伴随模式目前仅支持少数简单物理过程，在实际计算中忽略了湿物理过程。

2.3 试验设计

批量试验时间为2021年7月1—31日，每天00时(世界时，下同)和12时起报，预报时效为12 h，计算内蒙古睿图预报系统区域内观测对该系统12 h预报的影响。背景场x_b来自美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)全球预报系统(Global Forecast System, GFS)水平分辨率为0.25°×0.25°的格点预报资料在相应试验起报时刻的初始场。分析场x_a由背景场同化常规探空和地面观测资料所得，为了得到更加良好的分析同化效果，采用混合(Hybrid/3DEnVar)同化方法(其背景误差协方差中的25%源于3DVar变分框架中的静态背景误差协方差，75%源于集合预报的动态背景误差协方差)。其中，静态背景误差协方差使用WRFDA同化系统的gen_ be模块采用美国国家气象中心(National Meterological Center, NMC)方法和控制变量CV7选项生成，统计样本为2021年7月1—31日采用相同模式设置和以GFS格点预报资料为背景场的逐12 h起报的24 h和12 h区域模式预报场之间的差异；而动态背景误差协方差则由NCEP全球集合预报系统(Global Ensemble Forecast System, GEFS)格点集合预报资料30组集合成员在相应试验起报时刻的初始场相对于集合平均的扰动估计。大气参考状态(真实场)x_t由NCEP全球资料同化系统(Global Data Assimilation System, GDAS)水平分辨率为0.25°×0.25°的格点分析资料在相应试验起报时刻的初始场同化常规探空和地面观测资料后的分析场代表，即由下一起报时刻GDAS分析场代表当前起报时刻模式积分12 h时对应的大气参考状态(真实场)。

3 观测影响分析 3.1 观测影响线性近似代表性分析

观测影响计算的准确性取决于基于伴随的估计预报误差减小δe_a^b(线性近似)对实际预报误差减小Δe_a^b的代表程度。虽然δe_a^b不可能完全地反映出Δe_a^b的实际情况，但若δe_a^b能够对Δe_a^b提供合理的估计，其即可为观测影响计算提供有用的信息。

图 3为2021年7月00时和12时实际预报误差减小(黑线)及相应的基于伴随的估计预报误差减小(红线)的时间序列。可以看出，62个时次的试验中有44个时次(71%)出现了Δe_a^b小于零的情况，即多数时次的试验通过观测资料的同化产生了更准确的短期预报轨迹，改善了预报系统的12 h预报，减小了预报误差，观测对预报起正贡献作用。但有些时次的试验也存在Δe_a^b与δe_a^b正负号相反或偏差较大的δe_a^b对Δe_a^b估计非理想的情况。基于伴随的观测影响估计不准确主要有以下原因：首先，基于伴随的预报对观测敏感性计算没有考虑到湿物理和非线性过程，当出现了强的非线性天气过程时这种线性近似的不准确往往会更加明显；其次，批量试验同化的观测资料有限，尤其模式区域内俄罗斯南部和蒙古国等天气系统上游地区缺乏有效观测资料的输入(田伟红，2018)，同时也未进行气象卫星等观测资料的同化，导致分析增量的量级较小；此外，与一些学者在研究中采用将背景场预报轨迹提前36 h的方式以拉大背景场与大气参考状态(真实场)之间的差异从而增大分析增量的量级不同，为了达到更加贴近业务实际的效果，本研究中采用质量更高的GFS初始场作为背景场，但也在一定程度上导致分析增量的量级较小和一些负同化效果。唐兆康(2021)的研究也说明分析增量较小可能是影响FSO线性近似效果的因素之一。

整体上，基于伴随的估计δe_a^b较好地遵循了Δe_a^b的每日趋势，从绝对幅度上看，伴随计算基本可以解释批量试验中观测资料的同化对12 h预报误差实际影响的约3/4。尤其考虑到该结果是基于上述非理想的情况下取得的，可以认为批量试验中δe_a^b对Δe_a^b提供了合理且显著的估计。

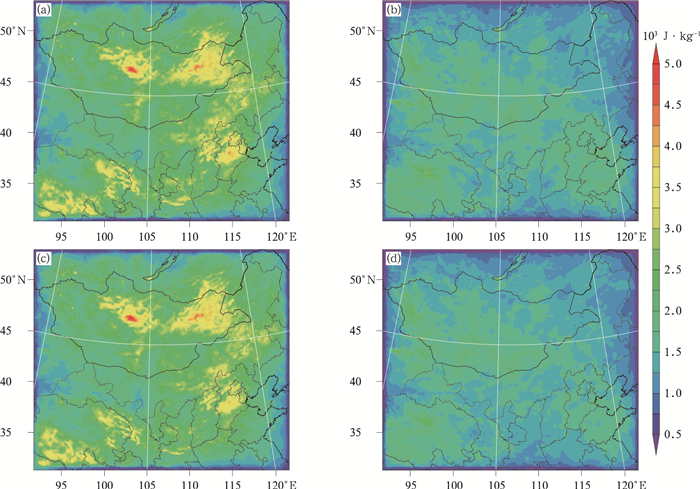
3.2 预报误差的空间特征分析

2021年7月00时和12时的时间平均能量加权垂直积分预报误差如图 4所示，误差综合考量了从地面到模式层顶的水平风场、位温和气压。可以看出，对于12 h短期预报误差，12时起报试验由于积分时段基本处于夜间，模式对辐射、对流等物理过程的描述具有的不确定性更小，导致12时起报的短期预报误差明显小于00时起报的，量值上约为前者的2/3。最大预报误差出现在00时起报试验的蒙古国中部和东部、华北平原北部和青藏高原东北部等地区，一方面是由于模式区域内杭爱山、祁连山和巴颜喀拉山等陡峭的山地和高原地区对于数值模式属于复杂的下垫面区域，导致模式预报误差增大；另一方面也与该季节中纬度地区活跃的天气尺度气旋和反气旋有关，如蒙古气旋源地等。此外，通过对探空和地面观测资料的同化，每个格点上的时间平均能量加权垂直积分预报误差平均从1747.3 J·kg^-1减小到1730.6 J·kg^-1，降低了约1%。

同时，分别利用批量试验背景场和分析场的12 h累计降水预报与模式区域内的1120个国家级地面自动站的降水资料进行TS降水评分计算来评估模式定量降水预报(quantitative precipitation forecast, QPF)效果(表 3)。可以看出，对于各量级降水评分，分析场预报的评分均较背景场预报评分高，尤其在大雨及以上量级评分中改善明显。结果表明, 同化探空和地面观测资料可以进一步提高定量降水预报效果。

2021年7月00时和12时的时间平均能量加权垂直积分实际预报误差减小及相应的基于伴随的估计预报误差减小如图 5所示。由图可见，尽管存在相当一部分实际预报误差减小为正的地区，如蒙古国、内蒙古东北部地区等，这可能是由于模式区域内天气系统上游地区缺乏有效观测资料的输入，同时也与同化系统对地面观测海拔与模式最低层高度差异质量控制设置较为严苛有关，导致大兴安岭等地形陡峭地区有一定量的地面观测未能通过同化系统的质量控制。但观测影响的总体总和为负，其中12时起报试验每个格点上的时间平均能量加权垂直积分实际预报误差减小平均为-19.5 J·kg^-1，对背景场预报误差的改善略优于00时起报试验的-13.6 J·kg^-1。这种负和正观测影响的组合反映了资料同化的统计性质。观测影响的总体总和为负说明观测的同化减小了预报误差，观测对预报起正贡献作用。这种正贡献作用在青藏高原东北部、黄土高原和华北平原北部等地区尤为显著。

同时，基于伴随的估计预报误差减小在空间分布上亦对实际预报误差减小提供了较为合理的估计，观测对预报起显著正贡献作用的地区均主要分布在模式区域的偏南部。从物理意义上看，可以将基于伴随的估计预报误差减小分布型理解为“上游地区的天气气候系统”，其将在12 h预报时效后演变成实际预报误差减小分布型。至此，可以使用同化系统的伴随模块将基于伴随的估计预报误差减小由网格空间扩展到观测空间来计算每个观测对预报误差减小的影响。此外，在华北平原等局部地区出现了极大值与极小值环状交替分布的现象，导致这种现象的原因有待进一步探讨和研究。

3.3 不同观测变量对预报的影响

图 6为2021年7月探空观测及地面观测按观测变量划分的观测影响的统计结果。结果表明，对12 h预报误差减小贡献最大的观测是来自探空观测的动力变量(U、V风分量)；而探空观测的比湿(q)变量与地面观测的动力变量、温度(T)变量的观测影响相当，对12 h预报误差减小的正贡献作用次之；探空观测的T变量与地面观测的气压(p)变量的观测影响相当，对12 h预报误差减小起正贡献作用但不显著，这可能是由于随着模式发展目前数值模式对温度场预报本身质量较高导致的。此外，探空观测的p变量是作为坐标变量输入同化系统的，因此地面观测是唯一能够产生p变量观测影响的观测，对预报误差减小亦起着不可或缺的作用；地面观测的q变量对12 h预报误差减小的平均贡献较弱，这可能是由于该湿度观测仅有地面一层，对湿度变量的敏感性较低导致的。

探空观测的各变量单时次平均观测使用数接近，明显多于地面观测。一方面是由于探空观测给出了各变量在垂直方向上的廓线，具有多个垂直层次，而地面观测仅有地面一层；另一方面也与同化系统对地面观测海拔与模式最低层高度差异质量控制设置较为严苛有关，导致一定量的地面观测未能通过同化系统的质量控制，观测资料同化率不高。结合各变量的单时次平均观测影响，给出各变量的单时次单位数量平均观测影响，结果表明：地面观测的动力变量对12 h预报误差减小的单位正贡献作用最大；探空观测的动力变量、q变量与地面观测的T变量、p变量的单位正贡献作用次之；探空观测的T变量与地面观测的q变量的单位正贡献作用较弱。

图 6d, 6h给出了探空观测及地面观测的单时次平均观测影响正负贡献观测数量对比，蓝色表示对12 h预报误差减小起正贡献作用的观测数量，红色表示对12 h预报误差减小起负贡献作用的观测数量，灰色表示对12 h预报误差减小贡献呈中性的观测数量(未能通过同化系统的质量控制)。结果表明：无论是探空观测还是地面观测，所有变量对12 h预报误差减小起正贡献作用的观测数量均大于起负贡献作用的观测数量。此外，探空观测同化率显著优于地面观测，也进一步反映出从观测角度推动数值模式发展所面临的涉及观测质量、同化系统参数设置及地形原因等提高地面观测同化率的问题和其蕴藏的巨大潜力。

3.4 不同观测类型对预报的影响

图 7为2021年7月探空观测及地面观测按观测类型划分的观测影响的统计结果。结果表明：无论是探空观测还是地面观测，单时次平均观测影响均为负，这说明观测在被同化系统同化时具有有利的影响，即从分析场x_a开始的预报比从背景场x_b开始的预报具有更小的误差。

探空观测提供了更多的观测数据，其对12 h预报误差减小的贡献也最大。而单时次单位数量平均观测影响探空观测的贡献约为地面观测的1/2。对于探空观测，对12 h预报误差减小起正贡献作用的观测数量占比为52.3%，起负贡献作用的观测数量占比为44.2%，贡献呈中性的观测数量占比为3.5%，具有较高的观测资料同化率；对于地面观测，对12 h预报误差减小起正贡献作用的观测数量占比为33.4%，起负贡献作用的观测数量占比为27.1%，贡献呈中性的观测数量占比为39.5%，有待进一步提高观测资料同化率。

3.5 观测影响时间序列

图 8为2021年7月探空观测及地面观测的观测影响的时间序列。结果表明，对于探空观测，85.5%的试验时次观测影响为负；对于地面观测，83.9%的试验时次观测影响为负。这说明无论是探空观测还是地面观测，绝大部分试验时次观测在被同化系统同化时对12 h预报误差减小起到了积极的作用。此外，对12 h预报误差减小起负贡献作用的试验时次与图 3中基于伴随的估计预报误差减小为正的时次有着高度一致的对应关系。其中仅有9日12时、13日12时、20日00时、25日00时和28日12时5个时次出现了探空观测与地面观测均对12 h预报误差减小起负贡献作用的情况，这可能是由于对背景误差和观测误差统计进行的假设和近似以及同化参数设置等很难在所有时次试验中均保持适合，导致在上述时次试验中无法获得更好的分析场。

3.6 观测影响空间垂直分布

根据观测的垂直层次对观测影响的统计结果进行划分具有指导意义，如图 9所示为2021年7月探空观测及地面观测按气压层次划分的观测影响的统计结果。对于探空观测，对12 h预报误差减小从近地面层至模式层顶均保持正贡献作用，可以看到2个极大值区域：一个位于对流层中低层850~500 hPa层，另一个位于对流层高空急流层300~200 hPa层附近；对于地面观测，对12 h预报误差减小起正贡献作用的层次可以从近地面层延伸至700 hPa，这可能是由于地面观测资料同化时在垂直方向上的传播导致的。整体上，地面观测在850 hPa以下低层正贡献占比明显。

综合探空观测及地面观测的整体观测影响的统计结果。结果表明，尽管500 hPa以上的观测数量更多(占总观测数量的54.3%)，但12 h预报误差的总减小量只有34.3%可归因于500 hPa以上的观测，约有65.7%归因于地面和500 hPa之间的观测。100 hPa以上的观测数量约占总观测数量的9%，主要是探空观测在平流层的观测资料，对本研究使用的预报误差测量没有实质性地减小。

3.7 观测影响空间水平分布

上述已经表明，大量观测资料的同化可以减小短期预报误差。然而，单个观测的影响可能有很大不同，基于伴随的计算可以以合理的准确性对模式区域内的每个单独的观测估计量化这种影响。图 10显示了2021年7月探空观测及地面观测的观测影响的空间分布。

对于探空观测，模式区域内的57个探空站在垂直廓线上观测的综合影响均为负，这说明探空观测在被同化时均总体具有有利的影响，也反映出探空观测数据稳定、质量较高的特征(张旭鹏等，2021；李秋阳等，2022)。对12 h预报误差减小贡献最大的3个探空站分别为：唐山市乐亭站(-24 602.3 J·kg^-1)、邢台市邢台站(-19 662.2 J·kg^-1)、通辽市通辽站(-17 639.5 J·kg^-1)；对12 h预报误差减小起正贡献作用次数最多的3个探空站分别为：呼伦贝尔市海拉尔站(52次)、鄂尔多斯市东胜站(51次)、昌吉回族自治州北塔山站(51次)。可以看出，高原地区探空站较其他地区探空站的正贡献作用和次数相对较弱，这可能是由于其垂直探测范围较窄导致的。

对于地面观测，尽管存在相当一部分观测影响为正的个别观测，但其观测影响的总体总和为负。这种负和正观测影响的组合反映了资料同化的统计性质。相较探空站，地面自动站的地面观测仅有地面一层，单个站点的观测影响要比探空站小一个数量级，但考虑到其站点数量巨大，因此累加得到的总体观测影响也可能是较大的。对12 h预报误差减小起正贡献作用的站点主要分布在嫩江平原、辽河平原上游、内蒙古中部偏南、黄河几字湾西南部以及华北平原南部和长江中下游平原北部，起负贡献作用的站点则主要分布在黄河几字湾东部以及华北平原北部，而模式区域西部观测资料较稀疏地区站点则主要表现为弱正贡献或贡献呈中性。对12 h预报误差减小贡献最大的3个国家级地面自动站分别为：石嘴山市陶乐站(-1106.8 J·kg^-1)、银川市永宁站(-1090.8 J·kg^-1)、鄂尔多斯市乌审旗站(-998.7 J·kg^-1)，均位于黄河几字湾西南部；对12 h预报误差减小起正贡献作用次数最多的3个国家级地面自动站分别为：包头市包头站(50次)、巴彦淖尔市五原站(50次)、邯郸市永年站(49次)，且在河套地区尤为显著。此外，也存在极个别站点对12 h预报误差减小起正贡献作用次数显著偏少的情况(红点，图 10d)，应着重排查观测资料是否存在问题。尤其值得关注的是，有一定量的地面观测未能通过同化系统的质量控制(灰点)，这些观测主要位于大兴安岭、燕山、太行山、吕梁山、秦岭以及青藏高原地区。可见，对于数值模式属于复杂下垫面的区域，应调整同化系统参数设置，本着容忍偏差、提高观测资料同化率的原则促进观测资料更多的吸收利用，才能更好地从观测角度推动数值模式发展，通过观测与预报互动使预报能力和观测能力同时不断迭代升级。

4 结论与展望

本文基于内蒙古睿图预报系统的低分辨率版本和WRFDA-FSO诊断工具，评估2021年7月现有探空和地面观测对内蒙古睿图预报系统预报的影响。该方法的一个显著优势是，可以有效地评估全局观测集或按观测变量、观测类型、气压层次、地理区域等划分的任何观测子集的观测影响。本研究中使用的代价函数为以干总能量为度量的分别以背景场x_b和分析场x_a为初始条件的短期预报x_b^f和x_a^f在验证时刻的预报误差之间的差异。得到如下结论：

(1) 尽管基于伴随的预报对观测敏感性计算没有考虑到湿物理和非线性过程，但基于伴随的预报误差减小估计δe_a^b(线性近似)对实际预报误差减小Δe_a^b提供了合理且显著的估计。从绝对幅度上看，伴随计算基本可以解释批量试验中观测资料的同化对12 h预报误差实际影响的约3/4。

(2) 12时起报试验的短期预报误差明显小于00时起报试验，量值上约为前者的2/3。最大预报误差出现在00时起报试验的蒙古国中部和东部、华北平原北部和青藏高原东北部等地区。此外，观测影响的总体总和为负，观测对预报起正贡献作用。

(3) 对12 h预报误差减小贡献最大的观测来自探空观测的动力变量(U、V风分量)，而单时次单位数量平均观测影响探空观测的贡献约为地面观测的1/2。

(4) 探空观测对12 h预报误差减小从近地面层至模式层顶均保持正贡献作用，并在对流层中低层和对流层高空急流层存在两个极大值区域；地面观测在850 hPa以下低层正贡献占比明显。此外，12 h预报误差的总减小量约有65.7%归因于地面和500 hPa之间的观测。

(5) 探空观测在被同化系统同化时总体具有有利的影响，也反映出探空观测数据稳定、质量较高的特征；地面观测对12 h预报误差减小起正贡献作用的站点主要分布在嫩江平原、辽河平原上游、内蒙古中部偏南、黄河几字湾西南部以及华北平原南部和长江中下游平原北部。对12 h预报误差减小起正贡献作用次数最多的区域在河套地区尤为显著。

此外，本研究模式区域内俄罗斯南部和蒙古国等天气系统上游地区缺乏有效观测资料的输入，同时，随着气象卫星辐射和反演资料在数值预报中逐步起到主导的贡献作用，还需在后续的研究中进一步加入上述观测资料，进行更多的预报对观测敏感性试验讨论与验证。尤其值得关注的是，一些地形陡峭地区有一定量的地面观测未能通过同化系统的质量控制，应调整同化系统参数设置，本着容忍偏差、提高观测资料同化率的原则促进观测资料更多的吸收利用。因此，针对上述不足进行完善，继续开展批量试验以验证预报对观测敏感性试验分析的结论，最终形成同化系统按观测影响分级的动态站点白名单等亦是至关重要的工作(杨国彬等，2021)。可以预见该项工作在提高地面观测同化率、不良观测的质量控制以及进一步改善分析同化效果方面还蕴藏着巨大的潜力有待挖掘。

致谢：中国气象局气象探测中心王佳对本文给予了宝贵建议和帮助，谨此致谢！