2. 重庆市气象台,重庆 401147;
3. 国家气象中心,北京 100081
2. Chongqing Meteorological Observatory, Chongqing 401147;
3. National Meteorological Centre, Beijing 100081
气温是天气预报中最重要的气象要素之一, 对农业、电力、交通以及人民日常生产生活都有重要的影响。尽管数值天气预报准确率越来越高, 但对近地面气温预报仍存在偏差。西南地区东部地形复杂、天气多变, 模式预报偏差较大。减小气温预报偏差, 一直是数值预报模式产品应用的研究重点。目前, 天气预报业务中多采用可信度高的站点观测资料开展站点上的模式统计释用, 以提高预报技巧(刘还珠等, 2004; 赵声蓉, 2006; Glahn et al, 2009; 赵声蓉等, 2012; 代刊等, 2016; 吴启树等, 2016; 薛谌彬等, 2019; 陈昱文等, 2020; 杨绚等, 2022; 陈鹤等, 2022; 杨彬等, 2024)。
模式统计释用通常涉及资料样本较长, 且计算复杂、计算量大。随着模式预报性能不断提高, 在天气预报应用中, 更多的是直接把模式气温预报插值到站点。但模式地形和真实地形存在差异, 尤其是地形复杂地区, 而地形又能显著影响气温预报(陶诗言, 1980; Oshima et al, 2002; LeMone et al, 2003; 曾晓青等, 2024), 特别是2 m气温, 紧随地形而变化, 因而模式地形与真实地形的高度偏差(简称模式地形高度偏差, 下同)是地形复杂地区气温预报偏差的重要来源, 对于这种偏差, 常依据垂直变率予以订正。气温作为一个随时间不断变化的三维要素场, 其垂直变率也是一个动态变量。已有研究表明, 气温订正方法对垂直变率的变化较为敏感, 使用定常的气温垂直变率(5.5~6.6 ℃·km-1), 在业务和研究中存在一定的局限性(杨昌军等, 2004; Minder et al, 2010; Holden and Rose, 2011; Shen et al, 2016; 李框宇等, 2019; He and Wang, 2020; 罗伦等, 2021)。
赵滨等(2016)利用模式三维预报变量和近地面要素预报产品, 设计了一种针对2 m气温的三维插值方法。该方法采用模式自身的多层预报变量进行垂直插值, 相当于获得一个动态的垂直变率, 其在不同格点、不同时次均提供不同的垂直变率量值, 以此获得更为准确的评估信息。赵瑞霞等(2023)利用模式地面气温预报随高程的变化关系, 实时统计地面气温垂直变率, 设计了动态垂直变率降尺度方法, 使智能网格气温预报性能得到有效提升。目前我国的气象网格预报体系中, 在进行短期、中期和延伸期气温客观分析时, 有考虑地理信息的订正作用, 将插值点气温订正到被插值点高度(金荣花等, 2019), 但气温递减率仍然采用固定经验值, 这对插值精度有一定的影响。智协飞等(2019)将模式地形高度偏差分成4个区间, 细致评估了不同区间内模式气温的预报性能, 指出较大的模式地形高度偏差严重影响模式预报性能, 导致2 m气温预报误差明显偏大; 而且模式地形高度偏差相较预报时效, 对模式预报技巧的影响更加显著。
上述研究在计算垂直变率时, 考虑了模式气温预报和模式地形, 尚未考虑实况气温和真实地形, 难以真实反映模式气温预报偏差和模式地形高度偏差之间的关系。此外, 垂直变率存在明显的时间和空间变化(王乙竹等, 2023; 赵瑞霞等, 2023), 即预报日不同、季节不同、观测站位置不同时, 垂直变率也不相同, 所以计算时需要考虑其时空演变特征。针对上述问题, 本研究综合考虑模式气温预报、模式地形和实况气温、真实地形之间相互关系, 基于模式气温预报偏差和模式地形高度偏差, 计算近似垂直变率。考虑近似垂直变率的季节变化, 利用准对称混合滑动方法(吴启树等, 2016), 逐月确定最优训练期, 形成训练集。考虑近似垂直变率的日变化和空间变化, 按预报日逐日滚动、逐站计算训练集中的平均近似垂直变率; 最后对模式气温预报进行订正。
1 资料和方法 1.1 资料本文使用ECMWF高分辨率数值模式(简称EC模式)2 m气温预报资料, 时间为2021年1月1日至2023年12月31日, 分辨率为0.125°×0.125°, 起报时间为20时(北京时, 全文), 预报时效为24~240 h, 取24 h内的最高和最低气温, 作为模式预报的日最高和最低气温。采用双线性插值方法, 将EC模式资料插值到观测站点上, 以获得站点处的模式气温预报和地形高度。观测资料为重庆158个气象观测站对应时间的日最高和最低气温, 158个站包括34个国家站和124个区域自动站(经质量控制)。地形资料为EC模式自带的高程数据和中国地面气象站资料提供的地理信息数据。
1.2 订正方法采用准对称混合滑动训练期方法, 利用训练期内观测站点气温的模式预报值和相同时间的实况, 计算更符合真实大气的近似垂直变率, 具体计算公式为:
| $ \gamma_{i, j}=\frac{F_{i, j}-O_{i, j}}{H_i-H_i^{\prime}} $ | (1) |
式中: γi, j为训练期内某一样本j在观测站点i处的近似垂直变率, Fi, j、Oi, j分别表示训练期内样本j在观测站点i处气温的模式预报值和实况值, Hi、H′i分别表示观测站点i处的模式地形和真实地形高度。
准对称混合滑动训练期样本由预报日之前N天、前一年预报日之前N天、预报日和预报日之后N-1天的资料, 随预报日滑动取样混合而成, 形成的训练样本有3N天。再计算观测站点在训练期内所有样本的平均近似垂直变率, 具体计算公式为:
| $ \bar{\gamma}_i=\frac{1}{3 N} \sum\limits_{j=1}^{3 N} \gamma_{i, j} $ | (2) |
式中, γi为滑动训练期内所有样本在观测站点i处的平均近似垂直变率。
采用反距离权重插值法(申友利等, 2017; 占龙飞等, 2018), 将观测站点的平均近似垂直变率插值到模式网格点上。然后将测站周围邻近4个模式格点的气温按照各自的近似垂直变率, 转化为与站点相同海拔高度平面上的气温:
| $ T_k=F_k-\bar{\gamma}_k\left(H_k-H_i^{\prime}\right) $ | (3) |
式中: Fk、Tk分别为第k个网格点上气温的模式预报值和订正值, Hk为第k个网格点上的模式地形高度, H′i为第k个网格点对应站点i的真实地形高度。计算出站点周围4个与其高度相同的网格点气温订正值后, 利用双线性插值方法生成该站点的气温订正值。
对上述站点气温订正值进行检验, 根据平均绝对误差最小化原则, 逐月确定最优滑动训练期。针对每个月, N取值范围为5~70 d, 间隔5 d, 则对应有14个训练样本集, 计算每个训练样本集下所有站点气温订正值的平均绝对误差, 预报时效内平均绝对误差最小时, 对应的N则为最优训练期, 其结果为最终的站点气温订正值。为了简化计算, 所有站点采用相同的训练期。
设计两种试验方案, 开展2023年2 m最高和最低气温订正试验, 以对比研究固定垂直变率(方案一)和动态近似垂直变率(方案二)对模式气温的订正效果。其中, 方案一基于固定垂直变率(6 ℃·km-1)来订正模式气温, 方案二采用文中设计的动态近似垂直变率来订正模式气温。
1.3 检验方法选取预报准确率、平均绝对误差(MAE)和平均误差(ME)对气温预报性能进行评估。预报准确率是气温预报绝对偏差≤2℃的百分率, MAE反映预报与实况总的偏离程度, ME反映统计区域内的系统性偏差(冯良敏等, 2019)。
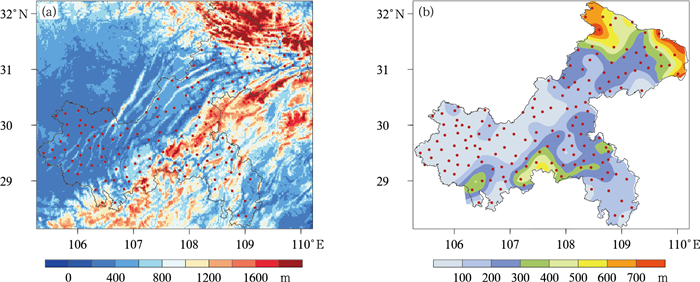
2 模式气温预报性能评估重庆地处青藏高原和长江中下游平原的过渡地带, 地形复杂, 气温预报难度大。如图 1所示, 重庆东北部有大巴山和巫山、东南部有武陵山、西南部有大娄山, 山高谷深, 海拔落差大; 西部和中部主要由丘陵和低山组成(图 1a)。文中使用的158个测站中, 位于东北部、东南部和西南部的站点模式地形高度偏差大(图 1b)。
|
图 1 (a) 重庆真实地形高度(填色)和158个气象观测站(圆点)分布, (b)EC模式地形和观测站(圆点)真实地形的高度偏差绝对值(填色)空间分布 Fig. 1 (a) Topography (colored) of Chongqing and 158 observation stations (dot), (b) spatial distribution of the absolute bias (colored) between topographic elevation of EC model and the actual elevation of observation stations (dot) |
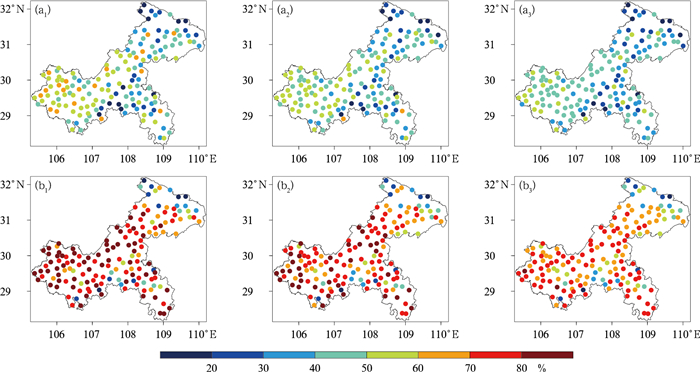
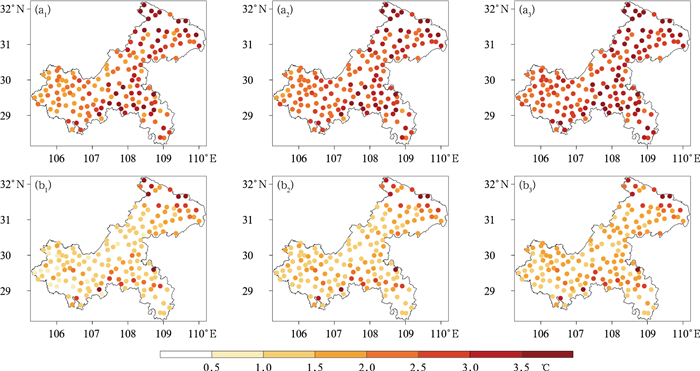
计算2023年EC模式不同预报时效最高和最低气温的预报准确率和MAE, 发现它们的空间分布特征基本相似(图略), 图 2和图 3给出了48 h、96 h和144 h时效的空间分布。总体来看, 模式对最高气温的预报准确率明显小于最低气温, MAE则明显大于最低气温; 随着预报时效延长, 气温预报性能降低。模式预报性能的空间差异大, 在模式地形高度偏差较大的地区, 预报性能较低, 在东北部偏北山区大部, 预报准确率小于40%, MAE在2℃以上; 在模式地形高度偏差较小的中西部, 预报性能较高; 例如48 h, 不同地区预报准确率的最大差值, 最高、最低气温分别达62.43%、88.71%(图 2a1, 2b1); 不同地区MAE的最大差值, 最高、最低气温均超过4℃(图 3a1, 3b1), 分别达4.87℃、4.21℃。
|
图 2 2023年EC模式不同预报时效的(a)最高和(b)最低气温预报准确率空间分布 (a1, b1)48 h, (a2, b2)96 h, (a3, b3)144 h Fig. 2 Spatial distribution of the forecast accuracy of (a) maximum and (b) minimum temperatures with different forecast lead-times by EC model in 2023 (a1, b1) 48 h, (a2, b2) 96 h, (a3, b3) 144 h |
|
图 3 2023年EC模式不同预报时效的(a)最高和(b)最低气温MAE的空间分布 (a1, b1)48 h, (a2, b2)96 h, (a3, b3)144 h Fig. 3 Spatial distribution of the MAE of (a) maximum and (b) minimum temperatures with different forecast lead-times by EC model in 2023 (a1, b1) 48 h, (a2, b2) 96 h, (a3, b3) 144 h |
从2023年不同预报时效最高和最低气温预报准确率、MAE随模式地形高度偏差绝对值的散点分布图(图略)可知, 随着模式地形高度偏差增大, 高低温的预报准确率明显降低, MAE逐渐增大。158个观测站中, 模式地形高度偏差最大为1009.3 m, 大于334 m的有35个站, 按6 ℃·km-1垂直变率计算, 因地形偏差造成的气温预报偏差最大达6.06℃, 有35个站偏差均在2℃以上。
综上可知, 模式地形高度偏差对模式气温预报性能有显著影响, 在模式气温订正时, 需予以考虑。
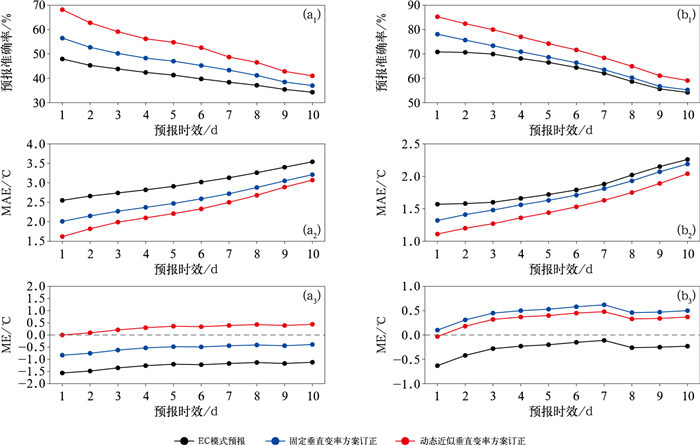
3 订正结果分析对2023年2 m最高和最低气温进行订正试验, 两个方案的订正结果如图 4所示。对比模式气温预报, 订正后的效果均有显著改善, 方案二更优; 随着预报时效延长, 订正效果呈下降趋势, 两个方案对高温的订正效果优于低温。
|
图 4 2023年EC模式预报的(a)最高和(b)最低气温经不同垂直变率方案订正前后各预报评估指标随预报时效的变化 (a1, b1)预报准确率, (a2, b2)MAE, (a3, b3)ME Fig. 4 Variation in forecast evaluation metrics with lead time of (a) maximum and (b) minimum temperatures by EC model and the correction by different vertical rate schemes in 2023 (a1, b1) forecast accuracy, (a2, b2) MAE, (a3, b3) ME |
对比EC模式预报, 方案一订正后, 最高气温预报准确率在24 h内提高了8.56%(相比模式的绝对值, 下同), 10 d平均提高了5.43%, MAE在24 h内降低0.54℃, 10 d平均降低0.43℃(图 4a1, 4a2); 最低气温预报准确率在24 h内提高了7.28%, 10 d平均提高了2.77%, MAE在24 h内降低0.25℃, 10 d平均降低0.11℃(图 4b1, 4b2); 最高气温的ME绝对值有所减小, 但负值仍然较大, 最低气温的ME由负值转为较大的正值(图 4a3, 4b3), 表明气温预报的系统性偏差仍然明显。方案二订正后, 最高气温预报准确率在24 h内提高了20.24%, 10 d平均提高12.71%, MAE在24 h内降低0.93℃, 10 d平均降低0.68℃(图 4a1, 4a2); 最低气温预报准确率在24 h内提高了14.45%, 10 d平均提高了8.30%, MAE在24 h降低0.46℃, 10 d平均降低0.30℃(图 4b1, 4b2); 最高和最低气温预报的系统性偏差小于方案一的订正结果(图 4a3, 4b3)。
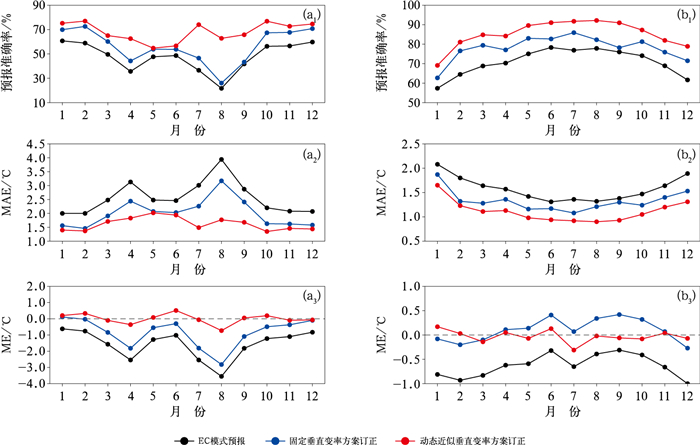
图 5是两个方案对24 h模式气温进行订正后, 其预报准确率、MAE和ME的逐月变化。对比模式预报, 订正后各月气温预报效果均有改善, 方案二更优; 两个方案对最高气温的订正效果优于最低气温。
|
图 5 2023年EC模式预报的24 h预报时效(a)最高和(b)最低气温经不同垂直变率方案订正前后各预报评估指标的逐月变化 (a1, b1)预报准确率, (a2, b2)MAE, (a3, b3)ME Fig. 5 Monthly variation in forecast evaluation metrics of (a) maximum and (b) minimum temperatures with 24 h lead time by EC model and the correction by different vertical rate schemes in 2023 (a1, b1) forecast accuracy, (a2, b2) MAE, (a3, b3) ME |
对比EC模式预报, 最高气温经方案二订正后, 各月预报准确率提高幅度差异大, 其中7月、8月明显高于其他月份, 8月最大(达41.1%), 全年月平均提高了20.34%, 明显高于方案一的8.56%;MAE在8月降低2.17℃, 全年月平均降低0.94℃, 高于方案一的0.55℃, 各月的值基本在2℃之内; 订正后各月预报准确率差异明显减小, 预报稳定性提高(图 5a1, 5a2)。最低气温经方案二订正后, 各月预报准确率提高幅度差异小, 相对来说2月、3月提高幅度较大, 全年月平均提高了14.44%, 高于方案一的7.24%;除1月、12月外, 其余月份预报准确率均在80%以上, 8月高达92%以上; MAE月平均降低0.46℃, 高于方案一的0.25℃(图 5b1, 5b2)。订正后, 高、低温各月ME在零值附近, 模式气温预报的系统性偏差显著减小(图 5a3, 5b3)。上述各月订正效果, 与冯良敏等(2019)采用15 d周期的滑动双权重平均法对EC模式四川2 m气温偏差订正效果相似。
上述结果表明, 不论从全年各时效还是从逐月订正效果来看, 基于动态近似垂直变率的订正方案, 都优于基于固定垂直变率的订正方案。
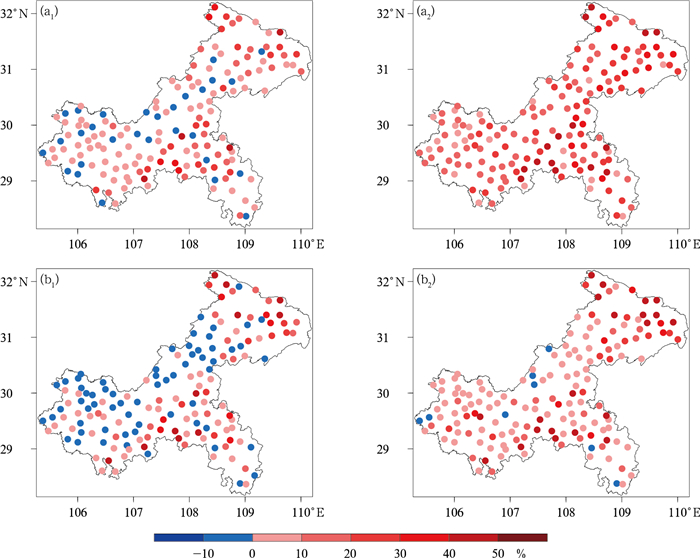
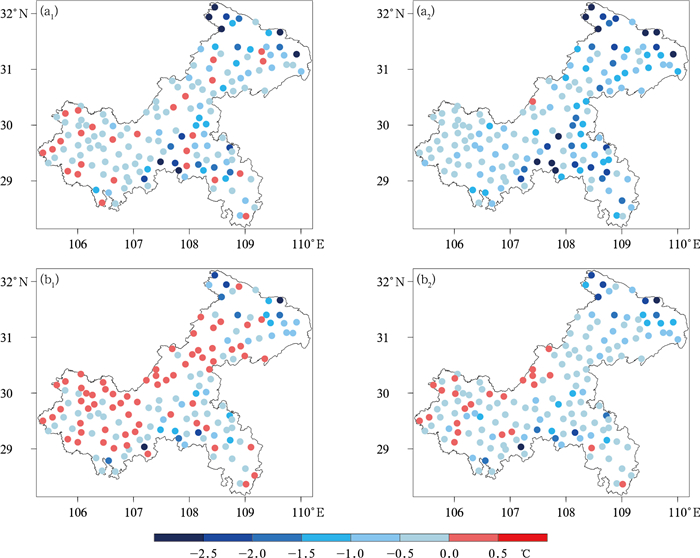
图 6和图 7分别是订正后气温预报准确率、MAE相比于EC模式预报偏差的空间分布。对比模式预报, 方案一订正后, 大部分站点最高气温预报效果有改善, 模式地形高度偏差越大, 效果改善越显著(图 6a1, 图 7a1); 在模式地形高度偏差较小的地区, 最低气温有弱的负订正效果; 在模式地形高度偏差较大的地区, 最低气温订正效果显著(图 6b1, 图 7b1)。方案二订正后, 高、低温预报效果绝大部分有改善, 模式地形高度偏差越大, 改善越显著, 明显优于方案一(图 6a2, 6b2; 图 7a2, 7b2); 在东北部偏北山区, 高、低温预报准确率提高极值大多在40%以上(图 6a2, 6b2), MAE减小极值超过2.5℃(图 7a2, 7b2)。
|
图 6 2023年EC模式预报的24 h预报时效(a)最高和(b)最低气温经不同垂直变率方案订正后的预报准确率变化空间分布 注: 填色为不同方案订正后的结果与EC模式预报值之差。 (a1, b1)固定垂直变率方案, (a2, b2)动态近似垂直变率方案 Fig. 6 Spatial distribution of variation in forecast accuracy by EC model of (a) maximum and (b) minimum temperatures with 24 h lead time after being corrected by different vertical rate schemes in 2023 (a1, b1) difference between Scheme One and EC model forecasts, (a2, b2) difference between Scheme Two and EC model forecasts |
|
图 7 2023年EC模式预报的24 h预报时效(a)最高和(b)最低气温经不同垂直变率方案订正后的MAE变化空间分布 注: 填色为不同方案订正后的结果与EC模式预报值之差。 (a1, b1)固定垂直变率方案, (a2, b2)动态近似垂直变率方案 Fig. 7 Spatial distribution of variation in MAE by EC model of (a) maximum and (b) minimum temperatures with 24 h lead time after being corrected by different vertical rate schemes in 2023 (a1, b1) difference between Scheme One and EC model forecasts, (a2, b2) difference between Scheme Two and EC model forecasts |
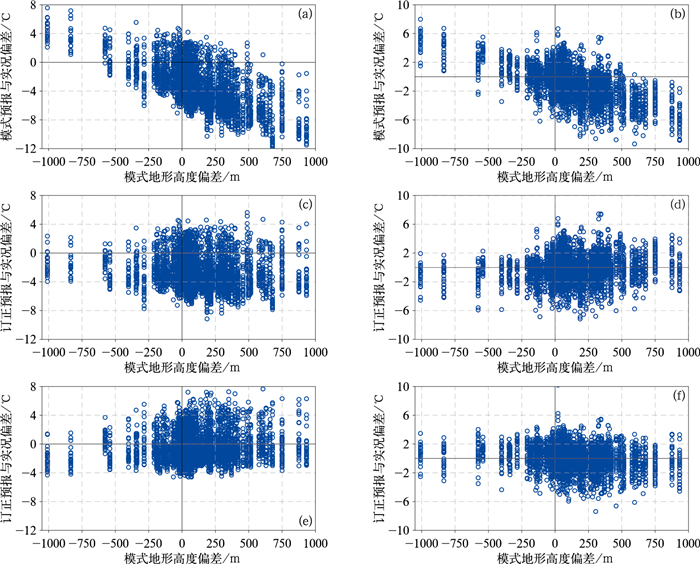
图 8给出了订正前后气温预报偏差与模式地形高度偏差的散点分布。可以看到, 模式气温预报偏差与地形高度偏差关系密切, 呈明显的反比例关系, 偏差以负值为主, 高温的负偏差大于低温, 偏差大值区主要集中在第四象限; 8月最高气温负偏差的极值在-12℃左右, 2月最低气温负偏差的极值在-9℃左右(图 8a, 8b)。两个方案订正后, 气温偏差显著减小, 与模式地形高度偏差的反比例关系减弱。方案二订正后, 效果改善更显著, 第四象限气温的负偏差得到有效控制, 气温偏差主要集中在-4~4℃区间内, 近似对称分布; 8月最高气温负偏差的极值减小到-4℃左右, 2月最低气温负偏差的极值在-6℃左右。表明基于动态近似垂直变率的订正方案能有效地减小模式气温预报偏差。
|
图 8 2023年24 h预报时效(a, c, e)8月最高气温和(b, d, f)2月最低气温的(a, b)EC模式预报及(c~f)不同垂直变率方案订正结果与实况的偏差随模式地形高度偏差的散点分布 (c, d)固定垂直变率方案, (e, f)动态近似垂直变率方案 Fig. 8 Scatter plot distribution of (a, b) forecast bias by EC model and (c-f) correction biases by different vertical rate schemes versus model topographic elevation bias for (a, c, e) maximum temperatures in August and (b, d, f) minimum temperatures in February with 24 h lead time in 2023 (c, d) difference between Scheme One and observations, (e, f) difference between Scheme Two and observations |
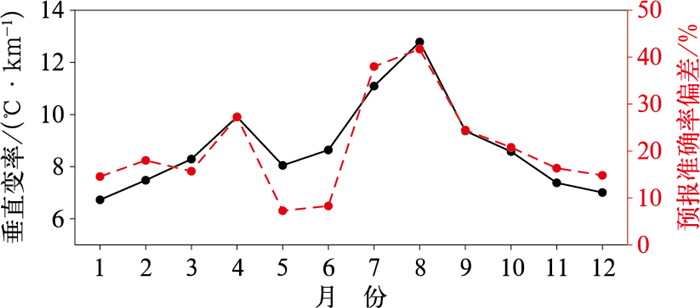
图 9给出了24 h时效最高气温预报准确率的偏差和近似垂直变率的逐月变化。方案二订正后, 预报准确率提升幅度与近似垂直变率的季节变化密切相关, 7月、8月订正效果最显著, 其次是4月, 近似垂直变率在这三个月出现极大值, 明显高于6℃· km-1。5月、6月的最高气温时刻对应降水偏多, 天气变化快, 采用方案二的订正效果有限。
|
图 9 2023年EC模式预报的24 h预报时效最高气温动态近似垂直变率(黑线)及经其订正后的预报准确率偏差(红线)的逐月变化 Fig. 9 Monthly variation of forecast accuracy bias (red line) of maximum temperatures by EC model with 24 h lead time after correction by dynamically approximated vertical rate (black line) scheme in 2023 |
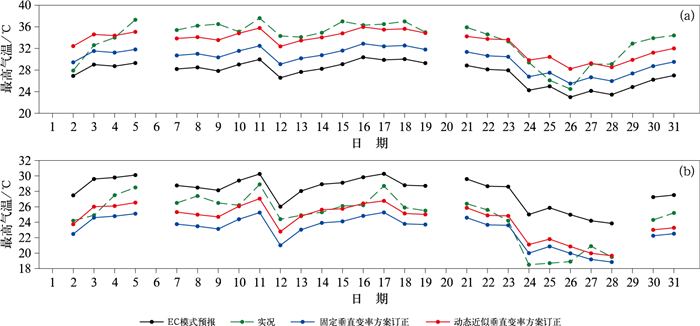
以模式地形高度偏差大的两个站点为例进一步分析, 武隆站和黔江八面山站模式地形减真实地形的高度差分别为418.65 m和-834.13 m。如图 10所示, 方案二订正后, 预报与实况更为接近, 气温预报相对稳定, 但是对8月24—26日的降温过程预报偏高; 对8月5日和月底的升温过程预报偏低。表明方案二对波动幅度较小的天气过程具有更好的订正效果, 对明显的升温和降温过程订正效果有限, 这与蔡怡等(2023)采用滑动双权重平均法对CMA-MESO 3 km模式2 m气温预报订正的结论相似, 是今后的重点改进方向。
|
图 10 2023年8月(a)武隆站和(b)黔江八面山站最高气温的EC模式预报、不同垂直变率方案订正结果与实况变化 Fig. 10 Variation of maximum temperature forecasts by EC model and the correction by different vertical rate schemes versus observations at (a) Wulong Station and (b) Qianjiang Bamianshan Station in August 2023 |
本文综合考虑模式气温预报、模式地形和实况气温、真实地形之间的相互关系, 采用随时空演变的动态近似垂直变率订正方法, 对2023年重庆158个观测站2 m模式最高和最低气温开展订正试验, 评估订正结果, 得到以下结论:
(1) EC模式对最高和最低气温预报性能的空间分布相似, 对最高气温的预报性能明显弱于最低气温且预报性能随预报时效延长而降低。模式地形高度偏差与模式气温预报偏差关系密切, 在模式地形高度偏差较小的地区, 气温预报性能较高, 反之亦然。
(2) 基于动态近似垂直变率的订正方案, 订正效果显著优于基于固定垂直变率的订正方案; 两个方案都能改善EC模式气温预报, 随预报时效延长订正效果下降, 对最高气温的订正效果优于最低气温。与EC模式预报相比, 基于动态近似垂直变率的订正结果, 最高和最低气温10 d平均预报准确率分别提高了12.71%和8.30%, MAE分别降低0.68℃和0.30℃, 系统偏差显著减小; 逐月预报效果都有改善, 24 h时效最高气温预报准确率月平均提高了20.34%, 4月、7月、8月提升幅度明显, 这与近似垂直变率的季节变化密切相关; 最低气温预报准确率月平均提高了14.44%, 除1月、12月外, 其余月份均在80%以上。订正后气温预报性能更加稳定。
(3) 基于动态近似垂直变率的订正方案, 其订正效果与模式地形高度偏差呈正相关, 即偏差越大的地区, 订正效果越显著。订正后, 在重庆东北部偏北的山区预报准确率提高幅度大, 气温预报系统性偏差显著减小, 8月最高气温负偏差极值由-12℃左右减小到-4℃左右, 2月最低气温负偏差极值由-9℃左右减小到-6℃左右, 气温偏差主要集中在-4~4℃。站点分析表明, 基于动态近似垂直变率的订正方案, 对波动幅度较小的天气过程具有较好的订正能力, 对明显的升温和降温过程订正能力有限。
深度学习方法在挖掘多源数据时空特征和推理效率上具有显著优势, 今后可利用动态近似垂直变率作为物理约束, 耦合LSTM/Transformer等模型, 引入更多的模式要素、雷达回波和小时尺度的观测数据等, 构建“模式-遥感-观测”联合订正框架, 提升复杂地形区和转折性天气过程的气温预报能力。
蔡怡, 徐枝芳, 朱克云, 等, 2023. CMA-MESO 3 km系统2 m温度预报诊断[J]. 气象, 49(4): 400-414. Cai Y, Xu Z F, Zhu K Y, et al, 2023. Diagnosis of 2 m temperature prediction by CMA-MESO system with 3 km resolution[J]. Meteor Mon, 49(4): 400-414 (in Chinese). DOI:10.7519/j.issn.1000-0526.2022.041501
|
陈鹤, 蔡荣辉, 陈静静, 等, 2022. 基于深度学习方法的气温预报技术应用与评估[J]. 气象, 48(11): 1373-1383. Chen H, Cai R H, Chen J J, et al, 2022. Application and evaluation of temperature forecast based on deep learning method[J]. Meteor Mon, 48(11): 1373-1383 (in Chinese). DOI:10.7519/j.issn.1000-0526.2022.070101
|
陈昱文, 黄小猛, 李熠, 等, 2020. 基于ECMWF产品的站点气温预报集成学习误差订正[J]. 应用气象学报, 31(4): 494-503. Chen Y W, Huang X M, Li Y, et al, 2020. Ensemble learning for bias correction of station temperature forecast based on ECMWF products[J]. J Appl Meteor Sci, 31(4): 494-503 (in Chinese).
|
代刊, 曹勇, 钱奇峰, 等, 2016. 中短期数字化天气预报技术现状及趋势[J]. 气象, 42(12): 1445-1455. Dai K, Cao Y, Qian Q F, et al, 2016. Situation and tendency of operational technologies in short- and medium-range weather forecast[J]. Meteorol Mon, 42(12): 1445-1455 (in Chinese). DOI:10.7519/j.issn.1000-0526.2016.12.002
|
冯良敏, 周秋雪, 康岚, 2019. 四川地区EC细网格模式2 m温度偏差订正研究[J]. 高原山地气象研究, 39(1): 34-40. Feng L M, Zhou Q X, Kang L, 2019. Study on 2 m temperature bias correction of EC model in Sichuan Province[J]. Plateau Mt Meteor Res, 39(1): 34-40 (in Chinese).
|
金荣花, 代刊, 赵瑞霞, 等, 2019. 我国无缝隙精细化网格天气预报技术进展与挑战[J]. 气象, 45(4): 445-457. Jin R H, Dai K, Zhao R X, et al, 2019. Progress and challenge of seamless fine gridded weather forecasting technology in China[J]. Meteor Mon, 45(4): 445-457 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.04.001
|
李框宇, 周梅, 陈玖英, 等, 2019. 一种适用于气温空间插值的改进梯度距离平方反比法[J]. 中国科学院大学学报, 36(4): 491-497. Li K Y, Zhou M, Chen J Y, et al, 2019. An approach of improved gradient plus inverse distance squared for spatial interpolation of temperature[J]. J Univ Chin Acad Sci, 36(4): 491-497 (in Chinese).
|
刘还珠, 赵声蓉, 陆志善, 等, 2004. 国家气象中心气象要素的客观预报——MOS系统[J]. 应用气象学报, 15(2): 181-191. Liu H Z, Zhao S R, Lu Z S, et al, 2004. Objective element forecasts at NMC——a MOS system[J]. J Appl Meteor Sci, 15(2): 181-191 (in Chinese).
|
罗伦, 旦增, 朱立平, 等, 2021. 藏东南色季拉山气温和降水垂直梯度变化[J]. 高原气象, 40(1): 37-46. Luo L, Dan Z, Zhu L P, et al, 2021. Vertical gradient changes of temperature and precipitation in the Sygera mountains, southeastern Qinghai-Xizang Plateau[J]. Plateau Meteor, 40(1): 37-46 (in Chinese).
|
申友利, 叶祖超, 张少峰, 等, 2017. 一种改进的Cressman插值方法在渤海表层总氮数据处理中的应用[J]. 海洋环境科学, 36(4): 622-628. Shen Y L, Ye Z C, Zhang S F, et al, 2017. A modified Cressman interpolation method applied to process total nitrogen data in Bohai surface waters[J]. Mar Environ Sci, 36(4): 622-628 (in Chinese).
|
陶诗言, 1980. 中国之暴雨[M]. 北京: 科学出版社. Tao S Y, 1980. Heavy Rainfalls in China[M].
Beijing: Science Press (in Chinese).
|
王乙竹, 王玮, 黄剑钊, 等, 2023. 利用地形高度差对ERA5气温降尺度的方法研究[J]. 气象研究与应用, 44(2): 33-38. Wang Y Z, Wang W, Huang J Z, et al, 2023. A methodological study of downscaling of ERA5 temperature using terrain height difference[J]. J Meteor Res and Appl, 44(2): 33-38 (in Chinese).
|
吴启树, 韩美, 郭弘, 等, 2016. MOS温度预报中最优训练期方案[J]. 应用气象学报, 27(4): 426-434. Wu Q S, Han M, Guo H, et al, 2016. The optimal training period scheme of MOS temperature forecast[J]. J Appl Meteor Sci, 27(4): 426-434 (in Chinese).
|
薛谌彬, 陈娴, 张瑛, 等, 2019. ECMWF高分辨率模式2 m温度预报误差订正方法研究[J]. 气象, 45(6): 831-842. Xue C B, Chen X, Zhang Y, et al, 2019. Bias correction method for the 2 m temperature forecast of ECMWF high resolution model[J]. Meteor Mon, 45(6): 831-842 (in Chinese). DOI:10.7519/j.issn.1000-0526.2019.06.009
|
杨彬, 马廷淮, 黄学坚, 2024. 基于注意力机制与自适应时序分解的气温预报模型[J]. 气象, 50(6): 723-732. Yang B, Ma T H, Huang X J, 2024. Air temperature forecasting model based on attention mechanism and AdaSTL[J]. Meteor Mon, 50(6): 723-732 (in Chinese). DOI:10.7519/j.issn.1000-0526.2024.031901
|
杨昌军, 陈渭民, 罗玲, 等, 2004. 高斯权重法在温度场插值中的应用研究[J]. 南京气象学院学报, 27(5): 606-614. Yang C J, Chen W M, Luo L, et al, 2004. Applications of Gaussian weighted method to the spatial interpolation of temperature[J]. J Nanjing Inst Meteor, 27(5): 606-614 (in Chinese).
|
杨绚, 代刊, 朱跃建, 2022. 深度学习技术在智能网格天气预报中的应用进展与挑战[J]. 气象学报, 80(5): 649-667. Yang X, Dai K, Zhu Y J, 2022. Progress and challenges of deep learning techniques in intelligent grid weather forecasting[J]. Acta Meteor Sin, 80(5): 649-667 (in Chinese).
|
曾晓青, 曹勇, 王玉, 等, 2024. 一种针对模式预报场的精细化插值新方法[J]. 大气科学, 48(5): 1879-1890. Zeng X Q, Cao Y, Wang Y, et al, 2024. A new fast refinement interpolation method for model forecasting[J]. Chin J Atmos Sci, 48(5): 1879-1890 (in Chinese).
|
占龙飞, 张传江, 胡菊芳, 等, 2018. 基于DEM的复杂地形气温空间插值研究[J]. 气象与减灾研究, 41(1): 57-62. Zhan L F, Zhang C J, Hu J F, et al, 2018. Spatial interpolation of temperature over complex terrain based on DEM[J]. Meteor Disast Reduct Res, 41(1): 57-62 (in Chinese).
|
赵滨, 李子良, 张博, 2016. 三维插值方法在2 m温度评估中的应用[J]. 南京信息工程大学学报: 自然科学版, 8(4): 343-355. Zhao B, Li Z L, Zhang B, 2016. Spatial and temporal characteristics of precipitation in Shijiazhuang during 1961-2014[J]. J Nanjing Univ Inform Sci Technol: Nat Sci Ed, 8(4): 343-355 (in Chinese).
|
赵瑞霞, 代刊, 王勇, 等, 2023. 动态垂直变率降尺度方法在气温智能网格预报中的应用[J]. 气象学报, 81(5): 788-800. Zhao R X, Dai K, Wang Y, et al, 2023. Application of a dynamic vertical change rate downscaling method in gridded temperature forecast[J]. Acta Meteor Sin, 81(5): 788-800 (in Chinese).
|
赵声蓉, 2006. 多模式温度集成预报[J]. 应用气象学报, 17(1): 52-58. Zhao S R, 2006. Multi-model consensus forecast for temperature[J]. J Appl Meteor Sci, 17(1): 52-58 (in Chinese).
|
赵声蓉, 赵翠光, 赵瑞霞, 等, 2012. 我国精细化客观气象要素预报进展[J]. 气象科技进展, 2(5): 12-21. Zhao S R, Zhao C G, Zhao R X, et al, 2012. The development of objective meteorological element forecast in China[J]. Adv Meteor Sci Technol, 2(5): 12-21 (in Chinese).
|
智协飞, 吴佩, 俞剑蔚, 等, 2019. GFS模式地形高度偏差对地面2 m气温预报的影响[J]. 大气科学学报, 42(5): 652-659. Zhi X F, Wu P, Yu J W, et al, 2019. Impact of topographic altitude bias of the GFS model on the 2 m air temperature forecast[J]. Trans Atmos Sci, 42(5): 652-659 (in Chinese).
|
Glahn B, Gilbert K, Cosgrove R, et al, 2009. The gridding of MOS[J]. Wea Forecasting, 24(2): 520-529. DOI:10.1175/2008WAF2007080.1
|
He Y Y, Wang K C, 2020. Contrast patterns and trends of lapse rates calculated from near-surface air and land surface temperatures in China from 1961 to 2014[J]. Sci Bull, 65(14): 1217-1224. DOI:10.1016/j.scib.2020.04.001
|
Holden J, Rose R, 2011. Temperature and surface lapse rate change: a study of the UK's longest upland instrumental record[J]. Int J Climatol, 31(6): 907-919. DOI:10.1002/joc.2136
|
LeMone M A, Ikeda K, Grossman R L, et al, 2003. Horizontal variability of 2-m temperature at night during CASES-97[J]. J Atmos Sci, 60(20): 2431-2449. DOI:10.1175/1520-0469(2003)060<2431:HVOMTA>2.0.CO;2
|
Minder J R, Mote P W, Lundquist J D, 2010. Surface temperature lapse rates over complex terrain: lessons from the Cascade mountains[J]. J Geophys Res Atmos, 115(D14): D14122.
|
Oshima N, Kato H, Kadokura S, 2002. An application of statistical downscaling to estimate surface air temperature in Japan[J]. J Geophys Res Atmos, 107(D10): ACL 14-1-ACL 14-10.
|
Shen Y J, Shen Y J, Goetz J, et al, 2016. Spatial- temporal variation of near-surface temperature lapse rates over the Tianshan mountains, central Asia[J]. J Geophys Res Atmos, 121(23): 14006-14017.
|
 2025, Vol. 51
2025, Vol. 51 
