引言

数值天气预报是天气预报业务和防灾减灾的核心科技，被称为气象领域的“国之重器”。数值天气预报涉及大气科学、数学、物理学、力学、地理学、计算机科学等多学科，是一门多学科综合交叉的科学，其系统的建立及其在天气预报和服务保障中的应用是高度复杂和严格的系统性工程。可以说，数值天气预报是气象科技水平的综合体现，是保障国计民生和国防安全的气象核心科技的重要组成部分。

中国数值天气预报研究和业务应用一直受到高度重视，在理论、方法和数值模式研究方面取得了有广泛国际影响的研究成果。沈学顺等(2020)系统回顾了新中国数值天气预报自主创新研究的成果，特别是对Global/Regional Assimilation and PrEdiction System(GRAPES)在半隐式半拉格朗日格点模式技术、物理过程、非静力全球模式四维变分同化以及区域/全球一体化确定性预报和集合预报系统业务的建立和应用等方面所取得的重要进展进行了综述。可以说，自主研发的数值天气预报全面业务体系的建立是中国数值预报发展历程中里程碑式的事件，是二十余年坚持既定科学技术方向以及研究和业务紧密结合、经验不断积累的结果，是中国自主发展数值天气预报技术并走向国际前列的重要起点。

本文在沈学顺等(2020)综述文章的基础上，针对新世纪以来GRAPES系统(后改命名为CMA模式)自主创新发展过程中取得的原创性成果进行综述。数值预报历经70余年的发展，欧美主要业务中心在数值模式、同化及观测资料同化应用等诸方面积累了较为成熟的技术方法(Bauer et al, 2015)。我国在借鉴已有科技成果的同时，在数值算法、物理过程、卫星资料同化等多方面做出了有特色、原创成果。

为了提高现有业务系统CMA-GFS(即原GRAPES_GFS)模式的时间、空间离散化精度，并提升系统的积分效率和稳定性，苏勇等(2018；2020)引入了基于气候态的三维参考廓线，张红亮和沈学顺(2021)、张红亮等(2022)按照预估-修正二时间层半隐式半拉格朗日的方案重新设计了动力学方程组的求解方法，以二者为主题构建了新版本的动力框架(Shen et al, 2023), 大幅度提升了系统的预报性能。面向未来全球千米尺度数值模拟、E级(百亿亿次级)超级计算下高精度和高可扩展性的需求，为解决CMA-GFS在计算精度、数值守恒性和并行扩展性方面的瓶颈，Li et al(2013；2020)基于立方球网格研发了多矩约束有限体积方法的动力框架。Tang et al(2021；2022)基于该方法，开发了一种在立方球网格上的高精度、守恒、无振荡、正定保形的全球平流方案，保证了模式对暴雨等极端天气的模拟能力。云物理过程的不确定性是数值模式误差主要来源之一，为解决CMA-GFS中云和降水预报精度不足的难题，刘奇俊等(2003)和Ma et al(2018；2022)研发了一套新的云物理方案，主要包括大尺度宏观云方案、次网格对流卷出对格点尺度的反馈方案、双参数云微物理方案和云量显式预报方案，并改进了冰云对辐射的影响作用，有效提高了CMA-GFS系统中云和定量降水的预报能力(马占山等，2021)。业务数值预报系统目前已达千米级，未来将达到百米级，边界层过程的合理参数化是我们面临的重要科学问题，Zhang et al(2018)发展了尺度自适应的三维湍流参数化方案，显著提高了高分辨率下模式对边界层和对流过程的描述能力。

卫星观测算子是连接数值模式和卫星观测数据的桥梁，快速辐射传输模式的发展对卫星资料同化至关重要，Weng et al(2020)和Yang et al(2020)研发了适用于国内外各种卫星辐射率资料的快速辐射传输模式ARMS(advanced radiative transfer modeling system), 并与CMA-GFS模式耦合业务运行，支撑了模式中卫星资料的同化应用，稳步提升了系统的预报性能。切线性模式与伴随模式是四维变分同化(4DVar)系统的核心组成部分，刘永柱等(2017)开发了基于CMA-GFS非静力全球模式的切线和伴随模式，并实现了较高的并行计算效率，为CMA-GFS 4DVar系统的研发构建、业务化应用与推广奠定了坚实基础，显著提升系统的同化能力和预报精度。为了减小卫星资料同化中观测和背景场的系统性偏差，Han(2014)、Han and Bormann(2016)发展了有约束的卫星资料偏差订正方法，有效解决了观测偏差向模式偏差的漂移问题。风云四号A星(FY-4A)携带有目前国际上少有的在静止轨道上运行的红外高光谱大气探测仪，对于强对流、台风等高影响天气的预报具有重要价值，尹若莹等(2019)和Han(2021)开发了FY-4探测仪资料同化的多项核心技术，突破了静止卫星大面阵、多探元、高光谱、高时间分辨率探测仪资料同化的多项难题，有效提高了业务数值天气预报的准确率。

本文第一部分回顾了在预估-修正半隐式半拉格朗日算法、多矩约束有限体积方法、高精度正定保形平流、双参数云物理方案和尺度自适应湍流参数化方案方面的自主创新发展，第二部分回顾了辐射传输模式、四维变分同化、卫星资料同化等方面的理论发展和方法创新，最后进行总结和讨论。

1 数值模式基础算法和物理过程方面 1.1 预估-修正半隐式半拉格朗日算法

半隐式半拉格朗日(SISL)技术可以使用较大的时间步长，大幅度地提高模式的积分效率，在过去几十年里广泛应用于世界各国的数值天气预报系统中(Staniforth and Côté, 1991)。通常半隐式计算时会引入参考廓线，将温度和压力方程中的右端项分解为线性项和非线性项，线性项隐式计算，非线性项一般外插处理，这种简单的外插可能增大计算误差或者导致模式积分溢出(Gospodinov et al, 2001；Hortal, 2002)。同时，传统的半拉格朗日算法假设质点做匀速直线运动, 使用中间时刻中间点的速度计算上游点的位置，该速度通常通过时间外插得到，同样会对计算精度和稳定性造成影响，特别是在急流轴、台风眼等速度不随时间线性变化的区域(Cordero et al, 2005)。

为了解决上述问题，Hortal(2002)将匀速直线运动的假设改为匀加速直线运动假设，设计了稳定外插的二时间层方案(SETTLS)，一定程度上提高了SISL算法的稳定性。但Durran and Reinecke(2004)指出SETTLS本质上仍然是时间外插方案，不能从根本上解决外插带来的计算不稳定问题。同时，Durran and Blossey(2012)、Kar(2012)提出通过预估-修正(Predictor-Corrector)的方法，对非线性项采用多步计算，避免外插的影响。加拿大气象局的Global Environmental Multiscale模式(Côté et al，1998)首先在二时间层-半隐式半拉格朗日(2TL-SISL)时间积分中使用了预估-修正算法，Cullen(2001)将预估-修正方法应用于ECMWF-IFS模式中，英国气象局的New Dynamical Core和Even Newer Dynamics for General atmospheric modelling environment(Wood et al, 2014)在其SISL时间积分中都采用基于预估-修正思路的算法。

另外，方程组线性化时参考廓线的选择对半隐式算法的精度和收敛性非常重要(Simmons and Temperton, 1997；Temperton et al, 2001)，通常要使得非线性项在量级上小于线性项，参考廓线一般满足静力平衡且不随积分发生变化。早期，Zeng et al(1989)基于标准大气层结和静力平衡关系构造了一维参考廓线，陈嘉滨和舒静君(1994)将该方法应用于ECMWF-IFS模式，有效地提高了模式的空间离散化精度。随后，研究人员就该问题开展了广泛的研究，目前各个天气模式、气候模式在求解动力学方程组的时候都会引入基于等温大气、一维或者二维基本态的参考廓线，以提高气压梯度力、复杂地形处平流计算等的空间离散化精度(Liang, 1996；Skamarock et al, 2012；Wu et al, 2008)。

CMA-GFS模式原先采用基于等温大气构造的参考廓线，在模式高层空间离散化误差较大，且会引发积分溢出。苏勇等(2018；2020)在CMA-GFS中引入基于气候场的三维参考廓线，其中位势温度和无量纲气压的参考态满足静力平衡，不随积分时间发生变化。相比于等温大气，预报方程在离散化之后右端会出现参考态的水平导数项，需放入线性项部分参加方程组的推导，增加了框架求解的复杂性。

线性化之后的预报方程可以写为下面的一般形式：

$ \frac{\mathrm{d} \psi(X, t)}{\mathrm{d} t}=L(X, t, \psi)+N(X, t, \psi) $

(1)

式中：X代表位置，ψ为预报变量，L是线性项，N是非线性项。设计预估-修正时间积分方案时，对非线性项在预估步采用Adams-Bashforth算法(Durran and Blossey, 2012；Kar, 2012)，在修正步采用线性内插法；对线性项在预估步采用Adams-Moulton算法(Durran and Blossey, 2012)，在修正步采用线性内插法。将两部分结合起来，就形成了二阶精度的预估-修正2TL-SISL时间积分方案(Shen et al, 2023)，公式如下：

$ \begin{gathered} \frac{\psi^*-\psi_d^n}{\Delta t}=N\left(\psi^*\right)^{n+\frac{1}{2}}+ \\ \alpha_1 L\left(\psi^*\right)+\left(1-\alpha_1\right) L_d\left(\psi^{n-1}\right) \\ \frac{\psi^{n+1}-\psi_d^n}{\Delta t}=\frac{1}{2}\left(N\left(\psi^*\right)+N_d\left(\psi^n\right)\right)+ \\ \frac{1}{2}\left(L\left(\psi^{n+1}\right)+L_d\left(\psi^n\right)\right)= \\ \left(1-\alpha_2\right)(L+N)_d^n+\alpha_2\left(N\left(\psi^*\right)+L\left(\psi^{n-1}\right)\right)\\ N\left(\psi^*\right)^{n+\frac{1}{2}} =\frac{3}{2} N\left(\psi^n\right)-\frac{1}{2} N\left(\psi^{n-1}\right) \\ \alpha_1 =\frac{3}{4}, \alpha_2=\frac{1}{2} \end{gathered} $

(2)

式中：下标d代表上游点，上标n，n+1/2, n+1为时间层，上标*为预估值，α为半隐式系数。

对于上游点的位置，在预估步仍然使用时间外插得到的n+1/2时刻中间点速度计算，在修正步使用预估计算的n+1时刻风速和前一步的n时刻风速内插得到n+1/2时刻中间点风速计算。

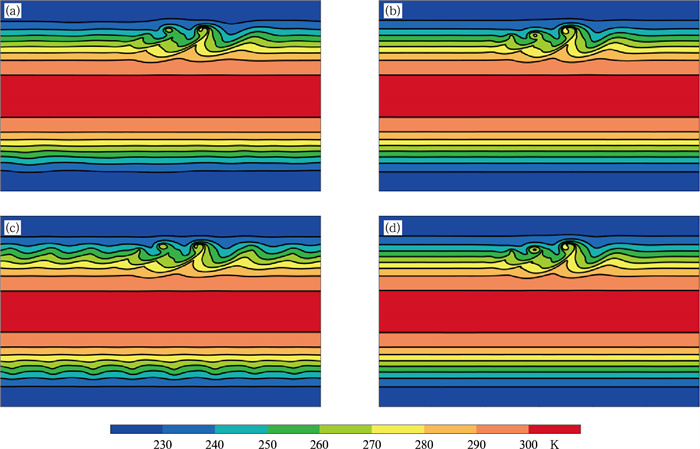
在稳定的地转平衡风场中叠加纬向风的扰动会触发斜压波动的产生，数值模式可以模拟斜压波的发生、发展和消亡过程(Jablonowski et al, 2008)。基于斜压波试验，测试采用预估-修正算法和三维参考廓线之后CMA-GFS动力框架计算精度的变化(图 1)。试验方案：采用0.5°水平分辨率，60层非均匀垂直分层，分别测试600、1200、1800 s的时间步长，积分15 d。

从图 1中可以看到，两组试验都可以模拟出积分9 d之后斜压波的分布，但也存在明显的区别：首先，在600 s时间步长的情况下，新框架模拟的斜压波(图 1b)相比于旧框架(图 1a)强度更强，更加接近于参考解(Jablonowski et al, 2008)；其次，当时间步长翻倍之后，旧框架无法维持波动的形态和强度(图 1c)，新框架在不同的时间步长之下可以维持相同的预报精度(图 1d)。这显示出新框架具有更高的时间、空间离散化精度，且在维持预报精度的情况下可以使用较大的时间步长，从而大幅提高模式积分效率。

1.2 多矩约束有限体积方法

在众核超算的驱动下(Yang et al，2016)，数值天气预报模式分辨率朝着全球千米级、区域百米级方向发展，我国现有业务数值天气预报CMA-GFS(沈学顺等，2017)模式动力框架(Chen et al，2008)在计算精度、数值守恒性以及并行可扩展性等方面存在瓶颈，无法满足精细化业务发展的需求。例如其基于点概念的半拉格朗日模式框架无法保证质量严格守恒，基于变量交叉分布网格的二阶中央差分离散气压梯度力使得模式框架理论精度不超过二阶，同时大型线性Helmholtz方程数值求解的全局并行通信使得模式在高分辨率下并行可扩展性较弱。因此，需要新的大气数值计算方法适应这种新的挑战。多矩约束有限体积方法(Xiao, 2004；Xiao et al, 2006；2013；Chen and Xiao, 2008；Ii and Xiao, 2009)是国际上能够充分利用众核计算、局地高阶重构发展新一代大气模式的代表性高精度数值方法之一(沈学顺等，2022)。

这是一种比较新颖的局地高阶数值重构的数值算法，它在单元网格内定义可用于描述物理场变量的点值(PV)、积分平均值(VIA)以及导数值(DV)，这些量称之为矩(moment)，通过施加多矩约束条件推导出预报变量的时间演变方程。不同于传统有限体积方法，多矩约束有限体积方法不仅使用了积分平均值，而且在局地数值重构时可采用点值和导数值，是对传统有限体积方法的拓展。下面从一维守恒律出发，简要介绍三点多矩约束有限体积方法的数值离散思想。考虑双曲守恒律方程:

$ \frac{\partial q}{\partial t}+\frac{\partial f(q)}{\partial x}=0 $

(3)

式中：q为预报变量，f(q)=uq为通量函数，u为速度。考虑一维计算域中的计算单元$ \varOmega_i= \left[x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}\right], i=1, 2, \cdots, I$，在计算单元Ω_i内的等距求解点$ x_{i 1}=x_{i-\frac{1}{2}}, x_{i 2}=\frac{x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}}}{2}, x_{i 3}=x_{i+\frac{1}{2}}$上定义预报变量q_ik, k=1, 2, 3。为了推导式(3)的多矩约束时间演变方程，定义两类矩：

VIA矩

$ \bar{q}_i(t)=\frac{1}{\Delta x_i} \int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} q(x, t) \mathrm{d} x $

(4)

式中：$ \Delta x_i=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}} $。

PV矩

$ q_{i 1}(t)=q\left(x_{i-\frac{1}{2}}, t\right), q_{i 3}(t)=q\left(x_{i+\frac{1}{2}}, t\right) $

(5)

通过施加这两类矩于式(3)，可得到其时间演变方程:

$ \left\{\begin{array}{l} \frac{\mathrm{d} \bar{q}_i}{\mathrm{~d} t}=-\frac{1}{\Delta x_i}\left(\hat{f}_{i+\frac{1}{2}}-\hat{f}_{i-\frac{1}{2}}\right) \\ \frac{\mathrm{d} q_{i 1}}{\mathrm{~d} t}=-\hat{f}_{x, i-\frac{1}{2}} \\ \frac{\mathrm{~d} q_{i 3}}{\mathrm{~d} t}=-\hat{f}_{x, i+\frac{1}{2}} \end{array}\right. $

(6)

式中：$ \hat{f}_{i-\frac{1}{2}}$与$ \hat{f}_{x, i-\frac{1}{2}}$分别表示计算单元界面$ x_{i-\frac{1}{2}}$的近似数值通量及其导数。利用三点辛普森公式 q_i=(q_i1+4q_i2+q_i3)/6，预报变量q_ik, k=1, 2, 3的更新方程可写为：

$ \left\{\begin{array}{l} \frac{\mathrm{d} q_{i 1}}{\mathrm{~d} t}=-\hat{f}_{x, i-\frac{1}{2}} \\ \frac{\mathrm{~d} q_{i 2}}{\mathrm{~d} t}=-\frac{3}{2 \Delta x_i}\left(\hat{f}_{i+\frac{1}{2}}-\hat{f}_{i-\frac{1}{2}}\right)+\frac{1}{4}\left(\hat{f}_{x, i-\frac{1}{2}}+\hat{f}_{x, i+\frac{1}{2}}\right) \\ \frac{\mathrm{d} q_{i 3}}{\mathrm{~d} t}=-\hat{f}_{x, i+\frac{1}{2}} \end{array}\right. $

(7)

值得注意的是，$ \hat{f}_{i-\frac{1}{2}}$可直接由界面处定义的q_ik和u_ik计算得到，而$ \hat{f}_{x, i-\frac{1}{2}}$则通过求解导数黎曼问题获得(Ii and Xiao, 2009)。多矩约束有限体积方法同先进的不连续伽辽金(Cockburn and Shu, 1989；Giraldo et al, 2002)、谱有限元(Taylor et al，1997；Giraldo and Rosmond, 2004)等方法属于同一类局地高阶重构数值算法，相比较而言，多矩算法的构造方式具有明确物理意义，数值离散、更新过程简洁，计算效率高。Smolarkiewicz et al(2016)指出大气动力框架是当前研究热点，多矩算法是近期利用高精度计算技术开发新动力框架的代表性工作之一。基于立方球网格的多矩守恒半拉格朗日平流算法在美国国家大气研究中心(NCAR)获得了应用(Erath and Nair, 2014)。

采用局地高阶数值重构的多矩约束有限体积方法，中国气象局发展下一代高精度、守恒、可扩展大气模式取得了一系列代表性研究成果。Li et al(2013)在笛卡尔坐标系下发展了具有三阶和四阶精度的完全可压缩守恒的二维非静力大气动力框架，标准数值试验测试表明该框架数值模拟能力同国际上基于不连续伽辽金方法发展的非静力大气动力框架相当，验证了多矩算法对大气非静力运动行为的仿真能力。Chen et al(2014)基于三阶多矩约束有限体积方法，发展了基于立方球网格、正二十面体网格及阴阳网格的浅水波模式，模式在不同球面网格上获得了一致三阶收敛。球面浅水模式标准算例试验表明，采用多矩约束有限体积方法在数值解的质量和计算简便性之间取得了很好的平衡，这为在不同球形网格上建立大气环流模式动力框架提供了准确而实用的依据。Qin et al(2019)将笛卡尔坐标系下二维非静力大气动力框架拓展到三维，孤立山理想数值结果表明，三维非静力模式动力框架模拟的背风坡湍流尾流与其他现有先进模式(Smolarkiewicz et al，2013)相当，且非静力山脉波更光滑合理，进一步验证该框架非常具有竞争力。基于前述研究基础，Chen et al(2023)基于球面立方球网格发展了高精度多矩完全可压缩守恒非静力大气模式动力框架，其水平采用四阶多矩有限体积方法显式求解，垂直采用守恒有限差分方法，而时间推进上采用水平显式垂直隐式时间积分。球面三维数值结果表明，多矩非静力模式数值模拟的质量与现有的先进模式相当，具备作为开发大气环流模式的巨大实用潜力。在示踪物平流模式方面，Tang et al(2022)在球面立方球网格上发展了三维正定守恒的多矩有限体积平流模式，该模式水平方向采用四阶无振荡的梯度调节转换方法，同时为了保证数值正定性，采用了单元边界通量订正技术(Li et al，2020)，而垂直采用基于有理函数重构的多矩守恒半拉格朗日方法。开展的各种基准测试包括三个代表性的平流测试和一个理想化的污染化学测试，其数值结果表明，与目前文献中的现有平流模式相比具有很强的竞争力并且适用于实际大气的模拟。至2025年，基于多矩约束有限体积方法发展的非静力大气模式动力框架，已经耦合了升级的CMA-GFS物理过程软件包，建成了具备完全自主知识产权的多矩非静力大气模式系统。

1.3 高精度正定保形平流方案

作为大气模式中的基本组成部分，准确模拟示踪物在实际大气模式中的运动一直是数十年来的研究热点。理想的数值方法应具备多方面的特性，例如精度、稳定性、局部性、守恒性、保形性以及计算效率(Rasch and Williamson, 1990)。低阶精度方法通常会产生较大的误差，该种误差将在大气模式中迅速积累，严重影响模式预报的可靠性。鉴于此，发展高精度的平流方案显得尤为重要。Jakob-Chien et al(1995)将谱方法用于模拟大气模式中的湿度场，并获得了高精度。然而，由于吉布斯振荡，模拟结果不可避免地会产生负的数值解。作为替代方案，基于点值的半拉格朗日方法(Staniforth and Côté, 1991)广泛应用于格点模式中。半拉格朗日方法具有良好的计算效率和稳定性，但基于点值的方法无法保证质量守恒。因此，许多学者提出了守恒的半拉格朗日方法，例如守恒单元积分半拉格朗日方法(Nair and Machenhauer, 2002)，结合分段抛物线重构(Nair et al, 2002)、分段三次多项式重构(Zerroukat et al, 2004)和分段样条重构(Zerroukat et al, 2007)的守恒级联半拉格朗日方法，守恒半拉格朗日多示踪物方法(Lauritzen et al, 2010)及其通量形式方法(Harris et al, 2020)等。近年来，基于局地高阶数值重构的方法因其在大规模并行计算机上的高可扩展性和网格灵活性，已成为现在大气数值模式平流方案研究的焦点。连续和不连续的伽辽金方法(Nair et al, 2002；Hall and Nair, 2013；Guo et al, 2016)是能够满足局地这一理想特性的代表性高阶方法。高阶方法有利于光滑场的模拟，但在间断及大梯度附近会产生非物理噪声。为了处理这种情况，需采取修正方法(Qiu and Shu, 2005；Zhang and Shu, 2010)来抑制数值解中的非物理振荡。

作为传统有限体积方法的扩展，具有局地重构的多矩有限体积(multi-moment finite-volume, MMFV)方法是一种在有限体积方法背景下获得高精度的新方法(Ii and Xiao, 2007；Chen and Xiao, 2008)。多矩约束有限体积方法借鉴了CIP(constrained interpolation profile)方法(Yabe and Aoki, 1991)的基本思想，在一个单元内引入多种类型的矩(见1.2节)，用于重构空间近似。不同类型的矩可通过不同的方法更新。例如，多矩约束有限体积方法中的积分平均值通过有限体积方法中的通量形式更新保证数值守恒性，而点值可以灵活地通过欧拉方法(Xiao et al, 2002；Sun et al, 2015)或半拉格朗日方法(Xiao et al, 2002；Ii and Xiao, 2007；Sun and Xiao, 2017)更新。如上所述，高阶方法在大梯度或间断附近会产生非物理振荡。为了抑制高阶多矩方法中的数值振荡，Xiao and Peng(2004)提出了一种保凸性的限制器，Xiao et al(2002)提出了一种无振荡的有理重构函数，Sun et al(2015)基于WENO(weighted essential non-oscillatory)设计了一种高精度的斜率限制器，Sun and Xiao(2017)设计了高阶边界梯度切换(BGS)限制器。

在实际大气模式中，除了需要考虑平流方案的守恒性、无振荡性和保形性等数值特性外，水平和垂直网格间距的巨大差异导致不同方向上库朗数(Courant number)的差别也需特别关注。因此，为了提高计算效率，平流方案应采用允许垂直方向上在较大库朗数条件下能稳定计算的数值方法。本部分的研究工作基于多矩思想发展了一种在立方球网格上的守恒、无振荡、正定保形的全球平流方案。该方案采用Strang维度分裂方法(Gottlieb, 1972)，在二维水平(球面)和一维垂直方向分别使用不同的数值方法进行更新。在水平方向上，采用高阶无振荡MCV3-BGS(three-point multi-moment constrained finite volume method with boundary gradient switching algorithm)方法(Deng et al, 2017)；在垂直方向上，采用允许大时间步长的半拉格朗日分段有理函数(piecewise rational method, PRM)方法(Xiao and Peng, 2004)，从而在计算上非常高效，适合实际应用。此外，该平流方案还采用了我们先前工作中提出的两种正定修正(Li et al, 2020；Tang et al, 2021)，以确保数值解的正定性。结合上述特征，新研制的平流方案称为MCV3_BGS-PRM方案。

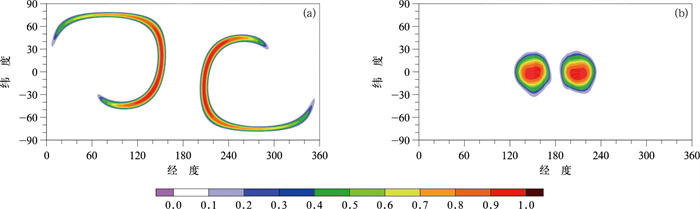
为验证平流方案在复杂流场中的数值特性，采用变形流试验进行测试。该试验中，初值会逐步发生变形，直至半周期时变形达到最大，在后半周期又逐渐回复到初始状态。试验设置与Kent et al(2014)一致，试验中有四种具有不同初始分布的平流物质。第一个平流物质(称为q₁，余同)是准光滑的余弦钟；q₂=0.9-0.8q₁²，与q₁非线性相关；q₃为有切口的圆柱，具有强间断，以验证平流方案抑制非物理数值振荡的性能；q₄与前三个线性相关，$ 1-\frac{3}{10}\left(q_1+q_2+q_3\right)$。试验所用分辨率与Kent et al(2014)相同，垂直为60层，网格间距Δz=200 m；水平方向立方球网格分辨率为45×45×6，相当于沿赤道的自由度分辨率为1°；时间步长为Δt=864 s。q₁在z=4900 m处半周期及一周期的试验结果如图 2所示，从图中可以看出，MCV3_BGS-PRM方案模拟结果无明显的上冲和下冲。

试验标准误差如表 1所示。标准误差定义为：

$ \begin{aligned} l_1 & =\frac{\int_{\varOmega}\left|q-q_t\right| \mathrm{d} \varOmega}{\int_{\varOmega}\left|q_t\right| \mathrm{d} \varOmega} \\ l_2 & =\sqrt{\frac{\int_{\varOmega}\left(q-q_t\right)^2 \mathrm{~d} \varOmega}{\int_{\varOmega} q_t^2 \mathrm{~d} \varOmega}} \\ l_{\infty} & =\frac{\max \left|q-q_t\right|}{\max \left|q_t\right|} \end{aligned} $

式中：Ω是全局计算区域，q是数值解，q_t是精确解。表中同时列出多个先进大气动力核心平流方案的模拟结果(Kent et al，2014；Hall et al，2016)，以进行对比分析。其中，CAM-FV为NCAR基于经纬度网格和有限体积法开发的动力核心，CAM-SE为NCAR基于立方球网格和谱元法开发的动力核心，MCore则是美国密歇根大学基于立方球网格和有限体积法开发的动力核心。从表中可以看出，对于准光滑的q₁，MCV3_BGS-PRM的结果比Mcore好(l₁误差除外)，与CAM-SE相当。但要逊于CAM-FV方案的结果差，主要原因可能是因为CAM-FV方案的自由度多于MCV3_BGS-PRM。在该试验中，CAM-FV在水平经纬度网格的总自由度为360× 180，而MCV3_BGS-PRM方案所用立方球网格的总自由度为24×45×45+2，两者之比大约为4∶3。对于具有强间断的q₃，MCV3_BGS-PRM的结果与其他方案相当，其中l_∞误差都好于其他方案。试验结果表明，该平流方案具备无振荡性、正定性，与国际同类型平流方案相比，在计算精度方面表现出较强的竞争力。

1.4 双参数云微物理

云物理方案是数值模式中最重要的物理方案之一。由于云降水粒子的相态、尺度和物理属性等差异显著，且在当前的水平分辨率下难以解析云的全部生消过程，数值模式对云微物理过程描述存在相当困难，云物理过程的不确定性是模式误差的主要来源之一(IPCC, 2022；Solomon et al, 2007)，对其正确描述已成为提高数值模式预报性能的关键。

在CMA-GFS模式发展初期，云微物理方案来自于区域天气预报模式，这些方案属于纯粹的微物理方案，仅在网格平均水汽达到饱和时才会考虑云的形成。然而，对于相对较粗分辨率的全球中期数值天气模式而言，要在几十千米分辨率内达到饱和状态并非易事，尤其是在对流活跃的热带地区将变得更加困难。因此，仅使用云微物理方案会明显低估低纬地区水凝物含量和网格尺度降水。同时，由于网格平均水汽难以饱和，热带地区云微物理过程会以蒸发为主，在大气云凝结层内除了对云的预报会出现不足外，也会出现云微物理方案以蒸发、降温大气为主要分布特征的不合理现象。

为解决这些问题，研发团队在调研世界主要数值预报中心全球模式中湿物理过程处理基础上(Tiedtke, 1993；Zhao et al, 1997；Harris et al, 2020；McTaggart-Cowan et al, 2019)，总结CMA-GFS模式影响热带地区云和降水预报低估的主要原因，经过多年持续研发与优化改进，建立了一套适宜于CMA-GFS动力框架和物理过程的新云物理方案(Ma et al，2018；谭超等，2013)，该方案于2016年在CMA-GFS版本升级中实现了业务化应用(沈学顺等, 2021)。对于水凝物预报而言，新云物理方案共包括大尺度宏观云方案、次网格对流卷出对格点尺度的反馈方案、双参数云微物理方案共三个子云方案。其中，大尺度宏观云物理方案是处理网格平均水汽达到相对湿度阈值时的云凝结问题，其关键点是新凝结量与相对湿度的合理分布；次网格对流卷出对格点尺度的反馈方案作为格点尺度水凝物和云量的一个重要源项，主要考虑对流卷出和补偿环境空气时对格点尺度云形成的影响；双参数云微物理方案则是处理云内水凝物粒子转化和地面降水的重要环节，通过水凝物的源汇项、含水量以及云加热廓线(温度倾向)等影响模式动力过程。同时，建立了一套云量显式预报方案，以提高辐射计算精度。

在CMA-GFS业务模式云物理方案中，水凝物混合比和数浓度以及云量的预报方程可以表征为：

$ \begin{gathered} \frac{\partial q_x}{\partial t}=A\left(q_x\right)+S_{\mathrm{conv}}\left(q_{\mathrm{c}} q_{\mathrm{i}}\right)+ \\ S_{\mathrm{macro}}\left(q_{\mathrm{c}} q_{\mathrm{i}}\right)+S_{\mathrm{micro}}\left(q_x\right)+D\left(q_x\right) \end{gathered} $

(8)

$ \begin{gathered} \frac{\partial N_x}{\partial t}=A\left(N_x\right)+S_{\mathrm{conv}}\left(N_{\mathrm{i}}\right)+S_{\text {marco }}\left(N_{\mathrm{i}}\right)+ \\ S_{\text {micro }}\left(N_x\right)+D\left(N_x\right) \end{gathered} $

(9)

$ \frac{\partial a}{\partial t}=A(a)+S_{\mathrm{conv}}(a)+S_{\mathrm{strat}}(a)+S_{\mathrm{evap}}(a) $

(10)

$ \frac{\partial T}{\partial t}=A(T)+S_{\mathrm{conv}}(T)+S_{\mathrm{marco}}(T)+S_{\mathrm{micro}}(T) $

(11)

式(8)~(10)中：q和N分别表示为水凝物的混合比和数浓度，下标x代表不同的水物质种类，分别用v、c、r、i、s和g表示水汽、云水、雨水、冰晶、雪和霰。由于双参数云微物理中未考虑云滴数浓度的预报，因此，N_x只表示雨滴、冰晶、雪和霰的数浓度。a为云量，T为温度。A(q_x)、A(N_x)和A(a)项表示动力过程的水平或垂直平流作用引起的水物质混合比、数浓度以及云量在网格体积边界的变化率。S_conv(q_cq_i)、S_conv(N_i)和S_conv(a)则是由于次网格对流卷出过程对格点尺度云水和冰晶的混合比、冰晶数浓度以及云量的贡献率。S_macro(q_cq_i)和S_macro(N_i) 是格点平均水汽达到相对湿度阈值时，由大尺度宏观云物理方案计算的云水和冰晶混合比以及冰晶混合比的变化率。S_micro(q_x)和S_micro(N_x)则是不同水物质在双参数云微物理方案中由于微物理转化过程发生的变化率。D(q_x)和D(N_x)是有落速的水凝物粒子在沉降过程中的变化率，此处x只代表雨水、冰晶、雪和霰。S_strat(a)是由于层云凝结过程所产生的云量生成率，S_evap(a)则是因为云边界的蒸发过程引起的云量减少率。式(11)右端第2~4项分别是次网格对流卷出反馈方案、大尺度宏观云物理方案和云微物理方案中由于相态变化引起的温度变化率。需要说明的是，在上述预报方程中的大尺度宏观云物理方案和次网格对流卷出反馈方案中只考虑对云水和冰晶的影响，新生成的云水和冰晶更新到网格平均尺度后，通过微物理转化过程参与到大粒子水凝物以及降水的形成过程。

CMA-GFS全球模式中的云微物理方案需要格点水汽达到液面或冰面饱和时才开始计算凝结过程，这在粗分辨率条件下，会导致低纬热带地区云和格点降水预报明显偏少的现象。为解决该问题，引入了大多全球模式中均采用的Sundqvist计算网格尺度上云生成的方案(Sundqvist, 1988；Sundqvist et al, 1989；McTaggart-Cowan et al, 2019)。格点尺度平均水汽状况达不到饱和的情况下，如果湿度达到一定的阈值，该方法可以通过模式热动力过程和其他物理过程引起的温度和水汽的变化，来计算格点内的次网格云凝结过程，并将次网格的云凝结和云预报过程反馈到格点尺度。由于该方案是以数值模式中的大尺度热动力和物理过程共同参数化格点尺度云的形成，因此该方法通常被称之为宏观云物理方案。

在CMA-GFS全球模式的原有云方案中，没有充分考虑对流参数化中的对流卷出对格点尺度云微物理过程的影响，因此不能很好地预报出热带低纬对流旺盛区域中水凝物含水量分布，导致云预报不足。为此，参考ECMWF-IFS模式的做法(ECMWF Documentation, 2012)，在云方案中加入次网格深对流和浅对流卷出过程，将次网格深浅对流中上升气流中的云水和云冰夹卷作用反馈到格点尺度，作为格点尺度云水和云冰的源项加入到预报方程中，格点尺度水凝物含水量和格点降水量明显增加(Ma et al, 2018；谭超等, 2013)。

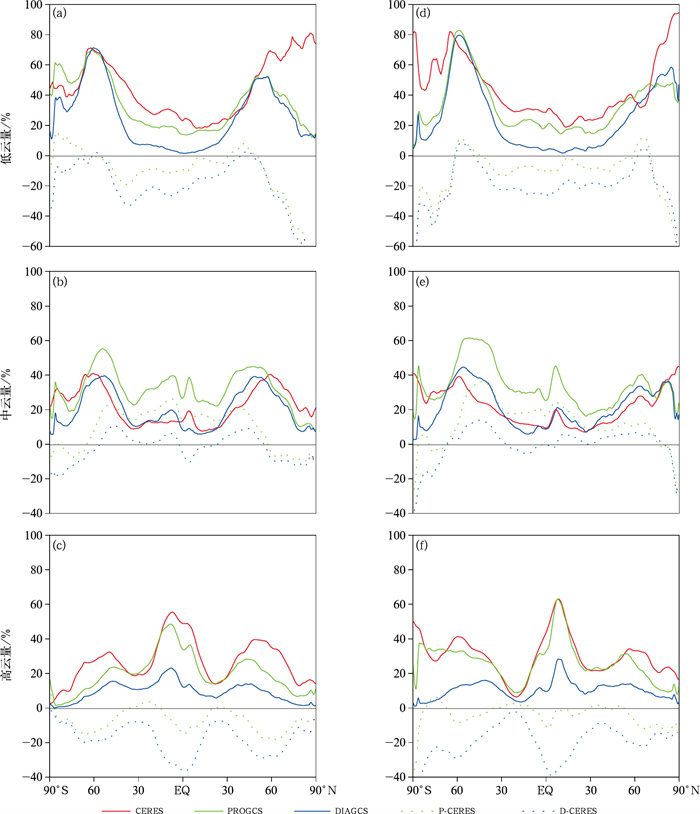
另外，基于Tiedtke(1993)的工作，Ma et al(2018)在CMA-GFS中建立新的云量显式预报方案，替代原有的通过相对湿度和大尺度网格平均凝结水混合比的函数关系来诊断云量的方案(Xu and Randall, 1996)。对比该云量预报方案与原有的将云量参数化为相对湿度和水凝物含量的诊断方案发现，云量预报方案能更好地模拟出海上层积云的日变化特征、改进低云量和高云量显著偏少的问题, 对总云量也有较明显的改进，但对中云量预报存在中低纬度偏多、正偏差增大现象(图 3)，云量的预报也显著提高了CMA-GFS模式的辐射计算精度。

在CMA-GFS全球模式中也引入由我国科学家自主研发的双参数云微物理方案，来描述格点平均层云形成及演变的微物理过程。双参数云微物理方案是由中国气象科学研究院胡志晋在20世纪80年代提出的(Hu and He, 1988; 1989)，其目的是为了研究层云和积云中的云微物理过程。刘奇俊等(2003)在此基础上进行了发展和改进，并将其耦合到了多个区域中尺度天气模式中。研究表明，该双参数云微物理方案能很好地模拟台风、暴雨和地形降水等天气过程(李喆等, 2019；2025；Ma et al, 2022)。在与CMA-GFS模式耦合过程中，充分考虑全球模式动力框架、物理过程以及粗分辨率的特点，对双参数云微物理方案进行了必要的调整和简化，以适应全球粗分辨率模式特征。

根据水的相态、尺度、形状、比重等将水物质分成六种，即水汽、云水、雨水、冰晶、雪和霰，云微物理特征参数为水汽和云滴的比含水量以及冰晶、雪、霰和雨水的比含水量和数浓度，其中云滴数浓度作为定值处理。同时，将云滴谱拓宽函数、冰晶和雪的凇附率也作为预报量，其目的是为了更加精确地表述云水到雨水的自动转化过程，以及冰晶到雪和雪到霰的转化过程。由于在新的云物理方案中凝结均是通过大尺度宏观云物理方案计算的，因此在双参数云微物理方案中不再考虑凝结过程，而只考虑当格点平均水汽小于相对湿度阈值时的蒸发过程，这包括云滴和雨滴的蒸发以及冰相水凝物(冰晶、雪团和霰)的升华过程。对于水凝物之间的转化过程包括：(1)云滴向雨滴、冰晶向雪团、冰晶向霰、雪团向霰的自动转化；(2)云滴和雨滴、云滴和冰晶、云滴和雪团、云滴和霰、冰晶和冰晶、冰晶和霰、冰晶和雪团、雪团和雪团的碰并；(3)冰晶的核化过程和繁生过程；(4)冰晶、雪团和霰的融化；(5)云滴、雨滴的冻结。

1.5 尺度自适应的三维湍流参数化方案

目前许多数值天气预报中心的业务模式水平分辨率已达到千米级，预计在未来几年内可能达到百米级(Hong and Dudhia, 2012)。模式向高分辨率发展不仅对动力框架在计算上提出了更高的要求，而且需要在物理上对各种参数化方案进行重新思考与认识。其中以湍流与边界层过程为代表的高分辨率下次网格尺度混合的参数化问题是最重要的方面之一(Dudhia, 2014)。

一般而言，模式的网格尺度不同，所使用的湍流参数化方案也应不同。次网格混合的参数化方案“本质上”应该依赖于模式的网格尺度。随着目前中尺度数值预报模式的分辨率越来越高，当模式网格距Δ与含能湍流的长度尺度l相当时(Δ~l)，模式的动力过程可解析(或表达)一部分湍流运动，但对另一部分湍流仍需进行参数化。Wyngaard(2004)将该区域称为“Terra Incognita(未知领域)”，通常也被称为湍流运动的“灰色区域”。次网格混合的参数化方案依赖于模式网格的尺度，“灰色区域”尺度下湍流参数化问题既不同于传统的行星边界层(PBL)参数化，也不同于大涡模拟(LES)的湍流参数化(郭建平等，2025)，因此有必要发展尺度自适应的湍流参数化方案。

在水平方向上，随着模式分辨率的提高，水平湍流输送和混合作用变得越来越重要，“灰色区域”内水平湍流通量与垂直湍流通量具有相当的量级，显然不满足水平均一性条件(Wyngaard, 2010)，因而湍流通量的水平梯度不可忽略，必须要考虑水平方向的混合作用。

另一方面，湍流在大气运动中是普遍存在的，不仅存在于边界层中，也可存在于边界层以上，甚至可达对流层顶(Marks et al, 2008)。对流云内的湍流及由此产生的湍流输送在湿对流过程的形成和发展中起着关键作用(Persing et al, 2013)。因此，在数值天气预报模式中准确且合理地参数化表征与湿对流过程相关的次网格湍流输送，对于准确预测和模拟强对流过程至关重要。

综上所述，从三维湍流的角度，发展尺度自适应的湍流混合参数化是十分必要的。同时，完善和改进三维湍流参数化方案，使其不只局限于PBL内，而是能够表征整个大气的三维湍流运动，是高分辨率数值预报模式湍流参数化方案发展的必然趋势。

1.5.1 尺度自适应三维湍流参数化方案(SMS-3DTKE)的发展

传统湍流方案只适用于大涡尺度模拟，为了对原方案进行扩展以适应于“灰色区域”尺度，需要确定两个关键的参数，分别为中尺度分辨率下的非局地项和垂直混合长度。对于特定的分辨率，次网格热通量可分为局地项和非局地项(NonLocal，简写为NL)。非局地次网格热通量$ \overline{w^{\prime} \theta^{\prime}} ^\mathrm{NL}$乘以由模式分辨率决定的权重函数P_NL(Δ/z_i):

$ \overline{{w}^{\prime} \theta^\prime}^{\varDelta, \mathrm{NL}}=\overline{w^{\prime} \theta^{\prime}} ^\mathrm{NL} P_{\mathrm{NL}}\left(\varDelta / z_i\right) $

(12)

当模式分辨率达到LES尺度时，P_NL(Δ/z_i)=0。其中z_i为PBL高度，P_NL(Δ/z_i)的具体形式参见Zhang et al(2018)。

在水平方向上，提出一种新的处理“灰色区域”尺度下水平混合作用的方案，通过引入随模式分辨率变化的函数，将Smagorinsky方案与由湍流动能(TKE)决定的扩散方案结合起来，从而实现水平混合的尺度自适应。

该方案通过构建依赖于湍流动能的水平扩散方案和求解完整的湍流动能预报方程，实现了垂直和水平方向次网格混合在物理和数学上的一致性，突破了传统大气边界层方案只有垂直一维方向的局限性；通过考虑非局地通量的尺度依赖性，实现了次网格湍流参数化方案从大涡尺度到中尺度的尺度自适应(Zhang et al, 2018)。该方案命名为SMS-3DTKE(Shanghai Meteorological Service-Three Dimensional Turbulent Kinetic Energy)，并被NCAR中小尺度气象实验室(MMM)新一代中尺度模式WRF所采用，于2020年4月在WRF4.2版本中正式公开发布。

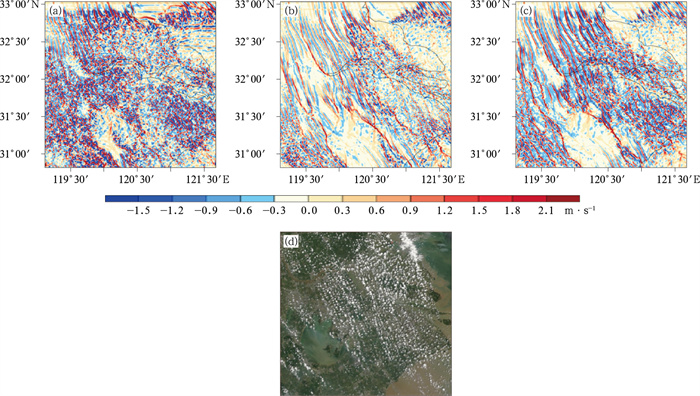
将SMS-3DTKE方案耦合进中尺度数值预报模式，并针对华东一次浅对流云街进行了模拟(图 4)，结果表明，SMS-3DTKE方案模拟的边界层浅对流云呈现线性结构分布，与卫星观测相近，效果与传统的一维边界层方案相当，具有取代一维边界层方案的潜力。

1.5.2 三维湍流参数化方案针对湿对流湍流的扩展

湍流不只存在于大气边界层中，也普遍存在于湿对流系统内。可显式表征深对流系统和对流尺度环流的对流允许尺度模式(水平分辨率≤4 km)依然无法完全解析个体对流云，导致在模式中出现部分可分辨和部分次网格通量特征，因此该尺度被称为“灰色区域”尺度。通过提升湍流方案对对流云内次网格湍流通量的表征是解决“灰色区域”问题的一个有效途径。传统的湍流方案通常采用梯度扩散方法来表征自由大气内的湍流混合，因此难以得到深对流云内的逆梯度湍流通量，而前人的研究表明逆梯度湍流通量是深对流云的一个重要特征，为更好表征深对流云内的湍流通量，将水平梯度湍流闭合(H-gradient closure)应用到自主研发的尺度自适应三维湍流方案(SMS-3DTKE)，使得该方案不仅能表征边界层内的湍流，而且能够表征整个大气的三维湍流运动，极大地扩展了方案的应用范围。修改的方案称为SMS-3DTKE-H方案(Ye et al, 2023)，其垂直方向的次网格通量表达式可写成如下形式：

$ \begin{gathered} \overline{w^{\prime} \theta^{\prime}}=-K_{\mathrm{h}} \frac{\partial \bar{\theta}}{\partial z}+{\overline{w^{\prime} \theta^{\prime}}}^{\mathrm{NL}} P\left(\varDelta / z_i\right)+ \\ C_{\mathrm{s}} \frac{\varDelta^2}{12}\left(\frac{\partial \overline{w}}{\partial x} \frac{\partial \theta}{\partial x}+\frac{\partial \overline{w}}{\partial y} \frac{\partial \theta}{\partial y}\right)_{\text {above PBL }} \end{gathered} $

(13)

式中：K_h为垂直标量扩散系数，C_s为可调常数，取为5；右侧第一项为梯度扩散项，第二项为非局地项，第三项为水平梯度湍流闭合项。

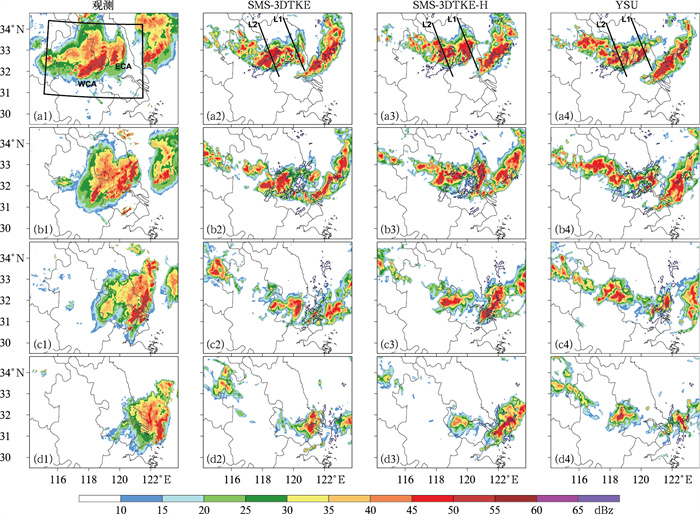
图 5给出了一次强对流天气过程的观测和三组模拟试验的雷达组合反射率。三组模拟试验都能较好再现2022年7月10日12时的线状对流系统，但对江苏省内对流系统的强度和演变特征的模拟存在明显差异。SMS-3DTKE方案模拟的江苏省内对流系统的强度偏弱且很快衰亡，并没有进一步发展。SMS-3DTKE-H方案能较好地再现江苏省内对流系统的强度和演变特征，对流的线状结构与观测更加接近。此外，SMS-3DTKE-H方案能较好抑制SMS-3DTKE和常用的边界层方案(YSU方案)中位于安徽北部和河南南部的虚假对流。

2 资料同化方面 2.1 ARMS辐射传输模式

卫星观测算子是连接数值预报模式的“状态变量”(如大气温度、湿度、风速、气压)与卫星实际观测数据的关键桥梁，其本质是基于大气辐射传输、散射等物理过程，将模式输出的“抽象大气状态”转化为“卫星可直接观测的物理量”的数学与物理模型。卫星观测资料在全球气象观测中的覆盖范围广泛，尤其对海洋和极地等地面观测稀缺地区至关重要(张鹏等，2025)。快速辐射传输模式的应用使得卫星辐射率资料的直接同化成为可能，这对于全球数值天气预报精度提升具有重要意义。

在中国业务数值天气预报模式研发过程中，卫星观测算子也经历了从依赖国外模式到自主创新的发展历程。早期主要采用欧洲研发的RTTOV模式(Saunders et al, 2018)。随着国产气象卫星(如风云系列卫星等)的蓬勃发展，为了促进国产气象卫星观测资料的遥感定量化应用尤其是在数值天气预报方面的同化应用，中国气象局针对风云卫星特有的载荷特性，研发了适用于国内外所有卫星辐射率资料的快速辐射传输模式ARMS(Weng et al, 2020；Yang et al, 2020)，并于2023年5月22日起随CMA-GFS V4.0一起正式业务运行。业务结果表明，ARMS能支撑CMA-GFS中所有卫星资料的同化应用，且其替换RTTOV后，CMA-GFS模式预报精度稳中有升。

ARMS的设计和开发充分借鉴了国外同类模式的先进经验，即插即用功能使得其高度兼容，便于国内外团队的科研合作。ARMS由四个子模型组成，其中包括前向模型、切线性模型、伴随模型和K-矩阵模型。前向模型主要用于模拟卫星仪器在不同天气和地表条件下的大气层顶辐射，该模型主要在卫星仪器定标/验证以及仪器设计方面应用；切线性模型、伴随模型和K-矩阵(雅可比)模型用于快速计算辐射相对于大气状态的灵敏度，这些模型在卫星遥感反演以及数值预报方面应用起到重要作用。

ARMS前向模型的主要组成部分包括大气气体吸收模块、粒子散射模块、地表发射率模块和辐射传输求解模块。其中粒子散射模块包括云(如液水、冰、雪、雨、霰、雹)粒子散射和气溶胶(如沙尘、海盐、黑碳、有机碳、硫化物)粒子的散射；地表发射率需要根据不同波段(如微波、红外)、不同地表类型(如海洋、森林、沙漠等)分别计算地表发射率。通过气体吸收模块、粒子散射模块和地表发射率模块中用于在一定天气和地表条件下的大气和地表光学特性，然后通过辐射传输求解模块，将这些光学特性和卫星仪器特征转化成大气层顶的辐射量或者亮温。

近年来，在ARMS模式中的全极化辐射传输求解方案、大气气体吸收计算方案、粒子散射、地表发射率等方面做了大量创新工作。在ARMS模式中集成的矢量辐射传输求解方案(VDISORT)，攻克了斯托克斯矢量辐射传输求解难题，核心突破性成果包括四方面：一是在相对方位角与天顶角方向离散矢量微分积分辐射传输方程，形成常微分方程组，可针对任意形状粒子散射介质，结合边界条件求解各谐波分量辐亮度矢量并求和得总辐射能量；二是基于海洋双尺度粗糙度模型，在微波与可见光波段精准推导下边界海面反射、发射项；三是重新定义微波波段热源矢量，使其契合太阳源矢量能量守恒框架；四是建立大气层顶斯托克斯辐亮度矢量与大气、海洋光学参数关联的数学表达式。该方案可以处理一般散射条件下的计算，能更准确地模拟可见光和紫外线仪器观测，可以支撑未来可见光资料在数值预报系统中的同化应用(Zhu et al, 2024)。

VDISORT方案求解以下辐射传输方程：

$ \begin{gathered} \mu \frac{\mathrm{d} \boldsymbol{L}(\tau, \mu, \phi)}{\mathrm{d} \tau}=\boldsymbol{L}(\tau, \mu, \phi)- \\ \frac{\omega}{4 \mathsf{π}} \boldsymbol{F}_0 \mathrm{e}^{-r / \mu_0} \boldsymbol{M}\left(\mu, \phi ;-\mu_0, \phi_0\right)-(1-\omega) \boldsymbol{B}- \\ \frac{\omega}{4 \mathsf{π}} \int_0^{2 \mathsf{π}} \mathrm{~d} \phi^{\prime} \int_{-1}^1 \boldsymbol{L}(\tau, \mu, \phi) \boldsymbol{M}\left(\mu, \phi ; \mu^{\prime}, \phi^{\prime}\right) \mathrm{d} \mu^{\prime} \end{gathered} $

(14)

式中：L代表辐射的斯托克斯矢量，是关于光学厚度τ、卫星观测天顶角μ和卫星观测方位角ϕ的函数。τ也表示位置信息，对于单层大气而言，τ=0表示在层顶，τ=τ₀表示在层底，τ₀为该层大气的光学厚度。ω是大气的单次散射反射率，反映大气散射强弱。M(μ, ϕ; μ′, ϕ′)为大气散射相矩阵，反映辐射能量从角度(μ′, ϕ′)散射到角度(μ, ϕ)的变化情况。F₀和B分别表示太阳入射辐射的斯托克斯矢量和大气普朗克函数(地球热红外发射辐射)的斯托克斯矢量。VDISORT求解方案模块是快速辐射传输模式的核心，其余各个模块用于计算该模块所需的大气、地表参数。

大气透过率模块用于计算各层大气气体吸收光学厚度τ_gas。在ARMS大气透过率计算模块中，为了更好地贴合星载仪器的观测特性，在计算过程中考虑了真实光谱响应函数：

$ \varGamma_{\mathrm{ch}, j}=\frac{\int_V \varGamma_j(v) \operatorname{SRF}(v) \mathrm{d} v}{\int_V \operatorname{SRF}(v) \mathrm{d} v} $

(15)

式中：Γ_{ch, j}表示从大气层顶到第j层大气的星载仪器通道下的大气透过率，Γ_j(v)和Γ_{ch, j}类似，表示单个频率v下的大气透过率，SRF(v)表示星载仪器通道光谱响应函数。此外，使用MonoRTM模型作为ARMS支持的微波仪器的大气透过率系数训练参考模型，增加了臭氧作为气体吸收的可变气体，并可以更加精确地支持未来的高频微波和太赫兹观测系统的新仪器模拟(Kan et al, 2024)。

粒子散射模块用于计算云、气溶胶散射光学性质。在ARMS粒子散射模块中，分别基于T-Matrix和离散偶极子近似(DDA)方法发展了云粒子和气溶胶粒子散射资料库，用于支撑数值预报模式中全天空卫星资料同化的应用(Yang et al, 2020)。在辐射传输模拟中，云单粒子散射特性通常需要耦合云粒子谱分布计算云粒子群的散射特性：

$ \beta_{\mathrm{s}}=\int_{D_{\min }}^{D_{\max }} \sigma_{\mathrm{s}}(D) n^{\prime}(D) \mathrm{d} D $

(16)

$ \beta_{\mathrm{e}}=\int_{D_{\min }}^{D_{\max }} \sigma_{\mathrm{e}}(D) n^{\prime}(D) \mathrm{d} D $

(17)

$ \boldsymbol{M}_0=\frac{\int_{D_{\min }}^{D_{\max }} \boldsymbol{m}(D) \sigma_{\mathrm{e}}(D) n^{\prime}(D) \mathrm{d} D}{\beta_{\mathrm{s}}} $

(18)

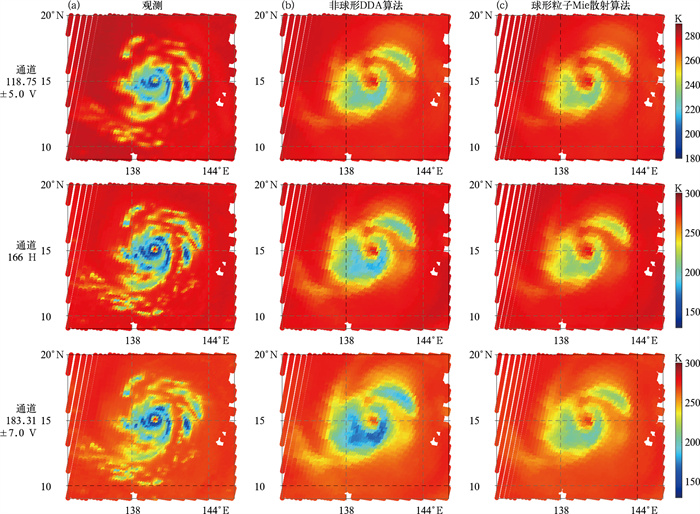
式中：σ_s(D)，σ_e(D)和m(D)分别表示单个云粒子的散射截面、消光截面和散射相矩阵；β_s，β_e和M₀分别表示云粒子群的质量散射截面、质量消光截面和散射相矩阵。云粒子消光光学厚度τ_clde和散射光学厚度τ_clds通过用β_e和β_s，与云水(冰)含量相乘计算得到。用于辐射传输方程求解的各个大气光学参数是综合了τ_gas和云、气溶胶散射光学性质的共同结果。值得注意的是，引入非球形粒子散射后，ARMS模式对高频微波散射的模拟能力显著提升(参见图 6)。

在ARMS中开发了基于双尺度海洋粗糙度模型的偏振双向反射分布函数(pBRDF)，完善了微波全极化海气耦合辐射传输模式的海气界面双向反射物理机制，构建了相应的海气界面边界条件，可以同时处理被动微波仪器的海洋发射率和主动微波仪器的归一化雷达截面，增强了支持主被动一体化辐射传输模拟能力(He and Weng, 2023)。在ARMS陆表发射率物理模型(LandEM)中，在Dobson土壤介电常数模型基础上，补充了0.3~1.3 GHz范围水的有效电导率参数的估算，以支持低频通道的模拟范围；发展了Mironov土壤介电常数模型，改善了土壤介电常数计算精度；在Ulaby常温植被介电常数模型基础上，发展了Matzler低温植被介电常数模型，支持低温情况下植被介电常数计算；发展了Chen-Weng粗糙地表反射率模型，改善植被到土壤反射率估算效果。基于FY-3卫星微波成像仪观测资料，使用一维变分回归算法反演出了旬更新的全球陆表微波发射率气候资料集，进一步改善了卫星微波仪器陆表亮温的模拟精度。

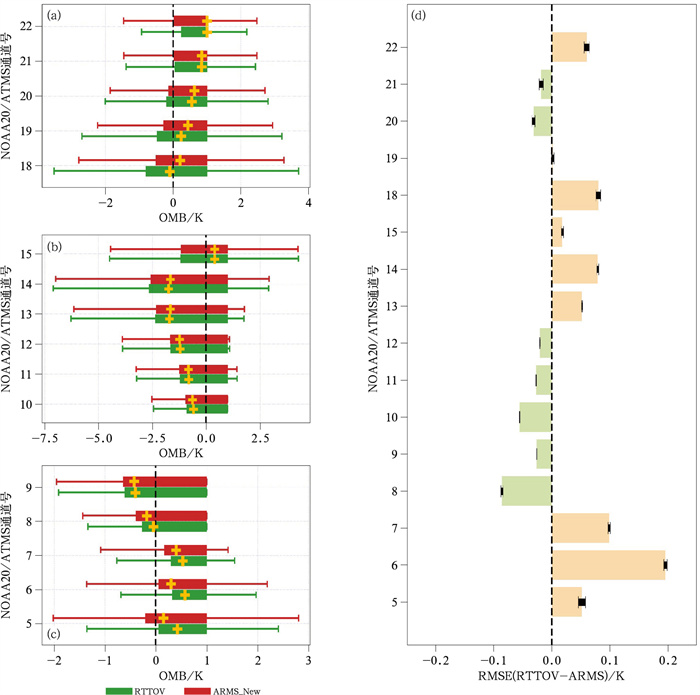
为了验证模式的精度，研究也使用ARMS模式模拟NOAA20/ATMS的观测亮温并将结果与RTTOV 13.2的模拟结果进行了对比。选择NOAA20/ATMS的观测是由于其资料质量相对较高，被广泛用于辐射传输模式的精度验证。背景场选择了137层ERA5大气再分析资料，其可提供较高垂直分辨率的温、湿度廓线。其对比结果如图 7所示, 整体而言，ARMS与RTTOV模拟精度大致相当。对于低层温度通道，ARMS相比于RTTOV模式整体更加贴近观测，但是方差相对偏大。对于高频水汽通道，ARMS的OMB的中位数略大于RTTOV，但是ARMS偏差更加稳定，方差较小。

随着中国气象卫星观测系统的进一步发展和业务数值天气预报走向地球系统数值预报模式，卫星观测算子将面临更高的技术要求。未来的气象卫星将具备更高的时空分辨率和更复杂的光谱信息，这对观测算子的精度和计算能力提出了更高的挑战。新一代的快速辐射传输模型需要在算法上进一步优化，才能适应更复杂的卫星观测和地球系统模式业务需求。此外，人工智能为观测算子的进一步优化提供了新的可能性，通过结合机器学习和深度学习技术，未来的辐射传输模型有望在保持高精度的同时，显著提高计算速度，从而更好地支撑实时天气预报和气候研究。

2.2 非静力全球模式切线和伴随模式 2.2.1 切线性模式和伴随模式基本原理

若CMA-GFS非线性预报模式(Non-Linear Model, NLM)用$ \mathscr{M}$表示，那么大气状态x随时间的演变积分方程可表示为：

$ \boldsymbol{x}\left(t_i\right)=\mathscr{M}\left(\boldsymbol{x}\left(t_0\right)\right) $

(19)

式中：向量 x代表模式所有的预报变量，$\mathscr{M} $表示从t₀时刻积分到t_i时刻的NLM算子，x(t₀)是初始时刻t₀的大气状态，x(t_i)是预报时刻t_i的大气状态。

如果初始时刻 x(t₀)增加一个小扰动δx(t₀)，即 x(t₀)+δx(t₀)，那么扰动δx随时间的演变为：

$ \delta \boldsymbol{x}\left(t_i\right)=\mathscr{M}\left(\boldsymbol{x}\left(t_0\right)+\delta \boldsymbol{x}\left(t_0\right)\right)-\mathscr{M}\left(\boldsymbol{x}\left(t_0\right)\right) $

(20)

根据泰勒展开公式，则有：

$ \begin{gathered} \mathscr{M}\left(\boldsymbol{x}\left(t_0\right)+\delta \boldsymbol{x}\left(t_0\right)\right)=\mathscr{M}\left(\boldsymbol{x}\left(t_0\right)\right)+ \\ \mathscr{M}^{\prime}\left(\boldsymbol{x}\left(t_0\right)\right) \delta \boldsymbol{x}\left(t_0\right)+O\left(\mathscr{M}^n\right) \end{gathered} $

(21)

式中O($ \mathscr{M}^n$)表示$ \mathscr{M}$泰勒展开的高阶项。如果忽略高阶项O($ \mathscr{M}^n$)，将式(21)代入式(20)，可以得到扰动δx随时间演变的近似描述为：

$ \delta \boldsymbol{x}\left(t_i\right) \approx \boldsymbol{M} \delta \boldsymbol{x}\left(t_0\right) $

(22)

式中$ \boldsymbol{M}=\mathscr{M}^{\prime}\left(\boldsymbol{x}\left(t_0\right)\right)$是$\mathscr{M}$的一阶导数，代表$ \mathscr{M}$的切线性模式预报算子。也就是说，切线性模式(TLM, Tangent Linear Model)是数值天气预报模式的一阶线性近似，它描述了初值扰动随时间的演变。

伴随模式(ADM, ADjoint Model)与切线性模式是一一对应的关系，数学表达式为：

$ \boldsymbol{x}^*\left(t_0\right)=\boldsymbol{M}^{\mathrm{T}} \boldsymbol{x}^*\left(t_i\right) $

(23)

式中：x^*(t₀)和x^*(t_i)分别代表在初始时刻t₀和某一后续时刻t_i的伴随向量(或称为伴随状态)，M^T是 M对应的伴随模式，即M模式的转置。

伴随模式的核心作用在于能够根据末态(如某一时刻)目标函数或响应函数的梯度信息，逆向推算初态的梯度分布。这一特性在数值天气预报、资料同化、敏感性分析及误差诊断等领域具有重要的应用价值。切线性模式与伴随模式的代码开发过程极为复杂、挑战性较高。尽管目前已有多种自动化工具可用于代码生成，但自动生成的代码往往存在可读性差、维护困难、运行效率低下，甚至潜在错误等问题。因此，切线性与伴随模式的高质量开发仍需大量人工参与和严格的测试验证。

2.2.2 CMA-GFS切线性模式(TLM)和伴随模式(ADM)

(1) 总体设计

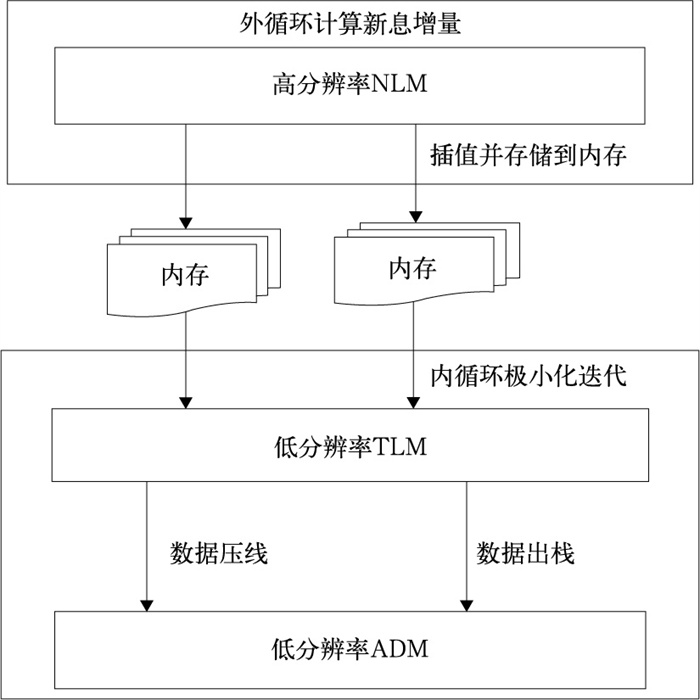
TLM与ADM均需共享由非线性预报模式(NLM)生成的模式轨迹(基态)，以保证线性化过程的准确性。CMA-GFS系统将程序结构划分为“线性模块”(如极区滤波、扩散等不依赖基态的过程)与“非线性模块”(如上游点插值、Helmholtz方程求解等依赖基态的过程)。基态获取采用“以内存传递为主、重复计算为辅”的策略：在NLM或TLM积分过程中，将各步基态预存至数组或通过栈结构管理；TLM在积分时可实时补充少量中间基态，而反向积分的ADM则需全部读取预存的基态数据。以Helmholtz方程为例，ADM 1.0版本每步需先计算非线性基态，2.0版本则由TLM一次性预存全步长基态，虽然增加了内存消耗，但避免了重复的非线性计算，使全球ADM计算耗时减少约20%，4DVar整体流程效率提升约10%。如图 8所示，CMA-GFS 4DVar流程中，外循环高分辨率NLM生成观测增量，并将轨迹插值至低分辨率后存入内存；内循环迭代过程中，TLM读取轨迹并再次存储基态栈，供后续ADM调用。TLM已通过线性近似和伴随一致性检验，能够满足4DVar同化及奇异向量计算的需求。

(2) 切线性物理过程设计

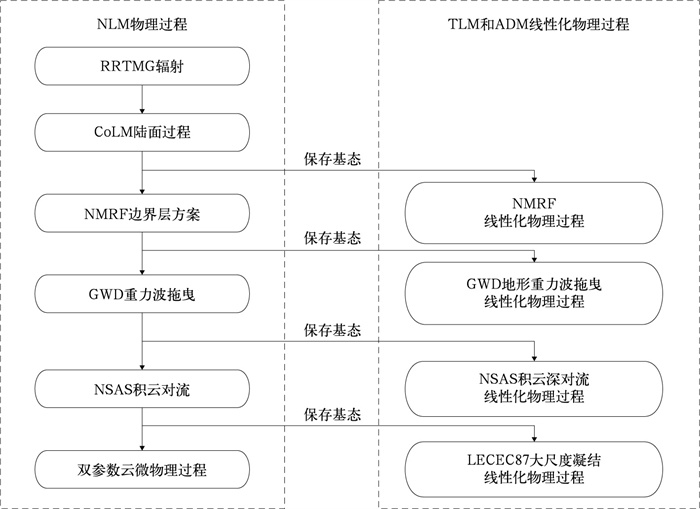
CMA-GFS 4DVar系统采用增量式框架，其中外循环的NLM分辨率为0.25°，内循环的TLM和ADM分辨率为1°，以聚焦大尺度过程并有效抑制非线性误差的影响。线性化物理过程的实现分为四个阶段(Liu et al, 2018)：①对非线性物理方案进行简化，保留其核心物理特征；②开发并测试切线性方案；③通过规约化方法抑制扰动的异常增长；④基于规约化代码自动生成伴随模式并进行测试。当前已实现的线性化物理方案包括MRF边界层、GWD地形重力波拖曳、NSAS深对流以及LCEC87大尺度凝结(见图 9)，这些方案能够显著抑制绝热TLM在低层的扰动增长，提升湿温变量的线性近似精度，从而改善同化与预报效果(刘永柱等, 2019；2023)。在4DVar运行过程中，外循环NLM负责计算MRF边界层过程，并将轨迹基态插值存储于内存，供内循环TLM/ADM调用，实现了：①高质量的基态轨迹；②TLM/ADM仅需计算简化物理方案，提高计算效率；③非线性与线性物理方案的松耦合，便于独立开发与维护。

(3) 计算效率

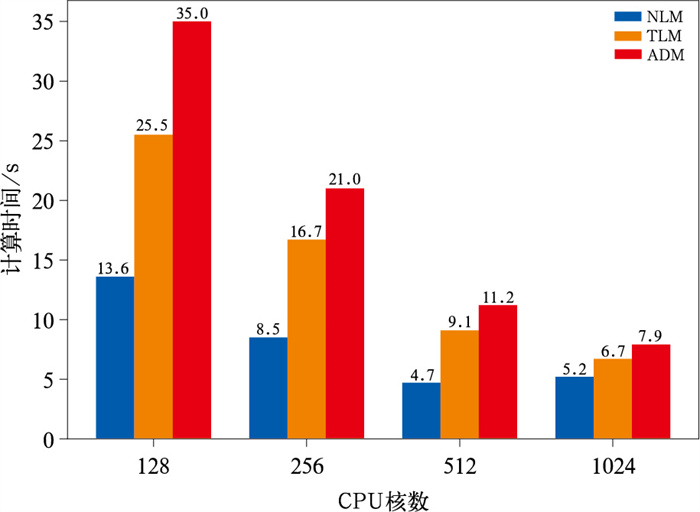
在仅包含动力框架的条件下，TLM、ADM与NLM采用相同的程序模块，计算量具有可比性，可用于评估TLM和ADM计算代码的效率。基于中国气象局曙光高性能计算平台进行测试，试验设置为：水平分辨率1°，垂直层数60层，预报时长6 h，积分步长1200 s。由于TLM和ADM在设计上需保存大量基态信息，内存需求较高，测试自4个计算节点(每节点32核)起逐步扩展。结果如图 10所示，TLM的计算时间约为NLM的2倍，ADM的计算时间约为TLM的1.3倍；当核数扩展至1024时，TLM与ADM的并行效率超过NLM。其原因在于节点数量增加带来充足内存，预存轨迹策略的带宽优势得以充分发挥(刘永柱等，2017)。

2.3 有约束卫星资料偏差订正

变分同化系统要求观测和背景场误差符合无偏高斯分布。然而卫星观测、辐射传输模式以及背景场都存在系统性偏差。为解决这一问题，通常在同化之前或同化过程中，使用参数化模型对卫星观测偏差进行订正(Harris and Kelly, 2001)。随着数值预报精度不断提高，对于卫星观测偏差订正的要求也越来越高，偏差订正是卫星辐射率资料同化能否对分析预报有正贡献的关键技术(Eyre et al, 2022)。近年来，自适应方法如变分偏差订正(VarBC)得到广泛应用(Auligné et al, 2007)。VarBC依赖于同化系统中的无偏锚定观测来约束模式偏差和观测偏差。对于那些存在无偏观测充分覆盖且模式偏差较小的区域，VarBC可以取得很好的效果。然而，当缺乏足够的锚定观测或模式偏差较大时，VarBC难以区分模式偏差和观测偏差，导致观测偏差订正值向模式偏差漂移。

2012年前后，GRAPES全球同化预报系统的模式偏差较大，特别是热带高层暖偏差显著，而此区域又缺乏足够的锚定观测。为解决卫星辐射率偏差订正向模式偏差漂移难题，需要发展新的方法。此前，ECMWF等数值预报中心采用的方法，是对某些受模式偏差影响较大的卫星通道(如AMSU-A通道14)采用无偏差订正同化(McNally, 2007；Han and McNally, 2010)。这种方法假设这些特定通道的观测偏差远小于模式偏差。然而，这种做法忽视了客观存在的观测偏差，如扫描角依赖偏差以及卫星与卫星之间的系统性偏差等。Han(2014)首次在观测偏差订正中引入卫星辐射率资料定标不确定性信息做为先验约束，基于数学物理反问题中“极小模解”的思想，在变分同化目标泛函中增加卫星观测偏差上界估计的正则化项，见式(24)，发展了卫星辐射率资料有约束偏差订正方法(CBC)，较好解决了观测偏差向模式偏差的漂移问题。

$ \begin{gathered} 2 J(x, \beta)=\left(x_{\mathrm{b}}-x\right)^{\mathrm{T}} \boldsymbol{B}_x^{-1}\left(x_{\mathrm{b}}-x\right)+ \\ \left(\beta-\beta_{\mathrm{b}}\right)^{\mathrm{T}} \boldsymbol{B}_\beta^{-1}\left(\beta-\beta_{\mathrm{b}}\right)+ \\ {[y-H(x)-h(x, \beta)]^{\mathrm{T}} \boldsymbol{R}^{-1}[y-H(x)-h(x, \beta)]+} \\ \alpha^2\left[h(x, \beta)-b_0\right]^{\mathrm{T}} \boldsymbol{R}_{\mathrm{b}}^{-1}\left[h(x, \beta)-b_0\right] \end{gathered} $

(24)

式中：左端J为目标泛函，x为分析变量，β为待估计的偏差参数。右端第一项为大气状态的背景约束项，x_b为大气背景状态，B为背景误差协方差矩阵；第二项为VarBC约束项，β_b为偏差参数的背景值，B_β为偏差参数的背景误差协方差矩阵；第三项为观测约束项，y为观测值，H为观测算子，R为观测误差协方差矩阵；第四项为CBC的约束项，b₀是观测偏差的先验估计，R_b是偏差先验估计的不确定性指标，其应与卫星仪器绝对定标中的不确定性相关。α²是用于衡量第三项和新约束项相对重要性的正则化参数。

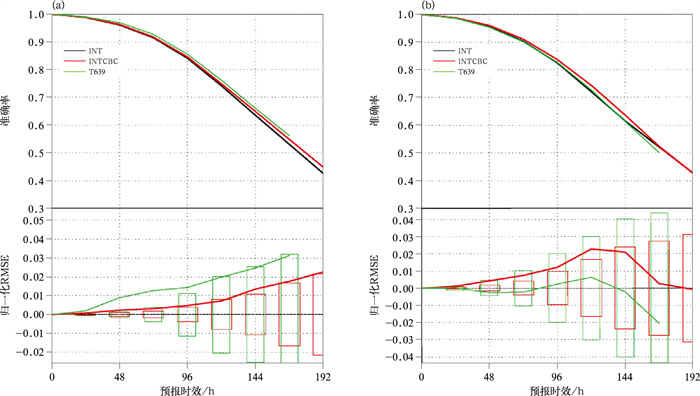
为验证有约束偏差订正方法在我国全球数值预报系统中的应用效果，开展了对比试验(图 11)。采用2013年5—6月的数据对比原有偏差订正方案和有约束偏差订正方案的预报性能。从500 hPa位势高度场预报误差来看，该方案在南北半球均表现出改进效果。其中，在北半球，3~7 d预报时效上相对于原有方案的归一化均方根误差降低约2%~3%；在南半球，改进更为显著，5 d预报时效误差降低约5%。该结果表明，有约束偏差订正方法在解决高层温度通道偏差订正向模式暖偏差漂移问题的同时，并未对中低层的中期预报产生负面影响，反而带来了一定的正贡献。这验证了有约束偏差订正方法既能有效约束观测偏差订正，又能改善数值预报水平。

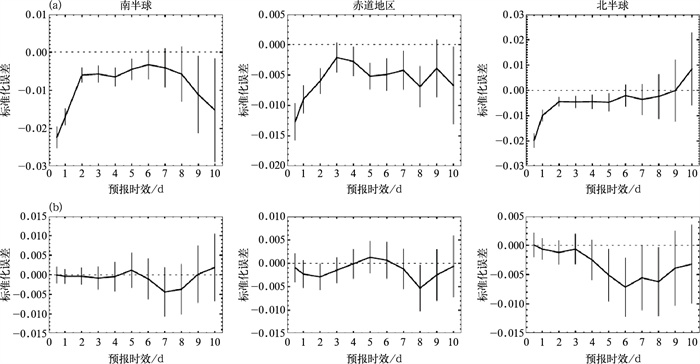
此外，该技术后续在ECMWF-IFS系统中得到进一步发展和应用。Han and Bormann(2016)将CBC方法扩展为有约束变分偏差订正技术(CVarBC)，解决了困扰ECMWF多年的卫星微波高层温度通道偏差订正向模式暖偏差漂移的问题(Di Tomaso and Bormann, 2011)，提高了平流层温度分析和预报的精度(图 12)，并对全球中期预报有显著正贡献。这项技术2018年在ECMWF-IFS(CY45R1)中业务化应用，之后应用于其新一代全球大气再分析ERA6中首颗红外高光谱卫星雨云4号卫星IRIS的同化(Bell et al, 2023)，解决了20世纪70年代全球再分析高层暖偏差问题。德国气象局在微波湿度探测通道同化中也采用了CBC(Faulwetter, 2023)，克服了模式湿度偏差对卫星湿度探测通道偏差订正的影响。有约束偏差订正既实现了对扫描偏差和卫星之间偏差等已知偏差的订正，又通过弱约束限制了观测偏差订正的不合理漂移，是有效解决偏差订正漂移的新方法(Eyre et al, 2022)。

2.4 FY-4红外高光谱同化

我国2016年发射的FY-4A与2021年发射的FY-4B，都搭载有干涉式大气垂直探测仪GIIRS，是目前国际上仅有的两台在静止轨道上运行的红外高光谱大气探测仪，能够实现覆盖东亚区域2 h时间分辨率的高分辨率大气温湿度三维探测，对于强对流、飑线、雷暴等短生命史、影响大的高影响天气预报、以及台风等海上系统的发生发展预报具有重要价值。我国学者成功开发了FY-4探测仪资料同化多项核心技术，突破了静止卫星大面阵、多探元、高光谱、高时间分辨率探测仪资料同化的多项难题，实现了业务同化应用，提高了我国业务数值天气预报准确率。

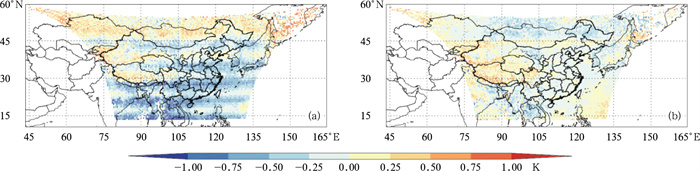
区别于极轨卫星高光谱仪器观测算子采用全球大气廓线的计算方式，Di et al(2018)利用FY-4观测区域的典型大气廓线样本，采用逐线辐射传输模式LBLRTM，应用加权最小二乘算法，发展了基于局地训练的静止卫星探测仪辐射率观测算子。为了在我国业务数值预报系统中更好地发挥FY-4应用效益，尹若莹等(2019)研制了基于业务数值天气预报背景误差和观测误差的静止卫星红外高光谱通道选择等关键技术并建立了业务流程。此外，GIIRS观测采用大面阵探测方式，具有128个观测探元，Yin et al(2020)研发了大面阵多探元有约束偏差订正方法，在我国数值预报系统中实现了高时间分辨率红外探测仪GIIRS业务同化应用。图 13所示为GIIRS在偏差订正前后区域分布，可以看到偏差订正可以有效消除静止卫星大面阵观测带来的条带现象，从而反映模式背景本身的偏差特征。此外，Han(2021)发展了风云卫星红外高光谱大气探测仪在轨参数最优估计技术，基于“大气指纹”的非线性最优化算法，能识别红外高光谱探测仪的光谱变化规律，提高了定标精度和稳定性，为静止卫星探测仪的光谱监视和定标优化，提供了新技术途径，也为后续探测仪发展优化提供了支撑。

FY-4A GIIRS长波通道观测于2018年12月(中波通道观测于2023年5月)在我国业务数值预报系统中实现业务应用，同时针对FY-4B GIIRS的同化技术也已研发完成，已于2024年12月接替FY-4A实现业务同化。

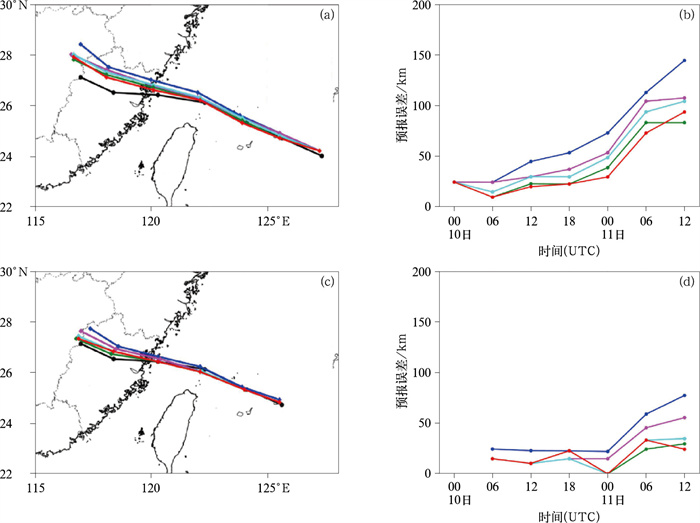
除了常规观测同化应用，我国学者还发展了初值敏感区识别技术(刘永柱等，2013)，实现了预报需求驱动的探测仪时间分辨率和观测区域优化选择；建立了静止卫星探测仪目标观测和同化的业务流程；开展了实时业务环境下探测仪加密观测和数值预报同化的星地协同工作；充分发挥了静止轨道卫星的探测优势，在国际上第一次在业务中实现了静止气象卫星探测仪目标观测和同化应用。图 14显示GIIRS首次目标观测(2018年台风“玛丽亚”)对台风路径预报的影响(Yin et al, 2021), 显然，同化GIIRS目标观测资料能够改善“玛丽亚”的路径预报，并且随着GIIRS同化观测时间分辨率的提高，路径预报误差降低越显著。其他多次目标观测试验均表明(Han et al, 2023)，交互式“观测-预报”技术可以精准提高对目标天气系统和重点保障区域天气的预报水平和服务能力，在台风等灾害天气预报和重大气象服务保障中发挥了重要作用。

3 讨论

我国业务数值天气预报的全面自主创新始于2000年初，至2015年底实现了从区域千米分辨率快速循环到全球中期预报、中尺度集合到全球集合预报的全面业务应用(沈学顺等，2020)。在此过程中，在数值方法、微物理和湍流混合、非静力模式四维变分同化、卫星资料同化核心技术包括辐射传输模式和有约束偏差订正等方面取得了原创性成果，象征着我国在数值预报基础研究方面开始有新的突破性的进展。随着上述核心技术的持续改进和分辨率的逐步提高，我国数值预报系统的性能也稳步提升，与国际先进中心预报能力的差距逐步缩小。以CMA-GFS为例，目前水平分辨率为0.125°(约12.5 km)，垂直方向87层，模式层顶约0.1 hPa，北半球全年平均的可预报天数(高度场距平相关系数大于0.6)稳定超过8 d，但仍落后于ECMWF、NCEP和MetOffice等先进中心。本文回顾和综述了这些原创性的成果，同时也想传达“基础研究的突破存在于持之以恒的实践中”这一地学等传统科学的基本规律。

在全球变暖加速演进的背景下，近年来，极端天气事件多发频发重发，在世界范围内给人民生命财产安全甚至国家安全带来严重威胁。世界经济论坛近五年均将极端天气事件列为全球重大威胁(https://www.weforum.org/)。应对极端天气，数值天气预报在理论和方法上、以及工程技术等方面均需有重大突破：一方面建立高精度、高可扩展的数值模式动力内核，并发展多圈层耦合的天气气候一体化地球系统模式和耦合资料同化技术，以延长预报时效、实现更加精准的复合极端天气灾害的预报预警；另一方面发展全球千米分辨率和区域百米分辨率的模式同化技术和物理参数化算法，以实现对造成极端灾害的天气系统直接解析计算，实现模式预报能力的突破性进展。

发展上述系统，地球系统数值预报面临诸多挑战，包括对地球系统复杂物理过程的认识仍有待深化、计算资源对模式分辨率的制约、高性能异构平台对模式算法的挑战等方面。异构众核E级计算以及近年来突飞猛进的人工智能(AI)技术，为解决上述重大科学与技术挑战带来了机遇。AI正成为引领地球系统预报变革的核心驱动力，有望催生“第二次数值预报革命”，推动预报范式从以物理为中心向“物理-数据”双轮驱动转变。物理驱动的数值方法和数据驱动的AI技术优势互补，相互融合是必然趋势。

未来我们在强化数值预报基础研究和产出具有国际水平的原创性成果方面，一方面将利用好AI技术解决好高分辨率地球系统数值预报“算得精算得快”的科学和技术问题；另一方面将强化与高性能计算厂商和计算机科学的深度融合，从高性能计算机的软硬件设计之初实现协同发展；同时，还应重视多学科多行业交叉与数值预报的耦合定量应用方法和模型的研究，实现精细化的影响预报和风险评估。