2. 中国气象科学研究院灾害天气科学与技术全国重点实验室, 北京 100081;
3. 国家气象中心, 北京 100081
2. State Key Laboratory of Severe Weather Meteorological Science and Technology, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. National Meteorological Centre, Beijing 100081
大气运动具有高度的非线性和混沌特征,单一确定性预报难以充分描述未来天气演变的不确定性。20世纪60年代初,Lorenz(1963)通过理想模型试验揭示了初始条件微小差异即可导致预报结果巨大分歧的现象,即著名的“蝴蝶效应”,表明大气预报存在内在的不可预报性极限。这一发现奠定了在天气预报中引入不确定性分析的理论基础。此后,学者们在70年代开始探索集合预报思想,通过在数值预报中加入随机扰动来模拟预报的不确定性。Epstein(1969)提出了利用随机过程产生天气预报集合的概念,Leith(1974)进一步验证了蒙特卡罗方法在理论上的预报效果,初步证明集合方法可用于量化预报的不确定性。
经过多年研究,到20世纪80年代中后期,集合预报的可行性和价值逐渐被认识。集合预报一般是指针对同一预报时刻,针对初始状态或模型方案进行多次扰动试验,从而得到一组不同的预报结果集合(图 1)。通过对这些集合成员结果的离散性和一致性进行统计分析,可以估计预报的不确定性范围并提高预报产品的可靠性。1985—1992年,欧洲中期天气预报中心(ECMWF)和美国国家环境预报中心(NCEP)率先开展了集合预报模型的科学试验,并于1992年12月几乎同时将全球集合预报系统投入业务运行。例如,ECMWF于1992年建立了基于奇异向量(SV)扰动的全球中期集合预报系统(Buizza and Palmer, 1995),而NCEP同期发展了基于繁殖增量(BV)的方法,用于生成初始集合成员(Toth and Kalnay, 1993)。这些开创性工作标志着集合预报由理论走向业务应用。
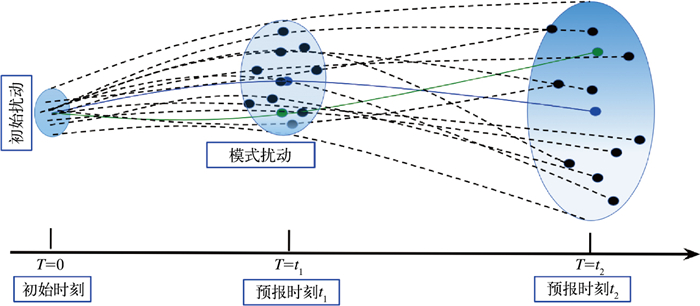
|
图 1 现代集合预报单一模式的概念图 注:黑色虚线:集合扰动成员,绿线:集合控制预报,蓝线:集合预报平均。 Fig. 1 Concept map of a single model for modern ensemble prediction |
进入20世纪90年代后期至21世纪初,集合预报系统迎来快速发展时期。世界主要气象中心如加拿大环境与气候变化部(ECCC)、英国气象局(UKMet)、日本气象厅(JMA),以及中国气象局(CMA)等相继建立了各自的全球集合预报业务系统。同时,各机构间开展集合预报合作计划,例如北美集合预报系统(NAEFS)将美加两国的集合预报进行集成(Buizza et al,2005;Zhu,2005;Candille,2009);世界气象组织(WMO)发起了“全球交互大集合预报”(TIGGE),建立全球集合预报资料库供研究和应用(Swinbank et al,2016);还有美国的次季节预报试验(SubX)(Pegion et al,2019;Guan et al,2019)和WMO的次季节至季节(S2S)集合预报项目等(Vitart et al,2017)。这些举措推动了多模式集合预报的发展,通过集成不同模式的预报来减小预报误差,改善集合预报的离散度,从而进一步提高预报技巧, 减小由于单一模式所造成的离散度偏低(过度自信)的情况。
集合预报技术的发展与高性能计算的进步密切相关。随着计算资源的提升,集合预报能够使用更高的分辨率和更多的集合成员,提高了预报的精细度和稳定性。例如,ECMWF早期由于计算限制,其集合预报的水平分辨率一直低于确定性预报,但近年来随着超级计算机升级,已将集合预报提升到与高分辨率确定性预报相当的9 km网格。然而,集合预报成员数受到计算成本制约,各主要预报中心的全球集合成员一般为15~50个。有限的成员数可能导致对概率分布取样不足,特别是对低概率的极端事件刻画不充分。因此,在保证预报质量的同时,提高集合规模或发展更高效的集合生成方法,一直是集合预报领域的重要研究方向。
与此同时,近年来深度学习、云计算、大数据等技术的飞速发展,让基于数据驱动方法(如生成式对抗网络、扩散模型、变分自编码器等)的集合预报成为可能。这些模型直接或间接地从历史观测和再分析数据中学习大气演变的不确定性规律,通过高效的神经网络推断便可在极短时间内生成多个具有物理合理性和丰富变异特征的预报成员。此类人工智能(AI)集合预报方法不仅显著降低了运行成本,而且在捕捉极端天气方面往往表现优异。一些最新研究表明,包括GenCast(Price et al,2025)、FuXi-Ens (Zhong et al,2024)和AIFS-CRPS(Simon et al,2024)等,AI生成的集合在均方根误差(RMSE)、连续分级概率评分(CRPS)、极端天气概率预报等指标上与传统物理模式集合相当甚至更优,预示着在不久的将来,数据驱动方法有望突破计算瓶颈,为集合预报扩增成员规模和提高精度提供全新方案。国际主要预报中心(ECMWF、NCEP、CMA等)也已纷纷启动AI集合预报探索,期待在下一代业务系统中实现“人机融合”的预报范式转型。
综上所述,集合预报经过数十年发展,已成为数值天气预报业务和科研中不可或缺的工具。它通过量化预报不确定性,提高了预报产品的可信度和实用性。本文将系统回顾集合预报的关键技术和应用进展。第一、二节分别介绍集合预报的初始扰动技术和模式扰动技术的发展;第三节讨论各国主要的全球与区域集合预报系统现状;第四节总结集合预报的统计后处理与预报诊断评估方法; 第五节展示集合预报在极端天气和灾害预警中的应用; 第六节重点综述最新的人工智能与数据驱动的集合预报新进展,包括新一代AI集合预报模型的原理与性能及国内外研究动态与未来发展方向。最后给出本文的结论和展望。
1 初始扰动技术的发展初始条件的不确定性是数值天气预报误差的重要来源之一。大气初始场来自不完备的观测和同化分析,存在观测误差、采样误差和同化算法近似所导致的偏差。这些初始误差在预报积分中会非线性增长,引起预报结果与真实演变的偏离。为了模拟初始场误差对预报的影响,集合预报在起报时刻引入初始扰动,生成一组经过扰动的初始状态来驱动多个预报集成。对比不同扰动成员的预报,可以评估初值误差对预报的不同影响,并通过集合平均减少随机误差,提高预报稳定性。
初始扰动技术经历了从简单到复杂的演变过程。早期最简单的方法是对初始分析场施加随机噪声扰动,即蒙特卡罗方法。这种方法思想简单,但可能导致非物理性的扰动结构。后来发展出针对模式快速增长误差方向的繁殖增量扰动法(简称繁殖法)。该方法由美国NCEP的Toth and Kalnay (1993;1997)提出和改进,通过反复积分和尺度缩放,提取大气最不稳定的误差增长模态。NCEP在1992年首次将繁殖法用于全球集合预报初值扰动。该方法实现简单,能高效捕捉主要误差增长方向,曾在NCEP业务应用多年。与此同时,ECMWF发展了基于SV的初始扰动方法。SV方法源自线性最优扰动理论,寻找预报时效内使预报误差增长最大的初始扰动方向。ECMWF的研究表明,只需少数几个SV即可有效表征中期预报的主要不确定性方向。因此ECMWF自1992年起采用SV作为初始扰动生成方法。经典SV方法的代表性成果包括Buizza and Palmer(1995)的研究。
此后,初始扰动技术进一步融合了现代同化理论成果。集合卡尔曼滤波(EnKF)等同化方法不仅可用于资料同化,也可用于生成分析场的不确定性估计。加拿大气象局在EnKF的发展中,采用分析误差的集合估计方法来构建初始扰动场。ECMWF则在21世纪00年代中期提出集合资料同化(EDA)方案,运行一个由多组带噪声扰动观测的同化系统来产生集合分析。EDA为集合预报提供了一组由同化系统统计生成的初始状态,其离散度能够反映分析误差水平。例如,ECMWF业务中通过EDA生成初始分析集合,从而改进了集合预报初始不确定性的表征。相比之下,美国NCEP在逐步放弃繁殖法后,于2015年转向采用EnKF同化来构建初始扰动,并结合随机物理扰动等方法改进初值扰动质量。自集合资料同化方法(EDA/EnKF)被引入数值预报系统以来,集合-变分混合同化技术已逐渐发展成为集合预报初始不确定性的主要来源(Hamill and Snyder, 2000)。这一技术突破性地将集合预报提供的流依赖误差协方差与变分同化框架相结合,显著改善了初始场的质量。如Lorenc (2003)所述,混合同化通过整合集合协方差的流依赖特性,能够更准确地表征天气系统演变过程中的不确定性。研究表明,这种混合方法在热带气旋路径预报和中纬度天气系统预报等方面均展现出显著优势(Kleist and Ide, 2015)。
此外,Mu et al(2003;2010)提出的条件非线性最优扰动(CNOP)方法为初始扰动研究提供了新的思路。CNOP通过非线性最优化方法求解在约束条件下导致预报偏差最大的初始扰动。Mu et al(2003;2010)研究了CNOP在ENSO预测等问题上的应用。CNOP考虑了预报系统的非线性,有助于识别传统线性方法遗漏的误差增长模式,在理论上拓展了初始扰动方法的范畴。目前CNOP仍主要用于研究领域,但为集合预报初值扰动提供了宝贵参考。
综上所述,初始扰动技术包括随机扰动、繁殖扰动、奇异向量、集合同化、条件非线性最优扰动等多种方法,各有特点并在不同预报系统中应用组合。例如,ECMWF全球集合系统长期采用SV与EDA相结合,NCEP则逐步由繁殖扰动转向EnKF分析扰动,ECCC使用EnKF,英国等也尝试SV和EnKF的融合。无论方法差异,其共同目标是科学表征初始场不确定性,优化集合离散度与预报误差的匹配,在提升集合均值稳定性的同时保留极端事件预报能力。
2 模式扰动技术的发展除初始条件外,数值模式本身的不完善(如物理过程参数化的不确定性)同样会导致预报误差。为此,集合预报引入模式扰动技术,即在模式积分过程中对模型物理过程或参数进行随机或系统扰动,以模拟模式误差带来的预报不确定性。模式扰动的目的是弥补模式自身局限性,生成一组考虑模型差异影响的预报成员,从而扩大集合离散度。模式扰动技术大致包括以下几类:
(1) 随机动力学扰动:直接在模式的动力方程中引入随机项以模拟未解析尺度过程对大尺度的影响。例如,随机动能后向散射(SKEB)方案向模式动能方程添加随机噪声,将潜在的未解析小尺度能量回馈到较大尺度上。Shutts (2005)的研究首先将SKEB应用于集合预报,通过随机涡旋强迫来模拟次网格尺度的不确定性。又如涡度局地化(VC)方法(Shutts and Allen, 2007),通过随机扰动模式涡度场,补偿数值扩散耗散的小尺度能量。这些随机动力学方法在中高层大气预报中有效增加了集合离散度,改善了集合预报对不稳定天气系统的捕捉。
(2) 随机物理参数化扰动:针对模式物理参数化过程的不确定性,在参数化计算过程中加入随机扰动。例如,ECMWF于1999年提出并进行业务应用的随机物理倾向扰动(SPPT)方案(Buzza et al,1999),即在每一个时间步长将模式所有物理参数化过程产生的预报倾向乘以一个随机空间场,从而引入预报倾向的随机波动。SPPT方法以较小的代价显著增加了集合离散度,被许多业务中心广泛借鉴。此外,还有针对特定物理过程的扰动方法,如Tompkins and Berner(2008)提出的湿度参数扰动(SHUM),为边界层湿度引入随机扰动以模拟云和对流的不确定性。近期的发展趋势是随机参数扰动(SPP),即对关键物理参数(或过程)引入独立随机扰动。Leutbecher et al (2017)提出SPP的概念并在试验中证明其有效性。ECCC在2022年率先将SPP引入业务,McTaggart-Cowan et al (2022a; 2022b)的工作表明,加拿大全球集合预报系统通过随机扰动对流、湍流等参数化方案,提升了集合预报对模型不确定性的表示。
(3) 多物理方案集合:通过集成多套不同物理参数化方案或不同模式,从根本上反映模式物理过程处理的差异。Houtekamer and Derome(1995)最早提出多模式组合产生集合的方法并应用于ECCC的全球集合预报系统。另一个实例如美国短期集合预报曾采用同一模式不同物理选项配置成员或北美集合预报系统(NAEFS)和欧洲的多模式集成试验。多物理集合能显著增加成员间差异,但也可能因为模式偏差不同而增加均值误差,需要权衡与调整。此外,有研究提出在预报积分的不同时间段引入扰动而非仅初始时刻,即“时变扰动”,以模拟模式误差随预报时间积累的影响。
模式扰动技术已经成为各主要集合预报系统的标配。ECMWF在21世纪00年代初引入SPPT后,不断完善随机物理方案,目前其全球集合系统综合采用SPPT、SKEB等多种随机扰动。英国气象局、德国气象局等也都有各自的随机物理扰动方案。美国NCEP的全球集合预报则很早开始尝试总倾向随机扰动方案,最新的全球集合预报系统(GEFS) v12版本(Zhu et al,2018;2019;Zhou et al,2022)集成了多种模式扰动技术。模式扰动有效增加了集合离散度,使集合预报不仅反映初始不确定性,也涵盖模式不确定性来源。这对提高极端天气事件(如强对流、飓风等)的预报能力尤为重要,因为这些事件对模式物理过程的敏感性较高。实践表明,合理的模式扰动可以显著改善集合预报性能,尤其在提高概率预报的可靠性和极端事件捕捉能力方面。举例来说,SPPT具有明确的物理意义,尽管表现为随机过程,但它能够有效描述大气物理状态的变化。较强的模式倾向通常对应系统更快的增长,而这恰恰反映了大气中快速发展系统(如天气尺度扰动)的特征,这些系统也是数值预报中误差增长的主要来源之一。因此,合理引入模式倾向随机扰动有助于更好地捕捉大气中的快速变化过程,从而提升对极端天气事件的预报能力。
需要注意的是,模式扰动的引入也带来新的挑战:如何确定扰动的幅度和空间相关结构,既保证扰动足够大以增加不确定性,又避免扰动过强破坏模式的物理合理性。同时,模式扰动增加了预报系统复杂度和计算量,需要在效果与成本之间取得平衡。未来,随着对模式误差统计特征认识的加深,预计模式扰动技术将在物理更加合理、计算更加高效的方向进一步发展。
3 全球和区域集合预报系统 3.1 全球集合预报系统全球集合预报系统旨在针对行星尺度的大气环流提供不确定性预估,预报时效通常在中期(3~15 d)乃至延伸到季节尺度。自1992年ECMWF和NCEP开启全球集合预报业务以来,各主要数值预报中心的全球集合系统不断演进,在成员数、分辨率、物理方案等方面持续升级。
ECMWF的全球集合预报(ENS)被公认为当前世界领先的中期集合预报系统之一。目前运行51个成员(包括1个控制预报),预报时效15 d,水平分辨率约为9 km(与其确定性预报一致)。ECMWF-ENS以SV+EDA生成初始扰动,结合SPPT和SKEB等模式扰动方案。经过数十年发展,ECMWF-ENS在500 hPa高度场等指标上显示出极高的技巧和稳定的可靠性,在国际灾害性天气预警中发挥核心作用。例如,ECMWF集合预报产品中的极端预报指数(EFI)可有效提示极端天气事件发生的概率和强度异常。EFI由ECMWF研发,用集合预报与历史气候分布比较来度量未来天气异常程度,在欧洲风暴、强降水预警中应用广泛。由于EFI是一个无量纲指数,需要有对应的量化指标,研究表明,对温度预报来说,EFI=0.78相当于97.6% 偏态(Guan and Zhu, 2017)。
NCEP的全球集合预报系统(GEFS)也是国际上具有重要影响力的集合预报系统之一。NCEP最初于1992年12月开始运行2个成员的全球集合预报(当时采用繁殖法进行扰动)。此后GEFS经历多次升级:1998年提高水平分辨率,2006年扩展到20个成员并引入集合转换和重新尺度化等扰动改进技术(Wei et al,2006),2015年引入EnKF分析扰动替代繁殖法,并结合物理扰动以增加成员差异。最新业务版本GEFS v12(2020年上线)使用大气、陆面、海浪和海洋单向耦合模式,分辨率为25 km的成员数增加到31个,预报时间由16 d延伸至35 d,采用了5种时空尺度的SPPT方案和SKEB方案等现代技术(Zhu et al,2018;Zhou et al,2022),并提供了30年的集合预报回算(Guan et al,2022)。GEFS在热带气旋路径集合预报、北美极端天气概率预报等方面发挥着重要作用。例如,GEFS提供的飓风路径“集合同心圆”概率图和美国国家飓风中心(NHC) 预报的产品,是美国飓风预警决策的重要依据之一。
ECCC的全球集合预报系统以EnKF同化和多模式物理扰动为特色。加拿大在1996年前后建立了21个成员的全球集合,初始扰动来自EnKF分析误差,模式扰动采用多物理参数方案(不同物理组合)。近年加拿大集合已更新采用SPP并提高分辨率至0.35°,对高纬度天气预报提供了可靠的集合信息。加拿大还与美国NCEP共同推进NAEFS(Toth et al,2006),共享集合预报成员并统一概率预报产品,为北美地区提供改进的不确定性预报服务。
英国气象局(UKMet)的全球集合预报系统为Met Office Global and Regional Ensemble Prediction System-Global(MOGREPS-G)。英国早期在集合预报上进展稍慢,但2005年后建立了基于北半球25 km局地分析扰动的全球集合,后来转为采用ECMWF的SV技术和本国四维变分(4DVar) 同化分析扰动相结合的方法。当前MOGREPS-G约有20个成员,每天两次预报,在欧洲和热带的大尺度预报上与ECMWF互为重要参考。此外,英国还与欧洲其他国家合作开发多中心集合产品,例如欧洲季节-年际预测计划(EUROSIP)项目将ECMWF、英国气象办公室(UKMO)、法国气象局(Météo-France)集合预报进行集成,用于季节预测。
日本气象厅(JMA)自20世纪90年代末运行全球集合预报,当前的JMA Global Ensemble Prediction System(GEPS)包含27个集合成员,预报时长1个月,并与JMA独特的台风集合预报系统相结合。JMA集合预报对西北太平洋台风路径和强度预报提供了宝贵的不确定性信息,经常被亚太各国采用参考。近年来JMA也提升了集合分辨率并引入模式不确定性处理来改进集合性能。
中国气象局(CMA)的全球集合预报业务起步于20世纪90年代后期至21世纪00年代初期。并于2004年基于T213L31全球谱模式开展了集合预报试验,这是中国全球集合预报的早期探索(李晓莉等,2019)。21世纪10年代后,CMA逐步转向自主研发的GRAPES模式体系,并于2016年前后CMA-GEPS(原GRAPES-GEPS)实现业务化运行(陈静和李晓莉,2020;李晓莉等,2019),标志着技术完全自主化(沈学顺等,2025)。当前CMA-GEPS有31个成员,水平分辨率为50 km,采用奇异向量结合多物理方案扰动。中国的集合预报产品已在国家级天气预报和台风路径预报中应用,如台风路径集合概率图、袭击概率图等,提高了预报客观性和稳定度。随着“数值预报攻关”和新一代全球模式的建设,CMA计划进一步增加集合成员数和分辨率,并尝试引入EDA分析集合、随机参数扰动等先进技术,缩小与国际领先中心的差距。
值得一提的是,为促进全球集合预报资料共享和研究,WMO组织的TIGGE计划自2005年起建立了包含ECMWF、NCEP、CMA等十余个中心集合预报数据的共享库, 分别由ECMWF、NCAR和CMA承担。在项目实施的10年期间,各个中心根据自己的能力和条件,共享了多达73个气象要素的全球集合预报,为气象学界开展概率预报研究和服务提供了重要支撑(Swinbank et al,2016)。TIGGE的数据分析表明,不同中心集合预报各有优势,若进行多系统集成(如简单合并或加权平均),可在一定程度上提高预报技巧和可靠性。这印证了多模型集合的价值,也为各国改进各自系统提供了参考。另外,2015年启动的S2S计划扩展了集合预报在次季节至季节尺度的应用,通过汇集各中心延伸期集合预报(时效长达30~60 d)来研究热带大气季节内振荡(MJO)、季风等低频变率的可预报性。这些国际合作项目体现出集合预报在气象大数据共享时代的重要意义。
3.2 区域集合预报系统区域集合预报聚焦于有限区域(如单个国家或州、省)的高分辨率集合预报,侧重于短期(0~3 d)至中期(3~10 d)内的中小尺度天气系统的不确定性预报。随着20世纪末区域数值模式(WRF①、AROME②、ALADIN③等)的发展和计算资源增长,各国从20世纪90年代末开始建设区域集合预报系统,以提高本地高影响天气的预报能力。
①WRF-Weather Research and Forecasting
②AROME-Application of Research to Operations at Mesoscale
③ALADIN-Aire Limited Dynamic Adaptation International Development
区域集合预报通常采用更高的水平/垂直分辨率(几千米量级)以及更频繁的更新周期(例如每日4次以上初始化),以捕捉局地天气过程。例如,美国运行的短期集合预报(SREF)系统(Du et al,2003),结合多个区域模式(Eta④、RSM⑤、WRF等)和多物理方案,提供16~21个成员的北美区域集合预报。SREF产品对强对流风暴、暴雨等的风险预报提供了量化信息。近年美国又发展出高分辨率集合预报(HREF),集成多个对流尺度模型,实现对雷暴、龙卷等显著天气的不确定性预报。相似地,欧洲多个国家(如德国的COSMO①、英国的MOGREPS②、法国的PEARP③等)都建立了针对各自国土范围的区域集合预报系统,分辨率在2~10 km,着重预报剧烈天气和定量降水的不确定性。
④Eta-The Eta Vertical Coordinate Regional Model
⑤RSM-Regional Spectrum Model
①COSMO-The Consortium for Small-Scale Modeling
②MOGREPS-The Met Office Global and Regional Ensemble Prediction System
③PEARP-Prévision d'Ensemble ARPEGE
中国也非常重视区域集合预报的发展。陈静等(2005)在21世纪00年代初就开始了对区域集合预报系统的研究。中国气象局于2018年前后建成CMA-REPS (原GRAPES-REPS),覆盖东亚地区,水平分辨率约为15 km,提供20个成员的集合预报。该系统采用多初始扰动(来自全球集合降尺度及区域分析扰动)和多物理过程扰动,能够较好地给出我国短期强降水、强对流的预报不确定性(范宇思等,2022;张涵斌等,2022;王婧卓等,2025)。例如,在重大天气过程中,CMA-REPS的降水概率预报、雷暴风险概率等,为预报员判断极端降水落区提供了参考。目前CMA正在研发升级千米级的对流允许集合预报,以求更精细地刻画短时强降水和强对流风暴发生概率。
相比全球集合预报,区域集合预报的边界条件处理是一个独特问题。通常区域模式需要从全球预报获取边界条件,因而全球-区域集合嵌套是常用做法:将全球集合预报成员下传作为区域模式边界,从而产生区域集合预报的不同成员。这样区域集合既继承了全球尺度的不确定性,又能在本地放大细节差异。但也有研究采用在区域模型自身中引入随机边界扰动的方法(Houtekamer et al,1996;Marsigli et al,2001;Bowler et al,2008)。另一个挑战是高分辨率集合的计算量,比如一个3 km分辨率、20个成员的区域集合非常耗费资源。因此一些区域集合采用多模型集成而非同时运行众多成员的方式,例如美国HREF通过少量模式的组合替代大规模集合,欧洲的有限区域模式-集合预报系统(LAM-EPS)项目也探索了“元集合”(meta-ensemble)的方法。总体而言,区域集合预报正在向更高分辨率、更频繁、更新和更智能集成(同化雷达、卫星等高时空分辨率观测)方向发展。
区域集合预报在提升局地灾害天气预警方面成效显著。例如,其可为特定城市提供逐小时降水概率预报,或为机场提供雷暴大风发生概率预报,以支持精细化的决策服务。在复杂地形(山区、沿海)区域,局地集合预报对热力和动力细节的刻画明显优于全球集合,有助于改进山谷风、海陆风、地形降水等预报。在中国,华南前汛期暴雨、江淮梅雨锋降水等预报中,区域集合往往能比全球集合更早、更准确地给出可能的降水落区和极端值范围,成为预报员研判的重要依据。
4 统计后处理与预报诊断评估方法集合预报为同一预报时段提供了离散的多样本预报结果,需要经过适当的统计分析和后处理才能转化为用户易于理解和利用的信息。统计后处理(statistical post-processing)是指对原始集合预报进行统计校正和提炼,包括偏差订正、概率校准、空间降尺度、集合成员加权等,旨在去除系统误差并提高概率预报的可靠性。此外,为了评估集合预报的效果,需要应用预报诊断评估方法,如各类检验指标和图表,对集合预报的技巧、可靠性及不确定性信息进行定量评价(朱跃建,2020)。高质量的统计后处理与科学的诊断评估相结合,可以充分发挥集合预报的优势,使其产品更好地服务预报决策。
4.1 统计后处理方法统计后处理可参考世界气象组织出版的集合预报用户指南(WMO,2021)中的标准流程。一般包括以下几个方面:
(1) 偏差校正:针对集合预报整体存在的系统偏差进行校正,主要方法有:
(a) 线性/非线性回归:利用历史观测和预报资料建立预报值与实况之间的回归关系,校正集合预报的均值偏差。例如传统MOS方法通过线性回归消除模式偏差,在集合预报情景下可对集合平均进行回归校准。Glahn and Lowry (1972)的工作奠定了回归校正的基础。
(b) 卡尔曼滤波(Kalman filter)逐步校正:利用递推的方法实时更新预报偏差。具体做法是对于每个新预报时刻,用前一时次预报与实况之差估计当前偏差,并乘以衰减因子累积,从而修正当前预报。Cui et al (2012)将该方法应用于温度和降水集合预报偏差订正,取得良好效果。
(c) 频率匹配(frequency matching):主要针对降水等变量,比较预报值与观测值的累计频率分布,找到对应分位进行匹配调整。Zhu and Luo (2015)提出的频率匹配方法在很多业务部门降水集合预报订正中得到应用。它类似于分位数映射技术,通过调整预报量的分布使之与观测分布一致。
(d) 分位数映射(quantile mapping, QM): Hamill and Scheuerer (2018)提出了QM和秩加权最优成员修饰的概率性降水预报后处理方法。该方法首先利用分位数映射技术对原始集合预报进行系统性偏差校正,从而更准确地对预报降水的分布特征进行调整。随后,应用秩加权最优成员修饰方法,将历史最优预报成员的信息引入当前预报,通过对集合成员进行加权构建概率分布,提高预报的不确定性刻画能力。该方法能够有效提升降水概率预报的准确性和可靠性,尤其在极端降水事件的预报中展现出更优的性能。
(2) 概率校准:针对集合概率预报输出的校正,核心在于使预报概率与实际观测频率相一致。常用方法包括:
(a) 多元逻辑回归:建立集合预报统计量与观测发生与否之间的多元逻辑回归模型,输出校正后的事件概率。例如Eckel and Walters(1998)将多元回归用于降水概率预报校准。Wilks(2006)也讨论了回归校准概率的方法。
(b) 贝叶斯模型平均(BMA):Raftery et al(2005)提出,用一个加权的概率密度函数混合来表征集合预报的概率分布。BMA根据历史性能给每个集合成员赋予权重,再将各成员的概率分布线性组合成综合概率预报。这种方法在降水、温度等概率预报校准中效果良好,可明显提高概率预报的可靠性。
(c) 逻辑回归校准:针对二分类事件(如是否下雨),用逻辑回归将原始集合给出的发生概率进行偏差校正。Hamill and Colucci(1997)应用逻辑回归对降水概率进行后处理,提高了暴雨概率预报的命中率和可靠度。
(d) 组合校准:结合多种信息的混合校准方法。如Guan et al(2015)提出将实时滚动校正(Kalman滤波思想)与历史回报统计校正相结合,同时考虑模式近期误差趋势和历史气候偏差,构建混合概率校准方案。这种方法在中国区域降水概率预报中提升了稳定性。
(3) 集合成员加权与整合:针对集合预报成员贡献不等或多模型集合的情形,通过赋予不同权重来优化预报。例如:
(a) 最佳线性无偏组合:对集合成员按照线性加权求和,权重根据成员误差协方差确定,从而得到方差最小且无偏的合成预报。Gneiting and Raftery(2005)提出可将此技术用于集合预报后处理,尤其在多模型集合情形下优化集合结果。
(b) 集合成员历史性能加权:根据各成员过去一段时间的预报准确度指标,给予优秀成员较大权重、劣质成员较小权重,以此构建加权集合平均或概率分布。Leutbecher and Palmer(2008)证明这样的加权可提高集合平均技巧。Song et al(2018)也在多模式台风强度集合预报中采用成员加权,改善了预报效果。
(c) 多模型集合:采用多模式超级集合技术整合异构预报系统的集合成员,如北美集合预报系统(NAEFS)融合美国NCEP与加拿大气象中心(CMC)的全球集合预报产品。Candille(2009)指出多集合集成往往比任何单一集合表现更好。实际业务中多模型集合常辅以统计权重或校正以优化性能。
(4) 空间后处理:针对格点预报场的空间细节调整,包括降尺度,即利用高分辨率地面观测或雷达卫星等信息,将集合预报场插值并校正到更高分辨率,以提供局地预报。例如将10 km集合预报降尺度到1 km,以反映地形影响。Stensrud et al(2000)探讨了集合降尺度对局地暴雨预报的改进。Zhu and Cui(2007)提出的多模型降尺度方法在NAEFS地面要素预报中得到了很好的应用。
空间平滑:对集合预报场应用空间滤波,去除小尺度噪声,使概率预报图更清晰稳定。Atger(2001)研究了集合概率场的平滑技巧,发现适度平滑可提高用户对概率预报的解读度,同时不显著降低信息含量。
经过上述偏差订正、概率校准、成员加权和降尺度等步骤处理后,集合预报产品的准确性和可靠性都可得到提升。需要指出,不同预报对象和区域应采用相应的后处理方案,并依赖历史检验来优化参数。如温度预报适合用多元回归+概率校准,降水预报则更依赖分位数矫正+逻辑回归等。代刊等(2018)总结了集合预报模式定量降水预报统计后处理的技术和方法。近年来,随着机器学习的发展,出现了将神经网络、决策树等用于集合后处理的探索。例如,Haupt et al(2009)尝试用神经网络校正集合降水概率,杨绚等(2022)、代刊等(2025)对深度学习用于网格天气预报的进展进行了综述,其中也讨论了AI在集合预报结果解释中的应用。机器学习有望整合多种传统后处理方法,自动学习最佳校正策略,是未来值得关注的发展方向。
4.2 预报诊断评估方法为了量化集合预报的效果,需要对其进行多方面的检验评估。常用的集合预报诊断指标包括:
(1) 均方根误差和相关系数:计算集合平均(或中位数)与实况的均方根误差以及相关系数,以评估集合平均预报的准确性。一般来说,集合平均往往比任何单一成员更准确(误差更小),这是集合预报降噪作用的体现。
(2) 离散度-误差相关:衡量集合离散度(各成员之间的标准差)与集合平均误差的匹配程度。理想情况下,平均离散度应接近均方根误差的值,从而离散度可以作为预报不确定性的有效指示。若离散度远小于误差,说明集合低估了不确定性(过于自信);反之若离散度远大于误差,则可能过度发散(预报不够收敛)。预报中心常用离散度-误差图来调优集合扰动幅度。
(3) 概率分布检验:包括等级直方图和PIT(probability integral transform)图。等级直方图将观测在集合排序中的位置统计成直方图,以检查集合是否存在系统偏差或离散度问题。如果直方图平坦,表示集合成员分布与观测无偏且散布合理;若呈U型,说明观测常落在集合外侧,集合散度不足;若中间凸起,则集合散度过大。PIT图是连续变量的类似检验。
(4) 可靠度和解析性:针对概率预报,绘制可靠性曲线评估预报概率与实际频率的一致性。理想情况下曲线应接近对角线(如预报70%概率雨天,那么实际约70%发生)。同时用Brier评分来总结二类事件概率预报的均方根误差。Brier评分可分解为可靠性、解析性等部分,其中解析性表示不同预报概率值对结果的区分能力,可靠性表示预报概率的校准优劣。集合预报经过良好校准后应当可靠度高且具有一定解析性。
(5) 连续分级概率评分(CRPS):这是评价集合预报整体分布与观测差异的综合指标,相当于概率预报的均方根误差。CRPS数值越小表示集合给出的累积概率分布与实际观测更接近。CRPS能同时反映偏差和不确定性,因此广泛用于集合预报模型之间的优劣比较。例如,在验证AI集合模型时,常用CRPS衡量其相对于传统集合的改进幅度。
(6) 极端预报能力评估:利用集合预报可以计算极端事件的概率,比如“24小时降水超过50 mm的概率”等。这类概率预报可以用ROC曲线评估命中率和虚警率的折中(Guan and Zhu, 2017)。ROC曲线下面积定量表示区分能力。集合预报往往能提高极端事件的ROC得分,表明对于极端天气具有更好的探测能力。例如Hamill et al(2006)利用NCEP集合再预报数据集,显著改善了美国极端降水的概率预报技巧。
通过以上多层次的诊断评估,可以全面了解集合预报系统的性能,从而针对性地改进模型和后处理。Toth et al(2003)就概率预报的可靠性和解析性以及其他应用功能做了全面的介绍。另外,用户价值评估也是重要环节,如使用经济价值模型评估集合预报在决策中的效益。Richardson(2000)和Zhu et al(2002)研究了集合预报在航空、能源等行业决策中的相对经济价值。结果显示,相对于单一确定性预报,集合预报能够显著提高决策收益,尤其在需要权衡风险的场景下优势更为明显。
4.3 集合预报产品示例统计后处理和诊断评估的最终目的是将集合预报转化为直观、有用的预报产品提供给预报员和用户。常见的集合预报产品包括:
(1) 概率预报图:直接根据集合成员统计计算事件发生概率。如图 2所示,概率定量降水预报(PQPF)地图显示特定区域在未来24小时降水量超过阈值(如1 mm、10 mm等)的概率。再如最高气温超过35℃的概率分布图,用不同颜色表示高温发生概率范围。概率预报图是最典型的集合预报产品,已广泛应用于天气公报和灾害预警中。文中时间除标注外均为北京时。
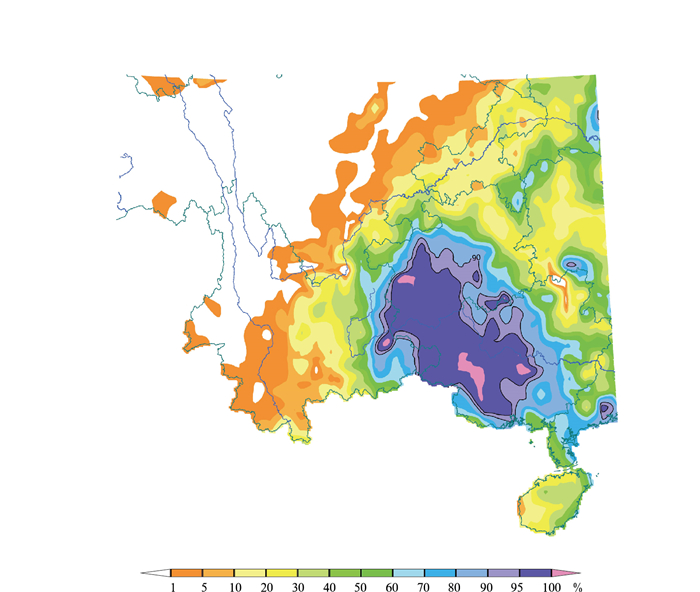
|
图 2 华南地区2025年9月25日08时至26日08时24小时累计降水≥10 mm的集合概率预报分布(起报时间为2025年9月25日20时,预报时效为0~24小时) Fig. 2 Distribution of the probabilistic forecast of 24 h accumulated precipitation ≥ 10 mm from 08:00 BT 25 to 08:00 BT 26 September 2025, initiated at 08:00 BT 25 September with 0-24 h forecast lead time in South China |
(2) 集合预报烟羽图和箱线图:用于展示集合预报在某地点的取值分布(图 3)。烟羽图通常以时间为横轴,将某格点各成员预报随时间的演变以折线表示,再叠加集合均值和观测值,直观反映预报不确定性随时间变化。箱线图则在特定时刻用箱型阐述集合分布的中位数、上(下)四分位和极值等。这些图表可以帮助预报员快速了解集合离散度和可能的极端情况。
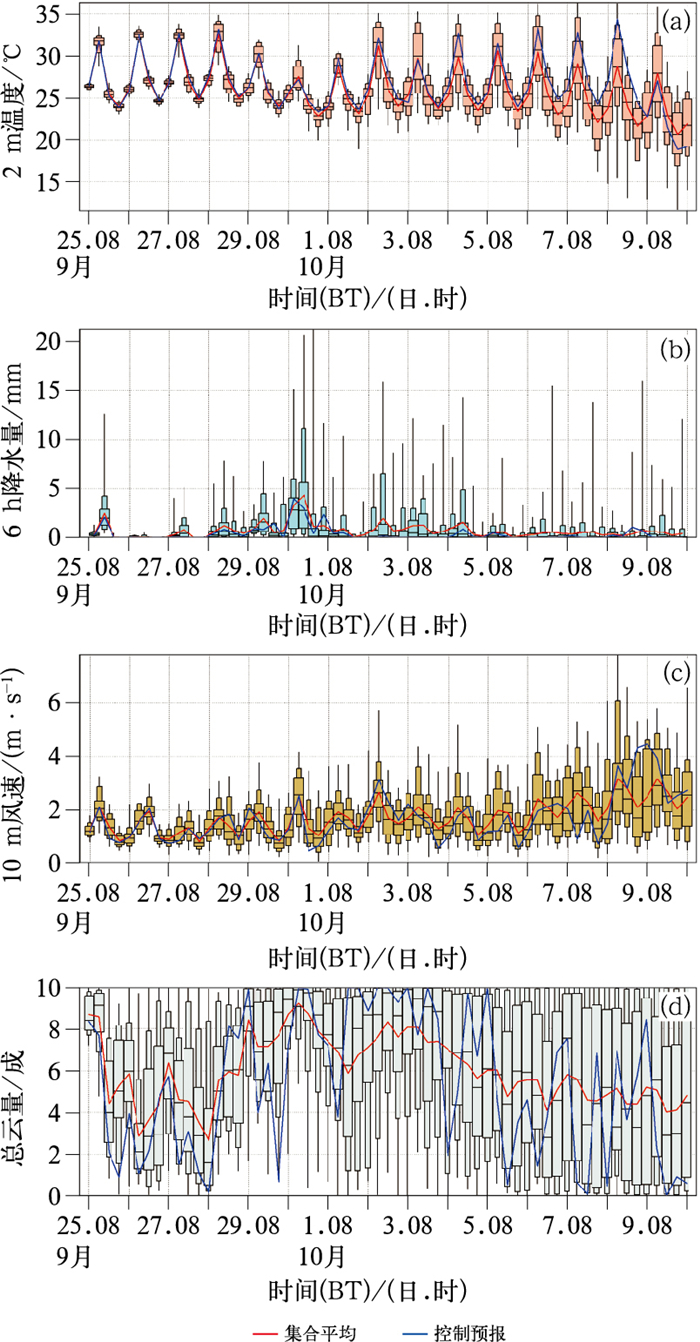
|
图 3 2025年9月25日08时至10月10日08时(起报时间为9月25日08时)北京站逐6小时数值模式集合预报的气象要素时间序列和箱线图(a)2 m气温,(b)6 h降水量,(c)10 m风速,(d)总云量 Fig. 3 Box plot with time series of meteorological elements of ensemble forecast by 6 h numerical model at Beijing Station from 08:00 BT 25 September to 08:00 BT 10 October 2025, initiated at 08:00 BT 25 September (a) 2 m temperature, (b) 6 h precipitation, (c) 10 m wind speed, (d) total cloud cover |
(3) 集合预报“邮票图”和“面条图”:“邮票图”通常是将多个集合成员对应的空间预报场以小图并列显示,如同一排排“邮票”,预报员可通过浏览这些并列图快速判断成员间对某天气系统的演变是否一致。如果多数成员显示相近的空间形态,则表示预报集中度高、可信度较高;若各成员出现截然不同的预报场,则暗示不确定性大, 需重点关注不同演变情景。“面条图”,在同一张地图上叠加多个集合成员某个关键等值线(如图 4中500 hPa高度场中的特定等值线)的分布情况,从而生成曲线相互交织、形如面条的图像。面条图更注重突出集合成员在特定气象要素(如高度场、温度场)的水平位置与幅度差异,适合展示中期预报对于槽脊、锋区等大尺度天气系统的定位分歧。两种方式都能在第一时间向预报员呈现集合成员对同一天气过程的不同预测结果,使其对预报不确定性有更直观的感受。
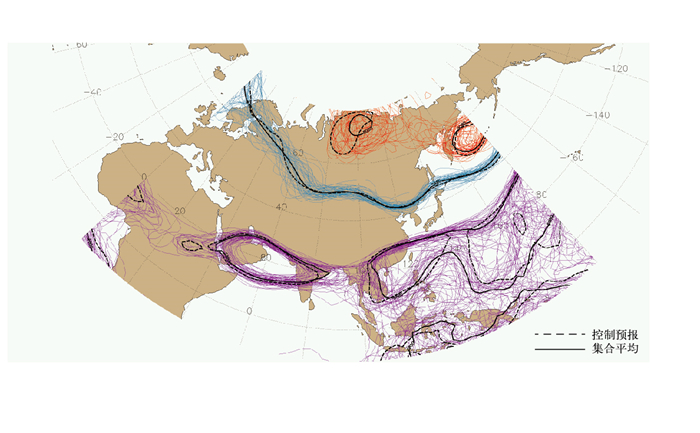
|
图 4 2025年11月9日08时(起报时间2日08时)数值模式集合预报的500 hPa高度场(单位:gpm)面条图 注:细线、黑实线、黑虚线分别为集合成员预报、集合平均和控制预报对应的500 hPa等高线,用于反映中高层环流的不确定性;蓝色面条线表示高纬度地区各集合成员的预报路径,紫色线表示南亚和热带地区的集合分布情况。 Fig. 4 Spaghtti plot of 500 hPa geopotential height (unit: gpm) of ensemble forecast by the numerical model at 08:00 BT 9 November 2025, initiated at 08:00 BT 2 November |
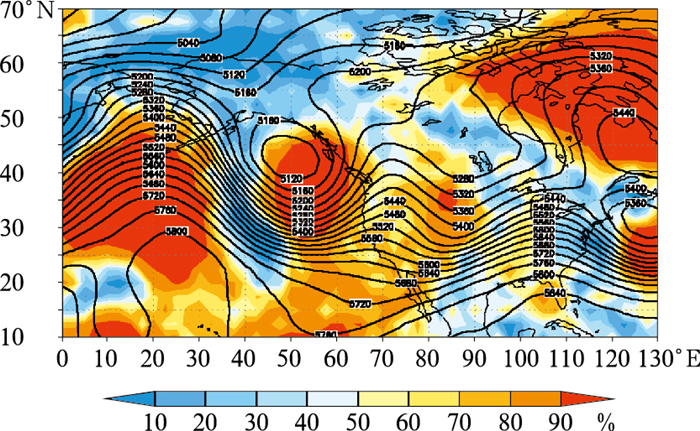
(4) 不确定性定量指标产品:例如可预报性信号图(Toth et al,2001),将集合离散信息转化为空间图形。图 5展示的相对可预报性(RMOP)即为一例。RMOP通过参考气候场方差,定量给出当前预报场相对可预报程度,通常用颜色或阴影显示:颜色深代表该地区集合预报一致、可预报性高;颜色浅或无色表示集合分歧大、预报不确定性高。类似地,ECMWF也提供集合信心指数图和预报显著性图,帮助预报员把握预报可靠度。
|
图 5 2011年4月13日00时(世界时, 初始时刻为8日00时)500 hPa高度5天预报的集合预报平均场(等值线,单位:gpm)和可预报性相对度量(填色) Fig. 5 The ensemble mean forecast field of 5 d geopotential height forecast (contour, unit: gpm) and the relative measure of predictability (colored) at 00:00 UTC 13 April 2011, initiated at 00:00 UTC 8 April |
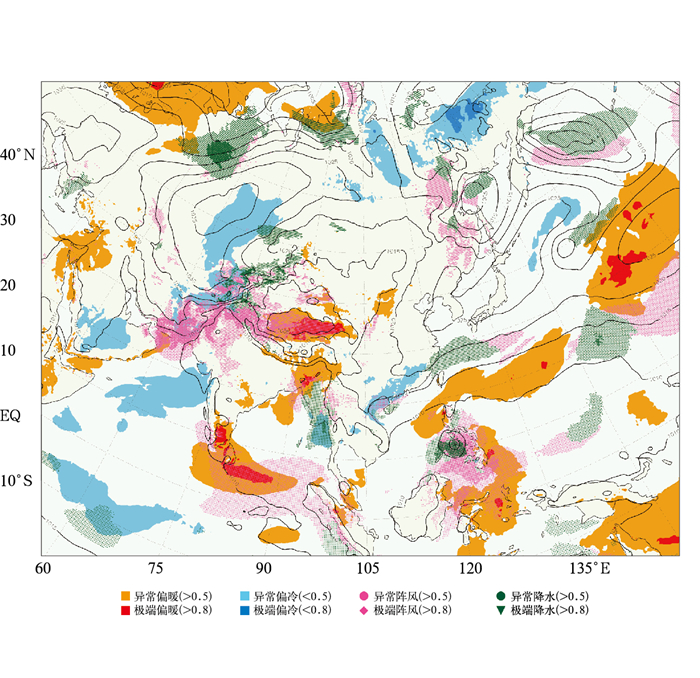
(5) 风险预警产品:这是面向用户和决策者的高级产品,将集合预报信息提炼成对特定灾害风险的预警。比如基于集合的暴雨红色预警信号,当未来24小时降水量大于100 mm的概率超过一定高阈值(如50%)时触发,以提醒相关部门提前准备。美国NCEP曾推出无偏异常预报产品,利用40年再分析气候基准计算当前预报的异常程度,如果超过历年第90%或95%分位值则判为显著异常。这类产品可以辅助识别极端事件。ECMWF的EFI也是一种风险指数输出,专门为极端天气预警服务,如图 6所示。再如风暴潮和洪水风险预报,将大气集合预报输出到海洋和水文模型,计算沿岸不同地点可能出现的风暴潮增水高度概率或河流洪峰流量概率。Pappenberger et al(2011)利用ECMWF集合为欧洲洪水预警系统提供了洪水风险预报示例。
|
图 6 2025年11月4日08时至5日08时(2日08时起报, 预报时效为第48~72小时)中国及邻近地区的集合数值模式极端天气指数预报产品空间分布 注:黑色等值线为同期海平面气压, 单位:hPa。 Fig. 6 Spatial distribution of extreme weather index forecast products of ensemble numerical models in China and its neighboring regions from 08:00 BT 4 to 08:00 BT 5 November 2025, initiated at 08:00 BT 2 November with 48-72 h forecast lead time |
通过丰富多样的产品形式,集合预报的不确定性信息得以及时传递给用户。在实际业务中,预报员会综合参考概率图、集合分布图以及确定性预报,与经验知识结合后对公众或特定用户发布风险提示。例如在台风预报中,除了传统的路径点和误差锥,现在中央气象台也使用基于集合的“概率葵花图”展示台风未来位置概率分布,使公众更直观地了解台风路径的不确定性。随着用户需求的发展,未来集合预报产品将更加多元化和智能化,例如通过交互式地图、概率情景叙述等形式,提高风险沟通的有效性。
5 集合预报在极端天气和灾害预警中的应用集合预报在极端天气事件预报和气象灾害预警中展现出独特的价值。由于极端事件往往具有发生概率低、影响严重、单一预报不确定性高的特点,集合预报提供的概率信息和备选情景对防灾决策尤为关键。以下举例说明集合预报在若干典型灾害性天气中的应用:
(1) 热带气旋(台风/飓风)路径和强度预报:热带气旋路径预报的误差随预报时长增大,而且对初始位置和引导气流的微小差异非常敏感。集合预报通过提供一组可能路径,可以直观反映未来路径的不确定范围。例如,ECMWF和NCEP的全球集合对5天左右台风路径预报的集合散点图,常用来生成“气旋路径概率锥”产品,表示未来几天台风中心可能出现的位置范围和概率密度。这有助于预警区合理制定防御半径。强度方面,集合预报也能给出不同成员的气压和风速预报分布,提供增强或减弱的概率。研究表明,集合平均的台风路径误差往往小于大多数单一模式,提高了预报稳定性;而集合可以捕捉到部分确定性预报遗漏的偏移情景,提高对转向等复杂路径的警觉性。在2018年台风“玛莉亚”、2019年台风“博罗依”(图 7)等案例中,集合预报成功提前指示出转向时机和可能的登陆区域,大大提升了预警的科学性。

|
图 7 2025年9月25日18时发布的2025年第20号台风“博罗依”未来120小时路径概率预报 注:紫线表示台风“博罗依”的实况路径,紫色阴影表示未来路径的不确定性区域(概率分布),同时标注各主要时刻的中心位置预报。 Fig. 7 Probability forecast of the 120 h track of Typhoon Bualoi issued at 18:00 BT 25 September 2025 |
(2) 暴雨洪涝预警:暴雨的落区和强度对初始条件和局地地形非常敏感,单一数值预报常有位置和强度误差。集合预报能够提供降水的多种可能分布,通过降水概率预报图,帮助识别高风险区域。例如,集合预报显示某流域有20%的成员出现极端大暴雨时,即便确定性预报未报出,该信息也可促使预报员提高警惕。欧洲洪水预警系统(EFAS)全面依赖ECMWF集合来驱动水文模型,Pappenberger et al(2011)统计显示,相比传统方法,集合驱动的洪水预警准确率提高约10%~20%,并能提供峰值流量的不确定性区间。在我国,集合降水预报也被用于山洪地质灾害风险预报模型,通过叠加土壤湿度初始不确定性场,给出泥石流和中小河流洪水发生概率,改进了地方防汛部门的预警流程。
(3) 强对流和雷暴大风:短时强降水、冰雹、龙卷等强对流天气发生具有较强的不确定性。对流尺度的集合预报(如CMA的对流允许集合试验)可生成如雷暴回波、风切变等的概率预报。在2019年夏季的华北龙卷事件中,虽然单一模式未明确预报,但集合预报给出了华北平原中部低压过境时产生剧烈天气的可能性,其成员中有部分出现了强风暴反射率回波的信号。这为临近预报提供了有益提示。国外研究亦表明,集合预报可以显著提高强对流风险的检测率。
(4) 高温和寒潮:极端高温和严寒事件通常由大型大气环流异常造成,但集合预报仍可给出持续时间和强度的不确定范围。Min and Zhang(2011)利用集合预报分析了中国历史上的极端高温和寒潮,结果表明集合方法能够较好地涵盖实际发生的极值情况。例如,2013年中国南方极端高温过程中,集合预报提前10天即提示副热带高压可能异常偏强,部分成员预报了40℃以上的极端高温,帮助政府部门早做准备。对于寒潮,集合预报可以预测冷空气南下路径的不确定性以及降温幅度概率,使得寒潮预警在时间和影响区域上更加从容。Vitart et al(2017)也指出,在季节预测中集合预报可提供未来1~2个月温度异常的概率信息,有助于提前部署能源调度和农业防灾。
(5) 森林火灾风险:极端高温干旱和大风是森林火灾发生和扩散的重要气象因素。集合预报可以结合火险指标(如火险气象指数)生成火险等级概率预报。Smith and Hughes(2020)对2019年澳大利亚山火季进行了事后分析,发现集合预报在多个地点提前预示了极端火险条件的持续,可靠度明显优于单次预报。在火情应对中,集合预报提供的不确定性信息(如火险高值出现概率、不同风力情景)可以帮助决策者制定更稳健的资源调配方案。
除了上述例子,集合预报还广泛应用于航空气象(如飞机颠簸和能见度预报)、海洋预报(如海浪高度和风暴潮)、环境气象(如沙尘暴路径、空气污染过程)等领域。例如多家中心联合的火山灰扩散集合预报,为航空提供了火山灰云影响概率预报图,使航线调整更加合理。再如欧洲空气质量预报集合项目(如大气成分与气候监测MACC)集成多个化学模式输出,改进了污染事件的不确定性评估。这些都体现了集合预报在各领域的适应性和重要性。
总的来说,集合预报通过提供概率预警取代了过去“报或不报”的二元预报模式,使预报产品更符合实际不确定性。它为防灾减灾提供了科学依据,让应急管理能够根据风险概率分级响应,避免漏报和过度预警的“双重损失”。随着集合预报的不断进步和与应用部门的磨合,其在极端事件预报中的作用将更加突出。
6 人工智能与数据驱动的集合预报新进展进入21世纪第三个10年,AI技术尤其是深度学习在天气预报领域取得令人瞩目的突破。基于海量历史再分析数据训练的AI天气预报模型,能够在极短时间内完成与数值模式相当精度的预报。例如美国NVIDIA公司开发的FourCastNet模型(基于深度神经网络)成功实现全球14天500 hPa高度场的预测,与ECMWF模式精度相当但速度快数万个数量级;华为团队的盘古天气模型利用3D神经网络预测全球逐小时多变量天气,达到全球业务中心同等水平并登上Nature期刊。这些模型主要用于确定性预报,但其巨大成功启发了概率预报的新思路——利用AI模型快速生成大规模集合成员,或直接学习预报概率分布,从而克服传统集合预报计算成本高、成员数受限的瓶颈。
Google研究团队在2024年提出了SEEDS模型(Li et al,2024)。SEEDS以美国NCEP的GEFS集合再预报数据为基础,采用扩散概率模型框架,旨在模拟传统集合预报的结果分布。其做法包括两个阶段:首先训练集合模拟器模块,使用少数GEFS集合成员的信息来重构GEFS的整体概率分布;然后训练生成后处理模块,将GEFS模拟的分布与历史ERA5再分析的不确定性信息相结合,纠正集合预报的系统偏差。最终,SEEDS能够在仅输入GEFS两个成员(控制及一个扰动)的条件下,快速生成上百个模拟成员,且生成集合的统计特征(如均值、方差、极端概率)与原始GEFS 30个成员集合非常接近。计算成本方面,SEEDS使用扩散模型逐步采样的方法,但因为只需少数输入成员,整体效率仍比直接跑数值模式生成大量成员要高出一个数量级以上。更重要的是,SEEDS输出的超大集合可以更好地表征稀有事件:在Google的试验中,生成1000个成员的SEEDS可以捕捉到原始30个成员集合未出现的一些极端降水情景,并以概率形式给出。SEEDS展示了AI生成模型与传统NWP结合的潜力——以较小成本显著扩大集合规模,从而改善极端事件的概率预报。
DeepMind团队在2023年底提出了另一个具有里程碑意义的模型GenCast。与SEEDS偏重于模拟已有集合不同,GenCast尝试完全由AI生成独立的集合预报。GenCast使用扩散模型框架,将天气预报问题视为逐步消除噪声还原大气状态的过程。它以ERA5再分析数据训练,可以从随机噪声出发,通过迭代“降噪”生成全球15天逐12小时的天气演变。GenCast的架构融合了深度神经网络提供的大尺度准确定性预测和扩散过程提供的不确定扰动,其单次运行即可输出一个随机的可能天气序列。通过多次运行GenCast并改变初始噪声种子,就能获得一个预报集合。性能方面,Price et al(2025)表明,GenCast在0.25°分辨率、15天预报对80多个大气和地表变量的预报技巧,超过了ECMWF的51个成员集合预报,在97.4%的检验指标上取得更高的技巧分数。尤其在降水极值、热带气旋路径等方面,GenCast对极端情况的捕捉能力优于传统集合。此外,GenCast生成一套20个成员左右的集合耗时仅几分钟,这相比ECMWF集合需要超级计算机运行几小时以上的情况,有巨大的效率优势。GenCast的出现标志着AI有望直接挑战乃至超越物理模式生成的集合预报。
FuXi-Ens是中国研究团队在AI集合预报方向的最新成果(Zhong et al,2024)。2024年初,有来自复旦大学等单位的学者在arXiv发表了FuXi-Ens模型的成果。FuXi-Ens借鉴了生成模型思想,但采用变分自编码器(VAE)框架来生成集合成员。其特点包括:(1)输入采用ERA5再分析数据,输出6小时步长、全球15天预报,与GenCast相似;(2)水平分辨率达到0.25°(约25 km),垂直方向包含13个等压面层和十余个地表变量;(3)利用VAE的隐空间随机采样性质来产生初始扰动和模拟模式随机误差。训练目标方面,FuXi-Ens没有像典型VAE那样仅用均方根误差,而是设计了结合连续分级概率评分(CRPS)和Kullback-Leibler(KL)散度的损失函数。CRPS部分确保生成的概率分布逼近真实分布(提升概率预报技巧),KL散度则约束生成样本不要偏离历史气候统计。通过这种特殊训练,FuXi-Ens在保留VAE高效单步生成能力的同时,提高了生成集合的可靠度和分散性。根据论文,FuXi-Ens与ECMWF集合在相同初始条件下对比测试,在360个检验指标中的98.1%上显著优于ECMWF集合预报,尤其是CRPS评分平均降低了约10%左右。FuXi-Ens不依赖任何传统NWP集合输入;与GenCast需要通过扩散多步生成不同,FuXi-Ens一次前向传播就输出所有变量的集合成员。这样在业务部署时,只需提供当前分析场,FuXi-Ens即可直接给出集合预报结果,极大简化了流程。
总的来说,人工智能集合预报仍处于起步阶段,但已有的成果足以表明其巨大潜力。一方面,AI模型能以远低于NWP的成本生成高质量集合,为提高成员数、分辨率提供了全新途径;另一方面,AI模型也面临诸多挑战,如如何保证物理一致性、防止奇异假象,以及在模式外推时的稳定性等。这需要气象科学与人工智能领域的深入交叉合作。未来,我们有理由期待一个“物理驱动和数据驱动结合”的新型预报范式。在这种范式下,集合预报将进一步减少不确定性、提高预报能力,在保障社会经济发展和防灾减灾中发挥更大作用。
7 结论与展望本文回顾了现代集合预报系统的发展历程、关键技术、业务应用以及最新的人工智能驱动进展。集合预报自20世纪下半叶兴起,解决了确定性预报无法量化不确定性的根本问题,通过各种扰动模拟提供了未来天气多种可能性的概率预报框架。传统集合预报技术在初始扰动方面发展出繁殖法、奇异向量、集合同化等方法,在模式扰动方面形成了随机物理方案、多模型集成等体系,不断改善了集合离散度与可靠性,使预报技巧稳步提升。各国建立的全球和区域集合预报系统,如ECMWF、NCEP、CMA的集合系统等,已成为业务天气预报和灾害预警的重要支撑。通过统计后处理,集合预报产品更加准确、稳定,以概率形式服务于各行业决策。在极端天气和气象灾害预警中,集合预报大幅提高了预报的提前量和信息量,为防灾减灾赢得宝贵时间。可以说,集合预报理念的普及是数值天气预报领域的一场范式革命。
进入大数据与人工智能时代,集合预报正迎来新的发展契机。深度学习等AI技术提供了全新的手段来表征和获取不确定性信息,突破了传统方法在计算成本和模式偏差上的瓶颈。新近出现的GenCast、SEEDS、FuXi-Ens、AIFS-CRPS等AI集合预报模型,展示了AI生成天气集合的可行性和巨大潜力;它们以更低成本、更高维度,达到甚至超过传统51个成员集合的预报性能,尤其在极端天气概率预报上表现突出。这预示着未来集合预报系统形态可能发生重大变化——通过AI模型,可以实时生成数百乃至上千个成员的超大型集合来探测极端事件概率分布,而不再受限于计算资源。同时,AI模型可以与物理模式融合,形成“AI+NWP”双引擎的集合预报系统:既有物理模型提供可靠性保障,又有AI模型拓展预报的广度和深度。
尽管如此,我们也需保持理性认识。目前AI集合预报尚处试验阶段,要替代或大规模应用于业务,还需解决诸多挑战。例如,如何确保AI生成的预报满足大气物理约束,不产生不合理的天气演变?如何在资料同化环节融合AI输出,提高初始场质量?如何建立AI集合预报的检验评估标准,确保其稳定性和可解释性?这些都需要进一步研究探索。另外,预报员角色也会因AI而改变,更需要关注概率预报解读和风险沟通,将复杂的不确定信息有效传达给用户。
总的来看,集合预报的发展体现了气象预报从确定性走向概率性的科学进步。它极大提升了我们面对不确定性的从容度。展望未来,随着高性能计算的发展和人工智能的深度介入,集合预报系统将更加智能、高效和精细化。不仅天气预报,在气候预测、环境预测乃至其他复杂系统(如水文、海洋、空间天气等)中,集合方法都将发挥越来越重要的作用。我们有理由相信,一个结合了物理机理和数据智能的新一代集合预报生态正在形成。这将帮助人类更好地预测和应对天气与气候的不确定性,为防灾减灾和可持续发展保驾护航。
致谢:感谢地球系统数值预报中心齐倩倩在文档整理方面的协助。
陈静, 李晓莉, 2020. GRAPES全球/区域集合预报系统10年发展回顾及展望[J]. 气象科技进展, 10(2): 9-18, 29. Chen J, Li X L, 2020. The review of 10 years development of the GRAPES global/regional ensemble prediction[J]. Adv Meteor Sci Technol, 10(2): 9-18, 29 (in Chinese).
|
陈静, 薛纪善, 颜宏, 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究[J]. 大气科学, 29(5): 717-726. Chen J, Xue J S, Yan H, 2005. A new initial perturbation method of ensemble mesoscale heavy rain prediction[J]. Chin J Atmos Sci, 29(5): 717-726 (in Chinese).
|
代刊, 杨绚, 周康辉, 等, 2025. 深度学习在数字智能天气预报中的应用[J]. 气象, 51(11): 1477-1494. Dai K, Yang X, Zhou K H, et al, 2025. Application of deep learning in digital intelligent weather forecasting[J]. Meteor Mon, 51(11): 1477-1494 (in Chinese). DOI:10.7519/j.issn.1000-0526.2025.110701
|
代刊, 朱跃建, 毕宝贵, 2018. 集合模式定量降水预报的统计后处理技术研究综述[J]. 气象学报, 76(4): 493-510. Dai K, Zhu Y J, Bi B G, 2018. The review of statistical post-process technologies for quantitative precipitation forecast of ensemble prediction system[J]. Acta Meteor Sin, 76(4): 493-510 (in Chinese).
|
范宇恩, 李红祺, 陈静, 等, 2022. CMA-REPS区域集合预报随机动能后向散射方案敏感性试验[J]. 气象, 48(9): 1077-1089. Fan Y E, Li H Q, Chen J, et al, 2022. Sensitivity experiments of a stochastic kinetic energy backscatter scheme within the CMA-REPS regional ensemble prediction system[J]. Meteor Mon, 48(9): 1077-1089 (in Chinese). DOI:10.7519/j.issn.1000-0526.2022.051201
|
李晓莉, 陈静, 刘永柱, 等, 2019. GRAPES全球集合预报初始条件及模式物理过程不确定性方法研究[J]. 大气科学学报, 42(3): 348-359. Li X L, Chen J, Liu Y Z, et al, 2019. Representations of initial uncertainty and model uncertainty of GRAPES global ensemble forecasting[J]. Trans Atmos Sci, 42(3): 348-359 (in Chinese).
|
沈学顺, 苏勇, 李兴良, 等, 2025. 中国业务数值天气预报自主发展中的理论和方法创新[J]. 气象, 51(11): 1293-1320. Shen X S, Su Y, Li X L, et al, 2025. Innovation of theory and methodology in the independent development of operational numerical weather prediction in China[J]. Meteor Mon, 51(11): 1293-1320 (in Chinese). DOI:10.7519/j.issn.1000-0526.2025.093001
|
王婧卓, 李红祺, 陈静, 等, 2025. 高分辨率区域集合预报混合侧边界扰动方法研究[J]. 气象, 51(9): 1029-1045. Wang J Z, Li H Q, Chen J, et al, 2025. Research on the mixed lateral boundary perturbation method for high-resolution regional ensemble forecast[J]. Meteor Mon, 51(9): 1029-1045 (in Chinese). DOI:10.7519/j.issn.1000-0526.2025.041401
|
杨绚, 代刊, 朱跃建, 2022. 深度学习技术在智能网格天气预报中的应用进展与挑战[J]. 气象学报, 80(5): 649-667. Yang X, Dai K, Zhu Y J, 2022. Progress and challenges of deep learning techniques in intelligent grid weather forecasting[J]. Acta Meteor Sin, 80(5): 649-667 (in Chinese).
|
张涵斌, 计燕霞, 陈敏, 等, 2022. 基于观测扰动的集合预报EDA初值扰动方法研究[J]. 气象, 48(4): 406-417. Zhang H B, Ji Y X, Chen M, et al, 2022. Study on the EDA initial condition perturbation method for ensemble prediction system based on observation perturbation[J]. Meteor Mon, 48(4): 406-417 (in Chinese). DOI:10.7519/j.issn.1000-0526.2021.102301
|
朱跃建, 2020. 基于最新全球集合预报系统的可预报性评估[J]. 大气科学学报, 43(1): 193-200. Zhu Y J, 2020. An assessment of predictability through state-of-the-art global ensemble forecast system[J]. Trans Atmos Sci, 43(1): 193-200 (in Chinese).
|
Atger F, 2001. Verification of intense precipitation forecasts from single models and ensemble prediction systems[J]. Nonlin Processes Geophys, 8(6): 401-417. DOI:10.5194/npg-8-401-2001
|
Bowler N E, Arribas A, Mylne K R, et al, 2008. The MOGREPS short-range ensemble prediction system[J]. Quart J Roy Meteor Soc, 134(632): 703-722. DOI:10.1002/qj.234
|
Buizza R, Houtekamer P L, Pellerin G, et al, 2005. A comparison of the ECMWF, MSC, and NCEP global ensemble prediction systems[J]. Mon Wea Rev, 133(5): 1076-1097. DOI:10.1175/MWR2905.1
|
Buizza R, Milleer M, Palmer T N, 1999. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system[J]. Quart J Roy Meteor Soc, 125(560): 2887-2908. DOI:10.1002/qj.49712556006
|
Buizza R, Palmer T N, 1995. The singular-vector structure of the atmospheric global circulation[J]. J Atmos Sci, 52(9): 1434-1456. DOI:10.1175/1520-0469(1995)052<1434:TSVSOT>2.0.CO;2
|
Candille G, 2009. The multiensemble approach: the NAEFS example[J]. Mon Wea Rev, 137(5): 1655-1665. DOI:10.1175/2008MWR2682.1
|
Cui B, Toth Z, Zhu Y J, et al, 2012. Bias correction for global ensemble forecast[J]. Wea Forecasting, 27(2): 396-410. DOI:10.1175/WAF-D-11-00011.1
|
Du J, DiMego G, Tracton M S, et al, 2003. NCEP short-range ensemble forecasting (SREF) system: multi-IC, multi-model and multi-physics approach[M]//Côté J. Research Activities in Atmospheric and Oceanic Modelling. CAS/JSC Working Group Numerical Experimentation (WGNE).
|
Eckel F A, Walters M K, 1998. Calibrated probabilistic quantitative precipitation forecasts based on the MRF ensemble[J]. Wea Forecasting, 13(4): 1132-1147. DOI:10.1175/1520-0434(1998)013<1132:CPQPFB>2.0.CO;2
|
Epstein E S, 1969. Stochastic dynamic prediction[J]. Tellus, 21(6): 739-759.
|
Glahn H R, Lowry D A, 1972. The use of model output statistics (MOS) in objective weather forecasting[J]. J Appl Meteor Climatol, 11(8): 1203-1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2
|
Gneiting T, Raftery A E, 2005. Weather forecasting with ensemble methods[J]. Science, 310(5746): 248-249. DOI:10.1126/science.1115255
|
Guan H, Cui B, Zhu Y J, 2015. Improvement of statistical postprocessing using GEFS reforecast information[J]. Wea Forecast ing, 30(4): 841-854. DOI:10.1175/WAF-D-14-00126.1
|
Guan H, Zhu Y J, 2017. Development of verification methodology for extreme weather forecasts[J]. Wea Forecasting, 32(2): 479-491. DOI:10.1175/WAF-D-16-0123.1
|
Guan H, Zhu Y J, Sinsky E, et al, 2019. Systematic error analysis and calibration of 2-m temperature for the NCEP GEFS reforecast of the subseasonal experiment (SubX) project[J]. Wea Forecast ing, 34(2): 361-376. DOI:10.1175/WAF-D-18-0100.1
|
Guan H, Zhu Y J, Sinsky E, et al, 2022. GEFSv12 reforecast dataset for supporting subseasonal and hydrometeorological applications[J]. Mon Wea Rev, 150(3): 647-665. DOI:10.1175/MWR-D-21-0245.1
|
Hamill T M, Colucci S J, 1997. Verification of Eta-RSM short-range ensemble forecasts[J]. Mon Wea Rev, 125(6): 1312-1327. DOI:10.1175/1520-0493(1997)125<1312:VOERSR>2.0.CO;2
|
Hamill T M, Scheuerer M, 2018. Probabilistic precipitation forecast postprocessing using quantile mapping and rank-weighted best-member dressing[J]. Mon Wea Rev, 146(12): 4079-4098. DOI:10.1175/MWR-D-18-0147.1
|
Hamill T M, Snyder C, 2000. A hybrid ensemble Kalman filter-3D variational analysis scheme[J]. Mon Wea Rev, 128(8): 2905-2919. DOI:10.1175/1520-0493(2000)128<2905:AHEKFV>2.0.CO;2
|
Hamill T M, Whitaker J S, Mullen S L, 2006. Reforecasts: an important dataset for improving weather predictions[J]. Bull Amer Meteor Soc, 87(1): 33-46. DOI:10.1175/BAMS-87-1-33
|
Haupt S E, Pasini A, Marzban C, 2009. Artificial Intelligence Methods in the Environmental Sciences[M].
New York: Springer Science and Business Media.
|
Houtekamer P L, Derome J, 1995. Methods for ensemble prediction[J]. Mon Wea Rev, 123(7): 2181-2196. DOI:10.1175/1520-0493(1995)123<2181:MFEP>2.0.CO;2
|
Houtekamer P L, Lefaivre L, Derome J, et al, 1996. A system simulation approach to ensemble prediction[J]. Mon Wea Rev, 124(6): 1225-1242. DOI:10.1175/1520-0493(1996)124<1225:ASSATE>2.0.CO;2
|
Kleist D T, Ide K, 2015. An OSSE-based evaluation of hybrid variational-ensemble data assimilation for the NCEP GFS[J]. Mon Wea Rev, 143(1): 178-191.
|
Leith C E, 1974. Theoretical skill of Monte Carlo forecasts[J]. Mon Wea Rev, 102(6): 409-418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2
|
Leutbecher M, Lock S J, Ollinaho P, et al, 2017. Stochastic representations of model uncertainties at ECMWF: state of the art and future vision[J]. Quart J Roy Meteor Soc, 143(707): 2315-2339. DOI:10.1002/qj.3094
|
Leutbecher M, Palmer T N, 2008. Ensemble forecasting[R]. Shinfield Park: ECMWF: 1-31.
|
Li L Z, Carver R, Lopez-Gomez I, et al, 2024. Generative emulation of weather forecast ensembles with diffusion models[J]. Sci Adv, 10(13): eadk4489. DOI:10.1126/sciadv.adk4489
|
Lorenc A C, 2003. The potential of the ensemble Kalman filter for NWP-a comparison with 4D-Var[J]. Quart J Roy Meteor Soc, 129(595): 3183-3203. DOI:10.1256/qj.02.132
|
Lorenz E N, 1963. Deterministic nonperiodic flow[J]. J Atmos Sci, 20(2): 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
|
Marsigli C, Montani A, Nerozzi F, et al, 2001. A strategy for high-resolution ensemble prediction.Ⅱ: limited-area experiments in four Alpine flood events[J]. Quart J Roy Meteor Soc, 127(576): 2095-2115.
|
McTaggart-Cowan R, Separovic L, Aider R, et al, 2022a. Using stochastically perturbed parameterizations to represent model uncertainty.Part Ⅰ: implementation and parameter sensitivity[J]. Mon Wea Rev, 150(11): 2829-2858. DOI:10.1175/MWR-D-21-0315.1
|
McTaggart-Cowan R, Separovic L, Charron M, et al, 2022b. Using stochastically perturbed parameterizations to represent model uncertainty. Part Ⅱ: comparison with existing techniques in an operational ensemble[J]. Mon Wea Rev, 150(11): 2859-2882. DOI:10.1175/MWR-D-21-0316.1
|
Min D, Zhang Q, 2011. Ensemble prediction of climate extremes: application to heat waves and cold waves[J]. Climate Dyn, 37(9): 1717-1731.
|
Mu M, Duan W S, Wang B, 2003. Conditional nonlinear optimal perturbation and its applications[J]. Nonlin Processes Geophys, 10(6): 493-501. DOI:10.5194/npg-10-493-2003
|
Mu M, Duan W S, Wang Q, et al, 2010. An extension of conditional nonlinear optimal perturbation approach and its applications[J]. Nonlin Processes Geophys, 17(2): 211-220. DOI:10.5194/npg-17-211-2010
|
Pappenberger F, Thielen J, Del Medico M, 2011. The impact of weather forecast improvements on large scale hydrology: analysing a decade of forecasts of the European Flood Alert System[J]. Hydrol Processes, 25(7): 1091-1113. DOI:10.1002/hyp.7772
|
Pegion K, Kirtman B P, Becker E, et al, 2019. The subseasonal experiment (SubX): a multimodel subseasonal prediction experiment[J]. Bull Amer Meteor Soc, 100(10): 2043-2060. DOI:10.1175/BAMS-D-18-0270.1
|
Price I, Sanchez-Gonzalez A, Alet F, et al, 2025. Probabilistic weather forecasting with machine learning[J]. Nature, 637(8044): 84-90. DOI:10.1038/s41586-024-08252-9
|
Raftery A E, Gneiting T, Balabdaoui F, et al, 2005. Using Bayesian model averaging to calibrate forecast ensembles[J]. Mon Wea Rev, 133(5): 1155-1174. DOI:10.1175/MWR2906.1
|
Richardson D S, 2000. Skill and relative economic value of the ECMWF ensemble prediction system[J]. Quart J Roy Meteor Soc, 126(563): 649-667. DOI:10.1002/qj.49712656313
|
Shutts G, 2005. A kinetic energy backscatter algorithm for use in ensemble prediction systems[J]. Quart J Roy Meteor Soc, 131(612): 3079-3102. DOI:10.1256/qj.04.106
|
Shutts G, Allen T, 2007. Sub-gridscale parametrization from the perspective of a computer games animator[J]. Atmos Sci Let, 8(4): 85-92. DOI:10.1002/asl.157
|
Simon L, Alexe M, Clare M C A, et al, (2024-12-20). AIFS-CRPS: ensemble forecasting using a model trained with a loss function based on the Continuous Ranked Probability Score[J/OL]. arXiv: 2412.15832.
|
Smith C, Hughes A, 2020. Ensemble forecasting for wildfires: case study of the 2019 Australian bushfire season[J]. Australian Meteor Oceanographic J, 70(2): 91-105.
|
Song X J, Zhu Y J, Peng J Y, et al, 2018. Improving multi-model ensemble forecasts of tropical cyclone intensity using Bayesian model averaging[J]. J Meteor Res, 32(5): 794-803. DOI:10.1007/s13351-018-7117-7
|
Stensrud D J, Bao J W, Warner T T, 2000. Using initial condition and model physics perturbations in short-range ensemble simulations of mesoscale convective systems[J]. Mon Wea Rev, 128(7): 2077-2107. DOI:10.1175/1520-0493(2000)128<2077:UICAMP>2.0.CO;2
|
Swinbank R, Kyouda M, Buchanan P, et al, 2016. The TIGGE project and its achievements[J]. Bull Amer Meteor Soc, 97(1): 49-67. DOI:10.1175/BAMS-D-13-00191.1
|
Tompkins A M, Berner J, 2008. A stochastic convective approach to account for model uncertainty due to unresolved humidity variability[J]. J Geophys Res Atmos, 113(D18).
|
Toth Z, Desmarais J G, Brunet G, et al, 2006. The North American ensemble forecast system (NAEFS)[R]. AGU Geophysical Research Abstracts.
|
Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC: the generation of perturbations[J]. Bull Amer Meteor Soc, 74(12): 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2
|
Toth Z, Kalnay E, 1997. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 125(12): 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2
|
Toth Z, Talagrand O, Candille G, et al, 2003. Probability and ensemble forecasts[M]//Jolliffe I T, Stephenson D B. Forecast Verification: A Practitioner's Guide in Atmospheric Science. Wiley: 137-163.
|
Toth Z, Zhu Y J, Marchok T, 2001. On the ability of ensembles to distinguish between forecasts with small and large uncertainty[J]. Wea Forecasting, 16: 436-477.
|
Vitart R, Ardilouze C, Bonet A, et al, 2017. The subseasonal to seasonal (S2S) prediction project database[J]. Bull Amer Meteor Soc, 98(1): 163-173. DOI:10.1175/BAMS-D-16-0017.1
|
Wei M Z, Toth Z, Wobus R, et al, 2006. Ensemble transform Kalman filter-based ensemble perturbations in an operational global prediction system at NCEP[J]. Tellus: Dyn Meteor Oceanogr, 58(1): 28-44. DOI:10.1111/j.1600-0870.2006.00159.x
|
Wilks D S, 2006. Statistical Methods in the Atmospheric Sciences[M].
2nd ed.London: Academic Press.
|
WMO, 2021. Guidelines on ensemble prediction system postprocessing[R]. WMO: 1-46.
|
Zhong X H, Chen L, Li H, et al, (2024-05-09). FuXi-Ens: a machine learning model for medium-range ensemble weather forecasting[J/OL]. Preprint at https://doi.org/10.48550/arXiv.2405.05925.
|
Zhou X Q, Zhu Y J, Hou D C, et al, 2022. The development of the NCEP global ensemble forecast system version 12[J]. Wea Forecasting, 37(6): 1069-1084. DOI:10.1175/WAF-D-21-0112.1
|
Zhu Y J, 2005. Ensemble forecast: a new approach to uncertainty and predictability[J]. Adv Atmos Sci, 22(6): 781-788. DOI:10.1007/BF02918678
|
Zhu Y J, Cui B, 2007. Statistical down-scaling for NAEFS ensemble forecasts[R]. NOAA.
|
Zhu Y J, Li W, Zhou X Q, et al, 2019. Stochastic Representation of NCEP GEFS to improve sub-seasonal forecast[M]//Randall D A, Srinivasan J, Nanjundiah R S, et al. Current Trends in the Representation of Physical Processes in Weather and Climate Models. Singapore: Springer: 317-328.
|
Zhu Y J, Luo Y, 2015. Precipitation calibration based on the frequency- matching method[J]. Wea Forecasting, 30(5): 1109-1124. DOI:10.1175/WAF-D-13-00049.1
|
Zhu Y J, Toth Z, Wobus R, et al, 2002. The economic value of ensemble- based weather forecasts[J]. Bull Amer M eteor Soc, 83(1): 73-84. DOI:10.1175/1520-0477(2002)083<0073:TEVOEB>2.3.CO;2
|
Zhu Y J, Zhou X Q, Li W, et al, 2018. Toward the improvement of subseasonal prediction in the national centers for environmental prediction global ensemble forecast system (GEFS)[J]. J Geophys Res Atmos, 123(13): 6732-6745. DOI:10.1029/2018JD028506
|
 2025, Vol. 51
2025, Vol. 51 