引言

次季节至季节(S2S)预测的时间尺度介于天气预报和季节预测之间，可衔接天气预报和气候预测以建立起无缝隙天气/气候预测系统，更好地满足水利、农业和公共卫生等部门的服务需求(金荣花等，2019；White et al，2017)。但受到大气初始信号快速衰减和边界条件难以充分表达的影响，次季节预测的预测技巧较天气预报和气候预测均相对较低，这也制约了次季节预测研究与业务化的进展(Wu et al，2022)。近年来，为了次季节预测技巧的提升及增进对其可预报性来源和应用的理解，世界气候研究计划等组织发起了S2S预测研究项目(Vitart et al，2017)，中国气象局作为S2S预测研究项目的参与成员，开发了北京气候中心第3代气候模式系统的第2代次季节至季节预测子系统(BCC-CPSv3-S2Sv2，以下简称CPSv3)模式，可提供未来60 d逐日预测和13个月的月预测，在2020年底投入准业务运行开展S2S预测(刘绿柳等，2023)。虽然S2S模式发展取得一定进步，但模式误差仍客观存在，因此对模式结果进行客观评估，是减小S2S模式预报误差和改进S2S模式预报能力的应用基础(Huang et al，2022；White et al，2022)。

目前已有许多学者对不同S2S模式的预报效果进行了检验，如Coelho et al(2018)检验了欧洲中期天气预报中心(ECMWF)S2S模式降水数据在南美的预测表现。也有学者对比分析了参与S2S项目的中国气象局(CMA)和ECMWF模式在北半球海洋性大陆次季节降水的预测技巧，发现ECMWF模式的预报性能整体优于CMA模式，但ECMWF模式随着预报时效的增加往往会产生湿偏差，而CMA模式在大部分地区提前2~4周预报的平均误差基本保持不变(Lyu et al, 2022)；Liu et al(2021)考察了大气环流模式(BCC_AGCM2.2)对中国东部夏季降雨的次季节预测能力，并基于多成员预报评估了中国东部夏季降雨的可预测性；林倩等(2019)对S2S预测研究项目11个预报中心发布的降水预测在全球尺度上进行了确定性评价；庞轶舒等(2021)分析了8个次季节模式对四川汛期极端降水事件的预测能力，发现各模式在川西高原的预测技巧较高，盆地东部、攀西地区预测技巧较低。

综上所述，许多学者对次季节预测的理论基础、模式发展等做了大量工作(Rivoire et al，2023；郭渠等，2021；de Andrade et al，2021)，但目前S2S模式的预测尤其是降水的预测与实况仍存在较大偏差，这也制约了S2S预测在各方面的应用(邵宇行等，2023；Baker et al，2020)。长江流域社会经济发展水平较高, 人口密度较大，科技产业密集，是我国重要的经济走廊，极端天气和气象灾害往往更易造成较大的经济损失(尹家波等，2021)。联合国政府间气候变化专门委员会(IPCC)最新评估报告指出，全球变暖增加了极端降水等发生的可能性和严重性(IPCC，2022)，而未来几十年是长江经济带建设、发展的关键期，客观上增加了对长江流域次季节降水预测的需求。因此无论是从发展天气气候尺度的无缝隙预报还是从社会需求的角度，在长江流域开展和实施S2S降水预测都具有重要的科学意义和广泛的社会应用价值(White et al，2017)。目前对于中国自主研发的CPSv3模式在长江流域S2S降水的预测结果进行评价的相关研究较少，且在美国第2代气候预测系统(CFSv2)、ECMWF等S2S模式次季节预测结果的检验分析订正研究中的预测尺度通常集中于4周以内，缺乏对4周之后的预测检验(肖颖等，2023；杨露等，2023)。因此，在长江流域开展CPSv3模式汛期次季节降水预测的检验评估，对于CPSv3模式推广应用和提升长江流域次季节降水预测能力有着重要意义(Wang et al，2020；Manzanas et al，2018；Yang et al，2017)。

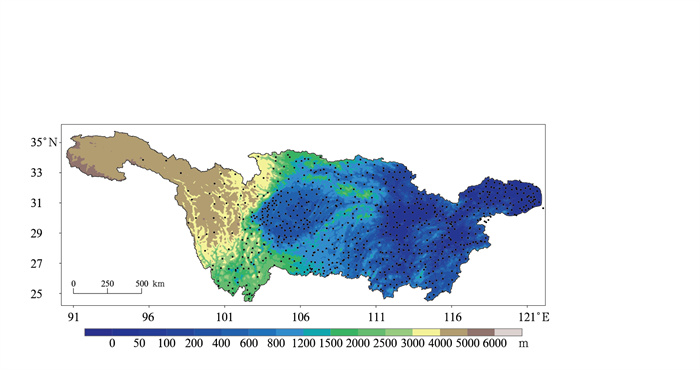
1 资料与方法 1.1 基础数据

本文所用的资料主要包括站点资料及CPSv3模式数据，其中站点资料来源于国家气象信息中心整编的约2400个国家级气象观测站逐日气候观测数据集，从中筛选出位于长江流域且连续性较好的675个站点，如图 1所示。模式数据则为CPSv3次季节尺度气候预测未来60 d的逐日降水数据，包括2008—2020年5—8月的回报数据以及2021—2022年的预测数据。预测数据为CPSv3模式5—8月逐日更新的未来60 d降水，每日启动4个并行作业，构成4个集合成员；而受限于计算资源，CPSv3只开展了部分起报日的模式回报，每次模拟包含4个成员，具体起报日期如表 1所列。

1.2 检验方法

将CPSv3模式输出降水数据通过双线性插值法插值到站点后进行检验分析，采用相关系数(CC)、均方根误差(RMSE)、符号一致率(SCR)、公平技巧评分(ETS)和偏差评分(BIAS)等方法，对模式4个成员降水预报的均值进行确定性评价；通过布里尔评分(BS)和受试者特征(ROC)曲线方法对模式多成员概率预报开展检验评估。为更细致地探讨模式的次季节预报能力，选取模式提前1~6旬的预测降水，以提前1旬为例，模式的起报时间为5月22—31日，对未来10 d即6月1—10日的降水进行预测，提前2~6旬预测, 以此类推。

CC可比较模式预测和站点实况之间的相关程度，能在统计意义上较好衡量模式的预测能力。

$ \mathrm{CC}=\frac{\sum\limits_{i=1}^N\left(o_i-\overline{o_i}\right)\left(f_i-\overline{f_i}\right)}{\sqrt{\sum\limits_{i=1}^N\left(o_i-\overline{o_i}\right)^2} \times \sqrt{\sum\limits_{i=1}^N\left(f_i-\overline{f_i}\right)^2}} $

(1)

式中：o_i和f_i分别代表站点观测和模式预测降水，o_i和f_i分别代表观测和模式预测降水均值，N为样本数，当N为格点总数时代表空间相关，N为时间序列时表示时间相关。相关系数越高，模式预测与实况越接近，模式性能越高(魏凤英，1999)。

RMSE是一种用于衡量模式在连续性数据上的预测精度的指标，其衡量了预测与真实降水之间的均方根差异，表示模式和观测之间的一致性和离散程度。RMSE越小表示模式与实况之间的误差越小，即模式的预测效果越好。

$ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^N\left(f_i-o_i\right)^2}{N}} $

(2)

SCR主要是以预测和实况的距平符号是否一致为判断依据，采用逐站评判。当预测和实况距平符号一致时认为该站预测正确，主要体现的是预测和实况在异常上的相似程度，符号一致率越高表示预测效果越好。

$ \mathrm{SCR}=\frac{N_i}{N} \times 100 \% $

(3)

式中：N_i代表模式与实测降水距平符号相同的站数，N为参评总站数。

ETS根据是否满足阈值(事件发生与否)，对预测、观测进行分类并统计观测点上预测、观测事件发生的次数，进而衡量不同量级降水预测的准确程度(Casati et al，2008)。相较于成功指数评分(TS)，ETS增加了对空报或漏报的惩罚，去除了随机预测的影响，评分结果更加公平。

$ \begin{aligned} & \mathrm{ETS}=\frac{N_{\mathrm{A}}-\gamma}{N_{\mathrm{A}}+N_{\mathrm{B}}+N_{\mathrm{C}}-\gamma} \\ & \gamma=\frac{\left(N_{\mathrm{A}}+N_{\mathrm{B}}\right)\left(N_{\mathrm{A}}+N_{\mathrm{C}}\right)}{N_{\mathrm{A}}+N_{\mathrm{B}}+N_{\mathrm{C}}+N_{\mathrm{D}}} \end{aligned} $

(4)

式中：N_A为降水预测正确的站数，N_B为漏报站数，N_C为空报站数，N_D为预测未发生且观测也未发生的站数。ETS越接近于1，表明对应的预测结果越准确(韦青等，2020)。

BIAS主要用于衡量模式对某一量级降水的预测偏差，为预测区域内满足降水阈值的总站数与对应的实况降水总站数的比值。与ETS类似，越接近于1，表明预测效果越好。

$ \mathrm{BIAS}=\frac{N_{\mathrm{A}}+N_{\mathrm{C}}}{N_{\mathrm{A}}+N_{\mathrm{B}}} $

(5)

BS是用于衡量均方概率误差的一种评价函数，综合考虑了可靠性和不确定性，被广泛应用于定量降水概率预测中(赵琳娜等，2015)。

$ \mathrm{BS}=\frac{1}{N} \sum\limits_{i=1}^N\left(f_i-o_i\right)^2 $

(6)

式中：f_i为预测概率，o_i为实况概率，当事件发生时o_i为1，事件不发生时o_i为0，N为参评总站数。BS范围为0~1，值越小则模式预测的准确率越高(Hersbach，2000)。

ROC曲线通过将连续变量设定出多个不同的临界值，从而计算出一系列真正率(TPR)和假正率(FPR)，再以假正率为横坐标、真正率为纵坐标绘制成曲线，曲线下面积(AUC)越大，预测准确性越高(Fawcett，2006)。

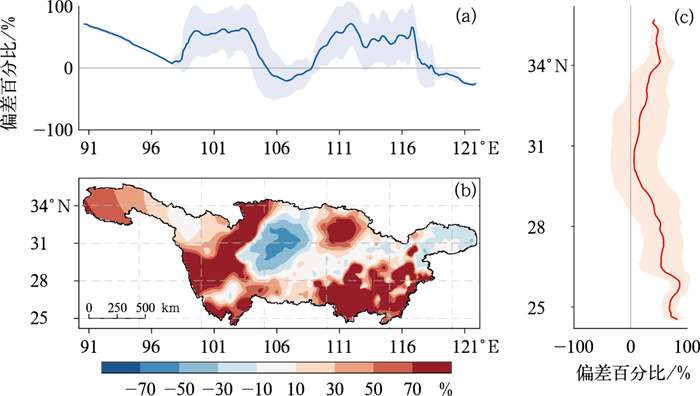
2 结果分析 2.1 整体预测性能评估

图 2给出了CPSv3模式2008—2022年5—8月逐日起报的降水与实况之间的平均偏差百分比。模式整体的降水预测相较实况偏大，同时存在明显的地区差异：对长江上游西部和两湖地区的60 d累计降水的高估超过了70%，但在嘉陵江流域模式预测对降水是低估的，在嘉陵江中部地区的偏差百分比甚至可达-50%左右。模式在长江中游干流区间和下游地区有较好表现，但无论是经向平均还是纬向平均，模式对于降水均有明显高估，表明模式存在系统性偏差。

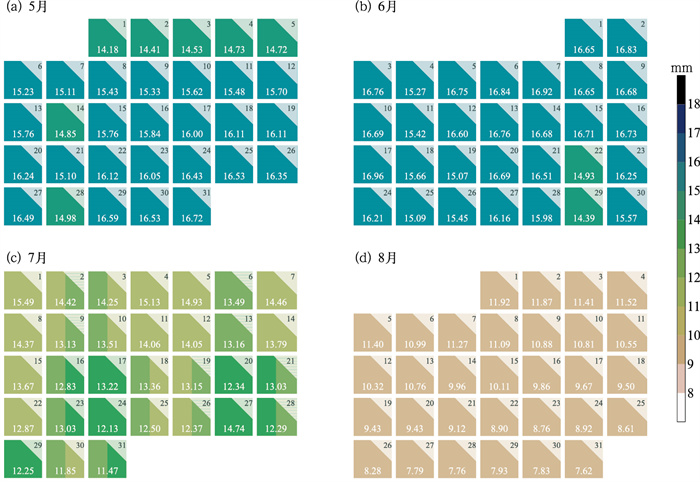
图 3给出了模式2008—2022年5—8月逐日起报的60 d降水RMSE日历图，其中部分起报日缺少回报，因此仅用到预测数据。模式在不同起报时间的多年平均RMSE在7~18 mm，随着起报时间的变化，RMSE经历了先减小后增大的变化过程。分月来看，8月尤其是8月下旬起报的预测结果明显好于其余月份，7月次之，5月底至6月起报未来60 d的RMSE是最大的。这与长江流域降水的气候特点密切相关：6月和7月是长江流域降水量最大的两个月，模式预测降水量的绝对误差也比较大，因此，5月底至6月的预测时段包含6月和7月，对应的RMSE也较大，而7月之后随着预测时段向后推移至盛夏乃至于秋季，降水量减小，模式预测的RMSE也随之减小。

2.2 确定性预测技巧分析

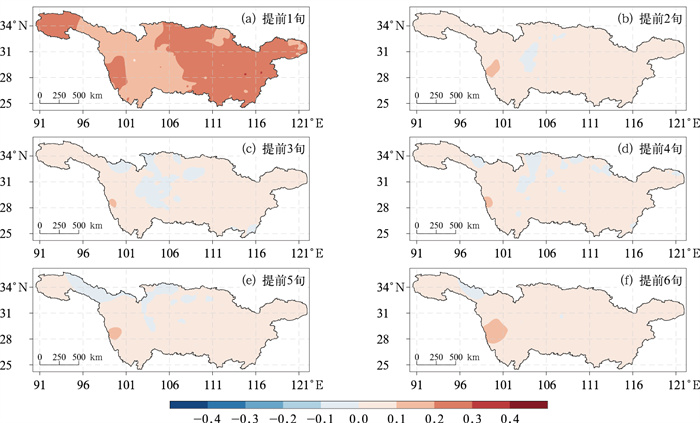
从提前1~6旬预测的2008—2022年长江流域汛期6—8月降水时间相关系数(TCC)的空间分布(图 4)来看，CPSv3模式提前1~6旬预测的汛期降水TCC在长江流域绝大多数地区均为正值，模式提前1旬预测的TCC显著高于其余起报时间，且在长江中下游大部地区超过0.2。提前2~3旬预测的TCC迅速下降，且在青藏高原东侧的四川盆地开始出现负值，即模式在该地区的预测效果不理想，这可能与复杂下垫面与地形的快速变化相关：地形高度从4 km及以上的高原降至海拔几百米乃至几十米的盆地平原地区，模式可能难以表征和模拟出空间场上环流要素的快速变化特征(周秋雪等，2019)。此外，模式在金沙江中部地区的TCC较高，提前1~6旬均是如此，即模式在金沙江中部有着稳定较好的预测技巧，提前2旬后模式预测降水的TCC变化较为平缓。

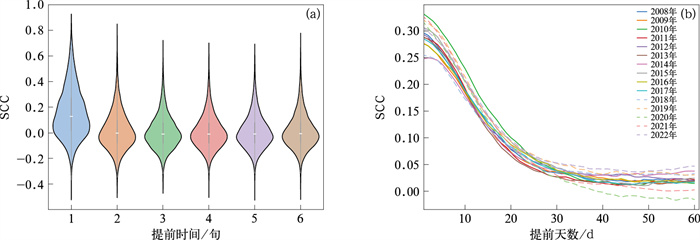
图 5为模式提前1~6旬预测长江流域汛期降水空间相关系数(SCC)的小提琴图和历年值。小提琴图作为箱形图与核密度图的结合体，除了能显示箱型图的统计数据外，还显示了数据的整体分布，小提琴图的宽度代表数据在该位置的密度，即较宽的部分代表SCC在对应值出现的概率较高，较窄的部分则对应于SCC在对应值较低的概率。提前1旬预测的SCC大部分分布在0~0.4，中位数在0.17左右，明显高于提前2旬的预测；提前2~6旬的SCC的峰值与中位数基本保持一致，仅比0值略大，表明提前2旬以后的降水预测在SCC上预测技巧非常有限。从图 5b可看出，提前1~30 d的SCC随起报时间的提前而快速下降，提前30 d后趋于稳定，而大部分年份的SCC均大于0。分年来看，预测效果最好的年份是2010年，该年提前1~30 d预测的降水SCC几乎均是所有年份中最高的；此外，提前30 d以上预测时，2022年的SCC最高而2020年却显著低于其余年份。从实况来看，2020年是长江流域汛期降水显著偏多年份，是1951年以来历史第2，而2022年汛期降水严重偏少，降水量是历史倒数第3。

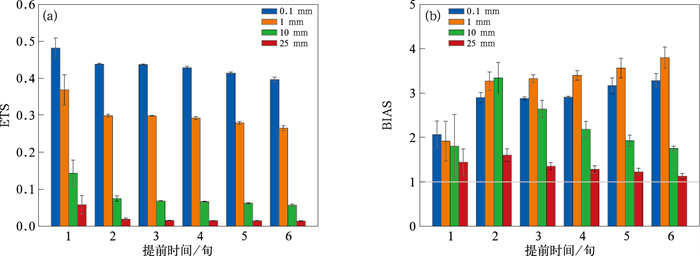
对模式汛期次季节降水进行偏差和相关检验分析后，对模式预测的逐日降水设定不同阈值进行评价，分别选取0.1、1、10和25 mm作为阈值，计算得到模式提前1~6旬的汛期逐日预测降水在不同阈值下的平均ETS和BIAS(图 6)。对于有无降水(0.1 mm阈值)，模式表现出较好的预测效果，提前1旬预测的ETS可达0.48左右，提前2~3旬预测的ETS大致相当，提前3旬后ETS呈梯级下降，但即使是ETS最低的提前6旬预测结果，评分也接近0.4。模式对于小雨(1 mm阈值)量级的降水也有较高技巧，ETS大都在0.3附近波动。但对于中雨(10 mm阈值)和大雨(25 mm阈值)，模式表现并不理想，尤其是对大雨量级的预测，提前1旬预测的ETS也仅达0.06左右，表明模式对强降水预测仍有一定的改进空间(King et al, 2020)。从BIAS来看，模式对所有量级降水提前1~6旬的预测BIAS都大于1，即模式的降水预测整体偏大，这与图 2中的模式降水预测存在系统性偏差一致。随着预测时间的提前，模式降水高估程度随之增大；当模式提前1旬预测时，对有无降水的高估程度最大，但提前2旬时小雨和中雨的BIAS最高，预报技巧最低，提前3~6旬时则是小雨的BIAS最高，0.1 mm和10 mm阈值的BIAS次之，即提前3~6旬时小雨的预测技巧低于对有无降水和中雨的预测技巧。这表明在提前1~2旬的预测中，模式对日降水的系统性高估主要是对于小雨和中雨的高估。

2.3 夏季降水异常的预测检验

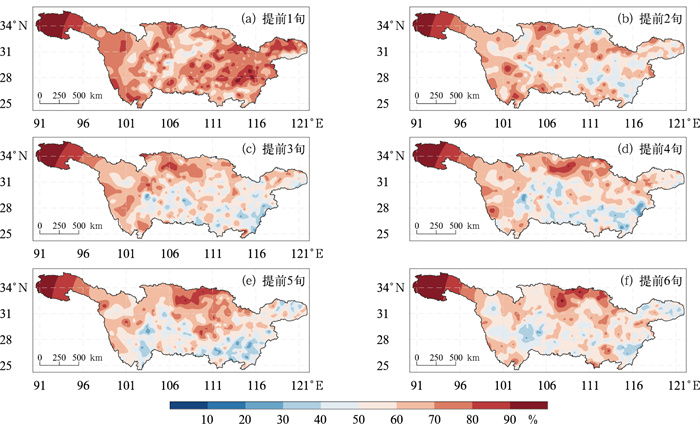
图 7给出了模式提前1~6旬预测长江流域汛期降水的距平符号一致率的空间分布。提前1旬时预测的长江流域汛期降水异常趋势与实况最为一致，大部分地区的距平符号一致率超过60%，其中长江中下游大部分地区在70%以上，局部超过80%；金沙江中下游西部的距平符号一致率超过70%(金沙江上游北部因为缺少观测站点而出现虚假高值区)，这表明提前1旬时预测的CPSv3模式结果对长江中下游和上游西部的汛期降水异常较为准确。提前2旬时模式预测效果明显减退，特别是在两湖地区；提前3旬时的距平符号一致率与提前2旬的分布较为一致，均是在长江上中游北部高而在中下游干流南部低；提前5~6旬时嘉陵江东部和汉江北部的距平符号一致率反而比之前更高。总体来看，模式提前1旬时对长江流域大部的汛期降水异常具备较好的预测能力，在提前2~6旬的次季节尺度上，对于长江上游北部、中流干流北部和金沙江西部仍具有一定的预测能力，但对于金沙江下游东部和两湖地区的汛期降水异常预测能力较弱。

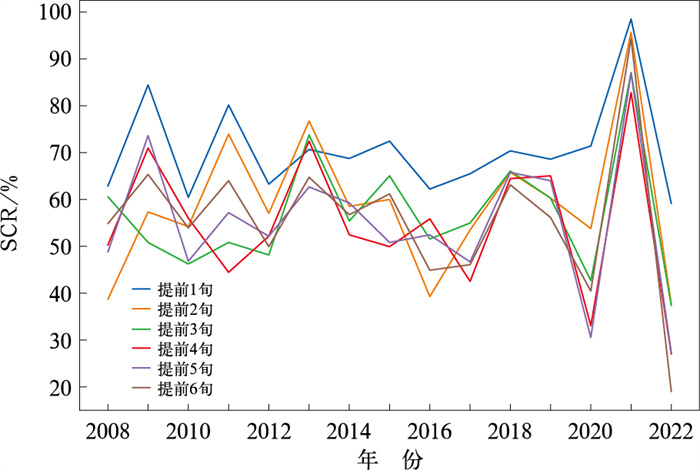
从各年的汛期预测降水与实况的距平符号一致率(图 8)来看，绝大多数年份的距平符号一致率在40%以上，距平符号一致率的年际波动较大；2021年的距平符号一致率是最高的，提前1~6旬的降水预测的距平符号一致率都超过了80%，提前1~3旬的降水预测的距平符号一致率更是超过了90%；模式表现较好的有2009年、2011和2013年，这些年份长江流域汛期整体降水均偏少，整体来看长江流域汛期降水偏少年份的距平符号一致率和SCC要好于降水偏多年份，这也表明模式在次季节尺度上对实况降水偏少情况下的逐日降水预测能力较强，而在汛期降水偏多年份下的预测技巧偏弱。但这一结论在2022年并不适用，2022年汛期极端少雨，距平符号一致率却是所有年份中最低的，甚至低于2020年这一极端多雨年，与之前对SCC的分析相反。以上分析表明尽管模式对汛期降水异常的预测在实际降水偏少时普遍表现较好，但对于极端异常少雨的预测在不同指标的评价下仍有不同。

2.4 概率性预测结果评价

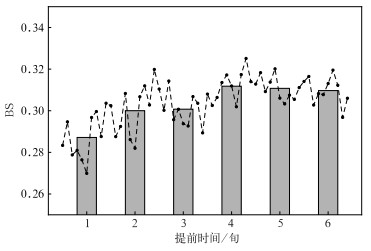
对于长江流域汛期降水的CPSv3模式各成员的预测结果，根据多年平均将各成员预测结果分为正异常和负异常，得到模式的概率预测结果，并计算了提前1~6旬的BS，结果如图 9所示。可以看到，逐日预测的BS呈波动上升趋势，表明预测效果随预测时间的提前而减弱，但提前5 d预测BS值要比提前1 d临近预测更小，而BS值越小则模式预测准确率越高，即提前5 d预测的效果最好。提前1旬预测的BS不到0.29，提前2旬和提前3旬的平均BS相接近，显著高于提前1旬，即预测效果明显差于提前1旬的预测；提前4~6旬的BS在0.31附近波动，无明显的变化特征。

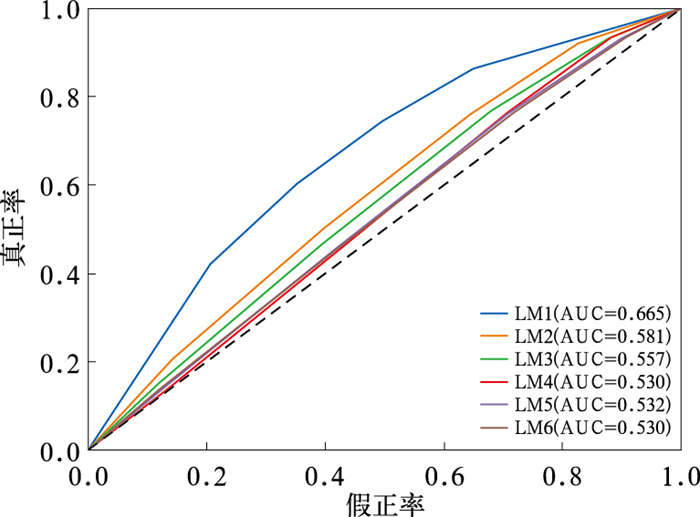
图 10给出了模式提前1~6旬预测长江流域汛期降水异常的ROC曲线。当ROC曲线越陡，即AUC越高时，模式预测效果越好；图 10中黑色虚线为对角线，其AUC为0.5，即随机预测结果；LM1~LM6分别为提前1~6旬的预测。从图 10可以看到，提前1旬预测夏季降水偏多或偏少概率时的AUC为0.665，与前文分析一致，提前1旬时的概率预测相对最为准确，提前2旬和3旬时的概率预测技巧显著低于提前1旬，AUC超过0.55，有一定的参考价值；提前3旬之后的ROC曲线几乎完全重合且贴近随机预测的虚线，表明提前3旬后模式的预测技巧十分有限。

3 结论与讨论

根据2008—2022年的CPSv3模式次季节预测和历史回报资料，对模式在长江流域汛期的预测效果采用多种方法进行检验，评估模式在长江流域汛期次季节逐日/逐旬降水异常的预测技巧，分析模式降水可用预测时效，得到以下主要结论：

(1) 模式对于长江流域汛期降水整体存在系统性高估，尤其是对长江上游西部和两湖地区降水的高估，这可能主要来源于模式提前1~2旬的预测中对于小雨和中雨日数的高估；模式对中雨及以上量级降水的预测能力仍有较大改进空间，对较强降水的落区及量值的把握仍有不足。

(2) 从模式预测技巧的空间分布来看，长江中下游的预测技巧高于长江上游，这一趋势在提前1旬的预测中尤为明显；此外模式对于金沙江西部的预测技巧也明显高于周边地区。

(3) 模式能较好把握长江流域汛期降水偏少的异常趋势，从各评分指标来看模式在长江流域汛期降水偏少情况下的降水预测技巧整体高于降水偏多情况。

(4) 从模式的有效预测时效来看，模式对于长江流域汛期逐日定量预测的有效预测时间为1旬左右，随着预测时间的提前，模式预测技巧随之下降。模式对于汛期降水异常的预测也与之类似，提前1旬预测的技巧最高，提前2~3旬的预测也有一定的参考价值；提前3旬后模式的预测结果仅比随机预测略好。

本文对CPSv3模式在长江流域的汛期次季节降水预测能力进行了检验评估，从逐日定量降水、汛期整体降水异常及异常概率预测等多方面分析了模式的预测性能。整体而言，CPSv3模式对长江流域汛期降水具备一定的预测能力，但也存在模式预测性能不稳定、对较强降水预测能力不足等问题。此外，对于次季节降水的有效预测时效仍有待进一步提高。本研究的主要工作集中于CPSv3模式的预测技巧和误差评估分析上，后期可进一步横向对比ECMWF、CFSv2等次季节模式的检验评估结果，并在此基础上分析不同模式的误差来源，以期为模式应用和预测改进提供条件(Pan et al，2021)；同时也可考虑对模式结果进行后处理订正，比较传统订正方法和机器学习算法对模式预测技巧改进的优劣(Wang et al，2021；Yang et al，2021)，以期提高长江流域次季节降水的预测水平。