2. 湖北省气象台, 武汉 430074
2. Hubei Meteorological Observatory, Wuhan 430074
内河航运系统凭借经济性优势在交通运输领域发挥巨大作用,被称为“自然的高速公路”(陈德山等,2022)。当前,内河航道沿线气象观测站点数量有限、分布不均,而且数值预报模式的精细化程度和对不同地形的适应程度不能满足新时期航运安全的需求(熊红梅等,2021;王甚男等,2023)。风是影响内河航运安全的重要气象因素,2015年6月1日的“东方之星”号客轮因突发大风强对流天气翻沉,事件造成442人遇难(郑永光等,2016; 孟英杰等,2023)。内河航道沿途地形复杂,研究适应不同地形的风速预报降尺度订正方法,对于提高风速预报的准确率十分重要。
目前,风速预报主要依靠数值预报模式,模式通过在给定初始值和边界值的情况下求解大气运动和热力学方程组,预测未来一段时间的风速变化,由于大气系统的不确定性,给定的初始值和边界值不可能完全准确,大气运动和热力学方程组不可能完备描述大气运动过程,导致风速预报不可避免地存在一定的误差(Lorenz,1965;曾庆存,1978;Mu et al,2002;常俊等,2015;徐景峰等,2023)。模式预报的空间分辨率一般较粗,对于精细地形的适应性有偏差,为了满足更加精细、准确的风速预报需求,对数值预报模式降尺度订正可有效提高预报准确率。
基于物理理论或统计规律的订正方法是传统的风速预报订正方法。陈豫英等(2006)采用多元线性和逐步回归的模式输出统计(MOS)方法进行风的精细化释用;胡海川等(2017)通过建立基于集合预报众数的10 m风速客观订正方法,利用沿海代表站观测资料对2013—2015年的欧洲中期天气预报中心(ECMWF)集合预报进行风速订正研究,提升了中长期时效大量级风速的预报能力;杨程等(2019)利用自动气象站观测资料采用偏最小二乘回归方法订正区域模式预报产品,对浙江不同地区的大部分站点风速订正都取得了较好的结果,且在西部地区站点订正效果好于东部地区;王在文等(2019)利用相似理论、大数据和集合预报思路等统计释用方法,结合运用集合预报相关概念形成订正后的确定预报及概率预报;申华羽等(2020)通过线性回归方法,对冷空气过程浮标站最大风速预报进行订正,该方法可以有效减小预报误差;张鑫宇等(2023)利用莫宁-奥布霍夫(Monin-Obukhov)相似理论,引入大气稳定度判定因子构建站点风速偏差订正方案,将地面风速预报由模式地形订正到实际地形产生了较好的订正效果。
随着人工智能技术的发展,相关技术与气象领域的结合越来越密切。钱燕珍等(2013)将支持向量机(SVM)回归方法应用于近海和登陆热带气旋的强度预报,对数值预报产品进行了释用;张颖超等(2016)利用极限学习机(ELM)对WRF模式预报风速进行了订正,该算法训练速度快,具有很好的泛化能力;杨晓君等(2019)基于常规海洋气象观测资料,采用BP人工神经网络开展多种模式的渤海海风预报订正研究;孙全德等(2019)采用LASSO回归、随机森林、深度学习三种机器学习算法对ECMWF预测的华北地区10 m风速进行订正,订正结果好于MOS方法;任萍等(2020)开展基于XGBoost方法的数值预报多模式集成技术研究,研究发现10 m风的订正结果好于传统的等权重平均和线性回归方法;罗江珊等(2024)利用随机森林算法对青岛港区ECMWF细网格预报风速进行订正,预报精度有所提升。近年,随着大数据的兴起和算力的提升,深度学习算法逐渐成熟。Han et al(2021)提出了一种基于卷积神经网络的CU-Net深度学习方法,有效改善了中国北方ECMWF预测的10 m风速、风向的预报偏差,订正结果好于传统方法;张延彪等(2022)通过引入稠密卷积块改进了CU-Net,形成Dense-CUNet模型,并融合地形和多种气象要素特征构造出Fuse-CUNet模型,对ECMWF 10 m风速预报进行订正,订正效果较CU-Net模型有一定提升;刘志杰等(2022)基于黄渤海海域站点风速观测资料和TIGGE资料选择ECMWF、CMA、NCEP、ECCC的集合预报产品,对传统订正方法(集成平均、动态权重、变权偏差订正)和LSTM深度学习方法进行了对比,发现LSTM方法好于传统方法;徐景峰等(2023)开展了基于北京快速更新无缝隙融合与集成预报系统(RISE系统)预报的北京冬奥会延庆及张家口赛区100 m分辨率的冬季近地面10 m风速数据的偏差订正,构建新的CU-Net++订正模型,订正结果优于CU-Net模型。
上述方法多采用站点订正,通过插值的方式获取模式预报的站点数据,再根据站点的实况观测信息开展订正研究,但是站点订正的问题在于没有站点的区域不能构建订正模型,内河航道沿线站点分布不均,致使站点订正模型不能全面覆盖内河航道区域。对于格点订正,一般采用ECMWF的第五代全球再分析数据产品(ERA5)作为格点参照数据,空间尺度上比较粗,没有将数值模式预报订正与降尺度结合起来,不能满足内河航道风速预报精细化的需求。本研究参照1 km高分辨率格点风实况产品,采用改进的U-Net++模型,开展数值天气预报模式风速数据降尺度订正研究,利用区域特点和时次变化规律构建分区域、分起报时间、分预报时次的订正模型,并将航道项与地形项加入损失函数,实现航道风速的精细化订正预报。
1 资料与方法 1.1 资料数值天气预报产品采用2022年1月1日至2023年12月31日ECMWF高分辨率大气模式确定性预报产品(EC-HRES)与中国气象局中尺度天气数值预报系统(CMA-MESO)10 m风预报数据,实况参照数据采用中国区域多源融合实况分析1 km分辨率产品(ART_1 km,地面)10 m风数据(表 1)。数据源自国家气象信息中心天擎气象大数据云平台。全文所用时间均为北京时。
|
|
表 1 模式预报和实况产品信息 Table 1 Information of model forecast and real-time products |
资料研究区域选择湖北西部与重庆相邻的丘陵地带,以及湖北中部与湖南交接的平原地带,如图 1所示。丘陵地区地形较为复杂,平均海拔为1058 m,平原地区地形较为开阔平坦,平均海拔为52 m,两处研究区域均覆盖了部分长江航道。
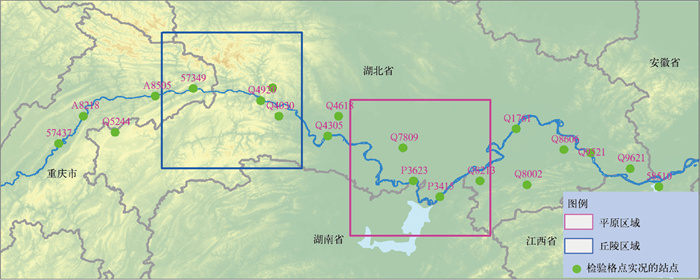
|
图 1 研究区域及格点实况产品检验站点位置 Fig. 1 Location of research areas and test stations of grid real-time products |
为便于研究区域的实况和模式预报产品检验分析以及模型样本构建,需要对三种模式数据进行区域裁切、时空对齐处理,流程见图 2,所有数据处理为空间分辨率为0.01°×0.01°, 宽高为192×192的单层格点区域。192的宽高便于模型构建时下采样处理,每次下采样都会将数据宽高减半,模型采用4次下采样过程,因此要求格点大小至少是16的倍数,同时本文的区域订正与徐景峰等(2023)的订正区域选取方法不同,本研究同一个模型只订正固定区域,能够更好地体现区域的统计特征,区域太大包含的地形会更复杂,难以研究不同地形对于统计特征的影响,太小会降低研究区域的覆盖面积,影响区域统计特征的普适性。采用最近邻插值的方式将预报数据处理为与实况同等宽高和分辨率的格点,目的是保持数据的原始状态,使数据检验时更为客观,双线性或三线性等插值方法有更好的视觉效果,但对原始数据是一种失真处理。
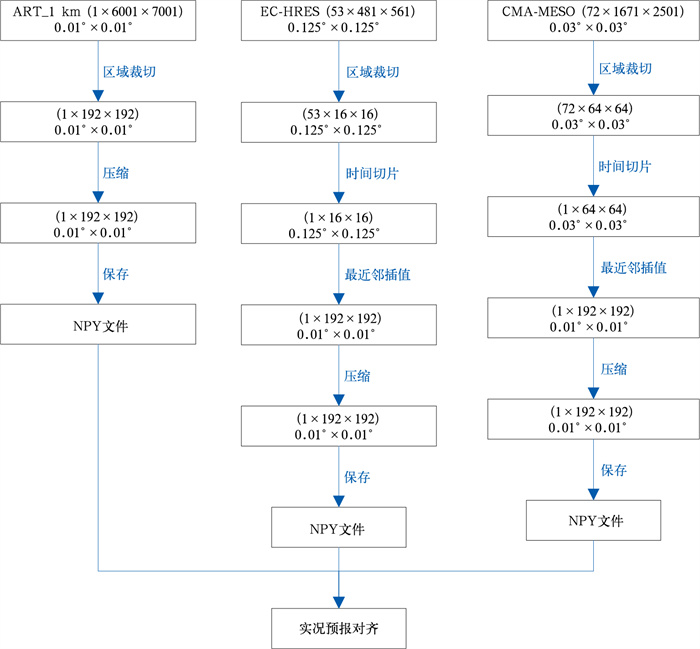
|
图 2 ART_1 km、EC-HRES和CMA-MESO数据处理流程 注:“1×6001×7001”表示数据的层数、经向、纬向格点数,“0.01°×0.01°”表示数据的空间分辨率,以此类推。 Fig. 2 Data processing flow of ART_1 km, EC-HRES and CMA-MESO |
模式预报和订正结果数据采用以格点为单位的检验,检验指标有三个:样本的区域格点均方根误差(RMSE)、平均绝对误差(MAE)和平均误差(ME),计算方式如下:
| $ \mathrm{RMSE}=\frac{1}{M} \sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(y_i-x_i\right)^2} $ | (1) |
| $ \operatorname{MAE}=\frac{1}{M}\left(\frac{1}{N} \sum\limits_{i=1}^N\left|y_i-x_i\right|\right) $ | (2) |
| $ \mathrm{ME}=\frac{1}{M}\left[\frac{1}{N} \sum\limits_{i=1}^N\left(y_i-x_i\right)\right] $ | (3) |
式中:N表示研究区域单个样本的格点数,M为样本个数,xi、yi分别表示单个格点模式预报和实况的风速值。RMSE、MAE两个指标用于检验模式数据对于实况产品的误差程度,越大表示在研究区域模式预报与实况产品的差距越大,也反映出模式对于该区域的预报适用性越差,MAE更适合作为预报模式订正模型的检验指标。ME用于检验模式数据对于实况产品是否存在系统性的偏差,负数表示模式预报相较于实况产品有系统性的偏大,正数表示模式预报相较于实况产品有系统性的偏小。
1.4 U-Net++模型构建方法U-Net深度学习网络模型(Ronneberger et al,2015)自2015年被提出后,其广泛应用于图像分割、图像超分领域,取得了很好的成果。Han et al(2021)将其应用于温度、湿度、风速、风向等要素数值天气预报的偏差订正,并改进了上采样过程,采用了Shi et al(2016)提出的Sub-Pixel Convolution子像素卷积模块,使得上采样过程参数化,提高了模型的表达能力,取得了较好的订正效果。Zhou et al(2020)等提出了U-Net++网络,该网络在原有网络的基础上增加了密集的跳联,从而使得网络能够学习到更多的非线性特征,增强网络的表达能力。本文应用的U-Net++网络模型,将下采样的最大池化替换为步长为2的卷积,上采样使用Shi et al(2016)提出的Sub-Pixel Convolution,从而将上、下采样参数化,增加模型的学习能力。图 3展示了模型架构。
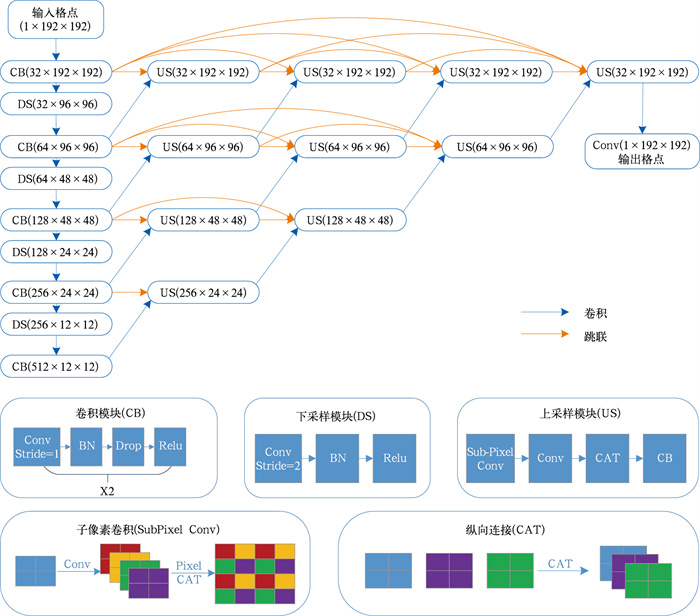
|
图 3 U-Net++网络模型框架 Fig. 3 The framework of U-Net++ network model |
本文降尺度订正采用格点订正,订正区域包含了长江部分航道。传统的站点订正不会考虑站点周围的因素,并且对于没有站点的位置,只能通过邻近站点插值获得,订正效果的好坏与插值算法以及被插值点周边环境有关,不会考虑周边点作用于被插值点的统计规律,而格点的降尺度订正,恰好可以弥补这一点。本文将模型以区域、起报时间、预报时次进行分类,发掘特定于上述分类条件的统计规律,利用U-Net++模型学习这些规律,从而达到模式降尺度订正的目的。
损失函数(Loss)包含三个部分:
| $ \begin{gathered} \text { Loss }=\frac{1}{N_{\mathrm{a}}} \sum\limits_{i=1}^{N_{\mathrm{a}}}\left(y_i-x_i\right)^2+\frac{\lambda}{N_{\mathrm{w}}} \sum\limits_{i=1}^{N_{\mathrm{a}}}\left[\left(y_i-x_i\right)^2 m_i\right]+ \\ \frac{\xi}{N_{\mathrm{s}}} \sum\limits_{k=1}^{N_{\mathrm{s}}}\left[\operatorname{std}\left(Y_k\right)-\omega \operatorname{std}\left(T_k\right)\right]^2 \end{gathered} $ | (4) |
| $ \operatorname{std}\left(Y_k\right)=\operatorname{sqrt}\left\{\frac{1}{N_{\mathrm{o}}} \sum\limits_{j=1}^{N_{\mathrm{o}}}\left[y_{k_j}-\frac{1}{N_{\mathrm{o}}} \sum\limits_{j=1}^{N_{\mathrm{o}}}\left(y_{k_j}\right)\right]^2\right\} $ | (5) |
| $ \operatorname{std}\left(T_k\right)=\operatorname{sqrt}\left\{\frac{1}{N_{\mathrm{o}}} \sum\limits_{j=1}^{N_{\mathrm{o}}}\left[t_{k_j}-\frac{1}{N_{\mathrm{o}}} \sum\limits_{j=1}^{N_{\mathrm{o}}}\left(t_{k_j}\right)\right]^2\right\} $ | (6) |
式(4)中,第一部分是研究区域模式预报与实况风速格点均方误差,Na表示研究区域格点总和,yi表示实况格点风速值,xi表示预报格点风速值;第二部分是航道区域预报与实况的RMSE,Nw表示研究区域被航道覆盖的格点数,mi表示航道掩膜格点值:航道区域点为1,其他点为0,此项作用是提高模型对于航道区域风速订正的效果;第三部分采用Yu et al(2022)在研究风速空间降尺度模型提出的地形指导方法,其通过大量相关统计发现,风速标准差[std(Yk)]与地形标准差[std(Tk)]具有某种不确定关联,标准差计算见式(5)、式(6),此项可以使模型学习局地复杂地形对于风速的影响,提高模型的鲁棒性,Yk为局地待订正格点数据,Tk为对应局地地形格点数据,此处为8×8的格点,即No的值为64,Ns为局地区域总数,本文的研究区域维度为192×192,因此Ns为24,λ、ξ、ω均为超参数,取值区间为(0, 1)。
2 风速误差分析 2.1 实况资料分析韩帅等(2018)利用2016年1月1日至12月31日的2380个国家级气象观测站的小时观测数据,对ART_1 km产品进行了质量评估。同时,选取2023年1月1日至12月31日部分沿江站点对ART_1 km产品进行风速误差检验,站点位置如图 1所示,检验结果见表 2,所有站MAE的平均值约为0.116 m·s-1。对于ART_1 km 10 m风实况产品,两次检验结果均较好,且在沿江区域的适用性较好,能够作为模式风速预报检验和模式订正的目标数据使用。
|
|
表 2 2023年ART_1 km风速产品沿江站点MAE(单位:m·s-1) Table 2 MAE of ART_1 km wind product at stations along the Yangtze River in 2023 (unit: m·s-1) |
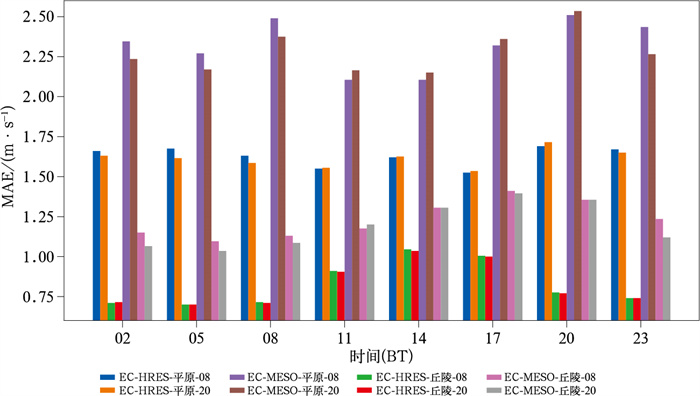
对2022年1月1日至2023年12月31日,为期两年在平原与丘陵区域的EC-HRES、CMA-MESO未来48 h预报时次,逐3 h间隔的数据进行分区域、分起报时间和分预报时次的检验,RMSE和MAE的结果见图 4。由图可知,两个模式在不同区域的误差均呈现波动增长,RMSE与MAE变化趋势一致,因此可以使用RMSE作为模型训练的损失函数,通过减小RMSE、降低MAE实现预报订正;EC-HRES的分辨率虽然低于CMA-MESO,但是不同研究区域EC-HRES风速预报的RMSE和MAE均小于CMA-MESO,EC-HRES对于研究区域的适应性更好;两个模式的风速预报在丘陵区域的MAE小于平原区域,即在丘陵区域模式预报产品与ART_1 km实况产品更为接近。为分析昼夜、起报时间对于模式预报的影响,图 5展示了平原区域与丘陵区域一天内不同起报时间MAE的日变化。由图可知,两个模式在丘陵区域的预报误差白天较大,晚上较小,EC-HRES在14时误差最大,CMA-MESO在17时误差最大,平原区域这个现象不明显;起报时间对于两个模式的影响不大,08时起报的误差略大于20时起报误差。由上可见,模式预报对于不同区域、预报时次、起报时间的误差都呈现出一定的规律性,这也为模型分类订正提供了依据。
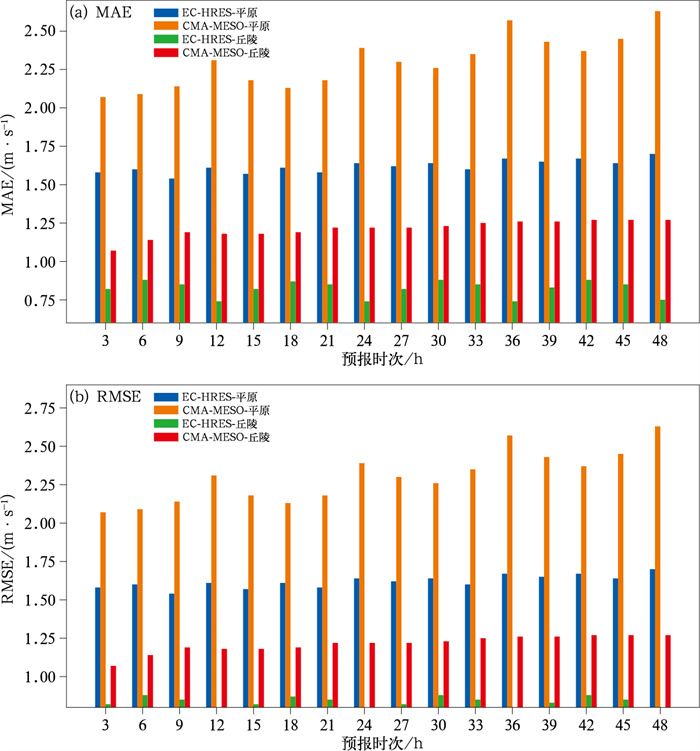
|
图 4 2022年1月1日至2023年12月31日EC-HRES和CMA-MESO在平原与丘陵区域48 h预报时次的风速预报(a)MAE和(b)RMSE Fig. 4 Variation of wind forecast (a) MAE and (b) RMSE by EC-HRES and CMA-MESO in plain and hilly areas in 48 h forecast time from 1 January 2022 to 31 December 2023 |
|
图 5 2022年1月1日至2023年12月31日EC-HRES和CMA-MESO在平原与丘陵区域不同起报时间的风速预报MAE日变化 Fig. 5 Daily variation of wind forecast MAE by EC-HRES and CMA-MESO at different initial times in plain and hilly areas from 1 January 2022 to 31 December 2023 |
表 3展示了EC-HRES与CMA-MESO在不同区域的平均误差,即误差统计样本不再区分预报时次和起报时间。由表 3可知,两个模式参照ART_1 km实况产品,在风速预报上均有不同程度偏大的系统性偏差,平原区域的误差较丘陵区域更大,CMA-MESO误差较EC-HRES更大。ART_1 km实况是由多源数据叠加精细化地形得到的,更符合局地地形特性,EC-HRES和CMA-MESO的模式风速预报都呈现一定的趋势性,不能很好体现精细地形因素对于风速的影响,这个现象在平原区域更为明显,这也是平原区域误差更大的原因之一,因此本研究将地形数据添加到损失函数中,从而增加模型的鲁棒性。
|
|
表 3 2022年1月1日至2023年12月31日在平原与丘陵区域EC-HRES和CMA-MESO风速预报的误差(单位:m·s-1) Table 3 The total average error of EC-HRES and CMA-MESO wind forecasts in plain and hilly areas from 1 January 2022 to 31 December 2023(unit: m·s-1) |
打乱2022年1月1日至2023年12月31日的样本并拆分,将5/6的样本用于模型训练,1/6的样本用于模型检验,两个样本集数据不重叠,订正结果分析采用的数据全部来自于检验样本生成的数据。对EC-HRES和CMA-MESO的10 m风速进行分起报时间(08时、20时), 不同预报时次3、6、9、12 h, 分区域(平原、丘陵)的订正结果分析,表 4、表 5分别展示了应用训练好的模型针对测试样本的订正结果,由表可知,EC-HRES和CMA-MESO在平原和丘陵区域都有正向的订正效果;订正后EC-HRES的MAE依然小于CMA-MESO,但两种模式订正后的MAE差距明显减小;订正后丘陵区域的MAE依旧小于平原区域。
|
|
表 4 2022年1月1日至2023年12月31日检验样本EC-HRES风速预报订正前后的MAE(单位:m·s-1) Table 4 Comparison of MAE before and after correction for EC-HRES wind forecast on test samples from 1 January 2022 to 31 December 2023 (unit: m·s-1) |
|
|
表 5 2022年1月1日至2023年12月31日检验样本CMA-MESO风速预报订正前后的MAE(单位:m·s-1) Table 5 Comparison of MAE before and after correction for CMA-MESO wind forecast on test samples from 1 January 2022 to 31 December 2023 (unit: m·s-1) |
为对比模型改进前后的效果,采用预报订正前后相对于实况MAE的降低比率(RMAE)来评价模型的订正效果,如式(7)所示:
| $ R_{\mathrm{MAE}}=\frac{E_y-E_{y^{\prime}}}{E_y} \times 100 \% $ | (7) |
式中:Ey表示预报MAE,Ey′为预报订正MAE,RMAE值越大降尺度订正效果越好。
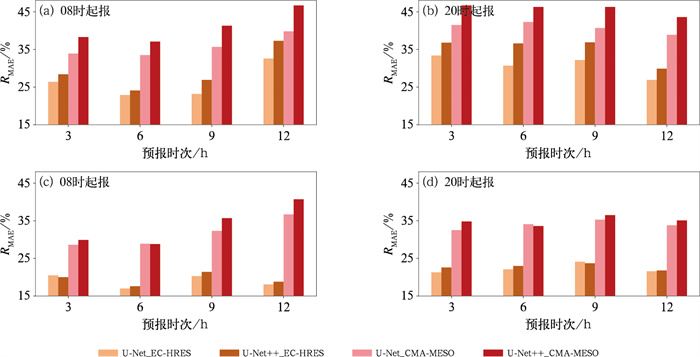
图 6展示了U-Net和U-Net++模型在不同模式、区域、起报时间、预报时次的RMAE。由图可知CMA-MESO的降尺度订正程度好于EC-HRES,平原区域要好于丘陵区域,这与2.2节预报检验中CMA-MESO以及平原区域MAE更大有关,也进一步说明国内外模式,以及平原、丘陵区域订正后的结果有趋同性;U-Net和U-Net++两个模型订正结果对比,除了个别区域、时次外,U-Net++网络模型要好于U-Net,U-Net++的总平均RMAE为32.73%,U-Net的总平均RMAE为30.06%,平均订正效果提升了2.67个百分点(表 6,表 7)。
|
图 6 2022年1月1日至2023年12月31日检验样本不同起报时间(a, b)平原与(c, d)丘陵区域U-Net和U-Net++模型风速预报的RMAE Fig. 6 RMAE of U-Net and U-Net++ wind forecasts on test samples at different initial times in (a, b) plain and (c, d) hilly areas from 1 January 2022 to 31 December 2023 |
|
|
表 6 2022年1月1日至2023年12月31日检验样本不同起报时间平原区域U-Net与U-Net++模型风速预报的RMAE(单位:%) Table 6 Comparison of RMAE between U-Net and U-Net++ wind forecasts in plain area on test samples at different initial times from 1 January 2022 to 31 December 2023 (unit: %) |
|
|
表 7 2022年1月1日至2023年12月31日检验样本不同起报时间丘陵区域U-Net与U-Net++模型风速预报的RMAE(单位:%) Table 7 Comparison of RMAE between U-Net and U-Net++ wind forecasts in hilly area on test samples at different initial times from 1 January 2022 to 31 December 2023 (unit: %) |
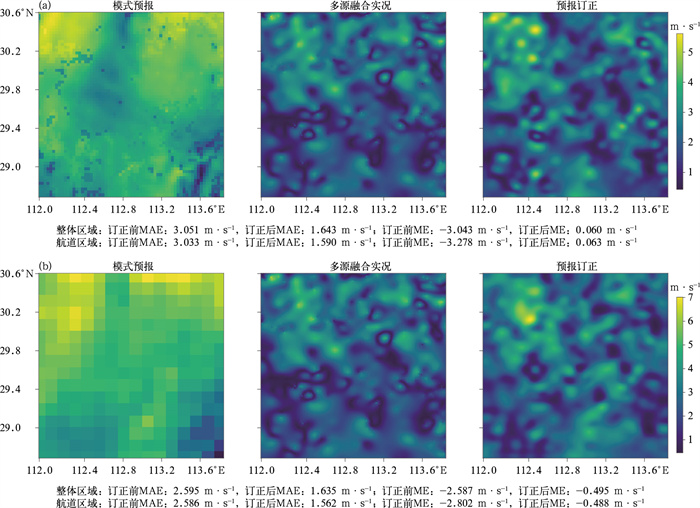
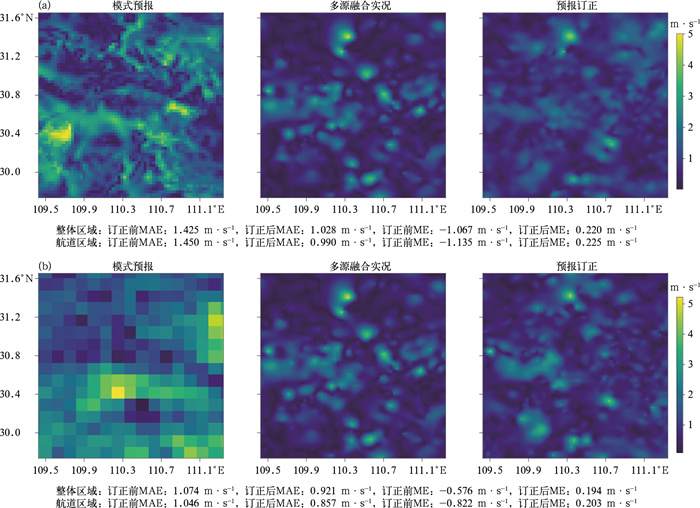
为对比损失函数中加入地形对模型订正效果的影响,本文采用U-Net++网络模型选取6 h预报时次进行研究,由表 8可知,模型在迭代500次后,不加地形的订正效果好于加入地形的效果,1000次迭代后,丘陵区域加入地形的效果好于不加地形的效果,且不加地形的模型订正效果会回退,出现过拟合现象,平原区域加入地形的效果提升不明显。在损失函数中加入航道区域项,对于航道区域的订正效果提升较好,无论是在丘陵或平原,模型的订正效果提升了约2个百分点(表 9)。图 7和图 8分别为EC-HRES和CMA-MESO预报测试样本订正结果个例展示。由图可见,CMA-MESO的预报精细化程度较EC-HRES更高,多源融合实况ART_1 km局地特征很明显,订正模型能够学习到这些局地特征,使订正结果也呈现出明显的局地特征,图中评价数据显示,模型基本消除了系统偏差,订正效果在航道区域好于整体区域。
|
|
表 8 2022年1月1日至2023年12月31日检验样本损失函数在加入地形标准差前后U-Net++模型的RMAE(单位:%) Table 8 Comparison of RMAE of U-Net++ model before and after adding terrain standard deviation to the loss function on test samples from 1 January 2022 to 31 December 2023 (unit: %) |
|
|
表 9 2022年1月1日至2023年12月31日检验样本损失函数在加入航道区域误差前后U-Net++模型在航道区域的RMAE和订正效果提升 Table 9 Comparison of RMAE and improvement of correction effect of U-Net++ model before and after adding channel area error to loss function on test samples in channel area from 1 January 2022 to 31 December 2023 |
|
图 7 2022年1月5日(a)CMA-MESO和(b)EC-HRES在平原区域08时起报6 h预报时次的风速订正效果 Fig. 7 Comparison of model correction effects of wind forecast between (a) CMA-MESO and (b) EC-HRES in plain areas for 6 h forecast time initiated at 08:00 BT 5 January 2022 |
|
图 8 2023年6月21日(a)CMA-MESO和(b)EC-HRES在丘陵区域08时起报6 h预报时次的风速订正效果 Fig. 8 Comparison of model correction effects of wind forecast between (a) CMA-MESO and (b) EC-HRES in hilly areas for 6 h forecast time initiated at 08:00 BT 21 June 2023 |
首先利用中国多源融合实况分析ART_1 km 10 m风要素产品分析了EC-HRES和CMA-MESO预报10 m风要素在航道研究区域的适应性,EC-HRES和CMA-MESO相较于实况产品,均有偏大的系统性误差,EC-HRES的误差相对较小,丘陵区域风速误差相对较小,风速误差随着预报时次的增加逐步增大,并呈现周期性波动,丘陵区域白天误差大于夜晚。
利用U-Net++深度神经网络对EC-HRES和CMA-MESO风速预报数据进行降尺度订正,将EC-HRES的0.125°、CMA-MESO的0.03°分辨率格点订正到0.01°。根据检验结果发现,平原区域的降尺度订正程度好于丘陵区域,CMA-MESO的降尺度订正程度好于EC-HRES,但订正后平原区域的MAE依旧大于丘陵区域,订正后CMA-MESO的MAE依旧大于EC-HRES,差距明显减小,也进一步说明国内外模式,以及平原、丘陵区域订正后的结果有趋同性;U-Net++网络模型对于格点模型风速预报的订正效果平均提升了32.73%,好于U-Net网络模型;对损失函数加入地形和航道项前后进行了订正效果对比,发现加入航道项后,对于航道区域的订正效果提升约2个百分点,加入地形项后,对于平原区域的订正效果不明显,对于丘陵区域订正效果平均提升了约1个百分点。
U-Net++网络模型对于模式风速预报有很好的订正效果,风是一个矢量气象要素,既有大小又有方向,对于同一风速,可能风向完全不同,航道区域不同的风向对于航道通行风险的影响也不同,后续考虑将风的U、V分量加入订正模型,同时进行风速、风向降尺度订正,提高航道区域风预报能力。在模型方面,U-Net++网络模型利用卷积实现了订正模型的空间特征提取,采用编解码的方式实现了模式风的空间订正,风是一个随着时间变化的物理量,风每一个时刻的状态都与前几个时次有着密切的关系,后续考虑结合LSTM网络,提取模式风的时间特征,从而进一步提高降尺度订正效果。
常俊, 彭新东, 范广洲, 等, 2015. 结合历史资料的数值天气预报误差订正[J]. 气象学报, 73(2): 341-354. |
Chang J, Peng X D, Fan G Z, et al, 2015. Error correction of numerical weather prediction with historical data[J]. Acta Meteor Sin, 73(2): 341-354.
|
陈德山, 范腾泽, 元海文, 等, 2022. 内河航运系统监管技术现状与展望[J]. 交通运输系统工程与信息, 22(6): 1-14. |
Chen D S, Fan T Z, Yuan H W, et al, 2022. Review and prospect on system operation supervision technology of inland river navigation system[J]. J Transp Syst Eng Inf Technol, 22(6): 1-14.
|
陈豫英, 陈晓光, 马金仁, 等, 2006. 风的精细化MOS预报方法研究[J]. 气象科学, 26(2): 210-216. |
Chen Y Y, Chen X G, Ma J R, et al, 2006. A study on subtle MOS forecasting method of wind[J]. Sci Meteor Sin, 26(2): 210-216.
|
韩帅, 师春香, 姜志伟, 等, 2018. CMA高分辨率陆面数据同化系统(HRCLDAS-V1.0)研发及进展[J]. 气象科技进展, 8(1): 102-108, 116. |
Han S, Shi C X, Jiang Z W, et al, 2018. Development and progress of high resolution CMA land surface data assimilation system[J]. Adv Meteor Sci Technol, 8(1): 102-108, 116.
|
胡海川, 黄彬, 魏晓琳, 2017. 我国近海洋面10 m风速集合预报客观订正方法[J]. 气象, 43(7): 856-862. DOI:10.7519/j.issn.1000-0526.2017.07.009 |
Hu H C, Huang B, Wei X L, 2017. Objective correction method of ensemble forecast of 10 m winds on Chinese offshore[J]. Meteor Mon, 43(7): 856-862.
|
刘志杰, 刘彬贤, 王锐, 等, 2022. 基于传统和深度学习技术的黄渤海域大风预报方法研究[J]. 海洋预报, 39(6): 34-43. |
Liu Z J, Liu B X, Wang R, et al, 2022. Research on the gale prediction methods in the Yellow Sea and Bohai Sea based on traditional and deep learning technologies[J]. Marine Forecasts, 39(6): 34-43.
|
罗江珊, 杨凡, 毕玮, 等, 2024. EC细网格10 m风场产品在青岛港区的预报检验和随机森林订正[J]. 海洋预报, 41(3): 110-119. |
Luo J S, Yang F, Bi W, et al, 2024. Verification and random forest correction of the EC fine-grid model 10 m wind in Qingdao Port[J]. Marine Forecasts, 41(3): 110-119.
|
孟英杰, 田刚, 明绍慧, 等, 2023. 长江航运智慧气象服务的实践[J]. 中国水运(上半月), 23(1): 10-12. |
Meng Y J, Tian G, Ming S H, et al, 2023. Practice of smart meteorological services for Yangtze River shipping[J]. China Water Transp (1st Half), 23(1): 10-12.
|
钱燕珍, 孙军波, 陈佩燕, 等, 2013. 用数值预报释用方法做近海及登陆热带气旋强度预报[J]. 气象, 39(6): 710-718. DOI:10.7519/j.issn.1000-0526.2013.06.007 |
Qian Y Z, Sun J B, Chen P Y, et al, 2013. Interpretation method of numerical weather prediction for intensity forecast of offshore and landing tropical cyclones[J]. Meteor Mon, 39(6): 710-718.
|
任萍, 陈明轩, 曹伟华, 等, 2020. 基于机器学习的复杂地形下短期数值天气预报误差分析与订正[J]. 气象学报, 78(6): 1002-1020. |
Ren P, Chen M X, Cao W H, et al, 2020. Error analysis and correction of short-term numerical weather prediction under complex terrain based on machine learning[J]. Acta Meteor Sin, 78(6): 1002-1020.
|
申华羽, 方艳莹, 涂小萍, 等, 2020. ECMWF细网格10 m风预报在浙江沿海的评估与订正[J]. 气象, 46(11): 1485-1494. DOI:10.7519/j.issn.1000-0526.2020.11.009 |
Shen H Y, Fang Y Y, Tu X P, et al, 2020. Verification of ECMWF 10 m wind forecast for coastal Zhejiang Province[J]. Meteor Mon, 46(11): 1485-1494.
|
孙全德, 焦瑞莉, 夏江江, 等, 2019. 基于机器学习的数值天气预报风速订正研究[J]. 气象, 45(3): 426-436. DOI:10.7519/j.issn.1000-0526.2019.03.012 |
Sun Q D, Jiao R L, Xia J J, et al, 2019. Adjusting wind speed prediction of numerical weather forecast model based on machine learning methods[J]. Meteor Mon, 45(3): 426-436.
|
王甚男, 李彦, 王翔, 等, 2023. 泸州长江航道运输安全气象保障策略研究[J]. 中国信息化, (2): 73-74. |
Wang S N, Li Y, Wang X, et al, 2023. Research on meteorological guarantee strategy for transportation safety of the Yangtze River Channel in Luzhou[J]. iCHINA, (2): 73-74.
|
王在文, 陈敏, Monache L D, 等, 2019. 相似集合预报方法在北京区域地面气温和风速预报中的应用[J]. 气象学报, 77(5): 869-884. |
Wang Z W, Chen M, Monache L D, et al, 2019. Application of analog ensemble method to surface temperature and wind speed prediction in Beijing Area[J]. Acta Meteor Sin, 77(5): 869-884.
|
熊红梅, 田刚, 张勤, 等, 2021. 交通强国背景下内河航运气象保障发展思考[J]. 中国水运(下半月), 21(8): 22-24. |
Xiong H M, Tian G, Zhang Q, et al, 2021. Development considerations for meteorological support of inland waterway transportation under the background of a transportation power[J]. China Water Transp (2nd Half), 21(8): 22-24.
|
徐景峰, 宋林烨, 陈明轩, 等, 2023. 冬奥会复杂山地百米尺度10 m风速预报的机器学习订正对比试验[J]. 大气科学, 47(3): 805-824. |
Xu J F, Song L Y, Chen M X, et al, 2023. Comparative machine learning-based correction experiment for a 10 m wind speed forecast at a 100 m resolution in complex mountainous areas of the Winter Olympic Games[J]. Chin J Atmos Sci, 47(3): 805-824.
|
杨程, 姜瑜君, 余贞寿, 等, 2019. 基于偏最小二乘回归的区域换式风速预报订正技术研究[J]. 气象, 45(5): 676-684. DOI:10.7519/j.issn.1000-0526.2019.05.009 |
Yang C, Jiang Y J, Yu Z S, et al, 2019. Correction technology of regional wind speed forecasting based on partial least square regression[J]. Meteor Mon, 45(5): 676-684.
|
杨晓君, 张楠, 陈宏, 等, 2019. 基于人工神经网络算法的渤海海风预报方法研究[J]. 干旱气象, 37(1): 146-152. |
Yang X J, Zhang N, Chen H, et al, 2019. Study on forecast method of sea wind in Bohai Sea based on artificial neural network algorithm[J]. J Arid Meteor, 37(1): 146-152.
|
曾庆存, 1978. 计算稳定性的若干问题[J]. 大气科学, 2(3): 181-191. |
Zeng Q C, 1978. Some aspects of the computational stability[J]. Sci Atmos Sin, 2(3): 181-191.
|
张延彪, 陈明轩, 韩雷, 等, 2022. 数值天气预报多要素深度学习融合订正方法[J]. 气象学报, 80(1): 153-167. |
Zhang Y B, Chen M X, Han L, et al, 2022. Multi-element deep learning fusion correction method for numerical weather prediction[J]. Acta Meteor Sin, 80(1): 153-167.
|
张颖超, 肖寅, 邓华, 2016. 基于ELM的风电场短期风速订正技术研究[J]. 气象, 42(4): 466-471. DOI:10.7519/j.issn.1000-0526.2016.04.010 |
Zhang Y C, Xiao Y, Deng H, 2016. Modification technology research of short-term wind speed in wind farm based on ELM method[J]. Meteor Mon, 42(4): 466-471.
|
张鑫宇, 陈敏, 范水勇, 2023. 基于莫宁-奥布霍夫相似理论的地面站点风速预报偏差订正[J]. 气象, 49(5): 624-632. DOI:10.7519/j.issn.1000-0526.2022.101201 |
Zhang X Y, Chen M, Fan S Y, 2023. Correction of wind speed forecast deviations at ground stations based on Monin-Obukhov similarity theory[J]. Meteor Mon, 49(5): 624-632.
|
郑永光, 田付友, 孟智勇, 等, 2016. "东方之星"客轮翻沉事件周边区域风灾现场调查与多尺度特征分析[J]. 气象, 42(1): 1-13. DOI:10.7519/j.issn.1000-0526.2016.01.001 |
Zheng Y G, Tian F Y, Meng Z Y, et al, 2016. Survey and multi scale characteristics of wind damage caused by convective storms in the surrounding area of the capsizing accident of cruise ship "Dongfangzhixing"[J]. Meteor Mon, 42(1): 1-13.
|
Han L, Chen M X, Chen K K, et al, 2021. A deep learning method for bias correction of ECMWF 24-240 h forecasts[J]. Adv Atmos Sci, 38(9): 1444-1459.
|
Lorenz E N, 1965. A study of the predictability of a 28-variable atmospheric model[J]. Tellus, 17(3): 321-333.
|
Mu M, Duan W S, Wang J C, 2002. The predictability problems in numerical weather and climate prediction[J]. Adv Atmos Sci, 19(2): 191-204.
|
Ronneberger O, Fischer P, Brox T, 2015. U-Net: convolutional networks for biomedical image segmentation[C]//Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015: Part Ⅲ. Munich: Springer: 234-241.
|
Shi W Z, Caballero J, Huszár F, et al, 2016. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//29th IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: Institute of Electrical and Electronics Engineers: 1874-1883.
|
Yu T Z, Yang R Y, Huang Y, et al, 2022. Terrain-guided flatten memory network for deep spatial wind downscaling[J]. IEEE J Sel Top Appl Earth Obs Remote Sens, 15: 9468-9481.
|
Zhou Z W, Siddiquee M M R, Tajbakhsh N, et al, 2020. UNet++: redesigning skip connections to exploit multiscale features in image segmentation[J]. IEEE Trans Med Imaging, 39(6): 1856-1867.
|
 2025, Vol. 51
2025, Vol. 51 
