2. 山东省气象数据中心,济南 250031;
3. 山东省气候中心,济南 250031;
4. 山东省气象台,济南 250031
2. Shandong Meteorological Data Center, Jinan 250031;
3. Shandong Climate Center, Jinan 250031;
4. Shandong Meteorological Observatory, Jinan 250031
IPCC在第六次气候变化评估报告中指出,受全球变暖的影响,未来如果不能将升温幅度控制在1.5℃之内,由于人类活动和自然系统的变化,极端天气气候事件发生频率和强度将可能进一步增加。强降水作为极端天气和气候事件的一种重要形式,是在全球不同区域经常会发生的自然现象,易诱发暴洪、地质灾害和城市内涝等次生灾害,对粮食安全、经济活动和水资源都会产生深远的影响,因此引起社会的广泛关注和重视。同时,全球变暖加剧了强降水事件的区域不均衡性,导致近年来强降水事件在全球各地频繁发生,其中短时强降水主要由中小尺度天气系统造成,并且呈现出极端性突出、生命史短、尺度小、雨量大、预测难度大、影响严重等特征(唐永兰等,2022;高帆等,2022;刘菲凡等,2023;崔慧慧等,2023)。值得关注的是,受气候系统异常的影响,强降水事件呈现出频率增加、强度增大的趋势,由于主汛期强降水的落区不确定性、突发性和高强度性,给预报业务和科学研究带来了巨大的挑战,同时严重威胁着人民生产生活和经济社会发展,因此研究多时间尺度的强降水变化频率和危险性对研究气候变化和防灾减灾有重要意义。
关于强降水事件的频率和强度可能在21世纪增加的问题已经在政府间气候变化委员会达成共识(周天军等,2024),重现期表示强降水致灾危险性超过某一阈值的频率,对于全面了解区域强降水导致的风险和应对未来可能发生的气候挑战极其重要。以往的研究虽然认识到重现期指标作为量化强降水、干旱等致灾危险性的重要性,但评价方法实质是将多影响因素简化为单变量,导致依赖单变量刻画重现期的方法丢失关键致灾因子的关联信息(程攀等,2022;谭红梅等,2023)。为避免依赖单变量计算导致的重现期高估问题,有学者尝试建立刻画致灾事件危险性的多变量模型(Vergni et al, 2015; 王颖等,2024)。然而,传统的多变量模型要求变量间互相独立且服从特定的边缘分布(Zhang and Singh, 2007),但在实际致灾场景中,这些条件很难同时满足,因此,基于这些严格假设条件的多变量模型方法难以应用于大多数致灾场景。为了更加灵活地刻画各种致灾场景中多变量的依存关系,克服假设条件中同时满足独立性和边缘分布类型的约束,近年来,有学者提出采用Copula函数刻画多变量间的依存关系(Sklar, 1959)。Copula函数已在干旱事件风险识别中广泛应用,Li et al(2015)研究了北京干旱事件的联合重现期,并评估了干旱风险对冬小麦生长的影响。张洁祥等(2023)采用基于Copula函数的多变量风险评估方法,分析了长江流域发生的高温复合型干旱事件重现期。Wen et al(2023)通过Copula函数建立干旱风险模型,揭示了河南省干旱变量间的响应关系。同时,Copula函数在洪涝事件灾害风险分析中也得到应用,de Michele and Salvadori(2003)首次提出采用Copula函数刻画强降水频率,并通过广义帕累托分布拟合了自然降水持续时长和降水强度之间的关系。Tong et al(2015)利用选定的Copula函数分析了洪峰随时间长度的变化情况。Haile et al(2023)通过对洪峰和洪量特征进行二元建模,证明了Copula函数在洪水管理中的有效性。曹伟华等(2016)尝试利用2005—2014年逐小时降水资料建立二元联合分布模型,计算北京地区强降水重现期并开展危险性分析。以上研究均表明Copula函数是分析干旱或洪涝等极端事件有效工具,但是目前对强降水事件灾害风险的研究主要集中在通过日降水量和降水日数分析强降水频率特征(Utsumi and Kim, 2022;程攀等,2022;谭红梅等,2023),难以凸显短时强降水带来的致灾危险性。
山东省属于暖温带季风气候区,地处东部沿海,受到海陆位置和下垫面差异的影响,强降水落区分布和降水频率变化有显著差异,城市内涝等灾害频发。已有研究表明,强降水对山东年降水量贡献已累计超过52.0%(董旭光等,2014;2017),21世纪以来大雨与暴雨降水量和降水日数占比呈增大趋势(丁一汇,2019)。目前针对山东强降水的研究多为强降水演变的时空分布特征和强降水个例的成因分析,针对降水持续时长和降水量两者耦合的强降水频率以及空间分布特征的相关研究尚未开展。因此,本文采用小时降水资料研究山东强降水变化的频率特征,通过Copula函数构建降水持续时长和降水量间的关系,并利用该函数估算重现期,然后从重现期的角度分析山东多场景强降水的变化和联系,进一步得到强降水频率的时空分布特征和致灾危险性,以期对提高山东防灾减灾水平和科学决策能力提供积极参考。
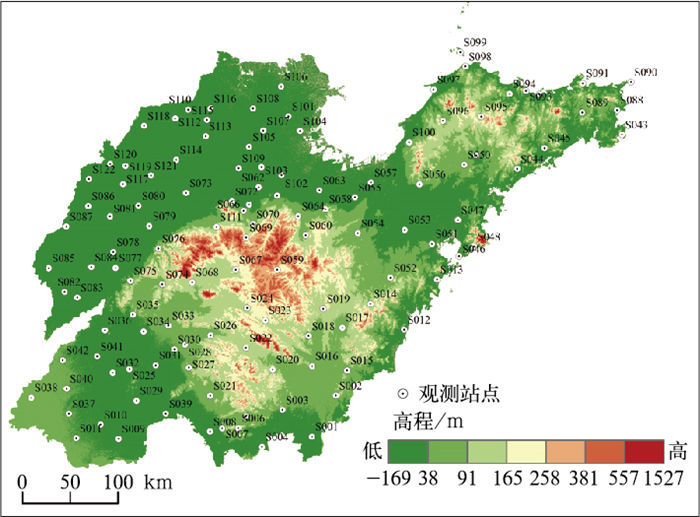
1 资料与方法 1.1 资料本研究所用数据为图 1所示的1966—2023年山东122个国家级气象观测站(简称山东122个观测站)逐小时降水资料,是山东省气象数据中心通过质量控制剔除可疑和错误数据后的整编数据。针对超过30年(气候平均值参考年份)观测年限的小时降水整编数据,在定义强降水过程时采用如下标准:当出现降水量大于0 mm的时刻作为降水过程的开始时间,若之后连续2小时无降水,则视为该次降水过程的结束时间;对于降水过程中出现的无降水间歇期,将间隔1小时的降水过程合并为同一次降水过程。在此基础上,筛选整个降水过程中至少有1小时降水量达到或超过20 mm的过程作为强降水事件(佘敦先等,2011;王莉萍等,2023)。需要说明的是,本文中的降水持续时长是指从降水开始到结束的整个过程时长(包括弱降水时段),而降水量则指一次降水过程中所有小时降水量的累计值。本文以强降水事件的样本为基础估算重现期。
|
图 1 山东站点空间分布以及地形高度分布 Fig. 1 Spatial distribution of stations and the height of terrain in Shandong Province |
本文采用的Copula统计模型由变量的最优边缘分布函数构成,考虑到不同区域强降水事件概率分布的差异性和模型估算结果的可靠性,候选边缘分布函数选用以往强降水特征研究中应用最广泛的适用类型(王沁,2006;Rauf and Zeephongsekul, 2014;Salvadori and de Michele, 2015)。选取广义极值分布(简称GEV分布)、对数正态分布(简称Ln分布),Gamma分布(简称Gam分布)、Weibull分布(简称Wbl分布)、指数分布(简称Exp分布)、广义帕累托分布(简称Gp分布),然后采用K-S(Kolmogorpv-Smirnov)检验对比候选边缘分布函数的拟合优度(Massey, 1951;李琼芳等,2024),依此选定最优函数类型。
1.2.2 选取Copula联合分布函数类型Copula联合分布函数源于1959年被提出的Sklar定理(Sklar,1959),又被称为“连接”函数,即如果是两个随机变量,并且有各自拟合的边缘分布函数u(x)和v(y),那么可以找到唯一的Copula联合分布函数将以上两个变量的边缘分布“连接”起来,得到C(u(x), v(y))。
由于Copula函数的结构相对灵活,不依赖于特定的边缘分布函数,因此可以更好地描述两个随机变量的依存关系。Copula函数本质上是一类特殊的多变量概率分布函数,其特点是边缘分布均为标准均匀分布。本文选用Copula函数簇中的Gumbel、Frank、Clayton等类型作为候选,表 1列出了3种函数的表达式及其参数域,其中参数θ刻画了变量间的依赖程度,可通过最大似然估计法求得。采用赤池信息量准则(简称AIC)法(蒋金良和林广明,2008;宋亚轩等,2023)评估各候选函数的拟合优度,并依此选取最优的Copula函数类型。
|
|
表 1 3种候选Copula函数及参数域 Table 1 Three candidate functions of Copula and their parameter domains |
利用Copula联合分布函数估算重现期的方法可以计算两个变量共同影响下的强降水的频率特征,与以往的重现期计算方法相比(Adamowski,2000;王莉萍等,2023),其优点在于其不需要依赖单一的指标变量,比如可以体现短时强降水的致灾危险性,联合重现期TC的计算公式为(Kao and Govindaraju, 2007):
| $ \begin{aligned} T_{\mathrm{C}}= & \frac{T}{N \cdot p(x \geqslant X \mid y \leqslant Y)}= \\ & \frac{T}{N\left[1-\frac{C(u(x), v(y))}{v(y)}\right]} \end{aligned} $ | (1) |
式中:T为强降水事件的年数,N为强降水事件的次数,p(x≥X|y≤Y)是过程降水量大于X、降水持续时长小于Y的强降水事件条件概率(沈永平和王国亚,2013),u(x)和v(y)分别为降水量和降水持续时长的边缘分布函数。
单变量重现期适用于单一因素主导或变量间相关性弱的情况,在强降水分析中,则表示大于等于一定降水量的强降水事件的平均发生间隔,单变量重现期Tm的计算公式为:
| $ T_{\mathrm{m}}=\frac{T}{N[1-u(x)]} $ | (2) |
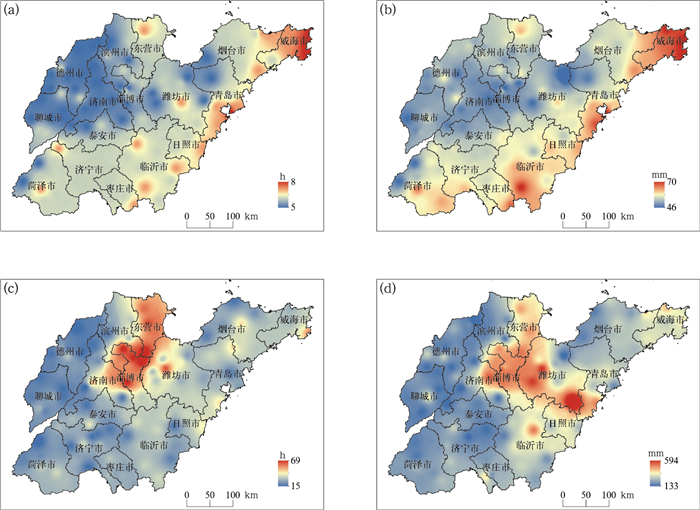
1966—2023年山东122个观测站均出现强降水,降水持续时长主要集中在24小时以内,且短历时特征明显。山东122个观测站均出现过1小时内的强降水,最长平均持续时长出现在威海(8 h),最短则出现在菏泽(5 h)。各站强降水过程的平均降水量为58 mm,最大平均降水量出现在滨州(75 mm),最小则出现在潍坊(46 mm)。降水过程最长持续时长出现在淄博(70 h),最大降水量出现在潍坊(595 mm)。总体而言,山东强降水事件的降水平均持续时长为5~8 h,降水持续时长总体较短,并且以强对流为主(孙继松和陶祖钰,2012;侯淑梅等,2023)。1966—2023年强降水贡献的平均降水量每小时可达9 mm,并且强降水的空间分布极为不均,从图 2可以看出,降水平均持续时长和平均降水量的空间分布较一致,高值区域均集中在威海、青岛、日照、临沂等地区(图 2a,2b);降水最长持续时长和最大降水量的空间分布也较一致,高值区域集中在东营、淄博、潍坊、济南(图 2c,2d),由此可推断出强降水事件的持续时长和降水量存在相关性。
|
图 2 1966—2023年山东强降水(a)平均持续时长,(b)平均降水量,(c)最长持续时长和(d)最大降水量 Fig. 2 (a) Mean duration, (b) mean precipitation amount, (c) the longest duration and (d) maximum precipitation amount of heavy precipitation in Shandong Province during 1966-2023 |
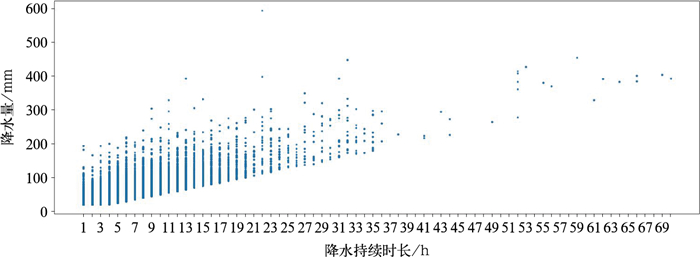
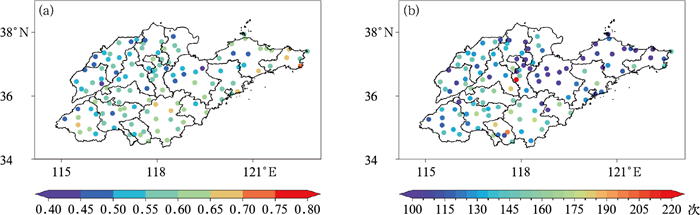
采用Kendall秩相关系数计算特征变量间的相关性,该系数不受总体分布限制、对异常值不敏感且与Copula函数存在直接的函数关系,较Pearson和Spearman相关系数更适合用于Copula函数的构建(Wilks, 2023)。山东1966—2023年强降水均发生在5—9月,降水量和降水持续时长的Kendall秩相关系数在0.4~0.8(已通过0.01显著性水平检验),且降水量随着持续时长的增加而增加,呈现明显的正相关(图 3),平均相关系数达到0.6。由Kendall秩相关系数的空间分布(图 4a)可以看出,在沿海和鲁南地区相关性较明显。受水汽输送、热力差异、地形等因素的影响(高理等,2013;任建成等,2024),山东强降水频次分布存在明显的地区差异,由1966—2023年5—9月山东122个观测站强降水次数的空间分布(图 4b)可以看出,1966—2023年的强降水大致集中在鲁南区域。发生的频次平均约为130次,其中强降水最为频繁的区域出现在枣庄站(196次),最低频次出现在潍坊昌乐站(67次)。总体而言,山东强降水的降水量随着降水持续时长的增加而持续增加,两者之间存在显著的依赖关系,适用于通过Copula函数构建联合分布估算重现期。为了更加突出强降水的致灾危险性,以下选用过程累计降水量大于50 mm、持续时长小于24 h的强降水事件计算重现期。
|
图 3 1966—2023年山东强降水的降水量与降水持续时长散点分布 Fig. 3 Scattered distribution of precipitation amount and duration of heavy precipitation in Shandong Province during 1966-2023 |
|
图 4 1966—2023年山东强降水(a)降水量与降水持续时长的Kendall秩相关系数和(b)降水次数的空间分布 Fig. 4 Spatial distribution of (a) Kendall correlation coefficients between precipitation amount and duration and (b) frequency of heavy precipitation in Shandong Province during 1966-2023 |
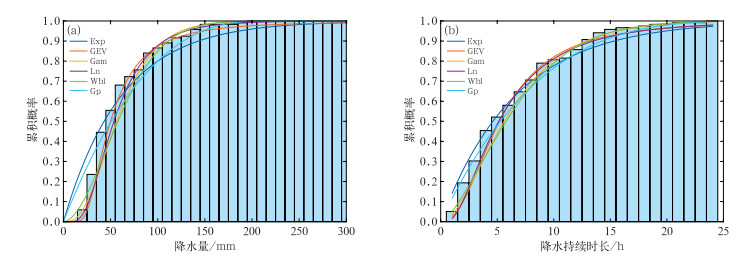
为选取适当的降水持续时长和降水量的最优边缘概率分布拟合类型,利用K-S检验对候选的6种边缘概率分布(GEV、Ln、Gam、Wbl、Exp、Gp)做拟合优度检验。采用K-S检验评估时,p>0.05表示样本数据与理论分布不存在显著差异,因此在众多候选分布中选择K-S统计量最小且p>0.05的边缘分布函数作为最优拟合类型(Wilks, 2023)。以青岛崂山站降水持续时长小于6 h的50 mm以上的强降水情景为例,依据上述检验方法筛选出降水持续时长最优边缘概率密度函数为Ln分布,降水量最优拟合函数类型为GEV分布,两者的K-S统计量分别为0.086和0.064,显著优于其他分布函数。通过对比崂山站降水持续时长和降水量的6种候选边缘分布拟合匹配程度(图 5), 验证上述两种边缘分布的适配度。对山东122个观测站分别进行上述拟合优度检验,统计每种分布函数被选为最优拟合类型的站点数量,并计算其在总站点数中的占比,得到图 6所示的最优分布类型占比。结果表明,对于降水持续时长序列,47%的站点以Ln分布为最优拟合类型;对于降水量序列,76%的站点适合采用GEV分布。总体而言,山东地区强降水事件的持续时长和降水量的边缘分布适合选取Ln分布和GEV分布类型。
|
图 5 1966—2023年崂山站强降水的(a)降水量和(b)降水持续时长的频率分布及候选边缘分布拟合 Fig. 5 Frequency distribution and candidate marginal distribution fitting of (a) precipitation amount and (b) duration of heavy precipitation at Laoshan Station during 1966-2023 |
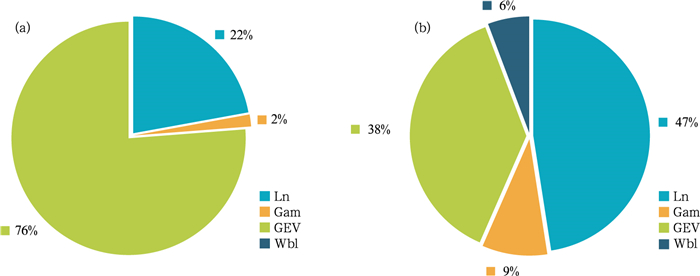
|
图 6 1966—2023年山东122个观测站强降水的(a)降水量和(b)降水持续时长最优边缘分布占比 Fig. 6 Percentage of optimal marginal distribution of (a) precipitation amount and (b) duration of heavy precipitation at 122 stations in Shandong Province during 1966-2023 |
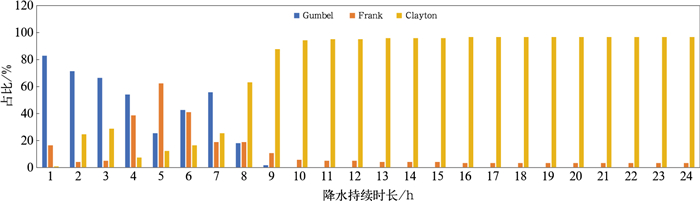
为选取强降水事件的最优二元Copula联合分布类型,本文对每个站点分别拟合3种候选Copula函数(Gumbel、Frank、Clayton),采用AIC评估各函数的拟合优度,AIC值越小说明该函数对站点数据的匹配程度越高。以青岛崂山站强降水为例:在降水持续时长小于7 h且降水量大于50 mm的情景下,Gumbel Copula的AIC值为-245.3,明显小于Clayton Copula(-238.6)和Frank Copula(-232.1),因此选择Gumbel Copula作为该情景下的最优联合分布类型。通过对山东122个观测站分别计算不同降水持续时长情景下的AIC值,统计每种Copula函数被选为最优拟合类型的站点数量及其占比,得到图 7所示的各类型占比随降水持续时长的变化特征。结果表明,对于降水持续时长在8 h以上的情景,大多数站点适用于Clayton Copula联合分布函数类型;而降水持续时长在8 h以下的情景中,站点的最优联合分布函数类型以Gumbel Copula和Clayton Copula为主,这两类联合分布函数对于山东大多数站点拟合程度较好。值得注意的是,在降水持续时长为5 h且降水量大于50 mm的特定情景下,少数站点最优拟合函数类型为Frank Copula,这表明此地区的强降水联合分布特征可能具有特殊性,有待进一步研究。至此,构建完成了山东强降水Copula联合分布,为分析该地区强降水重现期及致灾性奠定了基础。
|
图 7 1966—2023年山东强降水不同降水持续时长的最优拟合Copula联合分布函数类型占比 Fig. 7 Percentage of types of best-fit Copula joint distribution functions for different durations of heavy precipitation in Shandong Province during 1966-2023 |
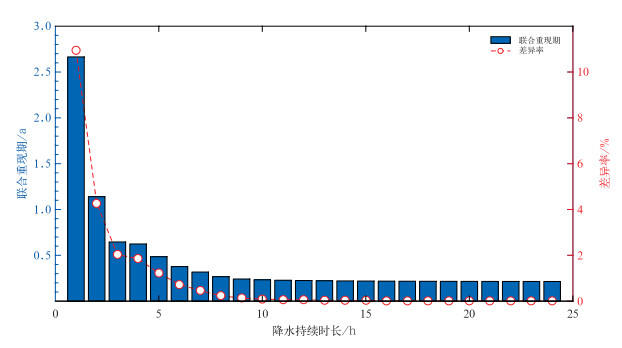
图 8为1966—2023年山东强降水持续时长随联合重现期变化情况,可看出,随着降水持续时长的延长, 联合重现期逐渐减小,降水持续时长在小于8 h时,联合重现期衰减较明显,降水持续时长大于8 h时,联合重现期逐渐趋近于0.5 a且趋于稳定。将联合重现期与单变量重现期的相对差值定义为差异率,从图 8可以看出,随着降水持续时长的增加,联合重现期与差异率均呈现递减趋势,当降水持续时长低于8 h时差异率较大,而降水持续时长大于8 h时差异率迅速减小。以上结果表明,在降水持续时长小于8 h的短时强降水情景中,结合降水持续时长和降水量来计算强降水的频率对于科学分析其致灾危险性尤为重要。
|
图 8 1966—2023年山东强降水不同降水持续时长的联合重现期及差异率 Fig. 8 Joint return period and the rate of difference with different durations of heavy precipitation in Shandong Province during 1966-2023 |
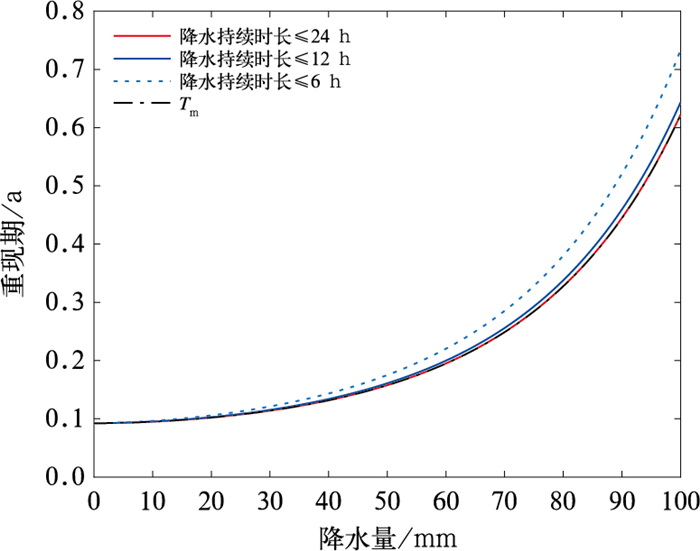
图 9为1966—2023年崂山站强降水不同降水持续时长联合重现期与单变量重现期的变化关系,可以发现,当降水持续时长相同时,随着降水量的增加,联合重现期相应延长;降水量相同时,随着降水持续时长的减小,联合重现期也相应延长。事实上,估算联合重现期的Copula函数同时将降水持续时长与降水量考虑在内,也就意味着相同降水量的情况下,降水持续时长越小,其平均降水强度会越大,发生概率也就越低,联合重现期越长,说明此类强降水事件在相同的承灾条件下,致灾的危险程度会随之增大。因此,利用Copula函数估算联合重现期可以区分不同强降水情况下的致灾危险程度。
|
图 9 1966—2023年崂山站强降水不同降水持续时长的联合重现期与单变量重现期对比 Fig. 9 Comparison of joint and univariate return periods for different precipitation durations of heavy precipitation at Laoshan Station during 1966-2023 |
由图 9可以明显看出,降水持续时长为24 h的联合重现期结果与单变量重现期的结果几乎一致。崂山站1966—2023年强降水事件的最长降水持续时长为26 h,接近联合重现期估算的降水持续时长24 h,因此,当崂山站的降水持续时长的阈值为24 h时,其单变量重现期和联合重现期的估算结果几乎一致。与单变量重现期仅依赖降水量的估算方法相比,联合重现期是在降水持续时长小于某一阈值的条件下估算出的强降水发生频率,当降水持续时长越大,两种估算方法的差异越小,持续时长的阈值足够大时,两种重现期估算值的差接近于0。
值得关注的是,在强降水过程的灾害风险评估工作中,将日累计降水量作为计算重现期或者评价致灾危险程度的指标,相当于在降水持续时长接近24 h时估算单变量重现期,对于客观评价山东强降水的致灾危险程度有较大局限性。考虑到山东大多数的强降水事件的历时较短,使得基于单变量重现期估算和联合重现期估算存在较大差别,因此,以往仅依据日降水量计算的指标值会严重低估短时强降水过程的危险性和致灾程度(程攀等,2022;谭红梅等,2023)。利用Copula函数估算的强降水联合重现期描述了降水持续时长与降水量之间的依存关系,该估算方法将降水强度考虑在内,可以更客观地描述不同历时强降水下的频率信息,因此有利于更合理地描述不同情景强降水致灾因子的危险程度。
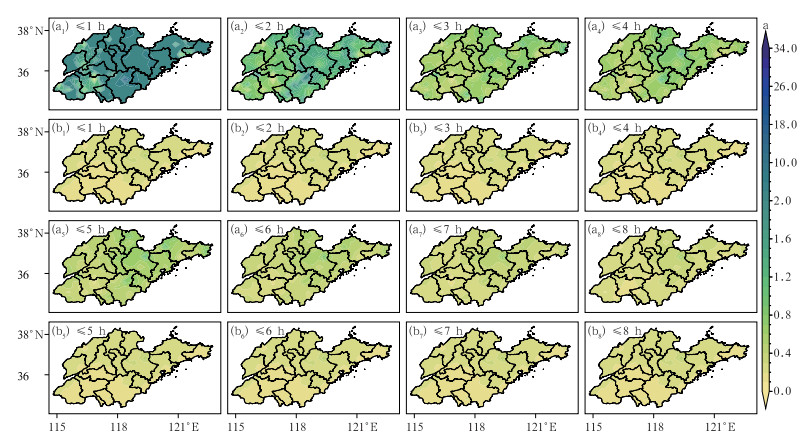
2.3.2 多情景强降水重现期空间分布在山洪地质灾害的防灾减灾和城市排水系统建设中,为了更加科学地规划防灾减灾的区域布局,不仅应该了解研究区域的强降水事件的频率信息,还应该了解研究区域强降水事件致灾因子的空间分布。因此,针对强降水事件的降水量超过50 mm的情景,对比降水持续时长小于8 h阈值下的联合重现期和单变量重现期在山东的空间分布(图 10),此时以上情景的强降水有可能引发泥石流、城市内涝和山体滑坡等灾害,分析以上情景的联合重现期对于强降水灾害的防灾减灾和城市排水系统建设提供决策依据有积极意义。从图 10中可以看出,强降水联合重现期空间分布随着降水持续时长阈值的变化呈现出明显差异,而仅基于降水量的单变量重现期在不同持续时长阈值下的空间分布则相对一致。降水量超过50 mm,降水持续时长阈值低于1 h的情景,联合重现期空间分布的高值大致集中在鲁东和鲁南东部区域,鲁西地区强降水的发生频率相对较低,随着降水持续时长逐渐增大,联合重现期的高值区域逐渐缩小至鲁东区域,联合重现期的低值区域在鲁西地区不断扩大。降水量超过50 mm,降水持续时长阈值为5 h的情景与阈值为3 h的空间分布差异不大,说明山东大部分强降水的降水持续时长不超过5 h的样本中,大多数降水持续时长低于3 h。相较于降水持续时长阈值为8 h的情景,降水持续时长的阈值为1 h情景下的联合重现期高出86%,以上两种情景的空间分布有明显差异,且联合重现期的高值集中在鲁东和鲁南等区域,说明以上地区的强降水事件的降水持续时长在1 h内发生频率更高,其致灾风险也随之较高,联合重现期空间分布同时也说明了短时强降水带来的影响(郑祚芳等,2014)。以上不同降水持续时长阈值的重现期的空间分布差异表明,结合强降水的持续时长和降水量分析强降水致灾风险,可以更加客观地描述不同情景下强降水的致灾风险因子的强度和频率的空间分布特征。
|
图 10 1966—2023年山东强降水(降水量≥50 mm)在不同降水持续时长阈值下的(a)联合重现期与(b)单变量重现期空间分布 Fig. 10 Spatial distribution of (a) joint and (b) univariate return periods of heavy precipitation with precipitation ≥50 mm for different precipitation duration thresholds in Shandong Province during 1966-2023 |
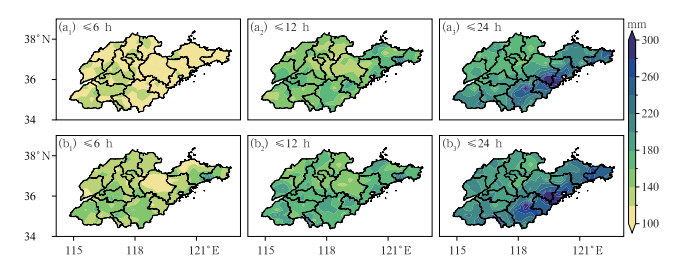
科学估算不同情景的强降水重现期的降水量是城市建设规划排水系统的重要参考依据。本文通过Copula联合分布估算重现期为30 a和60 a的降水量阈值,并给出以上两种情景降水量的空间分布特征,将其作为分析强降水致灾危险性的重要参考。由图 11可见,降水量阈值均伴随着降水持续时长的延长逐渐增大,相比30年一遇的情景(图 11a),60年一遇情景的降水量最大增加幅度达到65%。重现期为30 a的情景下,降水持续时长在6 h内的降水量阈值均在200 mm以下(图 11a1),山东降水持续时长在12 h和24 h内降水量高值的空间分布大致集中鲁南和鲁东地区(图 11a2, 11a3)。重现期为60 a的情景下,降水量阈值随着降水持续时长的增加在鲁南部分区域逐渐扩大(图 11b),预计超过300 mm。以上分析表明,通过Copula联合分布计算出的联合重现期刻画强降水致灾危险程度可以更加客观地反映强降水的频率和强度信息。综合以上结果分析,不同情景的强降水事件的致灾危险性有明显的地区差异,其中60年一遇的强降水事件在鲁东和鲁南等地区的危险程度较高,建议重点考虑以上区域城市雨水系统的建设和洪涝防灾减灾的规划。
|
图 11 山东不同降水持续时长在(a)30年一遇和(b)60年一遇联合重现期下的降水量阈值 Fig. 11 Precipitation thresholds for different durations at the joint return periods of (a) 30 a and (b) 60 a in Shandong Province |
由于受到全球变暖等多种因素的影响,极端天气气候事件发生愈加频繁,科学估算和分析强降水致灾频率和危险程度对于防灾减灾和风险管理规划有积极作用。本文以山东122个观测站逐小时强降水资料为基础建立了同时考虑降水持续时长和降水量的Copula二元联合分布,在此基础上计算能够反映强降水事件致灾风险的联合重现期,并依据联合重现期统计分析了山东不同情景强降水过程对应的重现期特征。基于Copula联合分布估算联合重现期的方法能够更客观地反映不同情景强降水致灾危险程度,为山东强降水的灾害风险评估提供新途径。主要结论如下:
(1) 1966—2023年山东强降水短历时特征明显,均出现过1 h内的强降水,强降水频次分布有明显的地区差异,强降水事件大致集中在鲁南地区。降水持续时长和降水量的最大Kendall秩相关系数达到0.7,两者存在显著的依存关系,满足Copula联合分布计算重现期的适用条件。
(2) 通过K-S检验评估强降水事件指标变量的边缘分布的最优拟合类型发现,对于1966—2023年山东强降水样本适合采用Ln分布和GEV分布拟合强降水事件的持续时长和降水量,Gumbel Copula和Clayton Copula联合分布函数较适合刻画山东强降水二元变量的依存结构,但针对降水持续时长在8 h以上的情景,更适合采用Clayton Copula联合分布函数。
(3) 由于山东近60年强降水持续时长短、强度大等特征明显,大多数降水持续时长在3 h以内,由日降水量估算的重现期可能会严重低估短时强降水的致灾危险性。利用Copula联合分布估算联合重现期的方法刻画了降水持续时长和降水量的依存结构,同时描述了不同历时强降水情景下的频率信息,特别是短时强降水带来的影响。相同降水量的情景下,降水持续时长越短,其平均降水强度越大,其发生概率越低,联合重现期也就越长,说明此类强降水事件在相同的承灾条件下,致灾的危险程度会随之增大。
(4) 由Copula联合分布估算的山东强降水联合重现期随着降水持续时长延长有明显的空间差异,随着降水持续时长逐渐增大,联合重现期的高值由鲁东和鲁南等区域逐渐缩小至鲁东区域,特别是60年一遇强降水在鲁东和鲁南等地区致灾危险性较高。基于Copula联合分布可以辨识不同情景强降水致灾危险性,估算出的联合重现期相比于以往依赖单变量估算重现期的方式,能够更加合理地刻画出强降水致灾因子的二维强度和频率信息,可为山东强降水事件的防灾减灾规划及其灾害风险管理提供科学依据。
(5) 采用Copula函数对山东1966—2023年发生的强降水事件的两个特征变量进行重现期估算,发现Copula函数可以刻画降水持续时长和累计降水量两个变量间复杂的相依关系,进而联合重现期可以有效捕捉降水特征变量间的相互作用关系,相比单一变量的分析能够更完整地刻画降水事件的特征,同时更准确地评估短时强降水的风险,避免仅考虑降水量而低估降水风险的问题。由于缺乏历史强降水的数据,本文仅收集1966—2023年的强降水事件特征变量,时间序列相对较短,但Copula函数有效体现了估算多维特征变量重现期的优势。现阶段Copula函数在水文气象领域的应用主要集中于二维联合分布分析。然而,随着计算技术的快速发展和研究问题的日益复杂化,构建三维及高维Copula函数模型已成为可能,这对其参数估计方法、函数族的选择准则等理论问题提出了新的挑战。同时,扩充历史观测数据的样本量和延长时间序列长度对提高重现期计算方法的可靠性具有重要意义。这些研究的深入开展,将为Copula函数在自然灾害风险评估中的推广应用奠定坚实基础。
曹伟华, 梁旭东, 赵晗萍, 等, 2016. 基于Copula函数的北京强降水频率及危险性分析[J]. 气象学报, 74(5): 772-783. Cao W H, Liang X D, Zhao H P, et al, 2016. Copula-based frequency analysis and its application in hazard risk assessment of heavy rainfall in Beijing[J]. Acta Meteor Sin, 74(5): 772-783 (in Chinese).
|
程攀, 杨萌, 孙虹雨, 等, 2022. 基于复合极值模型的辽宁省极端降水重现期研究[J]. 暴雨灾害, 41(6): 662-670. Cheng P, Yang M, Sun H Y, et al, 2022. Study on the return period of extreme precipitation in Liaoning Province based on the compound extreme value model[J]. Torr Rain Dis, 41(6): 662-670 (in Chinese).
|
崔慧慧, 李荣, 郜彦娜, 等, 2023. "7·20"郑州极端特大暴雨降水细节特征和成灾过程研究[J]. 灾害学, 38(2): 114-120, 149. Cui H H, Li R, Gao Y N, et al, 2023. Study on the precipitation details and disaster formation process of "7·20" extreme rainstorm in Zhengzhou[J]. J Catastrophol, 38(2): 114-120, 149 (in Chinese).
|
丁一汇, 2019. 中国暴雨理论的发展历程与重要进展[J]. 暴雨灾害, 38(5): 395-406. Ding Y H, 2019. The major advances and development process of the theory of heavy rainfalls in China[J]. Torr Rain Dis, 38(5): 395-406 (in Chinese).
|
董旭光, 顾伟宗, 曹洁, 等, 2017. 山东省汛期小时极端强降水分布和变化特征[J]. 气象, 43(8): 953-961. Dong X G, Gu W Z, Cao J, et al, 2017. Variation features of hourly precipitation in Shandong Province in flood season during 1961-2012[J]. Meteor Mon, 43(8): 953-961 (in Chinese). DOI:10.7519/j.issn.1000-0526.2017.08.006
|
董旭光, 顾伟宗, 孟祥新, 等, 2014. 山东省近50年来降水事件变化特征[J]. 地理学报, 69(5): 661-671. Dong X G, Gu W Z, Meng X X, et al, 2014. Change features of precipitation events in Shandong Province from 1961 to 2010[J]. Acta Geogr Sin, 69(5): 661-671 (in Chinese).
|
高帆, 俞小鼎, 尹承美, 等, 2022. 山东一次浅薄冷空气触发强降水过程的对流系统组织形态演变分析[J]. 气象, 48(8): 993-1006. Gao F, Yu X D, Yin C M, et al, 2022. Analysis on the evolution of convective system organization in a process of severe precipitation triggered by shallow cold air in Shandong[J]. Meteor Mon, 48(8): 993-1006 (in Chinese). DOI:10.7519/j.issn.1000-0526.2022.040901
|
高理, 胡桂芳, 孙莎莎, 2013. 山东夏季强降水的时空演变特征及成因[J]. 干旱气象, 31(4): 690-694, 731. Gao L, Hu G F, Sun S S, 2013. Temporal-spatial evolution feature of summer heavy rainfall in Shandong Province and causes analysis[J]. J Arid Meteor, 31(4): 690-694, 731 (in Chinese).
|
侯淑梅, 朱晓清, 史茜, 等, 2023. 冷涡背景下山东省"5·17"极端强对流天气环境条件分析[J]. 气象, 49(11): 1328-1342. Hou S M, Zhu X Q, Shi Q, et al, 2023. Analysis of the environmental conditions of "5·17" extremely severe convective weather in Shandong Province under the background of cold vortex[J]. Meteor Mon, 49(11): 1328-1342 (in Chinese). DOI:10.7519/j.issn.1000-0526.2023.053101
|
蒋金良, 林广明, 2008. 基于ARIMA模型的自动站风速预测[J]. 控制理论与应用, 25(2): 374-376. Jiang J L, Lin G M, 2008. Automatic station wind speed forecasting based on ARIMA model[J]. Control Theory Appl, 25(2): 374-376 (in Chinese).
|
李琼芳, 方凯悦, 韩幸烨, 等, 2024. 基于多维Copula函数的澜沧江-湄公河流域气象干旱特征分析[J]. 水资源保护, 40(1): 52-59. Li Q F, Fang K Y, Han X Y, et al, 2024. Analysis of meteorological drought characteristics in the Lancang-Mekong River Basin based on multi-dimensional Copula function[J]. Water Res Prot, 40(1): 52-59 (in Chinese).
|
刘菲凡, 郑永光, 罗琪, 等, 2023. 京津冀及周边一般性降水与短时强降水特征对比[J]. 应用气象学报, 34(5): 619-629. Liu F F, Zheng Y G, Luo Q, et al, 2023. Comparison of characteristics of light precipitation and short-time heavy precipitation over Beijing, Tianjin, Hebei and neighbouring areas[J]. J Appl Meteor Sci, 34(5): 619-629 (in Chinese).
|
任建成, 谷山青, 卢晓宁, 2024. 基于REOF分析的山东省年降水区域特征及趋势分析[J]. 水土保持研究, 31(1): 224-231. Ren J C, Gu S Q, Lu X N, 2024. Regional characteristics and trend analysis of annual precipitation in Shandong Province based on REOF[J]. Res Soil Water Conserv, 31(1): 224-231 (in Chinese).
|
佘敦先, 夏军, 张永勇, 等, 2011. 近50年来淮河流域极端降水的时空变化及统计特征[J]. 地理学报, 66(9): 1200-1210. She D X, Xia J, Zhang Y Y, et al, 2011. The trend analysis and statistical distribution of extreme rainfall events in the Huaihe River Basin in the past 50 years[J]. Acta Geogr Sin, 66(9): 1200-1210 (in Chinese).
|
沈永平, 王国亚, 2013. IPCC第一工作组第五次评估报告对全球气候变化认知的最新科学要点[J]. 冰川冻土, 35(5): 1068-1076. Shen Y P, Wang G Y, 2013. Key findings and assessment results of IPCC WGI Fifth Assessment Report[J]. J Glaciol Geocryol, 35(5): 1068-1076 (in Chinese).
|
宋亚轩, 索梅芹, 刘丽博, 2023. Copula函数在漳河上游联合干旱特征分析中的应用[J]. 水电能源科学, 41(10): 1-5. Song Y X, Suo M Q, Liu L B, 2023. Application of copula function in analysis of joint drought characteristics in Zhanghe upstream[J]. Water Res Power, 41(10): 1-5 (in Chinese).
|
孙继松, 陶祖钰, 2012. 强对流天气分析与预报中的若干基本问题[J]. 气象, 38(2): 164-173. Sun J S, Tao Z Y, 2012. Some essential issues connected with severe convective weather analysis and forecast[J]. Meteor Mon, 38(2): 164-173 (in Chinese). DOI:10.7519/j.issn.1000-0526.2012.02.004
|
谭红梅, 贺中华, 陈莉会, 等, 2023. 贵州省极端降雨特征及其影响因子[J]. 山地学报, 41(5): 748-758. Tan H M, He Z H, Chen L H, et al, 2023. Characteristics of extreme rainfall and its influencing factors in Guizhou Province, China[J]. J Mt Sci, 41(5): 748-758 (in Chinese).
|
唐永兰, 徐桂荣, 万蓉, 2022. 2020年主汛期长江流域短时强降水时空分布特征[J]. 大气科学学报, 45(2): 212-224. Tang Y L, Xu G R, Wan R, 2022. Temporal and spatial distribution characteristics of short-duration heavy rainfall in the Yangtze River Basin during the main flood season of 2020[J]. Trans Atmos Sci, 45(2): 212-224 (in Chinese).
|
王莉萍, 王韫喆, 向欣, 等, 2023. 基于耿贝尔-线性矩和K-Means算法的短时强降水等级划分研究[J]. 地球物理学报, 66(8): 3171-3184. Wang L P, Wang Y Z, Xiang X, et al, 2023. Research on classification of short-duration heavy rain based on Gumbel-Linear Moment and K-Means algorithm[J]. Chin J Geophys, 66(8): 3171-3184 (in Chinese).
|
王沁, 2006. 生成Copula的两种简单方法[J]. 浙江大学学报(理学版), 33(2): 129-130. Wang Q, 2006. Method of creating Copula[J]. J Zhejiang Univ (Sci Ed), 33(2): 129-130 (in Chinese).
|
王颖, 杨佳希, 杨宝钢, 等, 2024. 利用短序列高密度台站资料推算暴雨重现期方法研究及应用[J]. 气象学报, 82(4): 510-521. Wang Y, Yang J X, Yang B G, et al, 2024. Estimating the rainstorm return period based on short-sequence high-density station data: meteorology and application[J]. Acta Meteor Sin, 82(4): 510-521 (in Chinese).
|
Wilks D S, 2023. 大气科学中的统计方法: 第4版[M]. 朱玉祥, 译. 北京: 气象出版社. Wilks D S, 2023. Statistical Methods in the Atmospheric Sciences[M]. Zhu Y X, trans. 4th ed. Beijing: China Meteorological Press(in Chinese).
|
张洁祥, 吕娟, 张学君, 等, 2023. 基于Copula的2022年长江流域极端干旱重现期研究[J]. 人民长江, 54(8): 32-39. Zhang J X, Lyu J, Zhang X J, et al, 2023. Return period of extreme drought over Changjiang River Basin of 2022 based on Copula function[J]. Yangtze River, 54(8): 32-39 (in Chinese).
|
郑祚芳, 高华, 王在文, 等, 2014. 北京地区降水空间分布及城市效应分析[J]. 高原气象, 33(2): 522-529. Zheng Z F, Gao H, Wang Z W, et al, 2014. Analysis on spatial distribution of precipitation in Beijing and its city effect[J]. Plateau Meteor, 33(2): 522-529 (in Chinese).
|
周天军, 陈晓龙, 张文霞, 等, 2024. 气候变化与碳中和[J]. 自然杂志, 46(1): 1-11. Zhou T J, Chen X L, Zhang W X, et al, 2024. Climate change and carbon neutrality[J]. Chin J Nat, 46(1): 1-11 (in Chinese).
|
Adamowski K, 2000. Regional analysis of annual maximum and partial duration flood data by nonparametric and L-moment methods[J]. J Hydrol, 229(3-4): 219-231. DOI:10.1016/S0022-1694(00)00156-6
|
de Michele C, Salvadori G, 2003. A generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas[J]. J Geophys Res: Atmos, 108(D2): ACL15.
|
Haile M M, Khosa R, Abebe A K, et al, 2023. Copula-based joint flood frequency analysis: the case of Guder River, Upper Blue Nile Basin, Ethiopia[J]. Adv Meteor, 2023: 7637884.
|
Kao S C, Govindaraju R S, 2017. A bivariate frequency analysis of extreme rainfall with implications for design[J]. J Geophys Res: Atmos, 112(D13): D13119.
|
Li Y, Gu W, Cui W J, et al, 2015. Exploration of Copula function use in crop meteorological drought risk analysis: a case study of winter wheat in Beijing, China[J]. Nat Hazards, 77(2): 1289-1303. DOI:10.1007/s11069-015-1649-2
|
Massey Jr F J, 1951. The Kolmogorov-Smirnov test for goodness of fit[J]. J Am Stat Assoc, 46(253): 68-78. DOI:10.1080/01621459.1951.10500769
|
Rauf U F A, Zeephongsekul P, 2014. Copula based analysis of rainfall severity and duration: a case study[J]. Theor Appl Climatol, 115(1-2): 153-166. DOI:10.1007/s00704-013-0877-1
|
Salvadori G, de Michele C, 2015. Multivariate real-time assessment of droughts via Copula-based multi-site hazard trajectories and fans[J]. J Hydrol, 526: 101-115. DOI:10.1016/j.jhydrol.2014.11.056
|
Sklar A, 1959. Fonctions de Répartition à N Dimensions et Leurs Marges[M]. Paris: Publications de l'Institut Statistique de l'Université de Paris: 229-231.
|
Tong X, Wang D, Singh V P, et al, 2015. Impact of data length on the uncertainty of hydrological Copula modeling[J]. J Hydrol Eng, 20(4): 05014019. DOI:10.1061/(ASCE)HE.1943-5584.0001039
|
Utsumi N, Kim H, 2022. Observed influence of anthropogenic climate change on tropical cyclone heavy rainfall[J]. Nat Clim Chang, 12(5): 436-440. DOI:10.1038/s41558-022-01344-2
|
Vergni L, Todisco F, Mannocchi F, 2015. Analysis of agricultural drought characteristics through a two-dimensional Copula[J]. Water Resour Manage, 29(8): 2819-2835. DOI:10.1007/s11269-015-0972-4
|
Wen Y L, Zhou L W, Kang L, et al, 2023. Drought risk analysis based on multivariate copula function in Henan Province, China[J]. Geomat, Nat Haz Risk, 14(1): 2223344.
|
Zhang L, Singh V P, 2007. Bivariate rainfall frequency distributions using Archimedean Copulas[J]. J Hydrol, 332(1-2): 93-109.
|
 2025, Vol. 51
2025, Vol. 51 
